Superconvergent eigenvalue bending plate element

Abstract

In the development of mass models, one may form an admissible mass matrix in parametric form and define its parameters such that the corresponding eigenvalue problem results in the best possible solution in terms of some error measures. This article uses the mentioned inverse strategy and develops a mass formulation for a plate element in bending with superconvergent eigen-properties. The parameters of mass formulation are obtained by setting the element formulation low-order discretization errors to zero. In situations where the error terms cannot be set to zero, the mass model parameters are defined in such a way that the residual errors in adjacent nodes are equal in magnitudes but with opposite signs. This creates zero bias error in the associated eigen-problem and leads to an element model with super convergent eigenvalue properties. The obtained mass matrix using the proposed procedure produces accurate estimates of plate eigenvalues with a higher rate of convergence compared to the existing mass models.

Keywords:

• mass matrix
• discretization error
• inverse method
• plate element

1. Introduction

Thin plates are the most elementary and essential structural components in modern engineering such as construction engineering, aerospace and aircraft structures, nuclear power plant components and naval structures. Because of their vast application, knowledge of dynamic characteristics, i.e. natural frequencies and mode shapes has been the focus of research in solid mechanics for more than a century 1,2. Although analytical solutions for the bending of thin plates have been intensively developed during the past decades, the analytical solutions for thin plates are still not completed properly 1. Therefore numerical solutions such as finite element method (FEM), finite difference method (FDM) etc., are of interest to researchers.

Since the early days of developing FEM, the concept of a lumped mass model has received much attention. Lumped mass matrices are diagonal and their inversion requires negligible computational costs. In solving dynamic problems, there are also various time-stepping schemes for which a diagonal mass matrix is very advantageous. In spite of these advantages, the lumped mass matrix produces a slow rate of convergence in estimating the eigenvalues of the system. Another disadvantage of lumped mass formulation is that in some cases, for example, when the element has rotational degrees of freedom (DOF), they do not lead to a positive definite mass matrix.

The improvement in mass matrix formulations was made by developing consistent mass matrices. Consistent mass matrices have proved to be more accurate in representing the physical properties of an element, such as its mass moments of inertia, compared to lumped mass matrices. Also based on Rayleigh's principle, when both the mass and stiffness matrices are developed using permissible shape functions, the resultant eigen-solution produces an upper bound estimate of the exact solution.

Considerable effort in finite element modelling is focused on obtaining an element formulation that gives a small discretization error and fast convergence 3,4. Based on the fact that the consistent finite element formulation leads to an overestimation of eigenvalues and the lumped finite element formulation usually leads to lower bounds of eigenvalues, several researchers concluded that an intermediate formulation should exist that is accurately superior to both formulations. Kim 5 studied the performance of non-consistent mass matrices of bars and beams obtained by the linear combination of lumped and consistent ones. Sauer and Wolf 6 constructed new mass matrices for bar and beam elements using the element eigenvectors when they are scaled using the exact eigenvalues of the element. The proposed mass formulations by Kim 5 and Sauer and Wolf 6 produce accurate estimation of higher modes, but their convergence rate is slow compared to some other models. More recently, Fried et al. 7,8 showed that a super-convergent finite element formulation exists for bar and membrane eigen-problems and used a linear combination of lumped and consistent mass matrices to obtain super-convergent element formulations. More recently, Madoliat and Ghasemi 9 produced bilinear rectangular element matrices for diffusion problems via an inverse method. They showed that this rectangular element matrix is superior to the consistent and lumped finite element formulations.

The optimum non-consistent mass matrix with super-convergent property is not, in general, a linear combination of the lumped and consistent mass matrices. They can be obtained by setting up a parametric form for the mass matrix and assigning the parameters such that the required convergence properties are achieved. Apparently, it was Stavrinidis et al. 10 who first used this type of analysis for assessing the discretization error in rod and beam elements. They showed that the discretization error in the solution of a finite element model can be expressed by a series in powers of Δ x, where Δ x is the element characteristic length. The coefficients of the series are linear combinations of the mass matrix parameters. The optimum values for the parameters are determined by minimizing the discretization errors in the finite element solution and hence obtaining a super-convergent element formulation.

The objective in this article is to set up an admissible parametric mass matrix for a rectangular plate element and define the parameters by minimizing the discretization errors in the finite element formulation. Discretization errors are those associated with replacing the continuous media by one composed of finite elements. If the characteristic lengths of the elements approach zero, the discretization error vanishes, assuming convergence.

In general, an admissible mass model must meet certain requirements. Consider an element with d degrees of freedom and r rigid-body modes, . The mass matrix M is symmetric, positive definite and of rank d. If the rigid-body modes, are defined on the principal co-ordinates of an element with six DOF at each node, then (1) where m is the element total mass and I_xx, I_yy and I_zz are the mass moments of inertia. Moreover, if the element has some symmetric properties, then the mass model reflects these properties; rotation of the element about its symmetry axes does not change the mass matrix. It is possible to define an admissible parametric mass matrix for an element that satisfies these requirements but depend upon few parameters. Established elements in the literature are members of this admissible family of models. By using finite element error analysis, we are able to establish the accuracy of a model that arises from specified shape functions with known parameters, and to find the optimum values of the parameters.

In this article, a mass formulation is developed for a four-node plate element in bending by minimizing the discretization errors and achieving a super-convergent eigenvalue formulation. An admissible parametric form of mass matrix having 12 parameters is developed. Then by comparing the eigen-equations in discrete form with exact eigen-equations of bending plate and minimizing the differences, optimum values of the parameters are determined. The literature reports discretization error analysis of element models; starting from the lowest order terms, the errors are set to zero until all parameters are exhausted and the element model is identified. This article introduces a different approach in minimizing the errors by distributing the errors uniformly over the entire domain and setting the cumulative errors to zero. This do not affect the accuracy of the eigenvalue predictions but exhausts less parameters compared to the conventional method and allows more accurate models to be identified. The obtained mass model produces highly accurate eigenvalues having fast rate of convergence.

The rest of this article is organized as follows. The basic concepts of developing a super-convergent mass formulation involving developing an admissible element mass model in parametric form and minimization of discretization errors in the finite element model are illustrated in Section 2 using a simple rod element. Section 3 uses the inverse parameter identification method demonstrated for rod element to establish a super-convergent eigenvalue formulation for the bending plate model. Section 4 studies the performance of the obtained mass formulation using numerical examples, followed by the concluding remarks in Section 5.

2. Three nodes rod element

A uniform quadratic rod element with the length of 2dx shown in Figure 1 has an admissible parametric mass matrix M satisfying the following two requirements:

(i) Out of plane rotation of the element about its mid node by 180° does not change its mass distribution:

(2)

(ii) The total mass of element normalized using the unit length density is 2dx. This requirement can be imposed on the mass matrix using rigid body mode φ as

(3)

Figure 1. The rod model (a) element DOFs and (b) assembled model node numbering.

An admissible parametric mass matrix is defined using three independent parameters, satisfying the above two requirements, as (4)

The developed admissible mass matrix along with the element stiffness matrix obtained using quadratic shape functions 11, (5) are used in this article to model free vibrations of a uniform rod with free boundary conditions. The choice of free boundary conditions is because the assembled finite element models inherently satisfy these natural boundary conditions. The assembled finite element model shown in Figure 1 consists of N similar elements with 2N + 1 DOF.

The predicted eigenvalues of the finite element model are compared with the exact values, λ, obtained from the corresponding boundary value problem: (6)

Therefore, it is a natural choice to compare the set of discrete finite element eigen-problem with the corresponding boundary value problem and specify the unknown parameters of the model by minimizing the residuals, i.e. the discretization errors.

Discrete eigen-equations formed corresponding to a typical node i at the interface between two elements and its neighbouring mid element nodes i − 1 and i + 1 are (7)

Following Stavrinidis et al. 10, we consider the deformation u_i to be the exact analytical solution and rewrite the deformations in other neighbouring nodes using Taylor series expansion of u_i in those nodes. This converts the discrete eigen-equations given in Equation (7) to continuous series equations in powers of dx: (8) (9) (10)

It is seen from Equation (8) that the eigen-equations are of odd orders of dx in the internal nodes of the assembled model. In a similar manner, it can be shown that the two boundary nodes of the free rod, i = 0, N + 1, contain all orders of dx starting from zero order: (11) (12)

The characteristic length of element dx is an independent variable; therefore, in comparing the obtained series equations with the exact boundary value problem, we start from the lowest order terms and assign the mass parameters to minimize the difference between the two models. When an order of smallness is reached so that these parameters are exhausted and the series terms cannot be reconciled with the classical boundary value equation, the residual error is minimized and order of the discretization error has been determined.

The lowest order terms are in Equation (9) of order dx⁰ and correspond to the free conditions at the boundary nodes: (13) The first requirement on the mass matrix parameters is obtained by considering coefficients of the order dx¹ in Equation (8b) which forms the following: (14)

The rod mass model would represent the boundary value problem defined in Equation (6) if one sets: (15)

Enforcing this requirement into the mass matrix results the first-order terms of the assembled model at the elements’ interface nodes, i = 3, 5, …, 2N − 1, the elements’ mid nodes, j = i ± 1 and the boundary nodes, r = 1, 2N + 1, to form the rod eigen-equations, respectively, as (16)

Next, to find the remaining two unknown parameters in the mass matrix, we consider the third-order terms in all nodes: (17)

Using a conventional approach 10,12, one may assign the two remaining unknowns by satisfying the obtained requirements individually and construct an element mass matrix that produces eigen-solutions of the fourth-order accuracy. In this article, we propose an alternative approach and set the residual errors in adjacent nodes equal in magnitude but with opposite signs. This produces a uniformly distributed error with zero means over the solution domain and as the eigenvalues are global properties of the assembled model, this effectively produces no bias error in the estimates of the eigenvalues. The proposed approach exhausts only one unknown parameter, enabling us to find a more accurate mass model by satisfying the fifth-order requirements.

The cumulative error of third-order terms are set to zero by requiring the mass coefficients to satisfy the following: (18)

The two requirements given in Equations (12) and (15) lead to an element mass matrix with one parameter: (19)

The lumped mass matrix is obtained by setting m₁₁ = 1/3, and the consistent mass matrix is produced by selecting m₁₁ = 4/15. Both of these element models result in eigen-solutions with the fourth-order accuracy. To find the optimum value for m₁₁, we consider the fifth-order terms: (20)

In order to satisfy the fifth-order terms, one requires to set m₁₁ = 14/45; the determined mass matrix produces eigen-solutions with the sixth-order accuracy.

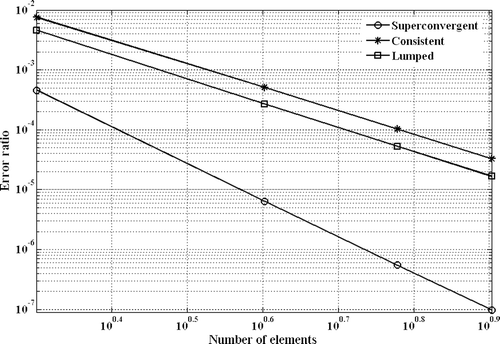
Figure 2 shows the eigenvalue convergence of a free rod model using the lumped, consistent and the obtained mass matrices. As indicated in Figure 2 the order of convergence in models formed using lumped and consistent mass models is of fourth order while the order of error in the model formed using the obtained mass matrix is of sixth order, consistent with the error analysis preformed in this study. Fried and Chavez 7 obtained the same mass matrix using a weighted combination of the lumped and consistent mass matrices () and calculated the optimum value for the weighting coefficient γ = 2/3 using numerical studies. Despite this finding, it is important to note that in general, the best mass formulation of many elements, e.g. elements with rotational DOF, cannot be obtained by linear combination of their lumped and consistent mass matrices 10. This makes the mass matrix parameterization procedure a crucial step in the success of obtaining the optimum mass formulation.

Figure 2. Convergence of fundamental eigenvalue of a unit length rod using different mass models.

The rod example demonstrates the important steps of parameterization of mass matrix and identification of its parameters by minimizing the discretization errors. Identification of mass parameters is achieved by minimizing cumulative sums of the residual errors. The same steps will be followed in Section 3 to construct a super-convergent mass matrix for a rectangular thin plate element.

3. Rectangular thin plate element

In this section, a new mass matrix is presented for a uniform out-of-plane rectangular bending plate element with four nodes/12 DOF. The element mass matrix and its displacement vector are defined as (21) where are 3 × 3 sub-matrices. The mass matrix has 78 parameters that can be reduced using its geometrical symmetries, total mass and moments of inertia requirements.

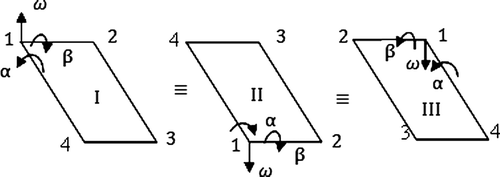
The rectangular plate element, shown in Figure 3, has two symmetry axes and rotation of mass matrix about these axes does not change its mass distribution: (22) (23)

Figure 3. Symmetry properties of rectangular plate element.

Further constraints are imposed on the entries of the rectangular plate mass matrix by considering rotation of the element about an axis normal to its plane. The element has an aspect ratio of p = Δ y/Δ x and rotation of the element about this third axis by π/2 radians would change p to 1/p in the formulation: (24)

It will be shown in the following equations that the dependency of mass matrix entries to the aspect ratio of the element does not affect the low-order residual errors and may be ignored in the mass formulation without compromising the model accuracy. Therefore, by transforming the mass matrix using Q, we require the mass matrix to remain unchanged. Applying the three geometrical symmetry requirements, one obtains a mass matrix with 14 parameters as (25) (26)

The total mass and moments of inertia requirements of the element are also imposed on the mass matrix formulation to reduce the number of its independent parameters. These requirements are defined using the rigid body modes of the element Φ_R as (27)

These requirements are satisfied by specifying two more parameters as (28) (29) and brings the total number of unattributed parameters of the parametric mass matrix to 12. These 12 parameters are determined by minimizing the discretization errors of the element formulations. The obtained parametric mass matrix is used along with the element stiffness matrix to form a parametric free vibration formulation and allowing identification of the unattributed parameters by minimizing the discretization errors.

Various stiffness matrices are reported in the literature for a rectangular thin plate element. In this study, we choose the stiffness matrix proposed by Ahmadian, Friswell and Mottershead (AFM) 12. Their proposed stiffness matrix is based on the Kirchoff bending plate theory and is obtained by minimizing the discretization errors in the element formulation. This stiffness model produces sixth-order errors in the internal nodes when the aspect ratio of the element is one, i.e. square plate element and errors of fourth order at other aspect ratios. The other stiffness models reported in the literature produce fourth-order errors at the best situation.

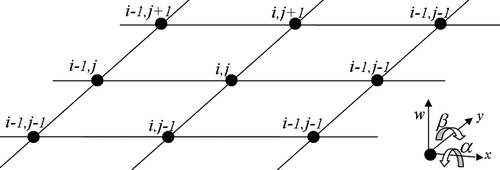
We assemble the plate elements with area Δ A = Δ x × Δ y to create a regular mesh for a rectangular plate with free edges as shown in Figure 4. In the assembled model, three discrete eigen-equations for a typical internal node (i, j) is formed. These discrete eigen-equations are then converted to continuous series form by defining the deformations in the neighbouring nodes using Taylor series expansions of deformations in node (i, j): (30)

Figure 4. Assembled plate model, node numbering and their DOFs.

This process transforms the discrete finite element equations into three continuous eigen-equations having terms of increasing order of smallness . First, we try comparing the second-order terms with the classical plate eigen-equation, and if it is satisfied at that order of smallness, we proceed to investigate the fourth-order terms, and so on, until the unattributed mass parameters are exhausted.

The equations result from the second-order terms in the Taylor series corresponding to lateral DOFs of the mid node (i, j) represent the Kirchoff plate eigen-equation: (31)

For the sake of simplicity, the subscripts i, j of w are omitted. Also, it is worth mentioning that the second-order terms corresponding to the rotational DOFs are zero. Next, we consider the fourth-order terms in internal nodes, from which we obtain (32) (33) (34) when p = 1, the AFM stiffness matrix 12 has a fourth-order accuracy and, hence, the discretization error is of sixth order in the internal nodes. These equations represent the Kirchoff plate eigen-problem if we restrict the entries of mass matrix as (35) (36) These two requirements reduce the number of unattributed parameters of the mass matrix to 10.

The first-order equations associated with boundary nodes on plate edges revolve free boundary conditions: (37) while the second-, third- and fourth-order terms create Kirchoff plate eigen-equations. Similarly, the terms corresponding to the plate four corner nodes create plate eigen-equations up to the third orders.

Next, we consider fourth-order terms on the corner nodes, fifth-order terms on the plate edges and the mid nodes, sixth-order terms. These three different order terms effectively create discretization errors of the same order due to number of nodes associated with each term. On physical grounds, we start with minimizing the mid nodes, sixth-order terms, based on the fact that the errors on the boundaries have less effect on the higher modes of the plate.

The sixth-order terms contain three equations, each corresponding to one of the internal nodes’ DOF. These equations are functions of element aspect ratio of orders 1/p², p⁰ and p² and as the aspect ratio is an independent parameter, we select to minimize the discretization error in each order independently. The terms with coefficient p⁰ are as follows: (38) (39) (40)

It is obvious that by assigning any values to the unattributed mass parameters, neither the residuals of sixth-order terms in the mid nodes nor their sums will vanish. Residuals in Equation (30), apart from some constants, are given as (41)

Column sums of the coefficient matrix in Equation (31) are minimized to reduce the cumulative (bias) error in estimates of equation of motion coefficients in each node. Minimizing these cumulative errors in least squares sense leads to (42)

On the other hand, the row sums represent the residual errors and minimizing them defines the coefficients α and β uniquely. The obtained solution is consistent with the results obtained in Equation (32) and leads to two more requirements on the mass parameters as (43)

Next we consider the sixth-order terms in the internal nodes with coefficient 1/p² and p². The terms with coefficient 1/p² and p² are similar and only those with coefficients p² are reported here as (44)

Residuals of Equation (34), apart from some constants, are given as (45)

Similar to the previous steps, first column sums of coefficient matrix in Equation (35) are minimized to reduce the bias errors in estimates of eigen-equations; then, the row sums of residuals are minimized. This leads to two more requirements on the mass parameters as (46)

Applying all these requirements reduces the number of unattributed parameters to six. The remaining mass parameters are obtained by minimizing the errors of fifth-order terms on the boundary and fourth-order terms on the corner nodes in a similar manner as described above. However, unconstraint minimization of the errors leads to a mass matrix which is not positive definite. To remove this obstacle, one may minimize these error terms subject to positive definiteness of the element mass matrix. The constraint minimization problem is solved numerically using genetic algorithm and leads to the following parameters: (47)

The obtained mass model along with its companion stiffness matrix produces discretization errors of sixth order in the internal nodes of the plate. The discretization errors on free edges and free corners are of the fifth and fourth orders, respectively. It is important to note that the existing finite element models produce fourth-order discretization errors in the internal nodes of the plate. The performance of the obtained mass matrix and its convergence rate in calculating the plate eigenvalues are demonstrated in Section 4.

4. Numerical case study

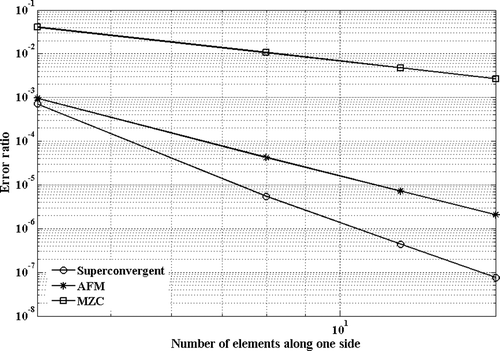
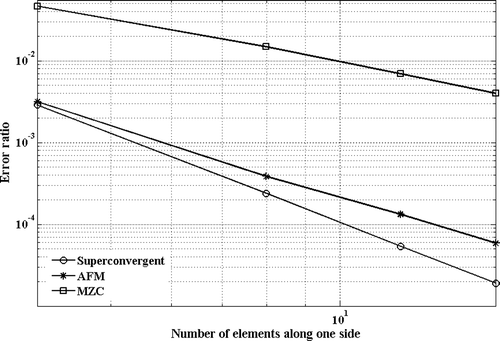
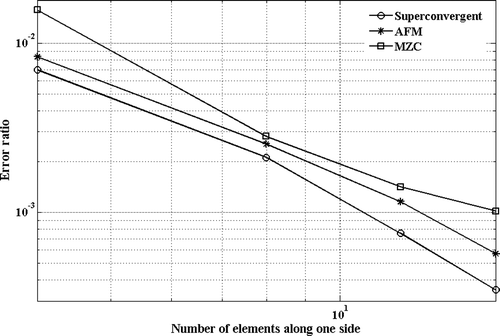
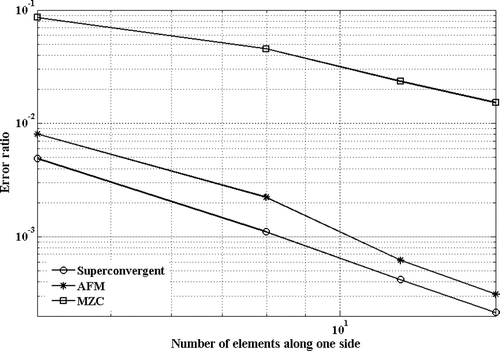
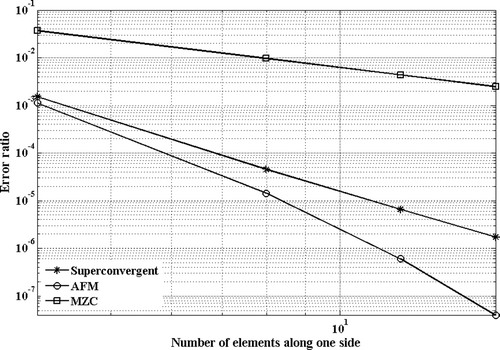
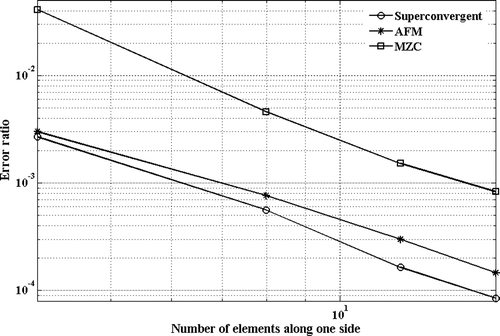
Performance of the proposed mass matrix is demonstrated by comparing its convergence properties against other mass formulations in numerical case studies. In these studies, eigenvalue predictions using different mass formulations for thin plates with various boundary conditions of simply supported, clamped, free and a combination of them are compared. The convergence rate of each formulation is determined by evaluating the errors in eigenvalue estimations using reference eigenvalues reported in 13. The finite element formulations used in this study are those proposed by AFM and non-conforming element MZC; reference 12 provides error analysis for different rectangular plate elements and finds that among all consistent models, the MZC formulation predicts the plate eigenvalues more accurately. The MZC plate element produces fourth-order errors while the errors in AFM model in the internal nodes are of sixth-order.

The errors in the estimates of the fundamental mode are calculated for square plates with various boundary conditions and are shown in Figures 5–8. As expected, the MZC model predictions have a slower rate of convergence and the proposed mass model of this article provides the highest rate of convergence in predictions of the fundamental mode. The AFM model and the proposed one share the same stiffness matrix and their difference is in their mass formulations. In the AFM model, the error terms are minimized in a least squares sense 12, creating a bias error in coefficients of equation of motion. In the proposed mass formulation, the sum of errors in equations of motions in each node is minimized. This effectively distributes the error with near-zero means over the solution domain creating more precise eigenvalue estimates using the proposed mass matrix.

Figure 5. Error in estimation of first eigenvalue of a simply supported square plate.

Figure 6. Error in estimation of first eigenvalue of a clamped square plate.

Figure 7. Error in estimation of first eigenvalue of a free square plate.

Figure 8. Error in estimation of first eigenvalue of a square clamped-free simply supported free plate.

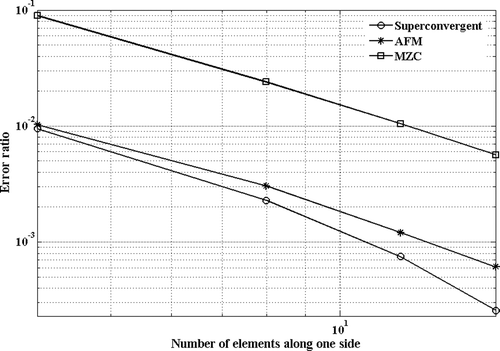
Another study is performed to evaluate the convergence sensitivity of these element models to the element aspect ratio. In this study, eigenvalue predictions for a rectangular plate (p = 2) with clamped, simply supported and free boundary conditions are performed using AFM, non-conforming MZC consistent mass formulation and the formulation proposed in this article. The errors in estimations of the rectangular plate fundamental mode are calculated with various boundary conditions and are shown in Figures 9–11. The results show the convergence rate of proposed mass model is insensitive to the element aspect ratio, and it produces much faster convergence compared to the existing models.

Figure 9. Error in estimation of first eigenvalue of a clamped rectangular plate (p = 2).

Figure 10. Error in estimation of first eigenvalue of a simply supported rectangular plate (p = 2).

Figure 11. Error in estimation of first eigenvalue of a free rectangular plate (p = 2).

The super-convergent eigenvalue non-consistent plate element proposed in this article improves the eigenvalue estimation procedure and minimizes the errors in model prediction at no extra computational cost compared to the conventional consistent element formulations.

5. Conclusions

An accurate plate element mass matrix is obtained by minimizing the discretization error in the finite element formulation. By employing an inverse approach, we consider what criteria the element mass model must satisfy and form a parametric family of admissible mass matrices. The parameters of the mass model are then obtained by minimizing the discretization error in the element formulation. In minimizing the discretization errors, special attention is paid on reducing the sum of errors in each node, hence creating a model with minimum bias errors. The benefit of using the proposed approach is that it produces a model with highest convergence rate for the element under consideration. The improvements in estimating the eigenvalues are presented using numerical case studies. The added accuracy in the new model requires no extra computational effort and it may be implemented easily into existing finite element codes.