Comparative application of CGM and Wiener filtering techniques for the estimation of heat flux distribution

Abstract

The conjugate gradient method (CGM), formulated with the adjoint problem, is adopted in this study as the functional minimization tool for the solution of the 2-D steady-state linear inverse heat conduction problem with the aim of estimating the heat flux density distribution on a given surface using the temperature distribution as input data. The robustness of the solution strategy, based on an iterative regularization scheme, is compared with another consolidated estimation methodology adopted in the literature to handle the same problem: the Wiener filtering technique. The comparison is performed by adopting a noisy test signal aimed at simulating infrared temperature maps. Using a comparative approach, the problem's particular difficulties related to the high number of unknowns and to the deficiency of the estimation techniques at the domain's geometrical boundaries are discussed.

Keywords:

• inverse heat conduction problem
• conjugate gradient method
• Wiener filter

Nomenclature

	=	Signal amplitude, A (°C)
	=	Spatial domain, D
	=	Error, Equation (33), E
	=	Heat flux density, g (W m−2)
	=	Performance function, J (°C2)
	=	J/M, J* (°C2)
	=	Total number of sensors, M
	=	Direction of the descent, q (W m−2)
	=	Heat rate generation per unit volume, qg (W m−3)
	=	Thickness, s (m)
	=	Temperature, T (°C)
	=	Spatial coordinates, x, y, X, Y (m)
	=	Search step size, β
	=	Dirac delta function, δ
	=	Noise, ε (°C)
	=	Conjugation coefficient, γ
	=	Lagrange multiplier, η (m2 °C)
	=	Thermal conductivity, λ (W m−1 °C−1)
	=	Variance of the signal, µ (°C2)
	=	Variance of the noise, ν (°C2)
	=	Measured temperature, Θ (°C)
	=	Standard deviation, σ (°C)
	=	Laplace operator, ▿2 (m−2)

Subscripts

	=	Boundary conditions, b
	=	Index of temperature sensor, i
	=	Initial guess, 0

Superscripts

	=	Gradient operator, ‘
	=	Mean value, –
	=	Iteration number, K

1. Introduction

To estimate the heat flux density distribution and then estimate the local convective and radiation heat transfer coefficients and/or the heat source distribution on a given surface, one must solve the inverse heat conduction problem (IHCP) in the solid domain. The well-known difficulties involved in inverse heat transfer problems and the IHCP stem primarily from the fact that they are often ill-posed and, consequently, very sensitive to small perturbations in the input data.

A growing number of papers published in the literature report estimation methodologies of both the local and the surface averaged heat transfer coefficients, which ‘de facto’ circumvent the difficulties embedded in the IHCP by assuming some type of approximation in the problem's formulation.

A more general and appropriate approach aimed at estimating the convective coefficient on a given surface should instead be framed within either parameter- or function-estimation problems, which consist, respectively, of finite- and infinite-dimensional optimization problems. The heat flux density distribution is then regarded as being unknown and non-uniform both spatially and/or temporally. The desired information is then suitably restored from either the steady or the unsteady local energy balance in the wall by solving the corresponding steady or unsteady inverse heat conduction problem (also referred to, respectively, as SIHCP and UIHCP) with the temperature distribution as input data 1–3. More precisely, because the unknown quantity is a boundary surface function, this problem is often referred to as a boundary inverse heat transfer problem 4–6.

Regarding the development of the solution methods of the IHCP, it must be noted that the possibility of detecting highly space- and time-resolved surface temperature distributions, mainly achieved by means of infrared focal plane array detectors or thermochromic liquid crystal thermography, represented a real breakthrough. In fact, only the possibility of performing remote and non-contact thermal monitoring permitted the practical application of many of the solution strategies of the IHCP, which have been developed mostly theoretically using simulated noisy signals. An application of the inverse solution approach to infrared thermographic data can be found, for instance, in 7, with regard to the restoration of heat line sources and boundary conditions, and in 8, with regard to the estimation of the local heat transfer coefficient. A comprehensive review of the development reported in the scientific literature on the solution techniques of the UIHCP is reported in 9.

The growing interest reported in the literature regarding this research topic attests to the fact that the solution to the IHCP has developed from being a pure mathematical/theoretical challenge to becoming an important tool in engineering design. The analysis of the literature in this field reveals that most of the efforts have been directed towards UIHCPs, whereas the steady-state formulation (SIHCP) has been less extensively investigated. Moreover, the solutions in one spatial dimension are most frequently studied. In particular, among both parameter- and function-estimation approaches, the most widely studied class of IHCPs regards the determination of unknown boundary conditions or thermophysical properties from temperature histories at one or more internal locations 2,10,11. The majority of the solution strategies for the UIHCP deal with its ill-posed nature, and, in particular, the instability of the system response with respect to random errors in the input data. These strategies reformulate the problem as a well-posed problem by minimizing an objective function, which generally expresses the squared difference between measured and estimated temperature discrete data. To overcome the problem's instability, the regularization scheme suggested by Tikhonov and Arsenin 12 has proven to be very successful when applied in both the temporal and the spatial domains 2,13, although the selection of the regularization parameter requires some care. Other alternative regularization approaches, described in detail by Özisik and Orlande 3 are Beck's sequential function specification method 2 or Alifanov's iterative regularization methods 1. Both these approaches have been applied to simulated and experimental data and on both one-dimensional 14,15 and multi-dimensional UIHCPs 16,17. The adaptive iterative filter 18,19 and the Bayesian inference method 20 are examples of a probabilistic approach, as opposed to the above described methodologies, which are generally referred to as determinist methods. Evolutionary algorithms have also been suggested to handle inverse transfer problems 21.

As already observed, the SIHCP has been less extensively investigated in the literature. Although it can be regarded as a special case of the UIHCP, some care is needed in the application of standard inverse solution strategies to the SIHCP. In fact, the elliptical nature of the partial differential equation (PDE), which expresses the steady-state local energy balance, makes the estimation procedure based on the solution of the SIHCP more complex. In fact, in the steady formulation, the destructive effect of noise is amplified by the necessity of estimating the desired information from the signal Laplacian and not from the signal's first temporal derivative, as it often occurs in the classical formulation of the UIHCP. Hensel and Hills 22 solved a two-dimensional SIHCP using the usual least-square approach coupled with regularization to estimate an unknown boundary condition on a portion of the domain. Throne and Olson 23 adopted the generalized eigensystems method and compared it to the conventional regularization approach to recover steady-state temperature and heat flux distribution on the inner boundary given the boundary condition on the outer boundary. Martin and Dulikravich 24 adopted the boundary element method to estimate an unknown boundary condition on an inaccessible portion of the domain in the steady-state regime when the remaining thermal boundary conditions and heat sources distribution were known.

A more general inverse heat transfer problem is represented by the case in which the heat flux is instead unknown on the whole domain and the retrieval of the local heat transfer coefficient is the main goal. This particular issue has been analysed by Matsevity and Moultanovsky 6 and Matsevity et al. 25. The peculiar difficulties of this kind of SIHCP are mainly related to the high number of degrees of freedom of the problem (i.e., to the number of unknowns) and therefore to the computational cost of the solution algorithm. These difficulties are, for instance, found in applications in which the input temperature data are acquired by infrared or thermochromic liquid crystal thermography with the aim of inversely estimating an equal number of unknown quantities. This peculiarity makes most of the available solution strategies impracticable. The computational requirements, for instance, of Tikhonov's regularization technique are very onerous when handling the solution of this general IHCP.

With regard to this and other similar problems, the iterative procedures described in 4,5,26 have proven to be very effective. According to the approach followed in 26, the temperature distribution on a thin wall obtained by numerically solving the corresponding direct problem is forced to match the experimental noisy data acquired by means of infrared thermography by tuning the local value of the heat transfer coefficient under the constraint given by the sensitivity of the adopted experimental facility. This solution method has proven to be a robust tool in the reconstruction of the local heat transfer coefficient both in single- and two-phase convective heat transfer, in both the internal and the external flow conditions and on both smooth and enhanced surfaces 26. An alternative and still innovative solution method for IHCPs is the one based on the filtering of the raw temperature data, which, by removing the unwanted experimental noise, makes the direct calculation of the signal's Laplacian feasible. In this regard, it must be observed that the consecutive application of the Wiener filter with an adjustable window has been successfully applied to high-quality infrared temperature maps 8,27. When using the technique based on the Wiener windows, the necessity of a finite neighbourhood around each element of the data matrix causes the estimation procedure to fail in the region close to the domain boundaries. This limitation can be partially amended by adopting a variable size of the filter window, as discussed by Rainieri et al. 27.

Ay et al. 28 claim to directly solve the same steady-state energy balance equation by processing temperature distributions acquired by infrared thermography to recover both local and average heat transfer coefficients in a tube-and-fin assembly in both the in-line and the staggered arrangements.

Regarding the minimization techniques adopted to achieve the solutions of IHCPs, the conjugate gradient method (CGM) with adjoint problem formulation represents a more general and straightforward approach. The solution strategy on which the CGM is based is essentially a regularization procedure that is implemented iteratively by searching for the optimal minimum of the objective function expressing the squared difference between the measured and estimated temperature discrete data.

As noted by Alifanov and Mikhailov 29, Alifanov et al. 30 and Park and Chung 31, in the estimation procedure based on the CGM, the vanishing of the gradient of the conjugate direction at the domain's boundary forces the unknown function never to be updated along the iterative process by causing a systematic local error in the reconstruction of the unknown function. This defect is discussed by Park and Chung in relation to the solution of the UIHCP applied to estimate the time-varying strength of a 2-D heat source distribution. The inadequacy of correctly estimating the unknown function at the final time has been bypassed by these authors by adopting a hybrid method based on both the direct differentiation method and the adjoint variable method for evaluating the gradient of the objective function. This possibility, although attractive, is restricted to applications in which the number of unknowns is limited. (Park and Chung 31 formulate this approach for a maximum number of unknowns equal to 51.) If the number of unknowns is too large, such as in cases where the desired information has to be reconstructed with high spatial resolution, as often happens in inverse estimation methods based on thermographic input data, the calculation becomes impracticable due to the enormous computation time required.

The CGM solution methodology has been successfully applied by Huang and Tsai 32 to the 3-D IHCP to estimate the local convective heat transfer coefficient. A multidimensional approach to the IHCP is adopted by Jarny et al. 33 and Alifanov and Nenarokomov 34,35. Regarding the UIHCP, a CGM with an adjoint variable has been also adopted to estimate the heat source distribution by means of the iterative regularization methodology 36.

The present investigation is intended to apply a solution methodology for the SIHCP based on the iterative regularization scheme to the general case in which the steady-state temperature map, consisting of about 500,000 discrete data, are used to restore the heat flux exchanged locally on a given thin surface. The tool adopted to perform the required functional minimization is the CGM with the adjoint formulation, which, being an intrinsically self regularization method, reduces the computational time compared with other minimization techniques (genetics, Monte-Carlo, etc.). This approach is of practical interest in engineering applications in which the thermal boundary condition is frequently ascribable to both convection and radiation heat transfer modalities, and a homogeneous or inhomogeneous heat source term can also be present.

To evaluate the effectiveness of this solution strategy, which is essentially based on the restoration of the Laplacian of a raw temperature map, a simulated noisy signal has been considered. The solution method is compared to the Wiener filtering technique, which represents a well-established solution strategy that has already been adopted to handle the same problem 8, as previously described. The two methodologies are radically different; the method formulated by means of the CGM belongs to the iterative regularization scheme class, whereas the method based on the Wiener window is a simple pre-filtering technique. Despite their differences, they both provide a very effective approach in engineering applications that require solving the IHCP.

The effect of the noise level on the accuracy of the estimation and on the convergence of the solution algorithm has been analysed. Moreover, this study is focused on the investigation of the communal deficiency of the above-referenced solution methodologies related to the impossibility of recovering the value of the unknown function at the domain's geometrical boundary.

The repercussion of this systematic error in recovering the heat flux distribution has been discussed here and investigated by comparing the performance of the iterative regularization method with the CGM and the Wiener filtering technique.

2. Problem formulation: the direct and the inverse problem

In the present analysis, the steady-state heat conduction problem in a homogeneous and isotropic domain is considered. Under the assumption of constant thermal properties, the local energy balance in the system is expressed by adopting a Cartesian coordinate system with the following elliptic PDE: (1) where q_g is the in volumetric heat generation rate, λ is the medium thermal conductivity and ▿² is the Laplace operator, which in a three-dimensional Cartesian coordinate system is defined by ∂²/∂x²+ ∂²/∂y²+ ∂²/∂z².

The equation is then completed by a proper boundary condition on the domain's border.

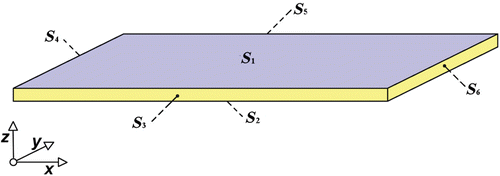
In the present investigation, the problem has been formulated on a rectangular thin plate, which is schematically shown in Figure 1, with the aim of analysing a typical condition to be found in plate-and-fin heat exchangers. Under the assumption of a thin plate of thickness s, the temperature distribution can be assumed to be uniform along the z coordinate, and the energy balance equation can be expressed in the form 37: (2) where g(x, y) expresses the overall heat flux density distribution, which accounts for both the heat flux exchanged by radiation and convection on the surfaces S₁ and S₂ and for the heat generated internally as follows: (3)

Figure 1. Geometrical domain with coordinate system and boundary conditions.

In the present analysis, the energy balance equation on the thin plate is considered to be completed by Dirichlet's condition on the domain's boundary as follows: (4)

The direct formulation of the problem is concerned with the determination of the surface temperature distribution when the heat flux distribution g(x, y), both boundary conditions on S₃–S₆ and the thermal proprieties are known. In the inverse formulation considered here, the heat flux distribution g(x, y) is instead regarded as being unknown, whereas the surface temperature T(x, y) is assumed to match the experimental data Θ(x, y).

From the knowledge of the heat flux density distribution g(x,y), the convective and/or radiation contribution may then be restored if the heat source term q_g is either known or null. Otherwise, if the convective and radiation contributions are known, the heat sources in the domain can be localized and quantified.

As described in detail in Section 1, the extreme sensitivity of the governing equation to even small errors or noise in the input experimental data makes the problem ill-conditioned and thus ill-posed. The strategies adopted here to inversely estimate the unknown heat flux distribution g(x, y) are the iterative regularization method coupled to the CGM with the adjoint equation as a functional minimization tool and the Wiener filtering technique. The CGM, as already pointed out in the Introduction, represents the more suitable functional minimization strategy in problems involving many design variables and a limited number of cost function 31, while the Wiener filtering technique is a pre-filtering data processing procedure to be applied to the experimental data to make the computation of the signal's Laplacian feasible 8.

3. The iterative regularization scheme by the CGM

The CGM is a gradient-based optimization procedure that, by using the steepest descent method, first evaluates the search direction, the gradient of the objective function with respect to the design variables, and then searches iteratively in this direction for the minimum of the performance function.

Under the adjoint equation approach, such a minimization procedure requires the solution of two auxiliary problems known as the sensitivity and the adjoint problems. These equations are then solved iteratively to minimize the objective function, represented by the error between the estimated and measured temperature distributions as originally formulated by 1 and applied, for instance, in 38.

The functional to be minimized in the problem under investigation is then: (5) where the matrices T(X_i, Y_i) and Θ(X_i, Y_i) express the estimated and measured temperature discrete maps, respectively, where the total number of elements is equal to M. The above equation can be suitably rewritten on the whole domain D as follows: (6) where δ is the Dirac delta function.

Although the CGM represents a well-known approach to perform the functional minimization required by the iterative regularization solution of IHCPs, its steady-state formulation in a 2-D domain in which the heat flux density is regarded as the unknown variable deserves a particular interest in relation to the application discussed above.

3.1. The CGM applied to the 2-D SIHCP

With the aim of estimating g(x, y) from Equation (2), the iterative procedure of the CGM is written as follows: (7) where β^k is the search step size at iteration K, and q^K is the direction of the descent, which is obtained as a linear combination of the gradient direction with the descent direction of the previous iteration.

The direction of descent for the CGM can be written as (8) where J′^K(x, y) is the gradient of the functional J(g(x, y)) and γ is the conjugation coefficient. Different versions of the CGM can be found in the literature, depending on how the conjugation coefficient is computed. Here, these parameters are obtained as follows: (9)

The search step size β^K appearing in the expression of the iterative procedure for the estimation of g(x, y) is obtained by minimizing the objective functional at each iteration along the specified direction of descent. This is performed by solving the ‘sensitivity problem’ and the ‘adjoint problem’, as outlined in the following sections.

3.2. Search step size

The search step size β^k is determined by minimizing the functional J[g(x, y)] given by Equation (5) with respect to β: (10)

By replacing g^K+1 with the expression given by Equation (7), the following expression can be obtained: (11)

By following a standard approach 32, a Taylor series expansion is adopted as follows: (12) where ΔT [q^K(x, y)] represents the change in T(x, y) with respect to a change in the heat flux density distribution g(x, y) = q^K(x, y), which is evaluated by solving the direct problem.

The calculation of ΔT [q^K(x, y)] can be performed either by the direct calculation of incremental ratios for each term or by solving the sensitivity problem, as explained in the following discussion.

To minimize Equation (12), its derivative with respect to β^k is set equal to zero: (13)

After rearrangement, the following expression can be obtained for the search step size β^k: (14)

3.3. The sensitivity problem

The sensitivity function, that is, the solution of the sensitivity problem, is defined as the directional derivative of T(x, y) in the direction of the perturbation of the unknown function. It is then obtained by assuming that the dependent variable g(x, y) is perturbed by Δg(x, y) when the input data T(x, y) are perturbed by ΔT(x, y).

The direct calculation of the sensitivity of T(x, y) to g(x, y) is unfeasible in the present problem because of the high computational cost resulting from the high number of variables considered (about 500,000). Therefore, it is obtained by replacing T(x, y, t) by T(x, y) + ΔT(x, y) and g(x, t) by g(x, y) + Δg(x, y) in the direct problem and then by subtracting the original direct problem from the resulting expressions, the following equation is then obtained: (15) with (16) in which Δg(x, y) is set equal to q^K(x, y) 1.

3.4. The adjoint problem

The calculation of the gradient J′^K(x, y) of the functional J[g(x, y)] to be minimized, under the adjoint equation approach, ends in the solution of a single direct problem.

To obtain the adjoint problem, the differential equation of the direct problem (Equation (2)) is multiplied by the Lagrange multiplier (or adjoint function) η(x, y), and the resulting expression is integrated over the whole domain. The resulting expression is then added to the right-hand side of Equation (6) to obtain the following extended expression for the functional J [g(x, y)]: (17)

Clearly, when T(x, y) is the exact solution of the problem, the second term on the right-hand side vanishes and Equation (17) reduces to Equation (6).

It is then assumed that the extended functional given by Equation (17) is perturbed by an amount ΔJ, when the heat flux distribution g(x, y) is perturbed by Δg(x, y) and the temperature distribution T(x, y) is perturbed by ΔT(x, y). By subtracting the original Equation (17) from the resulting expression and by neglecting the second-order terms it follows that: (18)

By integrating the second term at the right-hand side of the above equation by parts and rearranging terms, Equation (18) assumes the form: (19)

In the above equation, ∂/∂n is the directional derivative in the direction of the outward pointing normal to the line element dl. After rearrangement, Equation (19) assumes the form: (20)

The boundary and initial conditions of the sensitivity problem are substituted into the resulting expression, which is then allowed to go to zero. The vanishing of the integral terms containing ΔT(x, y) results in the following adjoint problem for the determination of the Lagrange multiplier η(x, y): (21) (22)

Finally, in this limiting process, the only integral term left on the right-hand side of Equation (20) is (23)

Moreover, by knowing that (24) and by comparing Equations (23) and (24), the following gradient equation for the functional J can be obtained: (25)

After developing the expressions for the search step size (Equations (14–16)) and for the gradient direction (Equations (21), (22) and (25)), the iterative algorithm of the CGM can be implemented until a given stopping criterion is satisfied, as discussed in the following section.

3.5. The stopping criterion

If the input data are not affected by noise, the classical convergence criterion is (26) where ξ is a small specified number. However, because the experimental temperature data are inevitably affected by uncertainties, the stopping criterion can be defined by adopting the approach called the discrepancy principle, originally formulated by Morozov 39 and later on implemented for filtering technique and applied by many authors 5,40,41. According to this principle, the inverse problem solution is regarded to be sufficiently accurate when the difference between the estimated and measured temperatures is close to the standard deviation σ of the measurements. Thus, the stopping criterion is as follows: (27) where M is the total number of experimental data.

3.6. The computational algorithm

The computational procedure that implements the solution of the present inverse problem based on the iterative regularization methodology by the CGM with adjoint equation is summarized below.

By assuming that a guess estimate value for g(x, y) is available at iteration K, the steps are as follows:

Step 1

solve the direct problem given by Equations (2–4) using the initial guess distribution g^K(x, y) to determine the estimated temperature distribution T^K(x, y);

Step 2

check the stopping criterion given by Equation (27) and continue if not satisfied;

Step 3

solve the adjoint problem given by Equations (21) and (22) using T^K(x, y) and obtain the Lagrange multiplier η(x, y);

Step 4

compute the gradient J′(x, y) of the functional J(x, y) from Equation (25);

Step 5

compute the conjugation coefficient γ^K from Equation (9) and then the direction of descent q^K(x, y) from Equation (8);

Step 6

solve the sensitivity problem given by Equations (15–16) to obtain ΔT[q^K(x, y)] by setting Δg^K(x, y) = q^K;

Step 7

compute the search step size β^K from Equation (14);

Step 8

compute the new estimate g^K+1(x, y) from Equation (7) and return to Step 1.

The direct, sensitivity and adjoint problems are solved here by implementing the finite-difference method in the Matlab® environment; a perfect correspondence between the location of the measurement points and of the nodes of the computational grid has been assumed.

4. The Wiener filtering technique

The Wiener filtering technique has been shown to be a successful and simple tool in handling the ill-conditioned nature of the SIHCP 8. In this regard, it must be remembered that the experimental noise represents the main impediment in the estimation processes aimed to the restoration of the information contained in the Laplacian of a raw signal. In fact, the direct calculation of a discrete noisy data set is not feasible because even small fluctuations are tremendously amplified by the Laplace operator. The Wiener filtering technique enables one to locally remove the noise from a raw signal, and it achieves the best results when the power spectra of the theoretical undisturbed signal and of the noise are known 42. Usually, some theoretical assumption on the expected denoised signal can be made, and the power spectrum of the noise can be easily measured (see, e.g. 43). On this basis, the filter can be applied in its full formulation 44. However, this adaptive filter also works well if this information is not known, but at least some assumptions on the signal and noise spectra can be made. For instance, if, as in many practical applications 8, the pure signal presents a narrow-band spectrum while the noise presents a wide-band spectrum, the noise variance can be simply estimated by considering the average variance on the whole range of the signal.

If this assumption cannot be made, this technique is not able to distinguish between the measured data fluctuations that reflect real process changes and noise. In this case, the application of this filter inevitably throws out not only the noise but also a part of the signal 42.

With regard to the SIHCP, the consecutive application of two Wiener filters applied to pre-process the raw temperature maps has proven to be effective in the estimation of the heat flux density exchanged at the wall–fluid interface. This information, which represents a relevant variable in the design of heat transfer apparatuses, is directly related to the Laplacian of the temperature signal, as predicted by the local energy balance in the wall. The success of this approach is due to the fact that the Wiener filter tailors itself to the local noise level in the signal, and it then performs a better smoothing than other filtering techniques.

The filtering function uses a local adaptive filtering procedure based on statistics estimated from the neighbourhood of each data value. By defining the local mean and variance around each discrete temperature data using the following equations, (28) (29) where π is the n·m local neighbourhood of each discrete temperature data value, the restored two-dimensional signal is estimated by the Wiener filter as follows: (30) where ν is the variance of the noise, assumed to be additive Gaussian white noise, which is estimated before doing the filtering by considering the average variance on the whole range of the signal.

For a successful application of this technique, it is necessary to adjust the range of action of the filter, defined by the size of the data neighbourhood, according to the noise level present in the signal.

This requires identifying a finite window around each element of the data matrix, and this causes the technique to fail in the region close to the domain boundaries or close to signal discontinuities. This problem can be partially overcome by varying the size of the window used to perform the local statistical processing close to the domain's boundaries 27. Although this problem is also present in the iterative regularization method by the CGM approach, the Wiener filtering technique has the great advantage of not requiring any iterative procedure because it is a simple data restoration technique, which is particularly effective in the reconstruction of a raw signal's Laplacian.

5. Results and discussion

To estimate the robustness of the previously described estimation methods, a simulated temperature signal, expressed by an analytical function with different additive noise levels ε, has been considered. In particular, the two-dimensional function, (31) defined on a rectangular domain, has been considered. Due to the fact that its n-th derivatives persist to be a non-vanishing function over the whole domain, the signal addressed here represents a significant benchmark for the validation of the SIHCP solution techniques implemented in this study. The signal has been mapped on a discrete domain with 800 × 600 equally spaced elements. This choice has been made to consider the novel application of the iterative regularization method by the CGM to the problem characterized by a high number of unknowns.

By assuming (W/°C), the estimation procedure addressed here implies the inverse reconstruction of the unknown term g(x,y), whose exact expression is in this case given by (32)

As the signal-to-noise ratio is the relevant variable in the inverse estimation problems, in the present analysis, two representative cases have been considered: Gaussian white noise with a null average value and a standard deviation σ such that σ/A = 2% and σ/A = 6%.

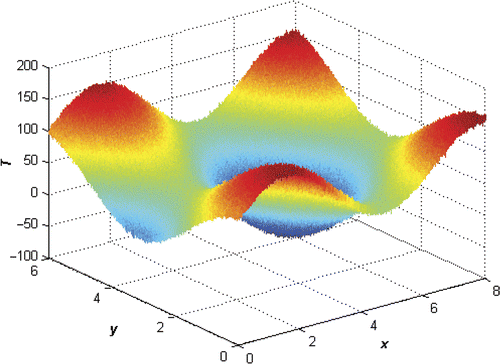
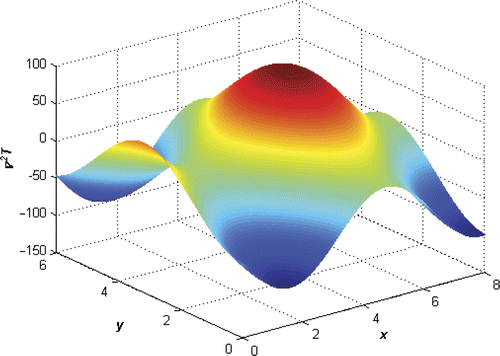
The distributions of the noisy test signal and of its Laplacian are reported in Figures 2 and 3. The convergence of the algorithm and the accuracy of the solution method have been quantified by means of an estimation error defined as follows: (33) where is the usual L₂-norm.

Figure 2. Noisy test signal for the case A = 50, dx = dy = 0.001 m and σ/A = 6%.

Figure 3. Exact signal Laplacian for the case A = 50 and dx = dy = 0.001 m.

To discuss the peculiar behaviour of the estimation procedure close to the domain's boundary, the estimation error has been evaluated both on the whole domain and on a limited domain region, namely on the central region corresponding to an area of 200 × 300 elements of the discrete rectangular domain on which the problem has been formulated.

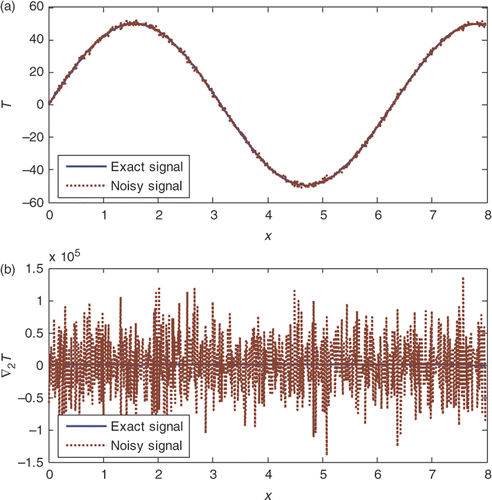
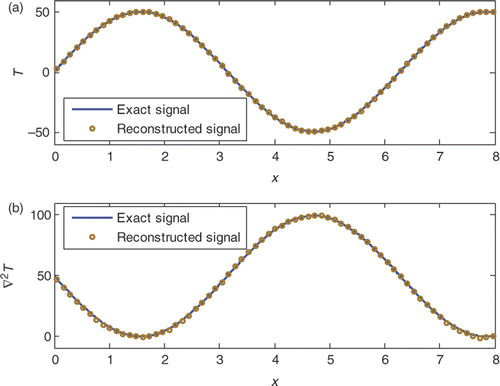
In Figure 4(a), the exact signal along the centreline of the domain is compared with the noisy data. The main objective is to correctly recover the Laplacian of the function, which is inaccessible by means of a direct differentiation, as shown in Figure 4(b).

Figure 4. Exact and noisy test signals and signal's Laplacian along the domain centreline for the case A = 50, dx = dy = 0.001 m and σ/A = 2%.

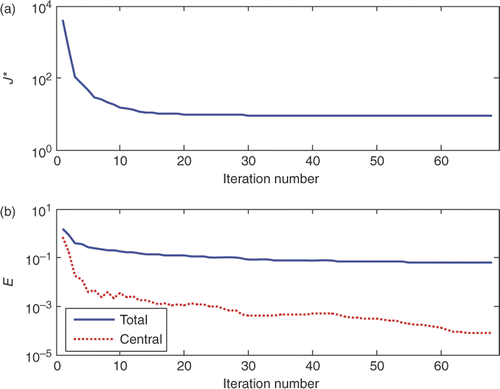
The CGM with adjoint problem formulation, implemented with the algorithm described in the previous paragraph, has been applied to reconstruct the unknown term g(x,y) to express the heat flux distribution over the surface, which is related to the second derivative of the input signal. The initial guess of the unknown function g⁰(x, y) has been assumed to vary linearly between the values assumed at the domain's boundaries, which have been set equal to the known exact values. Figures 5 and 6 report both the objective function divided by the number of experimental data J* and the estimation error versus the iteration number for the two levels of noise considered. J* approaches the value assumed by the noise standard deviation, as imposed by the stopping criterion value, Equation (27), and the trend of the estimation error proves the rapid convergence and then the robustness of the solution method addressed here for the SIHCP. Moreover, the data reveal that the estimation error has a different behaviour if evaluated in the central region of the domain as opposed to over the whole domain. While the overall error decreases slowly, by increasing the iteration number, the error evaluated in the central region decreases rapidly by assuming values lower than 0.1% after 30 and 40 iterations, respectively, for the case σ/A = 2% and σ/A = 6%.

Figure 5. Objective function J* and estimation error during iteration number for the case A = 50, dx = dy = 0.001 m and σ/A = 2%.

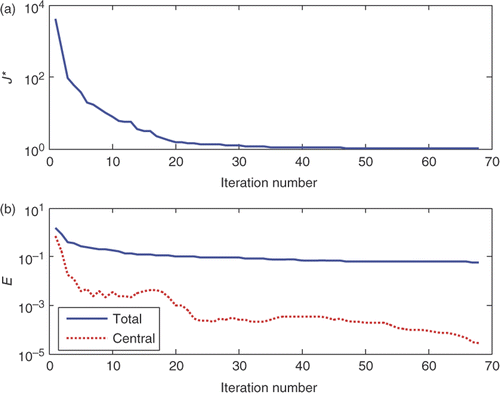
Figure 6. Objective function J* and estimation error during iteration number for the case A = 50, dx = dy = 0.001 m and σ/A = 6%.

This behaviour is due to the systematic failure of the estimation procedure close to the boundary, as discussed in the previous paragraphs. In fact, although the exact value for the initial guess of the unknown function has been imposed at the domain's boundary, the constraint given by the first-kind thermal boundary condition produces a systematic local failure of the estimation procedure.

The corresponding estimated distribution of the unknown function g(x, y) is compared to the exact function in Figure 7 for the representative case σ/A = 6%. The data prove the optimal performance of the methodology addressed here when the exact value is assumed as initial guess along the domain's boundaries for the unknown term.

Figure 7. Exact and reconstructed signal and signal's Laplacian along the domain centreline for the case A = 50, dx = dy = 0.001 m and σ/A = 6%.

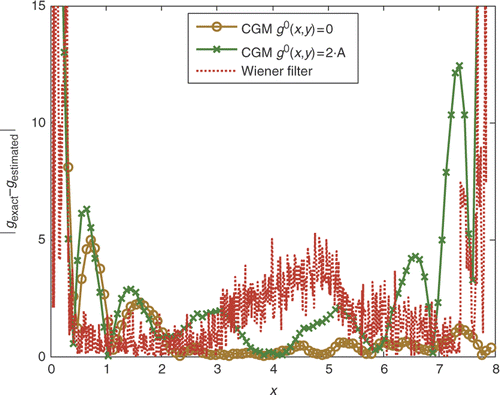
Although the iterative regularization method by the CGM, formulated here with the adjoint problem, converges rapidly to the exact solution, it has the major defect of being incapable of recovering the value of the unknown function close to the domain's boundary when an arbitrary value is assumed for its initial guess in the solution algorithm, as discussed in the previous paragraphs. In fact, the vanishing of the gradient of the conjugate gradient direction at the boundary forces the unknown function never to be updated along the iterative process. The repercussion of this systematic error on the solution has been investigated here by considering two different functions for the initial guess g^o(x, y): the null function and a function that assumes a constant value equal to 2A, where A is the amplitude of the temperature signal. In Figures 8 and 9, the reconstructed unknown function g(x, y) is reported along the centreline of the domain with the two initial guess values considered for the signal given by Equation (30) with σ/A = 2% an σ/A = 6%, respectively.

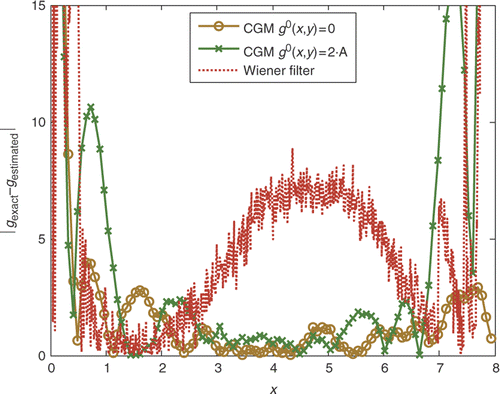
Figure 8. Exact and reconstructed signal's Laplacian, along the domain centreline, obtained by the CGM with two different initial guess of the unknown function and by the Wiener filtering technique for the case A = 50, dx = dy = 0.001 m and σ/A = 2%.

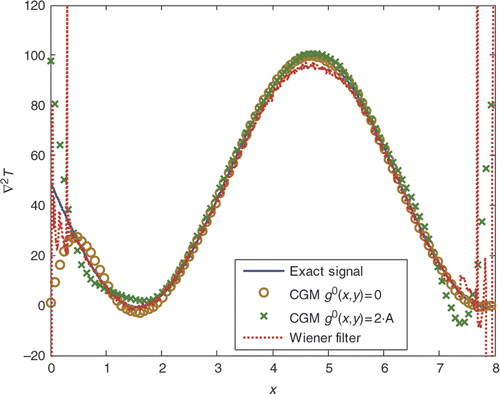
Figure 9. Exact and reconstructed signal's Laplacian, along the domain centreline, obtained by the CGM with different initial guess of the unknown function and by the Wiener filtering technique for the case A = 50, dx = dy = 0.001 m and σ/A = 6%.

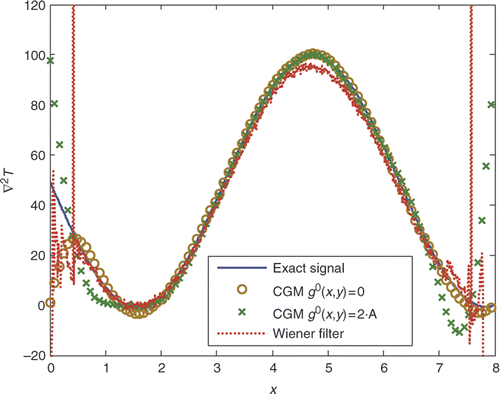
As expected, at the domain's boundaries, the reconstructed signal's Laplacian is affected by the systematic error related to the values adopted for its initial guess at the starting step of the iterative estimation procedure. As already observed, the method suggested by Park and Chung 31 to overcome this problem, which is based on a hybrid method between the adjoint formulation and the direct differentiation method, is impracticable for the present application due to the enormous amount of computing time required. Nevertheless, it can be observed that the error damps out by moving towards the central region of the domain, where the wanted information is restored with high accuracy. In the same figures, the signal's Laplacian, estimated by means of the consecutive application of two Wiener filters with adjustable window's sizes, as described by Rainieri et al. 30, is reported for the same test case. As expected, an analogous border effect is observed. The comparison between the CGM and the Wiener filtering technique, quantified by the data reported in Figures 10 and 11, which report the local deviation between the reconstructed and exact signals, respectively, for the cases of σ/A = 2% an σ/A = 6%, enables one to conclude that for the test function considered in the present analysis, the Wiener filter with a variable window size works better than the CGM in the region close to the domain's boundaries. Nevertheless, the unavoidable signal attenuation associated with the noise reduction effect of the filtering technique produces a less accurate estimation of the signal's Laplacian amplitude. This weakness of the Wiener filtering technique makes it suitable only for signals characterized by intrinsic high signal-to-noise ratios, as already noted by Rainieri et al. 27. The signal's attenuation associated with the Wiener filter is, in fact, amplified with a higher noise level (Figures 9 and 11), whereas, under the same condition, the CGM still proves its robustness in restoring the unknown heat flux distribution.

Figure 10. Local deviation between the exact and reconstructed signal's Laplacian, along the domain centreline, obtained by the CGM with different initial guess of the unknown function and by the Wiener filtering technique for the case A = 50, dx = dy= 0.001 m and σ/A = 2%.

Figure 11. Local deviation between the exact and reconstructed signal's Laplacian, along the domain centreline, obtained by the CGM with different initial guess of the unknown function and by the Wiener filtering technique for the case A = 50, dx = dy = 0.001 m and σ/A = 6%.

6. Conclusions

The development of a non-intrusive and accurate methodology to estimate the amount of heat exchanged locally on a given solid surface represents an important goal in optimal heat exchanger design. This is particularly true, for instance, in the assessment of the performance of a given heat transfer enhancement technique, in both single and two-phase convection modalities. The methodology addressed here, based on the application of the iterative regularization scheme by the CGM to the solution of the 2-D SIHCP in the wall, using the temperature map as input data, has proved to be a robust tool for achieving this goal. A simulated noisy signal is used to test the robustness of this solution strategy as compared with another consolidated estimation methodology adopted in the literature to handle the same test case, namely, the Wiener filtering technique.

The two approaches are radically different because the method formulated by means of the CGM belongs to the iterative regularization scheme class, whereas the method based on the Wiener window is a simple pre-filtering technique. Despite these differences, they both provide an effective data processing procedure for engineering applications that involve the solution of the SIHCP.

Some peculiar difficulties of these problems related to a high number of unknowns and to the failure of the estimation techniques at the domain's geometrical boundaries are discussed. In particular, the comparative application of the iterative regularization scheme by the CGM with adjoint problem formulation and of the Wiener filtering technique to the same test case highlights the benefits of each method.

Acknowledgements

The authors are grateful to Prof Giorgio Pagliarini for the helpful and valuable discussion on the results presented here. An MIUR grant is also gratefully acknowledged.