Multi-deme, twin adaptive strategy hp-HGS

Abstract

The article presents a twin adaptive, effective stochastic strategy for solving difficult inverse problems formulated as global optimization ones. It is especially dedicated to multimodal, noisy problems. The hp-hierarchic genetic strategy (hp-HGS) strategy offers two ways to decrease computational and memory costs. Firstly, it decreases the number of objective evaluations by using an adaptation of the inverse problem accuracy (HGS strategy). Secondly, the cost of the direct problem solution, necessary for objective evaluation, is decreased by the proper scaling of the finite element method error using the hp adaptation technique. The theory of hp-HGS mentioned in this article can guarantee its asymptotic correctness in the probabilistic sense i.e. the possibility of finding all solutions from a specified set. The theoretical results make the comparison of the expected computational cost of a single genetic epoch at a particular level of the hp-HGS tree possible. Moreover, Theorem 3.1 verifies the hp-HGS applicability condition (the Lipschitz continuity of the energy functional) for heat conduction problems. A simple computational test for the heat conduction inverse problem in an L-shape domain shows the hp-HGS behaviour in the case of objective bimodality.

Keywords:

• finite element method
• hp-adaptivity
• hierarchical genetic search
• multi-modal problems
• heat transfer

1. Problem definition

The inverse problems to be solved are related to a particular class of direct problems: (1) where stands for the total energy of the modelled physical system, and V is the proper Sobolev space shifted by the Dirichlet boundary condition. The form of the functionals a, l depend on physical phenomena (e.g. linear elasticity, heat conduction) and their parameters d ∈ 𝒟, where 𝒟 is a regular compact in ℝ^N, N < +∞. We assume that the above problem is well-posed in the sense of Hadamard and its solution u ∈ V can be obtained as the limit of the sequence {u_h,p} ⊂ V of solutions of finite dimensional problems obtained by the hp-adaptive finite element method (hp-FEM) assuming h → 0 and p → +∞ 1.

The inverse problem under consideration consists of finding the unknown, physical parameter while the energy of the exact solution u ∈ V to (1) is assumed to be known (e.g. it is measured in situ or in the laboratory). Because the exact energy J(d) is impossible to compute effectively for each d ∈ 𝒟, we can only find the approximation ĝ ∈ 𝒟 of the exact parameter so that: (2) where J_h,p(d) = E(d; u_h,p) stands for the energy of the approximate solution u_h,p obtained for the parameter d.

The inverse problem (2) may be classified as a global optimization one because of the frequent ambiguity of its solution (multiple solutions), manifested as the objective multi modality caused by its physical nature and/or the uncertainty of the mathematical model, as well as errors in the numerical objective evaluation. As a result, not only the global minimizers, but also the local ones with sufficiently low objective values, may represent the solutions. The other difficulty is the usually high computational cost of the objective evaluation.

A large variety of such problems in mechanics and other branches may be found in the literature e.g. in 2, where the ambiguity of the global minimizers was mathematically proven.

One possible way of solving such problems is to find all the local minimizers that satisfy the additional criterion (e.g. the objective is lower than the assumed threshold). Niching genetic algorithms as well as multi-start strategies were often applied as robust methods for finding multiple minimizers (see e.g. 3,4). Adaptive strategies that can significantly decrease the number of objective evaluations are also highly regarded (see e.g. 5).

We propose a new strategy, called hp-hierarchic genetic strategy (hp-HGS), composed of the adaptive numerical method hp-FEM 1,6,25,26, which allows a very effective direct problem solving up to the assumed accuracy expressed by the energy error of the physical phenomenon, and the multi-deme, HGS 7, which allows an economic global search with the adaptive accuracy in the parameters domain. The nature of HGS allows many local minimizers to be found in parallel. The proper rule of scaling the error of solving the direct problem versus inverse problem error decreases the computational cost of the single objective evaluation.

This article contains a detailed definition of the hp-HGS strategy and briefly reports the results of its formal analysis (asymptotic guarantee of success, efficiency, etc.), already published in the conference proceedings 8–13. The theoretical results are extended by verifying the Lipschitz continuity of the energy functional, which is crucial when studying the hp-HGS applicability and by tuning its main parameter. This condition is proved for linear heat conduction problems (see Section 3). We also attach new computational results obtained by using a new version of hp-HGS routine when solving the inverse bimodal problem of heat conductivity identification in an L-shape domain (see Section 6).

2. The main course of hp-HGS

The hp-HGS strategy is based on the HGS introduced by Kołodziej and Schaefer (see e.g. 7,14), which enables effective solving of global optimization problems using variable, dynamically adapting accuracy. Various HGS implementations and evidence supporting their efficiency for solving global optimization problems are presented in 7,14–18.

HGS produces a tree-structured, dynamically changing set of dependent demes. The depth of the HGS tree is limited by m < +∞. Currently, the evolution of each deme is governed by a separate instance of the simple genetic algorithm (SGA) 19. All demes work asynchronously and are synchronized by the message-passing mechanism if necessary.

The low-order demes (closer to the root) perform a more chaotic search with lower accuracy, while the high-order demes perform a more accurate, local search. The search accuracy is obtained by the various encoding precision and by the various length binary strings as the genotypes in demes of different orders. The unique deme of the first order (root) utilizes the shortest genotypes, while the leaf utilizes the longest ones. To obtain the search coherency for demes of different orders, a special kind of hierarchical, nested encoding is used. First, the densest mesh of phenotypes in 𝒟 for the demes of the m-th order is defined. Next, the meshes for the lower order demes are recursively defined by selecting some nodes from the previous ones. The maximum diameter of the mesh δ_j associated with the demes of the order j determines the search accuracy at this level of the HGS tree. Obviously, the mesh parameters satisfy δ₁ > ··· > δ_m.

Each deme expecting leaf-demes sprouts the new child-deme after the constant number of genetic epochs K called the metaepoch. The child-deme is activated in the promising region of the evolutionary landscape surrounding the best fitted individual, distinguished from the parental deme at the end of the metaepoch.

HGS also implements two mechanisms that allow a reduction in the search redundancy. The first one, called conditional sprouting, disables the sprouting of new demes in regions already occupied or explored by the brother-deme (another child-deme of the same order sprouted by the same parent). The second mechanism, called branch reduction, reduces the branches of the same order that perform searches in the common landscape region or in the regions already explored.

Let us apply HGS in order to solve the inverse problem (2). The fitness function for the particular deme should be based on the energy error (3) computed by using hp-FEM, which approximates the objective function of the global optimization problem (2) for the particular values of h and p. As previously, denotes the exact parameter value and the known, exact energy of the exact solution, while J_h,p(g) denotes the approximated value of energy computed by hp-FEM, with respect to the parameter value g ∈ 𝒟, obtained from the HGS individuals' genotype.

Let us assume that g represents the parameter value decoded from the genotype that appears in the HGS deme of the j-th order, j ∈ {1, … , m}. Using Lemma 2 in 12 and the formula (8) in 10 which show the regression of the error (3) while improving the hp-FEM approximation, we obtain (4)

The left-hand side stands for the energy error, while the first right-hand-side component is the relative error decrement in the single hp-FEM step 1. Moreover, L stands for the Lipschitz constants of the functional J, and is the error of the inverse problem solution that characterizes the individuals belonging to the HGS demes of the j-th order. It is easy to observe that corresponds to δ_j. The above formula shows that the error of the energy evaluation over the fine FEM mesh is estimated by the relative FEM error on the coarse FEM mesh solution with respect to the fine mesh solution, by the absolute FEM error over the coarse FEM mesh and by the accuracy of the proper HGS branch.

The main idea of hp-HGS is to dynamically adjust the accuracy of the objective computation to the particular value of the parameter g encoded in the individuals' genotype, as well as for the inverse problem error that characterizes the current HGS branch. This may be obtained by balancing the components of the FEM error given by the right-hand side of the formula (4), assuming δ_j as the accuracy of the inverse problem solved by the branch of the j-th order. We will perform then the hp-adaptation of the FEM solution of the direct problem while the quantity err_FEM/δ_j is greater than the assumed Ratio, which stands for the parameter of this strategy. The value of the parameter Ratio corresponds to the Lipschitz constant L, because the first two components the right-hand side of (4) asymptotically vanish as a consequence of the hp-FEM convergence.

Please note that no matter how the fitness of the individual i is computed by iterative processes of the hp-FEM adaptation, the fitness function f_j is well-defined for all individuals in branches of the j-th order (it is not a random variable).

A draft of the single hp-HGS deme activity is depicted in the pseudo-code Algorithm 1. The function branch_stop_condition(P) returns true if it detects a lack of evolution progress of the current deme P. The separate module continuously checks whether a satisfactory solution has been found or hp-HGS cannot find any more local extremes. If yes, the global_stop_condition signal is sent to all the computing demes. The conditional sprouting mechanism is implemented as follows. Each branch, except the root, computes the average of its phenotypes and sends it to its parental deme. These values are analysed by the children_comparison(x) procedure and compared with the phenotype of the best fitted individual x distinguished from the parental deme. This procedure returns true if x is sufficiently close to the existing child-demes. The branch reduction mechanism is omitted in the Algorithm 1 for the sake of simplicity.

Algorithm 1. Pseudo-code of the j-th order deme P in the hp-HGS tree.

3. Lipschitz continuity of the energy functional

In this section, we provide a result of the Lipschitz dependence of the heat energy functional on the scalar heat conductivity coefficient. The energy is associated with the linear variational elliptic equation, which is the direct problem and considered as a model for heat conduction. As we mentioned in Section 2, the Lipschitz condition for the energy functional is crucial in the estimation of error in (4).

Let Ω be an open bounded subset of ℝⁿ with Lipschitz boundary Γ. Let Γ_D and Γ_N be two disjoint sets in Γ so that Γ = Γ_D ∪ Γ_N ∪ N where m(Γ_D) > 0 and m(N) = 0. Let V = {v ∈ H¹(Ω) ∣ γv = 0 on Γ_D}, where γ: H¹(Ω) → L²(Γ) denotes the trace operator. For simplicity, we will use v instead of γv. Since m(Γ_D) > 0, it is well-known that V is a Hilbert space endowed with the norm where | · | denotes the norm in ℝⁿ. Due to the Poincaré inequality (cf. Chapter 3.9 of 20), this norm is equivalent on V to the usual norm on H¹(Ω). We denote by V* the dual space to V. Given the constants 0 < α ≤ β < ∞, we introduce the set of admissible heat conductivities by We define a : 𝒦 × V × V → ℝ and l : V → ℝ by (5) (6) where f₁ ∈ L²(Ω) and f₂ ∈ L²(Γ_N). Then it is clear that for all k ∈ 𝒦 the form a(k; ·, ·) is bilinear, continuous on V × V (i.e. |a(k; u, v)| ≤ β‖u‖‖v‖ for u, v ∈ V), coercive uniformly with respect to k (i.e. a(k; v, v) ≥ α‖v‖² for v ∈ V) and the linear functional l is continuous (i.e. l ∈ V*). Exploiting the Lax–Milgram lemma (cf. Chapter 2.7 of 21), we deduce that for every k ∈ 𝒦, there exists u = u(k) ∈ V a unique solution to the problem (7) and (8) We remark that for the functional l ∈ V* of the form (6), we have where ‖γ‖ is the norm of the trace operator in ℒ(H¹(Ω), L²(Γ)). Moreover, since for all k ∈ 𝒦 the bilinear form a(k; ·, ·) is symmetric on V × V (i.e. a(k; u, v) = a(k; v, u) for u, v ∈ V), it is well-known (cf. Chapter 2.7 of 21) that for all k ∈ 𝒦 the problem (7) is equivalent to the following minimization problem: (9) with the heat energy functional E: 𝒦 × V → ℝ given by (10)

Theorem 3.1

Let the energy functional E be of the form (10) with a and l defined by (5) and (6), respectively. Then there is a constant L > 0 such that for all k₁, k₂ ∈ 𝒦, we have where u(k_i) ∈ V is the unique solution to (7) corresponding to k_i for i = 1, 2.

Proof

Let k₁, k₂ ∈ 𝒦 and u₁ = u(k₁), u₂ = u(k₂) be the unique solutions to (7) which correspond to k₁ and k₂, respectively. First, we show (11) where M = α⁻²‖l‖. Since u₁, u₂ ∈ V are solutions to (7), we have a(k₁; u₁, v) = l(v) and a(k₂; u₂, v) = l(v) for all v ∈ V. Hence a(k₁; u₁ − u₂, v) = −a(k₁−k₂; u₂, v) for all v ∈ V. From the latter, using the coercivity of the form a, (8) and the Hölder inequality, we get which implies (11). Next, using (8), we have (12) Using (11) and the elementary inequality |ξ|² − |η|² ≤ |ξ − η|² for all ξ, η ∈ ℝⁿ, we deduce (13) Similarly, from (11), we easily obtain (14) In view of (12)–(14), we have which completes the proof.▪

4. Asymptotic features of hp-HGS

The asymptotic analysis presented below leads to a comparison of hp-HGS with two other strategies by solving the inverse problem (2). The first strategy is the coupling of HGS with the same SGA engines in each branch as in hp-HGS, but with the fitness function f_m computed as in hp-HGS leaves (e.g. by solving the direct problem with the maximum accuracy) and then applied to all lower order branches. Notice that such induction is well-defined because of the nested HGS encoding (all phenotypes in branches of the order j are also phenotypes in branches of the j + 1 order). The second strategy is the single population SGA with the same fitness f_m as previously. The size of the SGA population ensures the same initial local coverage of the domain 𝒟 by the SGA individuals as by individuals of all the hp-HGS leaves.

We will intensively use the theory of the SGA heuristic (genetic operator) and its fixed points, developed by Vose 19, as well as the convergence results of SGA sampling measures 14, Chapter 4]. Let us denote by Ω_j the SGA genetic universum of binary codes and by the genetic operator (heuristic) of all branches (SGA demes) of the order j. It depends only on the number of genotypes r_j, the fitness function f_j and the genetic operations applied in branches of the order j. Moreover, the unit simplex stands for the set of frequency vectors of all possible demes of the order j. We assume that each genetic operator G_j has the unique fixed point z_j in that represents the population limit (e.g. the infinite cardinality population after the infinite number of genetic epochs, understood as behaviour of the algorithm when the size of population and time tends to infinity). The fixed point z_j is assumed to be the global attractor of G_j on (i.e. lim_t→+∞(G_j)^t(x) = z_j for all ).

Each deme of the order j induces the probabilistic measure Θ(x) on 𝒟 given by the formula Θ(x)(A) = ∑_{i;code(i)∈A} x_i where A ⊂ 𝒟 is an arbitrary measurable set (see Section 4.1.2 in 13 for details). Let us denote further Θ(z_j) by Θ_j for the sake of simplicity. Moreover, we denote by μ_j the cardinality of an arbitrary deme of the order j in hp-HGS and HGS. We assume that SGAs governing the evolution of the hp-HGS branches of the j-th order j ∈ {1, … , m} are well-tuned 14, Definition 4.63]. The same assumptions are made for the strategy in which the fitness f_m is implemented in all HGS branches and for the single population SGA.

The course of verifying the asymptotic guarantee of success for hp-HGS exactly follows the method introduced by Kołodziej 15, and Schaefer and Kołodziej 7 for HGS. It consists of proving the compliance of the limit sampling measure of the analysed strategy with the limit sampling measure of the genetic algorithm, for which the asymptotic guarantee of success has already been checked. The single population SGA with the f_m fitness was selected as the reference algorithm that possesses the desired features 14,19. In other words, we are only obliged to prove that both hp-HGS and SGA can find the same set of local minimizers.

Let t₀ be the number of genetic epochs after which hp-HGS has b branches of maximal degree m and no new branches are sprouted. Then for all ϵ, η > 0, we can find N ∈ ℕ and W(N) > t₀ such that for the arbitrary measurable set A ⊂ 𝒟, we have (15) where (16)

The inequality (15) proved in 13 delivers the stochastic convergence of the mean sampling measure (16) on 𝒟 that governs the search performed by all hp-HGS leaves to the measure Θ_m imposed by the fixed point of the G_m operator. Then the hp-HGS may asymptotically find the same set of global and local minimizers as the infinite single population SGA governed by G_m after an infinite number of genetic epochs.

Next, we briefly report on other advantageous asymptotic features of hp-HGS that are presented and proved in detail in 13. Corollary 1 in 13 provides the formula for the expected computational cost of the single genetic epoch in all hp-HGS branches (17) where a_j stands for the average cost of solving the direct problem for individuals of the hp-HGS deme of the j-th order. It it obvious that a_j > a_i if j > i. In particular, when we assume the particular linear regression of the inverse problem error δ_j the average number of degrees of freedom n_j is (θ(j − 1) + β)^γ where the constants θ > 0, β ≥ 0 and γ > 1 depend on the inverse problem under consideration (see Corollary 4 and its proof in 13). The growth of the number of degrees of freedom from j to j + 1 level of the hp-HGS tree can be estimated as where γ = 3 for typical 3D problems. The computational cost of the robust multi-frontal solver is where b is the parameter depending on the sparsity of the matrices. It implies that the growth of the computational cost is of the order 𝒪(2^2γ) in this case.

The coefficient κ^j < 1 stands for the expected ratio of active branches of the order j. The expected computational cost of a single HGS epoch applied to the same inverse problem (18) is much greater than the one given by the formula (17). Both HGS and hp-HGS costs are less than the single deme SGA expected cost that may be approximated by ♯Ω_m−1μ_ma_m (see Corollaries 2 and 3 in 13).

5. Sample inverse problem

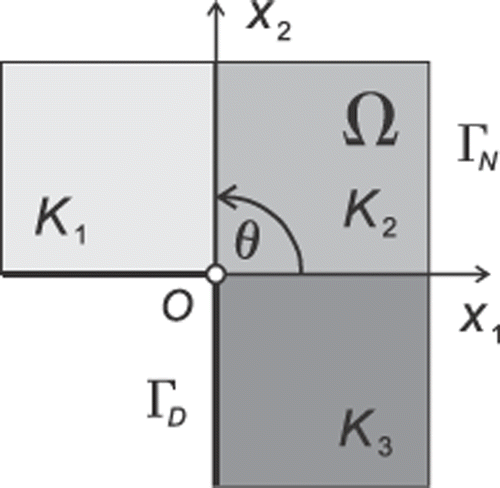
The sample inverse problem originates from the classical L-shape domain direct problem, a model academic problem formulated in 22,23, to test the convergence of the p- and hp-FEM adaptive algorithms. The direct L-shape domain problem consists of computing the temperature distribution over the L-shape domain, presented in Figure 1, with fixed zero temperature in the internal part of the boundary Γ_D, and the Neumann boundary condition prescribing the heat transfer on the external boundary Γ_N. There is a single singularity in the central point O of the domain, where the gradient of temperature ‖∇u‖ goes to infinity, so the accurate numerical solution, in terms of H¹ norm, requires a sequence of adaptations in the direction of the central point.

Figure 1. The L-shape domain problem.

We omit here and later the physical units of temperature, heat flux and heat conduction coefficients, since a dimensionless formulation is used.

The strong formulation of the direct problem consists of finding the temperature distribution u ∈ C²(ℝ²) so that (19) with the boundary conditions (20) with n being the unit normal outward vector to the ∂Ω, and (r, θ) the radial system of coordinates with the origin point O (see Figure 1). The heat conduction coefficient K takes the constant values K₁, K₂, K₃ over three parts of the domain, as illustrated in Figure 1.

We consider the following weak formulation of the problem (19)–(20): find u ∈ V = {v ∈ H¹(Ω) ∣ γv = 0 on Γ_D} such that: (21) where d = (K₁, K₂, K₃) ∈ 𝒟 = [0, 3]³ ⊂ ℝ³ is the vector of parameters.

The inverse problem to be computed is formulated in the following way: find values of the heat transfer coefficients ĝ ∈ 𝒟 that satisfy (2). The energy of the ‘exact’ solution was computed as , where are the assumed values of the heat transfer coefficients. In order to obtain the energy close to the , the L-shape domain problem was computed once with the very high relative accuracy 10⁻⁵ by using the self-adaptive hp-FEM code.

As both boundary conditions are symmetric with respect to the domain geometry (e.g. with respect to the axis θ = π/4) then the parameter vector gives the same energy as , so the inverse problem (2) has at least two solutions in this case.

6. Computational test

We applied the three level hp-HGS strategy for solving the inverse problem described in Section 5. All parameter settings of the strategy are listed in Table 1. The 9b length code increment between consecutive levels causes an increase in search accuracy in the hp-HGS tree. The large population size in the root allows sufficient diversity and the desired globality of the search. A much lower population size of leaves protects the enormous computational cost of many local searches. The algorithm was tuned by choosing the mutation and crossing rates on each level. The implementation utilizes random number generator 27. In order to undertake it properly we utilize the result of analysis of standard phenotype deviations for different values of the binary mutation rate previously published (see Table II in 8). The final settings of these parameters (see Table 1) ensures the proper intensification of local search in the deeper hp-HGS levels.

Table 1. Final parameters of the hp-HGS tree applied by solving the sample inverse problem.

	Level 1	Level 2	Level 3
Code length	9	18	27
δj	58 × 10^−4	11 × 10^−6	22 × 10^−9
Population size	100	50	20
Crossing rate	0.5	0.5	0.5
Mutation rate	0.2	0.2	0.02

Table 2. Leaf statistics obtained for the selected hp-HGS setting.

	Test 1	Test 2	Test 3
Number of leaves	6	6	3
Ratio	44.739242 × 10^6	22.3696213 × 10^7	44.739242 × 10^7
errfit	19	89	4316
min eucl1	0.09	0.06	0.14
min eucl2	0.007	0.02	1.33
aver errfit	1008	5147	6766
aver eucl1	0.09	1.18	0.26
aver eucl2	0.04	0.02	1.33

The assumed maximum number of metaepochs is used as the stopping condition of our strategy. Our test leads to the study of how the selection of the error scaling coefficient Ratio affects the error of fitness minimization . We intend to study how to relate the err_FEM with respect to the assumed accuracy δ_j in the hp-HGS branches and leaves by setting various Ratio coefficients. Of course, the proper Ratio setting depends on the conditioning of the particular inverse problem (see Theorem 3.1).

The fitness function originally expressing the gap between the exact and current energy of the solution was supplemented by a small regularization term of the Tikhonov type, which slightly improves the problem conditioning.

We do not obtain the possible minimum computational costs in this series of tests, but rather try to show the potential hp-HGS skill by finding multiple solutions and the influence of the main strategy coefficient Ratio on its accuracy in the case of difficult, ill-posed inverse problems. Therefore, the current hp-HGS instance does not use branch reduction and conditional sprouting, the policies that can significantly reduce computational cost, described in Section 2. Moreover, the total computational cost might be reduced by the proper local stop conditions, which quickly remove the leaves and branches that do not search effectively (e.g. the progress in their mean fitness becomes too slow).

The results found by the hp-HGS strategy for three different values of Ratio, together with the corresponding fitness values expressing the difference between the energy of ‘exact’ and currently computed solutions, are presented in Table 2. We choose three Ratio values 44.739242 × 10⁶, 22.3696213 × 10⁷ and 44.739242 × 10⁷, so that the err_FEM in leaves estimated by Ratio/δ₃ is equal to 1, 5 and 10, respectively. The ‘min eucl₁’ and ‘min eucl₂’ mean the smallest Euclidean distance between the computed solutions and the first exact solution and the second exact solution , respectively. The values ‘aver eucl₁’, ‘aver eucl₂’ are the averages of the Euclidean distance between the best solutions found by leaves in the attractor of the proper exact solution. The ‘err_fit’ and the ‘aver err_fit’ stand for the value of the fitness function for the best solution and the average of the fitness function values.

We now obtained much better solutions for and than those published in 9 (see Table 2). The best Euclidean distance to each of them is of the range 10⁻². It resulted from better tuning of the strategy and the new hp-FEM solver utilized for solving the direct problem, as well as from introducing mild regularization.

The strategy seems to behave regularly. Both minimum fitness ‘err_fit’ and the average error fitness ‘aver err_fit’ decrease with the increasing accuracy of solving the direct problem (decreasing err_FEM), which are related to the decreasing values of Ratio. In Tests 1 and 2, both solutions were found to be reasonably accurate, with comparable accuracy, however the minimum distance 0.007 from one solution was found in the first test with the smaller Ratio. We may then conclude that the smallest Ratio in the first test delivers unnecessary overestimation of the direct solver accuracy, and then the harmful growth of computational cost. The third test shows that excessively low accuracy (too large Ratio value) might prevent finding both solutions with satisfactory accuracy. The strategy was nearer to the first solution at the distance 0.14, not much better than the distance obtained in the first two tests. The best distance 1.33 to the second solution obtained in these tests seems to be unsatisfactory. Summing up, the better choice of Ratio for solving the inverse problem under consideration by using hp-HGS is the value used in Test 2.

Although the values of ‘err_fit’ and ‘aver err_fit’ are much better than the results of our previous tests 9, one may ask about the possibility of successive accuracy improvement. It seems that it can be obtained mainly by adding the next, 4th, level in the HGS tree below the current leaves. Of course, this will result in a denser network of phenotypes than the smaller maximum error δ₄ of the HGS search. A significant growth in computational cost is also unavoidable. The increase in the regularization terms can be dangerous when solving multimodal inverse problems. No matter how regularization improves its conditioning and makes its solution less tiring, the change in the fitness function may result in reducing the number of solutions found, especially those associated with the local fitness minimizers.

Another problem eliminated in the current series of tests, but observed in the previous ones 9 are artefacts (the points recognized as local fitness minima, but not being local minima at all). They appeared because two exact solutions are linked to each other through the shallow ‘valley’ and the expected distance of the offspring from the parent in the leaf populations is above half of the distance between these solutions. A similar artefact, appearing like the global minimizer found, was described e.g. by Galar and Karcz-Dulęba 23 and called evolutionary channel.

7. Conclusions

•	The hp-HGS strategy offers two ways to decrease computational and memory costs. Firstly, it decreases the number of objective evaluations by using an adaptation of the inverse problem accuracy (HGS strategy). Secondly, the cost of the direct problem solution, which is necessary for fitness evaluation, is decreased by the proper scaling of the FEM error using the hp adaptation technique.
•	The asymptotic theory of hp-HGS can guarantee its asymptotic correctness with respect to the same set of solutions as a huge population SGA with heuristics similar to the heuristics of the hp-HGS leaves 12. Other results proved in 12 make the comparison of the expected computational cost of the single genetic epoch at a particular level of the hp-HGS tree possible (see (17), (18)). Moreover, Theorem 3.1 verifies the hp-HGS applicability condition (the Lipschitz continuity of the energy functional) for heat conduction problems.
•	In comparison to our previous tests 8,9 we obtained much better solutions for and to the bimodal L-shape inverse, heat conduction problem (see Table 2). The best Euclidean distance to each of them is of the range 10−2. This was obtained mainly by the better tuning of the strategy and the new hp-FEM solver utilized for the direct problem.
•	The strategy seems to behave regularly. Both minimum fitness ‘errfit’ and the average error fitness ‘aver errfit’ decrease with the increasing accuracy of solving the direct problem (decreasing errFEM), which are related to the decreasing values of Ratio. Too low accuracy (too large Ratio value) might prevent finding both solutions with satisfactory accuracy.
•	The error versus Ratio dependence analysis might be helpful by selecting the compromise value of this parameter, which guarantees satisfactory accuracy of the inverse problem solution by moderate computational cost (e.g. the Ratio value used in the second test).
•	Further improvements in the test results' accuracy can be obtained mainly by adding the next, 4th, level in the HGS tree below the current leaves. Of course, this will result in a denser network of phenotypes than the smaller maximum error δ4 of the HGS search. A significant growth in computational cost is also unavoidable.
•	The intensive regularization can improve problem conditioning; however, the resulted fitness modifications may reduce the number of solutions found, especially those associated with the local fitness minimizers.

Acknowledgement

The work has been partially supported by the Foundation for Polish Science under the Homing Program, and by the Polish Ministry of Scientific Research and Information Technology grant nos NN 519 447 739, NN 519 405 737 and NN 519 401 637.