The linear sampling method in a lossy background: an energy perspective

Abstract

In this article we propose a physical approach to the linear sampling method (LSM) for a possibly inhomogeneous and lossy background, whereby the modified far-field equation at the basis of the method can be regarded as a constraint on the power fluxes carried by the Poynting vector associated with the scattered field. Under appropriate assumptions on the flow lines of this Poynting vector, the general theorem inspiring the LSM (and concerning the existence of approximate solutions to the modified far-field equation) can be reformulated in a different way, which is more appropriate to explain the performance of the method.

Keywords:

• qualitative inverse scattering
• linear sampling method

AMS Subject Classifications::

• 45A05
• 65R20
• 65R30
• 65R32
• 78A46

1. Introduction

The linear sampling method (LSM) 1–4 is a well-known algorithm for visualizing the support of an unknown object by processing the data of a time-harmonic scattering experiment, and it can be considered the first of a set of qualitative methods 5 in the field of inverse scattering. The strong points of these methods (intrinsic linearity, short computational times, no need for a priori information on the scatterer, etc.) make them an effective approach for a large variety of inverse scattering problems.

However, qualitative methods are based on equations that are artificially formulated, i.e. do not derive from physical laws. This lack of a physical foundation seems to be responsible for at least one of the open problems 5,6 concerning, in particular, the LSM. Indeed, the far-field equation at the basis of the LSM is known to admit approximate solutions whose L²-norms behave as good indicator functions for the support of the scatterer (i.e., functions bounded inside and arbitrarily large outside the unknown object), but there is a priori no reason why computing the L²-norm of a (Tikhonov) regularized solution of the far-field equation, as requested by the implementation of the LSM, should provide one of these indicator functions.

In order to overcome this difficulty, the far-field equation at the basis of the LSM can be modified so to obtain a different qualitative method, i.e. the factorization method (FM), first formulated in 7 and extensively described in 8. The theoretical foundation of the FM is much more sound than that of the LSM; moreover, the FM can provide a deep insight into the LSM, as shown in 9–11. In particular, in 10 the LSM is reformulated and mathematically justified by means of results holding for the FM. However, this approach is restrictive from the viewpoint of scattering conditions, since the FM is, so far, significantly less general than the LSM 5,6.

This gap motivated the physics-based approach to the LSM proposed in a recent article 12, whereby the far-field equation of the LSM is regarded as a constraint on the power fluxes carried by the Poynting vector associated with the scattered electromagnetic field. It is shown there that, under some assumptions on the flow lines of this Poynting vector in the background, any approximate (and, in particular, the Tikhonov regularized) solution of the far-field equation behaves as a good indicator function for the support of the unknown target. This approach is explained in detail in the case of a homogeneous and lossless background, and for an experimental set-up consisting of emitting and receiving antennas placed in the far-field region. However, the LSM can also be formulated when a lossy and inhomogeneous background is taken into account, and all the antennas are placed in the near-field region 13–15. Hence, in this article we want to show how the investigation pursued in 12 can be adapted to this more complex scenario. The main advantage of this approach is that the material properties of the scatterer (and, to a large extent, of the background) are irrelevant: we focus on the two-dimensional, penetrable case only to fix ideas and notations, but the key role in our framework is just played by the behaviour of the flow lines of the Poynting vector in the background medium (and not inside the scatterer). However, so far, this is also a limitation of our approach, since such behaviour is a posteriori observed by means of numerical simulations, and not theoretically predicted. Progress in this direction would probably require sophisticated tools of topological dynamics (see, e.g. 16), and is beyond the scope of the present investigation.

This article is organized as follows. In Section 2 we formulate the direct and the inverse scattering problems we are interested in, we summarize the LSM and highlight the theoretical open issue we want to address. Section 3 is concerned with the propagation of electromagnetic power flux throughout the background: in particular, the role of the flow lines of the Poynting vector field associated with the scattered field is emphasized. Section 4 shows how the analysis of power fluxes can give an insight into the LSM when emitters and receivers are placed in the near-field and the far-field region, respectively: to this end, the investigation of 12 is adapted to the case of a lossy and inhomogeneous background. In Section 5 we perform some numerical simulations in order to catch the typical behaviour of the flow lines of the Poynting vector field, and we explain how this behaviour is related to the performance of the LSM. Section 6 addresses the situation where both emitters and receivers are in the near-field region, by pointing out its link with the case of far-field receivers, considered in the previous sections. Finally, our conclusions and hints for future work are presented in Section 7.

2. The direct and inverse scattering problems

We consider a time-harmonic electromagnetic wave of angular frequency ω > 0. First, we describe its propagation inside the background medium. The latter is assumed to be a penetrable, isotropic, infinitely long cylinder, whose physical and geometrical properties are the same on each plane perpendicular to its axis â. Let us choose any of these planes and identify it with ℝ². Following the conventions of Section 9.1 in 17, we assign the refraction index of the background as (1) where . We assume that there exists R₀ > 0 such that ϵ(x) = ϵ₀ > 0 and σ(x) = 0 , with . In Ω₀ the wavenumber is , while the refraction index is n₀ = 1. Then, if we define m(x) ≔ 1 − n(x), the support of m (denoted by supp m) is compact: we also require that supp m is piecewise homogeneous, i.e. there exists a finite number J of open C²-domains Ω_j ⊂ ℝ² where n(x) = n_j ∈ ℂ ∀x ∈ Ω_j, for j = 1, … , J, such that Ω_i ∩ Ω_j = ∅ for i ≠ j and . Accordingly, the wavenumber is given by (with Im[k(x)] ≥ 0) ∀x ∈ Ω_j and ∀j = 0, … , J. The magnetic permeability is assumed to be constant everywhere, i.e. μ(x) = μ₀ > 0 ∀x ∈ ℝ².

The incident electric field is generated by a line source parallel to â, whose intersection x₀ with the plane of interest is placed in Ω₀. Accordingly, we can choose a coordinate system such that the incident field is expressed as (2) where is the Hankel function of the first kind and of order zero (the dependence of the fields on the source point x₀ will often be omitted in the following). This means that we are considering TM-polarized waves: then, the scattered and total electric field can be expressed as E^s(x) = (0, 0, u^s(x)) and E(x) = (0, 0, u(x)), respectively. Starting from the time-harmonic and rescaled Maxwell equations (see Section 9.1 in 17) (3) and imposing the continuity of the tangential components of the total fields E and H across the surfaces where n(x) is discontinuous, easy computations show that the scattering problem can be formulated as follows: given the incident field uⁱ as in (2), find the total field u ∈ C¹(ℝ² ∖ {x₀}) such that 13 (4) where the last relation expresses the Sommerfeld radiation condition. More precisely, Equation (4a) is written for each open domain Ω_j and complemented by the transmission conditions imposing the continuity of both u and its normal derivative across the discontinuity surfaces of n(x). Moreover, for each j = 1, … , J, ∀x ∈ Ω_j: it follows from (4a) that u satisfies the Helmholtz equation in each homogeneous portion Ω_j of the background, whence u is real-analytic in Ω_j itself 5 (of course, it is also real-analytic in Ω₀ ∖ {x₀}). Since an analogous argument shows that uⁱ, given by (2), is real-analytic in ℝ² ∖ {x₀}, the regularity properties of u also hold for the scattered field u^s = u − uⁱ, except that u^s is real-analytic in x₀ too.

The direct scattering problem (4) is equivalent 13,17 to the Lippmann–Schwinger equation (5) where B_m ≔ supp m. In particular, the integral formulation (5) of problem (4) allows proving the well-posedness of the latter: if B is any open ball, centred at the origin, such that and , the solution u of (4) in depends continuously on uⁱ with respect to the maximum norm in .

Now assume that a smooth, penetrable and cylindrical scatterer (with the same axis â and the same magnetic permeability μ₀ as the background) is located in : more precisely, we assume that it takes up the closure of an open, bounded and C²-domain , such that is connected and the lines of discontinuity of the refraction index are C²-curves. Accordingly, definition (1) is replaced by (6) with , while the corresponding wavenumber is now given by . The previous discussion is easily extended to this new framework: it suffices to replace everywhere n(x) with (x). We consider the same incident field (2) as before, and we denote the new total and scattered fields as ũ and ũ^s respectively. In particular, it is easy to realize 13,14 that (7) is the field scattered by when u, which is the Green's function for the background medium described by (1), is regarded as the incident field.

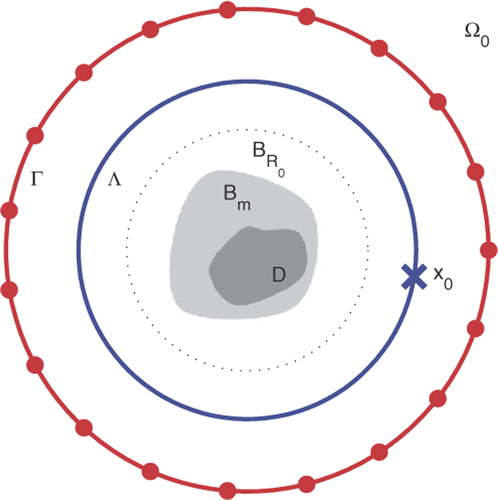
The qualitative inverse scattering problem considered here is to visualize the support of the scatterer by processing the data of an appropriate scattering experiment, starting from the knowledge of the background, i.e. of the refraction index n(x). We assume that the source point x₀ can be moved along a circle Λ ≔ {x ∈ ℝ² : |x| = R_Λ}, while the receivers are located on a circle Γ ≔ {x ∈ ℝ² : |x| = R_Γ}, with R_Λ, R_Γ > R₀. A schematic (and not in scale) representation of the physical set-up is shown in Figure 1.

Figure 1. Schematic representation of the physical set-up. (Available in colour online.)

The LSM (as outlined, in particular, in 13,14) is a procedure for solving this inverse problem. It is based on the modified far-field operator (8) and the corresponding modified far-field equation (9) written for each z in the investigation domain T, contained in the disk of boundary Γ. We point out that, in spite of the name of Equation (9), emitters and receivers are usually placed in the near-field region, as is reasonable when an inhomogeneous background is taken into account. In general, Equation (9) is unsolvable for almost all z ∈ T 14. However, the following theorem 13,14 ensures that (9) admits ε-approximate solutions whose L²(Λ)-norm can be used as an indicator function for , since it is bounded inside D, blows up on ∂D and can be made arbitrarily large outside D.

Theorem 2.1

Let D, F, k₀ be as above and assume that k₀ is not a transmission eigenvalue. Then:

i.	if z ∈ D, for every ε > 0 there exists a solution of the inequality (10) such that, for each z* ∈ ∂D, (11)
ii.	if , for every ε > 0 there exists a solution of inequality (10); moreover, every satisfying (10) is such that (12)

Inspired by this theorem, the LSM visualizes the scatterer by computing the Tikhonov regularized solution of Equation (9) and by plotting its L²(Λ)-norm for each sampling point z ∈ T. However, the main problem with this approach is that there is no guarantee that behaves as the ε-approximate solution exhibited by the theorem (see 5,6,8–10,15 for a detailed discussion of this point). Rather, remembering also that regularization prevents ε from vanishing (at least in presence of noise), an ‘ideal’ version of Theorem 2.1 would be the following: (i) if z ∈ D and ε > 0 is small enough, then any satisfying (10) is such that limit (11) holds; (ii) if and ε > 0 is small enough, there exists no satisfying (10).

Nevertheless, without any further hypothesis, this ‘ideal’ version is clearly false: e.g. the new point (ii) is made impossible by point (ii) of Theorem 2.1. Then, the key-problem now is: what further hypotheses can we reasonably add in order to obtain the desired statement? To face this problem, in the following sections we shall analyse how time-averaged electromagnetic power is transported in the background medium, from both the analytical and numerical viewpoints.

3. The Poynting vector and the transport of power fluxes

As suggested by (8) and (9), the field u^d plays a crucial role in the implementation of the LSM: then, in our framework, it is important to analyse u^d from the viewpoint of energy transport. From E^d(x) = (0, 0, u^d(x)) and the first equation of (3), we find the corresponding magnetic field . Then, remembering that , we can compute the time-averaged Poynting vector associated with the scattered electromagnetic field (E^d, H^d) as 18,19: (13) The previous regularity discussion implies that each component of 𝒮^d is in C⁰(ℝ²) and real-analytic in for each j = 0, … , J. We shall come back to this point later.

It is well known 18,19 that the integral of the time-averaged Poynting vector field over a closed surface Σ with outward unit normal represents the real power outgoing from Σ. Of course, in our two-dimensional setting, we consider plane curves instead of surfaces: then, if γ is a non-autointersecting and piecewise smooth curve in ℝ² (as always assumed in the following), we define the power flux of the field u^d across γ as the power flux of the corresponding Poynting vector (13), i.e. (14) where ν(x) is the unit normal to γ at the point x and dl(x) denotes the standard linear measure on γ. In particular, if γ is the boundary (with outward unit normal) of a bounded, connected and regular domain E_γ ⊂ ℝ² ∖ D, we can prove that the flux (14) is not greater than zero, since the background is, in general, lossy. To this end, it suffices to apply Gauss's divergence theorem in E_γ: remembering (13), (14) and observing that u^d satisfies Equation (4a) in , we get (15) where we used , with and Im[n(x)] ≥ 0 by (1). Of course, if the domain E_γ is a subset of the lossless region Ω₀, the equality holds true at the end of (15).

It is now interesting to discuss the particular case where E_γ is a finite flow strip of u^d in the background medium. To this end, we first recall that, given a point x₁ ∈ ℝ² ∖ D, the flow line of the plane vector field 𝒮^d starting from x₁ is defined as the solution x(τ) (for τ ≥ 0) of the Cauchy problem (16) For simplicity, we shall often refer to such x(τ) as the flow line of u^d starting from x₁, although it is actually a flow line of 𝒮^d. We observe that if x₁ is taken inside one of the domains Ω_j, the real-analyticity of 𝒮^d in Ω_j (remarked above) ensures the local existence and uniqueness of ; instead, if x₁ is chosen just on the boundaries ∂D or ∂Ω_j, the continuity of 𝒮^d (in particular, the fact that it is not Lipschitz in a neighbourhood of x₁) does not suffice to ensure the uniqueness of . In other terms, when x₁ belongs to a discontinuity curve of (x), it may be a ramification point of u^d, i.e. a point whence more than one flow line of u^d can start. We shall denote with the subset of ℝ² ∖ D where ramification points may occur.

Then, let us consider finite flow strips of u^d: they are open, connected and (almost everywhere) regular domains E_γ ⊂ ℝ² ∖ D obtained via the following construction. Take two distinct points x₁, x₂ ∈ ℝ² ∖ D and assume that they are neither ramification points, nor do they belong to the same flow line. Consider the two corresponding flow lines , and fix two other points, x₃ in the image of and x₄ in the image of . Hence, the arcs and are finite portions of flow lines and form the lateral boundary of a flow strip. Next, we close the latter by tracing two transverse sections, i.e. we consider two non-intersecting curves γ₁ and γ₂ connecting x₁ with x₂ and x₃ with x₄, respectively. The closed curve γ formed by γ₁, γ₂ and the arcs , is the boundary of the open domain E_γ, which shall be called a finite flow strip of u^d. Now, by virtue of (15), we have that ℱ_γ(u^d) ≤ 0; on the other hand, the power flux across the two arcs of flow lines is clearly zero. This amounts to saying that , with outward unit normals ν₁ to γ₁ and ν₂ to γ₂; but we can change the orientation of one of them (say ν₁, which then becomes inward), so that we find . The last inequality expresses the property that the power outgoing from the finite flow strip through γ₂ is not greater than the power ingoing through γ₁, as expected in a possibly lossy background.

In general, the flow tubes of the Poynting vector field are responsible for the power transport throughout the propagation medium: in other terms, they transmit the energy of the electromagnetic field from one point to another in space. In our physical interpretation of the LSM, we are interested in tracking this transport phenomenon in the case of the Poynting vector 𝒮^d given by (13). To this end, we need to assume that the flow strips of u^d starting from ∂D reach the observation circle Γ with a regular behaviour. This means that a flow strip E_γ, with lateral boundary formed by two flow lines and , should not intersect the scatterer D (in particular, and should not refold on D); furthermore, both and must intersect Γ in exactly one point. We shall fix these properties by means of appropriate definitions in the following.

We are now ready to use the concepts introduced above for investigating the modified far-field equation (9) from a power-flux perspective. Then, we conclude this section by pointing out that, although focused on the field u^d, the previous discussion can be easily extended to any scattered field.

4. Power fluxes and the modified far-field equation: far-field measurements

As a first step, let us assume, for the moment, that the observation circle Γ is placed in the far-field region, i.e. R_Γ → ∞: this assumption simplifies our framework and allows us to rely on the results of 12. We shall discuss the case of near-field measurements in Section 6; in any case, the emitters are placed on the near-field circle Λ.

We begin by stating the concept of (far-field) regularity for the flow lines and flow strips of the field u^d.

Definition 4.1

Given a point x₁ ∈ ℝ² ∖ D, a flow line of u^d starting from x₁ is called regular if the following properties hold:

1.	;
2.	, with large enough, ∃! τ1(R) > 0 such that ;
3.	if denote the polar coordinates of the point , then .

Moreover, an infinite flow strip E_γ of u^d is called regular if it is delimited by two distinct and regular flow lines , and E_γ ∩ D = ∅. If ϕ_∞(x₁) and ϕ_∞(x₂) are the asymptotic polar angles of and respectively, the quantity ψ_∞(x₁, x₂) ≔ |ϕ_∞(x₁) − ϕ_∞(x₂)| is called the far-field width of the flow strip E_γ.

Point (3) states that the flow line must approach a definite direction in the far-field region. This is in agreement with the Silver–Müller radiation condition 17, which entails the transversality of radiating electric and magnetic fields far enough from the source, and then the radiality of the corresponding Poynting vector field.

Then, by using for the field u^d, given by (7), the asymptotic behaviour of radiating solutions of the Helmholtz equation 17, i.e., (17) (where (r, ϕ) are the polar coordinates of x), and remembering Sommerfeld radiation condition (4c), it is possible to show that (cf. Theorem 8.17 in 17 for the three-dimensional case) (18) which holds uniformly in ϕ.

Now, let us consider an infinite regular flow strip delimited by two regular flow lines and of u^d, with asymptotic polar angles ϕ_∞(x₁) ≤ ϕ_∞(x₂) respectively: then, by virtue of (14) and (18), we can compute the power outgoing from the far-field observation angle [ϕ_∞(x₁), ϕ_∞(x₂)] as (19)

In the far-field approximation, the modified far-field operator (8) becomes (20) by virtue of (17), and the corresponding modified far-field equation reads (21) where u_∞ is the far-field pattern of the field u solving problem (4). With obvious changes, Theorem 2.1 remains valid in this far-field approximation 15: in particular, an ε-approximate solution of (21) satisfies (22) Hence, for any observation interval [ϕ₁, ϕ₂] ⊂ [0, 2π] in the far-field region, we have (23) Since, in general, the following implications hold: (24) setting and yields (25) By decreasing ε, one can make the right-hand side of (25) arbitrarily small. We also note that, by superposition 17, is the far-field pattern of the field (26) Then, remembering (19), inequality (25) allows the modified far-field equation (21) to be a constraint on energy fluxes: indeed, (25) means that the power outgoing from any observation interval [ϕ₁, ϕ₂] and radiated by the field (defined in (26)) can be made arbitrarily close to the power outgoing from the same interval and radiated by an elementary source located at the sampling point z. In this perspective, requiring that the presence of such source is always detectable in [ϕ₁, ϕ₂], in spite of the power loss along the path from the source itself to the receivers, is not too restrictive: it simply prevents the term u_∞(ϕ; z) in (21) from becoming (in part or at all) irrelevant. This requirement, formalized in the following Assumption 4.1, is ultimately made on n(x): it means that the absorption due to its imaginary part must not be too large.

Assumption 4.1

For any observation interval [ϕ₁, ϕ₂] in the far-field region, there exists a constant c_1,2 > 0 such that for all z in the investigation domain T.

We are now in a position to conclude that all the theorems and results presented in 12 are still true (by slight changes in the proofs) in the current framework, provided that the flow lines of u^d behave appropriately. In order to investigate this behaviour, a numerical approach seems to be more viable and direct than an analytical one: then, in the next section, we shall present and discuss the results of such investigation.

5. Numerical investigation: far-field measurements

We performed several numerical experiments in different scattering conditions, and the purpose of this section is to summarize their results by focusing on a single, but representative enough, simulation. The frequency of our experiment is ν = 1.0 GHz, corresponding to a wavelength λ₀ ≡ λ = 3.0 × 10⁻¹ m in vacuum. The background is formed by an ellipse and the vacuum outside it. The ellipse, characterized by relative permittivity ε_r = 2.0 and conductivity σ = 1.0 × 10⁻² S m⁻¹, is centred at the origin of the investigation domain, and its semiaxes have lengths a = 4.0 × 10⁻¹λ, b = 2.5 × 10⁻¹λ. The scatterer is a circle centred at (2.0, 0.0) × 10⁻¹λ and with radius r = 1.0 × 10⁻¹λ; its electrical parameters are ε_r = 5.0 and σ = 3.0 × 10⁻² S m⁻¹. We use N = 20 emitters, uniformly spaced on a circle Λ of radius R_Λ = 1.0λ, and N = 20 receivers, uniformly spaced on a far-field circle Γ of radius R_Γ = 1.2 × 10¹λ.

The direct scattering data are computed by means of a code based on the method of moments 20, and are then collected into an N × N matrix F; to this end, the investigation domain T is discretized into square cells whose side is shorter than 21, where δ is the minimum skin depth of the propagation media. Each entry of F is then affected by 3% Gaussian noise. Next, these noisy data are inverted by means of a standard implementation of the LSM, as described, e.g. 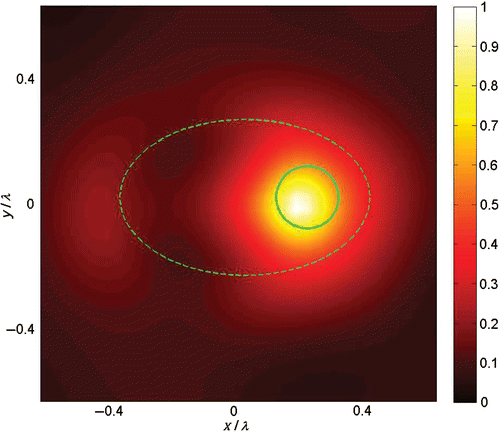in 2: in particular, Tikhonov regularization, together with Morozov's discrepancy principle, is applied to a discretized and noisy version of (21), in order to compute its regularized solution for each sampling point z in a grid 𝒵 covering T. 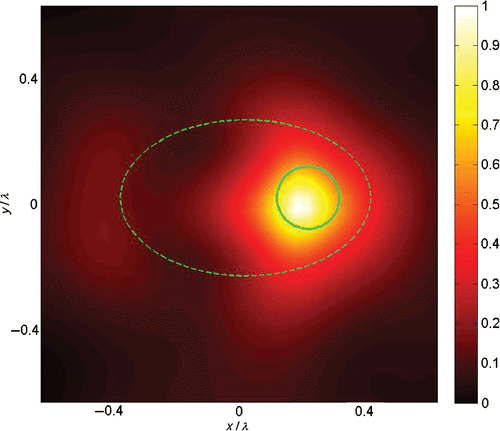In Figure 2 we show the visualization obtained by plotting (rescaled to [0, 1]) as indicator function on a square domain T of side 1.4λ. We superimpose a dashed and a solid line to represent the true profiles of the background ellipse and of the circular scatterer, respectively: as expected, only the latter is visualized.

Figure 2. LSM-visualization (for far-field measurements) of a lossy circular scatterer (solid line) inside a lossy elliptic object (dashed line). (Available in colour online.)

The direct code and the LSM-algorithm provide a discretized version of the integrand in (26): then, for each z of interest, we can easily compute the field and the corresponding Poynting vector field (cf. (13)) on an appropriate grid 𝒳 of points. Hence, for a given z ∈ 𝒵, the behaviour of the flow lines of can be visualized by plotting the unit vector on the points of 𝒳, where is obviously obtained by normalizing .

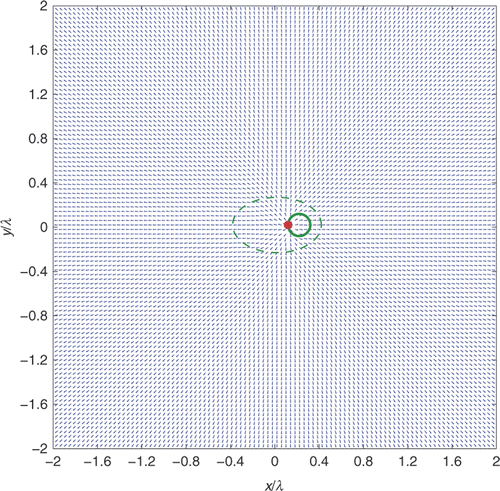
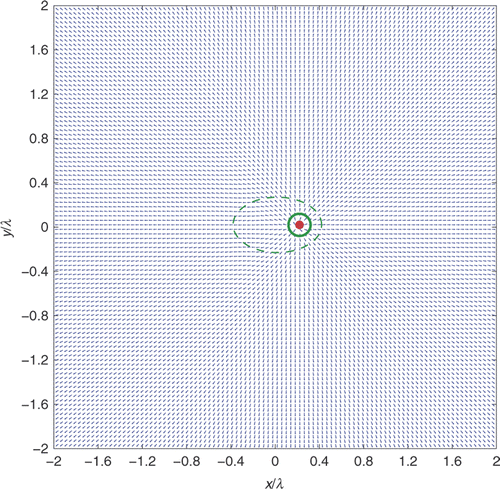
The typical behaviour of can be described as follows. When the sampling point z is taken inside the scatterer or even on its boundary ∂D, the flow lines are almost radially divergent from z itself, thus resembling the behaviour of the Green's function u(·, z) (cf. (4)) of the mere background: this situation is visualized in Figures 3 and 4. More precisely, both figures show the behaviour of the vector field when the sampling point z is respectively chosen as either the centre of the circular scatterer or a point on its boundary. Moreover, analogous figures (not shown here) visualizing the normalized Poynting vector field associated with the Green's function u(·, z) for the same sampling points z turn out to be essentially identical to Figures 3 and 4. The circle Γ where the receivers are placed cannot be contained in these pictures, but no anomaly of the flow lines is observed when the visualization domain is extended up to the far-field region. In particular, the flow lines starting from ∂D are regular in the sense of Definition 4.1, and any z ∈ ∂D is a ramification point of , i.e. a beam of several flow lines originates from z.

Figure 3. Behaviour of the vector field (for far-field measurements) when the sampling point z (red bullet) is taken inside the scatterer.

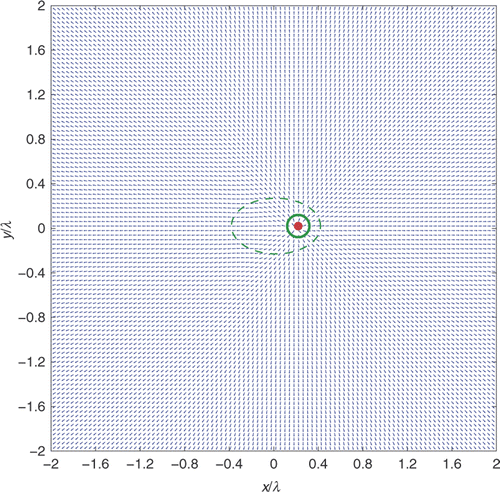
Figure 4. Behaviour of the vector field (for far-field measurements) when the sampling point z (red bullet) is taken on the boundary of the scatterer.

Let us briefly recall how this behaviour of the flow lines allows the conclusion that the L²[0, 2π]-norm of the approximate solution of Equation (21) must blow up as the sampling point z approaches a boundary point z* ∈ ∂D (for details, we refer to 12). Consider a sequence of points such that lim_n→∞|z_n − z*| = 0 and a corresponding sequence of collapsing circles centred at z* and with radius . Let be the portion of the circle not contained in D, i.e. , and let us assume that, for each n ∈ ℕ, the flow strip of starting from is regular, with non-vanishing far-field width as n → ∞, in the sense of Definition 4.1. If we assume, by contradiction, that the sequence is bounded in L²[0, 2π], two contradictory facts can be proved. First, we can show that the power flux across vanishes as n → ∞, since the length of the integration domain tends to zero, while the integrand function remains bounded. Second, the same flux must be greater than or equal to the far-field flux of the regular flow strip starting from : but, according to inequality (25), by choosing ε small enough this far-field flux can be made arbitrarily close to that of the elementary source u(·; z_n) across the same (non vanishing) far-field width of the flow strip. Then, by Assumption 4.1 and inequality (25), respectively, the far-field fluxes of both u(·; z_n) and are bounded from below by a positive constant, and then the same property holds for the near-field flux . This contradiction is removed by dropping the hypothesis of boundedness for the sequence .

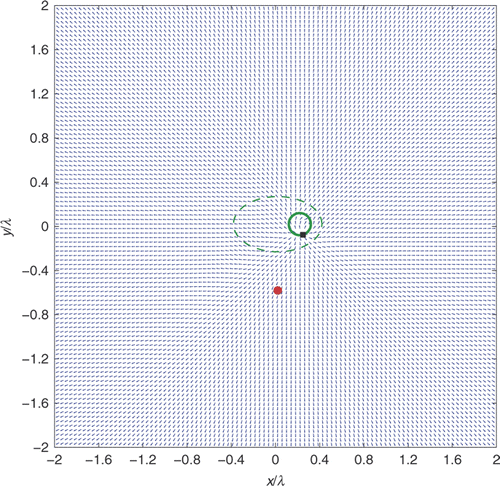
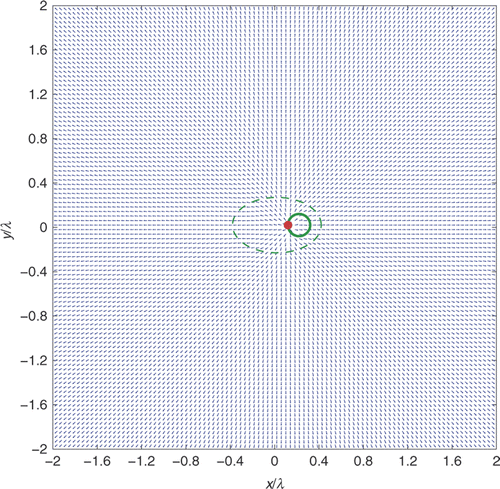
Now let us see what happens when the sampling point z is taken outside the scatterer D. The situation is shown in Figure 5: the vector field by no means resembles the Poynting vector field associated with the background Green's function u(·, z). Moreover, a ramification point z₀ of is detectable on the boundary ∂D, as highlighted by the small black box on the boundary of the scatterer in Figure 5.

Figure 5. Behaviour of the vector field (for far-field measurements) when the sampling point z (red bullet) is taken outside the scatterer: a ramification point (black box) appears on its boundary.

The behaviour of the flow lines outgoing from z₀ suggests introducing the following definition.

Definition 5.1

The field u^d defined in (7) is called partially pseudo-radial with respect to a ramification point z₀ ∈ R if there exist at least two regular flow lines of u^d, say and , starting from z₀ and with asymptotic polar angles , respectively, such that the flow strip delimited by them is regular with non-zero far-field width . Moreover, if is the set of the asymptotic polar angles of all such flow lines, we define the far-field width of this beam of flow lines as .

We can now apply a contradiction argument very similar to the previous one, to conclude that, if ε is small enough, there cannot exist such that the field is partially pseudo-radial with respect to a ramification point z₀ ∈ R and inequality (22) is satisfied.

We point out that in both cases, i.e. for z → z* ∈ ∂D and for z ∉ D, the core of the argument is the fact that the far-field power flux outgoing from the regular flow strips of the field is bounded from below by a positive constant, and Assumption 4.1 (which is trivially verified in the framework of 12) is ultimately a way of ensuring this lower boundedness condition.

We can now summarize the above investigation by stating our version of the approximation Theorem 2.1: it is based on tracking the power loss in the flow strips of starting from the boundary of the scatterer and reaching the observation curve Γ, placed in the far-field region. This tracking is made possible by the behaviour of the flow lines, as observed in this section: in other terms, our theorem relies on some assumptions on the flow lines, but these assumptions do not follow from a theoretical investigation, but are rather the formalization of a numerically observed behaviour. In this sense, ours is an a posteriori approach. In spite of this limitation, the strong point of our new version of Theorem 2.1 is that any ε-approximate solution of the far-field equation (9) behaves as a good indicator function (i.e. its L²[0, 2π]-norm blows up as z approaches ∂D and when z ∉ D) for a small enough (but a priori non-vanishing) bound ε on the discrepancy .

Theorem 5.2

Under Assumption 4.1 and the same hypotheses of Theorem 2.1:

i.

let z* ∈ ∂D and let be a neighbourhood of z*. For any ε > 0 and for each , let satisfy the inequality: (27) Moreover, let Cz(z*) be the circle with centre at z* and radius r ≔ |z − z*|, and define : for small enough, is an arc of extreme points for each . Finally, we assume that, for each , the two flow lines , of (starting from , , respectively) delimit a regular flow strip with far-field width , such that , i.e. . Then, if ε is small enough, it holds that (28)

ii.

let z ∈ ℝ2 ∖ D: then, if ε is small enough, there does not exist such that the field is partially pseudo-radial with respect to a point z0 ∈ R and inequality (27) is satisfied.

Proof

We shall adapt to the current framework the arguments proving Theorems 5.1 and 6.1 in 12.

i.	Let z* ∈ ∂D and assume, by contradiction, that limit (28) is false. Hence, it is possible to find a constant K > 0 and a sequence with the following properties: limn→∞|zn − z*| = 0 and ∀n ∈ ℕ.

According to (7), for each n ∈ ℕ we have that , where and are defined in analogy with (26). By the same arguments used for the proof of Theorem 5.1 in 12, we can obtain uniform bounds for both and , as well as their derivatives. To this end, we recall that m(x) ≔ 1 − n(x) and B_m ≔ supp m; then, we also set and . Next, we define , with R₁ > 0 such that R₁ < R₀ (i.e. , where is defined soon below (1)) and ; finally, let . Then, as explained in 12, there exists Q > 0 such that, for all n ∈ ℕ and for all , the following inequalities hold: (29) Accordingly, the fields and remain bounded ∀n ∈ ℕ and . As a consequence, we find (30) since the integral defining the flux (cf. (14)) is performed on a domain of vanishing measure, while the integrand function remains bounded.

On the other hand, if we track up to infinity the flux along the regular flow strip delimited by the two flow lines and of , we find that the power outgoing from this flow strip in the far-field region is not greater than , owing to the possible power loss along the path. Let us formally write this property: by using (14), (19), (25), (26) and assuming (with no actual restriction) that , for each n ∈ ℕ we can write (31) Now, by hypothesis we have ; in particular, there exist ϕ₁, ϕ₂ ∈ [0, 2π], with ϕ₁ < ϕ₂, such that for all n large enough, say n ≥ N. Then, from (31), Assumption 4.1 and taking (32) (with δ > 0 arbitrarily small), we easily find that there exists c > 0 such that (33) whence we have , in contradiction with (30).

(ii) Let z ∉ D: by contradiction, we assume that there exist ε > 0 and such that inequality (27) is verified and the field is partially pseudo-radial with respect to a ramification point z₀ ∈ R. According to Definition 5.1, if ψ_∞(z₀) > 0 is the far-field width of the beam of flow lines outgoing from z₀, there exists a regular flow strip delimited by two flow lines , starting from z₀ and with asymptotic polar angles , respectively, such that the corresponding far-field width is strictly positive.

Then, let {C_n(z₀)}_n∈ℕ be a sequence of circles centred at z₀ and with radius r_n, such that lim_n→∞r_n = 0, and let us set for j = 1, 2. Accordingly, the intersection between the flow strip delimited by the flow lines , and the circle C_n(z₀) identifies an arc of extreme points and . Then, by the same arguments used in the proof of Theorem 6.1 in 12, we can prove that (34)

As in the previous point (i), we can also track the power flux outgoing from up to the far-field region, by considering the regular flow strip delimited by the flow lines and of starting from z₀. Analogously to (31), we can write (35) We observe that the lower bound in (35) is now independent of n ∈ ℕ; moreover, since , we have by Assumption 4.1. Then, in order to obtain a contradiction between (34) and (35), it suffices to choose ε such that (36) This concludes the proof.▪

Remark 1

Theorem 5.2 deals with ε-approximate solutions of (21), then Tikhonov regularized solutions are a particular case. Since blows up only if α → 0, Theorem 5.2 foresees a vanishing α for z → z* ∈ ∂D and for z ∈ ℝ² ∖ D. This is in qualitative agreement with the well-known behaviour of α in the LSM-algorithm: its values inside the scatterer are notably larger than those on its boundary or outside 2.

6. Power fluxes and the modified far-field equation: near-field measurements

It is now interesting to see how the above discussion on power fluxes can give an insight into the modified far-field equation (9) or, better, into its approximate version (10), for an observation circle Γ placed in the near-field region. Differently from the genuine far-field equation considered in 12, or from the case of far-field measurements as addressed in the previous section, at first sight inequality (10) seems to have nothing to do with power fluxes: indeed, as highlighted by definition (14), the power flux of any field involves both the field itself and its derivatives; on the other hand, having a control over the L²(Γ)-norm of a field, as is the case for (10), does not entail, in general, any control over its derivatives and, consequently, over its flux.

We can give an alternative description of the above difficulty. The most direct way for adapting the results of the previous section to the case of near-field measurements consists in the following two steps: first, one should assume the (near-field) regularity of the flow strips, in the sense of the following definition.

Definition 6.1

Given a point x₁ ∈ {x ∈ ℝ² : |x| < R_Γ} ∖ D, a flow line of u^d starting from x₁ is called regular if

i.	;
ii.	∃!τ1 > 0 such that .

Moreover, a flow strip E_γ of u^d is called regular if it is delimited by two distinct and regular flow lines , and E_γ ∩ D = ∅.

Second, it should be required that the power flux outgoing from the flow strips across their intersection with the observation circle Γ is bounded from below by a positive number. Nevertheless, the latter requirement is now very unnatural, since inequality (10) has a priori nothing to do with power fluxes.

In order to overcome this difficulty, we observe that the investigation domain T ⊂ ℝ² where the sampling point can vary is a closed region surrounded by the circle Γ where the receivers are placed, i.e. . Accordingly, for each and for every ε > 0, the radiating field (cf. definition (26)) satisfies the Helmholtz equation (with wavenumber k₀) in ; moreover, it certainly holds that . Hence, by virtue of Theorem 3.21 in 17, we can conclude that there exists a constant C such that (37) where is the far-field pattern of . Hence, having a near-field control over the L²(Γ)-norm of the latter field enables a control over the L²[0, 2π]-norm of its far-field pattern (while the converse is clearly false, cf. 17 and Remark 3.1 in 12). In particular, as seen in the previous section (cf. relations (19), (23) and (25)), we can make the total fluxes and as close to each other as we want, by choosing ε small enough. This observation has a twofold consequence.

First, if we choose [ϕ₁, ϕ₂] = [0, 2π], we have that the difference between the total fluxes and ℱ_[0, 2π](u(·; z)) in the far-field region can be made arbitrarily small; but the observation circle Γ is placed in the outmost lossless region, then it holds that and ℱ_[0, 2π](u(·; z)) = ℱ_Γ(u(·; z)). Hence, inequality (10) entails a constraint on the two total power fluxes across Γ, whereby they must be close enough to each other. Note that equation (9), whence inequality (10) follows, is linear in the unknown , while imposing a constraint directly on power fluxes, e.g. via the equation , would give rise to a non-linear problem.

Second, if we consider the flow lines of the field beyond the observation circle Γ, i.e. up to the far-field region, the current framework becomes completely analogous to that of the previous section. Of course, Assumption 4.1 is now inelegant in that the detectability of the point source is required in the far-field region, while the measurements are made in the near-field. However, we can first replace Assumption 4.1 by its near-field analogous, i.e. by requiring that, for any circular portion Γ_1,2 ⊂ Γ, there exists a constant c_1,2 such that for all z in the investigation domain T. Then, we can take into account the typical behaviour of the flow lines of the field u(·; z) radiated by a point source placed at z: although they are not exactly radial with respect to z, these flow lines typically spread out from z and are regular up to the far-field region. Accordingly, we can reasonably conclude that Assumption 4.1 is implied by its near-field analogous, owing to the conservation of the power flux carried by each flow strip through the lossless medium, i.e. from Γ to the far-field region.

Summarizing, the case of near-field observations can be made analogous to that of far-field measurements, as long as the flow lines of the scattered field are considered not only inside , but also in all ℝ², up to the far-field region. In particular, the near-field version of Theorem 5.2 is simply obtained by replacing inequality (27) with the more general (10).

Then, as a last check, let us repeat the numerical experiment considered in Section 5, by only changing the radius R_Γ of the observation circle Γ, which has now to be in the near-field region: we choose R_Γ = 1.0 λ. The visualization provided by the LSM is given in Figure 6 and is almost identical to the previous one, plotted in Figure 2.

Figure 6. LSM-visualization (for near-field measurements) of a lossy circular scatterer (solid line) inside a lossy elliptic object (dashed line). (Available in colour online.)

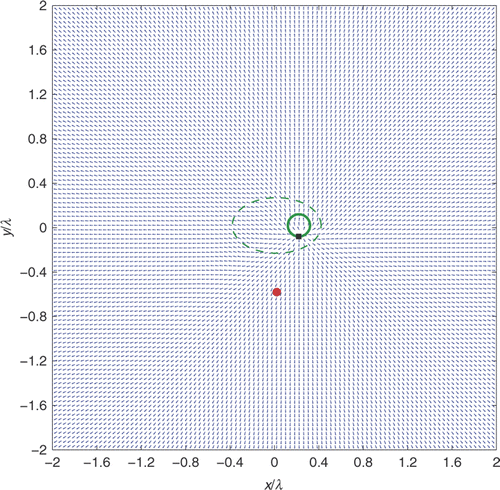
Then, Figures 7–9 show the behaviour of the vector field for z ∈ D, z ∈ ∂D and z ∉ D, respectively, for the same sampling points considered in Figures 3–5: for each of the three corresponding pairs of pictures, an immediate comparison between the two images highlights that they are very similar. Hence, also from a numerical viewpoint, the case of near-field measurements can be discussed within the framework outlined for far-field measurements.

Figure 7. Behaviour of the vector field (for near-field measurements) when the sampling point z (red bullet) is taken inside the scatterer.

Figure 8. Behaviour of the vector field (for near-field measurements) when the sampling point z (red bullet) is taken on the boundary of the scatterer.

Figure 9. Behaviour of the vector field (for near-field measurements) when the sampling point z (red bullet) is taken outside the scatterer: a ramification point (black box) appears on its boundary.

7. Conclusions

Our energy-based approach inspires a new form of the approximation theorem at the basis of the LSM. This reformulation provides a better explanation of the behaviour of the indicator function exploited by the LSM.

With respect to 12, the generalization is threefold: here the background can be inhomogeneous and/or lossy, while the receivers can also be placed in the near-field region. The inhomogeneity of the background implies that, a priori, the flow lines of the difference field u^d = ũ^s − u^s may have ramification points not only on the boundary ∂D of the scatterer, but also on any curve where the refraction index (x) is discontinuous. However (and interestingly), numerical simulations suggest that ramification points of can only show up on ∂D, as if the corresponding difference cancelled out the effect of all discontinuities of (x) except that on ∂D: this sounds reasonable and in agreement with the idea of ‘subtracting the background’, which underlies the formulation of the LSM considered in this article.

The lossiness of the background implies that electromagnetic energy is not conserved any more along the flow strips of u^d: however, the key arguments of 12 still hold by assuming that the absorption due to the imaginary part of n(x) is not too large, i.e. the presence of the elementary source in the investigation domain is always detectable by the receivers, in the sense of Assumption 4.1.

Finally, when the receivers are placed on a circle Γ in the near-field region, the modified far-field equation (9) cannot be directly regarded as a constraint on power fluxes, differently from the case of far-field measurements considered in 12 or in Section 4 (cf. (25)) of this article. However, having a control on the L²(Γ)-norm of a scattered field in the near-field region allows controlling the L²[0, 2π]-norm of its far-field pattern (cf. (37)): accordingly, taking into account the flow lines of the field up to the far-field region, the whole framework can be traced back to the far-field case.

Further developments concern both theoretical and numerical issues. From the theoretical viewpoint, a major achievement would consist of predicting the key-features (regularity, ramification points, etc.) of the flow lines, starting from the knowledge of the scattering conditions: this would make our physical interpretation a mathematical justification of the LSM. From a numerical viewpoint, it is interesting to investigate how much the LSM-algorithm (which accounts for discretization, noise, regularization, etc.) deviates from the continuous and noise-free framework. For example, our Theorem 5.2 requires that ε is small enough: indeed, depending on z, ε must be less than some upper bounds related to the far-field widths of appropriate flow strips (cf. inequalities (32) and (36)). On the other hand, such theoretical bounds have a priori nothing to do with the numerical values of the discrepancy as computed in the LSM-algorithm by means of Morozov's discrepancy principle: then, it would be interesting to check whether these values are consistent with their corresponding upper bounds. The investigation pursued in the simpler framework of 12 supports this consistency, but a more general and methodical approach to this problem is still missing.

Acknowledgments

Massimo Brignone was supported by a grant from the Istituto Nazionale d'Alta Matematica (INdAM), Roma, Italy.