An inverse solution for reconstruction of the area-moment-of-inertia of a beam using deflection data

Abstract

The main purpose of this study was to develop a mathematical model that could be used to determine the changes in the structural characteristics – such as changes that could occur due to corrosion in the cross-sectional area-moment-of-inertia of a bridge – from the knowledge of its loading and deflection. Reconstruction of the cross-sectional area-moment-of-inertia of a bridge from the knowledge of its loading and deflection is an inverse problem. In this investigation, the cross-sectional area-moment-of-inertias of a scaled model of simply supported steel bridge (with simulated corrosion) are reconstructed using the deflection and load data. The deflection data used in this inverse problem were numerically generated using the finite element method and the ANSYS software. The deflection data for each model were then used in the inverse problem to reconstruct the cross-sectional area-moment-of-inertias for the model. To solve the inverse problem, the solution domain was discretized into finite number of elements and nodes. The nodal deflections and slopes were represented by Hermite shape functions. For each element, the strain energy and the work done by the external forces were formulated. The minimum total potential energy principle was then used to create the stiffness matrices and reconstruct the area-moment-of-inertia for each element. The inverse model creates a set of linear equations that must be solved simultaneously. Moreover, since the formulation led to more equations than unknowns, the least squared method was used to minimize the errors associated with the solutions, and to match the number of equations with unknowns. Comparison of the inverse solutions with the direct solutions confirms that the variations in the area-moment-of-inertia for a bridge cross-section can be reconstructed, with good accuracy, from the knowledge of its loading and deflection.

Keywords:

• inverse problem
• structural health monitoring
• steel bridge
• Hermite shape functions
• minimum total potential energy

AMS Subject Classifications::

• 65R32
• 65M32
• 65M60

1. Introduction

In recent years, much has been reported about the condition of US infrastructure, particularly the bridges 1–19. According to the American Society of Civil Engineers: ‘Between 2000 and 2003, the percentage of the nation's 590,750 bridges rated structurally deficient or functionally obsolete decreased slightly from 28.5% to 27.1%. However, it will cost $9.4 billion a year for 20 years to eliminate all bridge deficiencies.’ The recent collapse of the I-35 W Bridge in Minnesota in the US has brought attention once again to the area of Structural Health Monitoring (SHM) and its significance in averting similar tragedies. As the name implies SHM refers to techniques that are used to measure, predict and monitor the health of a structure in carrying load safely and reliably. Typically, two basic elements are monitored, temporal changes in the characteristics of a structure and the level of change.

In the earlier stages of SHM research, the primary focus was on non-destructive testing 20,21 with emphasis on reinforced concrete beams and bridges 22,23. Moreover, sensors and instrumentation were developed to improve the quality of measurement response 24,25. Methods similar to system identification were also developed to perform damage assessment 26–28. Other research included the use of dynamic test results, or computer-generated data to analyse stay cables using open-source finite element codes 29. To model cracks in a simply supported beam, crack models such as reduced stiffness, discrete spring and complex models in two or three dimensions were also developed 30. No investigator has considered static deflection and slope data as a means of health monitoring and hence the reason for our investigation and this article.

The SHM research has led to many field applications and pilot testing, such as Minnesota's new I-35W bridge and Pennsylvania's Tacony-Palmyra and Burlington-Bristol bridges 31. However, the majority of bridges in the US are still inspected using conventional methods. The traditional testing/assessment programs requires bridge inspectors to attend a 2-week training course which covers topics, such as evaluation of bridge element damage and deterioration, evaluation and condition rating of steel bridges, corrosion of steel and rehabilitation techniques for bridges. Furthermore, most of the inspection techniques rely primarily on visual examination. At times, non-destructive tests such as using dye to penetrate cracks in steel or ultrasound for detecting corroded or missing ‘rebars’ are used. Typically, the bridge inspections are done annually or once every 2 years for newer bridges. The underwater inspections on pier foundation are done by scuba divers who are engineers or are under the supervision of engineers. As a part of inspection records, video tape, images of the bridges are taken and archived. If problems are detected then critical elements are monitored more closely and are inspected more frequently. It is important to note that with most of these techniques, particularly the visual inspection, detecting internal problems such as corrosion is very difficult. Bridges are designed for safety, but also with cost in mind. As a result, the criterion of cost, sometimes, leads to designs where components could be difficult to examine visually. Another important fact is that despite a 2-week training course and field training, bridge inspection/rating is still subjective. The subjective nature of traditional assessments along with insufficient funds to maintain the bridges affect their safety.

The main purpose of this study was to develop a mathematical model that could be used to determine the changes in structural characteristics such as area-moment-of-inertia (second moment of area) of a bridge cross-section from the knowledge of its loading and deflection. The approach does not require engineers to monitor the bridge continuously and generate an overwhelming amount of data, which can be costly 31. The inverse mathematical model developed in this article uses the change in deflection – under static loading introduced once a year – to detect corrosion and cracks within the structural members of the bridge. In practice, sensors and instruments such as load cell, LVDT, laser beam and tilt meter, and data logging systems could be used to obtain the load and deflection data 24 annually or as needed. The inverse model developed in this article is novel in approach and formulation, and because of its originality, it contributes to the state-of-the-art applied computational algorithms. No other investigator has approached an SHM problem in the manner formulated in this article. Moreover, in our study, in order to examine the validity and accuracy of the proposed inverse model, and as a first step, numerical experiments were conducted to generate the deflection profile for a beam under two point loads. The deflection and load data were then fed into our inverse model to reconstruct the area-moment-of-inertial for the bridge cross-section.

2. The direct problem

In civil engineering, when you design a bridge, you size the system characteristics such as the length, width, the cross-sectional size and the materials from which the bridge should be constructed. You also design for a specific traffic load, so you have information about the load. An additional design concern is the amount by which the bridge deflects under a traffic load. To solve this direct problem, using the finite element method (FEM), the solution domain is first discretized into finite number of elements and nodes. The nodal deflections and slopes are next represented by Hermite shape functions. For each element, the strain energy and the work done by the external forces are computed. The minimum total potential energy principle is then used. The finite element formulation of the direct problem 32 leads to the following set of linear equations that are customarily represented in a compact matrix form in the following manner: (1)

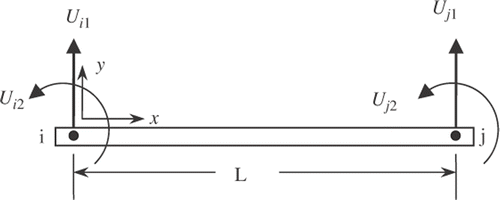
In the relationship (1), [K] represents the stiffness matrix, ‘system characteristics’, {U } is the deflection matrix, ‘the solution’, and {F } is the load matrix. For this situation, the deflection of the bridge represents a solution to this direct problem. In a direct problem formulation, we know the values of [K ] and {F } matrices and solve for values of {U } matrix. Let us discuss the FEM formulation steps in more detail now. A simple beam element consists of two nodes is shown in Figure 1.

Figure 1. A beam element.

Generally, a third-order polynomial with four unknown coefficients is used to represent the displacement field: (2)

The element's end conditions are then used to solve for the unknowns, c₁, c₂, c₃ and c₄. For node i, the vertical displacement, and the slope at (3) (4)

Similarly, for node j, the vertical displacement and the slope at (5) (6)

Solving for c₃ and c₄, and substituting into Equation (2), and regrouping the terms results in (7) where, S_i1, S_i2, S_j1 and S_j2 are called the ‘Hermite shape functions’ and are given by (8) (9) (10) (11)

In addition, the strain energy for an arbitrary beam element (e) is given by (12)

Substituting for v from Equation (7) into Equation (12) and minimizing the total potential energy with respect to the nodal displacements: (13)

We get the relationship, [K]{U} = {F }, where the elemental stiffness, nodal displacement and the point load matrices are given by (14) (15) (16)

In Equation (16), F_i1 and F_j1 are the point loads, which are applied in a downward direction at nodes i and j of the beam element.

3. The inverse problem

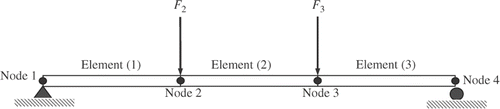
As mentioned in Section 1 of this article, SHM refers to techniques that are used to measure, predict and monitor the health of a structure in carrying load safely and reliably. Typically, two basic elements are monitored, temporal changes in the characteristics of a structure and the level of change. The inverse problem developed in this article makes use of such techniques, whereby the loading and deflection of a bridge could be monitored and used to detect changes (due to corrosion or fatigue) in the cross-sectional area-moment-of-inertia of the beams making up the bridge. Simply stated, if we know the values of {U} and {F} matrices, using the inverse model, we can then determine information about the [K] matrix. For the sake of simplicity of presentation, we develop the inverse problem using a model that has three elements and four nodes as shown in Figure 2. However, please note that the inverse method developed in this article can be applied to a model with more elements and nodes. The purpose of using only a three-element model is to show all the steps in detail.

Figure 2. The inverse model.

For the model shown in Figure 2, the relationship among the global stiffness, displacement, and load matrices for the given problem are then given by: (17)

After applying the boundary conditions U₁₁ = 0 and U₄₁ = 0, we have: (18)

If we factor out I⁽¹⁾ in row 1 and I⁽³⁾ in row 6, we will have the following identities: (19) (20)

Since I⁽¹⁾ and I⁽³⁾ cannot be zero, the terms in the bracket must be zero, which renders rows 1 and 6 ineffective in reconstructing the I-values. As a result, we end up with the following four equations and three unknowns. (21)

If we factor out I⁽¹⁾, I⁽²⁾ and I⁽³⁾, we will have the following four equations: (22) (23) (24) (25)

Since there are four equations and three unknowns, mathematically speaking, it is not possible to find solutions that exactly satisfy all four equations. Instead we have to make use of the least squared method to minimize the errors that may arise in the solutions of Equations (20)–(23). Representing Equations (20)–(23) in a compact matrix form, we have: (26) where the a and b coefficients are: and

Since the three solutions to Equation (24) do not exactly satisfy all four equations, errors are generated. These errors are given by (27)

Factoring out the {b} matrix and rewriting Equation (25), we have: (28)

And the sum of errors squared is given by (29) where are determined from: (30) (31) (32)

Similarly, , and are given by (33) (34) (35)

Next, the idea is to minimize the sum of the errors squared with respect to I⁽¹⁾, I⁽²⁾ and I⁽³⁾, which results in three equations: (36) (37) (38)

Evaluating Equation (34), we get: (39) where [B] matrix is the sum of all symmetrical matrices and is given by (40)

Making use of symmetry, Equation (37) then simplifies to (41)

Similarly, evaluating Equation (35), we get: (42) (43)

And evaluating Equation (36), we get: (44) (45)

We now have three equations (Equations (39), (41) and (43)) and three unknowns I⁽¹⁾, I⁽²⁾ and I⁽³⁾. These three equations can be solved simultaneously to obtain the I-values for each element. It is worth noting again that the least squared method described above can be applied to a model with more elements and nodes. The purpose of using only a three-element model was to show all the steps in detail in the development of the inverse method without introducing unnecessary complexity.

4. Numerical experiments

A series of numerical tests were performed to validate the inverse model developed in this article. For the numerical experiments (using three-element model), we used a span length of 600 mm, equal element length, L = 200 mm, a cross-sectional dimensions of 5 mm high and 25 mm deep with a cross-sectional area, A = 125 mm², and second-moment-of-area, I = 260.4167 mm⁴. A 20-Newton point load was applied at nodes 2 and 3 (F₂ = F₃ = 20 N). The numerical experiments were then conducted in the following manner:

Experiment 1:

A.	The model was divided into three elements and four nodes with equal length, width and cross-sectional moment-of-inertia (I-values). This direct problem was solved to obtain the displacement data for a homogeneous beam.
B.	We reconstructed the I-value for each element using the displacement data generated in Step A. Experiment 2:
C.	We picked element one and introduced a random change (between 5% and 15%) in the selected element's original value of the cross-sectional area-moment-of-inertia. This problem was solved directly to obtain the displacement values.
D.	The displacement values obtained in Step C were then used in the inverse problem to reconstruct the I-value for each of the three elements. Experiments 3 and 4:
E.	The procedure described in Steps C and D was repeated by picking elements 2 and 3 and introducing a random change in their I-values. Experiments simulating data noise:
F.	To study the effect of noise in the deflection data and how it may influence the reconstruction of I-values, we introduced a random noise between −2.5% and 2.5% in the displacement data in Experiments 2–4.
G.	The displacement results from Step F were then used in the inverse model to reconstruct the I-value for each element.

5. Discussion of result

5.1. The direct problem – displacement solutions

The deflection data that were used in the inverse model was generated numerically from the direct solutions using ANSYS. The deflection results of the direct problem are summarized in Table 1.

Table 1. The displacement results for the direct problem.

	Experiment 1 (Perfect model)	Experiment 2 (a random change of 5.7710% in I^(1))	Experiment 3 (a random change of 9.8254% in I^(2))	Experiment 4 (a random change of 6.28297% in I^(3))
U11	0	0	0	0
U12	−0.01536000	−0.01572600	−0.01619700	−0.01547400
U21	−2.56000000	−2.60180000	−2.72740000	−2.58290000
U22	−0.00768000	−0.00757550	−0.00851680	−0.00779440
U31	−2.56000000	−2.58090000	−2.72740000	−2.60580000
U32	0.00768000	0.00778450	0.00851680	0.00756560
U41	0	0	0	0
U42	0.01536000	0.01546500	0.01619700	0.01576000

5.2. The inverse problem – cross-sectional second-moment-of-inertia solutions

The displacement results of Section 4 were then fed into the inverse model to reconstruct the I-value for each element. The I-values obtained from the inverse model are shown in Table 2. Also shown in Table 2 are the actual I-values and the percent errors between the actual and inverse results for each experiment. It is self evident that the percent errors are insignificant.

Table 2. The three-element inverse model results and their comparison to direct solutions.

Experiment	Actual I-values (mm^4)	I-values from inverse solution (mm^4)	Percent error
1. Perfect model	I^(1) = 260.4167	I^(1) = 260.4167	0.00
	I^(2) = 260.4167	I^(2) = 260.4167	0.00
	I^(3) = 260.4167	I^(3) = 260.4167	0.00
2. A random change of 5.7710% in I^(1)	I^(1) = 245.3870	I^(1) = 245.4222	0.01
	I^(2) = 260.4167	I^(2) = 260.4416	0.01
	I^(3) = 260.4167	I^(3) = 260.5856	0.06
3. A random change of 9.8254% in I^(2)	I^(1) = 260.4167	I^(1) = 260.3963	0.01
	I^(2) = 234.8296	I^(2) = 234.8238	0.00
	I^(3) = 260.4167	I^(3) = 260.3963	0.01
4. A random change of 6.2829% in I^(3)	I^(1) = 260.4167	I^(1) = 260.3418	0.03
	I^(2) = 260.4167	I^(2) = 260.3757	0.02
	I^(3) = 244.0547	I^(3) = 243.9986	0.02

Numerical tests also were performed using a four-element and five-node model. For the four-element model, we used a span length of 600 mm, equal element length, L = 150 mm, a cross-sectional dimensions of 5 mm high and 25 mm deep with a cross-sectional area, A = 125 mm², and second-moment-of-area, I = 260.4167 mm⁴. A 15-Newton point load was applied at nodes 2–4 (F₂ = F₃ = F₄ = 15 N). For this model, a change in I was introduced randomly in elements 2 and 4 simultaneously. The results of these experiments are shown in Table 3.

Table 3. The four-element inverse model results and their comparison to direct solutions.

Experiment	Actual I-values (mm^4)	I-values from inverse solution (mm^4)	Percent error
Perfect model	I^(1) = 260.4167	I^(1) = 260.4167	0.00
	I^(2) = 260.4167	I^(2) = 260.4167	0.00
	I^(3) = 260.4167	I^(3) = 260.4167	0.00
	I^(4) = 260.4167	I^(4) = 260.4167	0.00
A random change of 5.7710% in I^(1)	I^(1) = 245.3870	I^(1) = 245.3825	0.00
	I^(2) = 260.4167	I^(2) = 260.5148	0.04
	I^(3) = 260.4167	I^(3) = 260.5322	0.04
	I^(4) = 260.4167	I^(4) = 260.6184	0.08
A random change of 9.8254% in I^(2)	I^(1) = 260.4167	I^(1) = 260.5611	0.06
	I^(2) = 234.8296	I^(2) = 234.4849	0.15
	I^(3) = 260.4167	I^(3) = 260.4715	0.02
	I^(4) = 260.4167	I^(4) = 260.5627	0.06
A random change of 6.2829% in I^(3)	I^(1) = 260.4167	I^(1) = 260.5611	0.06
	I^(2) = 260.4167	I^(2) = 260.4743	0.02
	I^(3) = 244.0547	I^(3) = 244.1441	0.04
	I^(4) = 260.4167	I^(4) = 260.5936	0.07
A random change of 13.6059% in I^(4)	I^(1) = 260.4167	I^(1) = 260.6120	0.07
	I^(2) = 260.4167	I^(2) = 260.5283	0.04
	I^(3) = 260.4167	I^(3) = 260.5187	0.04
	I^(4) = 224.9846	I^(4) = 224.9759	0.00
A random change of 9.8254% in I^(2) and a random change of 13.6059% in I^(4)	I^(1) = 260.4167	I^(1) = 260.6120	0.07
	I^(2) = 234.8296	I^(2) = 234.8472	0.01
	I^(3) = 260.4167	I^(3) = 260.5187	0.04
	I^(4) = 224.9846	I^(4) = 224.9589	0.01

5.3. Data noise

The main purpose of this article was to develop the mathematical theory for the stated inverse problem. In order to show the theory works, we performed a series of numerical experiments and used deflection data that were generated by ANSYS. Even though the data used up to this point contained no noise, it is still important that we introduce some random noise in the deflection data to evaluate the response of our model. To shed more light on this point, we introduced a random noise between −2.5% and +2.5% (5% range) in the deflection data (of the three-element model) using Excel®'s RAND function. First, random noise-percent values were generated. These values are shown in columns 3, 6 and 9 of Table 4. Next, the ± per cent values were multiplied by the U-values given in columns 2, 5 and 8, and added to the original U-values. For example, to the U₂₂ = −0.00757550, a randomly generated noise of (+2.42182214%)(−0.00757550) was added, resulting in U₂₂ = −0.00739203. The complete deflection data with random noise are shown in Table 4. As a means of comparison, the clean deflection data are also shown in Table 4. The deflection data with random noise were then fed into the inverse model to generate the I-value for each element. The results of these experiments are shown in Table 5. From examining Table 5, it is clear that because of the integral nature of the method presented here, the random noise in the data did not amplify too much and the resulting I-values are still in reasonable agreements. However, there are two major sources that contribute to percent error values as shown in Table 5:

1.	Due to the presence of noise in the data, Equations (18a) and (18b) are no longer zero, that is:

Table 4. The deflection data with and without random noise.

	Experiment 2 with noise			Experiment 3 with noise			Experiment 4 with noise
	U-values	Random noise between −2.5% and +2.5%	U-values with random noise	U-values	Random noise between −2.5% and +2.5%	U-values with random noise	U-values	Random noise between −2.5% and +2.5%	U-values with random noise
U12	−0.01572600	−0.17905428	−0.01575416	−0.01619700	−0.72022916	−0.01631366	−0.01547400	−0.77477280	−0.01559389
U21	−2.60180000	1.43153948	−2.56455421	−2.72740000	1.40482725	−2.68908474	−2.58290000	−2.04950705	−2.63583672
U22	−0.00757550	2.42182214	−0.00739203	−0.00851680	0.65994779	−0.00846059	−0.00779440	1.72650181	−0.00765983
U31	−2.58090000	−0.29404887	−2.58848911	−2.72740000	1.15514926	−2.69589446	−2.60580000	−0.17022396	−2.61023570
U32	0.00778450	−0.80933038	0.00784750	0.00851680	1.91318851	0.00835386	0.00756560	1.43309717	0.00745718
U42	0.01546500	−0.14178870	0.01548693	0.01619700	1.57928394	0.01594120	0.01576000	−0.92832095	0.01590630

Table 5. The actual and inverse model I-values and their relative percent errors.

Experiment	Actual I-values (mm^4)	I-values from inverse solution (mm^4)	Percent error
1. A random change of 5.7710% in I^(1) with random noise in deflection data (Table 3)	I^(1) = 245.3870	I^(1) = 186.0788	24.17
	I^(2) = 260.4167	I^(2) = 224.3383	13.85
	I^(3) = 260.4167	I^(3) = 254.1666	2.40
2. A random change of 9.8254% in I^(2) with random noise in deflection data (Table 3)	I^(1) = 260.4167	I^(1) = 239.1053	8.18
	I^(2) = 234.8296	I^(2) = 226.9139	3.37
	I^(3) = 260.4167	I^(3) = 273.9717	5.20
3. A random change of 6.28297% in I^(3) with random noise in deflection data (Table 3)	I^(1) = 260.4167	I^(1) = 251.3600	3.48
	I^(2) = 260.4167	I^(2) = 232.7736	10.61
	I^(3) = 244.0547	I^(3) = 217.1548	11.02

To get rid of the effects of the noise in the data, the following relations should then be zero: (46) (47)

Similarly, the introduction of noise into the deflection data U₁₂, U₂₁, U₂₂, U₃₁, U₃₂ and U₄₂ in Equations (20)–(23) will results in four additional equations containing noise in the data that should be zero. That is: (48) (49) (50) (51)

These six additional equations, Equations (18c), (18d), (20a), (21a), (22a) and (23a) must be considered when reconstructing the I-values. The authors are currently working on developing an error reduction model that would make use of these equations to handle the data noise better. The details of the error analysis will be presented in a follow-up paper.

1.	We had to reduce the number of equations to match the number of unknowns (I-values). This procedure also contributes to the percent errors shown in Table 5.

Finally, it is self-evident that all measurements, regardless of how carefully they are carried out, will have a certain level of noise. And as is the case in all engineering situations, when a measurement is made and data collected, before proceeding with further manipulation of data, one should first address the accuracy of data and the level of the noise that could be present. There are two basic types of noise: intrinsic and extrinsic. As the names imply, the intrinsic noise is created by the internal sources (e.g. the circuit elements making the measurement) while the extrinsic noise is created by the external sources, such as power supplies. It is also well-established that the first step of any measurement should include the calibration of the measurement system against known inputs. The calibration process will provide information about the level and the nature of the noise, and usually, during the calibration process sources of fixed noise could be identified and eliminated. Once the nature and the origin of the noise are identified, then we can resort to noise reduction techniques that are universally accepted. Examples of these techniques include differential measurement, averaging, polynomial smoothing and so on. In most situations, the accuracy of collected data can be increased if differential measurements are made. This technique works well because the noise on the high input closely resembles the noise on the low input and they cancel each other out. Another common technique involves averaging of data. For a steady signal, averaging provides a simple yet effective way of reducing random noise in a set of measured data. Polynomial smoothing using least square fits and cubic splines are examples of additional noise reduction techniques that have been proven effective. Finally, unlike finite differencing approaches, the integral approach developed in this article will not amplify any noise that could exist in experimental data. In general, integral approaches tend to average out random noise in the data. The authors are currently developing a sum-of-error-squared-scheme to improve the model in dealing with noise of larger magnitudes. This is a study by itself and will be presented in another article later.

6. Reliability analysis

A complete discussion of the reliability analysis of a structural system with the inclusion of the updated information from the results of the inverse problem presented here would be extensive and is beyond the scope of this article. However, in the following paragraphs, a simplified schematic version is presented to illustrate the potential application of the inverse problem study in reliability analysis.

For the beam shown in Figure 2, there are three elements or components. In reliability analysis, we may consider this beam as a series system in which the failure of the beam is the same as the failure of its weakest link (or element) 33,34. Then, the probability of failure of the beam becomes (52) where P_i represents the probability of failure of element i. Moreover, an element fails when the stress due to loading exceeds the strength of the element. For a steel beam, the strength can be defined as allowable stress σ_a, and the stress due to loading can be determined from the following relationship: (53)

In Equation (45), M is the internal bending moment due to the applied loads, y represents the distance from the neutral axis to the extreme fibre of the cross-section of the beam and I is the moment of inertia. The upper case symbols in Equation (45) signify random variables. Hence, the probability of failure of each element becomes (54)

During the SHM, if we apply a known load to the beam and measure the deflection and rotation at each node (Figure 2), from the inverse problem analysis presented here, we can then obtain an updated moment of inertia values such as those given in Table 3. A new average value for the moment of inertia for each element would then be used to replace the initial (design) values. Next, an updated probability of failure of the beam can be determined from Equations (46) and (44).

The sensors and test equipment may introduce random noise in the collected data, which in turn could influence the values of reduced moment of inertia as generated by inverse model. To remedy this situation, we can incorporate the variations into the reliability analysis by replacing the standard deviation of the random variable I with the deviation due to the random noise.

7. Concluding remarks

In this article, we discussed an inverse problem dealing with the reconstruction of cross-sectional second-moment-of-area for a beam from the knowledge of its loading and deflection data. To develop the inverse model, the solution domain was discretized into finite number of elements and nodes. The nodal deflections and slopes were represented by Hermite shape functions. For each element, the strain energy and the work done by the external forces were computed. The minimum total potential energy formulation along with minimum least squared technique was then used to create the stiffness matrices and reconstruct the area-moment-of-inertia for each element. In this study, the deflection data were generated from the solutions of direct problem. To simulate corrosion, for our numerical experiments, we introduced a random reduction in the I-value of an element. Moreover, to simulate noise in a physical experimental data set, we introduced random noise in the deflection data. Comparison of the inverse solutions with the direct solutions confirms that the variations in the area-moment-of-inertia for a bridge cross-section can be reconstructed, with good accuracy, from the knowledge of its loading and deflection. The reduced moment of inertia values due to crack or corrosion can be used to assess the reliability of the beam as discussed in section 6.

Acknowledgement

The first author thanks Professor Ernest True of Norwich University's Mathematics Department for his discussions related to error analysis.

Appendix

Symbol definition

E	=	modulus of elasticity, N m−2
F	=	load matrix, N
I	=	second moment of area, m4
K	=	stiffness matrix, N m−1
L	=	element length, m
M	=	internal bending moment, N · m
P	=	probability of failure
S	=	shape function
U	=	deflection matrix, m
v	=	displacement field, m
x	=	spatial coordinate, m
y	=	distance from the neutral axis to the extreme fibre of the cross-section, m

Subscripts

a	=	allowable
i	=	node reference
j	=	node reference

Superscript

e

=

element reference

Greek symbols

Λ	=	element strain energy, N m
Π	=	element total potential energy, N m
σ	=	stress, N m−2