A meshless method for an inverse two-phase one-dimensional linear Stefan problem

Abstract

We extend the meshless method of fundamental solutions proposed in [B.T. Johansson, D. Lesnic, and T. Reeve, A method of fundamental solutions for the one-dimensional inverse Stefan problem, Appl. Math. Model. 35 (2011), pp. 4367–4378] for the one-dimensional one-phase inverse Stefan problem to the two-phase change case. The implementation and analysis are more complicated and meaningful since one needs to handle composite layered materials. Furthermore, the inverse problem is ill-posed since small errors in the input data lead to large deviations in the solution. Therefore, the inverse problem is intractable to classical methods of linear inversion, and regularization is employed in our study. Numerical results obtained when the input data is either exact or contaminated with random noise are compared with the analytical solution, where available, or with the numerical results obtained by other methods, [D.D. Ang, A. Pham Ngoc Dinh, and D.N. Tranh, Regularization of an inverse two-phase Stefan problem, Nonlinear Anal. 34 (1998), pp. 719–731], otherwise.

Keywords:

• heat conduction
• method of fundamental solutions
• inverse Stefan problem
• two-phase change

AMS Subject Classifications::

• 35K05
• 35A35
• 65N35
• 80A22

1. Introduction

Heat conduction problems with phase change of state are of importance in several practical applications in metallurgy, ingot solidification, continuous casting of steel, scrap melting, ablation of metals using laser beams, welding of two materials, etc. 1. All these involve solving (in general, numerically) some Stefan-type problems for the parabolic heat equation. The classical Stefan problem has the essential specific peculiarity of imposing simultaneously both the local thermodynamic equilibrium and the dynamical compatibility condition on the unknown free boundary 2.

The direct Stefan problem requires determining both the temperature and the moving free surface when the initial and boundary conditions, as well as the thermal properties of the medium involved, are known. In contrast, in inverse problems some part of the cause of a physical phenomenon is unknown and it is compensated for by the knowledge of some part of the effect. Consequently, inverse Stefan problems require determining some initial temperature and/or boundary conditions, and/or thermal properties from additional information, which may involve the partial knowledge of the free surface, its normal velocity or the interior temperature measured at some points inside the medium 3. For example, in the process of recrystallization one has to solve the inverse Stefan problem which requires determining the temperature and the heat flux at the fixed surface that control the flatness of the crystallization front 4.

Prior to this study, much of the work on the inverse Stefan problem has been done for one-phase flow, see e.g. 5–10. However, the literature on solving numerically the two-phase inverse Stefan problem is much more scarce, see 11–13. A reason for this, as it has been pointed out earlier in the literature, is that standard direct problem domain discretization methods such as the finite-element method and the finite-difference method are not straightforward to adjust to the case of internal (interface) boundaries. Instead, integral equation-based methods are more attractable to use for these type of problems. In 11, the problem was reduced to a Volterra integral equation of the second kind and solved by regularization; however, their numerically obtained solution appears rather unstable. We also mention that, more recently, 12 employed the alternating phase truncation method combined with genetic algorithms and Tikhonov regularization for identifying a piecewise constant convective heat transfer coefficient. However, this latter heat transfer coefficient identification problem will not be investigated herein. Instead, we shall concentrate on extending the numerical method developed by the authors in 5 for the one-dimensional one-phase inverse Stefan problem to the two-phase case. We shall also compare our numerical results to those obtained in 11 by using the different method briefly abstracted above.

The plan of this article is as follows. In Section 2, we give the mathematical formulation of the one-dimensional two-phase inverse Stefan problem and point out its ill-posedness. In Section 3, we describe the numerical meshless method which is employed to approximate the solution of the inverse problem and its regularization. Section 4 presents and discusses numerical results obtained for some benchmark test examples. Noise is added to the input data in order to investigate the stability of the numerical solution. In one example, the analytical solution is available, whilst in the second one we compare our numerical results to those obtained in 11, where a different method was employed. Finally, Section 5 presents conclusions and possible future work.

2. Mathematical formulation

Consider a one-dimensional two-phase Stefan model for a slab of thickness l > 0 consisting partly of water and partly of ice separated by the moving interface x = s(t). Mathematically, the problem consists of determining two functions u₁ and u₂ satisfying the one-dimensional linear heat equations (1) (2) subject to the initial conditions at t = 0 (3) (4) the Stefan interface conditions along the curve x = s(t), (5) (6) and a Dirichlet or Neumann boundary condition at x = l, i.e. (7)

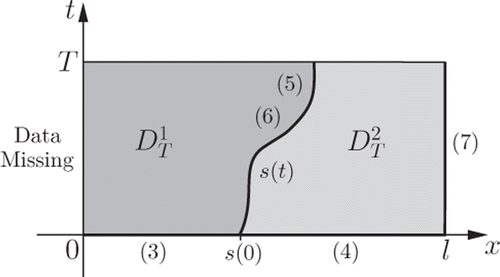
Figure 1 depicts the two-phase inverse Stefan problem under investigation. We mention that the corresponding one-phase inverse Stefan problem investigated in 5 is given by Equations (1) and (3), (8) and (9)

Figure 1. Representation of the two-phase inverse Stefan problem, with locations of the initial and boundary conditions (3–7).

In the above model, T > 0 is a given final time of interest, α_i = k_i/(ρ_ic_i) are the thermal diffusivities of water (i = 1) and ice (i = 2), k_i, ρ_i and c_i are the thermal conductivities, densities and specific heats, respectively, K_i = k_i/(ρ₂L) where L is the latent heat, and all the preceding physical quantities are constant, positive and given. The functions and represent the given initial data and satisfy the compatibility conditions at x = s(0), namely (10) where s(0) is assumed to be in the interval (0, l). We also require the compatibility condition at x = l, namely (11) in the case of the Dirichlet or Neumann data in (7), respectively.

The Stefan boundary conditions (5) and (6) reflect, respectively, the facts that the temperature at the interface must be equal to the initial temperature u*(t) (usually taken to be zero in melting processes, for simplicity) and that the rate of melting is proportional to the rate of absorption of heat energy at the interface 14.

Denote by the two-phase rectangular solution domain (0, l) × (0, T] which is subdivided into two subdomains and

The direct Stefan problem then requires finding the temperatures and the interface s ∈ C([0, T] ) ∩ C¹((0, T] ) satisfying s(t) ∈ (0, l) for 0 ≤ t ≤ T, Equations (1–11) and a boundary condition at x = 0, namely (12) where f₀, or g₀, or E are given functions satisfying the compatibility conditions (13) The well-posedness of the above direct two-phase Stefan problems were accomplished by Cannon and his co-workers in 15–17. The infinite differentiability of the free surface function x = s(t) has also been established in 18.

In contrast to the above direct nonlinear and well-posed Stefan problem, which requires finding the solution (u₁, u₂, s) satisfying Equations (1–13), the inverse linear and ill-posed Stefan problem requires finding the solution (u₁, u₂) satisfying Equations (1–11) only, but the additional information is that the interface x = s(t) is now known. The problems in which the additional information is the position of the moving interface are called design problems 12. In particular, all the quantities defined in Equation (12) and satisfying (13) are unknown and need to be determined. The more difficult inverse nonlinear Stefan problem which requires finding the solution (u₁, u₂, s) satisfying Equations (1–5), (10) and the Cauchy data at x = l (compare Equations (7–11)), namely (14) with (15) see 19, is deferred to a future work.

An initial attempt would be to split the two-phase inverse Stefan problem (1–11) into a direct problem for u₂ in followed by a one-phase inverse Stefan problem for u₁ in More specifically, one can first solve, using for example the method of fundamental solutions (MFS) presented in 20, the direct well-posed problem for u₂ in satisfying Equations (2), (4), (7), (11) and (16) where (17) and given s(t) ∈ (0, l) for 0 ≤ t ≤ T, to determine the partial derivative (18) This output can then be introduced into (6) to yield (19) Then, Equations (1), (3), (19) and (20) satisfying (21) and given s(t) ∈ (0, l) for 0 ≤ t ≤ T, form a one-phase inverse linear and ill-posed Stefan problem which has been previously solved using the MFS by the authors in 5.

The above splitting is useful in concluding the uniqueness of the solution of the two-phase one-dimensional inverse Stefan problem (1–11). Namely, the direct problem given by Equations (2), (4), (7), (11), (16) and (17) has a unique solution u₂, see 21, whilst the one-phase one-dimensional inverse Stefan problem given by Equations (1), (3), (19–21) also has a unique solution u₁, see 22. Moreover, uniqueness of a solution of this latter inverse problem also holds even if the initial condition (3) is not prescribed but is unknown, see 23.

However, when the data or g_l are contaminated with noise the retrieval of the heat flux derivative (18) is numerically unstable, see 24,25. Moreover, the inverse one-phase Stefan problem for u₁ given by Equations (1), (3), (19–21) is ill-posed since small errors in the input data cause large errors in the output data (12), see 6,9,26. Thus, in order to obtain stable solutions, both the above problems need to be regularized; however, using Tikhonov regularization this involves choosing two different regularization parameters. It would seem better if we could have instead a non-splitting approach of solving Equations (1–11) simultaneously using a regularization procedure which involves only choosing a single regularization parameter. This combined approach has been used before by the authors for simultaneously determining a heat source and the initial temperature in the standard parabolic heat equation, see 27. Therefore, in this article, we address finding the solution (u₁, u₂) by solving Equations (1–11) simultaneously. We will also investigate the case when the initial condition (3) is not prescribed, see the corresponding one-phase case, which has been recently investigated by the authors in 28.

3. The MFS

We approximate the solution (u₁, u₂) of the heat equations (1) and (2) using the MFS for the transient heat conduction in layered materials, recently developed by the authors in 29,30.

Let (22) where H the Heaviside function be the fundamental solutions of the heat equations (1) and (2). In the MFS, we approximate u₁ and u₂ by linear combinations of fundamental solutions (22) of the form (23) (24) In expressions (23) and (24), the source points for n = 1, 2 and are located outside their corresponding solution domains in the following way: (25) (26) where h > 0, M = 4M₁ and for We also define for . 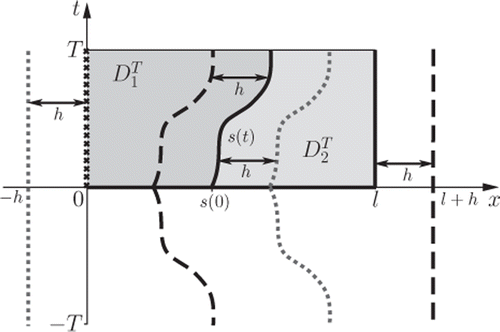A representation of the domains, boundaries and possible placement of source points is shown in Figure 2.

Figure 2. Representation of the two-phase problem with domains and , unknown boundary data (×), and source points (·····) and (- - -) placed externally to the domains and , respectively.

The MFS approximations (23) and (24) are motivated by the denseness properties shown in 5,29 in the standard L²-spaces on the respective boundaries of the solution domains. Alternatively, one could choose points below the bottom surface at points with coordinates (27) as suggested in 31 (under-determined situation), or at both these latter points and the top half of the lateral points (25) and (26), as suggested in 32 (over-determined situation). However, in this article we employ only the more natural determined situation given by the selection (25) and (26), and for which we know denseness properties of the approximation due to the proofs provided in 5,29.

3.1. Determination of the coefficients in the MFS

We now discuss how to determine the coefficients for n = 1, 2, and We shall collocate the initial conditions (3) and (4), the interface conditions (5) and (6) and the boundary condition (7) at certain collocation points. For the ease of implementation we select a uniform distribution of collocation points given by (28) and collocate Equations (3–11) as follows: (29) (30) (31) (32) Note that it is not important whether we impose (31) at i = 0 or not.

In total, via (23) and (24), Equations (29–32) form a system of (4M₂ + 4 + 2K) linear equations with 2M = 8M₁ unknown coefficients A necessary condition for a unique solution is that (33) Based on (23) and (24) we can write the system of Equations (29–32) in matrix form as (34) with the obvious notation. As pointed out in 25,33 the matrix A will have a high condition number both because of the ill-conditioning of the numerical MFS used and the ill-posedness of the mathematical problem. In order to handle this lack of stability, we consider the Tikhonov regularization method, which solves the modified stabilized system of linear equations (35) instead of the ill-conditioned system of Equations (34), where the superscript tr denotes the transpose of a matrix, I is the identity matrix and λ > 0 is a regularization parameter to be chosen. The now well-conditioned linear system of equations (35) can be solved using any classical method such as the Gaussian elimination method. The regularization parameter λ can, for example, be chosen according to the L-curve criterion, 34. We note that solving the system of Equations (35) yields an approximation to the vector of coefficients c which in turn, via the MFS approximants (23) and (24), produces the desired missing boundary data (12).

4. Numerical results and discussion

In this section, we apply the MFS outlined in the previous section to the inverse two-phase Stefan problem (1–11). Preliminary investigations indicate that the MFS parameter h, giving the distance between the boundary and the source points, should be chosen neither too small nor too large and in this section we present the numerical results obtained with a typical value of h = 2. Other values of h in the range (0.5, 4) produced similar results.

In the first example we have an analytical solution available. For this example we also investigate the case when the initial condition (3) for the function u₁ is not given and is part of the unknowns. In the second example, since an analytical solution is not available, we compare our numerical results with those obtained in 11 where a different method was used.

4.1. Example 1

In this example, we consider a melting problem in which both liquid and solid phases are present initially. Let us take T = 1, l = 1, α₁ = 0.5, α₂ = 1, k₁ = 0.5, k₂ = 1, L = 1, ρ₂ = 1, K₁ = 0.5 and K₂ = 1. We also choose in Equations (3) and (4) the initial conditions (36) (37) where γ = 0.479611, t⁰ = 0.695571, and erf and erfc are the error and complementary error functions, respectively, given by We also take (38) and then Equation (5) is satisfied with u* ≡ 0, i.e. (39) One can also check that the condition (6) is satisfied. Finally, the boundary condition at x = l = 1 is taken as (40) The analytical solution of the problem (1), (2), (6), (36), (37), (39) and (40) is then given by, 29,35, (41) (42) which can be verified by direct substitution. Of particular interest is to recover the data (12) at the inaccessible (hostile) boundary x = 0, given by (43)

As always with inverse and improperly posed problems, behaviour of the numerical solution in the presence of noise is an important part of the stability testing process. Noise could be added in the initial data (36), (37) or the moving boundary (38), see 12, but this case is not pursued herein. In our example, considering only the Dirichlet boundary condition in (40) given by (44) we add to it random additive noise generated as (45) where N(0, σ²) represents the normal distribution with mean zero and standard deviation (46) where δ represents the percentage of noise level. It was assumed that the initial data (36), (37) and the moving boundary (38) would be known fairly accurately, and the measurement error would concentrate mostly in the boundary temperature (45) or the heat flux (49) part of the data.

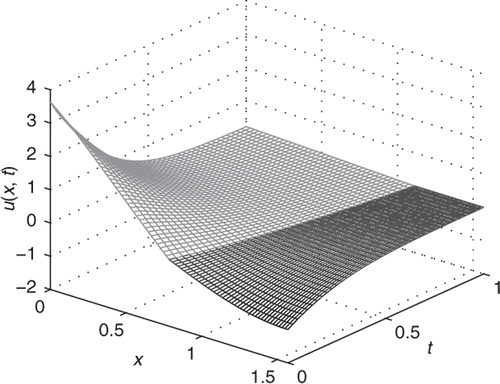
Figure 3(a) is a plot of the exact solution given by Equations (41) and (42), over the whole domain (x, t) ∈ [0, 1] × [0, 1]. Figures 3(b) and (c) show plots of the absolute error, when no noise is applied to u₂(1, t), i.e. δ = 0. From these figures it can be seen that more accurate approximations can be obtained by increasing the number of collocation and source points.

Figure 3. (a) The exact solution u(x, t) for all (x, t) ∈ [0, 1] × [0, 1], (b) the absolute error for all (x, t) ∈ [0, 1] × [0, 1], obtained with K = 20, M₁ = 10, M₂ = 20 (124 equations and 80 unknowns) and λ = 10⁻¹² and (c) the absolute error for all (x, t) ∈ [0, 1] × [0, 1], obtained with K = 40, M₁ = 20, M₂ = 40 (244 equations and 160 unknowns) and λ = 10⁻¹⁴. Additionally, for plots (b) and (c), h = 2 and δ = 0, for Example 1.

Figures 4(a) and (b) show the plots of the exact solution and exact normal derivative, respectively, in comparison with the MFS approximations for various noise levels added in the input data (45). From these figures one can see that the error in the approximation is of the same order as the noise level everywhere except for time t close to the final time T = 1. This conclusion is consistent with previous studies on the inverse heat conduction problems, see 36–38, which showed that if one wishes to determine a stable and accurate approximation for the boundary temperature and the heat flux in (10) for all times closer to the upper final time t = T, then one needs to consider and use the input Cauchy data (12) over a slightly future time interval (0, T + r), where r > 0 is related to the concept of Beck's future temperatures, see 39.

Figure 4. (a) The exact solution u₁(0, t) (–-) and the MFS approximations and (b) the exact normal derivative u_1x(0, t) (–-) and the MFS approximations. Both plots are for δ = 1% (•) with λ = 10⁻⁹, δ = 3% (▪) with λ = 10⁻⁷ and δ = 5% (▴) with λ = 10⁻⁷, and obtained with h = 2, K = 20, M₁ = 10, M₂ = 20 (124 equations and 80 unknowns) for Example 1.

In Figure 5(a) the exact solution and the MFS approximation for the best, average and least accurate approximations after 10 trials are plotted, and in Figure 5(b) the absolute error is plotted for the noise level δ = 5%.

Figure 5. (a) The exact solution u(0, t) (–-) and the best (•), average (▪) and least (▴) accurate MFS approximations from 10 different sets of noisy data with noise level δ = 5% and (b) the absolute error for all (x, t) ∈ [0, 1] × [0, 1] for noise level δ = 5%. Both plots obtained with h = 2, λ = 10⁻⁷, K = 20, M₁ = 10 and M₂ = 20 (124 equations and 80 unknowns) for Example 1.

Next, we look at the case when the initial condition (36) is not imposed. In this case, Equation (29) is collocated only for n = 2 and this together with (30–32) then forms a system of (4M₂ + 4 + K) linear equations with 2M = 8M₁ unknown coefficients . A necessary condition for a unique solution is that (47) compare with (33). To further highlight the flexibility of the proposed MFS approximation, in the remaining figures in this example we apply the Neumann boundary data in (40), instead of the Dirichlet data (44), given by (48) We further add to it random additive noise generated as (49) where (50)

Figures 6(a) and (b) show the plots of the absolute error when δ = 0 and δ = 5%, respectively. Again, even when we are missing the initial data (36), we obtain accurate and stable results.

Figure 6. (a) The absolute error for δ = 0 and λ = 10⁻¹², and (b) the absolute error for δ = 5% and λ = 10⁻⁶, for all (x, t) ∈ [0, 1] × [0, 1]. Both plots obtained with h = 2, K = 20, M₁ = 10 and M₂ = 20, (104 equations and 80 unknowns) for Example 1, when the initial condition (3) is not imposed.

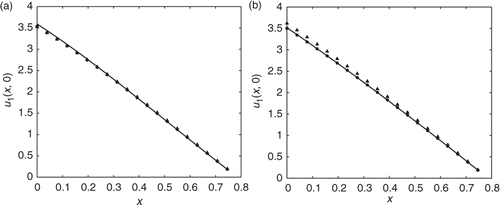
Lastly, Figures 7(a) and (b) show the plots of the exact solution and the best, average and least accurate MFS approximations after 10 trials along the boundary at x = 0 and the initial data at t = 0 for 0 ≤ x ≤ s(0), respectively. All plots in this example have shown the flexibility of the MFS to handle different and noisy boundary data and produce accurate and stable results.

Figure 7. The exact solution u(x, t) (–-) and the best (•), average (▪), both with λ = 10⁻⁶ and least (▴) with λ = 10⁻⁵, accurate MFS approximations from 10 different sets of noisy data with noise level δ = 5%, for: (a) (x, t) ∈ {0} × [0, 1] and (b) (x, t) ∈ [0, s(0)] × {0}. Both plots obtained with h = 2, K = 20, M₁ = 10 and M₂ = 20 (104 equations and 80 unknowns) for Example 1, when the initial condition (3) is not imposed.

4.2. Example 2

In this example, taken from 11, an analytical solution is not available. The input data are given by , α₁ = 2, α₂ = 1, K₁ = 1, K₂ = 2, u* ≡ 0, (51) (52) Noise is added in the zero Neumann data (52) as (53) We also tested adding noise to the initial data (51), but this appeared to be less influential on the obtained approximation.

Note that, in the similar example in 11, the initial data (3) was additionally imposed as However, it is unlikely that a solution to this inverse problem exists. Moreover, the plot presented in 11 is not clearly explained and since their numerically obtained solution appears not to match the given initial condition at x = t = 0, this seems to indicate the lack of a solution. Therefore, we relaxed the problem and took the initial data to be an additional unknown function to be determined. Since, as it is highlighted at the end of Section 2, the existence and uniqueness of the solution in is guaranteed, from the given Cauchy data on the interface s(t) it should be possible, due to analytic continuation 22, to determine a solution in provided that there are no additional redundant boundary or initial conditions imposed. This is further indicated by the numerical results below, in which a stable numerical solution with the expected physical properties is obtained. The inverse problem given by Equations (1), (2), (5), (6), (51) and (53) is then solved. In Figure 8(a) and (b), we plot the MFS approximations when T = 1 and T = 7, respectively, for different levels of noise applied in (53). The plots show that the temperature decays to zero as t increases, which is expected due to the diffusive nature of heat transfer. Figures 9(a) and (b) show the plots of the MFS approximations for the initial data (3). In both plots we observe that stable and accurate results are obtained. Finally, for completeness, Figure 10 shows the MFS approximation for all (x, t) ∈ [0, π/2] × [0, 1].

Figure 8. Plots of the MFS approximations for u₁(0, t), for t ∈ [0, T] , obtained with h = 2, K = 40, M₁ = 20, M₂ = 40, (204 equations and 160 unknowns), δ = 0 (–-) with λ = 10⁻⁸, δ = 1% (•) with λ = 10⁻⁶, and δ = 5% (▴) with λ = 10⁻⁵, for (a) T = 1 and (b) T = 7, for Example 2.

Figure 9. Plots of the MFS approximations for u₁(x, 0) for , obtained with h = 2, K = 40, M₁ = 20, M₂ = 40, (204 equations and 160 unknowns), δ = 0 (–-) with λ = 10⁻⁸, δ = 1% (•) with λ = 10⁻⁶, and δ = 5% (▴) with λ = 10⁻⁵, for (a) T = 1 and (b) T = 7, for Example 2.

Figure 10. Plot of the MFS approximation u(x, t), for all , obtained with h = 2, T = 1, δ = 0, λ = 10⁻⁸, K = 40, M₁ = 20, M₂ = 40 (204 equations and 160 unknowns), for Example 2.

5. Conclusion

In this article, a regularized MFS has been developed for solving an inverse two-phase one-dimensional linear Stefan problem. The numerical results show that the method is accurate and stable with respect to noise added in the input data. Future work will concern extending the MFS developed in this study to three-phase and two-dimensional inverse Stefan problems, see 26 and 40, respectively.

Acknowledgements

The third author thanks EPSRC for the financial support received. The comments and suggestions made by the referees are gratefully acknowledged.