Hyperbolic methods for the Landau–Lifschitz inverse scattering problem

Abstract

In this article, we present a direct approach to the Landau–Lifschitz scattering problem. A special fixed point problem is derived, which must be satisfied by the solution of the inverse scattering problem. A uniqueness result under a certain regularity condition is given and numerical methods based on the fixed point iteration and the layer stripping method are presented and illustrated.

Keywords:

• inverse scattering problems
• auxiliary linear problem for the Landau–Lifschitz equation
• overdetermined boundary-value problem for a hyperbolic system

AMS Subject Classifications::

• 78A46
• 34L25
• 34A55
• 35L50
• 65M32

1. Introduction

Let where p₁, p₂ and q are real-valued functions on ℝ satisfying and p* is the complex conjugate of p. We are interested in the problem of recovering Q(x) from scattering data, which is defined as follows in terms of special solutions of (1) Suppose that Q(x) is smooth enough and converges sufficiently rapidly to as x → ±∞. Then the matrix Jost solutions J^± are defined to be the solutions of (1.1) having the asymptotic behaviour There then exists a transition matrix 𝒯(ζ) satisfying The left and right reflection coefficients are defined on the real line as Although in general a(ζ) may have zeros on ℝ, throughout this article we make the technical assumption that A bound state is a square integrable vector solution to (1.1) which can occur only if ζ = ζ_n is a zero of a(ζ) in ℂ⁺, the upper half of the complex plane. Corresponding norming constants C_l,n, C_r,n are also defined as The inverse scattering problem is to recover Q(x) from the left scattering data {L(ζ), ζ_n, C_r,n} or the right scattering data {R(ζ), ζ_n, C_l,n}. We refer the reader to 1 for full treatment of this problem.

A principle motivation for consideration of this problem is that it is associated as part of a Lax pair with the Landau–Lifschitz (LL) nonlinear evolution equation (2) arising in ferromagnetism 2,3, hence we will refer to it as the LL inverse scattering problem (LLISP) and (1.1) as the LL system. In particular, analytical or numerical results for LLISP will have corresponding implications for the theory or computation of solutions of (1.2).

In this article, our main interest is in certain computational techniques for LLISP. The most common analytical methods, as in most other one-dimensional inverse scattering problems, involve integral equations of Gelfand–Levitan or Marchenko type, and numerical methods can be derived based on these. An alternative, which we investigate here, is to replace LLISP by an equivalent overdetermined problem for a hyperbolic system. Such an approach has been developed in the case of the scalar Schrödinger inverse scattering problem (see, e.g. 4) and leads to fast and stable numerical methods. A similar technique was developed for use in connection with a simpler system (see (1.3) below) in 5, but details were not given there.

It is known starting from the work of 6 that LLISP is related to the more well-known inverse scattering problem (ZSISP) for the Zakharov–Shabat (ZS) system (3) where which is in turn connected to the cubic Schrödinger equation via the inverse scattering transformation. Here s is a complex valued function on ℝ. We refer the reader to 7–11 for a comprehensive survey of the ZSISP and the general inverse scattering theory. The most refined results about the LLISP may be derived from this relationship and the known results about the ZSISP (see, e.g. 12). The exact connection between the two scattering problems is given by Equations (2.15a) and (2.17). Note that † denotes the Hermitian conjugate. This relationship is somewhat analogous to the correspondence between scalar scattering problems for the linear Schrödinger equation and the impedance form equation When the coefficients are sufficiently smooth a straightforward change of variables transforms one equation to the other, and likewise the scattering data are related in a simple manner. However the correspondence is that so that in cases of low regularity the transformation may be difficult to work with (e.g. η ∈ H¹) or may break down entirely (η ∈ L^∞ or even BV). Similarly, differentiability or at least absolute continuity of Q is required for the transformation of the LLISP to the ZSISP.

It is hence of interest to study the LLISP directly, rather than rely on theory of the ZSISP. Also, a direct method for numerical solution of the LLISP could be a useful device for numerical solution of the ZSISP. Our main quests in this article are

•	derivation of a computational method for the LLISP and
•	analysis and numerical simulation of our method.

Throughout this article we will assume that Q(x) − Λ is supported in [0, ∞). One might say that as long as Q(x) − Λ is rapidly enough decaying as x → −∞ then effectively it has this support property, where the support starts at x = 0 without loss of generality. We will also assume that there are no bound states, thus the scattering data consists of only the left reflection coefficient, L(ζ). Both of these restrictions can be removed by further development of the method – we will comment more on this at the end of Section 5. We point out that the smallness condition guarantees that there are no bound states 12,13. Throughout this article, we say a matrix function (or a vector function) A(x) is in L¹, if |A(x)|, the standard matrix 2-norm is in L¹. Similarly, usual function spaces (e.g. L², L^∞, W^1,1, etc.) can be defined for matrix functions (or vector functions).

Under these assumptions we derive two different overdetermined hyperbolic boundary-value problems connecting the coefficient matrix Q to the data L in a manner which is convenient for calculation. We also show that there is a unique solution which is absolutely continuous when L(ζ) satisfies a certain condition. Numerical examples, however, show that our method is not restricted to this case, that is, we successfully reconstruct discontinuous Q as well. Mathematical analysis of cases of piecewise continuous Q is ongoing work.

The outline of this article is as follows. In Sections 2 and 3, we derive two overdetermined boundary-value problems, which we will refer to as time-domain problems I and II, both of which are equivalent to the inverse scattering problem for the LL system (1.1) under the additional assumptions stated above. Problem I will exhibit explicitly a form of the known connection to the corresponding inverse scattering problem for the ZS system. Problem II is somewhat simpler in appearance, although not necessarily simpler to analyse, and is more suitable for use in cases of low regularity Q. In Section 4, we investigate the direct problem of the hyperbolic system and present auxiliary results. A fixed point problem is derived, which is equivalent to time-domain problem II in Section 5. We show that they have unique solutions as well. In the last section, we give numerical examples based on the fixed point iteration and the layer stripping method.

2. Time-domain problem I

Here, we derive the first of the two overdetermined hyperbolic boundary-value problems. As mentioned earlier, we assume that Q has no bound states and Q − Λ is supported in [0, ∞). We further assume that Q is sufficiently smooth for the moment. Applying the Fourier transform to the LL system (1.1) yields (4) where If the initial condition (5) is assumed, the boundary condition for (2.1) is given by (6) Indeed, since u⁽¹⁾(x, t) is an incoming wave from the left, u⁽¹⁾(x, t) = 0 for x < 0 and t ≠ x. Thus Note that u⁽¹⁾(x, t) is continuous on {t > x} because Q is assumed to be sufficiently smooth.

We seek a suitable additional boundary condition for (2.1) at x = t so that it is an overdetermined problem. To this end, we use the propagation of singularity for the wave equation (see, e.g. 14,15). Let { f_k(x)} be a sequence of functions, so that The solution of (2.1) and (2.2) with Q(x) = Λ is , thus near the characteristic t = x we should have (7) Inserting these expansions into (2.1) and matching the coefficients of the most singular terms we get (8) and the coefficients in subsequent terms, (9) From the conditions (2.2) and (2.3), we set (10) (11)

Now we show the uniqueness of u₀ satisfying (2.5) and (2.7). Multiplying (2.6) by , the Hermitian conjugate of u₀, for k = 1 yields (12) (13) and thus |u₀| = 1 from (2.7). Suppose that v is a column vector satisfying (2.5) and (2.7). Then v = e^−iθ(x)u₀ for a real-valued function θ(x) such that θ(0) = 0. It follows that which implies v = u₀.

Next, we compute u₁. Since is orthogonal to u₀, there exist scalar functions such that (14) We substitute this representation into (2.6) for k = 1 to obtain Similar to (2.10), applying to (2.6) for k = 2 yields Then we have the following differential equation due to the representation of (2.11). The initial condition is obtained from (2.7), (2.8), (2.10) and (2.11). From the integration by parts and (15) Thus (16) It follows from (2.4) that the additional boundary condition is given by

Now we introduce Problem I based on above argument as follows.

Time-domain problem I for the LLISP (TD1)

Given L = L(ζ), determine Q = Q(x) such that there exists u satisfying (17) (18) (19) Here Q and u₁ are related in the following manner:

1.	Solve the differential equation (2.13) for .
2.	Compute u0 from (2.12).
3.	, where is a matrix whose columns are u0 and .

One way to see that Q may be uniquely determined by means of (TD1) is to make a connection to a corresponding problem for the ZS system, provided that Q is sufficiently smooth. Let F = F(x) denote the solution of (20) (21) and set v = F^†u. One may then check that (22) (23) where (24) In addition, It follows from (2.17) that (25) The equations (2.16a), (2.16b) and (2.18) amount to a overdetermined hyperbolic boundary-value problem for v(x, t), which is already known in the literature, which may be used to recover S(x). For example in 16 it is proved that is uniquely determined on [0, X] from knowledge of on [0, 2X]. A direct analysis of (TD1) could be given, but we will instead derive an alternate problem in the next section, and analyse that one more closely.

Finally, we remark that this connection between these two overdetermined hyperbolic problems is parallel to, and predictable from, the earlier known results connecting the LLISP and ZSISP, and those connecting (1.2) and the cubic Schrödinger equation.

3. Time-domain problem II

In the time-domain problem 1 above, the direct relation between Q and u₁ is somewhat complicated. Furthermore, the boundary data at x = 0 may be difficult to work with if Q has a low regularity. Indeed, for some discontinuous Q. Thus, we are motivated to construct a more transparent system which is equivalent to (2.14) and which may be more easily used in the case of low regularity boundary data and Q. This can be done by a simple change of variables.

We define After some straightforward calculations using (2.6) and (2.14), we obtain Clearly (26) and since u₀ is a normalized eigenvector of Q corresponding to the eigenvalue 1, (3.1) can be rewritten as

Hence, we have the following time-domain problem.

Time-domain problem II for the LLISP (TD2)

Given L = L(ζ) determine Q = Q(x) such that there exists w satisfying (27) (28) (29)

Note that implies that (30) assuming w⁽¹⁾(x) ≠ 0 and q(x) ≠ −1.

We note that the additional boundary conditions (3.2c) (or (3.3) have an obvious sense even for discontinuous Q.

4. Direct problem

In this section, we discuss the well-posedness for (3.2a)–(3.2b) and investigate properties of solutions under various conditions for . We rewrite (3.2a)–(3.2b) on the domain T which is bounded by x = t, x = 0, and t = 2X − x. (31) (32) Here we do not limit w₀ to the form of (3.2b).

The well-posedness of (4.1) is a well-known result for smooth enough Q and w₀. For the case of less regularity, we define a weak solution;

Definition 1

w ∈ L²(T) is a weak solution to (4.1), provided for any smooth vector function ϕ(x, t) such that , (33)

Recall that we say a vector function (or a matrix function) w is in L², if |w|, the standard matrix 2-norm is in L² and V(w;(a, b)), the total variation of a vector function w over (a, b), is defined as

We now state the well-posedness for the direct problem (4.1) as follows.

Proposition 1

Suppose that Q ∈ L²(0, X) and w₀ ∈ L²(0, 2X). Then there exists a unique weak solution w ∈ L²(T) to (4.1) such that (34) Moreover, if then w ∈ W^1,s(T) such that (35) and if w₀ ∈ BV(0, 2X) then (36)

The proof can be found in the appendix. We close this section by stating two lemmas which will be used in the next section.

Lemma 1

Suppose that w solves (4.1) for given Q ∈ L²(0, X) and w₀ ∈ W^1,1(0, 2X). Then w, the trace of w at t = x, belongs to L¹(0, X) ∩ L^∞(0, X) and is such that (37) Here C is independent of Q.

Proof

The fact that w ∈ L¹(0, X) follows from Proposition 1 and the standard trace theorem. We consider w(x, ·) for fixed x to show that w is bounded. Since then from the embedding theorem, w(x, ·) is continuous up to the boundary of the interval (x, X − 2x) and there is a constant C, which is independent of x and Q, such that Hence we obtain (4.6).▪

Lemma 2

For given w₀ ∈ W^1,1(0, 2X), define Then 𝒲 is equicontinuous over [0, X].

Proof

First, we assume that w₀ ∈ W^2,1(0, 2X). Then w_t solves (4.1) with boundary data . As a corollary of Lemma 1 Since Q is bounded, w_x(x, x) = −Q(x)w_t(x, x) is also in L^∞(0, X). It follows that w is differentiable and (38) This implies that w′ is uniformly bounded since the constant C is independent of Q. For the case that w₀ ∈ W^1,1(0, 2X), we consider a sequence {w_0,n} ⊂ W^2,1(0, 2X) converging to w₀ in W^1,1. Since w_n, which is the trace of the solution w_n corresponding to w_0,n, uniformly converges to w due to (4.6), we obtain the desired result.▪

5. Fixed point problem

We next propose and study a direct approach to (TD2) by recasting it as a fixed point problem. Fix X > 0 and let For given w₀, we define an operator ℒ as (39) where is the trace of the solution w to Equation (4.1) with Q given by One may check that for w₀ ∈ W^1,1(0, 2X), ℒ is a well-defined map from Z to itself from Lemma 1 as long as (40)

We now observe that (TD2) is equivalent to the fixed point problem for the operator ℒ for (41) under certain regularities on . From direct calculation, we have (42) Hence q is a fixed point of ℒ in Z if and only if the characteristic boundary condition (3.2c) holds, provided the condition (5.2) is satisfied.

Proposition 2

For given L(ζ), Q solves (TD2) if and only if the corresponding q is a fixed point of ℒ with w₀ defined in (5.3), provided

We remark that under certain properties on L(ζ), one can show that (43) if either Q solves (TD2) or q is a fixed point of ℒ. Indeed, as a corollary of Lemma 3, one can see that (5.5) holds if Q solves (TD2) for . The other case follows from Theorem 1 as well.

Lemma 3

Suppose that w solves the overdetermined boundary-value problem (4.1) and (3.2c) for Q ∈ L²(0, X) and w₀ ∈ W^1,1(0, X) such that and (44) Then

Proof

Let w_0,n ∈ W^2,1(0, 2X) be a sequence converging to w₀ in W^1,1 such that (45) satisfying (5.6). Since w is continuous due to Lemma 2 and w_n, which is the trace of the solution w_n corresponding to w_0,n, uniformly converges to w due to Lemma 1, it is sufficient to show that From direct calculation, we have Then from (4.7) and (3.2c), we obtain which yields the desired result.▪

Next we turn our attention to the existence and uniqueness of a fixed point of ℒ. Due to the condition (5.2), ℒ(q) may not be in Z in general. For this reason, we analyse the fixed point problem locally. Namely, we consider a local map ℒ_α over the domain T_α (Figure 1) for each α ∈ [0, X) and some fixed h > 0. ℒ_α(q) is given by (5.1) for q in Z_α, which is a projection of Z over [α, α + h], and w is the trace of w satisfying (4.1a) in T_α with the boundary condition for given w_α(t). Note that we regard h as X − α in the case of α > X − h.

Figure 1. Domain T_α.

Lemma 4

For given α ∈ [0, X), suppose that w_α(t) ∈ W^1,1(α, 2X − α) and is of bounded variation such that (46) and for some constant M (47) Then there exists h > 0, which depends only on M, such that ℒ_α is a contraction mapping from Z_α to itself.

Proof

Fix h = h₁ > 0. Since w is continuous on [α, α + h₁] from Lemma 2, ℒ_α(q) ∈ Z_α provided |w| ≠ 0. Indeed, this is the case. Due to the assumption (5.8) and Lemma 2, we can take 0 < h₂ ≤ h₁ such that (48) Thus ℒ_α is well-defined from Z_α to itself for h = h₂. We note that h₂ depends only on thus M.

Next we show that ℒ_α is a contraction map by re-defining h other than h₂ if necessary. Let p, q ∈ Z_α, P, Q be the matrices corresponding to p, q, respectively, and w(x) = w(x,x), v(x) = v(x, x). Here w(x, t), v(x, t) solve the following equations over T_α. We deduce that (49) To estimate |w − v|, we assume that w_α ∈ W^2,1(α, 2X − α) for the moment. Let u = w − v and R = P − Q. Then u(x, t) solves the following problem over T_α, By Duhamel's principle, u is given by where K(x − y, t, y) solves Here T_y is a subdomain of T_α (Figure 2). Note that R(y)v_t(y, ·) is in W^1,1(y, 2X − y) for almost every y due to Proposition 1. Moreover, (4.4) implies that For any x ∈ [α, α + h₂], For the last inequality, we use (4.4) again. It follows from the Sobolev embedding theorem that for some constant C which is independent of x and α, Hence, together with (5.10) and (5.11), we obtain We re-define h as so that (50)

For the case of w_α satisfying the assumption in the lemma, we consider a sequence {w_α,n} ⊂ W^2,1(α, 2X − α) converging to w_α in W^1,1 such that for some N₁ (51) Such a sequence exists because the total variation of is assumed to be bounded. Let and ℒ_α,n be the map over [α, α + h] corresponding to w_α,n. Then ℒ_α,n converges to ℒ_α uniformly since w_n uniformly converges to w due to (4.6) for any given q. Here w_n is the trace of solutions w_n corresponding to w_α,n. Hence, for any ϵ > 0, there is N₂ such that for any q ∈ Z_α (52) Then for n ≥ max{N₁, N₂} Hence ℒ_α is a contraction mapping over [α, α + h].▪

Figure 2. Domain T_y.

Now we state the existence and uniqueness of the fixed point for the global operator ℒ.

Theorem 1

Suppose that w₀ ∈ W^1,1(0, 2X) and is of bounded variation satisfying Then the corresponding operator ℒ has a unique fixed point in Z. Moreover the fixed point is continuous.

Proof

Let Then, there exists h > 0 such that ℒ₀ has a fixed point in L²(0, h) due to Lemma 4. By the construction of the fixed point, w(x) is continuous and |w(x)| ≥ 1/2 on [0, h], which is the trace of the solution w(x, t) of (4.1) with the corresponding Q. It follows from (5.4) that is, (w, Q) solves the overdetermined boundary-value problem (4.1) and (3.2c) over [0, h]. Lemma 3 implies that |w(x)| = 1 for all x ∈ [0, h]. Now we consider ℒ_h with the boundary condition Since and due to Proposition 1, we can find a fixed point of ℒ_h over [h, 2h]. We continue this procedure to find a fixed point q of ℒ over [0, X]. Since h is independent of x, the induction step terminates in a finite number of steps.

The continuity of the fixed point follows from Lemma 2.▪

As a corollary of Proposition 2 and Theorem 1, we have the following uniqueness result for the LLISP.

Corollary 1

Suppose that there are no bound states for LLISP with Q such that Q − Λ is supported in [0, ∞). Then Q is uniquely determined on [0, X] from the knowledge of on [0, 2X] if (53) In this case, Q is continuous on [0, X].

We remark that it is possible to solve the half line LLISP without bound state information by a Darboux kind of transformation similar to the ZSISP described in 5. Indeed, assuming that Q − Λ is supported in the right half line, the left reflection coefficient can uniquely determine the bound state data {ζ_n, C_r,n}. Then is the left reflection coefficient for Q^[0] without bound states and Q can be uniquely restored from Q^[0]. The case without a support assumption can be handled as well by a splitting method using step-like coefficients. For given Q, we split it to Q_l, Q_r such that Then one can extract the right reflection coefficient for Q_l and the left reflection coefficient for Q_r from the relation Here 𝒯_l, 𝒯_r are the transition matrices corresponding to Q_l, Q_r, respectively. For more details we refer the reader to 12.

6. Numerical methods

In this section, we illustrate two numerical methods for (TD2). The first is based on fixed point iteration for the mapping method described in the previous section, and the second is a layer stripping method.

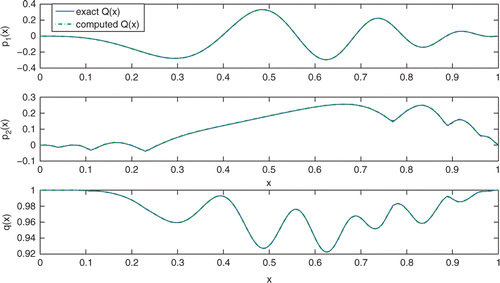
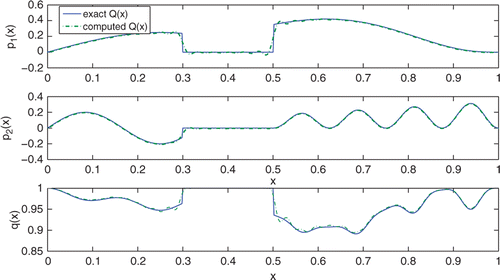
Figure 3 shows a numerical example of p and q reconstructed on [0, 1] from the fixed point method after eight integrations. The residual norm at each iteration is given in Table 1. In this example, Q is chosen so that , a condition known to guarantee that there are no bound states as mentioned in Section 1. To obtain the sampled left reflection coefficient L(ζ_j) for ζ_j = jΔζ, j = −M, … , M, we solve the LL system by an ODE solver. 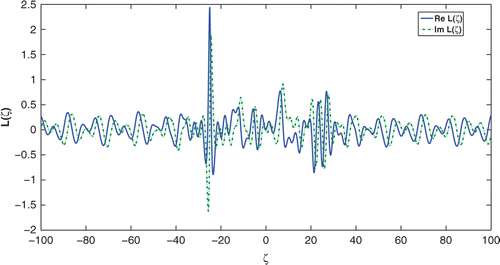Then L(ζ_j) is given by Figure 4 shows the sampled left reflection coefficient L(ζ).

Figure 3. Reconstruction of Q from the contraction mapping method.

Figure 4. The sampled left reflection coefficient.

Table 1. Residual norm at each iteration step.

n	1	2	3	4	5	6	7	8
	2.09e−1	2.24e−2	3.78e−3	6.05e−4	9.03e−5	1.29e−5	1.75e−6	2.12e−7

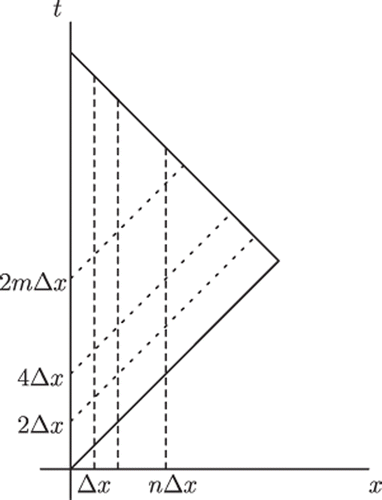
In computing the boundary data , we used the simple trapezoid rule after computing by the fast Fourier transform algorithm with zero padding L(ζ_j) values to the interval of [−(M + M′)Δζ, (M + M′)Δζ]. In the contraction mapping method, we have to solve the hyperbolic system (3.2a)–(3.2b) at each iteration step. For this, we adopt the idea in 17. We deduced that (54) (55) Consider the mesh points described in Figure 5 We obtain finite difference equations for (6.1) along the characteristic lines by the first-order backward scheme, (56) (57) Here w_n,m = w(x_n, t_n,m), p_n = p(x_n), and q_n = q(x_n). Let Then (6.2) yields where A · B denotes an entrywise product. We remark that A_n is invertible as long as q_n ≠ −1. Since we assume that the actual Q satisfies that , it is reasonable to assume that q_n > −1 at every step. Note that for all the examples given in this section, we choose M = 10⁴, M′ = 10⁶, Δζ = 0.01, Δx = 0.002 and q = [0 1]^T as the initial guess.

Figure 5. The finite difference grids.

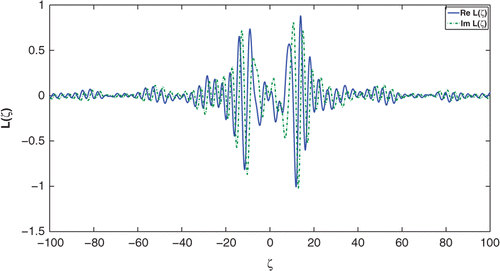
We applied this method to a discontinuous Q although our theory is restricted to continuous Q and there is a non-uniqueness result for the LLISP with discontinuous Q 12. Moreover, the corresponding may include Dirac delta functions in this case so that is not satisfied anymore. Nevertheless, our method can successfully reconstruct Q as shown in Figure 6. The corresponding scattering data, the left reflection coefficient is shown in Figure 7.

Figure 6. Reconstruction of discontinuous Q after eight iterations.

Figure 7. The sampled left reflection coefficient for discontinuous Q.

Next we illustrate a layer-striping method to solve (TD2) directly. Suppose that p_j, q_j are already reconstructed for j ≤ n − 1. Then we can find w_n,m (m = 0, 1, 2, …) from the following equation derived by the first-order forward method. Then p_n, q_n are computed as Since p₀ = 0 and q₀ = 1, we can construct p_n, q_n for all n by the induction.

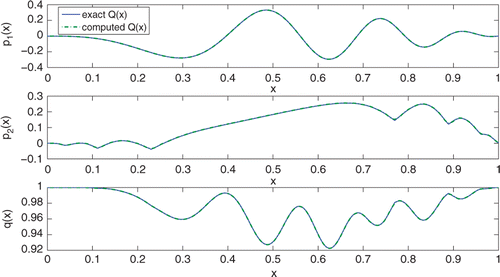
Figure 8 shows a numerical example via the layer-striping method described above.

Figure 8. Reconstruction of Q from the layer-striping method.

Acknowledgments

The author would like to thank Professor Paul Sacks for helpful discussions. A part of this article is presented in the author's Ph.D thesis.

Appendix

Here we provide the proof of Proposition 1.

First, we consider piecewise constant Q such that , where x₀ = 0 and x_N = X. Define a translation operator 𝒫_k such as from W^1,2(x_k−1, 2X − x_k−1) to W^1,2(T_k). Here T_k = {(x, t) ∈ T: x_k−1 < x < x_k}. Then the linear operator 𝒫_k satisfies the following properties: With these notations and a Hermitian matrix F_k such that Q_kF_k = F_kΛ, we define on each T_k, where w_k−1(·) = w(x_k−1,·). Since for any smooth v₀, 𝒫_kv₀ solves w solves (4.1). Moreover, if w₀ ∈ W^1,2(0, 2X) is assumed then w ∈ W^1,2(T) since w is continuous across x = x_k. Indeed, the properties of 𝒫_k yield that for any 0 ≤ α < α + h ≤ X (58) and especially

For general Q ∈ L²(0, X), we consider a sequence of piecewise constant Q_n converging to Q. From the above argument, there is w_n ∈ W^1,2(T) solving (4.1) for each Q_n and a fixed w₀ ∈ W^1,2(0, 2X). Since w_n is uniformly bounded in W^1,2(T), we can extract a subsequence such that

We now claim that w is a weak solution to (4.1). For any test function ϕ, (59) Here ⟨·, ·⟩ denotes the standard inner product on L²(T). Since weakly converges to w in W^1,2(T) and is uniformly bounded by a square integrable function, the first and the third term on the right-hand side converge to 0 as n_k → ∞. The boundedness of a weakly convergent sequence yields which converges to 0. Since is a solution for , for all n_k. Thus, (6.4) implies which gives (4.2) as desired.

Moreover, since weakly converges to w_t in L^s(T_α)(s = 1, 2) for any α, h (see Figure 1), it follows from (6.3) that Since α, h are arbitrary, we have energy estimation (4.4) for almost all x.

For the uniqueness, we have to derive an energy estimation without using the method to construct solutions. Let w ∈ W^1,2(T) be a solution for Q ∈ L²(0, X) and w₀ ∈ W^1,2(0, 2X). By applying Stokes's theorem to over T₀, we have Since |w|² ≥ |w^†Qw|, we conclude that which gives the uniqueness for the case of w₀ ∈ W^1,2(0, 2X).

The existence and uniqueness of a weak solution for a general w₀ ∈ L²(0, 2X) follows from a simple change of variables. For given w₀ ∈ L²(0, 2X), we define Then above argument implies that there exists unique solving (4.1) for the boundary data . That is, for any test function ϕ, since ϕ_t is also a test function. Integration by parts yields Thus, solves (4.3) for w₀ ∈ L². The energy estimation (4.3) follows from (4.4).

To derive (4.5), we consider a sequence {w_0,n} ⊂ W^1,1(0, 2X) converging to w₀ in L² and Let w_n(x, t) be the solution of (4.1) with boundary data w_0,n. Then for any test vector function such that Since w_n(x, ·) converges to w(x, ·) in L²(x, 2X − x), sending n to the infinity and taking supremum over all such φ yields (4.5).