Recovery of the integral kernel in the kinetic fragmentation equation

Abstract

Recovery of the fragmentation kernel for the time-dependent fragmentation kinetics is a nonlinear inverse problem. We propose a new method for such a recovery based on the transformation of the problem to the inverse problem for the right-hand side of the equation with a modified linear operator. To minimize the variational functional, we develop an algorithm based on the system of three equations: the direct, adjoint and control equations. Then working backwards we recover the kernel in the original problem. We assume that the only available information are partial observations of the solution at two time instants.

Keywords:

• inverse problems
• integral kernel recovery
• fragmentation kernel
• adjoint equations

AMS Subject Classifications::

• 45Q05
• 65R32
• 86A22

1. Introduction

Consider the fragmentation equation 1: (1)

The general inverse problem is: given c_obs = c(x, T), T < ∞ and c⁽⁰⁾ = c(x, 0) ≥ 0, find c(x, t) and F in (1).

Let F(x, y) = F(x + y), then (1) can be rewritten as

If F ≡ 1 then (2) and the exact solution to (2) is as follows 1: (3) and, then we sought solution c(x, t) is in the neighbourhood of c₀(x, t).

For example for c⁽⁰⁾(x) = e^−sx, (4)

In this article, we address the problem of recovering the fragmentation kernel F assuming that F is in the neighbourhood of a constant. Without loss of generality let the constant be equal to 1. This nonlinear inverse problem should be simplified by the linearization. The necessity of the linearization approach is justified in many publications including the review paper 2. We set F(x) = 1 + f(x), and, to apply the linearization let c = c₀ + g. Then neglecting the terms of the second order, we obtain from (1)

But, in view of (2), and we arrive at the linear equation for g(x, t): (5)

We define the linear operators A as follows:

Let us designate the right-hand side of (5) (6)

Then (5) becomes (7)

In the next section we state the inverse problem and prove uniqueness of the solution, in Section 3 we solve the inverse source problem and find v, the right-hand side of (7). In Section 4 we discuss how to find the fragmentation function f(x). Given v, the problem of solving (6) for f is ill-posed in view of its non-uniqueness. To fix this we introduce the corresponding natural space. In Section 5 we discuss the numerical issues and the results.

2. Uniqueness of the solution

The inverse problem is to find g, v such that: (8)

It it obvious that the inverse problem (8) has an infinitely large number of solutions. To check this it is sufficient to take any smooth function g(x, t), substitute it in (8) and obtain v(x, t). However, under additional constraint it is possible that solution to the inverse problem (8) is unique.

Theorem 1

If f(x) has a distinguished sign then the inverse problem (8) has a unique solution.

Proof

To show that the solution to the inverse problem (8) is unique, it is sufficient to show that the solution to the following problem must lead to g ≡ v ≡ 0: (9)

To solve the partial integrodifferential equation (9) we let h(x, t) = c₀(x, t)f(x) and take the Laplace transform of both sides of the equation. Then

where

Since then the approximated problem becomes: (10)

The solution to (10) is:

Recall that, then, let then,

Since f(x) has a distinguished sign, we can see that H_p also has a distinguished sign and since , H_p has a distinguished sign, and c⁽⁰⁾(x) is nonnegative, then H_p ≡ 0 ∀p ∈  [p₁, p₂], and therefore, the original inverse problem (8) has a unique solution.▪

3. Inverse source problem

Due to the unboundedness of the operator A: L₂[0, ∞) ↦ L₂[0, ∞) where , we will restrict the inverse problem (8) to x ∈ [0, H] where H < ∞.

Let T < ∞, X = [0, H]) × [0, T] , and A be a linear operator from L₂(X) ↦ L₂(X).

Define  = .

Then the inverse problem is to find g, v ∈ L₂(X) such that: (11)

Following 2–4, we consider the correspondence variational problem: find g, v such that the quadratic functional below is minimized: (12)

In this last expression we seek g, v such that the minimum is attained. Here α = constant ≥ 0.

Supposing that the problem (12) has the solution, we get (13) (14) where δv is an independent variation, whereas δg is defined from the corresponding Cauchy problem (15)

We introduce the adjoint equation (16) where A*: L₂(X) ↦ L₂(X)

Let us take the inner product of (15) and q and the inner product of (16) and δg. Subtracting one equation from the other and taking into account the zero initial condition in (15), we obtain

Comparing this expression with (14) we see that we should put (17) then we obtain from (14) the equation (18)

If δv ∈ L₂(X) is arbitrary, we obtain from (18) the so-called control equation (19)

Combining (13), (16), (17) and (19), we arrive at the system of variation equations (20)

On the basis of the above analysis, we conclude that for sufficiently small values α > 0 and under additional constraints the solution to the problem (20) can be regarded as an approximation to the problem (12). Therefore, we now discuss the question concerning the numerical solution to the problem (20).

Following 5 we can consider various iterative algorithms for solving (20) and, thus, finding v(x): where arbitrary initial value v⁰ ∈ L₂(X).

4. Recovery of the fragmentation kernel in the natural space

Given v(x, t), in this section we address Equation (6) to find f(x). Variable t is treated in (6) as a parameter. The principal difficulty in solving (6) is that its solution is non-unique. We show this property and then introduce the natural space in which the solution is unique and, thus, allows to develop the corresponding numerical algorithm.

To find f(x) we differentiate (6) in x and obtain

The functions on the right-hand side of the above expression depend on t but the function f(x) on the left should not depend on t. The terms on right depend on t as an outer parameter. We omit the parameter t for a while.

Here K is a constant to be determined. After integration, (21)

It is easy to see that constant K is equal to f(1, t). However, expression (21) satisfies (6) for any constant K and, thus, solution (21) is non-unique. To show this, we substitute (21) into (6):

In view of the identity (22) we arrive at v(x) = v(x) and see that f(1) cannot be uniquely determined. To investigate this issue, we make in (6) the substitution h = c₀f and now consider the equation: (23)

The adjoint of (23) is written as (24)

The inner product in L₂(0,H] of (23) and j(x) becomes: (25) and the inner product of (24) and h(z) is as follows: (26)

Let us now subtract (26) from (25):

The aim is to find another expression for integral in (23) in terms of p(z).

We want to choose p(x) such that .

Then let (27)

As we see function p depends on x and depends on y. To emphasize this dependency we write p = p(x; y). Then, (24) becomes: (28)

This means j also depends on x and z. So, j = j(x; z).

Definition 1

Natural space generated by equation (23) is the space of Lebesgue's measurable functions h(x) such that the integral exists. Here j(x; z) is the solution to the adjoint equation (28).

Let us now return back and solve (28) taking (27) into account. This is a Volterra equation with a piecewise continuous right-hand side. Consequently, (28) has a unique solution in the space of Lebesgue's integrable functions on each compact set on [0, ∞). We solve (28) and obtain:

Referring to the definition of the natural space, we see that for any x > 0 the improper integral should be bounded. That is why constant K in the solution (21) must be zeroed: K = 0, or f(1) = 0.

Finally, we arrive at the following solution to (6), which is unique in the above-determined natural space: (29)

5. Numerical example

In order to perform the numerical calculations we consider a finite domain where 0 ≤ x ≤ M < ∞. Our approach is to start with a known function f(x) which will be used to compare with our result, then we do the calculations pretending that we do not know the value of f(x).

We use the algorithm developed in the previous sections to calculate the right-hand side v(x), then work backwards to recover f(x, t) based on (29) and finally the value of f(x) will be calculated as the average of f(x, t) over t, that is, .

We solve the forward fragmentation equation numerically over the finite domain for the same initial condition c⁽⁰⁾(x) mentioned earlier and for F ≡ 1. this will be our c₀(x, t).

Recall that our intention is to recover the kernel F(x) = 1 + f(x). We consider the following small f(x):

Recall the right-hand side:

We calculate v(x, t) numerically over the finite domain and based on c₀(x, t) and f(x) from the above. We use this calculation of v(x, t) later on to compare it with the calculated v(x, t) based on our algorithm. We use the algorithm to recover v(x) and then use (29) to calculate f(x, t) and, thus, find the fragmentation kernel.

We use the explicit difference scheme to estimate the derivatives and Simpson's method to estimate the integrals.

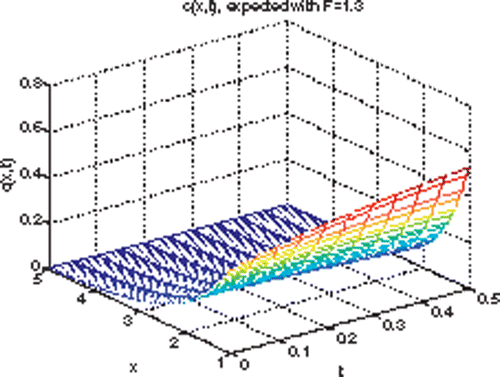
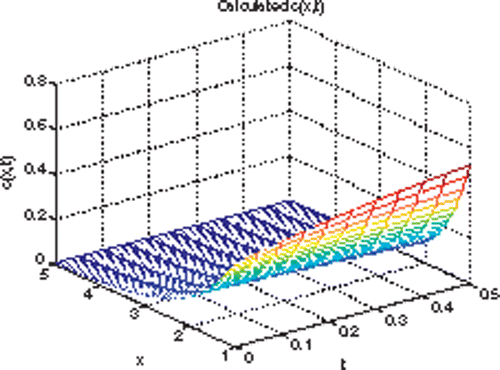
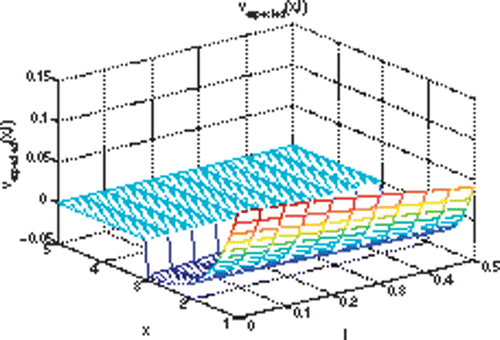
Figures 1–5 clarify our results: Figure 1 shows the expected solution of the forward fragmentation equation with Kernel F = 1.3, 1 ≤ x ≤ 5 and 0 ≤ t ≤ 0.5. This solution was calculated numerically as explained earlier. Figure 2 shows the solution of the inverse fragmentation equation over 1 ≤ x ≤ 5 and 0 ≤ t ≤ 0.5. This solution was calculated based on the algorithm developed in this article. Figure 3 shows the expected solution of the right-hand side v(x, t) over 1 ≤ x ≤ 5 and 0 ≤ t ≤ 0.5, the solution was calculated numerically as follows:

Figure 1. Expected c(x, t).

Figure 2. Calculated c(x, t).

Figure 3. Expected v(x, t).

Figure 4. Calculated v(x, t).

Figure 5. Calculated and exact f (x).

Recall, and we choose

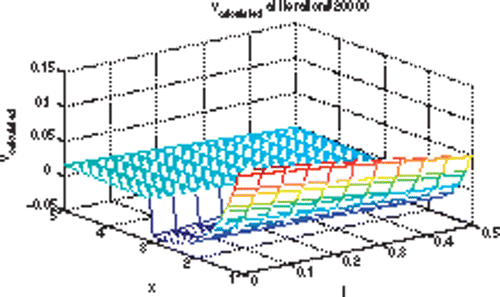
Figure 4 shows the calculated solution of the right-hand side v(x,t) over 1 ≤ x ≤ 5 and 0 ≤ t ≤ 0.5. This calculation was obtained by the algorithm outlined earlier. We can see that the calculated value of the right-hand side v(x, t) in Figure 4 is very close to the exact solution in Figure 3.

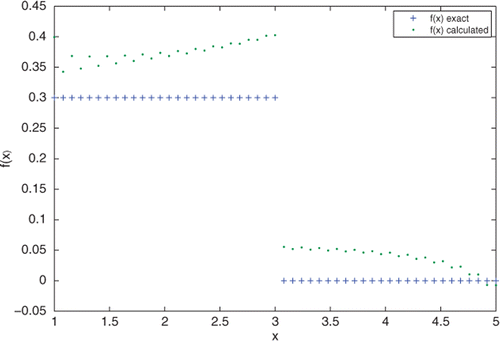
Figure 5 shows a side-by-side comparison between the expected value of f(x) showing in plus signs and the calculated value of f(x) showing in dots over 1 ≤ x ≤ 5. The calculated value of f(x) was obtained by averaging f(x, t) over t. We can see that the calculated value of f(x) is somewhat close to the expected value.

6. Summary

In this article, we have addressed the problem of recovering the integral kernel in the kinetic fragmentation equation. We started with a nonlinear inverse problem which was linearized and transformed to the inverse problem of recovering the right-hand side.

We have developed and justified an algorithm to solve the problem numerically. The recovery of the right-hand side was based on the variational approach leading to a system of three basic equations: original equation, adjoint equation and control equation.

To solve this system, we have analysed the corresponding linear operator, constructed a computational method and implemented this method numerically. In parallel, we have introduced the notion of natural space, then showed that the solution to the problem falls into the natural space and is unique in that space.

The numerical results show a good coincidence of the constructed algorithm and the results of the presented computations.

Acknowledgements

The authors are grateful to the referee for his valuable remarks leading to the improvement of this article.