The inverse determination of the thermal contact resistance components of unidirectionally reinforced composite

Abstract

This article considers the problem of determination of the thermal contact resistance in unidirectionally reinforced composite. The problem formulated in such a way should be treated as an inverse heat transfer problem in a non-homogenous material. The thermal conductivities of constituents (fibres and matrix) and fibre arrangement are known. The calculations are carried out for a composite with the fibres arranged in a matrix in a regular manner by a square grid.

Keywords:

• thermal contact resistance
• inverse heat transfer problem
• boundary collocation method
• Levenberg–Marquardt method

1. Introduction

In the literature, the following problems are considered to be the classical inverse heat conduction problems:

i.	determination of heat sources (e.g. 1–3),
ii.	determination of heat transfer coefficient (e.g. 4–7),
iii.	Cauchy problem (e.g. 8–10),
iv.	determination of temperature-dependent thermal conductivity (e.g. 11,12),
v.	the backward heat conduction problem (BHCP) (e.g. 13,14),
vi.	determination of the shape of the unknown boundaries (e.g. 15,16).

The inverse heat conduction problem considered in this study does not exactly belong to any of the above-mentioned problems (i–vi), but it is the closest to the last problem (vi). However, in this case we are not determining the shape of the boundary, but with a known shape of the boundary between two different materials the thermal contact resistance at this boundary is determined. In contrast to the aforementioned problems applied to homogeneous materials, the problem considered in this article examines composite materials.

The effective thermal conductivity of a composite material has been a topic of theoretical interest for about a century. The first paper on this subject appeared at the end of the nineteenth century 17. Generally speaking, it was found that the effective thermal conductivity was a function of the thermal conductivity, the geometric distribution and the volume fraction of each component. Some of the experimental results 18–20 showed that the effective thermal conductivity of composites can be affected by the thermal barrier resistance at the interface between the individual components, which result from the existence of the interfacial gaps, which are formed mainly because of the mismatch in the thermal expansion coefficients of the constituents during the cooling process of the manufacturing.

Some of the most important composites are fibre-reinforced composites which have been used extensively in many applications from space shuttles to electronic devices. The effective thermal conductivity for a unidirectional fibrous composite is defined by the effective thermal conductivity tensor. This tensor is determined by two independent components, one longitudinal and one transverse. The longitudinal component follows the rule of mixture and is a rather trivial problem. The evaluation of the transverse component, however, is a non-trivial matter and was considered by many authors. The first theoretical paper on the subject of the transverse effective thermal conductivity for a fibrous composite with perfect thermal contact between fibres and matrix was published most likely by Springer and Tsai 21. Afterwards, many papers on the subject of the transverse thermal conductivity for unidirectional fibrous composite have been published and it would be impossible to discuss all of them. We would like to mention only two of them, which are pretty important in our opinion, namely, Perrins et al. 22, and Han and Cosner 23.

There are considerably less papers published on the subject of the transverse thermal conductivity with imperfect thermal contact between the fibres and matrix. The first theoretical paper on the subject of the effective thermal conductivity for a fibrous composite with the interfacial thermal resistance was published by Hasselman and Johnson 24. The authors modified the theory of Rayleigh permitting for the derivation of the expression for the effective thermal conductivity with spherical, cylindrical and flat geometry. Benveniste et al. 25 extended the generalized self-consistent method and applied the Mori–Tanaka method to solve the interfacial thermal contact resistance and coated fibres. The theories 26 related to the spherical inclusions were extended to derive the expression for the longitudinal and transverse effective thermal conductivity of an isotropic matrix uniaxially reinforced with ortrotropic fibres for the finite interfacial thermal conductance values. Nicorovici et al. 27 studied the analytic properties of the effective dielectric constant of square arrays of coated cylinders by the same approach as the one used by Perrins et al. 22. Goncalves and Kołodziej 28 applied the boundary collocation method for the determination of the thermal conductivity in fibrous composites with an imperfect thermal contact between constituents for fibres arranged in square array. Lu and Lin 29 developed the boundary collocation method for three types of problems for the square and the hexagonal arrays: the coated inclusion, the debonded inclusion and the constant resistance problem. The effect of the interfacial characteristics on the effective conductivities of the composites containing randomly distributed aligned long fibres was studied in 30. Two types of interface are considered: one with finite thickness and one with no thickness but with certain thermal barriers. Zou et al. 31 derived an analytical expression for the transverse thermal conductivities of fibre composites with a thermal barrier based on the electrical analogy technique and on the cylindrical filament-square packing array unit cell model. The Hasselman–Johnson model for predicting the effective transverse thermal conductivity of a 2D-SiCf/SiC composite with a fibre–matrix thermal barrier was assessed experimentally and by comparing numerical FEM predictions 32. Agreement within 5% was predicted for composites with fibre volume fractions of 0.5 or less and with fibre-to-matrix conductivity ratios less than 10. The effective thermal conductivity of the nonlinear composite media with a contact resistance was considered in 33. The authors used the nonlinear constitutive equations (the generalized Fourier law) for the matrix and fibre materials. Lee et al. 34 applied a generalized self-consistent method for the calculation of the effective thermal conductivity of the composites with the interfacial contact conductance. In contrast to the studies mentioned above, Drygas and Mityushev 35 applied the method of the functional equations for the calculation of the effective conductivity of the composite with the unidirectional cylinders with the interfacial resistance. Kushch 36 developed an analytical method for a computer simulation of the transverse conductivity of the fibre reinforced composites with a partially debonded matrix–fibre interface. Yan et al. 37, for a unit cell approach, use the eigenfuction expansion-variational method which is in fact a Trefftz method with the special purpose Trefftz functions (which fulfil exactly the boundary conditions on the interfaces between fibre and matrix). Yan et al. 38 proposed a new complex variable method for the two-dimensional steady-state heat conduction problems of cylindrically orthotropic fibres. The method is based on a unit cell for the analysis of the effective thermal conductivity.

In all the papers discussed above, the direct problem related to the determination of the effective thermal conductivity in the fibrous composites with an imperfect thermal contact was considered. We define a direct problem as the determination of the effective thermal conductivity of composite based on a given thermal conductivity of constituents, the geometric distribution and the volume fraction of each component, and the thermal resistant between constituents.

Currently in the literature there are only few papers considering the inverse problem associated with the effective thermal conductivity. In 39, the thermal conductivity of one component of the composite is calculated as an inverse problem from the effective thermal conductivity of the composite taking into account the thermal resistance between the constituents. In 40, the inverse determination of volume fraction of fibres in reinforced composites based on the knowledge of the effective thermal conductivity of the composite and thermal conductivity of constituents was considered.

One way to determine the thermal resistance between the components in the composite is to consider the inverse problem, where we know the coefficients of the thermal conductivity of the components, their volumetric fraction and the effective thermal conductivity coefficient. It is much easier to measure experimentally the effective thermal conductivity of the composite than to determine the thermal resistance between the components in a composite. The first paper, in which the inverse problem for the interfacial barrier conductivity of a composite based on the measured values of the effective thermal conductivity for the spherical inclusions was determined, is 41. The experimental measurements of the interfacial thermal resistance between an epoxy resin and thin nickel wires tight in the mould before the epoxy transfer is described in 42. The heating of the wire was provided by the Joule effect and its temperature was obtained through the recording of its electrical resistance.

The purpose of this article is to propose an analytic-numerical algorithm for the determination of the thermal resistance between the components in a fibrous composite to obtain a given value of the transverse effective thermal conductivity, . Such problem can be treated as a type of inverse problem heat conduction problem for a composite material.

A brief outline of this article is as follows. In Section 2 the algorithm for the inverse problem is considered. Based of this algorithm, the results of the numerical experiment of the determination of the thermal resistance in a composite for a given effective thermal conductivity is considered in Section 3. Concluding remarks are presented in Section 4.

2. Inverse problem: determination of the thermal contact resistance components of composite

In real composite materials, the contact surface between the components is a transitional layer of a certain thickness with the mechanical, thermal and chemical interactions between the components. The transition layer of finite thickness is taken into account in the formulation of contact condition of fibre–matrix in the form of the so-called Kapitza condition: (1) where are the temperature field of the fibre and matrix, respectively, is the thermal conductivity of fibres, is the factor determining the thermal contact resistance components of the composite. When  → 0 we have a case of an ideal insulation, and when  →  there is a perfect contact between the components.

Let us consider a unidirectional composite with fibres arranged in a matrix in a regular, square array with an imperfect thermal contact between the fibre and matrix (Figure 1a), where is the radius of the fibres, is the distance between the neighbouring fibres, , and is the volume fraction of fibres. In this article the concept of representative volume element (RVE), which was introduced in 43 will be used. Here the RVE is the repeated element of the composite (Figure 1).

Figure 1. A unidirectional reinforced fibrous composite with fibre arrangement according to a square array for the imperfect thermal contact between fibre and matrix: (a) general view, (b) formulation of a nondimensional boundary value problem in a repeated element.

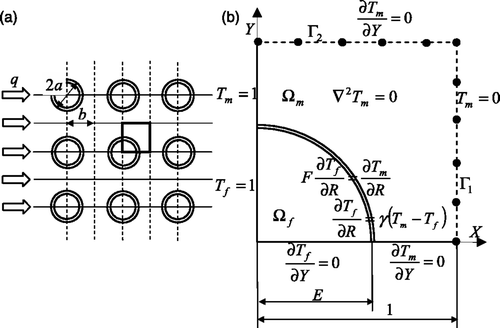
Figure 1(b) shows the formulation of the nondimensional boundary value problem in a repeated element where is the dimensionless resistance number.

The ratio of thermal conductivity of fibres to matrix is denoted as , is the dimensionless radius, are dimensionless Cartesian coordinates, is the dimensionless temperature field, , are the temperature on the left and on the right boundary in a repeated element, respectively.

In order to solve the nondimensional boundary value problem in the repeated element of the composite (Figure 1b), the Trefftz functions and the boundary collocation method are used 44. The general solution of the Laplace equation in the polar coordinate system has the form: (2) where are constants.

After determining strictly some of the constants from the conditions at the bottom and at the left side and from the contact conditions of fibre-matrix of the repeated element (Figure 1b), marking the remaining constants as and cutting off an infinite number of test functions to N expressions, we obtain a solution for the temperature field of the fibre and matrix: (3) (4)

The transverse effective thermal conductivity is defined by the formula: (5) where b is the distance between the isothermal boundaries, is the difference of temperature at the isothermal edges and q is the value of the global heat flux through the unit region of the considered element: (6)

After taking into consideration the definition of the non-dimensional temperature and coordinates in formula (5), the value of effective thermal conductivity with relation to the thermal conductivity of the matrix can be calculated from the relationship: (7) or (8) The constants and the unknown resistance number γ are determined from the boundary conditions: (9) (10) and from the additional condition defined by:

a.	known value of temperature in N3 points located on the matrix:

(11)

a.	known value of the temperature in N3 points located on the upper edge:

(12)

a.	known value of the effective thermal conductivity (8):

(13)

Denoting , from the collocation of the boundary condition (9) in N1 points on the right edge Γ₁, the boundary condition (10) in N2 points on the upper edge Γ₂ and from condition (11) we obtain a system of Ne = N1 + N2 + N3 nonlinear equations in Nu = N + 1 unknowns . Assuming that _, this system of non-linear equations can be solved in least squares sense: (14)

For solving this problem, the Levenberg–Marquardt method can be used according to the following algorithm:

Step 1

Choose initial guess for the fitted parameters .

Step 2

Compute according to formula (12).

Step 3

Pick a modest value for , say .

Step 4

Solve the linear system of equations: (15) where: , ,

Step 5

Evaluate .

Step 6

If , and go to Step 4.

Step 7

If , , update the trial solution .

If , STOP, or go back to Step 4.

The functions are described by conditions (9)–(11), while the derivatives have the following form: and

3. The results of the numerical experiment

The results of the inverse determination of the resistance number can be compared with the results for the direct problem. Figure 2 shows the values of the effective thermal conductivity as a function of the radius fraction of fibres for the assumed value of the coefficient and the resistance number for the direct problem.

Figure 2. The effective thermal conductivity as a function of radius of fibres in the matrix for different values of the ratio of thermal conductivity fibres to the matrix, F, and for different values of resistance number, γ.

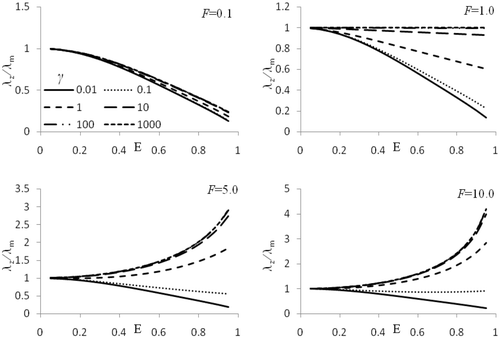
In order to verify the accuracy of the proposed method, two different versions of the additional condition are considered. Its values are known from solving the simple problem for a composite with a known value of the resistance .

In the first test example for the composite with the known fraction of fibres E = 0.7, the knowledge of the temperature at N3 points of the matrix and the effective thermal conductivity of the composite was used. The boundary condition is collocated on the right edge in 6 points and on the upper edge in 5 points. The results of the calculations for various values of the ratio of thermal conductivity of fibres to matrix : and for different number N3 points of the matrix are presented in Table 1.

Table 1. The value of resistance number γ for E = 0.7, for the different values of F for known temperature in M3 points in the matrix and for known λ_z/λ_m.

Datas		Results
		N3 = 10				N3 = 8		N3 = 6		N3 = 5
					Iter		Iter		Iter		Iter
0.1	0.518357	100.00	7.86E−06	3.16E−04	1096	100	130	100.00	1612	0.0073	425
	0.509996	10.00	8.77E−06	3.59E−04	489	10	479	10.00	1097	0.0170	282
	0.474349	1.00	1.07E−05	4.44E−04	54	1	1271	1.00	239	0.0005	1675
	0.446793	0.10	1.16E−05	4.85E−04	12	0.1	24	0.10	71	0.1020	132
	0.442058	0.01	1.17E−05	4.91E−04	93	0.01	113	0.01	180	0.0371	498
1	0.994556	100.00	1.61E−08	1.84E−06	1748	100	1703	100.00	1213	0.0002	1421
	0.949967	10.00	9.78E−08	3.46E−06	1431	10	1369	10.00	1428	0.0001	1604
	0.723159	1.00	3.97E−06	1.56E−04	11	1	12	1.00	14	0.9415	1909
	0.493099	0.10	1.02E−05	4.25E−04	11	0.1	11	0.10	12	0.1002	150
	0.447123	0.01	1.16E−05	4.84E−04	615	0.01	65	0.01	217	0.0130	909
5	1.687394	100.00	1.09E−05	7.80E−04	17	100	17	100.00	17	99.6320	17
	1.639267	10.00	8.42E−06	6.12E−04	14	10	14	10.00	14	0.0003	1394
	1.307356	1.00	2.22E−07	4.27E−05	11	1	11	1.00	12	0.9996	9
	0.672712	0.10	5.50E−06	2.23E−04	10	0.1	11	0.10	11	0.1000	8
	0.469287	0.01	1.09E−05	4.56E−04	11	0.01	20	0.01	40	0.0113	283
10	1.921272	100.00	1.70E−05	1.21E−03	17	100	17	100.00	17	99.6425	219
	1.886550	10.00	1.49E−05	1.07E−03	14	10	14	10.00	14	9.9915	418
	1.613496	1.00	3.90E−06	3.31E−04	11	1	11	1.00	12	0.9998	9
	0.850962	0.10	2.00E−06	7.72E−05	10	0.1	8	0.10	11	0.1000	9
	0.496224	0.01	1.01E−05	4.22E−04	185	0.01	46	0.01	213	0.0105	57

In addition to the error of fulfilling the boundary conditions (columns 4, 5), the columns 6, 8, 10 and 12 of Table 1 contain the number of iterations (Iter) after which the results have been achieved. With one exception, the expected values of the resistance numbers were obtained. Namely, for N3 = 5, the Levenberg–Marquardt method coincided with the error, the unexpected value of resistance number.

In the second test example, the additional condition defines the knowledge of the temperature in the N3 points located on the upper edge of the repeated element and the knowledge of the values of the effective thermal conductivity. These results identify that the resistance number γ (Table 2) are similar when compared with the previous example (Table 1). In this case the Levenberg–Marquardt method is a faster convergent.

Table 2. The value of resistance number γ for E = 0.7, for the different values of F for known temperature in M3 points on the upper boundary and for known λ_z/λ_m.

Datas		Results
		N3 = 10				N3 = 8		N3 = 6		N3 = 5
					Iter		Iter		Iter		Iter
0.1	0.518357	100.00	7.86E−06	3.16E−04	16	100.00	17	100.00	17	98.71	16
	0.509996	10.00	8.77E−06	3.59E−04	13	10.00	13	10.00	14	10.04	18
	0.474349	1.00	1.07E−05	4.44E−04	13	1.00	13	1.00	13	0.99	216
	0.446793	0.10	1.16E−05	4.85E−04	12	0.10	12	0.10	12	0.07	18
	0.442058	0.01	1.17E−05	4.91E−04	12	0.01	12	0.01	12	0.02	119
1	0.994556	100.00	1.61E−08	1.84E−06	20	100.00	20	100.00	20	98.91	20
	0.949967	10.00	9.78E−08	3.46E−06	16	10.00	16	10.00	16	9.98	16
	0.723159	1.00	3.97E−06	1.56E−04	13	1.00	13	1.00	13	1.00	13
	0.493099	0.10	1.02E−05	4.25E−04	11	0.10	11	0.10	11	0.10	11
	0.447123	0.01	1.16E−05	4.84E−04	9	0.01	9	0.01	9	0.01	211
5	1.687394	100.00	1.09E−05	7.80E−04	20	100.00	20	100.00	20	98.82	24
	1.639267	10.00	8.42E−06	6.12E−04	17	10.00	17	10.00	17	9.98	17
	1.307356	1.00	2.22E−07	4.27E−05	13	1.00	13	1.00	13	1.00	12
	0.672712	0.10	5.52E−06	2.24E−04	11	0.10	11	0.10	11	0.10	11
	0.469287	0.01	1.09E−05	4.56E−04	8	0.01	8	0.01	8	0.01	8
10	1.921272	100.00	1.70E−05	1.21E−03	20	100.00	20	100.00	20	98.48	20
	1.886550	10.00	1.49E−05	1.07E−03	17	10.00	17	10.00	17	9.98	17
	1.613496	1.00	3.90E−06	3.31E−04	13	1.00	13	1.00	13	1.00	12
	0.850962	0.10	2.01E−06	7.73E−05	11	0.10	11	0.10	11	0.10	11
	0.496224	0.01	1.01E−05	4.22E−04	8	0.01	8	0.01	8	0.01	168

For the composite with the same thermal conductivity of the fibre and matrix F = 1, and for the effective thermal conductivity close to unity, γ = 100 was determined, which indicates the correctness of the results. For the smallest values of coefficient for all the considered values of F, the calculated value of the resistance number is small γ = 0.01, indicating a high insulation composite.

The test calculations carried out for data from the known exact solutions of the direct problem are a certain idealization of reality. While solving the inverse heat conduction problem in a composite, the input data (known temperature in N3 points) will come from the measurement, which is, as we know not exactly accurate, but disturbed by some error. In order to consider the measuring error, the exact data (from the solution of the direct problem) are loaded with some random disturbance value , where ΔT = 0.1% is a disturbance coefficient and is a random number. The results for the disturbed data for the all test examples, for two forms of the additional condition, in the form of the maximal relative error of fulfilling the boundary conditions are presented in Tables 3 and 4, respectively.

Table 3. The value of resistance number γ for E = 0.7, for the different values of F for known temperature in N3 = 10 points in the matrix and for known λ_z/λ_m for disturbed data ΔT = 0.1%.

Datas		Results
N3 = 10, ΔT = 0.1%
					Iter
0.1	0.518364	46.4075	1.03E−02	2.57E−01	216
	0.510004	11.5292	7.00E−03	1.70E−01	1424
	0.474358	1.0646	5.91E−03	1.44E−01	12
	0.446802	0.1170	4.89E−03	1.01E−01	103
	0.442067	0.0162	3.12E−03	6.04E−02	818
1	0.994556	88.4183	1.08E−03	2.81E−02	131
	0.949967	10.4162	5.63E−03	1.39E−01	2230
	0.723163	0.9863	1.18E−02	2.88E−01	26
	0.493107	0.1003	5.04E−03	1.26E−01	12
	0.447132	0.0091	5.65E−03	1.43E−01	12
5	1.687399	148.0763	1.78E−02	4.35E−01	1423
	1.639269	10.1771	2.97E−03	7.63E−02	1258
	1.307353	0.9948	1.45E−02	3.58E−01	401
	0.672717	0.0997	1.11E−02	2.79E−01	12
	0.469296	0.0095	6.47E−03	1.62E−01	9
10	1.921281	363.9451	5.34E−03	1.33E−01	973
	1.886557	10.4811	1.51E−02	3.69E−01	1743
	1.613494	1.0004	1.52E−02	3.78E−01	14
	0.850965	0.0998	8.91E−03	2.06E−01	143
	0.496232	0.0098	9.49E−03	2.51E−01	210

Table 4. The value of resistance number γ for E = 0.7, for the different values of F for known temperature in N3 = 10 points on the upper boundary and for known λ_z/λ_m for disturbed data ΔT = 0.1%.

Datas		Results
N3 = 10, ΔT = 0.1%
					Iter
0.1	0.518364	114.9104	1.42E−04	1.70E−03	10
	0.510004	10.1615	3.71E−05	1.94E−03	17
	0.474358	1.0169	7.84E−05	5.70E−03	13
	0.446802	0.0893	1.64E−04	5.50E−03	12
	0.442067	0.0150	7.73E−05	3.09E−03	10
1	0.994556	97.2524	1.98E−05	1.13E−03	407
	0.949967	10.0536	2.69E−05	2.73E−03	16
	0.723163	0.9993	1.04E−04	1.25E−03	14
	0.493107	0.1003	8.88E−05	3.16E−03	12
	0.447132	0.0092	2.10E−04	6.23E−03	9
5	1.687399	101.5508	1.26E−04	1.75E−03	352
	1.639269	10.1046	6.54E−05	3.87E−03	18
	1.307353	0.9984	1.09E−04	6.09E−03	14
	0.672717	0.0999	2.63E−05	2.49E−03	12
	0.469296	0.0099	1.04E−04	3.08E−03	9
10	1.921281	–	–	–	–
	1.886557	10.0029	1.44E−04	2.44E−03	18
	1.613494	1.0007	2.29E−05	1.60E−03	14
	0.850965	0.1001	2.11E−05	3.48E−03	11
	0.496232	0.0100	5.58E−05	3.61E−03	9

The inclusion of the measurement error considerably worsens the results of the identification of the resistance number, especially for large values of . As for undisturbed data, more accurate results are obtained for the examples with a known value of temperature in the N3 points situated on the upper boundary of the considered domain of a composite.

For one example (Table 4), i.e.: for F = 10 and the method proved to be divergent.

Table 5 presents the impact of the number of collocation points on the accuracy of the inverse problem of identification of the resistance number γ.

Table 5. The impact of the number of collocation points on the value of the resistance number and the maximum error of fulfilling the boundary conditions at control points.

		,,			,,
3	2	10	7.45E−03	7.96E−02	10	7.13E−04	6.64E−03
4	3	9.99976725	1.64E−03	2.85E−02	10.0000025	1.43E−04	2.14E−03
5	4	9.99994733	3.76E−04	9.42E−03	9.99999798	2.90E−05	6.16E−04
6	5	1.8799939	8.31E−04	6.81E−02	10.0000039	6.17E−06	1.75E−04
7	6	10	7.45E−03	7.96E−02	10.0000846	1.92E−07	1.01E−05
8	7	–	–	–	10.188653	5.11E−03	4.26E−02
		,,			,,
3	2	10	8.58E−03	6.58E−02	10	1.17E−02	8.47E−02
4	3	9.99999937	1.58E−03	1.80E−02	9.99999919	2.12E−03	2.18E−02
5	4	9.99998335	2.77E−04	3.85E−03	10.0000016	3.60E−04	4.03E−03
6	5	10.0000116	4.60E−05	6.10E−04	9.99999056	5.56E−05	3.35E−04
7	6	10.0000139	8.41E−06	6.12E−04	9.99998628	1.49E−05	1.07E−03
8	7	9.17472511	3.35E−03	6.44E−02	10.2050555	1.81E−04	6.01E−03

The best results are obtained for 5 collocation points on the right boundary of the large element, for example, where F = 0.1, and for N1 = 7 points for the other three test examples. The increase in the number of the collocation points does not improve the quality of the results.

An important issue in solving the inverse problem of the identification of resistance number γ is the convergence of the Levenberg–Marquardt iterative method.

Table 6 presents the convergence of the Levenberg–Marquardt method for four test examples.

Table 6. Convergence of the Levenberg–Marquardt method for the four test examples.

	,			,		,		,
Iter			Iter
1	1.68E−03	1.02022	1	8.66E−01	1.21766	1.17E−01	1.9160	7.57E−02	2.0771
2	2.23E−03	1.04077	2	1.32E−01	1.19667	4.62E−02	3.4278	1.64E−02	3.7247
3	3.05E−03	1.06168	3	1.30E−01	2.00207	9.10E−03	5.6657	2.53E−03	6.0614
4	4.02E−03	1.08302	4	1.13E−01	3.82916	8.75E−04	8.1147	2.05E−04	8.4486
5	5.06E−03	1.10482	5	1.36E−02	6.36371	2.23E−05	9.6437	3.70E−06	9.7593
84	1.88E−04	9.15282	6	1.76E−03	8.67281	2.66E−08	9.9873	2.04E−09	9.9942
85	6.36E−06	9.90740	7	2.56E−05	9.82066	4.33E−14	10.0000	6.85E−16	10.0000
86	1.09E−09	9.99865	8	8.23E−09	9.99668	3.53E−24	10.0000	8.93E−29	10.0000
87	8.38E−17	10.0	9	1.48E−15	10.0
88	4.07E−24	10.0	10	2.41E−23	10.0

For F = 0.1 after 88 iterations, the correct result of the identification of the resistance number γ was obtained. For the majority of the tested examples, correct results were obtained with an error after less than 10 iterations.

4. Conclusions

The presented method of determining the resistance number γ of the composite is easy to implement and very effective with the exception of the cases of the maximum fibre density (E = 1), the excellent thermal resistance (β → 0) and the perfect contact (β → ∞) at the border of the components. It can be easily applied to the other configurations of the regular arrangement of fibres in the matrix, for example to a triangular or hexagonal mesh.

To solve the inverse problem of identification of the resistance number γ, two different formulations of the additional condition have been used:

•	the known temperature in some points in the matrix and the known value of the effective thermal conductivity,
•	the known temperature on the upper edge and the known value of the effective thermal conductivity.

The test calculations were carried out for the data from the known exact solutions and also for noisy data with random disturbance which simulate the measurement error. It was shown that the method using the knowledge of the effective thermal conductivity in relation to the thermal conductivity of the matrix λ_z/λ_m and the values of the temperature at several points of the upper edge of the large element is the most accurate for both exact and perturbed data. In addition, the impact of the number of collocation points (N1, N2) on the quality of the results was examined. It turns out that increasing the number of collocation points does not reduce the error of approximation of the boundary conditions while it leads to the ill-conditioning of the system of equations. Because the iterative Levenberg–Marquardt method was used, the convergence had to be considered. The method was not always quickly convergent.

Acknowledgements

Work by J.A. Kołodziej was supported by the grant 4917/B/T02/2010/39.