Numerical reconstruction of unknown boundary data in the Cauchy problem for Laplace’s equation

Abstract

This study explores an application of the quasi-solution and the Fourier methods used to solve a mixed initial-boundary problem involving Laplace’s equation in a rectangle. The problem is reduced to a system consisting of mutually dependent direct and adjoint problems. The explicit formula for the quasi-solution is obtained using the Fourier method. Computational experiments are performed for different types of synthetic data, and admissible parameter ranges are established.

Keywords:

• ill-posed problems
• Laplace’s equation
• inverse problem
• quasisolution method
• Fourier method
• numerical reconstruction

Classification:

• 35J05
• 35P99
• 35R25
• 35R30
• 49K20

1 Introduction

Laplace’s and Poisson’s equations are commonly studied mathematical models used in applications involving both direct and inverse problems. In many practical cases, a whole boundary for a given domain is unavailable, and boundary data cannot be stated explicitly. For instance, in geophysical applications, much of the boundary of an object of interest is not available for measurement. Hence, recovery of the boundary data is an important and practical problem [1, 2]. All possible measurements for the available portion of the boundary are used as additional information. This work concerns the application of Fourier and quasi-solution methods to solve mixed initial-boundary problem using Laplace’s equation in a rectangle. This is a classical inverse problem studied by many authors [3–8]. We consider the same statement given in [5], but we neither minimise the residual functional by any gradient method, nor do we use other iterative methods. Instead, we find a solution to the given problem by using a necessary minimum condition for the residual.

Use of the Fourier method to investigate the Cauchy problem for Laplace’s equation was applied for the first time in [7]. An iterative method used to solve an initial-boundary problem using Laplace’s equation was developed in [6], where initial data were complemented by additional data on one side of the boundary. The quasi-solution method [9] is the most useful method for an investigation of problems of this type [5–10]. By this method, a given inverse problem is reduced to an optimal control problem that can be solved using corresponding techniques. In many cases, the gradient of the residual functional is expressed in terms of the solution to the adjoint problem [3, 5, 10–16].

Therefore, this solution is useful for the numerical calculation of the gradient [3, 5, 6, 10–13]. Under certain conditions, the optimal control can be expressed in terms of the solutions to direct and adjoint problems [11, 16–21]. Necessary optimality conditions lead to the joined system that consists of direct and adjoint problems [16–21]. The solution, if it exists, satisfies the necessary optimality conditions. If the residual functional is convex, then a necessary condition is also sufficient for optimality. To the best of our knowledge, authors of [16, 17, 20] pioneer to use such an approach to an optimal control problem concerning processes in distributed objects. The solvability of a system consisting of mutually dependent direct and adjoint problems was first considered in [21] in the case of the 1D quasi-linear parabolic equation. Further, this problem was investigated in detail in [22]. We are not aware of any reference to the application of Fourier methods for numerical solutions to such systems.

In most cases, optimal control conditions lead to a nonlinear system; therefore, the Fourier method cannot be applied directly. In many cases, the solution to an adjoint problem is used to find a gradient of the functional, but a simultaneous solution for coupled direct and adjoint problems is not considered [3, 5, 6, 10–13].

We consider the same statement as in [5], but we do not minimise the residual functional by any gradient method and do not use other iterative methods, as is done in [5]. Instead, we find a solution to the given problem by using a necessary minimum condition for the residual. The system forms the necessary optimality condition that expresses the equality to zero at the first variation of the functional at the extremum point. In [5], the solution to the adjoint problem is used only to find a gradient of the residual. Compared with [5], the main difference of the presented work is that we directly solve a coupled system consisting of direct and adjoint problems. Then, we obtain an explicit formula for the solution of the given inverse problem. Furthermore, we do not apply any gradient methods to obtain numerical solutions. In [5], only one example of the numerical solution corresponding to the first harmonic has been considered; in the present work, we analyse different cases with a high number of harmonics and a discontinuous sought-for function.

This method makes it possible to realise a large number of numerical simulations and find admissible values of a regularisation parameter in different cases. The explicit formula for the solution allows one to study the solution in detail; this is an additional advantage of the presented method. The problems concerning convexity of the residual functional and sufficient conditions of optimality are outside the scope of this work.

The paper is organised as follows: in Section 2, the statement of the problem is given, and the residual functional is constructed; in Section 3, the explicit formula for the solution to a system consisting of mutually dependent direct and adjoint problems is derived using the Fourier method; and results of computational experiments are presented in Section 4.

2 The statement to the problem

We consider the following problem:

Find the function $U(a,y)$ at the boundary $x=a$ where $U(x,y)$ is the solution to the initial-boundary value problem for Poisson’s equation1 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 Assume that$$\begin{array}{c}\hfill \begin{array}{c}f(x,y)\in C(\overline{\mathrm{\Omega }}),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ q_1(x),q_2(x)\in C[0,a]\hfill \\ p_1(y),p(y)\in C[0,b],\hfill \end{array}\end{array}$$and the following consistence conditions hold true2 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 Let us rewrite the statement (2.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 )-(2.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ). The solution U(x,y) to the problem (2.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 )-(2.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ) can be represented as $U(x,y)=V(x,y)+u(x,y)$, where functions $V(x,y)$ and $u(x,y)$ are the solutions to the problems formulated below:3 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{V}_{xx}+V_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ V(x,0)=q_1(x),V(x,b)=q_2(x),\hfill \\ V(0,y)=p_1(y),\hfill \\ V(a,y)=(1-y/b)q_1(a)+(y/b)q_2(a),\hfill \end{array}\right.\end{array}$$3 and4 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ u(0,y)=0,\hfill \\ u_x(0,y)=p(y)-V_x(0,y)\equiv g(y).\hfill \end{array}\right.\end{array}$$4 Here the function $u(a,y)=r(y)$ is unknown:5 $$\begin{array}{c}\hfill u(a,y)=r(y)-?\end{array}$$5 Then, the sought-for function is expressed as$$\begin{array}{c}\hfill U(a,y)=r(y)+V(a,y)\end{array}$$The problem (2.33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{V}_{xx}+V_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ V(x,0)=q_1(x),V(x,b)=q_2(x),\hfill \\ V(0,y)=p_1(y),\hfill \\ V(a,y)=(1-y/b)q_1(a)+(y/b)q_2(a),\hfill \end{array}\right.\end{array}$$3 ) is a classical statement of the Dirichlet problem for Poisson’s equation and is solved uniquely by $V(x,y)\in C(\overline{\mathrm{\Omega }})\bigcap C^2(\mathrm{\Omega })$. The normal derivative $V_x(0,y)$ on the boundary $x=0$ exists and is continuous [23]. Therefore, the original problem (2.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 )-(2.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ) is reduced to the initial boundary value problem (2.44 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ u(0,y)=0,\hfill \\ u_x(0,y)=p(y)-V_x(0,y)\equiv g(y).\hfill \end{array}\right.\end{array}$$4 ) for Laplace’s equation. Let us apply the quasi-solution method [9] to the problem (2.44 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ u(0,y)=0,\hfill \\ u_x(0,y)=p(y)-V_x(0,y)\equiv g(y).\hfill \end{array}\right.\end{array}$$4 )-(2.55 $$\begin{array}{c}\hfill u(a,y)=r(y)-?\end{array}$$5 ). Namely, the required function $r(y)$ will be found as a solution to the following minimisation problem:6 $$\begin{array}{c}\hfill J(r)=\frac{1}{2}\underset{0}{\overset{b}{\int }}{(u_x(0,y;r)-g(y))}^{2}dy+\frac{1}{2}\mathit{\beta }\underset{0}{\overset{b}{\int }}{r}^2(s)ds\to \underset{r(·)}{min}.\end{array}$$6 Here, the derivative $u_x(x,0;r)$ is obtained by the following: we define the function $r(y)$, use it as a boundary condition at the boundary $y=b$, solve the Dirichlet problem for the function $u(x,y)$, and find $u_x(0,y)$. Here, $\mathit{\beta }>0$ is a regularisation parameter [24].

We consider the following set of admissible functions $r(y$):$$r(y)\in C[0,b],r(0)=0,r(b)=0.$$Let us introduce the following adjoint problem:7 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_{xx}+v_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ v(x,0)=0,v(x,b)=0,\hfill \\ v(0,y)=u_x(0,y,r)-g(y)\hfill \\ v(a,y)=0,\hfill \end{array}\right.\end{array}$$7 Authors of [5] have shown that the solution to the minimisation problem (2.66 $$\begin{array}{c}\hfill J(r)=\frac{1}{2}\underset{0}{\overset{b}{\int }}{(u_x(0,y;r)-g(y))}^{2}dy+\frac{1}{2}\mathit{\beta }\underset{0}{\overset{b}{\int }}{r}^2(s)ds\to \underset{r(·)}{min}.\end{array}$$6 ) is expressed as8 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 Using the formula (2.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) in (2.44 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ u(0,y)=0,\hfill \\ u_x(0,y)=p(y)-V_x(0,y)\equiv g(y).\hfill \end{array}\right.\end{array}$$4 ) as a boundary condition, we obtain the following coupled system of direct and adjoint problems, which need to be solved simultaneously:9 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,\hfill \\ v_{xx}+y_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \end{array}\right.\end{array}$$9 10 $$\begin{array}{c}\hfill \begin{array}{c}v(x,0)=0,v(x,b)=0,\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ v(a,y)=0,u(0,y)=0,\hfill \\ \mathit{\beta }·u(a,y)-v_x(a,y)=0,\hfill \\ u_x(0,y;r)-v(0,y)=g(y).\hfill \end{array}\end{array}$$10

3 The solution to the problem

The problem (2.99 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,\hfill \\ v_{xx}+y_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \end{array}\right.\end{array}$$9 )-(2.1010 $$\begin{array}{c}\hfill \begin{array}{c}v(x,0)=0,v(x,b)=0,\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ v(a,y)=0,u(0,y)=0,\hfill \\ \mathit{\beta }·u(a,y)-v_x(a,y)=0,\hfill \\ u_x(0,y;r)-v(0,y)=g(y).\hfill \end{array}\end{array}$$10 ) is a linear one. As the Fourier method is useful in solving linear problems, we shall apply it. First, we follow the standard procedure by separating the variables. Then, we find the function $u(x,y)$ in the following form:11 $$\begin{array}{c}\hfill u(x,y)=\sum _1^{\infty }[a_{k}cosh(\mathit{\pi }kx/b)+b_{k}sinh(\mathit{\pi }kx/b)]sin(\mathit{\pi }ky/b).\end{array}$$11 Analogously, do the same for v(x,y):12 $$\begin{array}{c}\hfill v(x,y)=\sum _1^{\infty }{c}_{k}sinh(\mathit{\pi }k(x-a)/b)sin(\mathit{\pi }ky/b)\end{array}$$12 The presentation (3.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 ), (3.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ) automatically obeys the conditions for $u(x,y)$ and $v(x,y)$ at the boundaries $y=0,y=b$, and the boundary condition for the function $v(a,y)$. Now, we find the coefficients of the series (3.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 ) and (3.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ) to satisfy the conditions for $u(0,y),u(a,y),v(0,x)$. Let the function $g(y)$ be represented by its Fourier series, which exists based on the assumptions, as follows:13 $$\begin{array}{c}\hfill g(y)=\sum _1^{\infty }{g}_{k}sin(\mathit{\pi }ky/b).\end{array}$$13 Next, we substitute the above formulas into the boundary conditions: $x=0$. Then, we have:$$u(0,y)=\sum _1^{\infty }{a}_{k}sin(\mathit{\pi }ky/b)=0.$$This yields$$a_k=0,k=1,2,...,$$Now, by writing (3.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 ) and (3.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ) for $x=0$ and $x=a$, and taking derivatives, we obtain the following expressions:14 $$\begin{array}{c}\hfill \begin{array}{c}v(0,y)=-\sum _1^{\infty }{c}_{k}sinh(\mathit{\pi }ka/b)sin(\mathit{\pi }ky/b)\hfill \\ u_x(x,y)=\sum _1^{\infty }{b}_k\frac{\mathit{\pi }k}{b}cosh(\mathit{\pi }kx/b)sin(\mathit{\pi }ky/b)\hfill \\ u_x(0,y)=\sum _1^{\infty }{b}_k\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }ky/b)\hfill \\ v_x(x,y)=\sum _1^{\infty }{c}_k\frac{\mathit{\pi }k}{b}cosh(\mathit{\pi }k(x-a)/b)sin(\mathit{\pi }ky/b)\hfill \\ v_x(a,y)=\sum _1^{\infty }{c}_k\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }ky/b)\hfill \end{array}\end{array}$$14 Next, we substitute the above formulas into the boundary conditions:15 $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\beta }u(a,y)-v_x(a,y)=\sum _1^{\infty }[b_k\mathit{\beta }sinh(\mathit{\pi }ka/b)-c_k\frac{\mathit{\pi }k}{b}]sin(\mathit{\pi }ky/b)=0,\hfill \\ u_x(0,y)-v(0,y)=\sum _1^{\infty }[b_k\frac{\mathit{\pi }k}{b}+c_{k}sinh(\mathit{\pi }ka/b)]sin(\mathit{\pi }ky/b)=\sum _1^{\infty }{g}_{k}sin(\mathit{\pi }ky/b).\hfill \end{array}\end{array}$$15 Using (3.55 $$\begin{array}{c}\hfill u(a,y)=r(y)-?\end{array}$$5 ), we obtain a linear algebraic system defining $b_k$ and $c_k$:16 $$\begin{array}{c}\hfill \begin{array}{c}{b}_k\mathit{\beta }sinh(\mathit{\pi }ka/b)-c_k\mathit{\pi }k/b=0,\hfill \\ b_k\mathit{\pi }k/b+c_{k}sinh(\mathit{\pi }ka/b)=g_k.\hfill \end{array}\end{array}$$16 The explicit formula for the solution is17 $$\begin{array}{c}\hfill \begin{array}{c}{b}_k=\frac{g_k\mathit{\pi }k/b}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}\hfill \\ c_k=\frac{g_k\mathit{\beta }sinh(\mathit{\pi }ka/b)}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}\hfill \end{array}\end{array}$$17 Now, we are ready to determine the sought-for function r(y) using the formula (2.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ):18 $$\begin{array}{c}\hfill \begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)={\mathit{\beta }}^{-1}\sum _1^{\infty }{c}_k\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }ky/b)\\ \hfill ={\mathit{\beta }}^{-1}\sum _1^{\infty }\frac{g_k\mathit{\beta }sinh(\mathit{\pi }ka/b)}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}·\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }ky/b)\\ \hfill =\sum _1^{\infty }\frac{g_{k}sinh(\mathit{\pi }ka/b)}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}·\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }ky/b)\end{array}\end{array}$$18 However, we have to justify the convergence of the series (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ). First, we need to estimate the order of diminishing coefficients. We take into account that for sufficiently large values of $k$ we have$$\begin{array}{c}\hfill sinh(\mathit{\pi }ka/b)\approx exp(\mathit{\pi }ka/b)/2.\end{array}$$Then, for large $k$ it holds that:19 $$\begin{array}{c}\hfill r_k\approx \frac{2exp(-\mathit{\pi }ka/b)}{\mathit{\beta }}\frac{\mathit{\pi }k}{b}{g}_k.\end{array}$$19 The estimate above guarantees the convergence of the series (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) for each $\mathit{\beta }>0$ because $g(y)$ belongs to $C[0,b]\subset L_2[0,b]$. As a by-product of the formula (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ), we obtain an estimate for $r(y)$ in terms of $g(y)$ as follows:20 $$\begin{array}{c}\hfill \begin{array}{c}\hfill ∥r∥=\sqrt{\frac{b}{2}\sum _1^{\infty }{\left|r_k\right|}^2}\le \frac{\sqrt{2}\mathit{\pi }}{\mathit{\beta }\sqrt{b}}\sqrt{\sum _1^{\infty }\frac{k^2{g}_k}{{sinh}^2(\mathit{\pi }ka/b)}}\\ \\ \hfill \le \frac{\sqrt{2}\mathit{\pi }}{\mathit{\beta }\sqrt{b}}\sqrt{\sum _1^{\infty }\frac{k^2}{{sinh}^2(\mathit{\pi }ka/b)}}∥g∥.\end{array}\end{array}$$20 Here, we have used Holder’s inequality. Because the last sum in the expression (3.1010 $$\begin{array}{c}\hfill \begin{array}{c}v(x,0)=0,v(x,b)=0,\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ v(a,y)=0,u(0,y)=0,\hfill \\ \mathit{\beta }·u(a,y)-v_x(a,y)=0,\hfill \\ u_x(0,y;r)-v(0,y)=g(y).\hfill \end{array}\end{array}$$10 ) is dominated by the integral$$\begin{array}{c}\hfill \underset{1}{\overset{\infty }{\int }}{x}^2{sinh}^{-2}(\mathit{\pi }xa/b)dx,\end{array}$$we obtain the following estimate in $L_2$-norm:21 $$\begin{array}{c}\hfill ∥r∥\le \frac{C(a,b)∥g∥}{\mathit{\beta }}\end{array}$$21 Note that if the set of functions $g(y)$ is restricted by a finite number of harmonics in (3.33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{V}_{xx}+V_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ V(x,0)=q_1(x),V(x,b)=q_2(x),\hfill \\ V(0,y)=p_1(y),\hfill \\ V(a,y)=(1-y/b)q_1(a)+(y/b)q_2(a),\hfill \end{array}\right.\end{array}$$3 ), then the formula (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) covers the case $\mathit{\beta }=0$ as well. It follows from [7] that, in this case, the system (2.99 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,\hfill \\ v_{xx}+y_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \end{array}\right.\end{array}$$9 )-(2.1010 $$\begin{array}{c}\hfill \begin{array}{c}v(x,0)=0,v(x,b)=0,\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ v(a,y)=0,u(0,y)=0,\hfill \\ \mathit{\beta }·u(a,y)-v_x(a,y)=0,\hfill \\ u_x(0,y;r)-v(0,y)=g(y).\hfill \end{array}\end{array}$$10 ) has the only solution $v\equiv 0$, and the initial-boundary problem for the function $u(x,y)$ can be solved independently using the Fourier method as noted above. Then, the solution to the problem (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) is defined for $\mathit{\beta }=0$ and is given by the formula:$$\begin{array}{c}\hfill r(y)=b\sum _1^L\frac{g_{k}sinh(\mathit{\pi }ka/b)}{\mathit{\pi }k}·sin(\mathit{\pi }ky/b)\end{array}$$The value of the functional is defined by a finite number of terms in (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) as well. The functional in this case vanishes; therefore, in the above mentioned finite-dimensional case the formula (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) gives the exact solution.

We now find the expression for the residual functional corresponding to the obtained r(y). Using the last line of (2.1010 $$\begin{array}{c}\hfill \begin{array}{c}v(x,0)=0,v(x,b)=0,\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ v(a,y)=0,u(0,y)=0,\hfill \\ \mathit{\beta }·u(a,y)-v_x(a,y)=0,\hfill \\ u_x(0,y;r)-v(0,y)=g(y).\hfill \end{array}\end{array}$$10 ), we substitute (3.44 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \\ u(x,0)=0,u(x,b)=0,\hfill \\ u(0,y)=0,\hfill \\ u_x(0,y)=p(y)-V_x(0,y)\equiv g(y).\hfill \end{array}\right.\end{array}$$4 ) and (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) into (2.66 $$\begin{array}{c}\hfill J(r)=\frac{1}{2}\underset{0}{\overset{b}{\int }}{(u_x(0,y;r)-g(y))}^{2}dy+\frac{1}{2}\mathit{\beta }\underset{0}{\overset{b}{\int }}{r}^2(s)ds\to \underset{r(·)}{min}.\end{array}$$6 ) and integrate:$$\begin{array}{cc}\hfill J(r)& =\frac{1}{2}\underset{0}{\overset{b}{\int }}{v}^2(0,y)dy+\frac{1}{2}\mathit{\beta }\underset{0}{\overset{b}{\int }}{r}^2(s)ds\hfill \\ & =\frac{b}{4}\sum _0^{\infty }{c}_k^2{sinh}^2(\mathit{\pi }ka/b)+\hfill \\ & \frac{b}{4\mathit{\beta }}\sum _0^{\infty }{c}_k^2\frac{{\mathit{\pi }}^2{k}^2}{b^2}\hfill \\ & =\frac{b}{4}\sum _0^{\infty }{c}_k^2\left({sinh}^2,(\mathit{\pi }ka/b),+,\frac{{\mathit{\pi }}^2{k}^2}{\mathit{\beta }{b}^2}\right).\hfill \end{array}$$Finally, by using expressions (3.77 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_{xx}+v_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ v(x,0)=0,v(x,b)=0,\hfill \\ v(0,y)=u_x(0,y,r)-g(y)\hfill \\ v(a,y)=0,\hfill \end{array}\right.\end{array}$$7 ) for $c_k$, we obtain:$$\begin{array}{c}\hfill J(r)=\frac{b}{4}\sum _0^{\infty }\frac{\mathit{\beta }{g}_k^2{sinh}^2(\mathit{\pi }ka/b)}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}.\end{array}$$If $\mathit{\beta }$ is positive then we can rewrite the formula above in the following form:22 $$\begin{array}{c}\hfill J(r)=\frac{b}{4}\sum _0^{\infty }\frac{g_k^2}{1+{\mathit{\pi }}^2{k}^2/(\mathit{\beta }{b}^2{sinh}^2(\mathit{\pi }ka/b))}.\end{array}$$22 As right hand side of (3.1212 $$\begin{array}{c}\hfill v(x,y)=\sum _1^{\infty }{c}_{k}sinh(\mathit{\pi }k(x-a)/b)sin(\mathit{\pi }ky/b)\end{array}$$12 ) are dominated by $\frac{b}{4}\sum _K^{\infty }{g}_k^2$, these series converge for $\mathit{\beta }>0$ on the given set of $g(y)$.

4 Synthesis of measured data

To solve an inverse problem, we need a synthetic function $g(y)$. First, we define a function $r(y)$ and then solve the direct problem. Then, by using this solution, we calculate its derivative $u_x(0,y)$ and use it as additional information in the inverse problem. We solve the direct problem numerically using the Fourier method with a finite number of harmonics.

Let the function $r(y)$ be presented by its Fourier series:23 $$\begin{array}{c}\hfill r(y)=\sum _1^{\infty }{r}_{k}sin(\mathit{\pi }ky/b),\end{array}$$23 The solution to the direct problem is found using the Fourier method and is given by the following formulas:$$\begin{array}{c}\hfill u(x,y)=\sum _1^{\infty }\frac{r_{k}sinh(\mathit{\pi }kx/a)}{sinh(\mathit{\pi }k)}sin(\mathit{\pi }ky/b).\end{array}$$Then its first derivative is defined as$$\begin{array}{c}\hfill u_x(x,y)=\sum _1^{\infty }\frac{\mathit{\pi }k}{a}\frac{r_{k}cosh(\mathit{\pi }kx/a)}{sinh(\mathit{\pi }k)}sin(\mathit{\pi }ky/b)\end{array}$$Therefore the synthetic function $g(y)$ can be written in the form24 $$\begin{array}{c}\hfill g(y)=u_x(0,y)=\sum _1^L\frac{\mathit{\pi }k}{a}\frac{r_k}{sinh(\mathit{\pi }k)}sin(\mathit{\pi }ky/b)\equiv \sum _1^L{g}_{k}sin(\mathit{\pi }ky/b).\end{array}$$24 Thus, we calculate the Fourier coefficients of the function $r(y)$, find the function $g(y)$,then forget the function $r(y)$, and recover it as if it were unknown.

4.1 Numerical method

Let us describe the numerical algorithm. In our numerical simulations we take values $a=1$ and $b=1$ only, and consider the unknown function at grid points $y_i=i/200,i=0,1,..,200$. The main steps of the numerical method are:

1.

Data synthesis a) Define the function $r(y)$ and a sufficiently large number $L$ of harmonics. In our simulations, we have tested $L=25,40,50,100$ b) Calculate coefficients $r_k,k=1,..,L$ of the series (4.11 $$\begin{array}{c}\hfill \begin{array}{c}{U}_{xx}+U_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ U(x,0)=q_1(x),U(x,b)=q_2(x),\hfill \\ U(0,y)=p_1(y),U_x(0,y)=p(y).\hfill \end{array}\end{array}$$1 ) numerically c) Find $g_k$ by (4.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ): $g_k=\mathit{\pi }k{r}_k{(asinh(\mathit{\pi }k))}^{-1}$

2.

Give the number $M\le L$ of harmonics for the function $r(y)$; calculate $r(y_i)$ using (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) and limiting by a finite number $M$ of harmonics:

$$\begin{array}{c}\hfill r(y_i)=\sum _1^M\frac{g_{k}sinh(\mathit{\pi }ka/b)}{\mathit{\beta }{sinh}^2(\mathit{\pi }ka/b)+{\mathit{\pi }}^2{k}^2/b^2}·\frac{\mathit{\pi }k}{b}sin(\mathit{\pi }k{y}_i/b)\end{array}$$In our numerical simulations, we have used different values of $L$. It turns out that for given cases, the difference between synthetic functions $g(y)$ obtained with $L=40$ and $L>40$ can be neglected; therefore, we use $L=40$.

Due to the linearity of the problem (2.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ) -(2.99 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}+u_{yy}=0,\hfill \\ v_{xx}+y_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b)\hfill \end{array}\right.\end{array}$$9 ), and according to (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ), any linear combination$$\begin{array}{c}\hfill g(y)=\sum _1^J{\mathit{\alpha }}_j{G}_j(y)\end{array}$$corresponds to the linear combination$$\begin{array}{c}\hfill r(y)=\sum _1^J{\mathit{\alpha }}_j{R}_j(y).\end{array}$$Therefore, in our investigation, we can consider the case of unique harmonic such as$$\begin{array}{c}\hfill r(y)=sin(\mathit{\pi }ky/b)\end{array}$$By (4.22 $$\begin{array}{c}\hfill q_1(0)=p_1(0),p_1(b)=q_2(0).\end{array}$$2 ), the $k$-th harmonic is presented in the function $g(y)$ with a coefficient$$\begin{array}{c}\hfill \frac{\mathit{\pi }k}{sinh(\mathit{\pi }k)}\end{array}$$that exponentially decreases with respect to $k$. This yields quality loss in the result when a frequency $k$ increases. When we analyse the formulas (3.88 $$\begin{array}{c}\hfill r(y)={\mathit{\beta }}^{-1}{v}_x(a,y)\end{array}$$8 ), we see that the coefficient corresponding to the frequency number k is equal to$$\begin{array}{c}\hfill \frac{g_k\mathit{\pi }k}{sinh(\mathit{\pi }k)}=\frac{{\mathit{\pi }}^2{k}^2{r}_k}{\mathit{\beta }a{sinh}^2(\mathit{\pi }k)},\end{array}$$and it decreases like$$\begin{array}{c}\hfill \frac{{\mathit{\pi }}^2{k}^{2}exp(-2k\mathit{\pi })}{\mathit{\beta }}.\end{array}$$

Figure 1. The recovery of only harmonic $r(y)=sin(10\mathit{\pi }y)$ for different $\mathit{\beta }$.

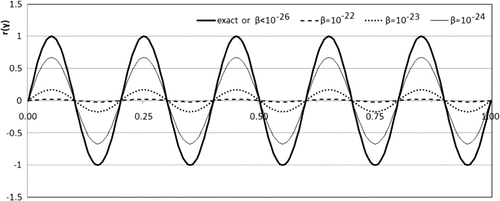
Therefore, to take into account these harmonics, we need to use a small value of $\mathit{\beta }$ for a high $k$. The higher $k$ we consider, the smaller a parameter $\mathit{\beta }$ need be. For instance, when $k=10$ we have obtained an admissible result for $\mathit{\beta }<{10}^{-30}$ only. The numerical results for different values of $\mathit{\beta }$ and $k=10$ are compared in Figure 1.

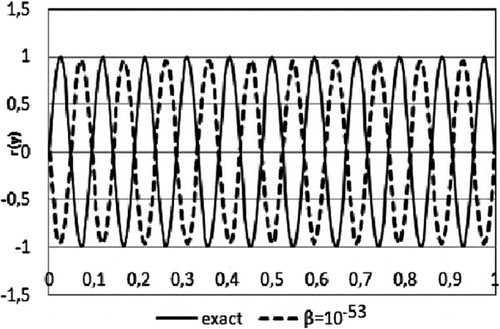
Table 1 contains corresponding values of the parameter $\mathit{\beta }$, frequencies, residual errors, and relative errors in the case $r(y)=sin(\mathit{\pi }ky)$. Here, the relative error is defined as$$\mathit{\delta }=\Vert r_{exact}-r_{recovered}{\Vert }_C/{\Vert r_{exact}\Vert }_C.$$When $16\le k\le 20$, we need to take $\mathit{\beta }$ close to machine precision. However, when we take $k>20$, the method does not work. For example, the result for $k=21$ reveals only the qualitative agreement with an exact solution (see Figure 2).

Table 1. Harmonic’s numbers $k$, corresponding admissible values of $\mathit{\beta }$ and relative errors $\mathit{\delta }$.

$k$	20	19	18	17	16	15	10
$\mathit{\beta }$	${10}^{-53}$	${10}^{-51}$	${10}^{-49}$	${10}^{-45}$	${10}^{-44}$	${10}^{-43}$	${10}^{-30}$
$\mathit{\delta }$	$0.03;$	$2\times {10}^{-2}$	$4\times {10}^{-5}$	$2\times {10}^{-3}$	$6\times {10}^{-5}$	$7\times {10}^{-3}$	$7\times {10}^{-7}$
$J(r)$	${10}^{-53}$	${10}^{-51}$	${10}^{-49}$	${10}^{-45}$	${10}^{-44}$	${10}^{-43}$	${10}^{-30}$
$\mathit{\delta }$ for $\mathit{\beta }=0$	$0.03;$	$3.4\times {10}^{-2}$	$1.5\times {10}^{-4}$	$1.3\times {10}^{-7}$	$1.8\times {10}^{-5}$	$8.5\times {10}^{-3}$	$5.0\times {10}^{-2}$

Figure 2. The recovery of the harmonic $r(y)=sin(21\mathit{\pi }y)$ for $\mathit{\beta }={10}^{-53}$.

Table 2. Relative errors $\mathit{\delta }$ for different parameter $\mathit{\beta }$ in the cases of discontinuous (c1) and smooth (c2) functions $r(y)$

$\mathit{\beta }$	${10}^{-6}$	${10}^{-13}$	${10}^{-14}$	${10}^{-15}$	${10}^{-20}$	${10}^{-24}$	${10}^{-30}$
c1) $\mathit{\delta }$	$0.52$	$0.6$	$0.58$	$0.56$	$0.49$	$0.52$	$0.49$
$J(r)$	${10}^{-6}$	${10}^{-13}$	${10}^{-14}$	${10}^{-15}$	${10}^{-20}$	${10}^{-24}$	${10}^{-30}$
c2) $\mathit{\delta }$	$1.0$	$0.6$	$0.15$	$0.02$	$3.2·{10}^{-3}$	$2.2$	$>{10}^4$
$J(r)$	${10}^{-6}$	$1.7\times {10}^{-13}$	$5\times {10}^{-14}$	$3.3\times {10}^{-14}$	$3.3\times {10}^{-14}$	$3.3\times {10}^{-14}$	$3.3\times {10}^{-14}$

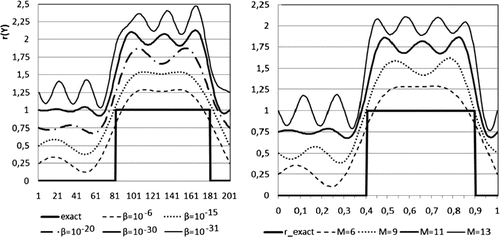
Figure 3. The influence of the regularization parameter $\mathit{\beta }$ and the number of harmonics $M$ to the solution in the case of discontinuous $r(y)$.

Figure 4. The influence of the regularization parameter $\mathit{\beta }$ to the quality of the solution for $r(y)=1-4{(y-0.5)}^2-sin(6\mathit{\pi }y)$.

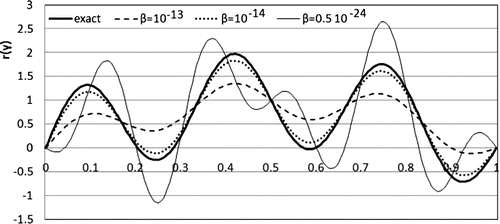
Further, more complicated cases of the function $r(y)$ are considered. We take up well-behaved functions $r$ as well as a discontinuous one. Relative errors for these two cases are compared in Table 2. It turns out that due to round-off errors, the case of small values of $\mathit{\beta }$ yields numerical instability for $M>20$. The use of $\mathit{\beta }<{10}^{-15}$ is not worthwhile (Figure 3, left). In Figure 3, for the sake of clarity, graphs corresponding to different parameters are shifted vertically.

Our numerical simulations show that in the case of strictly positive $\mathit{\beta }>0$, we need to limit the number of harmonics to no more than 15–18. Only in this case does the required function recover with satisfactory quality.

The case $\mathit{\beta }=0$ is considered as well. We recover the solution using the formula (3.77 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_{xx}+v_{yy}=0,(x,y)\in \mathrm{\Omega }=(0,a)\times (0,b),\hfill \\ v(x,0)=0,v(x,b)=0,\hfill \\ v(0,y)=u_x(0,y,r)-g(y)\hfill \\ v(a,y)=0,\hfill \end{array}\right.\end{array}$$7 ). Acceptable results are obtained for $M\le 13$ only.

The results in the case of discontinuous r(y) with $\mathit{\beta }=0$ and $M=11$ are similar to those with $\mathit{\beta }={10}^{-30}$ and $M=25$. The corresponding graphs are depicted in Figure 3. However, when the function $r(y)$ is a linear combination of no more than $M$ harmonics, the quality of recovery is high enough.

Numerical experiments show that the use of small $\mathit{\beta }\sim {10}^{-15}$ is preferable to $\mathit{\beta }=0$. From a practical point of view, if, by analysing the measured data $g(y)$ and other reasonable additional information, we estimate that the contribution of high harmonics with $k>15$ can be neglected, then we can choose the parameter $\mathit{\beta }\sim {10}^{-15}$ (Figure 4).

5 Conclusions

In our opinion, use of the Fourier method is an efficient way to solve the given problem. We can choose to either use it directly or to apply it using a quasi-solution approach. Numerical simulations show that the use of small $\mathit{\beta }>0$ leads to better results than applying the Fourier method directly by taking $\mathit{\beta }=0$. In addition, the case $\mathit{\beta }>0$ lets us consider a greater number of harmonics. We have determined more admissible values of the main parameters such as a harmonic number and a regularisation parameter. It turns out that the most useful range for $\mathit{\beta }$ is above ${10}^{-15}-{10}^{-16}$, and the most useful range for $M$ is 15–18.

Acknowledgments

The author is grateful to professors M. Otelbaev, T.S. Kalmenov, B.E. Kanguzhin, and M.A. Sadybekov and to other participants of the Fundamental Mathematics Seminar in Almaty, Kazakhstan for their attention to this work and for valuable discussion related to this work. The author is also grateful to the anonymous reviewers for their valuable comments that helped to improve the manuscript. This work has been supported by the Ministry of Education and Science of the Republic of Kazakhstan, grant number 1631-29.09.2012.