Numerical reconstruction in a three-spectra inverse Sturm–Liouville problem with mixed boundary conditions

Abstract

This paper proposes an algorithm for the numerical reconstruction of the coefficient (also called ‘potential’) function $q$ in the canonical Sturm–Liouville differential operator $L^{(q)}[u]:=-u^{\prime \prime }+q(x)u$ from three known sequences of its eigenvalues. These correspond respectively to three sets of mixed boundary conditions: Dirichlet type for the interval $[0,a]$, Dirichlet–Robin type for the interval $[0,a_0]$ and Robin–Dirichlet type for the interval $[a_0,a]$, where $a_0$ is an interior point of the interval $[0,a]$. This problem originates in an engineering application involving a string and its frequencies of oscillations when set into vibration. The method will be illustrated with numerical examples including both continuous and discontinuous potential functions.

Keywords:

• inverse Sturm–Liouville problem
• spectra
• Goursat boundary value problem
• Gelfand–Levitan–Marchenko kernel

AMS Subject Classifications:

• 34A55
• 34B24
• 34L20

Introduction

This paper proposes an algorithm to numerically reconstruct the unknown potential of the canonical Sturm–Liouville operator from three spectra, corresponding to three sets of mixed boundary conditions. This problem originates in the following vibrating string problem: an elastic, inaccessible string of negligible weight fixed at the end points is set into infinitesimal vertical vibrations. Its frequencies of oscillation are measured. Next, two more sets of frequencies of oscillation are measured, one set for each piece of the string, when the string has now an interior node attached to a spring with a known stiffness constant. Each piece of the string is set into infinitesimal, vertical vibrations independently of the other. From these measurements, one would like to determine the density of the string. Some details about problems of this type can be found in [1, Section 10.1].

Physical and mathematical arguments turn this problem into the following inverse spectral problem: obtain the coefficient (also called ‘potential’) function $q$ of the canonical Sturm–Liouville differential operator $L^{(q)}[u]:=-u^{\prime \prime }+q(x)u$ from three known sequences of real numbers with specific properties $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, and $\{\mathit{\nu }{\}}_{n\ge 1}$. These sequences will be the eigenvalues of the Sturm–Liouville operator mentioned above corresponding respectively to Dirichlet type boundary conditions on $[0,a]$, Dirichlet–Robin type boundary conditions on $[0,a_0]$, and Robin–Dirichlet type boundary conditions on $[a_0,a]$, where $a_0$ is an interior point of $[0,a]$, and the boundary parameter $H$ at the interior point $a_0$ being a given real number. Specifically, $\mathit{\lambda }$, $\mathit{\mu }$ and $\mathit{\nu }$ are respectively eigenvalues of such type, if there exist some non-identically zero functions (called eigenfunctions) $u\in H^2(0,a)$, $v\in H^2(0,a_0)$, $w\in H^2(a_0,a)$ such that:(1.1) $$\begin{array}{cc}\hfill & \{\begin{array}{cc}-u^{\prime \prime }(x)+q(x)u(x)=\mathit{\lambda }u(x),\hfill & x\in (0,a)\hfill \\ u(0)=0=u(a),\hfill \end{array}\hfill \end{array}$$(1.1) (1.2) $$\begin{array}{cc}\hfill & \{\begin{array}{cc}-v^{\prime \prime }(x)+q(x)v(x)=\mathit{\mu }v(x),\hfill & x\in (0,a_0)\hfill \\ v(0)=0=v^{\prime }(a_0)+Hv(a_0),\hfill \end{array}\hfill \end{array}$$(1.2) (1.3) $$\begin{array}{cc}\hfill & \{\begin{array}{cc}-w^{\prime \prime }(x)+q(x)w(x)=\mathit{\nu }w(x),\hfill & x\in (a_0,a)\hfill \\ w^{\prime }(a_0)+Hw(a_0)=0=w(a).\hfill \end{array}\hfill \end{array}$$(1.3) Here $H^2(a,b):=\{u\in C^1[a,b]:u^{\prime }(x)=\mathit{\alpha }+{\int }_a^{x}v(s)\mathit{ds}$, for some constant $\mathit{\alpha }$ and some $v\in L^2(a,b)\}$.

The overview of the method proposed is as follows (the meaning of the notations and concepts, and the details of the method will be provided in the subsequent sections). If $q$ is the unknown coefficient function of the canonical Sturm–Liouville operator to be recovered from the three types of eigenvalue sequences $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$ and $\{\mathit{\nu }{\}}_{n\ge 1}$, then these sequences will be respectively the zeros of the characteristic function for each type of eigenvalue problem (), (), or (). This information along with the following identity:(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) will suggest a way of obtaining two pairs of Cauchy data. One pair will correspond to $q_1:=q{|}_{[0,a_0]}$ and the other to ${\stackrel{\sim }{q}}_2$ which is the ‘reflection’ of $q_2:=q{|}_{[a_0,a]}$ about the line $x=a_0$. Since the recovery of the potential function from one pair of Cauchy data is already known in the literature (see [2]), our efforts will be focused towards determining two pairs of Cauchy data for the interval $[0,a_0]$, by following the guidelines suggested by the characteristic functions and the identity (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ). Once the Cauchy data are obtained, two coefficient functions for $[0,a_0]$ will be produced. Pasting together the first with the ‘reflection’ of the second, the coefficient function for the entire interval $[0,a]$ will be obtained.

The inverse Sturm–Liouville problem by three Dirichlet spectra (i.e. non-mixed boundary conditions) was discussed in [3]. The present work distinguishes itself from [3] in the following aspects: at the interior node $a_0$ the boundary condition is now of Robin type as opposed to Dirichlet type discussed in [3]; the fundamental identity (2.7) in [3] now becomes (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ) to highlight the characteristic function of the Sturm–Liouville problem with Dirichlet–Robin boundary conditions on the interval $[0,a_0]$. Another difference between [3] and the present work resides in the fact that the kernels in the integral representations of the characteristic functions for the Dirichlet eigenvalue problem and for the Dirichlet–Robin eigenvalue problem on $[0,a_0]$, respectively are different. Also, in [3] the kernel in the integral representation of the characteristic function$$\begin{array}{c}\hfill \mathit{\lambda }\to S(\mathit{\beta };p,\mathit{\lambda })\end{array}$$for the Dirichlet eigenvalue problem on the interval $[\mathit{\alpha },\mathit{\beta }]$, and the kernel in the integral representation of the function$$\begin{array}{c}\hfill \mathit{\lambda }\to S^{\prime }(\mathit{\beta };p,\mathit{\lambda })\end{array}$$were used to infer information about the Cauchy data. By contrast, in the present paper, information about the Cauchy data was obtained from the kernel in the integral representation of the characteristic function$$\begin{array}{c}\hfill \mathit{\lambda }\to S^{\prime }(\mathit{\beta };p,\mathit{\lambda })+h·S(\mathit{\beta };p,\mathit{\lambda })\end{array}$$for the Dirichlet–Robin eigenvalue problem on the interval $[\mathit{\alpha },\mathit{\beta }]$ with boundary parameter $h$, and the kernel in the integral representation of the function$$\begin{array}{c}\hfill \mathit{\lambda }\to S(\mathit{\beta };p,\mathit{\lambda }).\end{array}$$Various aspects on inverse three spectra problems were discussed by many other authors, and we mention here only a few: [4–9].

Preliminaries

Some notations are in order. Let $p\in L_{\mathbb{R}}^2(\mathit{\alpha },\mathit{\beta })$ and $\mathit{\lambda }\in \mathbb{C}$. We denote by $C(·;p,\mathit{\lambda })$ and $S(·;p,\mathit{\lambda })$ the weak (i.e. in $H^2(\mathit{\alpha },\mathit{\beta })$) solutions to the initial value problems:(2.1) $$\begin{array}{c}\hfill \{\begin{array}{c}-u^{\prime \prime }(x)+p(x)u(x)=\mathit{\lambda }u(x),\mathit{\alpha }<x<\mathit{\beta },\hfill \\ u(\mathit{\alpha })-1=0=u^{\prime }(\mathit{\alpha }),\hfill \end{array}\end{array}$$(2.1) and respectively(2.2) $$\begin{array}{c}\hfill \{\begin{array}{c}-u^{\prime \prime }(x)+p(x)u(x)=\mathit{\lambda }u(x),\mathit{\alpha }<x<\mathit{\beta },\hfill \\ u(\mathit{\alpha })=0=u^{\prime }(\mathit{\alpha })-1.\hfill \end{array}\end{array}$$(2.2) The notations were chosen suggestively, to remind of the solutions$$\begin{array}{c}\hfill \cos (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))\text{and}\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\end{array}$$to (2.1(2.1) $$\begin{array}{c}\hfill \{\begin{array}{c}-u^{\prime \prime }(x)+p(x)u(x)=\mathit{\lambda }u(x),\mathit{\alpha }<x<\mathit{\beta },\hfill \\ u(\mathit{\alpha })-1=0=u^{\prime }(\mathit{\alpha }),\hfill \end{array}\end{array}$$(2.1) ) and respectively (), when $p=0$.

Note that $\mathit{\lambda }$ is a Dirichlet–Robin eigenvalue on the interval $[\mathit{\alpha },\mathit{\beta }]$ of the canonical Sturm–Liouville operator $L^{(p)}$ (recall $L^{(p)}[u]:=-u^{\prime \prime }+p(x)u$) with boundary parameter $h$if and only if$$\begin{array}{c}\hfill S^{\prime }(\mathit{\beta };p,\mathit{\lambda })+h·S(\mathit{\beta };p,\mathit{\lambda })=0.\end{array}$$This can be seen as follows. If $\mathit{\lambda }$ is such an eigenvalue, let $u$ be its corresponding eigenfunction. So $u\in H^2(\mathit{\alpha },\mathit{\beta })-\{0\}$ such that $L^{(p)}[u]=\mathit{\lambda }u$, and $u(\mathit{\alpha })=0=u^{\prime }(\mathit{\beta })+h·u(\mathit{\beta })$. Hence, $u^{\prime }(\mathit{\alpha })\ne 0$, since otherwise the Dirichlet boundary condition $u(\mathit{\alpha })=0$ along with the ODE $-u^{\prime \prime }+p(x)u=\mathit{\lambda }u$ would imply that $u=0$. (The initial value problem that consists of this ODE and the initial conditions $u(\mathit{\alpha })=0=u^{\prime }(\mathit{\alpha })$ has only one solution, and the identically zero function is a solution to it). So $v:=\frac{u}{u^{\prime }(\mathit{\alpha })}$ is well defined. Moreover, it satisfies the above ODE since $u$ does. It also satisfies the initial conditions $v(\mathit{\alpha })=0$ and $v^{\prime }(\mathit{\alpha })=1$. Therefore, $v(x)=S(x;p,\mathit{\lambda })$, for all $x\in [\mathit{\alpha },\mathit{\beta }]$, because $S(·;p,\mathit{\lambda })$ is the only solution of this initial value problem. It follows then that$$\begin{array}{cc}\hfill S^{\prime }(\mathit{\beta };p,\mathit{\lambda })+h·S(\mathit{\beta };p,\mathit{\lambda })=& v^{\prime }(\mathit{\beta })+hv(\mathit{\beta })\hfill \\ \hfill =& \frac{u^{\prime }(\mathit{\beta })+hu(\mathit{\beta })}{u^{\prime }(\mathit{\alpha })},\text{by}\text{the}\text{definition}\text{of}v\hfill \\ \hfill =& 0,\text{by}\text{the}\text{property}\text{of}u\text{stated}\text{above}.\hfill \end{array}$$Conversely, if $\mathit{\lambda }$ is such that $S^{\prime }(\mathit{\beta };p,\mathit{\lambda })+h·S(\mathit{\beta };p,\mathit{\lambda })=0$, then by the definition of $S(·;p,\mathit{\lambda })$ above, $S(·;p,\mathit{\lambda })$ will be the eigenfunction corresponding to $\mathit{\lambda }$ for the Dirichlet–Robin boundary conditions. This means that $\mathit{\lambda }$ is a Dirichlet–Robin eigenvalue on $[\mathit{\alpha },\mathit{\beta }]$ of the Sturm–Liouville operator $L^{(p)}$.

So, the Dirichlet–Robin eigenvalues on $[\mathit{\alpha },\mathit{\beta }]$ of $L^{(p)}$ with boundary parameter $h$ are exactly the zeros of the function$$\begin{array}{c}\hfill \mathit{\lambda }\to S^{\prime }(\mathit{\beta };p,\mathit{\lambda })+h·S(\mathit{\beta };p,\mathit{\lambda }).\end{array}$$For this reason this function is called the characteristic function of the canonical Sturm–Liouville operator $L^{(p)}$ on $[\mathit{\alpha },\mathit{\beta }]$ with Dirichlet–Robin boundary conditions and boundary parameter $h$, by analogy with the matrix case. (A linear operator between two finite dimensional spaces can be represented by a matrix).

By similar arguments, the Dirichlet eigenvalues on $[\mathit{\alpha },\mathit{\beta }]$ of $L^{(p)}$ are exactly the zeros of the function$$\begin{array}{c}\hfill \mathit{\lambda }\to S(\mathit{\beta };p,\mathit{\lambda }),\end{array}$$called the characteristic function of the Sturm–Liouville operator $L^{(p)}$ on $[\mathit{\alpha },\mathit{\beta }]$ with Dirichlet boundary conditions.

Another important fact to be used later is that $\{\mathit{\nu },w(x)\}$ is a Robin-Dirichlet eigenpair of the Sturm–Liouville operator $L^{(p)}$ on $[a_0,a]$ with boundary parameter $H$if and only if$\{\stackrel{\sim }{\mathit{\nu }},\stackrel{\sim }{w}(\mathit{\xi })\}$ is a Dirichlet–Robin eigenpair of the Sturm–Liouville operator $L^{(\stackrel{\sim }{p})}$ on $[0,a_0]$ with boundary parameter $\stackrel{\sim }{H}$, where $\stackrel{\sim }{H}:=-\frac{a-a_0}{a_0}H$, $\stackrel{\sim }{\mathit{\nu }}:={(-\frac{a-a_0}{a_0})}^2\mathit{\nu }$, $\stackrel{\sim }{w}(\mathit{\xi }):=w(x)$, $\stackrel{\sim }{p}(\mathit{\xi }):={(-\frac{a-a_0}{a_0})}^{2}p(x)$, with $x:=a-\frac{a-a_0}{a_0}\mathit{\xi }$. (Here $\mathit{\xi }\in [0,a_0]$ and $x\in [a_0,a]$). This statement can be easily verified by the definition of an eigenpair corresponding to Robin-Dirichlet boundary conditions and respectively to Dirichlet–Robin boundary conditions, and the changes of variables indicated above.

It is known in the literature (see [10, p.255] and rescale $[0,1]$ to $[\mathit{\alpha },\mathit{\beta }]$ by the change of variables $x=\mathit{\alpha }+(\mathit{\beta }-\mathit{\alpha })s$, for $s\in [0,1]$) that the spectrum of the canonical Sturm–Liouville operator $L^{(p)}$ on $[\mathit{\alpha },\mathit{\beta }]$ with Dirichlet–Robin boundary conditions and boundary parameter $h\in \mathbb{R}$ is a sequence of real, simple eigenvalues, increasing and satisfying the asymptotic formula:(2.3) $$\begin{array}{c}\hfill {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{\mathit{\beta }-\mathit{\alpha }}\right)}^2+[p]+2\frac{h}{\mathit{\beta }-\mathit{\alpha }}+r_n,\text{for}n\ge 1,\end{array}$$(2.3) where $\{r_n{\}}_{n\ge 1}$ is an $l_2$ sequence of real numbers (i.e. $\sum _{n=1}^{\infty }{r}_n^2<\infty$). Here we denote the mean of $p\in L_{\mathbb{R}}^2(\mathit{\alpha },\mathit{\beta })$ by $[p]$ (i.e. $[p]:=\frac{1}{\mathit{\beta }-\mathit{\alpha }}\underset{\mathit{\alpha }}{\overset{\mathit{\beta }}{\int }}p(x)\mathit{dx}$).

It is also known (see [10, p.256], or [11, Theorem 1 (p.29), Theorem 2 (p.30), Theorem 4 (p.35)], or [12, Lemma 4.7 (p.135-136) and formula (4.25) on p.139], and rescale $[0,1]$ to $[\mathit{\alpha },\mathit{\beta }]$) that the spectrum of the canonical Sturm–Liouville operator $L^{(p)}$ on $[\mathit{\alpha },\mathit{\beta }]$ with Dirichlet boundary conditions is a sequence of real, simple eigenvalues, increasing and satisfying the asymptotic formula:(2.4) $$\begin{array}{c}\hfill {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{\mathit{\beta }-\mathit{\alpha }}\right)}^2+[p]+r_n,\text{for}n\ge 1,\end{array}$$(2.4) where $\{r_n{\}}_{n\ge 1}$ is an $l_2$ sequence of real numbers (i.e. $\sum _{n=1}^{\infty }{r}_n^2<\infty$). Here, as before, $[p]:=\frac{1}{\mathit{\beta }-\mathit{\alpha }}\underset{\mathit{\alpha }}{\overset{\mathit{\beta }}{\int }}p(x)\mathit{dx}$.

Therefore, if $q\in L_{\mathbb{R}}^2(0,a)$ and $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ are respectively the Dirichlet eigenvalues on $[0,a]$, the Dirichlet–Robin eigenvalues on $[0,a_0]$, and the Robin-Dirichlet eigenvalues on $[a_0,a]$ of the Sturm–Liouville operator $L^{(q)}$ with boundary parameter $H\in \mathbb{R}$ at the interior node $a_0$, then letting $q_1:=q{|}_{[0,a_0]}$, $q_2:=q{|}_{[a_0,a]}$ we can write by using () and () with the proper choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$, and the paragraph preceding the paragraph of ():(2.5) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+c_n,\text{for}n\ge 1,\hfill \end{array}$$(2.5) (2.6) $$\begin{array}{cc}\hfill & {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+[q_1]+2\frac{H}{a_0}+c_n^{(1)},\text{for}n\ge 1,\hfill \end{array}$$(2.6) (2.7) $$\begin{array}{cc}\hfill & {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+[{\stackrel{\sim }{q}}_2]+2\frac{\stackrel{\sim }{H}}{a_0}+{\stackrel{\sim }{c}}_n^{(2)},\text{for}n\ge 1,\hfill \end{array}$$(2.7) for some real-valued sequences $\{c_n{\}}_{n\ge 1}$, $\{c_n^{(1)}{\}}_{n\ge 1}$, and $\{{\stackrel{\sim }{c}}_n^{(2)}{\}}_{n\ge 1}$ in $l_2$. Here, ${\stackrel{\sim }{q}}_2(\mathit{\xi }):={(-\frac{a-a_0}{a_0})}^2{q}_2(x)$, for $\mathit{\xi }\in [0,a_0]\leftrightarrow x\in [a_0,a]$ given by $x:=a-\frac{a-a_0}{a_0}\mathit{\xi }$, $\stackrel{\sim }{\mathit{\nu }}:={(-\frac{a-a_0}{a_0})}^2\mathit{\nu }$, and $\stackrel{\sim }{H}:=-\frac{a-a_0}{a_0}H$. Dividing (2.7(2.7) $$\begin{array}{cc}\hfill & {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+[{\stackrel{\sim }{q}}_2]+2\frac{\stackrel{\sim }{H}}{a_0}+{\stackrel{\sim }{c}}_n^{(2)},\text{for}n\ge 1,\hfill \end{array}$$(2.7) ) by ${(-\frac{a-a_0}{a_0})}^2$ we obtain:(2.8) $$\begin{array}{c}\hfill {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+[q_2]-2\frac{H}{a-a_0}+c_n^{(2)},\text{for}n\ge 1,\end{array}$$(2.8) for ${\{c_n^{(2)}:=\frac{{\stackrel{\sim }{c}}_n^{(2)}}{{(-\frac{a-a_0}{a_0})}^2}\}}_{n\ge 1}\in l_2$.

Other important facts here are the integral representations with Gelfand–Levitan–Marchenko kernel of the function $S(·;p,\mathit{\lambda })$ and of its derivative $S^{\prime }(·;p,\mathit{\lambda })$. They are (see [12, Theorem 4.18 and Example 4.19, p.154–157] with similar calculations for $[\mathit{\alpha },\mathit{\beta }]$):(2.9) $$\begin{array}{c}\hfill S(x;p,\mathit{\lambda })=\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}+{\int }_{\mathit{\alpha }}^x\mathcal{K}(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\mathit{\alpha }\le x\le \mathit{\beta },\end{array}$$(2.9) which by differentiating with respect to $x$ gives:(2.10) $$\begin{array}{c}\hfill S^{\prime }(x;p,\mathit{\lambda })\&=\cos (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))+\mathcal{K}(x,x;p)\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\\ \hfill & +{\int }_{\mathit{\alpha }}^x{\mathcal{K}}_x(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\hfill \\ \hfill \&=\cos (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))+(\frac{1}{2}{\int }_{\mathit{\alpha }}^{x}p(s)\mathit{ds})\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\\ \hfill & +{\int }_{\mathit{\alpha }}^x{\mathcal{K}}_x(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\mathit{\alpha }\le x\le \mathit{\beta },\hfill \end{array}$$(2.10) where the Gelfand–Levitan–Marchenko kernel is $\mathcal{K}(x,t;p)$, the week solution to the Goursat boundary value problem:(2.11) $$\begin{array}{c}\hfill \{\begin{array}{cc}{\mathcal{K}}_{\mathit{xx}}-{\mathcal{K}}_{\mathit{tt}}-p(x)\mathcal{K}=0,\hfill & \mathit{\alpha }\le t\le x\le \mathit{\beta }\hfill \\ \mathcal{K}(x,x)=\frac{1}{2}{\int }_{\mathit{\alpha }}^{x}p(s)\mathit{ds},\hfill & \mathit{\alpha }\le x\le \mathit{\beta }\hfill \\ \mathcal{K}(x,\mathit{\alpha })=0,\hfill & \mathit{\alpha }\le x\le \mathit{\beta }.\hfill \end{array}\end{array}$$(2.11) We introduce some notations. For $q\in L_{\mathbb{R}}^2(0,a)$, the subscript $1$ or $2$ attached to $S(·;q,\mathit{\lambda })$ and $C(·;q,\mathit{\lambda })$ is meant to refer to the first subinterval $[0,a_0]$ of $[0,a]$, or to the second subinterval $[a_0,a]$ of $[0,a]$. That is for instance, $S_1(·;q,\mathit{\lambda })$ means $S(·;q{|}_{[0,a_0]},\mathit{\lambda })$, and $C_2(·;q,\mathit{\lambda })$ means $C(·;q{|}_{[a_0,a]},\mathit{\lambda })$. With these being said and $\stackrel{\sim }{\mathit{\lambda }}:={(-\frac{a-a_0}{a_0})}^2\mathit{\lambda }$, and $q_1$, ${\stackrel{\sim }{q}}_2$ as described in the paragraph of Equations (2.5(2.5) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+c_n,\text{for}n\ge 1,\hfill \end{array}$$(2.5) ) –(2.8(2.8) $$\begin{array}{c}\hfill {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+[q_2]-2\frac{H}{a-a_0}+c_n^{(2)},\text{for}n\ge 1,\end{array}$$(2.8) ), we recall Equation (2.7) of [3]:$$\begin{array}{c}\hfill S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+S_1^{\prime }(a_0;q_1,\mathit{\lambda })\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\end{array}$$Since at the interior node $a_0$ we have now a Robin type boundary condition, it is to our benefit to put the above equation into one that highlights the characteristic function of the canonical Sturm–Liouville operator with Dirichlet–Robin boundary conditions on $[0,a_0]$. So we subtract and add $H\frac{a-a_0}{a_0}{S}_1(a_0;q_1,\mathit{\lambda })S_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})$ in the right-hand side of the above equation, and then suitably combine the terms and factor out:$$\begin{array}{cc}\hfill S(a;q,\mathit{\lambda })=& S_1(a_0;q_1,\mathit{\lambda })S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+S_1^{\prime }(a_0;q_1,\mathit{\lambda })\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})\hfill \\ \hfill & -H\frac{a-a_0}{a_0}{S}_1(a_0;q_1,\mathit{\lambda })S_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+H\frac{a-a_0}{a_0}{S}_1(a_0;q_1,\mathit{\lambda })S_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})\hfill \\ \hfill =& S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})-H\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+{\mathit{HS}}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})\hfill \\ \hfill =& S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+{\mathit{HS}}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$which is Equation (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ) mentioned in Section  1. Here $\stackrel{\sim }{H}:=-\frac{a-a_0}{a_0}H$.

The method

Consider the canonical Sturm–Liouville differential operator $L^{(q)}[u]:=-u^{\prime \prime }+q(x)u$ having $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ as its Dirichlet, Dirichlet–Robin and Robin–Dirichlet eigenvalues on $[0,a]$, $[0,a_0]$, and $[a_0,a]$ where the boundary parameter at the interior node $a_0$ is $H\in \mathbb{R}$, a known number. Then, as noted in Section Section12 each sequence is a sequence of real numbers, increasing, the eigenvalues are simple and satisfy (2.5),  (2.6(2.6) $$\begin{array}{cc}\hfill & {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+[q_1]+2\frac{H}{a_0}+c_n^{(1)},\text{for}n\ge 1,\hfill \end{array}$$(2.6) ),  (2.8(2.8) $$\begin{array}{c}\hfill {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+[q_2]-2\frac{H}{a-a_0}+c_n^{(2)},\text{for}n\ge 1,\end{array}$$(2.8) ). It also follows that $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$ are the Dirichlet eigenvalues on $[0,a]$ corresponding to $q$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$ are the Dirichlet–Robin eigenvalues on $[0,a_0]$ corresponding to $q_1$ and boundary parameter $H$, and $\{{\stackrel{\sim }{\mathit{\nu }}}_n{\}}_{n\ge 1}$ are the Dirichlet–Robin eigenvalues on $[0,a_0]$ corresponding to ${\stackrel{\sim }{q}}_2$ and boundary parameter $\stackrel{\sim }{H}$ (see paragraph 5 in Section Section12). These further imply that (see paragraphs 2–4 in Section Section12):(3.1) $$\begin{array}{cc}\hfill & S(a;q,{\mathit{\lambda }}_n)=0,\text{for}n\ge 1,\hfill \end{array}$$(3.1) (3.2) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;q_1,{\mathit{\mu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\mu }}_n)=0,\text{for}n\ge 1,\hfill \end{array}$$(3.2) (3.3) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=0,\text{for}n\ge 1.\hfill \end{array}$$(3.3) Equation (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ) holds as well, and making $\mathit{\lambda }={\mathit{\mu }}_n$ in (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ) and using (3.2(3.2) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;q_1,{\mathit{\mu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\mu }}_n)=0,\text{for}n\ge 1,\hfill \end{array}$$(3.2) ) we obtain:(3.4) $$\begin{array}{c}\hfill S(a;q,{\mathit{\mu }}_n)=S_1(a_0;q_1,{\mathit{\mu }}_n)[S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)],\text{for}n\ge 1.\end{array}$$(3.4) Then making $\mathit{\lambda }={\mathit{\nu }}_n$ in (1.4(1.4) $$\begin{array}{cc}\hfill & S(a;q,\mathit{\lambda })=S_1(a_0;q_1,\mathit{\lambda })[S_1^{\prime }(a_0,{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }})]\hfill \\ \hfill & +[S_1^{\prime }(a_0;q_1,\mathit{\lambda })+H{S}_1(a_0;q_1,\mathit{\lambda })]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,\stackrel{\sim }{\mathit{\lambda }}),\text{for}\text{all}\mathit{\lambda }\in \mathbb{C}.\hfill \end{array}$$(1.4) ) and using (3.3(3.3) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=0,\text{for}n\ge 1.\hfill \end{array}$$(3.3) ) we obtain:(3.5) $$\begin{array}{c}\hfill S(a;q,{\mathit{\nu }}_n)=[S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n),\text{for}n\ge 1.\end{array}$$(3.5) Note that $S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)=0$if and only if${\stackrel{\sim }{\mathit{\mu }}}_n$ is a Dirichlet–Robin eigenvalue corresponding to ${\stackrel{\sim }{q}}_2$ and boundary parameter $\stackrel{\sim }{H}$ (see paragraphs 2–3 in Section Section12), which further happens if and only if${\mathit{\mu }}_n$ is a Robin–Dirichlet eigenvalue corresponding to $q_2$ and boundary parameter $H$ (see paragraph 5 in Section Section12). That means, if and only if${\mathit{\mu }}_n\in \{{\mathit{\nu }}_k{\}}_{k\ge 1}$. But if so, then by () we would have $S(a;q,{\mathit{\mu }}_n)=0$, which means (see paragraph 4 in Section Section12) that ${\mathit{\mu }}_n$ is a Dirichlet eigenvalue corresponding to $q$ (i.e. ${\mathit{\mu }}_n\in \{{\mathit{\lambda }}_k{\}}_{k\ge 1}$).

Also, $S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)=0$if and only if${\mathit{\nu }}_n$ is a Dirichlet–Robin eigenvalue corresponding to $q_1$ and boundary parameter $H$ (see paragraphs 2–3 in Section Section12). That means, if and only if${\mathit{\nu }}_n\in \{{\mathit{\mu }}_k{\}}_{k\ge 1}$. But if so, then by () we would have $S(a;q,{\mathit{\nu }}_n)=0$, which means (see paragraph 4 in Section Section12) that ${\mathit{\nu }}_n$ is a Dirichlet eigenvalue corresponding to $q$ (i.e. ${\mathit{\nu }}_n\in \{{\mathit{\lambda }}_k{\}}_{k\ge 1}$).

For these reasons we shall assume further that no two of the sets $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ overlap. It follows then by (3.4(3.4) $$\begin{array}{c}\hfill S(a;q,{\mathit{\mu }}_n)=S_1(a_0;q_1,{\mathit{\mu }}_n)[S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)],\text{for}n\ge 1.\end{array}$$(3.4) ) and (3.5(3.5) $$\begin{array}{c}\hfill S(a;q,{\mathit{\nu }}_n)=[S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)]\frac{a-a_0}{a_0}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n),\text{for}n\ge 1.\end{array}$$(3.5) ) that the quantities $S_1(a_0;q_1,{\mathit{\mu }}_n)$ and $S_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)$ are well defined. Specifically, they are given by:(3.6) $$\begin{array}{c}\hfill S_1(a_0;q_1,{\mathit{\mu }}_n)=\frac{S(a;q,{\mathit{\mu }}_n)}{S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)},\text{for}n\ge 1,\end{array}$$(3.6) and respectively by:(3.7) $$\begin{array}{c}\hfill S_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=\frac{S(a;q,{\mathit{\nu }}_n)}{S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)}·\frac{a_0}{a-a_0},\text{for}n\ge 1.\end{array}$$(3.7) Let $\mathcal{K}(x,t;q)$, for $0\le t\le x\le a$, $\mathcal{K}(x,t;q_1)$, for $0\le t\le x\le a_0$, and $\mathcal{K}(x,t;{\stackrel{\sim }{q}}_2)$, for $0\le t\le x\le a_0$ be respectively the solutions to the Goursat problems of type () with the appropriate choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$. Then using (2.9(2.9) $$\begin{array}{c}\hfill S(x;p,\mathit{\lambda })=\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}+{\int }_{\mathit{\alpha }}^x\mathcal{K}(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\mathit{\alpha }\le x\le \mathit{\beta },\end{array}$$(2.9) ),  (2.10(2.10) $$\begin{array}{c}\hfill S^{\prime }(x;p,\mathit{\lambda })\&=\cos (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))+\mathcal{K}(x,x;p)\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\\ \hfill & +{\int }_{\mathit{\alpha }}^x{\mathcal{K}}_x(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\hfill \\ \hfill \&=\cos (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))+(\frac{1}{2}{\int }_{\mathit{\alpha }}^{x}p(s)\mathit{ds})\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\\ \hfill & +{\int }_{\mathit{\alpha }}^x{\mathcal{K}}_x(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\mathit{\alpha }\le x\le \mathit{\beta },\hfill \end{array}$$(2.10) ) with $x=\mathit{\beta }$ and the appropriate choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$, and Equations (3.1(3.1) $$\begin{array}{cc}\hfill & S(a;q,{\mathit{\lambda }}_n)=0,\text{for}n\ge 1,\hfill \end{array}$$(3.1) ),  (3.2(3.2) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;q_1,{\mathit{\mu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\mu }}_n)=0,\text{for}n\ge 1,\hfill \end{array}$$(3.2) ),  (3.3(3.3) $$\begin{array}{cc}\hfill & S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=0,\text{for}n\ge 1.\hfill \end{array}$$(3.3) ) we obtain:(3.8) $$\begin{array}{cc}\hfill & 0=\frac{\sin (\sqrt{{\mathit{\lambda }}_n}a)}{\sqrt{{\mathit{\lambda }}_n}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\lambda }}_n}t)}{\sqrt{{\mathit{\lambda }}_n}}\mathit{dt},\text{for}n\ge 1,\hfill \end{array}$$(3.8) (3.9) $$\begin{array}{c}\hfill 0\&=\cos (\sqrt{{\mathit{\mu }}_n}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{q}_1(s)\mathit{ds}+H)\frac{\sin (\sqrt{{\mathit{\mu }}_n}{a}_0)}{\sqrt{{\mathit{\mu }}_n}}\\ \hfill & +{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1))\frac{\sin (\sqrt{{\mathit{\mu }}_n}t)}{\sqrt{{\mathit{\mu }}_n}}\mathit{dt},\text{for}n\ge 1,\hfill \end{array}$$(3.9) (3.10) $$\begin{array}{c}\hfill 0\&=\cos (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{\stackrel{\sim }{q}}_2(s)\mathit{ds}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}}\\ \hfill & +{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2))\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)}{\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}}\mathit{dt},\text{for}n\ge 1.\hfill \end{array}$$(3.10) Multiplying (3.8(3.8) $$\begin{array}{cc}\hfill & 0=\frac{\sin (\sqrt{{\mathit{\lambda }}_n}a)}{\sqrt{{\mathit{\lambda }}_n}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\lambda }}_n}t)}{\sqrt{{\mathit{\lambda }}_n}}\mathit{dt},\text{for}n\ge 1,\hfill \end{array}$$(3.8) ) by $\sqrt{{\mathit{\lambda }}_n}$,  (3.9(3.9) $$\begin{array}{c}\hfill 0\&=\cos (\sqrt{{\mathit{\mu }}_n}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{q}_1(s)\mathit{ds}+H)\frac{\sin (\sqrt{{\mathit{\mu }}_n}{a}_0)}{\sqrt{{\mathit{\mu }}_n}}\\ \hfill & +{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1))\frac{\sin (\sqrt{{\mathit{\mu }}_n}t)}{\sqrt{{\mathit{\mu }}_n}}\mathit{dt},\text{for}n\ge 1,\hfill \end{array}$$(3.9) ) by $\sqrt{{\mathit{\mu }}_n}$, and (3.10(3.10) $$\begin{array}{c}\hfill 0\&=\cos (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{\stackrel{\sim }{q}}_2(s)\mathit{ds}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}}\\ \hfill & +{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2))\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)}{\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}}\mathit{dt},\text{for}n\ge 1.\hfill \end{array}$$(3.10) ) by $\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}$, and solving for the integral terms we obtain:(3.11) $$\begin{array}{c}\hfill {\int }_0^a\mathcal{K}(a,t;q)\sin (\sqrt{{\mathit{\lambda }}_n}t)\mathit{dt}=-\sin (\sqrt{{\mathit{\lambda }}_n}a),\text{for}n\ge 1,\end{array}$$(3.11) (3.12) $$\begin{array}{c}\hfill {\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1))\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=-\sqrt{{\mathit{\mu }}_n}\cos (\sqrt{{\mathit{\mu }}_n}{a}_0)\\ \hfill -(\frac{a_0[q_1]}{2}+H)\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1,\end{array}$$(3.12) (3.13) $$\begin{array}{c}\hfill {\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2))\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}=-\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}\cos (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0)(\frac{a_0[{\stackrel{\sim }{q}}_2]}{2}+\stackrel{\sim }{H})\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1,\end{array}$$(3.13) where $[p]$ stands for the mean of the function $p$.

Letting $l_n^{(1)}$ denote the right-hand side of (3.6(3.6) $$\begin{array}{c}\hfill S_1(a_0;q_1,{\mathit{\mu }}_n)=\frac{S(a;q,{\mathit{\mu }}_n)}{S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)},\text{for}n\ge 1,\end{array}$$(3.6) ), and ${\stackrel{\sim }{l}}_n^{(2)}$ denote the right-hand side of (3.7(3.7) $$\begin{array}{c}\hfill S_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=\frac{S(a;q,{\mathit{\nu }}_n)}{S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)}·\frac{a_0}{a-a_0},\text{for}n\ge 1.\end{array}$$(3.7) ), and in (3.6(3.6) $$\begin{array}{c}\hfill S_1(a_0;q_1,{\mathit{\mu }}_n)=\frac{S(a;q,{\mathit{\mu }}_n)}{S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_n)},\text{for}n\ge 1,\end{array}$$(3.6) ) and (3.7(3.7) $$\begin{array}{c}\hfill S_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\nu }}}_n)=\frac{S(a;q,{\mathit{\nu }}_n)}{S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_n)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_n)}·\frac{a_0}{a-a_0},\text{for}n\ge 1.\end{array}$$(3.7) ) using again (2.9(2.9) $$\begin{array}{c}\hfill S(x;p,\mathit{\lambda })=\frac{\sin (\sqrt{\mathit{\lambda }}(x-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}+{\int }_{\mathit{\alpha }}^x\mathcal{K}(x,t;p)\frac{\sin (\sqrt{\mathit{\lambda }}(t-\mathit{\alpha }))}{\sqrt{\mathit{\lambda }}}\mathit{dt},\mathit{\alpha }\le x\le \mathit{\beta },\end{array}$$(2.9) ) with $x=\mathit{\beta }$ and the appropriate choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$, and solving for the integral terms we obtain:(3.14) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;q_1)\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=l_n^{(1)}\sqrt{{\mathit{\mu }}_n}-\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1\hfill \end{array}$$(3.14) (3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) We note now that solving the system of equations () for ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$, and the system of equations (3.14(3.14) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;q_1)\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=l_n^{(1)}\sqrt{{\mathit{\mu }}_n}-\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1\hfill \end{array}$$(3.14) ) for $\mathcal{K}(a_0,t;q_1)$, we get in the possession of one pair of Cauchy data, namely $\{\mathit{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{\}}$, because $H$ is prescribed. We can even get ${\mathcal{K}}_t(a_0,t;q_1))$ by direct differentiation of $\mathcal{K}(a_0,t;q_1)$. It is actually the pair $\{{\mathit{K}}_{\mathit{t}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{\}}$ that we need in order to use the algorithm in [2] to produce $q_1$.

Also, solving the system of equations () for ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$, and the system of equations (3.15(3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) ) for $\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ we obtain a second pair of Cauchy data, namely $\{\mathit{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{\}}$ from which the pair $\{{\mathit{K}}_{\mathit{t}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{\}}$ is immediately obtained and then used in the algorithm of [2] to produce ${\stackrel{\sim }{q}}_2$.

To solve numerically (3.11(3.11) $$\begin{array}{c}\hfill {\int }_0^a\mathcal{K}(a,t;q)\sin (\sqrt{{\mathit{\lambda }}_n}t)\mathit{dt}=-\sin (\sqrt{{\mathit{\lambda }}_n}a),\text{for}n\ge 1,\end{array}$$(3.11) ) – (3.15(3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) ), we shall use a truncated Fourier series expansion to represent each of the functions $\mathcal{K}(a,t;q)$, ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$, ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$, $\mathcal{K}(a_0,t;q_1)$ and $\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$. What would be an appropriate orthogonal basis of the space $L^2$ in each case? It depends on the known (or otherwise inferred) property of the function and of the eigenvalue sequences. The sequences$\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, and $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ we use for the reconstruction are real-valued, positive, strictly increasing and satisfying the asymptotic formulas:(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) (3.17) $$\begin{array}{cc}\hfill & {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+C_1+d_n^{(1)},\text{for}n\ge 1,\hfill \end{array}$$(3.17) (3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) So, because $\stackrel{\sim }{\mathit{\nu }}:={(-\frac{a-a_0}{a_0})}^2\mathit{\nu }$, the asymptotic formula:(3.19) $$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+{\stackrel{\sim }{C}}_2+{\stackrel{\sim }{d}}_n^{(2)},\text{for}n\ge 1,\end{array}$$(3.19) will hold as well. In (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ) – (3.19(3.19) $$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+{\stackrel{\sim }{C}}_2+{\stackrel{\sim }{d}}_n^{(2)},\text{for}n\ge 1,\end{array}$$(3.19) ), $\{d_n{\}}_{n\ge 1}$, $\{d_n^{(1)}{\}}_{n\ge 1}$, $\{d_n^{(2)}{\}}_{n\ge 1}$ and $\{{\stackrel{\sim }{d}}_n^{(2)}{\}}_{n\ge 1}$ are some $l_2^1$ real-valued sequences, and $M$, $C_1$, $C_2$, ${\stackrel{\sim }{C}}_2$ are real-valued constants related in a specific way (to be discussed at the end of this section).

About $\mathcal{K}(a,t;q)$ we know that:$$\begin{array}{cc}\hfill \mathcal{K}(a,0;q)=0,& \text{(by}\text{the}\text{second}\text{boundary}\text{condition}\text{of}\mathit{bad}\mathit{hbox}\hfill \\ \hfill & \text{with}p:=q\text{and}[\mathit{\alpha },\mathit{\beta }]:=[0,a],\hfill \end{array}$$and that$$\begin{array}{c}\hfill \mathcal{K}(a,a;q)=\frac{1}{2}{\int }_0^{a}q(s)\mathit{ds}=\frac{1}{2}a[q]=\frac{\mathit{aM}}{2}.\end{array}$$The first equality is due to the first boundary condition of () for $p:=q$ and $[\mathit{\alpha },\mathit{\beta }]:=[0,a]$, and the last equality follows by comparing the given asymptotics () with the asymptotics () the ${\mathit{\lambda }}_n$’s are supposed to satisfy, since they are expected to be the Dirichlet eigenvalues on $[0,a]$ corresponding to $q\in L_{\mathbb{R}}^2(0,a)$. From (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ), we have that$$\begin{array}{c}\hfill \sqrt{{\mathit{\lambda }}_n}=\frac{n\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{n}\right),\end{array}$$and so $\sin (\sqrt{{\mathit{\lambda }}_n}t)$ is close to $\sin \left(\frac{n\mathit{\pi }}{a}t\right)$, for $n$ large, making the matrix$$\begin{array}{c}\hfill {[{\int }_0^a\sin (\sqrt{{\mathit{\lambda }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}]}_{i,j}\end{array}$$almost diagonal, so easy to invert. All of these suggest we use $\{\sin \left(\frac{n\mathit{\pi }}{a}t\right){\}}_{n\ge 1}$ as an orthogonal basis of $L_{\mathbb{R}}^2(0,a)$ to represent not $\mathcal{K}(a,t;q)$ but rather $\mathcal{K}(a,t;q)-\frac{M}{2}t$, because both - the basis functions, and this latter function are zero at $t=0$ and $t=a$. Note that$$\begin{array}{c}\hfill {\left\{\sqrt{\frac{2}{a}}\sin \left(\frac{n\mathit{\pi }}{a}t\right)\right\}}_{n\ge 1}\end{array}$$is an orthonormal basis of $L_{\mathbb{R}}^2(0,a)$. (See [13, Example 2(d1), p.308-309].) So we write:(3.20) $$\begin{array}{c}\hfill \mathcal{K}(a,t;q)-\frac{M}{2}t\approx \sum _{j=1}^J{\mathit{\alpha }}_j\sin \left(\frac{j\mathit{\pi }}{a}t\right),\text{for}\text{all}t\in [0,a].\end{array}$$(3.20) Here $J$ is the number of available ${\mathit{\lambda }}_n$’s. Inserting (3.20(3.20) $$\begin{array}{c}\hfill \mathcal{K}(a,t;q)-\frac{M}{2}t\approx \sum _{j=1}^J{\mathit{\alpha }}_j\sin \left(\frac{j\mathit{\pi }}{a}t\right),\text{for}\text{all}t\in [0,a].\end{array}$$(3.20) ) into (3.11(3.11) $$\begin{array}{c}\hfill {\int }_0^a\mathcal{K}(a,t;q)\sin (\sqrt{{\mathit{\lambda }}_n}t)\mathit{dt}=-\sin (\sqrt{{\mathit{\lambda }}_n}a),\text{for}n\ge 1,\end{array}$$(3.11) ), we obtain a linear system to be solved for the Fourier coefficients ${\mathit{\alpha }}_j$’s:(3.21) $$\begin{array}{c}\hfill \sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\lambda }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j\approx -\sin (\sqrt{{\mathit{\lambda }}_i}a)\\ \hfill -\frac{M}{2}·({\int }_0^{a}t\sin (\sqrt{{\mathit{\lambda }}_i}t)\mathit{dt}),\text{for}i=1,\dots ,J.\end{array}$$(3.21) A similar discussion pertains to $\mathcal{K}(a_0,t;q_1)$ and also to $\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$. So we write:(3.22) $$\begin{array}{c}\hfill \mathcal{K}(a_0,t;q_1)-\frac{M_1}{2}t\approx \sum _{j=1}^{J_1}{\mathit{\beta }}_j^{(1)}\sin \left(\frac{j\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$(3.22) where $M_1:=[q_1]$, and $J_1$ is the number of available ${\mathit{\mu }}_n$’s. Also,(3.23) $$\begin{array}{c}\hfill \mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)-\frac{{\stackrel{\sim }{M}}_2}{2}t\approx \sum _{j=1}^{J_2}{\mathit{\beta }}_j^{(2)}\sin \left(\frac{j\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$(3.23) where ${\stackrel{\sim }{M}}_2:=[{\stackrel{\sim }{q}}_2]={(-\frac{a-a_0}{a_0})}^2[q_2]$ (because ${\stackrel{\sim }{q}}_2(\mathit{\xi }):={(-\frac{a-a_0}{a_0})}^2{q}_2(x)$, with $\mathit{\xi }\in [0,a_0]\leftrightarrow x\in [a_0,a]$ given by $x:=a-\frac{a-a_0}{a_0}\mathit{\xi }$ – see the paragraph of () - ()), so ${\stackrel{\sim }{M}}_2={(-\frac{a-a_0}{a_0})}^2{M}_2$, where $M_2:=[q_2]$. Here $J_2$ is the number of available ${\mathit{\nu }}_n$’s (and so of ${\stackrel{\sim }{\mathit{\nu }}}_n$’s). Inserting () into (3.14(3.14) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;q_1)\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=l_n^{(1)}\sqrt{{\mathit{\mu }}_n}-\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1\hfill \end{array}$$(3.14) ), and (3.23(3.23) $$\begin{array}{c}\hfill \mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)-\frac{{\stackrel{\sim }{M}}_2}{2}t\approx \sum _{j=1}^{J_2}{\mathit{\beta }}_j^{(2)}\sin \left(\frac{j\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$(3.23) ) into (3.15(3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) ), we obtain:(3.24) $$\begin{array}{c}\hfill \sum _{j=1}^{J_1}({\int }_0^{a_0}\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a_0}t\right)\mathit{dt}){\mathit{\beta }}_j^{(1)}\approx l_i^{(1)}\sqrt{{\mathit{\mu }}_i}-\sin (\sqrt{{\mathit{\mu }}_i}{a}_0)\frac{M_1}{2}·({\int }_0^{a_0}t\sin (\sqrt{{\mathit{\mu }}_i}t)\mathit{dt}),\text{for}i=1,\dots ,J_1\end{array}$$(3.24) and(3.25) $$\begin{array}{c}\hfill \sum _{j=1}^{J_2}({\int }_0^{a_0}\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}t)\sin \left(\frac{j\mathit{\pi }}{a_0}t\right)\mathit{dt}){\mathit{\beta }}_j^{(2)}\approx {\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{a}_0)\frac{{\stackrel{\sim }{M}}_2}{2}·({\int }_0^{a_0}t\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}t)\mathit{dt}),\text{for}i=1,\dots ,J_2.\end{array}$$(3.25) From (3.14(3.14) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;q_1)\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=l_n^{(1)}\sqrt{{\mathit{\mu }}_n}-\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1\hfill \end{array}$$(3.14) ) we only kept the first $J_1$ equations, and from () only the first $J_2$ equations to make square systems for the unknowns $\{{\mathit{\beta }}_j^{(1)}{\}}_{j=1}^{J_1}$, and respectively $\{{\mathit{\beta }}_j^{(2)}{\}}_{j=1}^{J_2}$. Note that the coefficient matrices in () and ()$$\begin{array}{c}\hfill {[{\int }_0^{a_0}\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a_0}t\right)\mathit{dt}]}_{i,j}\end{array}$$and respectively$$\begin{array}{c}\hfill {[{\int }_0^{a_0}\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}t)\sin \left(\frac{j\mathit{\pi }}{a_0}t\right)\mathit{dt}]}_{i,j}\end{array}$$are no longer almost diagonal, because by () and () we have:$$\begin{array}{c}\hfill \sqrt{{\mathit{\mu }}_n}=\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}+\mathcal{O}\left(\frac{1}{n}\right)\end{array}$$and$$\begin{array}{c}\hfill \sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}=\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}+\mathcal{O}\left(\frac{1}{n}\right),\end{array}$$and so $\sin (\sqrt{{\mathit{\mu }}_n}t)$ and $\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)$ are close to $\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)$, for $n$ large.

Next, the appropriate orthogonal basis for the Fourier series representation of ${\mathit{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{+}\mathit{H}\mathcal{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}$ and of ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ is $\left\{\sin \right(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t){\}}_{n\ge 1}$, because these functions are integrated against $\sin (\sqrt{{\mathit{\mu }}_n}t)$, and respectively $\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)$ (see () and ()), which we showed above are close to$$\begin{array}{c}\hfill \sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right).\end{array}$$The appropriateness of ${\left\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\right\}}_{n\ge 1}$ as an orthogonal basis in $L_{\mathbb{R}}^2(0,a_0)$ is strengthen by the fact that each of ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$ and ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ is zero when $t=0$ (by the second condition of the Goursat problem () with the appropriate choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$), as the functions $\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)$ are. Note that nothing can be said about ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$ and ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ when $t=a_0$. The fact that ${\left\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\right\}}_{n\ge 1}$ is an orthogonal basis of $L_{\mathbb{R}}^2(0,a_0)$ follows from the Auxiliary result 1 with $b=a_0$ (see Section Section17). So we write:(3.26) $$\begin{array}{c}\hfill {\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)\approx \sum _{j=1}^{J_1}{\mathit{\gamma }}_j^{(1)}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$(3.26) and(3.27) $$\begin{array}{c}\hfill {\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\approx \sum _{j=1}^{J_2}{\mathit{\gamma }}_j^{(2)}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0].\end{array}$$(3.27) Inserting () into (), and () into (), and keeping only the first $J_1$ equations from (), and respectively only the first $J_2$ equations from () we obtain two square linear systems to be solved for the Fourier coefficients $\{{\mathit{\gamma }}_j^{(1)}{\}}_{j=1}^{J_1}$ and $\{{\mathit{\gamma }}_j^{(2)}{\}}_{j=1}^{J_2}$, respectively:(3.28) $$\begin{array}{c}\hfill \sum _{j=1}^{J_1}({\int }_0^{a_0}\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}){\mathit{\gamma }}_j^{(1)}\approx -\sqrt{{\mathit{\mu }}_i}\cos (\sqrt{{\mathit{\mu }}_i}{a}_0)(\frac{a_0{M}_1}{2}+H)\sin (\sqrt{{\mathit{\mu }}_i}{a}_0),\text{for}i=1,\dots ,J_1\end{array}$$(3.28) (3.29) $$\begin{array}{c}\hfill \sum _{j=1}^{J_2}({\int }_0^{a_0}\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}){\mathit{\gamma }}_j^{(2)}\approx -\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}\cos (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{a}_0)(\frac{a_0{\stackrel{\sim }{M}}_2}{2}+\stackrel{\sim }{H})\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{a}_0),\text{for}i=1,\dots ,J_2.\end{array}$$(3.29) (Recall that $M_1:=[q_1]$, and ${\stackrel{\sim }{M}}_2:=[{\stackrel{\sim }{q}}_2]$.) The coefficient matrices in () and (), respectively$$\begin{array}{c}\hfill {[{\int }_0^{a_0}\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}]}_{i,j}\end{array}$$$$\begin{array}{c}\hfill {[{\int }_0^{a_0}\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}]}_{i,j}\end{array}$$are almost diagonal because $\sin (\sqrt{{\mathit{\mu }}_n}t)$ and $\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)$ are close to $\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)$, as discussed previously.

A great attention must be paid to $\{l_n^{(1)}{\}}_{n\ge 1}$ and $\{{\stackrel{\sim }{l}}_n^{(2)}{\}}_{n\ge 1}$. The linear systems () and () can be solved for $\{{\mathit{\beta }}_j^{(1)}{\}}_{j=1:J_1}$ and $\{{\mathit{\beta }}_j^{(2)}{\}}_{j=1:J_2}$, respectively only if $l_i^{(1)}$’s and ${\stackrel{\sim }{l}}_i^{(2)}$’s are known. Recall the definitions of $l_n^{(1)}$ and ${\stackrel{\sim }{l}}_n^{(2)}$ in the paragraph of (3.14(3.14) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;q_1)\sin (\sqrt{{\mathit{\mu }}_n}t)\mathit{dt}=l_n^{(1)}\sqrt{{\mathit{\mu }}_n}-\sin (\sqrt{{\mathit{\mu }}_n}{a}_0),\text{for}n\ge 1\hfill \end{array}$$(3.14) ) – (3.15(3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) ). Hence, using also () and () with $x=\mathit{\beta }$ and the appropriate choices of $p$ and $[\mathit{\alpha },\mathit{\beta }]$ we can write:(3.30) $$\begin{array}{c}\hfill \begin{array}{cc}{l}_i^{(1)}\hfill & :=\frac{S(a;q,{\mathit{\mu }}_i)}{S_1^{\prime }(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_i)+\stackrel{\sim }{H}{S}_1(a_0;{\stackrel{\sim }{q}}_2,{\stackrel{\sim }{\mathit{\mu }}}_i)}\hfill \\ \hfill & =\frac{\frac{\sin (\sqrt{{\mathit{\mu }}_i}a)}{\sqrt{{\mathit{\mu }}_i}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\mu }}_i}t)}{\sqrt{{\mathit{\mu }}_i}}\mathit{dt}}{\cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{\stackrel{\sim }{q}}_2(s)\mathit{ds}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}+{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2))\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\mathit{dt}}\hfill \\ \hfill & =\frac{\frac{\sin (\sqrt{{\mathit{\mu }}_i}a)}{\sqrt{{\mathit{\mu }}_i}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\mu }}_i}t)}{\sqrt{{\mathit{\mu }}_i}}\mathit{dt}}{\cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)+(\frac{a_0{\stackrel{\sim }{M}}_2}{2}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}+{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2))\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\mathit{dt}}\hfill \end{array}\end{array}$$(3.30) and respectively(3.31) $$\begin{array}{c}\hfill {\stackrel{\sim }{l}}_i^{(2)}\&:=\frac{S(a;q,{\mathit{\nu }}_i)}{S_1^{\prime }(a_0;q_1,{\mathit{\nu }}_i)+{\mathit{HS}}_1(a_0;q_1,{\mathit{\nu }}_i)}·\frac{a_0}{a-a_0}\\ \hfill & =\frac{\frac{\sin (\sqrt{{\mathit{\nu }}_i}a)}{\sqrt{{\mathit{\nu }}_i}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\mathit{dt}}{\cos (\sqrt{{\mathit{\nu }}_i}{a}_0)+(\frac{1}{2}{\int }_0^{a_0}{q}_1(s)\mathit{ds}+H)\frac{\sin (\sqrt{{\mathit{\nu }}_i}{a}_0)}{\sqrt{{\mathit{\nu }}_i}}+{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1))\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\mathit{dt}}·\frac{a_0}{a-a_0}\hfill \\ \hfill & =\frac{\frac{\sin (\sqrt{{\mathit{\nu }}_i}a)}{\sqrt{{\mathit{\nu }}_i}}+{\int }_0^a\mathcal{K}(a,t;q)\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\mathit{dt}}{\cos (\sqrt{{\mathit{\nu }}_i}{a}_0)+(\frac{a_0{M}_1}{2}+H)\frac{\sin (\sqrt{{\mathit{\nu }}_i}{a}_0)}{\sqrt{{\mathit{\nu }}_i}}+{\int }_0^{a_0}({\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1))\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\mathit{dt}}·\frac{a_0}{a-a_0}\hfill \end{array}$$(3.31) Due to (3.20(3.20) $$\begin{array}{c}\hfill \mathcal{K}(a,t;q)-\frac{M}{2}t\approx \sum _{j=1}^J{\mathit{\alpha }}_j\sin \left(\frac{j\mathit{\pi }}{a}t\right),\text{for}\text{all}t\in [0,a].\end{array}$$(3.20) ),  () and (), Equations () and () become:$$\begin{array}{c}\hfill l_i^{(1)}\approx \frac{\frac{1}{\sqrt{{\mathit{\mu }}_i}}·(\sin (\sqrt{{\mathit{\mu }}_i}a)+\sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j+\frac{M}{2}{\int }_0^{a}t\sin (\sqrt{{\mathit{\mu }}_i}t)\mathit{dt})}{\cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)+(\frac{a_0{\stackrel{\sim }{M}}_2}{2}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}+\sum _{j=1}^{J_2}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(2)}},\end{array}$$and so(3.32) $$\begin{array}{c}\hfill l_i^{(1)}\sqrt{{\mathit{\mu }}_i}\approx \frac{\sin (\sqrt{{\mathit{\mu }}_i}a)+\sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j+\frac{M}{2}{\int }_0^{a}t\sin (\sqrt{{\mathit{\mu }}_i}t)\mathit{dt}}{\cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)+(\frac{a_0{\stackrel{\sim }{M}}_2}{2}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}+\sum _{j=1}^{J_2}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(2)}},\end{array}$$(3.32) and respectively$$\begin{array}{c}\hfill {\stackrel{\sim }{l}}_i^{(2)}\approx \frac{\frac{1}{\sqrt{{\mathit{\nu }}_i}}·(\sin (\sqrt{{\mathit{\nu }}_i}a)+\sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\nu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j+\frac{M}{2}{\int }_0^{a}t\sin (\sqrt{{\mathit{\nu }}_i}t)\mathit{dt})}{\cos (\sqrt{{\mathit{\nu }}_i}{a}_0)+(\frac{a_0{M}_1}{2}+H)\frac{\sin (\sqrt{{\mathit{\nu }}_i}{a}_0)}{\sqrt{{\mathit{\nu }}_i}}+\sum _{j=1}^{J_1}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(1)}}·\frac{a_0}{a-a_0},\end{array}$$and so(3.33) $$\begin{array}{c}\hfill {\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}\approx \frac{\sin (\sqrt{{\mathit{\nu }}_i}a)+\sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\nu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j+\frac{M}{2}{\int }_0^{a}t\sin (\sqrt{{\mathit{\nu }}_i}t)\mathit{dt}}{\cos (\sqrt{{\mathit{\nu }}_i}{a}_0)+(\frac{a_0{M}_1}{2}+H)\frac{\sin (\sqrt{{\mathit{\nu }}_i}{a}_0)}{\sqrt{{\mathit{\nu }}_i}}+\sum _{j=1}^{J_1}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(1)}},\end{array}$$(3.33) because ${\stackrel{\sim }{\mathit{\nu }}}_i:={(-\frac{a-a_0}{a_0})}^2{\mathit{\nu }}_i$. In () and (), the Fourier coefficients $\{{\mathit{\alpha }}_j{\}}_{j=1}^J$, $\{{\mathit{\gamma }}_j^{(1)}{\}}_{j=1}^{J_1}$, $\{{\mathit{\gamma }}_j^{(2)}{\}}_{j=1}^{J_2}$ are the solutions to (),  () and (), respectively. So $\{l_i^{(1)}\sqrt{{\mathit{\mu }}_i}{\}}_{i=1}^{J_1}$ and $\{{\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{\}}_{i=1}^{J_2}$ can be calculated this way, and we can proceed with the calculations of $\{{\mathit{\beta }}_j^{(1)}{\}}_{j=1}^{J_1}$ and $\{{\mathit{\beta }}_j^{(2)}{\}}_{j=1}^{J_2}$ via () and (). Hence, approximations (via truncated Fourier series) for each of $\mathcal{K}(a,t;q)$, ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$, ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$, $\mathcal{K}(a_0,t;q_1)$ and $\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ will be available. Therefore, as mentioned in the two paragraphs immediately following (), $q_1$ and ${\stackrel{\sim }{q}}_2$ are the potential functions on $[0,a_0]$ that correspond to the pair of Cauchy data $\{{\mathit{K}}_{\mathit{t}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{\}}$ and respectively to the pair $\{{\mathit{K}}_{\mathit{t}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{\}}$, and$$\begin{array}{c}\hfill q=\{\begin{array}{cc}{q}_1,\hfill & \text{on}[0,a_0]\hfill \\ q_2,\hfill & \text{on}[a_0,a],\hfill \end{array}\end{array}$$where ${\stackrel{\sim }{q}}_2(\mathit{\xi }):={(-\frac{a-a_0}{a_0})}^2{q}_2(x)$, with $\mathit{\xi }\in [0,a_0]\leftrightarrow x\in [a_0,a]$ given by $x:=a-\frac{a-a_0}{a_0}\mathit{\xi }$.

The information gathered here will serve as a model in Section Section15. We need to say a few words about the relationship between the constants $M$, $C_1$, $C_2$, ${\stackrel{\sim }{C}}_2$ mentioned in ()– (3.19(3.19) $$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+{\stackrel{\sim }{C}}_2+{\stackrel{\sim }{d}}_n^{(2)},\text{for}n\ge 1,\end{array}$$(3.19) ), and how to estimate $[q]$, $[q_1]$, $[q_2]$, from the given asymptotics of ${\mathit{\lambda }}_n$’s, ${\mathit{\mu }}_n$’s, ${\mathit{\nu }}_n$’s. We shall work backwards from (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ) – (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ), since these will be assumed known in the inverse problem. It follows immediately from (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ) and (3.19(3.19) $$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\nu }}}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+{\stackrel{\sim }{C}}_2+{\stackrel{\sim }{d}}_n^{(2)},\text{for}n\ge 1,\end{array}$$(3.19) ) and the definition of ${\stackrel{\sim }{\mathit{\nu }}}_n$ (i.e. ${\stackrel{\sim }{\mathit{\nu }}}_n:={(-\frac{a-a_0}{a_0})}^2{\mathit{\nu }}_n$, for $n\ge 1$) that ${\stackrel{\sim }{C}}_2={(-\frac{a-a_0}{a_0})}^2{C}_2$. Next, comparing (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ) - (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ) with the asymptotics (2.5(2.5) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+c_n,\text{for}n\ge 1,\hfill \end{array}$$(2.5) ),  (2.6(2.6) $$\begin{array}{cc}\hfill & {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2+[q_1]+2\frac{H}{a_0}+c_n^{(1)},\text{for}n\ge 1,\hfill \end{array}$$(2.6) ) and (), the ${\mathit{\lambda }}_n$’s, ${\mathit{\mu }}_n$’s, ${\mathit{\nu }}_n$’s are supposed to satisfy, since they are expected to be the Dirichlet, Dirichlet–Robin and Robin-Dirichlet eigenvalues corresponding to the potential function $q\in L_{\mathbb{R}}^2(0,a)$ and boundary parameter $H\in \mathbb{R}$ on $[0,a]$, $[0,a_0]$ and $[a_0,a]$, respectively, we can write:(3.34) $$\begin{array}{c}\hfill \{\begin{array}{c}M=[q]\hfill \\ C_1=[q_1]+2\frac{H}{a_0}\hfill \\ C_2=[q_2]-2\frac{H}{a-a_0}.\hfill \end{array}\end{array}$$(3.34) Since $a[q]=a_0[q_1]+(a-a_0)[q_2]$, it follows by (3.34(3.34) $$\begin{array}{c}\hfill \{\begin{array}{c}M=[q]\hfill \\ C_1=[q_1]+2\frac{H}{a_0}\hfill \\ C_2=[q_2]-2\frac{H}{a-a_0}.\hfill \end{array}\end{array}$$(3.34) ) that:(3.35) $$\begin{array}{c}\hfill aM=a_0{C}_1+(a-a_0)C_2.\end{array}$$(3.35) Next, from (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ) – (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ) we infer that:$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2)=\underset{n\to \infty }{\lim }(M+d_n)=M,\text{because}\{d_n{\}}_{n\ge 1}\in l_2^1,\end{array}$$$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2)=\underset{n\to \infty }{\lim }(C_1+d_n^{(1)})=C_1,\text{because}\{d_n^{(1)}{\}}_{n\ge 1}\in l_2^1,\end{array}$$$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }({\mathit{\nu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2)=\underset{n\to \infty }{\lim }(C_2+d_n^{(2)})=C_2,\text{because}\{d_n^{(2)}{\}}_{n\ge 1}\in l_2^1.\end{array}$$It follows from these and (3.34(3.34) $$\begin{array}{c}\hfill \{\begin{array}{c}M=[q]\hfill \\ C_1=[q_1]+2\frac{H}{a_0}\hfill \\ C_2=[q_2]-2\frac{H}{a-a_0}.\hfill \end{array}\end{array}$$(3.34) ) that if only $\{{\mathit{\lambda }}_j{\}}_{j=1}^J$, $\{{\mathit{\mu }}_j{\}}_{j=1}^{J_1}$, $\{{\mathit{\nu }}_j{\}}_{j=1}^{J_2}$ are available, then:$$\begin{array}{c}\hfill [q]=M\approx {\mathit{\lambda }}_J-{\left(\frac{J\mathit{\pi }}{a}\right)}^2,\end{array}$$$$\begin{array}{c}\hfill M_1:=[q_1]=C_1-2\frac{H}{a_0}\approx {\mathit{\mu }}_{J_1}-{\left(\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2-2\frac{H}{a_0},\end{array}$$$$\begin{array}{c}\hfill M_2:=[q_2]=C_2+2\frac{H}{a-a_0}\approx {\mathit{\nu }}_{J_2}-{\left(\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+2\frac{H}{a-a_0}.\end{array}$$

Some remarks on (3.21(3.21) $$\begin{array}{c}\hfill \sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\lambda }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j\approx -\sin (\sqrt{{\mathit{\lambda }}_i}a)\\ \hfill -\frac{M}{2}·({\int }_0^{a}t\sin (\sqrt{{\mathit{\lambda }}_i}t)\mathit{dt}),\text{for}i=1,\dots ,J.\end{array}$$(3.21) ),  (),  (),  (),  ()

The reason we chose to solve for the first $J$ Fourier coefficients ${\mathit{\alpha }}_j$’s of $\mathcal{K}(a,t;q)-\frac{M}{2}t$, and not for any other $J$ coefficients is that the sequence of the partial sums $\left\{\sum _{j=1}^n{\mathit{\alpha }}_j\sin \right(\frac{j\mathit{\pi }}{a}t){\}}_{n\ge 1}$ converges to $\mathcal{K}(a,t;q)-\frac{M}{2}t$, and not any other sequence of finite sums. As another remark, from (3.11(3.11) $$\begin{array}{c}\hfill {\int }_0^a\mathcal{K}(a,t;q)\sin (\sqrt{{\mathit{\lambda }}_n}t)\mathit{dt}=-\sin (\sqrt{{\mathit{\lambda }}_n}a),\text{for}n\ge 1,\end{array}$$(3.11) ) we kept only $J$ equations in order to make a square system for the unknowns $\{{\mathit{\alpha }}_j{\}}_{j=1}^J$. If less than $J$ equations were kept, say $J^{\prime }<J$, then the corresponding linear system for the ${\mathit{\alpha }}_j$’s would have had more than one solution since at least $J-J^{\prime }\ge 1$ of the ${\mathit{\alpha }}_j$’s would have become parameters. On the other hand, if more than $J$ equations are kept, say $J^{\prime \prime }>J$, then it would be possible for some of the equations to be incompatible with each other, thus making the linear system not have a solution. Finally, we kept the first $J$ equations from (3.11(3.11) $$\begin{array}{c}\hfill {\int }_0^a\mathcal{K}(a,t;q)\sin (\sqrt{{\mathit{\lambda }}_n}t)\mathit{dt}=-\sin (\sqrt{{\mathit{\lambda }}_n}a),\text{for}n\ge 1,\end{array}$$(3.11) ), i.e. the equations that correspond to ${\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_J$, and not any other $J$ equations. Had we done otherwise, say by keeping the equations that correspond to ${\mathit{\lambda }}_{i_1},{\mathit{\lambda }}_{i_2},\dots ,{\mathit{\lambda }}_{i_J}$ with some $i_1<i_2<\dots <i_J$ not all in $\{1,2,\dots ,J\}$, then certainly $i_J$ would have been pushed outside the set $\{1,2,\dots ,J\}$. This would imply$$\begin{array}{ccc}\hfill {\int }_0^a\sin (\sqrt{{\mathit{\lambda }}_{i_J}}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}& =\hfill & \hfill {\int }_0^a\sin \left((\frac{i_J\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{i_J}\right))t\right)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt},\text{by}\mathit{bad}\mathit{hbox}\\ \hfill & \approx \hfill & \hfill {\int }_0^a\sin \left(\frac{i_J\mathit{\pi }}{a}t\right)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt},\text{as}{i}_J>J\text{is}\text{large}\\ \hfill & =\hfill & \hfill 0,\text{for}\text{all}j=1,2,\dots ,J.\end{array}$$That means that the last row of the $J\times J$ matrix associated with the linear system for the ${\mathit{\alpha }}_j$’s would have had all entries near zero, making the numerical computations of the ${\mathit{\alpha }}_j$’s difficult.

By similar arguments, the first $J_1$ Fourier coefficients of ${\mathcal{K}}_x(a_0,t;q_1)+H\mathcal{K}(a_0,t;q_1)$ and the first $J_1$ equations from () must be kept. Also, the first $J_2$ Fourier coefficients of ${\mathcal{K}}_x(a_0,t;{\stackrel{\sim }{q}}_2)+\stackrel{\sim }{H}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)$ and the first $J_2$ equations from () must be kept. That means that ${\mathit{\mu }}_1,\dots {\mathit{\mu }}_{J_1}$, and ${\mathit{\nu }}_1,\dots ,{\mathit{\nu }}_{J_2}$ must be involved. This implies that the first $J_1$ equations from (), and the first $J_2$ equations from (3.15(3.15) $$\begin{array}{cc}\hfill & {\int }_0^{a_0}\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}t)\mathit{dt}={\stackrel{\sim }{l}}_n^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}-\sin (\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_n}{a}_0),\text{for}n\ge 1.\hfill \end{array}$$(3.15) ) must be kept, and so the first $J_1$ Fourier coefficients of $\mathcal{K}(a_0,t;q_1)-\frac{M_1}{2}t$, and the first $J_2$ Fourier coefficients of $\mathcal{K}(a_0,t;{\stackrel{\sim }{q}}_2)-\frac{{\stackrel{\sim }{M}}_2}{2}t$ must be kept.

Therefore, the need for the first $J,J_1,J_2$ of the $\mathit{\lambda }$’s, $\mathit{\mu }$’s, $\mathit{\nu }$’s, respectively, is justified.

The numerical algorithm

Let $H$ be a given real number. Let $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ be three sequences of positive numbers, strictly increasing, satisfying the asymptotics (3.16(3.16) $$\begin{array}{cc}\hfill & {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+M+d_n,\text{for}n\ge 1,\hfill \end{array}$$(3.16) ) – (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ), for some real-valued sequences $\{d_n{\}}_{n\ge 1}$, $\{d_n^{(1)}{\}}_{n\ge 1}$, $\{d_n^{(2)}{\}}_{n\ge 1}$ in $l_2^1$, and some real-valued constants $M$, $C_1$, $C_2$ such that () holds. We assume further that no overlap holds between $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$, and they interlace in the following sense:$$\begin{array}{c}\hfill 0<{\mathit{\sigma }}_1<{\mathit{\lambda }}_1<{\mathit{\sigma }}_2<{\mathit{\lambda }}_2<\dots ,\end{array}$$where $\{{\mathit{\sigma }}_m{\}}_{m\ge 1}:=\{{\mathit{\mu }}_n{\}}_{n\ge 1}\bigcup \{{\mathit{\nu }}_n{\}}_{n\ge 1}$ arranged increasingly. Then $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ are the Dirichlet, Dirichlet–Robin and Robin-Dirichlet eigenvalues on $[0,a]$, $[0,a_0]$ and $[a_0,a]$, respectively, with boundary parameter $H$ at $a_0$, for some potential function $q\in L_{\mathbb{R}}^2(0,a)$.

Note that in practice only a few eigenvalues of each type are available: $\{{\mathit{\lambda }}_j{\}}_{j=1}^J$, $\{{\mathit{\mu }}_j{\}}_{j=1}^{J_1}$, $\{{\mathit{\nu }}_j{\}}_{j=1}^{J_2}$. But this is enough information for us to estimate the constants in () – (3.18(3.18) $$\begin{array}{cc}\hfill & {\mathit{\nu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+C_2+d_n^{(2)},\text{for}n\ge 1.\hfill \end{array}$$(3.18) ). Now we can present the reconstruction algorithm.

• Introduce the constants $M$, $M_1$, $M_2$, ${\stackrel{\sim }{M}}_2$by:$$\begin{array}{c}\hfill M:={\mathit{\lambda }}_J-{\left(\frac{J\mathit{\pi }}{a}\right)}^2,\end{array}$$$$\begin{array}{c}\hfill M_1:={\mathit{\mu }}_{J_1}-{\left(\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}\right)}^2-2\frac{H}{a_0},\end{array}$$$$\begin{array}{c}\hfill M_2:={\mathit{\nu }}_{J_2}-{\left(\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}\right)}^2+2\frac{H}{a-a_0},\end{array}$$$$\begin{array}{c}\hfill {\stackrel{\sim }{M}}_2:={(-\frac{a-a_0}{a_0})}^2{M}_2,\end{array}$$$$\begin{array}{c}\hfill \stackrel{\sim }{H}:=-\frac{a-a_0}{a_0}H.\end{array}$$

• Define$$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\mu }}}_j:={(-\frac{a-a_0}{a_0})}^2{\mathit{\mu }}_j,\text{for}j=1,\dots ,J_1,\end{array}$$$$\begin{array}{c}\hfill {\stackrel{\sim }{\mathit{\nu }}}_j:={(-\frac{a-a_0}{a_0})}^2{\mathit{\nu }}_j,\text{for}j=1,\dots ,J_2.\end{array}$$

• Solve the linear system (3.21(3.21) $$\begin{array}{c}\hfill \sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\lambda }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j\approx -\sin (\sqrt{{\mathit{\lambda }}_i}a)\\ \hfill -\frac{M}{2}·({\int }_0^{a}t\sin (\sqrt{{\mathit{\lambda }}_i}t)\mathit{dt}),\text{for}i=1,\dots ,J.\end{array}$$(3.21) ) for $\{{\mathit{\alpha }}_j{\}}_{j=1}^J$.

• Solve the linear system () for $\{{\mathit{\gamma }}_j^{(1)}{\}}_{j=1}^{J_1}$.

• Solve the linear system () for $\{{\mathit{\gamma }}_j^{(2)}{\}}_{j=1}^{J_2}$.

• Construct $\{l_i^{(1)}\sqrt{{\mathit{\mu }}_i}{\}}_{i=1}^{J_1}$ by ().

• Construct $\{{\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{\}}_{i=1}^{J_2}$ by ().

• Solve the linear system () for $\{{\mathit{\beta }}_j^{(1)}{\}}_{j=1}^{J_1}$.

• Solve the linear system () for $\{{\mathit{\beta }}_j^{(2)}{\}}_{j=1}^{J_2}$.

• Define$$\begin{array}{c}\hfill f_1(t):=\frac{M_1}{2}t+\sum _{j=1}^{J_1}{\mathit{\beta }}_j^{(1)}\sin \left(\frac{j\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$and$$\begin{array}{c}\hfill h_1(t):=\sum _{j=1}^{J_1}{\mathit{\gamma }}_j^{(1)}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0].\end{array}$$(The pair $\{f_1(t),h_1(t)\}$ is supposed to be the pair $\{\mathit{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{+}\mathit{H}\mathcal{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\mathit{q}}_{\mathsf{1}}\mathit{)}\mathit{\}}$.)

• Define$$\begin{array}{c}\hfill f_2(t):=\frac{{\stackrel{\sim }{M}}_2}{2}t+\sum _{j=1}^{J_2}{\mathit{\beta }}_j^{(2)}\sin \left(\frac{j\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0],\end{array}$$and$$\begin{array}{c}\hfill h_2(t):=\sum _{j=1}^{J_2}{\mathit{\gamma }}_j^{(2)}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right),\text{for}\text{all}t\in [0,a_0].\end{array}$$(The pair $\{f_2(t),h_2(t)\}$ is supposed to be the pair $\{\mathit{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{,}{\mathcal{K}}_{\mathit{x}}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{+}\stackrel{\sim }{\mathit{H}}\mathcal{K}\mathit{(}{\mathit{a}}_{\mathsf{0}}\mathit{,}\mathit{t}\mathit{;}{\stackrel{\sim }{\mathit{q}}}_{\mathsf{2}}\mathit{)}\mathit{\}}$.)

• Define$$\begin{array}{c}\hfill g_1(t):=h_1(t)-H{f}_1(t),\text{for}\text{all}t\in [0,a_0],\end{array}$$and$$\begin{array}{c}\hfill g_2(t):=h_2(t)-\stackrel{\sim }{H}{f}_2(t),\text{for}\text{all}t\in [0,a_0].\end{array}$$

• Use a divided difference scheme to obtain $f_1^{\prime }(t)$ from the known $f_1(t)$ and $f_1(a_0)=\frac{a_0{M}_1}{2}$.

• Use a divided difference scheme to obtain $f_2^{\prime }(t)$ from the known $f_2(t)$ and $f_2(a_0)=\frac{a_0{\stackrel{\sim }{M}}_2}{2}$.

• Use $\{f_1^{\prime }(t),g_1(t)\}$ in the algorithm of [2] to produce a function $q_1$ on $[0,a_0]$.

• Use $\{f_2^{\prime }(t),g_2(t)\}$ in the algorithm of [2] to produce a function ${\stackrel{\sim }{q}}_2$ on $[0,a_0]$.

• ’Reflect’ ${\stackrel{\sim }{q}}_2$ about the line $x=a_0$ to produce a new function $q_2$ on $[a_0,a]$. Precisely,$$\begin{array}{c}\hfill q_2(x):={(-\frac{a_0}{a-a_0})}^2{\stackrel{\sim }{q}}_2(\mathit{\xi }),\text{where}\mathit{\xi }\in [0,a_0]\leftrightarrow x\in [a_0,a]\text{by}x:=a-\frac{a-a_0}{a_0}\mathit{\xi }.\end{array}$$

• Paste together $q_1$ and $q_2$ to produce the function $q$ on $[0,a]$.

The best numbers of eigenvalues

In this section we are concerned with finding the best numbers $J$, $J_1$, $J_2$ such that the sequences $\{{\mathit{\lambda }}_j{\}}_{j=1}^J$, $\{{\mathit{\mu }}_j{\}}_{j=1}^{J_1}$, $\{{\mathit{\nu }}_j{\}}_{j=1}^{J_2}$ assure a good reconstruction of the potential function $q$. We start by noting that the quantities $\{l_i^{(1)}\sqrt{{\mathit{\mu }}_i}{\}}_{i=1}^{J_1}$ and $\{{\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}{\}}_{i=1}^{J_2}$ are needed to solve the linear systems () and () for $\{{\mathit{\beta }}_j^{(1)}{\}}_{j=1}^{J_1}$ and $\{{\mathit{\beta }}_j^{(2)}{\}}_{j=1}^{J_2}$, respectively. We see in () that the quantity$$\begin{array}{c}\hfill -\sin (\sqrt{{\mathit{\mu }}_i}{a}_0)-\frac{M_1}{2}·({\int }_0^{a_0}t\sin (\sqrt{{\mathit{\mu }}_i}t)\mathit{dt}),\end{array}$$and the numerator of $l_i^{(1)}\sqrt{{\mathit{\mu }}_i}$ in (),$$\begin{array}{c}\hfill \sin (\sqrt{{\mathit{\mu }}_i}a)+\sum _{j=1}^J({\int }_0^a\sin (\sqrt{{\mathit{\mu }}_i}t)\sin \left(\frac{j\mathit{\pi }}{a}t\right)\mathit{dt}){\mathit{\alpha }}_j+\frac{M}{2}{\int }_0^{a}t\sin (\sqrt{{\mathit{\mu }}_i}t)\mathit{dt}\end{array}$$are bounded (uniformly in $i$). Hence, in order for the right-hand side of () to be well defined, we need the denominator of $l_i^{(1)}\sqrt{{\mathit{\mu }}_i}$ in () to be non-zero, for all $i=1,\dots ,J_1$. Theoretically, they are so due to the non-overlap of $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$ with $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$. (See the three paragraphs immediately following ().) Numerically, they should not even be close to zero. So we need to require:(6.1) $$\begin{array}{cc}\hfill & |\cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)+(\frac{a_0{\stackrel{\sim }{M}}_2}{2}+\stackrel{\sim }{H})\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\hfill \\ \hfill & +\sum _{j=1}^{J_2}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(2)}|\gg 0,\text{for}i=1,\dots ,J_1.\hfill \end{array}$$(6.1) Similarly, in order for the right-hand side of () to be well defined, we need to require that the denominator of ${\stackrel{\sim }{l}}_i^{(2)}\sqrt{{\stackrel{\sim }{\mathit{\nu }}}_i}$ in () stay away from zero, for all $i=1,\dots ,J_2$. That is, we need to require:(6.2) $$\begin{array}{cc}\hfill & |\cos (\sqrt{{\mathit{\nu }}_i}{a}_0)+(\frac{a_0{M}_1}{2}+H)\frac{\sin (\sqrt{{\mathit{\nu }}_i}{a}_0)}{\sqrt{{\mathit{\nu }}_i}}\hfill \\ \hfill & +\sum _{j=1}^{J_1}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\mathit{\nu }}_i}t)}{\sqrt{{\mathit{\nu }}_i}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(1)}|\gg 0,\text{for}i=1,\dots ,J_2.\hfill \end{array}$$(6.2) We argue below that () and () will impose a constraint on the numbers $J_1$ and $J_2$. To this end, we shall take advantage of the orthogonality in $L^2(0,a_0)$ of the set ${\left\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\right\}}_{n\ge 1}$. We claim that if we hope () and () to hold, then:(6.3) $$\begin{array}{c}\hfill \frac{J_1-\frac{1}{2}}{a_0}\approx \frac{J_2-\frac{1}{2}}{a-a_0}.\end{array}$$(6.3) For if $\frac{J_1-\frac{1}{2}}{a_0}\gg \frac{J_2-\frac{1}{2}}{a-a_0}$, then $(J_1-\frac{1}{2})\frac{a-a_0}{a_0}\gg J_2-\frac{1}{2}$. Let ${\stackrel{\sim }{J}}_1$ be the positive integer such that ${\stackrel{\sim }{J}}_1-\frac{1}{2}\approx (J_1-\frac{1}{2})\frac{a-a_0}{a_0}$. Then ${\stackrel{\sim }{J}}_1-\frac{1}{2}\gg J_2-\frac{1}{2}$, so ${\stackrel{\sim }{J}}_1\gg J_2$ and$$\begin{array}{c}\hfill \sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}t)\&=\sin \left(\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}t\right)\\ \hfill & =\sin (\frac{a-a_0}{a_0}·(\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}+\mathcal{O}\left(\frac{1}{J_1}\right))t),\text{by}\mathit{bad}\mathit{hbox}\hfill \\ \hfill & \approx \sin \left(\frac{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}{a_0}t\right).\hfill \end{array}$$It follows that$$\begin{array}{cc}\hfill & {\int }_0^{a_0}\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\hfill \\ \hfill & \approx {\int }_0^{a_0}\sin \left(\frac{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}=0,\text{for}\text{all}j=1,\dots ,J_2,\hfill \end{array}$$(because $j\in \{1,\dots ,J_2\}$ and ${\stackrel{\sim }{J}}_1\gg J_2$ imply $j\ne {\stackrel{\sim }{J}}_1$) from which we have that(6.4) $$\begin{array}{c}\hfill \sum _{j=1}^{J_2}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(2)}\approx 0.\end{array}$$(6.4) Also,(6.5) $$\begin{array}{c}\hfill \frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}}\&=\frac{\sin \left(\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}{a}_0\right)}{\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}}\\ \hfill & \approx \frac{\sin (\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}·a_0)}{\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & \approx \frac{\sin (({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi })}{\frac{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & ={(-1)}^{{\stackrel{\sim }{J}}_1+1}\frac{a_0}{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}\hfill \\ \hfill & \approx 0,\text{because}{J}_1\text{is}\text{large,}\text{and}\text{so}\text{will}\text{be}{\stackrel{\sim }{J}}_1.\hfill \end{array}$$(6.5) And(6.6) $$\begin{array}{c}\hfill \cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}{a}_0)\&=\cos \left(\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}{a}_0\right)\\ \hfill & \approx \cos (\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}·a_0)\hfill \\ \hfill & \approx \cos (({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi })\hfill \\ \hfill & =0.\hfill \end{array}$$(6.6) Formulas (6.4(6.4) $$\begin{array}{c}\hfill \sum _{j=1}^{J_2}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}t)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(2)}\approx 0.\end{array}$$(6.4) ),  (6.5(6.5) $$\begin{array}{c}\hfill \frac{\sin (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}{a}_0)}{\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}}\&=\frac{\sin \left(\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}{a}_0\right)}{\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}}\\ \hfill & \approx \frac{\sin (\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}·a_0)}{\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & \approx \frac{\sin (({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi })}{\frac{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & ={(-1)}^{{\stackrel{\sim }{J}}_1+1}\frac{a_0}{({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi }}\hfill \\ \hfill & \approx 0,\text{because}{J}_1\text{is}\text{large,}\text{and}\text{so}\text{will}\text{be}{\stackrel{\sim }{J}}_1.\hfill \end{array}$$(6.5) ) and (6.6(6.6) $$\begin{array}{c}\hfill \cos (\sqrt{{\stackrel{\sim }{\mathit{\mu }}}_{J_1}}{a}_0)\&=\cos \left(\frac{a-a_0}{a_0}\sqrt{{\mathit{\mu }}_{J_1}}{a}_0\right)\\ \hfill & \approx \cos (\frac{a-a_0}{a_0}·\frac{(J_1-\frac{1}{2})\mathit{\pi }}{a_0}·a_0)\hfill \\ \hfill & \approx \cos (({\stackrel{\sim }{J}}_1-\frac{1}{2})\mathit{\pi })\hfill \\ \hfill & =0.\hfill \end{array}$$(6.6) ) show that () does not hold for $i=J_1$.

On the other hand, if $\frac{J_2-\frac{1}{2}}{a-a_0}\gg \frac{J_1-\frac{1}{2}}{a_0}$, then letting ${\stackrel{\sim }{J}}_2$ be the positive integer such that $\frac{{\stackrel{\sim }{J}}_2-\frac{1}{2}}{a_0}\approx \frac{J_2-\frac{1}{2}}{a-a_0}$ we have that $\frac{{\stackrel{\sim }{J}}_2-\frac{1}{2}}{a_0}\gg \frac{J_1-\frac{1}{2}}{a_0}$, so ${\stackrel{\sim }{J}}_2\gg J_1$. It follows that$$\begin{array}{c}\hfill \sin (\sqrt{{\mathit{\nu }}_{J_2}}t)\&=\sin \left((\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}+\mathcal{O}\left(\frac{1}{J_2}\right))t\right),\text{by}\mathit{bad}\mathit{hbox}\\ \hfill & \approx \sin \left(\frac{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}{a_0}t\right),\hfill \end{array}$$from which we can write:$$\begin{array}{cc}\hfill & {\int }_0^{a_0}\sin (\sqrt{{\mathit{\nu }}_{J_2}}t)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\hfill \\ \hfill & \approx {\int }_0^{a_0}\sin \left(\frac{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}=0,\text{for}\text{all}j=1,\dots ,J_1,\hfill \end{array}$$(because $j\in \{1,\dots ,J_1\}$ and ${\stackrel{\sim }{J}}_2\gg J_1$ imply $j\ne {\stackrel{\sim }{J}}_2$). This gives(6.7) $$\begin{array}{c}\hfill \sum _{j=1}^{J_1}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\mathit{\nu }}_{J_2}}t)}{\sqrt{{\mathit{\nu }}_{J_2}}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(1)}\approx 0.\end{array}$$(6.7) Also,(6.8) $$\begin{array}{c}\hfill \frac{\sin (\sqrt{{\mathit{\nu }}_{J_2}}{a}_0)}{\sqrt{{\mathit{\nu }}_{J_2}}}\&\approx \frac{\sin (\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}·a_0)}{\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}}\\ \hfill & \approx \frac{\sin (({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi })}{\frac{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & ={(-1)}^{{\stackrel{\sim }{J}}_2+1}\frac{a_0}{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}\hfill \\ \hfill & \approx 0,\text{because}{J}_2\text{is}\text{large,}\text{and}\text{so}\text{will}\text{be}{\stackrel{\sim }{J}}_2.\hfill \end{array}$$(6.8) And(6.9) $$\begin{array}{c}\hfill \cos (\sqrt{{\mathit{\nu }}_{J_2}}{a}_0)\&\approx \cos (\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}·a_0)\\ \hfill & \approx \cos (({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi })\hfill \\ \hfill & =0.\hfill \end{array}$$(6.9) Formulas (6.7(6.7) $$\begin{array}{c}\hfill \sum _{j=1}^{J_1}\left({\int }_0^{a_0}\frac{\sin (\sqrt{{\mathit{\nu }}_{J_2}}t)}{\sqrt{{\mathit{\nu }}_{J_2}}}\sin \left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a_0}t\right)\mathit{dt}\right){\mathit{\gamma }}_j^{(1)}\approx 0.\end{array}$$(6.7) ),  (6.8(6.8) $$\begin{array}{c}\hfill \frac{\sin (\sqrt{{\mathit{\nu }}_{J_2}}{a}_0)}{\sqrt{{\mathit{\nu }}_{J_2}}}\&\approx \frac{\sin (\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}·a_0)}{\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}}\\ \hfill & \approx \frac{\sin (({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi })}{\frac{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}{a_0}}\hfill \\ \hfill & ={(-1)}^{{\stackrel{\sim }{J}}_2+1}\frac{a_0}{({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi }}\hfill \\ \hfill & \approx 0,\text{because}{J}_2\text{is}\text{large,}\text{and}\text{so}\text{will}\text{be}{\stackrel{\sim }{J}}_2.\hfill \end{array}$$(6.8) ), and (6.9(6.9) $$\begin{array}{c}\hfill \cos (\sqrt{{\mathit{\nu }}_{J_2}}{a}_0)\&\approx \cos (\frac{(J_2-\frac{1}{2})\mathit{\pi }}{a-a_0}·a_0)\\ \hfill & \approx \cos (({\stackrel{\sim }{J}}_2-\frac{1}{2})\mathit{\pi })\hfill \\ \hfill & =0.\hfill \end{array}$$(6.9) ) show that () will not hold for $i=J_2$.

Thus, these calculations justify the constraint imposed by () and (): the numbers $J_1$ and $J_2$ must be taken such that (6.3(6.3) $$\begin{array}{c}\hfill \frac{J_1-\frac{1}{2}}{a_0}\approx \frac{J_2-\frac{1}{2}}{a-a_0}.\end{array}$$(6.3) ) holds. Bearing in mind the interlacing of $\{{\mathit{\lambda }}_n{\}}_{n\ge 1}$, $\{{\mathit{\mu }}_n{\}}_{n\ge 1}$, $\{{\mathit{\nu }}_n{\}}_{n\ge 1}$ (see the beginning of Section Section15), we also write:(6.10) $$\begin{array}{c}\hfill J=J_1+J_2\text{or}J=J_1+J_2-1.\end{array}$$(6.10)

Fig. 1 Examples for comparison of potentials (true and numerical).

Numerical examples

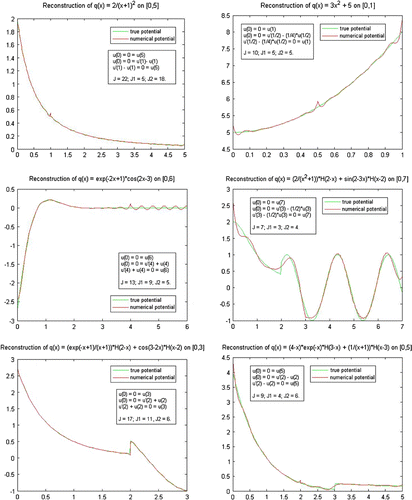
To illustrate the effectiveness of the algorithm presented in Section Section15, specific $q$’s were chosen and used in the software MATSLISE (see [14]) to produce three sequences of eigenvalues: Dirichlet on $[0,a]$, Dirichlet–Robin on $[0,a_0]$, and Robin-Dirichlet on $[a_0,a]$, with boundary parameter $H$ at the interior node $a_0$. These sequences were then used as the input data in the reconstruction algorithm of Section Section15. The comparison between the true potential (i.e. the one with which we generated the eigenvalues) and the numerically constructed potential is featured in Figure 1. In each picture, we indicate the three sets of boundary conditions for each inverse eigenvalue problem. Also the numbers $J$, $J_1$, $J_2$ of the $\mathit{\lambda }$’s, $\mathit{\mu }$’s, $\mathit{\nu }$’s that we used are indicated. The potential functions we chose to reconstruct are (from left to right, top to bottom):$$\begin{array}{c}\hfill q(x)=\frac{2}{{(x+1)}^2},\text{on}[0,5],\end{array}$$with $a_0=1$,$$\begin{array}{c}\hfill q(x)=3x^2+5,\text{on}[0,1],\end{array}$$with $a_0=\frac{1}{2}$,$$\begin{array}{c}\hfill q(x)=e^{-2x+1}\cos (2x-3),\text{on}[0,6],\end{array}$$with $a_0=4$,$$\begin{array}{c}\hfill q(x)=\{\begin{array}{cc}\frac{2}{x^2+1},\hfill & \text{for}0\le x<2\hfill \\ \sin (2-3x),\hfill & \text{for}2\le x\le 7,\hfill \end{array}\end{array}$$with $a_0=3$,$$\begin{array}{c}\hfill q(x)=\{\begin{array}{cc}\frac{e^{-x+1}}{x+1},\hfill & \text{for}0\le x<2\hfill \\ \cos (3-2x),\hfill & \text{for}2\le x\le 3,\hfill \end{array}\end{array}$$with $a_0=2$,$$\begin{array}{c}\hfill q(x)=\{\begin{array}{cc}(4-x)e^{-x},\hfill & \text{for}0\le x<3\hfill \\ \frac{1}{x+1},\hfill & \text{for}3\le x\le 5,\hfill \end{array}\end{array}$$with $a_0=2$.

Acknowledgments

I would like to thank Dr. Paul E. Sacks of Iowa State University for helpful discussions on the general topic of numerical reconstructions for inverse Sturm–Liouville problems.

Appendix

Auxiliary result 1 Let $b>0$. Then $\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right){\}}_{n\ge 1}$ is an orthogonal basis of $L^2(0,b)$.

Proof: We shall make use of the known statement: ‘Let $\{e_n{\}}_{n\ge 1}$ be an orthogonal sequence in a separable Hilbert space $H$. Then $\{e_n{\}}_{n\ge 1}$ is an orthogonal basis of $H$if and only if$\{e_n{\}}_{n\ge 1}$ is complete (i.e. the zero vector alone is perpendicular to all $e_n$’s).’ So, in order to establish the conclusion it is enough to prove that $\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right){\}}_{n\ge 1}$ is an orthogonal sequence in the Hilbert space $L^2(0,b)$, and it is complete in $L^2(0,b)$. We check orthogonality first. Let $m\ne n$. Then using the trigonometric formula$$\begin{array}{c}\hfill \sin A\sin B=\frac{\cos (A-B)-\cos (A+B)}{2},\end{array}$$we obtain:$$\begin{array}{c}\hfill {\int }_0^b\sin \left(\frac{(m-\frac{1}{2})\mathit{\pi }}{b}t\right)\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right)\mathit{dt}\&={\int }_0^b\frac{\cos \left(\frac{(m-n)\mathit{\pi }}{b}t\right)-\cos \left(\frac{(m+n-1)\mathit{\pi }}{b}t\right)}{2}\mathit{dt}\\ \hfill & =0.\hfill \end{array}$$Now we prove the completeness in $L^2(0,b)$ of $\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right){\}}_{n\ge 1}$. We shall make use of the completeness in $L^2(0,2b)$ of $\{\sin \left(\frac{m\mathit{\pi }}{2b}t\right){\}}_{m\ge 1}$. This latter sequence of functions is complete in $L^2(0,2b)$ due to the statement mentioned above (about the equivalence between orthogonal basis and complete sequence), and because it is an orthogonal basis of $L^2(0,2b)$ (see [13, Example 2(d1), p.308–309] with $L=2b$). Let $f\in L^2(0,b)$ be such that(8.1) $$\begin{array}{c}\hfill {\int }_0^{b}f(t)\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right)\mathit{dt}=0,\text{for}\text{all}n\ge 1.\end{array}$$(8.1) Consider the even reflection of $f(t)$ about the line $t=b$. That is, define(8.2) $$\begin{array}{c}\hfill \stackrel{\sim }{f}(t):=\{\begin{array}{cc}f(t),\hfill & \text{for}0\le t\le b\hfill \\ f(2b-t),\hfill & \text{for}b\le t\le 2b.\hfill \end{array}\end{array}$$(8.2) Then for all $m\ge 1$:(8.3) $$\begin{array}{cc}\hfill {\int }_0^{2b}\stackrel{\sim }{f}(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}& ={\int }_0^{b}f(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}+{\int }_b^{2b}f(2b-t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}\hfill \\ \hfill & ={\int }_0^{b}f(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}+{\int }_0^{b}f(\mathit{\tau })\sin (\frac{m\mathit{\pi }}{2b}(2b-\mathit{\tau }))d\mathit{\tau }\hfill \\ \hfill \text{(with}\mathit{\tau }:=2b-t\text{)}\\ \hfill & ={\int }_0^{b}f(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}+{\int }_0^{b}f(\mathit{\tau })\sin (m\mathit{\pi }-\frac{m\mathit{\pi }}{2b}\mathit{\tau })d\mathit{\tau }\hfill \\ \hfill & ={\int }_0^{b}f(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}-\cos (m\mathit{\pi })·({\int }_0^{b}f(\mathit{\tau })\sin \left(\frac{m\mathit{\pi }}{2b}\mathit{\tau }\right)d\mathit{\tau })\hfill \\ \hfill & ={\int }_0^{b}f(t)\sin \left(\frac{m\mathit{\pi }}{2b}t\right)\mathit{dt}-{(-1)}^m·({\int }_0^{b}f(\mathit{\tau })\sin \left(\frac{m\mathit{\pi }}{2b}\mathit{\tau }\right)d\mathit{\tau })\hfill \\ \hfill & =\{\begin{array}{cc}2{\int }_0^{b}f(t)\sin \left(\frac{(2n-1)\mathit{\pi }}{2b}t\right)\mathit{dt},\hfill & \text{if}m=2n-1\text{,}\text{with}n\ge 1\hfill \\ 0,\hfill & \text{if}m=2n\text{,}\text{with}n\ge 1\hfill \end{array}\hfill \\ \hfill & =0,\text{(by}\mathit{bad}\mathit{hbox}\hfill \end{array}$$(8.3) () and the completeness in $L^2(0,2b)$ of $\{\sin \left(\frac{m\mathit{\pi }}{2b}t\right){\}}_{m\ge 1}$ imply that $\stackrel{\sim }{f}(t)=0$, for all $t\in [0,2b]$. Hence, by () we obtain $f(t)=0$, for $t\in [0,b]$. Thus, the completeness in $L^2(0,b)$ of $\{\sin \left(\frac{(n-\frac{1}{2})\mathit{\pi }}{b}t\right){\}}_{n\ge 1}$ is proved.$\square$