Experimental design for vector output systems

Abstract

We formulate an optimal design problem for the selection of best states to observe and optimal sampling times for parameter estimation or inverse problems involving complex non-linear dynamical systems. An iterative algorithm for implementation of the resulting methodology is proposed. Its use and efficacy are illustrated on two applied problems of practical interest: (i) dynamic models of HIV progression and (ii) modelling of the Calvin cycle in plant metabolism and growth.

Keywords:

• optimal design
• inverse problems
• optimal selection of observables and sampling times
• HIV models
• plant metabolism and growth

Introduction

In many scientific fields where mathematical modelling is utilized, mathematical models grow increasingly complex, containing possibly more state variables and parameters, over time as the underlying governing processes of a system are better understood and refinements in mechanisms are considered. Additionally, as technology invents and improves devices to measure physical and biological phenomena, new data become available to inform mathematical modelling efforts. The world is approaching an era in which the vast amounts of information available to researchers may be overwhelming or even counterproductive to efforts. We explore a framework based on the Fisher Information Matrix (FIM) for a system of ordinary differential equations (ODEs) to determine when an experimenter should take samples and what variables to measure when collecting information on a physical or biological process that is modelled by a dynamical system.

Inverse problem methodologies are discussed in [1] in the context of dynamical system or mathematical model parameter estimation when a sufficient number of observations of one or more states (variables) are available. The choice of method depends on assumptions the modeller makes on the form of the error between the model and the observations (the statistical model). The most prevalent source of error is observation error, which is made when collecting data. (One can also consider model error, which originates from the differences between the model and the underlying process that the model describes. But this is often quite difficult to quantify.) Measurement error is most readily discussed in the context of statistical models. The three techniques commonly addressed are maximum likelihood estimators (MLE), used when the properties of the error distribution are known; ordinary least squares (OLS), for error with constant variance across observations; and generalized least squares (GLS), used when the variance of the data can be expressed as a non-constant function. Uncertainty quantification is also described for optimization problems of this type, namely in the form of observation error covariances, standard errors, residual plots, and sensitivity matrices. Techniques to approximate the variance of the error are also included in these discussions.

Experimental design using the FIM, which is based on sensitivity matrices, is described in [2] for the case of scalar data. Sensitivity matrices are composed of functions that relate the change in a variable to the change in the parameter. The first order quantifications of these relations are called traditional sensitivity functions and are useful in suggesting when a variable should be sampled to get the most information for estimating a particular parameter, especially when the first order sensitivity functions are used in conjunction with the so-called second order sensitivity functions. This work also examines the usefulness of generalized sensitivity functions,[3] which are calculated using the FIM, that are known to describe how information about the parameters is distributed across time for each variable. Both types of sensitivity functions are then used in numerical simulations to determine the optimal final time for an experiment of a process described by a logistic curve.

In [4], the authors develop an experimental design theory using the FIM to identify optimal sampling times for experiments on physical processes (modelled by an ODE system) in which scalar or vector data will be taken. The experimental design technique developed is applied in numerical simulations to the logistic curve, a simple ODE model describing glucose regulation and a harmonic oscillator example.

In addition to when to take samples, the question of what variables to measure is also very important in designing effective experiments, especially when the number of state variables is large. Use of such a methodology to optimize what to measure would further reduce testing costs by eliminating extra experiments to measure variables neglected in previous trials. In [5], the best set of variables for an ODE system modelling the Calvin cycle [6] is identified using two methods. The first, an ad-hoc statistical method, determines which variables directly influence an output of interest at any one particular time. A model using a subset of variables is determined via multivariate linear regression, and the efficacy of the model is then measured using the Akaike Information Criterion. The variables that appear in the best models at the most time points are then identified as the most important to measure. Such a method does not utilize the information on the underlying time-varying processes given by the dynamical system model. Extension of the second method first suggested in [5], based optimal design ideas, is the subject of our presentation here.

Building on the theory in [4] and [5], we formulate a previously unexplored optimal design problem to determine not only the optimal sampling variables out of a finite set of possible sampling variables but also the optimal sampling time distribution given a fixed final time. We compare the SE-optimal design introduced in [2] and [4] with the well-known methods of D-optimal and E-optimal design on a six-compartment HIV model [7] and a thirty-one dimensional model of the Calvin Cycle.[6] Such models where there may be a wide range of variables to possibly observe are not only ideal on which to test our proposed methodology, but also are widely encountered in applications.

Mathematical background

 

Mathematical and statistical models

We explore our experimental design questions using a mathematical model(1) $$\begin{array}{cc}\hfill \frac{d\overrightarrow{x}}{\mathit{dt}}(t)& =\overrightarrow{g}(t,\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\overrightarrow{q}),t\in [t_0,t_f],\hfill \\ \hfill \overrightarrow{x}(t_0;\overrightarrow{\mathit{\theta }})& ={\overrightarrow{x}}_0,\hfill \end{array}$$(1) where $\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }})$ is the vector of state variables of the system generated using a parameter vector $\overrightarrow{\mathit{\theta }}=({\overrightarrow{x}}_0;\overrightarrow{q})\in {\mathbb{R}}^{\mathbb{p}}$, $p=m+r$, that contains $m$ initial values and $r$ system parameters listed in $\overrightarrow{q}$, $\overrightarrow{g}$ is a mapping ${\mathbb{R}}^{\mathbb{1}+\mathbb{m}+\mathbb{r}}\to {\mathbb{R}}^{\mathbb{m}}$, $t_0\ge 0$ is the initial time, and $t_f<\infty$ is the final time. We define an observation process(2) $$\begin{array}{c}\hfill \overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\end{array}$$(2) where $C$ is an observation operator that maps ${\mathbb{R}}^{\mathbb{m}}\to {\mathbb{R}}^{\mathbb{N}}$, where $N$ is the number of variables observed at a single sampling time. If we were able to observe all states, each measured by a different sampling technique, then $N=m$ and $C={\mathbf{I}}^{m\times m}$; however, this is most often not the case because of the impossibility of or the expense in measuring all state variables. In other cases (such as the HIV example below) we may be able to directly observe only combinations of the states.

In order to discuss the amount of uncertainty in parameter estimates, we formulate a statistical model [1] of the form(3) $$\begin{array}{c}\hfill \overrightarrow{Y}(t)=\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t),t\in [t_0,t_f],\end{array}$$(3) where ${\overrightarrow{\mathit{\theta }}}_0$ is the hypothesized true value of the unknown parameters and $\overrightarrow{\mathcal{E}}$ is a vector random process that represents observation error for the measured variables. We make the standard assumptions:$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathrm{E}(\overrightarrow{\mathcal{E}}(t))=\overrightarrow{0},t\in [t_0,t_f],\hfill \\ \hfill \mathrm{V}\mathit{ar}(\overrightarrow{\mathcal{E}}(t))=V_0(t)=\mathrm{d}\mathit{iag}({\mathit{\sigma }}_{0,1}{(t)}^2,{\mathit{\sigma }}_{0,2}{(t)}^2,\dots ,{\mathit{\sigma }}_{0,N}{(t)}^2),t\in [t_0,t_f],\hfill \\ \hfill \mathrm{C}\mathit{ov}({\mathcal{E}}_i(t){\mathcal{E}}_i(s))={\mathit{\sigma }}_{0,i}{(t)}^2\mathit{\delta }(t-s),s,t\in [t_0,t_f],\hfill \\ \hfill \mathrm{C}\mathit{ov}({\mathcal{E}}_i(t){\mathcal{E}}_j(s))=0,i\ne j,s,t\in [t_0,t_f],\hfill \end{array}\end{array}$$where $\mathit{\delta }(0)=1$ and $\mathit{\delta }(t)=0$ for $t\ne 0$. Realizations of the statistical model (3(3) $$\begin{array}{c}\hfill \overrightarrow{Y}(t)=\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t),t\in [t_0,t_f],\end{array}$$(3) ) are written$$\begin{array}{c}\hfill \overrightarrow{y}(t)=\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathit{ϵ}}(t),t\in [t_0,t_f].\end{array}$$When collecting experimental data, it is often difficult to take continuous measurements of the observed variables. Instead, we assume that we have $n$ observations at times $t_j$, $j=1,\dots ,n$, $t_0\le t_1<t_2<\dots <t_n\le t_f$. We then write the observation process (2(2) $$\begin{array}{c}\hfill \overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\end{array}$$(2) ) as(4) $$\begin{array}{c}\hfill \overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t_j;\overrightarrow{\mathit{\theta }}),j=1,2,\dots ,n,\end{array}$$(4) the discrete statistical model as(5) $$\begin{array}{c}\hfill {\overrightarrow{Y}}_j=\overrightarrow{f}(t_j;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t_j),j=1,2,\dots ,n,\end{array}$$(5) and a realization of the discrete statistical model as$$\begin{array}{c}\hfill {\overrightarrow{y}}_j=\overrightarrow{f}(t_j;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathit{ϵ}}(t_j),j=1,2,\dots ,n.\end{array}$$If we were given ${\overrightarrow{\mathit{\theta }}}_0$, we could solve (1(1) $$\begin{array}{cc}\hfill \frac{d\overrightarrow{x}}{\mathit{dt}}(t)& =\overrightarrow{g}(t,\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\overrightarrow{q}),t\in [t_0,t_f],\hfill \\ \hfill \overrightarrow{x}(t_0;\overrightarrow{\mathit{\theta }})& ={\overrightarrow{x}}_0,\hfill \end{array}$$(1) ) for $\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)$, a process known as solving the forward problem. Alternatively, if we had a set of data ${\overrightarrow{y}}_j$, $j=1,2,\dots ,n$, we could estimate ${\overrightarrow{\mathit{\theta }}}_0$ in a process known as solving the inverse problem. We will use this mathematical and statistical framework to develop a methodology to identify sampling variables that provide the most information pertinent to estimating a given set of parameters and the most informative times at which the samples should be taken.

Formulation of the optimal design problem

Several methods exist to solve the inverse problem. A major factor [1] in determining which method to use is additional assumptions made about $\overrightarrow{\mathcal{E}}(t)$. It is common practice to make the assumption that realizations of $\overrightarrow{\mathcal{E}}(t)$ at particular time points are independent and identically distributed (i.i.d.). If, additionally, the distributions describing the behaviour of the components of $\overrightarrow{\mathcal{E}}(t)$ are known, then maximum likelihood methods may be used to find an estimate of ${\overrightarrow{\mathit{\theta }}}_0$. On the other hand, if the distributions for $\overrightarrow{\mathcal{E}}(t)$ are not known but the variance $V_0(t)$ (also unknown) is assumed to vary over time, weighted least squares methods are often used. We propose an optimal design problem formulation using a generalized weighted least squares criterion.

Let ${\mathcal{P}}_1([t_0,t_f])$ denote the set of all bounded distributions on the interval $[t_0,t_f]$. We consider the generalized weighted least squares cost functional for systems with vector output(6) $$\begin{array}{c}\hfill J_{\mathit{WLS}}(\overrightarrow{y},\overrightarrow{\mathit{\theta }})={\int }_{t_0}^{t_f}{[\overrightarrow{y}(t)-\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}(t)[\overrightarrow{y}(t)-\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})]{\mathit{dP}}_1(t),\end{array}$$(6) where $P_1(t)\in {\mathcal{P}}_1([t_0,t_f])$ is a general measure on the interval $[t_0,t_f]$. For a given continuous data set $\overrightarrow{y}(t)$, we search for a parameter $\hat{\mathit{\theta }}$ that minimizes $J_{\mathit{WLS}}(\overrightarrow{y},\overrightarrow{\mathit{\theta }})$.

We next consider the case of observations collected at discrete times. If we choose a set of $n$ time points $\mathit{\tau }=\{t_j\}$, $j=1,2,\dots ,n$, where $t_0\le t_1<t_2<\dots <t_n\le t_f$ and take(7) $$\begin{array}{c}\hfill P(t)=P_{\mathit{\tau }}=\sum _{j=1}^n{\mathit{\delta }}_{t_j},\end{array}$$(7) where ${\mathit{\delta }}_a$ represents the Dirac delta distribution with atom at $a$, then the weighted least squares criterion (6(6) $$\begin{array}{c}\hfill J_{\mathit{WLS}}(\overrightarrow{y},\overrightarrow{\mathit{\theta }})={\int }_{t_0}^{t_f}{[\overrightarrow{y}(t)-\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}(t)[\overrightarrow{y}(t)-\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})]{\mathit{dP}}_1(t),\end{array}$$(6) ) for a finite number of observations becomes$$\begin{array}{c}\hfill J_{\mathit{WLS}}^n(\overrightarrow{y},\overrightarrow{\mathit{\theta }})=\sum _{j=1}^n{[\overrightarrow{y}(t_j)-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}(t_j)[\overrightarrow{y}(t_j)-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$To select a useful distribution of time points and set of observation variables, we introduce the $N$ by $p$ sensitivity matrices $\left[\frac{\mathit{\partial }\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }\overrightarrow{\mathit{\theta }}}\right]$ and the $m$ by $p$ sensitivity matrices $\left[\frac{\mathit{\partial }\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }\overrightarrow{\mathit{\theta }}}\right]$ that are determined using the differential operator in row vector form $({\mathit{\partial }}_{{\mathit{\theta }}_1},{\mathit{\partial }}_{{\mathit{\theta }}_2},\dots ,{\mathit{\partial }}_{{\mathit{\theta }}_p})$ represented by ${\nabla }_{\overrightarrow{\mathit{\theta }}}$ and the observation operator defined in (2(2) $$\begin{array}{c}\hfill \overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\end{array}$$(2) ),(8) $$\begin{array}{cc}\hfill {\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{f}(t,\overrightarrow{\mathit{\theta }})& =\frac{\mathit{\partial }\overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }\overrightarrow{\mathit{\theta }}}\hfill \\ \hfill & =C\frac{\mathit{\partial }\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }\overrightarrow{\mathit{\theta }}}\hfill \\ \hfill & =C\left(\begin{array}{cccc}\hfill \frac{\mathit{\partial }{x}_1(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{x}_1(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \dots \hfill & \frac{\mathit{\partial }{x}_1(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \\ \hfill \frac{\mathit{\partial }{x}_2(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{x}_2(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \dots \hfill & \frac{\mathit{\partial }{x}_2(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & ⋮\hfill \\ \hfill \frac{\mathit{\partial }{x}_m(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{x}_m(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \dots \hfill & \frac{\mathit{\partial }{x}_m(t;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \end{array}\right)\hfill \\ \hfill & =C{\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}).\hfill \end{array}$$(8) Using the sensitivity matrix ${\nabla }_{\overrightarrow{\mathit{\theta }}}f(t,{\overrightarrow{\mathit{\theta }}}_0)$, we may formulate the Generalized Fisher Information Matrix (GFIM). Consider the set $\mathcal{C}\subset {\mathbb{R}}^{\mathbb{m}}$ of admissible observation maps and let ${\mathcal{P}}_2(\mathcal{C})$ represent the set of all bounded distributions $P_2(c)$ on $\mathcal{C}$. Then the GFIM may be written(9) $$\begin{array}{ccc}\hfill \mathcal{F}(P_1,P_2,{\overrightarrow{\mathit{\theta }}}_0)& \equiv \hfill & \hfill {\int }_{t_0}^{t_f}{\int }_{\mathcal{C}}\frac{1}{{\mathit{\sigma }}^2(t,c)}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0){\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0){\mathit{dP}}_2(c){\mathit{dP}}_1(t)\\ \hfill & ={\int }_{t_0}^{t_f}{\int }_{\mathcal{C}}\frac{1}{{\mathit{\sigma }}^2(t,c)}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}(c\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)){\nabla }_{\overrightarrow{\mathit{\theta }}}(c\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)){\mathit{dP}}_2(c){\mathit{dP}}_1(t).\hfill \end{array}$$(9) Taking $N$ different sampling maps in $\mathcal{C}$ represented by the $m$-dimensional row vectors $c_k$, $k=1,2,\dots ,N$, we construct the discrete distribution on $\mathcal{C}$(10) $$\begin{array}{c}\hfill P_C=\sum _{k=1}^N{\mathit{\delta }}_{c_k},\end{array}$$(10) where ${\mathit{\delta }}_a$ represents the Dirac delta distribution with atom at $a$. Using $P_C$ in (10(10) $$\begin{array}{c}\hfill P_C=\sum _{k=1}^N{\mathit{\delta }}_{c_k},\end{array}$$(10) ), we obtain the GFIM for multiple discrete observation methods taken continuously over $[t_0,t_f]$,(11) $$\begin{array}{cc}\hfill \mathcal{F}(P_1,P_C,{\overrightarrow{\mathit{\theta }}}_0)& ={\int }_{t_0}^{t_f}\sum _{k=1}^N\frac{1}{{\mathit{\sigma }}^2(t,c_k)}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}(c_k\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)){\nabla }_{\overrightarrow{\mathit{\theta }}}(c_k\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)){\mathit{dP}}_1(t)\hfill \\ \hfill & ={\int }_{t_0}^{t_f}\sum _{k=1}^N\frac{1}{{\mathit{\sigma }}^2(t,c_k)}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)c_k{}^{\text{T}}{c}_k{\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0){\mathit{dP}}_1(t)\hfill \\ \hfill & ={\int }_{t_0}^{t_f}\sum _{k=1}^N{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)c_k{}^{\text{T}}\frac{1}{{\mathit{\sigma }}^2(t,c_k)}{c}_k{\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0){\mathit{dP}}_1(t)\hfill \\ \hfill & ={\int }_{t_0}^{t_f}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)\sum _{k=1}^N\left(c_k{}^{\text{T}}\frac{1}{{\mathit{\sigma }}^2(t,c_k)}{c}_k\right){\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0){\mathit{dP}}_1(t)\hfill \\ \hfill & ={\int }_{t_0}^{t_f}{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0)(C{}^{\text{T}}{V}_0^{-1}(t)C){\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t;{\overrightarrow{\mathit{\theta }}}_0){\mathit{dP}}_1(t),\hfill \end{array}$$(11) where $C=(c_1,c_2,\dots ,c_N){}^{\text{T}}\in {\mathbb{R}}^{\mathbb{N}\times \mathbb{m}}$ is the observation operator in (2(2) $$\begin{array}{c}\hfill \overrightarrow{f}(t;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\end{array}$$(2) ) and (4(4) $$\begin{array}{c}\hfill \overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})=C\overrightarrow{x}(t_j;\overrightarrow{\mathit{\theta }}),j=1,2,\dots ,n,\end{array}$$(4) ) and $V_0(t)\in {\mathbb{R}}^{\mathbb{N}\times \mathbb{N}}$ is the covariance matrix as described in (3(3) $$\begin{array}{c}\hfill \overrightarrow{Y}(t)=\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t),t\in [t_0,t_f],\end{array}$$(3) ). Applying the distribution $P_{\mathit{\tau }}$ as described in (7(7) $$\begin{array}{c}\hfill P(t)=P_{\mathit{\tau }}=\sum _{j=1}^n{\mathit{\delta }}_{t_j},\end{array}$$(7) ) to the GFIM (12(12) $$\begin{array}{c}\hfill F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0)=F(P_{\mathit{\tau }},P_C,{\overrightarrow{\mathit{\theta }}}_0)=\sum _{j=1}^n{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t_j;{\overrightarrow{\mathit{\theta }}}_0)C{}^{\text{T}}{V}_0^{-1}(t_j)C{\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t_j;{\overrightarrow{\mathit{\theta }}}_0).\end{array}$$(12) ) for discrete observation operators measured continuously yields the discrete $p\times p$ FIM for discrete observation operators measured at discrete times(12) $$\begin{array}{c}\hfill F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0)=F(P_{\mathit{\tau }},P_C,{\overrightarrow{\mathit{\theta }}}_0)=\sum _{j=1}^n{\nabla }_{\overrightarrow{\mathit{\theta }}}{}^{\text{T}}\overrightarrow{x}(t_j;{\overrightarrow{\mathit{\theta }}}_0)C{}^{\text{T}}{V}_0^{-1}(t_j)C{\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{x}(t_j;{\overrightarrow{\mathit{\theta }}}_0).\end{array}$$(12) This describes the amount of information about the $p$ parameters of interest that is captured by the observed quantities described by the sampling maps $c_k$, $k=1,2,\dots ,N$, listed in $C$, when they are measured at the time points in $\mathit{\tau }$.

The questions of determining the best (in some sense) $C$ and $\mathit{\tau }$ are important questions in the optimal design of an experiment. Recall that the set of time points $\mathit{\tau }$ has an associated distribution $P_1(\mathit{\tau })=P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])$, where ${\mathcal{P}}_1([t_0,t_f])$ is the set of all bounded distributions on $[t_0,t_f]$. Similarly, the set of sampling maps $\{c_k\}$ has an associated bounded distribution $P_C\in {\mathcal{P}}_2(\mathcal{C})$. Define the space of bounded distributions $\mathcal{P}([t_0,t_f]\times \mathcal{C})={\mathcal{P}}_1([t_0,t_f])\times {\mathcal{P}}_2(\mathcal{C})$ with elements $P=(P_{\mathit{\tau }},P_C)\in \mathcal{P}$. Without loss of generality, assume that $\mathcal{C}\subset {\mathbb{R}}^{\mathbb{m}}$ is closed and bounded, and assume that there exists a functional $\mathcal{J}:{\mathbb{R}}^{\mathbb{p}\times \mathbb{p}}\to {\mathbb{R}}^{+}$ of the GFIM (10(10) $$\begin{array}{c}\hfill P_C=\sum _{k=1}^N{\mathit{\delta }}_{c_k},\end{array}$$(10) ). Then the optimal design problem associated with $\mathcal{J}$ is selecting a distribution $\hat{P}\in \mathcal{P}$ such that(13) $$\begin{array}{c}\hfill \mathcal{J}(\mathcal{F}(\hat{P},{\overrightarrow{\mathit{\theta }}}_0))=\underset{P\in \mathcal{P}}{\min }\mathcal{J}(\mathcal{F}(P,{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(13) where $\mathcal{J}$ depends continuously on the elements of $\mathcal{F}(P,{\overrightarrow{\mathit{\theta }}}_0)$.

The Prohorov metric [8] provides a general theoretical framework for the existence of $\hat{P}$ and approximation in $\mathcal{P}([t_0,t_f]\times \mathcal{C})$ (a general theoretical framework is developed in [2, 9]). The application of the Prohorov metric to optimal design problems formulated as (14(14) $$\begin{array}{c}\hfill \hat{C}={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F(\hat{\mathit{\tau }},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill \hat{\mathit{\tau }}={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },\hat{C},{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(14) ) is explained more fully in [2]: briefly, define the Prohorov metric $\mathit{\rho }$ on the space $\mathcal{P}([t_0,t_f]\times \mathcal{C})$, and consider the metric space $(\mathcal{P}([t_0,t_f]\times \mathcal{C}),\mathit{\rho })$. Since $[t_0,t_f]\times \mathcal{C}$ is compact, $(\mathcal{P}([t_0,t_f]\times \mathcal{C}),\mathit{\rho })$ is also compact. Additionally, by the properties of the Prohorov metric, $(\mathcal{P}([t_0,t_f]\times \mathcal{C}),\mathit{\rho })$ is complete and separable. Therefore, an optimal distribution $\hat{P}$ exists and may be approximated by a discrete distribution.

The formulation of the cost functional (14(14) $$\begin{array}{c}\hfill \hat{C}={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F(\hat{\mathit{\tau }},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill \hat{\mathit{\tau }}={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },\hat{C},{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(14) ) may take many forms. We focus on the use of traditional optimal design methods, D-optimal, E-optimal or SE-optimal design criteria, to determine the form of $\mathcal{J}$. Each of these design criteria are functions of the inverse of the FIM (assumed hereafter to be invertible) defined in (13(13) $$\begin{array}{c}\hfill \mathcal{J}(\mathcal{F}(\hat{P},{\overrightarrow{\mathit{\theta }}}_0))=\underset{P\in \mathcal{P}}{\min }\mathcal{J}(\mathcal{F}(P,{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(13) ).

In D-optimal design, the cost functional is written$$\begin{array}{c}\hfill {\mathcal{J}}_D(F)=\mathrm{d}\mathit{et}\left(F{(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0)}^{-1}\right)=\frac{1}{\mathrm{d}\mathit{et}(F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0))}.\end{array}$$By minimizing ${\mathcal{J}}_D$, we minimize the volume of the confidence interval ellipsoid describing the uncertainty in our parameter estimates. Since $F$ is symmetric and positive semi-definite, ${\mathcal{J}}_D(F)\ge 0$. Additionally, since $F$ is assumed invertible, ${\mathcal{J}}_D(F)\ne 0$, therefore, ${\mathcal{J}}_D:{\mathbb{R}}^{\mathbb{p}\times \mathbb{p}}\to {\mathbb{R}}^{+}$.

In E-optimal design, the cost functional is ${\mathcal{J}}_E$ is the largest eigenvalue of ${(F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0))}^{-1}$, or equivalently$${\mathcal{J}}_E(F)=\max \frac{1}{\mathrm{e}\mathit{ig}(F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0))}.$$To obtain a smaller standard error, we must reduce the length of the principal axis of the confidence interval ellipsoid. Since an eigenvalue $\mathit{\lambda }$ solves $\mathrm{d}\mathit{et}(F-\mathit{\lambda }I)=0$, an eigenvalue of $\mathit{\lambda }=0$ would mean $\mathrm{d}\mathit{et}(F)=0$, or that $F$ is not invertible. Since $F$ is positive definite, all eigenvalues are therefore positive. Thus, ${\mathcal{J}}_E:{\mathbb{R}}^{\mathbb{p}\times \mathbb{p}}\to {\mathbb{R}}^{+}$.

In SE-optimal design, ${\mathcal{J}}_{\mathit{SE}}$ is a sum of the elements on the diagonal of ${(F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0))}^{-1}$ weighted by the respective parameter values,[2, 4] written$$\begin{array}{c}\hfill {\mathcal{J}}_{\mathit{SE}}(F)=\sum _{i=1}^p\frac{{(F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0)))}_{i,i}^{-1}}{{\mathit{\theta }}_{0,i}^2}.\end{array}$$Thus in SE-optimal design, the goal is to minimize the sum of squared errors of the parameters normalized by the true parameter values. As the diagonal elements of $F^{-1}$ are all positive and all parameters are assumed non-zero in $\overrightarrow{\mathit{\theta }}\in {\mathbb{R}}^{\mathbb{p}}$, ${\mathcal{J}}_{\mathit{SE}}:{\mathbb{R}}^{\mathbb{p}\times \mathbb{p}}\to {\mathbb{R}}^{+}$.

In [4], it is shown that the D-, E- and SE-optimal design criteria select different time grids and yield different standard errors. We expect that these design cost functionals will also choose different observation variables (maps) in order to minimize different dimensions of the confidence interval ellipsoid.

Algorithm and optimization constraints

In most optimal design problems, there is not a continuum of measurement possibilities that may be used; rather, there are $N^{\ast }<\infty$ possible observation maps $c$. Denote this set as ${\mathcal{C}}_{N^{\ast }}\subset {\mathbb{R}}^{\mathbb{m}}$. While we may still use the Prohorov metric-based framework to guarantee existence and convergence of (14(14) $$\begin{array}{c}\hfill \hat{C}={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F(\hat{\mathit{\tau }},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill \hat{\mathit{\tau }}={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },\hat{C},{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(14) ), we have a stronger result first proposed in [5] that is useful in numerical implementation. Because ${\mathcal{C}}_{N^{\ast }}$ is finite, all probability distributions made from the elements of ${\mathcal{C}}_{N^{\ast }}$ have the form $P_2(\{c_k\})=P_C=\sum _{k=1}^N{\mathit{\delta }}_{c_k}$ for a fixed $N$. Moreover, the set of all distributions that use $N$ sampling methods ${\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})$ is also finite. For a fixed distribution of time points $P_{\mathit{\tau }}$, we may compute using (13(13) $$\begin{array}{c}\hfill \mathcal{J}(\mathcal{F}(\hat{P},{\overrightarrow{\mathit{\theta }}}_0))=\underset{P\in \mathcal{P}}{\min }\mathcal{J}(\mathcal{F}(P,{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(13) ) the set of all possible FIM $F(P_{\mathit{\tau }},P_C,\overrightarrow{\mathit{\theta }})$ that could be formulated from $c\in {\mathcal{C}}_{N^{\ast }}$. By the properties of matrix multiplication and addition, this set is also finite. Then the functional (14(14) $$\begin{array}{c}\hfill \hat{C}={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F(\hat{\mathit{\tau }},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill \hat{\mathit{\tau }}={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },\hat{C},{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(14) ) applied to all $F$ in the set produces a finite set contained in ${\mathbb{R}}^{+}$. Because this set is finite, it is well ordered by the relation $\le$ and therefore has a minimal element. Thus for any distribution of time points $P_{\mathit{\tau }}$, we may find at least one solution $\widehat{P_C}\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})$. Moreover, $\widehat{P_C}$ may be determined by a search over all matrices $C=(c_1,c_2,\dots ,c_N){}^{\text{T}}$ formed by $N$ elements from ${\mathcal{C}}_{N^{\ast }}$. Therefore, for a fixed $P_{\mathit{\tau }}$ and $N\le N^{\ast }<\infty$ a global optimal set of $N$ sampling methods may be determined.

Due to the computational demands of performing non-linear optimization for $n$ time points and $N$ observation maps (for a total of $n+N$ dimensions), and to the difference in techniques between searching for an optimal $P_C$ in the finite set ${\mathcal{C}}_{N^{\ast }}$ and searching for an optimal distribution of $n$ sampling times, we instead solve the coupled set of equations (14) $$\begin{array}{c}\hfill \hat{C}={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F(\hat{\mathit{\tau }},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill \hat{\mathit{\tau }}={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },\hat{C},{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(14) where $C\in {\mathbb{R}}^{\mathbb{N}\times \mathbb{m}}$ represents a set of $N$ sampling maps and $\mathit{\tau }=\{t_j{\}}_{j=1}^n$, $t_0\le t_1<t_2<\dots <t_n\le t_f$, is an ordered set of $n$ sampling times. These equations are solved iteratively as (15) $$\begin{array}{c}\hfill {\hat{C}}_i={\mathit{argmin}}_{\{C|P_C\in {\mathcal{P}}_2^N({\mathcal{C}}_{N^{\ast }})\}}\mathcal{J}(F({\hat{\mathit{\tau }}}_{i-1},C,{\overrightarrow{\mathit{\theta }}}_0)),\\ \hfill {\hat{\mathit{\tau }}}_i={\mathit{argmin}}_{\{\mathit{\tau }|P_{\mathit{\tau }}\in {\mathcal{P}}_1([t_0,t_f])\}}\mathcal{J}(F(\mathit{\tau },{\hat{C}}_i,{\overrightarrow{\mathit{\theta }}}_0)),\end{array}$$(15) where $\mathcal{J}$ is the D-, E- or SE-optimal design criterion. We begin by solving for ${\hat{C}}_1$ where ${\hat{\mathit{\tau }}}_0$ is specified by the user. The system (17(17) $$\begin{array}{c}\hfill {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(17) )-(18(18) $$\begin{array}{c}\hfill V_0\approx \hat{V}=\mathrm{d}\mathit{iag}\left(\frac{1}{n-p}\sum _{j=1}^n[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T\right),\end{array}$$(18) ) is solved until $|\mathcal{J}(F({\hat{\mathit{\tau }}}_i,{\hat{C}}_i,{\overrightarrow{\mathit{\theta }}}_0))-\mathcal{J}(F({\hat{\mathit{\tau }}}_{i-1},{\hat{C}}_{i-1},{\overrightarrow{\mathit{\theta }}}_0))|<\mathit{ϵ}$ or until ${\hat{C}}_i={\hat{C}}_{i-1}$. For each iteration, (17(17) $$\begin{array}{c}\hfill {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(17) ) is solved using a global search over all possible $C$. Since the sensitivity equations cannot be easily solved for in the models chosen to illustrate our method, we use a modified version of tssolve.m by A. Attarian,[10] which implements the myAD package developed by M. Fink.[11]

Solving (18(18) $$\begin{array}{c}\hfill V_0\approx \hat{V}=\mathrm{d}\mathit{iag}\left(\frac{1}{n-p}\sum _{j=1}^n[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T\right),\end{array}$$(18) ) requires using a non-linear constrained iterative optimization algorithm. While MATLAB’s fmincon is a natural choice for such problems, as reported in [4], it does not perform well in this situation. Instead, we use SolvOpt developed by A. Kuntsevich and F. Kappel [12] (which utilizes a modified version of Shor’s $r$-algorithm) to search for an optimal distribution local to an initial uniformly spaced time point distribution. There exist many types of constraints that may be placed on this optimization. The four constraints used in [4] are

1. Optimize all time points such that $t_0\le t_1\le t_2\le ...\le t_n\le t_f$. This method optimizes $n$ time points.

2. The initial and final time points are fixed as $t_1=t_0$ and $t_n=t_f$. The routine then optimizes over the remaining $n-2$ time points such that $t_j\le t_{j+1}$.

3. Optimize the time steps ${\mathit{\nu }}_j\ge 0$. Fix $t_1=t_0$ and $t_n=t_f$, and the remaining time points may be found by $t_{j+1}=t_j+{\mathit{\nu }}_j$, $j=1,2,\dots ,n-2$. Additionally, $t_f-t_0\ge \sum _{j=1}^{n-2}{\mathit{\nu }}_j$. This routine also optimizes over $n-2$ variables.

4. Optimize the time steps ${\mathit{\nu }}_j\ge 0$. Fix $t_1=t_0$. The remaining time points may be found by $t_{j+1}=t_j+{\mathit{\nu }}_j$, $j=1,2,\dots ,n-1$ such that $t_f-t_0=\sum _{j=1}^{n-1}{\mathit{\nu }}_j$. This method optimizes over $n-1$ variables.

We select for our use two constraints, (C2) and (C3), to reduce the complexity of the problem of time point distribution selection. Once either of the convergence requirements are met and $\hat{C}$ and $\hat{\mathit{\tau }}$ are determined, we compute standard errors using the asymptotic theory described in the next section.

Standard errors

In order to compare the ability of different optimal design criteria to minimize uncertainty in parameter estimation, we compute the standard errors associated with these parameters. We begin by selecting an ODE system, a nominal set of parameters $\overrightarrow{\mathit{\theta }}$ that we would estimate, the start and end times of the experiment $t_0$ and $t_f$, the number $N$ of sampling times $n$, and the number of observation maps we wish to use. After an optimal $\mathit{\tau }$ and $C$ are determined according to one of the three previously described optimal design methods, we compute the standard errors for the parameters in $\overrightarrow{\mathit{\theta }}$. There are multiple techniques [4] available to compute standard errors; here we choose to use asymptotic theory due to its ease of implementation.

Asymptotic theory for standard errors

If we assume that the covariance matrix $V_0(t)$ is constant over time ($V_0(t)\equiv V_0=\mathrm{V}\mathit{ar}(\overrightarrow{\mathcal{E}}(t_j))=\mathrm{d}\mathit{iag}({\mathit{\sigma }}_{0,1}^2,{\mathit{\sigma }}_{0,2}^2,\dots ,{\mathit{\sigma }}_{0,N}^2)$), then we may use an ordinary least squares (OLS) framework to estimate standard errors. Once an optimal $\mathit{\tau }=\{t_j{\}}_{j=1}^N$, $t_0\le t_1<t_2<\dots <t_n\le t_f$, and $C$ are determined, we obtain data from an experiment or simulate data $\{y_j\}$ as a realization of the random process $\{Y_j\}$ described in (5(5) $$\begin{array}{c}\hfill {\overrightarrow{Y}}_j=\overrightarrow{f}(t_j;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t_j),j=1,2,\dots ,n,\end{array}$$(5) ), and then we estimate the parameters in $\overrightarrow{\mathit{\theta }}$ by solving the inverse problem using the OLS criterion.[1] The discrete OLS estimator is defined as (16) $$\begin{array}{c}\hfill {\overrightarrow{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{Y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}[{\overrightarrow{Y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})],\end{array}$$(16) where $\mathrm{\Theta }$ is the set of all possible values of $\overrightarrow{\mathit{\theta }}$, such that each element of the difference vector ${\overrightarrow{Y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})$ is weighted using the variance of its corresponding sampling maps. One realization of this problem using data ${\overrightarrow{y}}_j$, $j=1,2,\dots ,n$, is written (17) $$\begin{array}{c}\hfill {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(17) However, calculating ${\hat{\mathit{\theta }}}_{\mathrm{OLS}}$ still requires the unknown $V_0$. If the number of parameters $p$ of a system is sufficiently small and number of observations $n$ large so that $p<n$, then we may calculate the bias adjusted estimate of the variances(18) $$\begin{array}{c}\hfill V_0\approx \hat{V}=\mathrm{d}\mathit{iag}\left(\frac{1}{n-p}\sum _{j=1}^n[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T\right),\end{array}$$(18) and find the estimate of ${\overrightarrow{\mathit{\theta }}}_0$ using (19) $$\begin{array}{c}\hfill {\overrightarrow{\mathit{\theta }}}_0\approx {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{\hat{V}}^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(19) Therefore, finding ${\hat{\mathit{\theta }}}_{\mathrm{OLS}}$ when $V_0$ is unknown requires solving the coupled system of equations (21(21) $$\begin{array}{c}\hfill {\mathit{\chi }}_j(\overrightarrow{\mathit{\theta }})={\mathit{\chi }}_j^n(\overrightarrow{\mathit{\theta }})=\left(\begin{array}{cccc}\hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \cdots \hfill & \hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \cdots \hfill & \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \end{array}\right).\end{array}$$(21) ) and (22(22) $$\begin{array}{c}\hfill {\mathrm{\Sigma }}_0^n\approx {\hat{\mathrm{\Sigma }}}^n={(\sum _{j=1}^n{\mathit{\chi }}_j^T({\hat{\mathit{\theta }}}_{\mathrm{OLS}}){\hat{V}}^{-1}{\mathit{\chi }}_j({\hat{\mathit{\theta }}}_{\mathrm{OLS}}))}^{-1}.\end{array}$$(22) ).

We may utilize the asymptotic properties of the OLS minimizer (19(19) $$\begin{array}{c}\hfill {\overrightarrow{\mathit{\theta }}}_0\approx {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{\hat{V}}^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(19) ) to learn about the behaviour of the model (1(1) $$\begin{array}{cc}\hfill \frac{d\overrightarrow{x}}{\mathit{dt}}(t)& =\overrightarrow{g}(t,\overrightarrow{x}(t;\overrightarrow{\mathit{\theta }}),\overrightarrow{q}),t\in [t_0,t_f],\hfill \\ \hfill \overrightarrow{x}(t_0;\overrightarrow{\mathit{\theta }})& ={\overrightarrow{x}}_0,\hfill \end{array}$$(1) ) and (3(3) $$\begin{array}{c}\hfill \overrightarrow{Y}(t)=\overrightarrow{f}(t;{\overrightarrow{\mathit{\theta }}}_0)+\overrightarrow{\mathcal{E}}(t),t\in [t_0,t_f],\end{array}$$(3) ). As the number of samples $n\to \infty$, ${\overrightarrow{\mathit{\theta }}}_{\mathrm{OLS}}$ has the following properties [1, 13, 14]$$\begin{array}{c}\hfill {\overrightarrow{\mathit{\theta }}}_{\mathrm{OLS}}\sim \mathcal{N}({\overrightarrow{\mathit{\theta }}}_0,{\mathrm{\Sigma }}_0^n)\approx \mathcal{N}({\hat{\mathit{\theta }}}_{\mathrm{OLS}},{\hat{\mathrm{\Sigma }}}^n),\end{array}$$where(20) $$\begin{array}{c}\hfill {\mathrm{\Sigma }}_0^n\approx {(\sum _{j=1}^n{\mathit{\chi }}_j^T({\overrightarrow{\mathit{\theta }}}_0)V_0^{-1}{\mathit{\chi }}_j({\overrightarrow{\mathit{\theta }}}_0))}^{-1}\end{array}$$(20) is the $p\times p$ covariance matrix, and ${\mathit{\chi }}_j(\overrightarrow{\mathit{\theta }})={\mathit{\chi }}_j^n(\overrightarrow{\mathit{\theta }})={\nabla }_{\overrightarrow{\mathit{\theta }}}\overrightarrow{f}(t_j;{\overrightarrow{\mathit{\theta }}}_0)$ is the $N\times p$ matrix(21) $$\begin{array}{c}\hfill {\mathit{\chi }}_j(\overrightarrow{\mathit{\theta }})={\mathit{\chi }}_j^n(\overrightarrow{\mathit{\theta }})=\left(\begin{array}{cccc}\hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \cdots \hfill & \hfill \frac{\mathit{\partial }{f}_1(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_1}\hfill & \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_2}\hfill & \hfill \cdots \hfill & \hfill \frac{\mathit{\partial }{f}_N(t_j;\overrightarrow{\mathit{\theta }})}{\mathit{\partial }{\mathit{\theta }}_p}\hfill \end{array}\right).\end{array}$$(21) The approximation ${\hat{\mathrm{\Sigma }}}^n$ to the covariance matrix ${\mathrm{\Sigma }}_0^n$ is(22) $$\begin{array}{c}\hfill {\mathrm{\Sigma }}_0^n\approx {\hat{\mathrm{\Sigma }}}^n={(\sum _{j=1}^n{\mathit{\chi }}_j^T({\hat{\mathit{\theta }}}_{\mathrm{OLS}}){\hat{V}}^{-1}{\mathit{\chi }}_j({\hat{\mathit{\theta }}}_{\mathrm{OLS}}))}^{-1}.\end{array}$$(22) We may use ${\hat{\mathrm{\Sigma }}}^n$ to approximate the standard errors of each parameter in ${\hat{\mathit{\theta }}}_{\mathrm{OLS}}$. For the $k$th element of ${\hat{\mathit{\theta }}}_{\mathrm{OLS}}$, written ${\hat{\mathit{\theta }}}_{\mathrm{OLS}\mathrm{,}\mathrm{k}}$, the asymptotic standard error is$$\mathit{ASE}({\overrightarrow{\mathit{\theta }}}_{0,k})=\sqrt{{\hat{\mathrm{\Sigma }}}_{0,\mathit{kk}}^n}\approx \mathit{ASE}({\hat{\mathit{\theta }}}_{\mathrm{OLS}\mathrm{,}\mathrm{k}})=\sqrt{{\hat{\mathrm{\Sigma }}}_{\mathit{kk}}^n},$$where ${\hat{\mathrm{\Sigma }}}_{0,\mathit{kk}}^n$ is the element in the $k$th row and $k$th column of ${\mathrm{\Sigma }}_0^n$, and ${\hat{\mathrm{\Sigma }}}_{\mathit{kk}}^n$ is the corresponding element in ${\hat{\mathrm{\Sigma }}}^n$. Additionally, since the FIM is defined to be the inverse of the covariance matrix, we may approximate the FIM using (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) by $F(\mathit{\tau },C,{\overrightarrow{\mathit{\theta }}}_0)\approx F(\hat{\mathit{\tau }},\hat{C},{\hat{\mathit{\theta }}}_{\mathrm{OLS}})={({\hat{\mathrm{\Sigma }}}^n)}^{-1}$.

Example 1: HIV model

After validating code results for time point selection on simple models such as those in [4], we examined the performance of both the time point and observable operator selection algorithms on the log-scaled version of the HIV model developed in [15]. While the analytic solution of this system cannot easily be found, this model has been studied, improved and successfully fit to and indeed validated with several sets of longitudinal data using parameter estimation techniques.[7, 16, 17] Additionally, the sampling or observation operators used to collect data in a clinical setting as well as the relative usefulness of these sampling techniques are known.[7] The model includes uninfected and infected CD$4^{+}$ T-cells, called type 1 target cells ($T_1$ and $T_1^{\ast }$, respectively), uninfected and infected macrophages (subsequently determined to more likely be resting or inactive CD$4^{+}$ T-cells), called type 2 target cells ($T_2$ and $T_2^{\ast }$), infectious free virus $V_I$, and immune response $E$ produced by cytotoxic T-lymphocytes CD$8^{+}$. The HIV model with treatment function $u(t)$ is given by(23) $$\begin{array}{cc}\hfill {\stackrel{·}{T}}_1& ={\mathit{\lambda }}_1-d_1{T}_1-(1-{\mathit{ϵ}}_{1}u(t))k_1{V}_I{T}_1,\hfill \\ \hfill {\stackrel{·}{T}}_2& ={\mathit{\lambda }}_2-d_2{T}_2-(1-f{\mathit{ϵ}}_{1}u(t))k_2{V}_I{T}_2,\hfill \\ \hfill {\stackrel{·}{T}}_1^{\ast }& =(1-{\mathit{ϵ}}_{1}u(t))k_1{V}_I{T}_1-\mathit{\delta }{T}_1^{\ast }-m_1{\mathit{ET}}_1^{\ast },\hfill \\ \hfill {\stackrel{·}{T}}_2^{\ast }& =(1-f{\mathit{ϵ}}_{1}u(t))k_2{V}_I{T}_2-\mathit{\delta }{T}_2^{\ast }-m_2{\mathit{ET}}_2^{\ast },\hfill \\ \hfill \stackrel{·}{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-[c+(1-{\mathit{ϵ}}_{2}u(t)){10}^3{k}_1{T}_1+(1-f{\mathit{ϵ}}_{1}u(t)){10}^3{k}_2{T}_2]V_I,\hfill \\ \hfill \stackrel{·}{E}& ={\mathit{\lambda }}_E+b_E\frac{T_1^{\ast }+T_2^{\ast }}{T_1^{\ast }+T_2^{\ast }+K_b}E-d_E\frac{T_1^{\ast }+T_2^{\ast }}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E.\hfill \end{array}$$(23) The log-scaled HIV model, which is used to alleviate difficulties due to the large differences in scales of the variables and the parameters, is(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) where $T_1={10}^{x_1}$, $T_2={10}^{x_2}$, $T_1^{\ast }={10}^{x_3}$, $T_2^{\ast }={10}^{x_4}$, $V_I={10}^{x_5}$ and $E={10}^{x_6}$.

In [7] this model’s parameters are estimated for each of 45 different patients who were in a treatment programme for HIV at Massachusetts General Hospital (MGH). These individuals experienced interrupted treatment schedules, in which the patient did not take any medication for viral load control. Seven of these patients adhered to a structured treatment interruption schedule planned by the clinician. We use the parameters estimated to fit the data of one of these patients, Patient 4 in [7], as our “true” parameters ${\overrightarrow{\mathit{\theta }}}_0$ for this model. This patient was chosen because the patient continued treatment for an extended period of time (1919 days) and the corresponding data set contains 158 measurements of viral load and 107 measurements of CD4 cell count ($T_1+T_1^{\ast }$) that exhibit a response to interruption in treatment, and the estimated parameters yield a model exhibiting trends similar to that in the data.

Table 1 Values of parameters in the HIV model (26).

Parameter	Value	Unit
${\mathit{\lambda }}_1$	4.633	$\frac{\text{cells}}{\mathit{\mu }\text{ml-blood}·\text{day}}$
$d_1$	0.004533	$\frac{1}{\text{day}}$
$k_1$	1.976e-6	$\frac{\text{ml}}{\text{virions}·\text{day}}$
${\mathit{ϵ}}_1$	${10}^{0.6017}$	-
${\mathit{ϵ}}_2$	${10}^{0.5403}$	-
$m_1$	0.02439	$\frac{\mathit{\mu }\text{ml}}{\text{cells}·\text{day}}$
$\mathit{\delta }$	0.1865	$\frac{1}{\text{day}}$
$f$	${10}^{0.53915}$	-
${\mathit{\lambda }}_E$	0.009909	$\frac{\text{cells}}{\mathit{\mu }\text{ml-blood}·\text{day}}$
$b_E$	0.09785	$\frac{1}{\text{day}}$
$K_b$	0.3909	$\frac{\text{cells}}{\mathit{\mu }\text{ml-blood}}$
${\mathit{\lambda }}_2$	0.1001	$\frac{\text{cells}}{\mathit{\mu }\text{ml-blood}·\text{day}}$
$d_2$	0.02211	$\frac{1}{\text{day}}$
$k_2$	5.529e-4	$\frac{\text{ml}}{\text{virions}·\text{day}}$
$m_2$	0.013099	$\frac{\mathit{\mu }\text{ml}}{\text{cells}·\text{day}}$
$c$	19.36	$\frac{1}{\text{day}}$
$N_T$	19.04	$\frac{\text{virions}}{\text{cell}}$
${\mathit{\delta }}_E$	0.0703	$\frac{1}{\text{day}}$
$d_E$	0.1021	$\frac{1}{\text{day}}$
$K_d$	0.8379	$\frac{\text{cells}}{\mathit{\mu }\text{ml-blood}}$

Sensitivity analysis performed in [15] and parameter subset selection carried out in [18] identified subsets of the 20 parameters and six initial conditions that would likely be reliably estimated when solving the corresponding inverse problems. Based on their results, we treat the subset of parameters $\overrightarrow{\mathit{\theta }}=({\mathit{\lambda }}_1,d_1,{\mathit{ϵ}}_1,k_1,{\mathit{ϵ}}_2,N_T,c,b_E,x_1^0,x_2^0,x_5^0)$ as unknown and fix all other parameters. The values for the fixed parameters and ${\overrightarrow{\mathit{\theta }}}_0$ are computed in [7] and given in Table 1. It is important to choose parameters to which the model is sensitive; a poor choice for the components of $\overrightarrow{\mathit{\theta }}$ will negatively affect sensitivity matrices and may lead to a near-singular FIM. Based on currently available measurement methods, we allow the possible types of observations including (1) infectious virus $x_5$, (2) immune response $x_6$, (3) total activated CD4 cells $x_1+x_3$ and (4) type 2 (resting or unactivated) target cells $x_2+x_4$, each with an assumed error variance of $10\%$ of the initial variable values given by ${\overrightarrow{x}}^0=(3.0799,1.2443,1.7899,-0.2150,5.9984,-0.7251){}^{\text{T}}$.

HIV observable selection results, times fixed

To simulate the experience of a clinician gathering data as a patient regularly returns for scheduled testing, we fix the sampling times and choose the optimal observables. We consider choices of $N=1,2,3$ sampling operators out of the four possible observables, all $N$ of which will be measured at $n=51,101,201,401$ evenly spaced times over 2000 days, corresponding to measurements every 40, 20, 10 and 5 days, respectively. The $N$ optimal sampling maps are determined for each of the three optimal design criteria, and the asymptotic standard errors (ASE) are calculated after carrying out the corresponding inverse problem calcualtions.

Table 2 Number of observables, number of time points, observables selected by D-optimal cost functional, and the minimum and maximum standard error and associated parameter for the parameter subset in the HIV model (27).

N	n	Observables	min(ASE)	max(ASE)
1	51	$x_1+x_3$	ASE$({\mathit{\lambda }}_1)=0.18$	ASE$({\mathit{\lambda }}_E)=6.35$
1	101	$x_1+x_3$	ASE$({\mathit{\lambda }}_1)=0.13$	ASE$({\mathit{\lambda }}_E)=4.40$
1	201	$x_1+x_3$	ASE$({\mathit{\lambda }}_1)=0.091$	ASE$({\mathit{\lambda }}_E)=3.03$
1	401	$x_1+x_3$	ASE$({\mathit{\lambda }}_1)=0.065$	ASE$({\mathit{\lambda }}_E)=2.13$
2	51	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.095$	ASE$(x_5^0)=2.31$
2	101	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.068$	ASE$(x_5^0)=1.52$
2	201	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.047$	ASE$(x_5^0)=1.26$
2	401	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.033$	ASE$(x_5^0)=1.13$
3	51	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.045$	ASE$(x_5^0)=2.26$
3	101	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.032$	ASE$(x_5^0)=1.43$
3	201	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.022$	ASE$(x_5^0)=1.23$
3	401	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.015$	ASE$(x_5^0)=1.12$

Table 3 Number of observables, number of time points, observables selected by E-optimal cost functional, and the minimum and maximum standard error and associated parameter for the parameter subset in the HIV model (27).

N	n	Observables	min(ASE)	max(ASE)
1	51	$x_5$	ASE$(d_1)=0.27$	ASE$({\mathit{\lambda }}_E)=4.27$
1	101	$x_5$	ASE$(d_1)=0.19$	ASE$({\mathit{\lambda }}_E)=3.11$
1	201	$x_5$	ASE$(d_1)=0.13$	ASE$({\mathit{\lambda }}_E)=2.27$
1	401	$x_5$	ASE$(d_1)=0.094$	ASE$({\mathit{\lambda }}_E)=1.63$
2	51	$x_5$, $x_2+x_4$	ASE$(d_1)=0.12$	ASE$({\mathit{\lambda }}_E)=2.18$
2	101	$x_5$, $x_2+x_4$	ASE$(d_1)=0.095$	ASE$({\mathit{\lambda }}_E)=1.52$
2	201	$x_5$, $x_2+x_4$	ASE$(d_1)=0.065$	ASE$({\mathit{\lambda }}_E)=1.10$
2	401	$x_5$, $x_1+x_3$	ASE$({\mathit{\lambda }}_1)=0.042$	ASE$({\mathit{\lambda }}_E)=0.86$
3	51	$x_5$, $x_6$, $x_1+x_3$	ASE$({\mathit{\lambda }}_E)=0.045$	ASE$(x_5^0)=0.77$
3	101	$x_5$, $x_6$, $x_1+x_3$	ASE$({\mathit{\lambda }}_E)=0.032$	ASE$(x_5^0)=0.73$
3	201	$x_5$, $x_6$, $x_1+x_3$	ASE$({\mathit{\lambda }}_E)=0.022$	ASE$(x_5^0)=0.69$
3	401	$x_5$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.032$	ASE$(x_5^0)=0.65$

Table 4 Number of observables, number of time points, observables selected by SE-optimal cost functional, and the minimum and maximum standard error and associated parameter for the parameter subset in the HIV model (27).

N	n	Observables	min(ASE)	max(ASE)
1	51	$x_5$	ASE$(d_1)=0.27$	ASE$({\mathit{\lambda }}_E)=4.27$
1	101	$x_5$	ASE$(d_1)=0.19$	ASE$({\mathit{\lambda }}_E)=3.11$
1	201	$x_5$	ASE$(d_1)=0.13$	ASE$({\mathit{\lambda }}_E)=2.27$
1	401	$x_5$	ASE$(d_1)=0.094$	ASE$({\mathit{\lambda }}_E)=1.63$
2	51	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.095$	ASE$(x_5^0)=2.31$
2	101	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.068$	ASE$(x_5^0)=1.52$
2	201	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.047$	ASE$(x_5^0)=1.26$
2	401	$x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_1)=0.033$	ASE$(x_5^0)=1.13$
3	51	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.045$	ASE$(x_5^0)=2.26$
3	101	$x_6$, $x_1+x_3$, $x_2+x_4$	ASE$({\mathit{\lambda }}_E)=0.032$	ASE$(x_5^0)=1.49$
3	201	$x_5$, $x_6$, $x_1+x_3$	ASE$({\mathit{\lambda }}_E)=0.022$	ASE$(x_5^0)=0.69$
3	401	$x_5$, $x_6$, $x_1+x_3$	ASE$({\mathit{\lambda }}_E)=0.015$	ASE$(x_5^0)=0.67$

Tables 2, 3 and 4 display the optimal observation operators determined by the D-, E- and SE-optimal design cost functions, respectively, as well as the lowest and highest ASE. In all three optimal design criteria, there was a distinct best choice of observables (listed in Tables 2, 3 and 4) for each pair of $n$ and $N$. When only $N=1$ observable could be measured, each design criterion consistently picked the same observable for all $n$; similarly, at $N=2$, both the D-optimal and SE-optimal design criteria were consistent in their selection over all $n$, and E-optimal only differed at $n=401$. Even at $N=3$, each optimal design method specified at least two of the same observables at all $n$.

The observables that were rated best changed between criteria, affirming the fact that each optimal design method minimizes different aspects of the standard error ellipsoid. At $N=1$ observable, D-optimal selects the CD4 cell count while E-optimal and SE-optimal choose the infectious virus count. As a result, the min(ASE) calculated for a parameter estimation problem using the D-optimal observables is approximately 1/3 lower than the min(ASE) of E- and SE-optimal for all tested time point distributions. Similarly, the max(ASE) calculated for E- and SE-optimal designed parameter estimation problems is approximately 1/3 lower than that of D-optimal. Thus at $N=1$, based on minimum and maximum asymptotic standard errors, there is no clear best choice of an optimal design cost function.

At $N=2$ allowed observables, both the D- and SE-optimal cost functions are minimized by an observation operator containing both activated CD4 cells (type 1 target cells) and type 2 target cells. The E-optimal cost function still favours infectious virus count in addition to type 2 target cells (at $n=51,101,201$) or type 1 target cells (at $n=401$). As a result, max(ASE) in the E-optimal design parameter estimation problem is $0\%$–$20\%$ lower than that of D- or SE-optimal; however, the D- and SE-optimal designs reduce min(ASE) by $20\%$–$30\%$ of the min(ASE) of E-optimal. Therefore at $N=2$, the E-optimal cost functional would be preferable if the largest ASE’s were to be reduced, but for the best overall improvement (as measured by percent reduction from the E-optimal ASE), D- and SE-optimal are recommended.

Table 5 Approximate asymptotic standard errors calculated by asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) using optimally spaced $n=35$ time points under constraints C2 (left set of 3) and C3 (right set of 3) and optimally selected $N=2$ observables for parameters of interest $\overrightarrow{\mathit{\theta }}$ of the HIV model (27). Smallest ASE per parameter is highlighted using bold font.

Time	C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE
Observe	$x_6,$	$x_5,$	$x_6,$	$x_6,$	$x_5,$	$x_6,$
	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$
ASE$({\mathit{\lambda }}_1)$	0.1077	0.2501	0.1164	0.1048	0.1297	0.1215
ASE$(d_1)$	0.0737	0.1523	0.0972	0.0683	0.0759	0.0817
ASE$(k_1)$	0.0967	0.0851	0.1404	0.1085	0.0920	0.1174
ASE$(N_T)$	0.2200	0.2722	0.2263	0.2257	0.2784	0.2398
ASE$(c)$	0.2455	0.2916	0.2505	0.2517	0.3098	0.2650
ASE$(b_E)$	0.0480	0.7788	0.0500	0.0476	0.8182	0.0494
ASE$(x_1^0)$	0.1148	0.1275	0.1366	0.1201	0.1081	0.1292
ASE$(x_2^0)$	0.2657	0.2456	0.2597	0.2635	0.2469	0.2654
ASE$(x_5^0)$	0.9450	0.4798	0.9234	0.9303	0.4629	0.9473

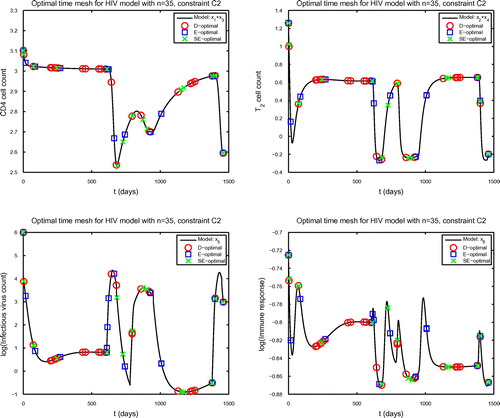
Fig. 1 Solution of (27) plotted using the observables log$({10}^{x_1}+{10}^{x_3})$ (upper left), log$({10}^{x_2}+{10}^{x_4})$ (upper right), $x_5$ (lower left) and $x_6$ (lower right). Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=35$ times under constraint C2.

When selecting $N=3$ observables, each of the three design criteria select many of the same observables. This is to be expected as $N^{\ast }=4$ in this simulation. For $n=51,101,201$, both total CD4 cell count and immune response $E(t)$ are selected by all design criteria. The D-optimal criterion also chooses type 2 cell count, so the lack of information on virus count as measured by $x_5(t)$ leads to its high max(ASE), $\mathit{ASE}(x_5^0)$. E-optimal (and at larger $n$, SE-optimal) choose to measure infectious virus count, reducing ASE$(x_5^0)$ and thus reducing the max(ASE) by more than $50\%$. While at low $n$, E-optimal has the lowest min(ASE) and max(ASE), SE-optimal performs better at high $n$, so when selecting $N=3$ observables, the number of time points $n$ may affect which optimal design cost function performs best.

HIV observables and time point selection results

When taking samples on a uniform time grid, D-, E- and SE-optimal design criteria all choose observation operators that yield favourable ASE’s, with some criteria performing best under certain circumstances. For example, the SE-optimal observables at $n=401$, $N=3$ yield the smallest standard errors; however, for all other values of $n$ at $N=3$, E-optimal performs best. At $N=2$, E-optimal is a slightly weaker scheme. The examples in [4] also reveal that D-, E- and SE-optimal designs are all competitive when only selecting time points for several different models. Now we wish to investigate the performance of these three criteria when selecting both an observation operator and a sampling time distribution using the algorithm described by Equations (17(17) $$\begin{array}{c}\hfill {\hat{\mathit{\theta }}}_{\mathrm{OLS}}={\mathit{argmin}}_{\overrightarrow{\mathit{\theta }}\in \mathrm{\Theta }}\sum _{j=1}^n{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T{V}_0^{-1}[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})].\end{array}$$(17) ) and (18(18) $$\begin{array}{c}\hfill V_0\approx \hat{V}=\mathrm{d}\mathit{iag}\left(\frac{1}{n-p}\sum _{j=1}^n[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]{[{\overrightarrow{y}}_j-\overrightarrow{f}(t_j;\overrightarrow{\mathit{\theta }})]}^T\right),\end{array}$$(18) ).

To maintain consistency across trials while slightly simplifying the parameter estimation problem, we allow the set of six parameters and three initial conditions $\overrightarrow{\mathit{\theta }}=({\mathit{\lambda }}_1$, $d_1$, $k_1$, $N_T$, $c$, $b_E$, $x_1^0$, $x_2^0$, $x_5^0)$ to be treated as unknowns and fix all other parameters. We again allow the possible observations of (1) infectious virus $x_5$, (2) immune response $x_6$, (3) CD4 cells $x_1+x_3$ and (4) type 2 target cells $x_2+x_4$, each with an assumed error variance of $5\%$ of the initial variable values given by ${\overrightarrow{x}}^0$. To reflect the often limited resources of a clinical trial, we allow $N=2$ observation maps to be included in the observation operators $C$ and examine the distribution of time points if $n=35$ or $n=105$ samples (consisting of all observables in the observation operator) which may be taken from $t_0=0$ through $t_f=1460$. We begin all simulations with uniformly spaced sample times, and use either time grid constraint C2 or C3. Both constraints assume that samples are taken at $t_0$ and $t_f$, so we in effect are optimizing the remaining 33 or 103 observation times.

When choosing $N=2$ observables and distributing $n=35$ time points using constraint C2, the D-optimal cost function yields the lowest ASE for the parameters $({\mathit{\lambda }}_1$, $d_1$, $N_T$, $c$, $b_E$, $x_1^0$), but the SE-optimals ASE are on the same order of magnitude (Table 5). Both the D- and SE-optimal cost functions selected the same observables, and they both were minimized by similar distributions of time points (Figure 1). The E-optimal design leads in the smallest ASE for $(k_1,x_2^0,x_5^0)$, with an ASE$(x_5^0)$ that is half that of D-optimal and SE-optimal. E-optimal, however, trails D- and SE-optimal in the accuracy of an estimate for $b_E$, with an ASE$(b_E)$ that is larger by one order of magnitude. The large difference in ASE’s for these two parameters may be related to the observables selected by each design criterion: E-optimal design chooses $x_5$ (the variable most closely related to $x_5^0$) as an observable when D- and SE-optimal choose $x_6$ (whose right hand side contains $b_E$). All three also chose $x_2+x_4$. The distribution of time points selected under each optimal design criterion focuses on regions very soon before or after a change in behaviour of the selected observables (Figure 1). This may indicate that fewer sampling points may be needed for parameter estimates of similar accuracy. For the experimental design constraints of 35 time point allocated using constraint C2, the D-optimal cost functional is best for most parameters, but E-optimal is best for some parameters.

The ASE calculated for choosing $N=2$ observables and distributing $n=35$ time points using constraint C3 are very similar (Table 5), and the selected observables remain unchanged; however, the optimal distribution of time points under each design criterion (Figure 2) is more uniform than when using constraint C2 (Figure 1). For small $n$ with $N=2$ observables under constraint C3, D-optimal design is best for most parameters, but E-optimal is best for the remaining few. While the choice of a particular time point distribution constraint does not greatly impact the calculated ASEs for the paramters of interest, the constraint C3 yields a measurement schedule that may be more feasible for a patient to follow in that it does not call for as many days of multiple observations.

Fig. 2 Solution of (27) plotted using the observables log$({10}^{x_1}+{10}^{x_3})$ (upper left), log$({10}^{x_2}+{10}^{x_4})$ (upper right), $x_5$ (lower left) and $x_6$ (lower right). Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=35$ times under constraint C3.

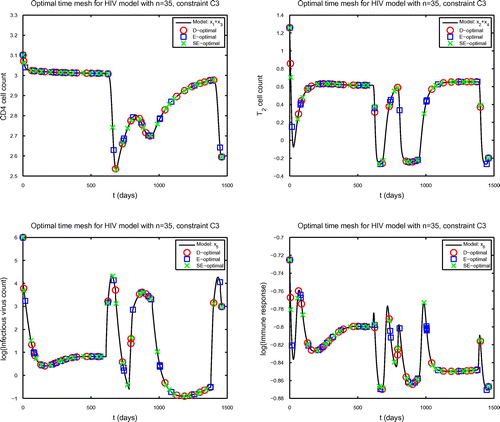
Table 6 Approximate asymptotic standard errors calculated by asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) using optimally spaced $n=105$ time points under constraints C2 (left set of 3) and C3 (right set of 3) and optimally selected $N=2$ observables for parameters of interest $\overrightarrow{\mathit{\theta }}$ of the HIV model (27). Smallest ASE per parameter is highlighted using bold font.

Time	C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE
Observe	$x_6,$	$x_1+x_3,$	$x_6,$	$x_6,$	$x_1+x_3,$	$x_6,$
	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$	$x_2+x_4$
ASE$({\mathit{\lambda }}_1)$	0.0687	0.0618	0.0607	0.0674	0.0475	0.0729
ASE$(d_1)$	0.0429	0.0541	0.0470	0.0441	0.0395	0.0475
ASE$(k_1)$	0.0658	0.0360	0.0681	0.0629	0.0388	0.0739
ASE$(N_T)$	0.1599	0.1437	0.1394	0.1192	0.1351	0.1423
ASE$(c)$	0.1785	0.1591	0.1551	0.1325	0.1500	0.1578
ASE$(b_E)$	0.0281	0.4560	0.0281	0.0266	0.4637	0.0299
ASE$(x_1^0)$	0.0810	0.0451	0.0793	0.0572	0.0490	0.0818
ASE$(x_2^0)$	0.2537	0.2004	0.2296	0.1823	0.2244	0.2330
ASE$(x_5^0)$	0.7042	0.4384	0.6825	0.0528	0.4491	0.6571

Fig. 3 Solution of (27) plotted using the observables log$({10}^{x_1}+{10}^{x_3})$ (upper left), log$({10}^{x_2}+{10}^{x_4})$ (upper right), $x_5$ (lower left) and $x_6$ (lower right). Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=105$ times under constraint C2.

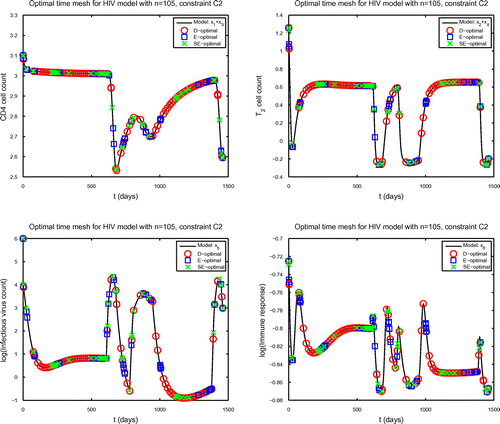
Choosing $N=2$ observables and distributing $n=105$ time points using constraint C2 leads to a different pattern in which optimal design criterion is best for which parameter. For the more dense time point distribution, SE-optimal design is a much stronger candidate against D- and E-optimal (Table 6). It yields the lowest ASE’s for $({\mathit{\lambda }}_1,N_T,c,b_E)$, while E-optimal is best for $(k_1,x_1^0,x_2^0,x_5^0)$ and D-optimal is best for $(d_1,b_E)$. The D- and SE-optimal cost functions again choose the same observables of $x_6$ and $x_2+x_4$, so their ASE’s for all parameters are similar. In this scenario, the E-optimal design has the largest percent reduction in ASE from those of D- and SE-optimal for the parameters $x_1^0$ and $x_5^0$. E-optimal also changed its selected observables to $x_1+x_3$ and $x_2+x_4$. The distribution of time points for the D-optimal design criteria appear very close to uniform (Figure 3), and the distributions for E- and SE-optimal are clustered near local maxima, local minima, and other large changes in behaviour of the observables; however, even slight differences between the distributions of the E- and SE-optimal costs functions are visible. Consider the graph of infectious virus count in Figure 3. There is a cluster of SE-optimal times between $t=1100$ and $t=1250$, but no E-optimal times occur during that interval. Very soon after, between $t=1250$ and $t=1400$, there is a cluster of E-optimal times but no SE-optimal times. These clusters may indicate that either these periods in the patient’s treatment history are key to characterizing the parameters or that fewer time points may be adequate to obtain sufficiently accurate parameter estimates.

Fig. 4 Solution of (27) plotted using the observables log$({10}^{x_1}+{10}^{x_3})$ (upper left), log$({10}^{x_2}+{10}^{x_4})$ (upper right), $x_5$ (lower left) and $x_6$ (lower right). Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=105$ times under constraint C3.

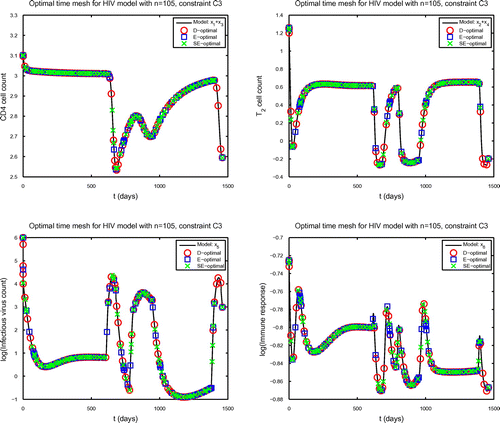
Table 7 Top: Optimal 5 observables chosen by each optimal design criterion when estimating the parameters ${\overrightarrow{\mathit{\theta }}}_a$ of the model in [6]. Bottom: Approximate asymptotic standard errors calculated using asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) for each parameter in ${\overrightarrow{\mathit{\theta }}}_a$ using the optimal 5 observables with time point constraints of uniform spacing, constraint C2, and constraint C3. Smallest ASE for each parameter per time point constraint is highlighted in bold font.

Method	Observables
D-opt	PGA, T3P, GOAc, SERc, F26BPc
E-opt	PGA, SERc, T3Pc, FBPc, F26BPc
SE-opt	PGA, SERc, T3Pc, FBPc, F26BPc
Time	Uniform			C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE	D	E	SE
ASE(KM${}_{11}$)	0.0014	0.0356	0.0356	0.0015	0.0033	8.7e-4	5.8e-4	0.0018	0.0018
ASE(KM${}_{521}$)	4.1811	4.0086	4.0086	0.1324	0.1078	0.6805	0.0750	0.1349	0.0532
ASE(KI${}_{523}$)	0.1173	0.1125	0.1125	0.0037	0.0030	0.0191	0.0012	0.0038	0.0015
ASE(KC)	0.0012	0.0353	0.0353	0.0012	0.0033	0.0019	0.0011	0.0018	0.0018
ASE(KM${}_{1221}$)	0.2805	1.3065	1.3065	0.2742	0.4330	0.5798	0.1460	0.5127	0.5136
ASE(KM${}_{1241}$)	0.2508	1.1764	1.1764	0.2451	0.3874	0.5183	0.1305	0.4582	0.4592

The strength of SE-optimal design for large $n$ does not hold for time grid constraint C3 (Table 6). E-optimal design provides the lowest ASE for the parameters $({\mathit{\lambda }}_1,d_1,k_1,x_1^0)$, D-optimal is best for $(N_T,c,b_E,x_2^0,x_5^0)$ and the ASE calculated using the SE-optimal designed experiment is often the largest. The observables selected in this case are the same as the $n=105$, constraint C2 case. The optimal time point distributions determined under all three design criterion are near uniform (Figure 4). Small differences between the distributions may be observed when the functions have a slope of high magnitude, indicating that the distributions are not exactly uniform. As the time point optimization routine is started with a uniform time point distribution, this may indicate that when samples are taken at many times during an experiment, a uniform distribution is somewhat near optimal for model (27) or, more significantly, that a uniform distribution is not an appropriate initial distribution to use to obtain the optimal time point distribution.

Between D- and E-optimal, there is no clear leader for optimal time point and observable selection in these examples for system (27). The SE-optimal criterion is useful in estimating some parameters under the constraint C2, and in most cases yields standard errors on the same order of magnitude of the leading optimal design criterion. The optimal design algorithm successfully identifies observables and a time distribution that optimizes an aspect of the Fisher Information Matrix as determined by the choice of optimal design cost functional; however, the time point distributions exhibit tendencies to cluster near times when the slopes of function solutions are changing. We proceed to examine the algorithm’s performance when presented with a system that allows many possible observables and does not require as many sampling times.

Example 2: Zhu’s Calvin Cycle model

The second model we use as an example is characteristic of the large differential equation systems that often appear in industrial problems. In [6], Zhu et al., present an ODE model for the Calvin Cycle in fully grown spinach. The Calvin Cycle, part of the light-independent reactions in photosynthesis, plays an important role in plant carbon fixation, which leads to the growth of the plant. This model contains 165 parameters and initial conditions, 31 ODEs and 7 concentration balance laws and involves 38 state variables (metabolite concentrations in different parts of the cell) as well as a calculation for photosynthetic CO${}_2$ uptake rate. The metabolites used in the model are denoted by RuBP, PGA, DPGA, T3P, FBP, E4P, S7P, ATP, SBP, NADPH, HexP, PenP, NADHc, NADc, ADPc, ATPc, GLUc, KGc, ADP in photorespiration, ATP in photorespiration, GCEA, GCA, PGCA, GCAc, GOAc, SERc, GLYc, HPRc, GCEAc, T3Pc, FBPc, HexPc, F26BPc, UDPGc, UTPc, SUCP, SUCc and PGAc, and the parameters are mainly initial conditions, maximum reaction velocities and Michaelis–Menten constants for reaction substrates, products, activators and inhibitors. The ‘c’ following some metabolite names indicates that the model compartment corresponds to the metabolite concentration in cytosol; compartment names lacking a ‘c’ are the metabolite in the chloroplast stroma. The full system of equations and parameter values may be found in the appendices of [6]. While the model has not been validated with data as completely as the family of HIV models discussed above, it is representative of the models used to describe plant enzyme kinetics and utilizes well-documented Michaelis–Menten enzyme kinetic model formulations.[19]

Fig. 5 Solutions of selected state variables in the Zhu model [6]. Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C2 when sampling the optimal 5 observables to estimate ${\overrightarrow{\mathit{\theta }}}_a$ (Table 7). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Fig. 6 Solutions of selected state variables in the Zhu model.[6] Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C3 when sampling the optimal 5 observables to estimate ${\overrightarrow{\mathit{\theta }}}_a$ (Table 7). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

In [5], sets of the optimal 3, 5, 10 and 15 metabolites are identified as the most useful to measure in an experiment in order to estimate a subset of 6 parameters, ${\overrightarrow{\mathit{\theta }}}_a$ = [KM${}_{11}$, KM${}_{521}$, KI${}_{523}$, KC, KM${}_{1221}$, KM${}_{1241}$]${}^{\text{T}}$ with true values ${\overrightarrow{\mathit{\theta }}}_{a0}$ = [0.0115, 0.0025, 0.00007, 0.0115, 0.15, 0.15]${}^{\text{T}}$, and a subset of 18 parameters, ${\overrightarrow{\mathit{\theta }}}_c$ =[RuBP${}_0$, SBP${}_0$, KM${}_{11}$, KM${}_{13}$, KI${}_{13}$, KE${}_4$, KM${}_9$, KM${}_{131}$, KI${}_{135}$, KE${}_{22}$, KM${}_{511}$, KM${}_{521}$, KI${}_{523}$, KC, KM${}_{1221}$, KM${}_{1241}$, V${}_9$, V${}_{58}$]${}^{\text{T}}$ with true values ${\overrightarrow{\mathit{\theta }}}_{c0}$ = [2, 0.3, 0.0115, 0.02, 0.075, 0.05, 0.05, 0.05, 0.4, 0.058, 0.02, 0.0025, 0.00007, 0.0115, 0.15, 0.15, 0.3242, 0.0168]${}^{\text{T}}$. The simulation was set in the framework of an experiment run for 3000 seconds over which 11 samples are taken at evenly spaced times for the optimization of estimates for ${\overrightarrow{\mathit{\theta }}}_a$ and 21 samples for estimation of ${\overrightarrow{\mathit{\theta }}}_c$.

We use a similar set up for our simulations in order to judge the ability of the time and variable selections to minimize the asymptotic standard errors of both ${\overrightarrow{\mathit{\theta }}}_a$ and ${\overrightarrow{\mathit{\theta }}}_c$ using $N=5$ and $N=10$ observables and $n=11$ time points over the time interval $t\in [0,3000]$. Each metabolite is assigned a variance of $5\%$ of its initial value, and to reduce computation time, all metabolites that do not change in concentration over time ($\mathit{dx}/\mathit{dt}=0$) are excluded from the search algorithm. As it is often possible to measure a particular metabolite’s concentration in plant tissue, we allow ${\mathcal{C}}_{N^{\ast }}$ to be composed of 28 vectors in ${\mathbb{R}}^{\mathbb{1}\times \mathbb{40}}$ that are composed of a one in the element corresponding to the position of the differential equation describing the dynamics of the metabolite in the vector of model ODEs and zero elsewhere.

We compare the ASE calculated for $n=11$ evenly spaced measurements over the interval $t\in [0,3000]$ against the optimally spaced $n=11$ time points according to constraints C2 and C3 and plot the D-, E- and SE-optimal time point distributions on the solutions of selected compartments in the Zhu model of [6]. The four compartments chosen for graphing are carbon uptake rate $A(t)$ (units $\mathrm{\mu }$mol m${}^{-2}$s${}^{-1}$), which is a rate calculated from the output of the model that describes the plant’s efficiency in using the available environmental resources to develop; adenosine triphosphate (ATP) in chloroplast stroma, which is a well-known metabolite active in photosynthesis; sucrose, a sugar, in cytosol (SUCc); and Ribulose-1,5-bisphosphate (RuBP), a metabolite connected to the enzyme RuBisCO, which is essential to carbon fixation.

The simplest scenario we test is the selection of the optimal $N=5$ observables (metabolites) and $n=11$ time points to use when estimating the six parameters in ${\overrightarrow{\mathit{\theta }}}_a$. For all three optimal design methods, the optimal observables determined under the uniform grid were also determined to be optimal after the time point distribution is optimized under constraints C2 and C3. These observables are listed in the upper portion of Table 7. All three optimal design methods identify the observables PGA, SERc and F26BPc, indicating that these three metabolites may be central to accurate estimates of the parameters in ${\overrightarrow{\mathit{\theta }}}_a$; moreover, the E-optimal and SE-optimal cost functions selected the same set of five observables.

The similarity in results, however, does not continue through the selected time point distributions. Under constraint C2 (Figure 5), the D-optimal distribution is loosely clustered about the center of the time interval, the E-optimal time points are clustered about $t=250$ seconds, and SE-optimal chooses a small cluster of time points around the initial bump and allows a few samples after the function reaches a steady state. Using constraint C3 (Figure 6), all three optimal design criteria chose a majority of their sampling times before $t=600$ and allow only a few sampling times after the system reaches a steady state. The optimization of time point distributions yields improved asymptotic standard errors from those of the uniform distribution – sometimes by an order of magnitude or more. For all three time point constraints, D-optimal yields the smallest ASE’s for the most number of parameters, and SE-optimal yields the smallest ASE’s for the second most number of parameters. Both optimal design criteria perform better with the C3 optimal times than the C2 optimal times. Therefore, in this simple case, using either the D- or SE-optimal design criterion with time point distribution constraint C3 would yield the best results.

The next scenario is the selection of the optimal $N=10$ observables and $n=11$ time points to use when estimating the six parameters in ${\overrightarrow{\mathit{\theta }}}_a$. For all three optimal design methods, the optimal observables determined under the uniform grid were also determined to be optimal after the time point distribution is optimized under constraints C2 and C3. These observables are listed in the upper portion of Table reftab:zhusps106. Of the 28 possible observables, 20 were selected by at least one optimal design criterion, 8 of which (DPGA, T3P, E4P, S7P, ATP, GCA, SERc, T3Pc) were selected by two criteria and one, GOAc, was selected by all three. The effect of adding five observables does not have a large effect on the estimated ASE for the six parameters of interest. The ASE’s listed in Table reftab:zhusps106 for the $N=10$ observable case are on the same order as those in Table 7 for the $N=5$ observable case for each time point constraint.

The optimal time point distributions also differ from those selected under the five observable case. Under constraint C2 (Figure 7), the D-optimal distribution is loosely clustered near the boundaries of the time interval while the E- and SE-optimal time points are scattered over the whole interval. Using constraint C3 (Figure 8), the D-optimal times are spread throughout the middle half of the time interval, E-optimal over the first half, and SE-optimal over the second half. While there are no easily discernible patterns between the distributions chosen under the C2 and C3 constraints, the optimization of time point distributions again yield improved asymptotic standard errors from those of a uniform time distribution. For all three time point constraints, D-optimal yields the smallest ASE’s for the most number of parameters, and SE-optimal yields the smallest ASE’s for the second most number of parameters. Other than for the parameters it estimates best, SE-optimal is often the worst criterion. The time point distribution under constraint C2 allows smaller ASE’s for the $N=10$ observable variables case. Therefore, using the D-optimal design criterion with time point distribution constraint C2 would yield the best results.

The addition of five observables for ${\overrightarrow{\mathit{\theta }}}_a$ does not greatly impact most of the calculated ASE’s. For the time point constraints C2 and C3, all but one of the minimum ASE’s remain on the same order of magnitude, and some of the ASE’s increase when $N=10$ observables are allowed from when $N=5$ observables are allowed. This may indicate that for a small parameter set such as ${\overrightarrow{\mathit{\theta }}}_a$, only a small amount of information is needed to obtain the best possible results; adding extra information (through additional observables) does not further improve the ASE’s.

Table 8 Top: Optimal 10 observables chosen by each optimal design criterion when estimating the parameters ${\overrightarrow{\mathit{\theta }}}_a$ of the model in [6]. Bottom: Approximate asymptotic standard errors calculated using asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) for each parameter in ${\overrightarrow{\mathit{\theta }}}_a$ using the optimal 10 observables with time point constraints of uniform spacing, constraint C2 and constraint C3. Smallest ASE for each parameter per time point constraint is highlighted in bold font.

Method	Observables
D-opt	RuBP, PGA, T3P, E4P, SBP, GOAc, SERc, GLYc, T3Pc, F26BPc
E-opt	DPGA, T3P, S7P, ATP, NADPH, NADHc, GCEA, GCA, GOAc, HexPc
SE-opt	DPGA, FBP, E4P, S7P, ATP, HexP, GCA, GOAc, SERc, T3Pc
Time	Uniform			C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE	D	E	SE
ASE(KM${}_{11}$)	0.0011	0.0013	0.0013	5.9e-4	0.0013	0.0013	0.0011	0.0013	0.0013
ASE(KM${}_{521}$)	4.0426	3.9710	3.9710	0.1104	0.7815	0.0588	0.1473	0.2715	0.0588
ASE(KI${}_{523}$)	0.1134	0.1114	0.1114	0.0031	0.0221	0.0016	0.0041	0.0076	0.0016
ASE(KC)	0.0009	0.0010	0.0010	9.1e-4	0.0010	0.0010	9.5e-4	0.0010	0.0010
ASE(KM${}_{1221}$)	0.2801	0.6740	0.6740	0.2531	0.6205	0.5808	0.3045	0.6136	0.6961
ASE(KM${}_{1241}$)	0.2504	0.6027	0.6027	0.2264	0.5548	0.5193	0.2722	0.5481	0.6227

Fig. 7 Solutions of selected state variables in the Zhu model [6]. Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C2 when sampling the optimal 10 observables to estimate ${\overrightarrow{\mathit{\theta }}}_a$ (Table 8). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Fig. 8 Solutions of selected state variables in the Zhu model [6]. Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C3 when sampling the optimal 10 observables to estimate ${\overrightarrow{\mathit{\theta }}}_a$ (Table 8). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Now consider the parameter vector ${\overrightarrow{\mathit{\theta }}}_c$. We identify the optimal $N=5$ observables and the optimal distribution of $n=11$ time points using the D-, E-, and SE-optimal cost functionals. Three metabolites, RuBP, SBP and F26BPc, are selected by all three cost functionals, indicating that these three observables may be important to measure to accurately estimate a large number of the parameters in ${\overrightarrow{\mathit{\theta }}}_c$. The inclusion of RuBP${}_0$ and SBP${}_0$ in ${\overrightarrow{\mathit{\theta }}}_c$ may also heavily influence the selection of observables. Many of the other metabolites selected by at least one of the cost functionals, namely, PGA, SERc and T3Pc, were also selected for ${\overrightarrow{\mathit{\theta }}}_a$ in the experimental setup of $N=5$ observables and $n=11$ time points, indicating that they are still relevant to some of the parameters in ${\overrightarrow{\mathit{\theta }}}_c$.

Using the uniform time point distribution yields standard errors that are up to six order of magnitude larger than the parameter (KI${}_{523}$ = 0.00007) and are typically two or three orders of magnitude larger than the parameter value (Table 9). Constraint C2 also leads to large standard errors when using the D- and E-optimal cost function. The E-optimal standard errors, in fact, do not change from those calculated using the uniform time point distribution, and as shown in Figure 9, the E-optimal time distribution under constraint C2 is uniform. The SE-optimal design criterion performs the best when using constraint C2 and produces much smaller standard errors, though the standard errors are still larger than the parameter values by orders of magnitude for most parameters. Both D- and SE-optimal perform favourably under constraint C3: the D-optimal, C3 design produces smaller ASE’s than the SE-optimal, C2 design, and the SE-optimal, C3 design yields the smallest ASE’s for almost all parameters. Under the constraint C3 and the SE-optimal cost functional, the calculated ASE’s are zero to one orders of magnitude larger than the parameter values.

The favourable performance of the SE-optimal design criterion under constraint C2 may be attributed to its selected time point distribution (Figure 9). The SE-optimal distribution is the only one that places a large number of time points (5 out of 11) before the solution approaches a steady state at $t=250$. The E-optimal design, as mentioned previously, selects the uniform distribution, and the D-optimal design suggests sampling after the solution has achieved a steady state. When using constraint C3, the E-optimal design selects a distribution that maintains the uniform spacing between points in the interior of the time interval (0,3000) (Figure 10), again leading to poor ASE’s. Both the D- and SE-optimal designs place the majority of the 11 time points in the first one-third of the time interval, thus capturing more of the dynamical system’s behaviour before it achieves a steady state. These front-heavy distributions greatly reduce the estimated ASE’s from those calculated using a uniform time distribution.

Table 9 Top: Optimal 5 observables chosen by each optimal design criterion when estimating the parameters ${\overrightarrow{\mathit{\theta }}}_c$ of the model in [6]. Bottom: Approximate asymptotic standard errors calculated using asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) for each parameter in ${\overrightarrow{\mathit{\theta }}}_c$ using the optimal 5 observables with time point constraints of uniform spacing, constraint C2 and constraint C3. Smallest ASE for each parameter per time point constraint is highlighted in bold font.

Method	Observables
D-opt	RuBP, PGA, SBP, SERc, F26BPc
E-opt	RuBP, SBP, PenP, SERc, F26BPc
SE-opt	RuBP, SBP, GCEAc, T3Pc, F26BPc
Time	Uniform			C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE	D	E	SE
ASE(RuBP${}_0$)	0.3162	0.3162	0.3162	0.3162	0.3162	0.2236	0.2235	0.3162	0.2222
ASE(SBP${}_0$)	0.1225	0.1225	0.1225	0.1225	0.1225	0.0866	0.0866	0.1225	0.0863
ASE(KM${}_{11}$)	10.81	17.08	15.66	12.93	17.08	0.0658	0.0373	20.63	0.0098
ASE(KM${}_{13}$)	69.74	116.02	88.10	68.45	116.02	1.1838	0.1084	147.67	0.0703
ASE(KI${}_{13}$)	39.68	45.02	71.89	53.46	45.03	4.8270	2.9386	56.67	0.9743
ASE(KE${}_4$)	23.33	23.97	15.12	12.89	23.97	0.9840	0.1781	48.76	0.0627
ASE(KM${}_9$)	11.35	19.67	8.7654	3.5664	19.67	1.5287	0.3212	25.59	0.1098
ASE(KM${}_{131}$)	109.58	7.8306	153.81	100.08	7.8306	1.1186	0.3684	7.9849	0.1399
ASE(KI${}_{135}$)	1.31e3	147.86	2.47e3	1.14e3	147.86	13.78	4.4908	115.39	1.7931
ASE(KE${}_{22}$)	26.15	47.41	27.36	21.92	47.41	0.1794	0.0941	40.85	0.0448
ASE(KM${}_{511}$)	4.3991	4.9372	0.1594	1.7103	4.9372	0.0050	0.1632	9.8977	0.0018
ASE(KM${}_{521}$)	330.93	402.73	18.64	396.04	402.73	8.4152	6.1770	377.72	0.1200
ASE(KI${}_{523}$)	9.2952	11.30	0.5225	11.12	11.30	0.2361	0.1736	10.60	0.0034
ASE(KC)	1.0948	1.5200	4.9411	0.9574	1.5200	0.5559	0.0789	2.4448	0.0292
ASE(KM${}_{1221}$)	40.12	61.53	621.18	49.80	61.53	14.24	0.7375	84.00	2.0692
ASE(KM${}_{1241}$)	36.04	55.30	557.93	44.71	55.30	12.91	0.6637	75.50	1.8290
ASE(V${}_9$)	28.26	47.99	38.76	7.9788	47.99	1.1204	0.1492	71.89	0.1373
ASE(V${}_{58}$)	0.5878	1.0247	0.1593	0.8311	1.0247	0.0866	0.0116	1.7824	7.8e-4

Fig. 9 Solutions of selected state variables in the Zhu model.[6] Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C2 when sampling the optimal five observables to estimate ${\overrightarrow{\mathit{\theta }}}_c$ (Table 9). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Fig. 10 Solutions of selected state variables in the Zhu model.[6] Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ times under constraint C3 when sampling the optimal five observables to estimate ${\overrightarrow{\mathit{\theta }}}_c$ (Table 9). Top left: Carbon uptake rate $A(t)$; top right: ATP; Bottom Left: SUCc; bottom right: RuBP.

The last case tested is designing experiments using each of the three cost functionals to estimate ${\overrightarrow{\mathit{\theta }}}_c$ when allowed $N=10$ observables and $n=11$ time points. As in the case of only allowing five observables for estimation of ${\overrightarrow{\mathit{\theta }}}_a$, the metabolites RuBP, SBP and F26BPc are selected by all three optimal design criteria. Additionally, PenP and SERc are selected by all three. A total of 15 different metabolites are chosen across the three optimal design criteria, of which only five are chosen by a single criterion and five selected by two criteria (Table 10). The three optimal design criteria show more agreement on which 10 observables are important to ${\overrightarrow{\mathit{\theta }}}_c$ than which 10 are important to ${\overrightarrow{\mathit{\theta }}}_a$ (in that case, a total of 20 different metabolites are chosen). This indicates that the three design criterion agree upon observables that are central to understanding the behaviour of the model but also select observables that help minimize their associated cost functionals.

Similar to the five observable cases for ${\overrightarrow{\mathit{\theta }}}_c$, the ASE’s calculated when using a time point distribution optimized under the C2 or C3 constraints are smaller than those of the uniform time point distribution (though the difference is much less pronounced). While the ASE’s from the D- and SE-optimal criteria are typically smallest under the uniform time point distribution, the E-optimal designed experiment yields the smallest ASE’s for the most number of parameters under constraint C2 (Table 10). The ASE’s for the D-optimal experiment under constraint C2 are typically larger than those for the D-optimal experiment with a uniform time distribution, and the SE-optimal ASE’s see only marginal improvements. For parameters when the E-optimal ASE’s are not as small as those for the D- and SE-optimal designs, the ASE’s are often still on the same order. These ASE’s are still orders of magnitude larger than the values of some parameters. The minimum ASE’s under constraint C3 are smaller than those under constraint C2 (and are notable improvements over those from the uniform time point distribution), but most are improved by only one order of magnitude or less. The D- and SE-optimal cost functions yield the smallest standard errors for more parameters under C3 than C2, as well.

The performance improvements seen in the D- and SE-optimal experimental designs from the C2-optimal time point distributions to the distributions optimal under constraint C3 can be easily explained. Under constraint C2, neither criterion produced clusters of time points (Figure 11). The distributions generated by both criteria are more similar to the uniform distribution that was used as the initial seed for the time point distribution optimization than to the highly clustered distributions seen for other selections of $n$ and $N$ (such as the one shown in Figure 10). The D-optimal distribution only contains one time point before $t=500$, as well, thus ignoring the early dynamics of the system. The E-optimal time point distribution contains clusters at the very beginning ($t<200$) and very end ($t>2900$) of the time interval as well as a loose cluster between $t=1500$ and $t=2000$.

All three optimal design criteria produce non-uniform distributions under constraint C3 (Figure 12). The time point distributions determined using the E- and SE-optimal cost functions place a majority of their time points before $t=1000$, capturing the dynamics early in the system solution. The D-optimal distribution also concentrates its sampling times before $t=1000$, but does not as tightly cluster the time points. All three cost functionals under time point constraint C3 produce smaller ASE’s than those calculated with a uniform time point distribution (Table 10). The distributions generated under both constraints C2 and C3 indicate that heavily weighting time periods when the system is changing its pattern of behaviour (such as transitioning from oscillations to a steady state) produce smaller standard errors than uniform or near-uniform distributions.

Table 10 Top: Optimal 10 observables chosen by each optimal design criterion when estimating the parameters ${\overrightarrow{\mathit{\theta }}}_c$ of the model in [6]. Bottom: Approximate asymptotic standard errors calculated using asymptotic theory (25(24) $$\begin{array}{cc}\hfill \stackrel{·}{x_1}& =\frac{{10}^{-x_1}}{\mathrm{l}n(10)}({\mathit{\lambda }}_1-d_1{10}^{x_1}-(1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_1+x_5}),\hfill \\ \hfill \stackrel{·}{x_2}& =\frac{{10}^{-x_2}}{\mathrm{l}n(10)}({\mathit{\lambda }}_2-d_2{10}^{x_2}-(1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}),\hfill \\ \hfill \stackrel{·}{x_3}& =\frac{{10}^{-x_3}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{1}u(t))k_1{10}^{x_5+x_1}-\mathit{\delta }{10}^{x_3}-m_1{10}^{x_6+x_3}),\hfill \\ \hfill \stackrel{·}{x_4}& =\frac{{10}^{-x_4}}{\mathrm{l}n(10)}((1-f{\mathit{ϵ}}_{1}u(t))k_2{10}^{x_5+x_2}-\mathit{\delta }{10}^{x_4}-m_2{10}^{x_6+x_4}),\hfill \\ \hfill \stackrel{·}{x_5}& =\frac{{10}^{-x_5}}{\mathrm{l}n(10)}((1-{\mathit{ϵ}}_{2}u(t)){10}^3{N}_T\mathit{\delta }({10}^{x_3}+{10}^{x_4})-c{10}^{x_5}\hfill \\ \hfill & -(1-{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_1{10}^3{k}_1{10}^{x_1+x_5}-(1-f{\mathit{ϵ}}_{1}u(t)){\mathit{\rho }}_2{10}^3{k}_2{10}^{x_2+x_5})\hfill \\ \hfill \stackrel{·}{x_6}& =\frac{{10}^{-x_6}}{\mathrm{l}n(10)}({\mathit{\lambda }}_E+\frac{b_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_b}{10}^{x_6}-\frac{d_E({10}^{x_3}+{10}^{x_4})}{{10}^{x_3}+{10}^{x_4}+K_d}{10}^{x_6}-{\mathit{\delta }}_E{10}^{x_6}),\hfill \end{array}$$(24) ) for each parameter in ${\overrightarrow{\mathit{\theta }}}_c$ using the optimal 10 observables with time point constraints of uniform spacing, constraint C2 and constraint C3. Smallest ASE for each parameter per time point constraint is highlighted in bold font.

Method	Observables
D-opt	RuBP, T3P, SBP, PenP, GCEA, GOAc, SERc, GLYc, T3Pc, F26BPc
E-opt	RuBP, PGA, T3P, E4P, S7P, SBP, PenP, GCEA, SERc, F26BPc
SE-opt	RuBP, PGA, SBP, PenP, GOAc, SERc, T3Pc, FBPc, HexPc, F26BPc
Time	Uniform			C2 Optimal			C3 Optimal
Method	D	E	SE	D	E	SE	D	E	SE
ASE(RuBP${}_0$)	0.3162	0.3162	0.3162	0.2236	0.3154	0.2236	0.2235	0.3132	0.3126
ASE(SBP${}_0$)	0.1225	0.1225	0.1225	0.0866	0.1224	0.0866	0.0866	0.1223	0.1221
ASE(KM${}_{11}$)	0.3753	0.8641	0.6406	0.5256	0.0245	0.6245	0.0909	0.0143	0.0116
ASE(KM${}_{13}$)	2.0637	4.6387	3.9718	2.9305	0.0576	3.9110	0.4995	0.0691	0.0620
ASE(KI${}_{13}$)	2.1607	2.6684	9.7853	3.2408	1.6959	9.4439	0.8757	1.2024	1.1163
ASE(KE${}_4$)	0.0111	0.0137	1.5091	0.1765	0.0115	1.4072	0.0079	0.0109	0.0359
ASE(KM${}_9$)	0.2489	0.2534	1.5764	0.5398	0.1759	1.5552	0.1727	0.1409	0.1264
ASE(KM${}_{131}$)	2.6863	2.2992	3.0282	4.2942	0.1250	2.9806	0.2176	0.0935	0.2603
ASE(KI${}_{135}$)	39.00	33.38	46.42	62.39	1.7950	45.67	3.1539	1.3321	3.6831
ASE(KE${}_{22}$)	0.0539	0.0925	2.2836	1.1505	0.0342	2.1316	0.0140	0.0125	0.0497
ASE(KM${}_{511}$)	0.0202	1.6256	0.0038	0.4271	0.0735	0.0038	0.0047	0.0176	0.0015
ASE(KM${}_{521}$)	8.6952	17.63	4.3969	133.86	1.3817	4.7393	2.6856	0.5071	0.1681
ASE(KI${}_{523}$)	0.2441	0.4942	0.1234	3.7574	0.0385	0.1330	0.0754	0.0142	0.0047
ASE(KC)	0.0514	0.0632	0.2632	0.0770	0.0402	0.2538	0.0216	0.0285	0.0303
ASE(KM${}_{1221}$)	0.3047	2.0413	0.3358	0.3230	0.7299	0.3486	0.2883	0.5776	0.2581
ASE(KM${}_{1241}$)	0.2726	1.8273	0.2953	0.2890	0.6535	0.3072	0.2579	0.5173	0.2313
ASE(V${}_9$)	0.2399	0.2467	2.4578	0.4956	0.1685	2.2104	0.1641	0.1393	0.1414
ASE(V${}_{58}$)	0.0236	0.1514	0.0030	0.5100	0.0078	0.0031	0.0052	0.0013	6.9e-4

Fig. 11 Solutions of selected state variables in the Zhu model.[6] Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ sampling times under constraint C2 when sampling the optimal 10 observables to estimate ${\overrightarrow{\mathit{\theta }}}_c$ (Table 10). Top left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Fig. 12 Solutions of selected state variables in the Zhu model.[6] Plotted on top of each curve are the D-optimal (circle), E-optimal (square) and SE-optimal (x) $n=11$ times under constraint C3 when sampling the optimal 10 observables to estimate ${\overrightarrow{\mathit{\theta }}}_c$ (Table 10). Top Left: Carbon uptake rate $A(t)$; top right: ATP; bottom left: SUCc; bottom right: RuBP.

Our computations using the Zhu model of [6] for the Calvin cycle indicate that both the selection of observables and the distribution of sampling times across the experiment affect the estimated asymptotic standard errors – sometimes by several orders of magnitude. While the ASE’s calculated for all exercises were often larger than the parameter values, this may be related to the model’s tendency to quickly reach a steady state.

Overall, the optimal design cost functions performed best under time point constraint C3, followed by C2 and finally the uniform distribution. While in some examples a particular cost functional would do particularly well (such as D-optimal in the ${\overrightarrow{\mathit{\theta }}}_a$, 10 observable case and SE-optimal in the ${\overrightarrow{\mathit{\theta }}}_c$, 5 observable case), it is hard to determine apriori – or even using the results of a uniform time distribution – which cost functional will perform best for a particular set of parameters and observables. The reduction in ASE’s gained from adding additional observables is also difficult to predict. Adding five observables to better estimate ${\overrightarrow{\mathit{\theta }}}_a$ did not result in noticeably smaller estimated asymptotic standard errors as calculated by asymptotic theory. The improvement may be better quantified using a different method to calculate asymptotic standard errors such as Monte Carlo simulations or bootstrapping, but that is beyond the scope of this initial investigation.

Conclusion

Expanding the efforts reported in [4] on time point distribution selection using the D-, E- and SE-optimal design criteria, we introduce a new methodology and algorithm for selecting both optimal observables and an optimal time point distribution. While the D- and E-optimal cost functions are well established in the literature, the SE-optimal design method is relatively new but competitive. We compare the abilities of these three design criteria to reduce the estimated asymptotic standard errors of selected subsets of parameters for two ordinary differential equation models representative of ODE systems used in industrial applications: the log-scaled HIV model (27) and the model of [6] for the Calvin cycle. These examples suggest the strengths of each design method in selecting appropriate observable variables and sampling times.

Collecting patient data for the treatment of HIV is limited by the types and expenses of assays available. In efforts with experimental data,[7] parameter estimation for the HIV model (27) has only been performed with one or two observed quantities. Our tests for determining the optimal sets of 1, 2 and 3 observables when data is collected at uniformly distributed times show that the SE-optimal design criterion performs very similarly to the D-optimal criterion; moreover, a small number of observables may be compensated for by allowing more sampling times. While only measuring one observable may not quite be adequate for accurate parameter estimates, taking either 201 or 401 measurements of two observables yielded similar standard errors when compared to an experiment in which three observables are sampled 51-101 times.

For the HIV model, we compared the performance of all three design criteria under time point distribution constraints C2 and C3. When determining the optimal distribution of 35 time points, D-optimal yields the smallest ASE’s for the most parameters, followed by E-optimal, for both time point constraints. When determining the optimal distribution of 105 time points, however, D-, E-, and SE-optimal each yield the smallest ASE’s for some of the parameters under C2, and both D- and E-optimal are strong performers under constraint C3. The SE-optimal standard errors, while not the lowest, are on the same order of magnitude as those of D- and E-optimal. Therefore for our selected parameter values, D- and E-optimal more reliably yield the smallest standard errors.

The Zhu model of [6] is representative of experimental environments where a great number of state variables may possibly be measured but the costs of measurements limit the number of observed variables that may be sampled. We compared the estimated asymptotic standard errors calculated using the observables and time point distributions determined with the D-,E-, and SE-optimal design methods. For the small parameter subset ${\overrightarrow{\mathit{\theta }}}_a$, a small number of observables is sufficient to obtain as small ASE’s as possible - adding more observables does not improve the ASE’s generated for any of the design methods. Optimizing the time point distribution under either constraint C2 or C3 improves the ASE’s by up to two orders of magnitude. At both 5 and 10 observables, the D-optimal design provides the smallest ASE’s for the most parameters, followed by SE-optimal. The E-optimal standard errors, however, are often on the same order of magnitude, indicating that it is still competitive.

When testing the treatment of the larger parameter subset ${\overrightarrow{\mathit{\theta }}}_c$ of the Zhu model by each of the three design methods, we found that while an excellent selection of observables and time points may still yield small standard errors (as with the SE-optimal design method with 5 observables under constraint C3), adding more information through more observables reduces the calculated ASE’s in the uniform time distribution. At 5 observables, the SE-optimal cost function performs the best and E-optimal time distribution optimization fails to venture far from the uniform grid initially used; at 10 observables, E-optimal performs best under constraint C2 and all three design criteria perform the best for different parameters under constraint C3. Thus for the Zhu model, it is difficult to predict which optimal design criterion will perform best in a particular case.

While the performance of each optimal design criteria is highly dependent upon the ODE system, parameter subset, number of observables allowed, number of time points allowed, and even constraints imposed on the time point distribution selection, the examples performed using the HIV model (27) and the Zhu model [6] demonstrate that the D-, E-, and SE-optimal design methods are all competitive and useful. Moreover, in the Zhu model examples, selection of optimal time points can reduce the estimated asymptotic standard errors of parameters by several orders of magnitude, thus providing data that is more useful in a parameter estimation problem without taking more samples or measuring more observables. Thus the new methodology developed and illustrated here can be an important tool in designing experimental protocols for obtaining data to be used in estimating parameters in complex dynamic models.

Acknowledgments

This research was supported in part (HTB and KLR) by grant number R01AI07 1915-07 from the National Institute of Allergy and Infectious Diseases and in part (KLR) by Fellowships from the CRSC and CQSB. The authors are grateful to Dr. Laura Potter of Bioinformatics, Syngenta Biotechnology, Inc., Research Triangle Park, NC, for her numerous conversations on plant biology experimentation and for initially providing, among a number of other references, the reference [6].