An alternating iterative procedure for the Cauchy problem for the Helmholtz equation

Abstract

We present a modification of the alternating iterative method, which was introduced by Kozlov and Maz’ya, for solving the Cauchy problem for the Helmholtz equation in a Lipschitz domain. The reason for this modification is that the standard alternating iterative algorithm does not always converge for the Cauchy problem for the Helmholtz equation. The method is then implemented numerically using the finite difference method.

Keywords:

• Helmholtz equation
• Cauchy problem
• alternating iterative method
• inverse problem
• ill-posed problem

View correction statement:

Corrigendum

Introduction

The Helmholtz equation

Let $\mathrm{\Omega }$ be a bounded domain in ${\mathbf{R}}^d$ with a Lipschitz boundary $\mathrm{\Gamma }$. Let $\mathrm{\Gamma }$ be divided into two disjoint parts ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ such that ${\overline{\mathrm{\Gamma }}}_0\cap {\overline{\mathrm{\Gamma }}}_1$ is Lipschitz, see Figure 1. We denote by $\mathit{\nu }$ the outward unit normal to the boundary $\mathrm{\Gamma }$ and consider the following Cauchy problem for the Helmholtz equation:(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) where the wave number $k$ is a positive real constant, ${\mathit{\partial }}_{\mathit{\nu }}$ denotes the outward normal derivative and f and g are specified Cauchy data on ${\mathrm{\Gamma }}_0$. We are considering real-valued solutions to problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ).

The Helmholtz equation arises in applications related to acoustic and electromagnetic waves. In the case of acoustic waves, u describes the pressure and the wave number is given by $k=\mathit{\omega }/c$, where $\mathit{\omega }>0$ is the frequency and $c$ is the speed of sound. For electromagnetic waves, the wave number k is given in terms of the electric permeability $\mathit{ϵ}$ and magnetic permeability $\mathit{\mu }$ by $k=\mathit{\omega }\sqrt{\mathit{ϵ}\mathit{\mu }}$; see [2, 3]. The Cauchy problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) has physical applications in optoelectronics [4] and characterization of sound sources.[5, 6]

The Cauchy problem is an ill-posed problem: its solution is unique but does not depend continuously on the Cauchy data; see [7–10]. A number of methods have been developed for solving the Cauchy problem for the Helmholtz equation such as the potential function method by Sun et al. [11], the modified Tikhonov regularization and the truncation method by Qin et al. [12, 13], the modified regularization method based on the solution given by the method of separation of variables by Wei and Qin [14], the method of approximate solutions by Regińska and Regiński [15] and the alternating boundary element method by Marin et al. [16]. For the latter, Marin et al. [16] implemented the alternating iterative algorithm formulated in [17] for a purely imaginary number k and in that case, they solved the Cauchy problem for the modified Helmholtz equation, i.e.$$\begin{array}{c}\hfill \mathrm{\Delta }u-k^{2}u=0.\end{array}$$They also noticed that the alternating algorithm does not always converge. In this paper, we propose a modification of the alternating algorithm that we used to solve the problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ). We also analyse the convergence of the modified method and present the numerical results.

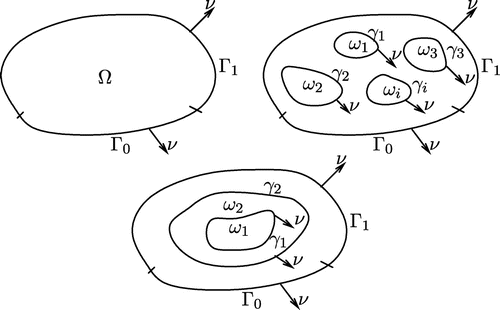
Fig. 1 The bounded domain $\mathrm{\Omega }$ with the boundary $\mathrm{\Gamma }$ divided into ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ is represented in the left. On the right and on the bottom, the choice of the artificial interior boundaries ${\mathit{\gamma }}_i$, $i=1,\dots ,m$ described in Section 1.4 are presented.

The alternating algorithm

The alternating algorithm was proposed by Kozlov and Maz’ya in [1] for solving ill-posed boundary value problems. Such algorithms preserve the differential equations and every step involves the solution of two well-posed problems for the original differential equation. The regularizing character of the algorithm is ensured solely by an appropriate choice of boundary conditions in each iteration. The method has been used for solving ill-posed problems originating from various applications; see [17–25].

In the alternating iterative algorithm for problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ), one considers the following two auxiliary problems:(2) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\end{array}$$(2) and(3) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\end{array}$$(3) where f and g are given in (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) and the functions $\mathit{\eta }$ and $\mathit{\varphi }$ are changed in each iteration of the algorithm. The standard alternating iterative procedure for solving the problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) is as follows:

1. The first approximation $u_0$ is obtained by solving (2(2) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\end{array}$$(2) ), where $\mathit{\eta }$ is an arbitrary initial approximation of the normal derivative on ${\mathrm{\Gamma }}_1$.

2. Having constructed $u_{2n}$, we find $u_{2n+1}$ by solving (3(3) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\end{array}$$(3) ) with $\mathit{\varphi }=u_{2n}$ on ${\mathrm{\Gamma }}_1$.

3. We then find $u_{2n+2}$ by solving (2(2) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\end{array}$$(2) ) with $\mathit{\eta }={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}$ on ${\mathrm{\Gamma }}_1$.

Recently, Johansson and Kozlov [26] modified the algorithm to solve the Cauchy problem for the Helmholtz equation and proved that the modified method converges. This modification applied to problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) can be described as follows: As an initial step, the solution $u$ is decomposed as $u=v+w$, where the function $v$ belongs to an explicitly defined subspace and w belongs to its complement. The original alternating algorithm described above is then applied to the problem of finding the function $v=u-w$. It is not easy to implement this algorithm. In this study, we propose another modification of the alternating algorithm which we use to solve the problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ). This modification is based on the choice of an artificial interior boundary $\mathit{\gamma }$ and a positive constant $\mathit{\mu }$. In the new algorithm, we alternate not only the Dirichlet–Neumann boundary conditions on ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$, but we also alternate boundary conditions on $\mathit{\gamma }$. More details about this modification can be found in [27].

Non-convergence of the standard algorithm

In this section, we show by an example that the original alternating iterative algorithm does not converge for large values of the constant $k^2$ in the Helmholtz equation. For this purpose, we consider the following Cauchy problem in the rectangle $\mathrm{\Omega }=(0,a)\times (0,b)$:(4) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u(x,y)+k^{2}u(x,y)=0,\hfill & 0<x<a,0<y<b,\hfill \\ u(x,0)=0,\hfill & 0\le x\le a,\hfill \\ {\mathit{\partial }}_{y}u(x,0)=0,\hfill & 0\le x\le a,\hfill \\ u(0,y)=u(a,y)=0,\hfill & 0\le y\le b,\hfill \end{array}\end{array}$$(4) where $k>0$. This problem is ill–posed.

Denoting ${\mathrm{\Gamma }}_0=(0,a)\times \{0\}$ and ${\mathrm{\Gamma }}_1=(0,a)\times \{b\}$, we observe for this problem that the Cauchy data $f$ and $g$ described in problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) are set to zero. Choosing an initial approximation of the normal derivative $\mathit{\eta }\in H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }$, we use the algorithm described in Section 1.2 and find that$$\begin{array}{c}\hfill u_0(x,y)=\sum _{n=1}^{\infty }\frac{A_n}{{\mathit{\lambda }}_n\cosh ({\mathit{\lambda }}_{n}b)}\sin \left(\frac{n\mathit{\pi }}{a}x\right)\sinh ({\mathit{\lambda }}_{n}y),\end{array}$$where ${\mathit{\lambda }}_n=\sqrt{a^{-2}{n}^2{\mathit{\pi }}^2-k^2}$ and $A_n=\frac{2}{a}{\int }_0^a\mathit{\eta }(x)\sin (\frac{n\mathit{\pi }}{a}x)\mathit{dx}$. Also, $u_{2m+1}$ and $u_{2m+2}$ are given by$$\begin{array}{c}\hfill u_{2m+2}(x,y)=\sum _{n=1}^{\infty }\frac{A_n{(\tanh ({\mathit{\lambda }}_{n}b))}^{2m+2}}{{\mathit{\lambda }}_n\cosh ({\mathit{\lambda }}_{n}b)}\sin \left(\frac{n\mathit{\pi }}{a}x\right)\sinh ({\mathit{\lambda }}_{n}y)\end{array}$$and$$\begin{array}{c}\hfill u_{2m+1}(x,y)=\sum _{n=1}^{\infty }\frac{A_n{(\tanh ({\mathit{\lambda }}_{n}b))}^{2m+1}}{{\mathit{\lambda }}_n\cosh ({\mathit{\lambda }}_{n}b)}\sin \left(\frac{n\mathit{\pi }}{a}x\right)\cosh ({\mathit{\lambda }}_{n}y),\end{array}$$respectively. Notice that the solution to (4(4) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u(x,y)+k^{2}u(x,y)=0,\hfill & 0<x<a,0<y<b,\hfill \\ u(x,0)=0,\hfill & 0\le x\le a,\hfill \\ {\mathit{\partial }}_{y}u(x,0)=0,\hfill & 0\le x\le a,\hfill \\ u(0,y)=u(a,y)=0,\hfill & 0\le y\le b,\hfill \end{array}\end{array}$$(4) ) is $u=0$. Let us define$$\begin{array}{c}\hfill A_n(y)=\frac{A_n{(\tanh ({\mathit{\lambda }}_{n}b))}^{2m+2}}{{\mathit{\lambda }}_n\cosh ({\mathit{\lambda }}_{n}b)}\sinh ({\mathit{\lambda }}_{n}y).\end{array}$$Using Parseval’s identity, we obtain that$$\begin{array}{c}\hfill \parallel u_{2m+2}{\parallel }_{L^2(\mathrm{\Omega })}^2=\frac{a}{2}\sum _{n=1}^{\infty }\frac{A_n^2{(\tanh ({\mathit{\lambda }}_{n}b))}^{4m+4}}{{\mathit{\lambda }}_n^2{\cosh }^2({\mathit{\lambda }}_{n}b)}\left(\frac{\cosh ({\mathit{\lambda }}_{n}b)\sinh ({\mathit{\lambda }}_{n}b)-{\mathit{\lambda }}_{n}b}{2{\mathit{\lambda }}_n}\right).\end{array}$$The sequence ${(u_{2m+2})}_{m=0}^{\infty }$ converges to 0 in $L^2(\mathrm{\Omega })$ when $|\tanh ({\mathit{\lambda }}_{1}b)|<1$, where$$\begin{array}{c}\hfill \tanh ({\mathit{\lambda }}_{1}b)=\{\begin{array}{cc}\tanh (\sqrt{a^{-2}{\mathit{\pi }}^2-k^2}b)\hfill & \text{if}{a}^{-2}{\mathit{\pi }}^2-k^2>0,\hfill \\ i\tan (\sqrt{k^2-a^{-2}{\mathit{\pi }}^2}b)\hfill & \text{if}{a}^{-2}{\mathit{\pi }}^2-k^2<0.\hfill \end{array}\end{array}$$The sequence ${(u_{2m+2})}_{m=0}^{\infty }$ diverges for$$\begin{array}{c}\hfill k^2\ge {\mathit{\pi }}^2(a^{-2}+{(4b)}^{-2}).\end{array}$$We, thus, conclude that the algorithm does not always converge for the Cauchy problem for the Helmholtz equation.

A modified alternating algorithm

To formulate the modified alternating algorithm for the geometries described in Figure 1 on the right and on the bottom, we first introduce an interior boundary $\mathit{\gamma }$ as follows: let ${\mathit{\omega }}_1,\dots ,{\mathit{\omega }}_m$ be open subsets inside the domain $\mathrm{\Omega }$ with $\overline{{\mathit{\omega }}_i}\subset \mathrm{\Omega }$ for $i=1,\dots ,m$, such that $\overline{{\mathit{\omega }}_i}\cap \overline{{\mathit{\omega }}_j}=\mathrm{\varnothing }$ for $i\ne j$. We assume that every ${\mathit{\omega }}_i$ is a Lipschitz domain. We denote by ${\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_m$ the boundaries of ${\mathit{\omega }}_1,\dots ,{\mathit{\omega }}_m$, respectively, and by $\mathit{\nu }$ the outward unit normal to the boundary ${\mathit{\gamma }}_i$. Let ${\mathrm{\Omega }}_1=\bigcup _{i=1}^m{\mathit{\omega }}_i$ with boundary $\mathit{\gamma }=\bigcup _{i=1}^m{\mathit{\gamma }}_i$ and ${\mathrm{\Omega }}_2=\mathrm{\Omega }\setminus ({\mathrm{\Omega }}_1\cup \mathit{\gamma })$. Then $\mathrm{\Omega }={\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup \mathit{\gamma }$.

Now let $u$ be a function defined in $\mathrm{\Omega }$ and put$$\begin{array}{c}\hfill u_1=u\text{in}{\mathrm{\Omega }}_1\text{and}{u}_2=u\text{in}{\mathrm{\Omega }}_2.\end{array}$$ We denote by$$\begin{array}{c}\hfill \left[u\right]=u_1{|}_{\mathit{\gamma }}-u_2{|}_{\mathit{\gamma }}\text{and}\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]={\mathit{\partial }}_{\mathit{\nu }}{u}_1{|}_{\mathit{\gamma }}-{\mathit{\partial }}_{\mathit{\nu }}{u}_2{|}_{\mathit{\gamma }}\end{array}$$ the jump of the function $u$ and the jump of the normal derivative ${\mathit{\partial }}_{\mathit{\nu }}u$ across $\mathit{\gamma }$, respectively. To describe the modified algorithm, we also choose a positive constant $\mathit{\mu }$ so that the bilinear form associated to the Helmholtz equation, the boundary $\mathit{\gamma }$, and the constant $\mathit{\mu }$ is positive, i.e.,(5) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla u{|}^2-k^2{u}^2)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS}>0,\end{array}$$(5) for $u\in H^1(\mathrm{\Omega })$ such that $u\ne 0$. The algorithm consists of solving in an alternating way the following two well–posed boundary value problems:(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) and(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) The modified alternating iterative algorithm for solving (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ) is as follows:

1. The first approximation $u_0$ is obtained by solving (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ), where $\mathit{\eta }$ is an arbitrary initial approximation of the normal derivative on ${\mathrm{\Gamma }}_1$ and $\mathit{\xi }$ is an arbitrary approximation of $[{\mathit{\partial }}_{\mathit{\nu }}{u}_0]+\mathit{\mu }{u}_0$ on $\mathit{\gamma }$.

2. Having constructed $u_{2n}$, we find $u_{2n+1}$ by solving (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) with $\mathit{\varphi }=u_{2n}$ on ${\mathrm{\Gamma }}_1$ and $\mathit{\phi }=u_{2n}$ on $\mathit{\gamma }$.

3. We then obtain $u_{2n+2}$ by solving the problem (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) with $\mathit{\eta }={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}$ on ${\mathrm{\Gamma }}_1$ and $\mathit{\xi }=\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}\right]+\mathit{\mu }{u}_{2n+1}$ on $\mathit{\gamma }$.

As for the original alternating iterative algorithm, this modification thus consists of solving well-posed mixed boundary value problems for the original equation.

Bilinear form and properties of traces

In this section, we introduce the function spaces, used in this paper. We define the bilinear form associated to the Helmholtz equation, the boundary $\mathit{\gamma }$ and the constant $\mathit{\mu }$. We also define the normal derivative of functions that satisfy the Helmholtz equation.

Function spaces

We denote by $L^2(\mathrm{\Omega })$ the space of square integrable functions in $\mathrm{\Omega }$. The Sobolev space $H^1(\mathrm{\Omega })$ consists of all functions in $L^2(\mathrm{\Omega })$ whose first-order weak derivatives belong to $L^2(\mathrm{\Omega })$. The space $H^1(\mathrm{\Omega })$ is a Hilbert space with the inner product$$\begin{array}{c}\hfill {(u,v)}_{H^1(\mathrm{\Omega })}={(u,v)}_{L^2(\mathrm{\Omega })}+\sum _{j=1}^d{({\mathit{\partial }}_{j}u,{\mathit{\partial }}_{j}v)}_{L^2(\mathrm{\Omega })},u,v\in H^1(\mathrm{\Omega }).\end{array}$$The corresponding norm is given by$$\begin{array}{c}\hfill \parallel u{\parallel }_{H^1(\mathrm{\Omega })}={({\int }_{\mathrm{\Omega }}{u}^2\mathit{dx}+{\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx})}^{1/2},u\in H^1(\mathrm{\Omega }).\end{array}$$We also define $H_0^1(\mathrm{\Omega })$ as the subspace to $H^1(\mathrm{\Omega })$ of functions in $\mathrm{\Omega }$ that vanish on $\mathrm{\Gamma }$. Let $H^{1/2}(\mathrm{\Gamma })$ be the space of traces of function in $H^1(\mathrm{\Omega })$ on $\mathrm{\Gamma }$. One of the equivalent norms in this space is given by$$\begin{array}{c}\hfill \parallel u{\parallel }_{H^{1/2}(\mathrm{\Gamma })}=({\int }_{\mathrm{\Gamma }}u{(x)}^2{\mathit{dS}}_x+{\int }_{\mathrm{\Gamma }}{\int }_{\mathrm{\Gamma }}\frac{{(u(x)-u(y))}^2}{|x-y{|}^d}{\mathit{dS}}_x{\mathit{dS}}_y{)}^{1/2},\end{array}$$where ${\mathit{dS}}_x$ and ${\mathit{dS}}_y$ denote surface measures. Similarly, we define $H^{1/2}(\mathit{\gamma })$ as the space of traces of function in $H^1(\mathrm{\Omega })$ on $\mathit{\gamma }$. We denote by $H^{1/2}({\mathrm{\Gamma }}_0)$ the space of restrictions of functions belonging to $H^{1/2}(\mathrm{\Gamma })$ to ${\mathrm{\Gamma }}_0$. The space $H^{1/2}({\mathrm{\Gamma }}_1)$ is defined similarly. We also denote by $H_{00}^{1/2}({\mathrm{\Gamma }}_1)$ the space of functions from $H^{1/2}(\mathrm{\Gamma })$ vanishing on ${\mathrm{\Gamma }}_0$. The norm in this space is given in Lions and Magenes (see [28, Chapter 1, Section 11.5]) by$$\begin{array}{c}\hfill \parallel u{\parallel }_{H_{00}^{1/2}({\mathrm{\Gamma }}_1)}=({\int }_{{\mathrm{\Gamma }}_1}\frac{u{(x)}^2}{\mathrm{dist}(x,{\mathrm{\Gamma }}_0)}{\mathit{dS}}_x+{\int }_{{\mathrm{\Gamma }}_1}{\int }_{{\mathrm{\Gamma }}_1}\frac{{(u(x)-u(y))}^2}{|x-y{|}^d}{\mathit{dS}}_x{\mathit{dS}}_y{)}^{1/2},\end{array}$$where $\mathrm{dist}(x,{\mathrm{\Gamma }}_0)$ is the distance from $x$ to ${\mathrm{\Gamma }}_0$. We will denote the dual space of $H^{1/2}(\mathrm{\Gamma })$ by $H^{1/2}{(\mathrm{\Gamma })}^{\ast }$. This space is equipped with the norm of dual spaces:$$\begin{array}{c}\hfill \parallel u{\parallel }_{H^{1/2}{(\mathrm{\Gamma })}^{\ast }}=\underset{v\in H^{1/2}(\mathrm{\Gamma })}{\sup }\frac{\left|〈u,v〉\right|}{\parallel v{\parallel }_{H^{1/2}(\mathrm{\Gamma })}}.\end{array}$$The space $H^{1/2}{(\mathit{\gamma })}^{\ast }$ is defined in the same way.

A bilinear form $a_{\mathit{\mu }}$ and a sufficient condition for $a_{\mathit{\mu }}$ to be positive definite

Let u be a smooth solution to the Helmholtz equation(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) Green’s formula and (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ) yield that(9) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}={\int }_{\mathit{\gamma }}\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(9) for all $u,v\in H^1(\mathrm{\Omega })$. Now assume that $\mathit{\mu }$ is a positive constant. By adding the expression $\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}$ to both sides of (9(9) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}={\int }_{\mathit{\gamma }}\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(9) ), we obtain that(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) for all $u,v\in H^1(\mathrm{\Omega })$.

Let us introduce a bilinear form $a_{\mathit{\mu }}$, defined by(11) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u,v)={\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}\text{for}u,v\in H^1(\mathrm{\Omega }).\end{array}$$(11) Since we assume that (5(5) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla u{|}^2-k^2{u}^2)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS}>0,\end{array}$$(5) ) holds, this form is an inner product on $H^1(\mathrm{\Omega })$ and the corresponding norm defined by $\parallel u{\parallel }_{a_{\mathit{\mu }}}=a_{\mathit{\mu }}{(u,u)}^{1/2}$ for every $u\in H^1(\mathrm{\Omega })$ is an equivalent norm in $H^1(\mathrm{\Omega })$; (see [29, Chapter 1, Section 1.2]).

We now prove a sufficient condition for the form $a_{\mathit{\mu }}$ to be positive definite on $H^1(\mathrm{\Omega })$.

Lemma 2.1

Put(12) $$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\mu }}=\underset{\begin{array}{c}\hfill u\in H^1(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }({\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS})\end{array}$$(12) and(13) $$\begin{array}{c}\hfill \mathrm{\Lambda }=\underset{\begin{array}{c}\hfill u\in W_0(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }{\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx},\end{array}$$(13) where $W_0(\mathrm{\Omega })=\{u\in H^1(\mathrm{\Omega }):u=0\text{on}\mathit{\gamma }\}$. Then there exists a positive constant $C$ such that(14) $$\begin{array}{c}\hfill \mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}\le C{\left(\frac{{\mathrm{\Lambda }}^3}{\mathit{\mu }}\right)}^{1/2}.\end{array}$$(14)

Proof

It follows directly from (12(12) $$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\mu }}=\underset{\begin{array}{c}\hfill u\in H^1(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }({\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS})\end{array}$$(12) ) and (13(13) $$\begin{array}{c}\hfill \mathrm{\Lambda }=\underset{\begin{array}{c}\hfill u\in W_0(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }{\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx},\end{array}$$(13) ) that ${\mathrm{\Lambda }}_{\mathit{\mu }}\le \mathrm{\Lambda }$. The infimum in (12(12) $$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\mu }}=\underset{\begin{array}{c}\hfill u\in H^1(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }({\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS})\end{array}$$(12) ) is attained for a function $u_{\mathit{\mu }}\in H^1(\mathrm{\Omega })$. Since $\parallel u_{\mathit{\mu }}{\parallel }_{L^2(\mathrm{\Omega })}=1$, formula (12(12) $$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\mu }}=\underset{\begin{array}{c}\hfill u\in H^1(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }({\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS})\end{array}$$(12) ) shows that(15) $$\begin{array}{c}\hfill {\int }_{\mathit{\gamma }}{u}_{\mathit{\mu }}^2\mathit{dS}\le \frac{\mathrm{\Lambda }}{\mathit{\mu }}.\end{array}$$(15) On the other hand, since $u_{\mathit{\mu }}$ solves (12(12) $$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{\mathit{\mu }}=\underset{\begin{array}{c}\hfill u\in H^1(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }({\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS})\end{array}$$(12) ),(16) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u_{\mathit{\mu }}·\nabla v\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}_{\mathit{\mu }}v\mathit{dS}={\mathrm{\Lambda }}_{\mathit{\mu }}{\int }_{\mathrm{\Omega }}{u}_{\mathit{\mu }}v\mathit{dx}\end{array}$$(16) for every function $v\in H^1(\mathrm{\Omega })$. The identity (16(16) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u_{\mathit{\mu }}·\nabla v\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}_{\mathit{\mu }}v\mathit{dS}={\mathrm{\Lambda }}_{\mathit{\mu }}{\int }_{\mathrm{\Omega }}{u}_{\mathit{\mu }}v\mathit{dx}\end{array}$$(16) ) now implies that(17) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }{u}_{\mathit{\mu }}+{\mathrm{\Lambda }}_{\mathit{\mu }}{u}_{\mathit{\mu }}=0\hfill & \text{outside}\mathit{\gamma },\hfill \\ u_{\mathit{\mu }}=u_{\mathit{\mu }}\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}{u}_{\mathit{\mu }}=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$(17) Now let $u_{\mathit{\mu }}=u_0+w$ be a decomposition of $u_{\mathit{\mu }}$, where $u_0\in H^1(\mathrm{\Omega })$ is harmonic outside $\mathit{\gamma }$ and satisfies$$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }{u}_0=0\hfill & \text{outside}\mathit{\gamma },\hfill \\ u_0=u_{\mathit{\mu }}\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}{u}_0=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$Using a result from [30, Chapter 7], we see that(18) $$\begin{array}{c}\hfill \parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}\le C\parallel u_{\mathit{\mu }}{\parallel }_{L^2(\mathit{\gamma })}.\end{array}$$(18) Replacing $u_{\mathit{\mu }}$ by $u_0+w$ in (17(17) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }{u}_{\mathit{\mu }}+{\mathrm{\Lambda }}_{\mathit{\mu }}{u}_{\mathit{\mu }}=0\hfill & \text{outside}\mathit{\gamma },\hfill \\ u_{\mathit{\mu }}=u_{\mathit{\mu }}\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}{u}_{\mathit{\mu }}=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$(17) ), we obtain the following problem:(19) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }w+{\mathrm{\Lambda }}_{\mathit{\mu }}w=-{\mathrm{\Lambda }}_{\mathit{\mu }}{u}_0\hfill & \text{outside}\mathit{\gamma },\hfill \\ w=0\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}w=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$(19) Multiplying the first equation of (19(19) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }w+{\mathrm{\Lambda }}_{\mathit{\mu }}w=-{\mathrm{\Lambda }}_{\mathit{\mu }}{u}_0\hfill & \text{outside}\mathit{\gamma },\hfill \\ w=0\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}w=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$(19) ) by $w\in H^1(\mathrm{\Omega })$, integrating by parts and taking into account the boundary conditions, we obtain that$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla w{|}^2-{\mathrm{\Lambda }}_{\mathit{\mu }}{w}^2)\mathit{dx}={\mathrm{\Lambda }}_{\mathit{\mu }}{\int }_{\mathrm{\Omega }}{u}_{0}w\mathit{dx}.\end{array}$$The Cauchy–Schwarz inequality now shows that(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla w{|}^2-{\mathrm{\Lambda }}_{\mathit{\mu }}|w{|}^2)\mathit{dx}\le {\mathrm{\Lambda }}_{\mathit{\mu }}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}\parallel w{\parallel }_{L^2(\mathrm{\Omega })}.\end{array}$$(20) We observe from (19(19) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }w+{\mathrm{\Lambda }}_{\mathit{\mu }}w=-{\mathrm{\Lambda }}_{\mathit{\mu }}{u}_0\hfill & \text{outside}\mathit{\gamma },\hfill \\ w=0\hfill & \text{on}\mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}w=0\hfill & \text{on}\mathrm{\Gamma }.\hfill \end{array}\end{array}$$(19) ) that the function $w$ belongs to $H^1(\mathrm{\Omega })$ and $w=0$ on $\mathit{\gamma }$. We thus have from (13(13) $$\begin{array}{c}\hfill \mathrm{\Lambda }=\underset{\begin{array}{c}\hfill u\in W_0(\mathrm{\Omega })\hfill \\ \hfill \parallel u{\parallel }_{L^2(\mathrm{\Omega })}=1\hfill \end{array}}{\inf }{\int }_{\mathrm{\Omega }}|\nabla u{|}^2\mathit{dx},\end{array}$$(13) ) that$$\begin{array}{c}\hfill \mathrm{\Lambda }\le \frac{{\int }_{\mathrm{\Omega }}|\nabla w{|}^2\mathit{dx}}{{\int }_{\mathrm{\Omega }}{w}^2\mathit{dx}}.\end{array}$$This relation together with (20(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla w{|}^2-{\mathrm{\Lambda }}_{\mathit{\mu }}|w{|}^2)\mathit{dx}\le {\mathrm{\Lambda }}_{\mathit{\mu }}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}\parallel w{\parallel }_{L^2(\mathrm{\Omega })}.\end{array}$$(20) ) give that$$\begin{array}{c}\hfill (\mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}){\int }_{\mathrm{\Omega }}|w{|}^2\mathit{dx}\le {\mathrm{\Lambda }}_{\mathit{\mu }}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}\parallel w{\parallel }_{L^2(\mathrm{\Omega })},\end{array}$$which leads to(21) $$\begin{array}{c}\hfill \parallel w{\parallel }_{L^2(\mathrm{\Omega })}\le \frac{{\mathrm{\Lambda }}_{\mathit{\mu }}}{\mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}.\end{array}$$(21) Since $\parallel u_{\mathit{\mu }}{\parallel }_{L^2(\mathrm{\Omega })}=1$, it follows from (21(21) $$\begin{array}{c}\hfill \parallel w{\parallel }_{L^2(\mathrm{\Omega })}\le \frac{{\mathrm{\Lambda }}_{\mathit{\mu }}}{\mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}.\end{array}$$(21) ) that$$\begin{array}{c}\hfill 1\le \parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}+\parallel w{\parallel }_{L^2(\mathrm{\Omega })}\le \frac{\mathrm{\Lambda }}{\mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}}\parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}.\end{array}$$Using the estimate (18(18) $$\begin{array}{c}\hfill \parallel u_0{\parallel }_{L^2(\mathrm{\Omega })}\le C\parallel u_{\mathit{\mu }}{\parallel }_{L^2(\mathit{\gamma })}.\end{array}$$(18) ) and the fact that $\mathrm{\Lambda }\ge {\mathrm{\Lambda }}_{\mathit{\mu }}$, we see that$$\begin{array}{c}\hfill \mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}\le C\mathrm{\Lambda }\parallel u_{\mathit{\mu }}{\parallel }_{L^2(\mathit{\gamma })}.\end{array}$$The result now follows from (15(15) $$\begin{array}{c}\hfill {\int }_{\mathit{\gamma }}{u}_{\mathit{\mu }}^2\mathit{dS}\le \frac{\mathrm{\Lambda }}{\mathit{\mu }}.\end{array}$$(15) ).$\square$

Theorem 2.2

If $\mathrm{\Lambda }$ is positive, then$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla u{|}^2-k^2{u}^2)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS}>0,\text{for}\text{all}u,u\ne 0\text{on}\mathit{\gamma }.\end{array}$$for sufficiently large $\mathit{\mu }$.

Traces and their properties

In this section, we define the trace spaces and their properties. We begin by giving the definition of a weak solution to the Helmholtz Equation (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ). Let us define $V(\mathrm{\Omega })=\{u\in H^1(\mathrm{\Omega }):u=0\text{on}\mathrm{\Gamma }\cup \mathit{\gamma }\}$.

Definition 2.3

A function $u\in H^1(\mathrm{\Omega })$ is called a weak solution to the Helmholtz equation (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ) if(22) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx}=0\end{array}$$(22) for every function $v\in V(\mathrm{\Omega })$.

Let $\mathcal{H}$ denote the space of weak solutions to (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ). Assume that $u\in C^2(\overline{\mathrm{\Omega }})$ is a classical solution to (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ). The identity (9(9) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}={\int }_{\mathit{\gamma }}\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(9) ) can be used to define the normal derivative ${\mathit{\partial }}_{\mathit{\nu }}u$ on $\mathrm{\Gamma }$ and on $\mathit{\gamma }$ for a solution to (8(8) $$\begin{array}{c}\hfill \mathrm{\Delta }u+k^{2}u=0\text{in}\mathrm{\Omega }\setminus \mathit{\gamma }.\end{array}$$(8) ). It follows from [28, Chapter 1, Section 9.2] that for any pair of functions ${\mathit{\psi }}_1\in H^{1/2}(\mathrm{\Gamma })$ and ${\mathit{\psi }}_2\in H^{1/2}(\mathit{\gamma })$, there exists a function $v\in H^1(\mathrm{\Omega })$ such that $v={\mathit{\psi }}_1$ on $\mathrm{\Gamma }$ and $v={\mathit{\psi }}_2$ on $\mathit{\gamma }$, satisfying(23) $$\begin{array}{c}\hfill \parallel v{\parallel }_{H^1(\mathrm{\Omega })}\le C(\parallel {\mathit{\psi }}_1{\parallel }_{H^{1/2}(\mathrm{\Gamma })}+\parallel {\mathit{\psi }}_2{\parallel }_{H^{1/2}(\mathit{\gamma })}),\end{array}$$(23) where the constant $C$ is independent of ${\mathit{\psi }}_1$ and ${\mathit{\psi }}_2$.

Lemma 2.4

There exists a bounded linear operator$$\begin{array}{c}\hfill G:\mathcal{H}⟶H^{1/2}{(\mathrm{\Gamma })}^{\ast }\times H^{1/2}{(\mathit{\gamma })}^{\ast }\end{array}$$such that for $u\in \mathcal{H}$ and $\mathit{\psi }=({\mathit{\psi }}_1,{\mathit{\psi }}_2)\in H^{1/2}(\mathrm{\Gamma })\times H^{1/2}(\mathit{\gamma })$,(24) $$\begin{array}{c}\hfill 〈G(u),\mathit{\psi }〉={\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx},\end{array}$$(24) where $v\in H^1(\mathrm{\Omega })$ satisfies $v{|}_{\mathrm{\Gamma }}={\mathit{\psi }}_1$ and $v{|}_{\mathit{\gamma }}={\mathit{\psi }}_2$. Moreover,$$\begin{array}{c}\hfill G(u)=({\mathit{\partial }}_{\mathit{\nu }}u,\left[{\mathit{\partial }}_{\mathit{\nu }}u\right])\text{if}u\in C^2(\mathrm{\Omega }).\end{array}$$

Proof

We first show that the right–hand side of (24(24) $$\begin{array}{c}\hfill 〈G(u),\mathit{\psi }〉={\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx},\end{array}$$(24) ) is independent of the choice of $v$. Let $u\in \mathcal{H}$. If $v_1,v_2\in H^1(\mathrm{\Omega })$ and $v_1=v_2={\mathit{\psi }}_1$ on $\mathrm{\Gamma }$ and $v_1=v_2={\mathit{\psi }}_2$ on $\mathit{\gamma }$, then the difference $v=v_1-v_2$ belongs to $V(\mathrm{\Omega })$. From (22(22) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx}=0\end{array}$$(22) ), we therefore have that$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx}=0.\end{array}$$ It follows that$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\nabla u·\nabla v_1\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}u{v}_1\mathit{dx}={\int }_{\mathrm{\Omega }}\nabla u·\nabla v_2\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}u{v}_2\mathit{dx}.\end{array}$$ Thus, the definition of $G(u)$ does not depend on $v$. We now show that $G(u)$ is a bounded operator from $\mathcal{H}$ to $H^{1/2}{(\mathrm{\Gamma })}^{\ast }\times H^{1/2}{(\mathit{\gamma })}^{\ast }$. Applying the Cauchy–Schwarz inequality to the right–hand side of (24(24) $$\begin{array}{c}\hfill 〈G(u),\mathit{\psi }〉={\int }_{\mathrm{\Omega }}\nabla u·\nabla v\mathit{dx}-k^2{\int }_{\mathrm{\Omega }}uv\mathit{dx},\end{array}$$(24) ), we get that$$\begin{array}{c}\hfill |〈G(u),\mathit{\psi }〉|\le (1+k^2)\parallel u{\parallel }_{H^1(\mathrm{\Omega })}\parallel v{\parallel }_{H^1(\mathrm{\Omega })}.\end{array}$$Together with (23(23) $$\begin{array}{c}\hfill \parallel v{\parallel }_{H^1(\mathrm{\Omega })}\le C(\parallel {\mathit{\psi }}_1{\parallel }_{H^{1/2}(\mathrm{\Gamma })}+\parallel {\mathit{\psi }}_2{\parallel }_{H^{1/2}(\mathit{\gamma })}),\end{array}$$(23) ), this yields that$$\begin{array}{c}\hfill |〈G(u),\mathit{\psi }〉|\le C\parallel u{\parallel }_{H^1(\mathrm{\Omega })}(\parallel {\mathit{\psi }}_1{\parallel }_{H^{1/2}(\mathrm{\Gamma })}+\parallel {\mathit{\psi }}_2{\parallel }_{H^{1/2}(\mathit{\gamma })}),\end{array}$$which shows that $G(u)$ belongs to $H^{1/2}{(\mathrm{\Gamma })}^{\ast }\times H^{1/2}{(\mathit{\gamma })}^{\ast }$ and that $G$ is bounded.$\square$

The main theorem

We now prove the main theorem in this paper. We denote the sequence of solutions to (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ), obtained from the modified alternating algorithm described in Section 1.4 by ${(u_n(f,g,\mathit{\eta },\mathit{\xi }))}_{n=0}^{\infty }$. The proof uses a similar argument as in [17].

Theorem 3.1

Suppose that assumptions on the choice of the interior boundary formulated in Section 1.4 and the positivity of the quadratic form (5(5) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\nabla u{|}^2-k^2{u}^2)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathit{dS}>0,\end{array}$$(5) ) are fulfilled. Let $f\in H^{1/2}({\mathrm{\Gamma }}_0)$ and $g\in H^{1/2}{({\mathrm{\Gamma }}_0)}^{\ast }$, and let $u\in H^1(\mathrm{\Omega })$ be the solution to problem (1(1) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\end{array}$$(1) ). Then, for every $\mathit{\eta }\in H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }$ and every $\mathit{\xi }\in H^{1/2}{(\mathit{\gamma })}^{\ast }$, the sequence ${(u_n)}_{n=0}^{\infty }$, obtained from the modified alternating algorithm, converges to $u$ in $H^1(\mathrm{\Omega })$.

Proof

Lemma 2.4 shows that ${\mathit{\partial }}_{\mathit{\nu }}u{|}_{{\mathrm{\Gamma }}_1}\in H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }$. Since$$\begin{array}{c}\hfill u=u_n(f,g,{\mathit{\partial }}_{\mathit{\nu }}u{|}_{{\mathrm{\Gamma }}_1},\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u{|}_{\mathit{\gamma }}),\end{array}$$ it follows that$$\begin{array}{c}\hfill u_n(f,g,\mathit{\eta },\mathit{\xi })-u=u_n(0,0,\mathit{\eta }-{\mathit{\partial }}_{\mathit{\nu }}u{|}_{{\mathrm{\Gamma }}_1},\mathit{\xi }-(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u{|}_{\mathit{\gamma }}\left)\right),\end{array}$$which means that we can assume that $f=g=0$. Then $u_{2n}$ solves problem (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) with $u_{2n}=0$ on ${\mathrm{\Gamma }}_0$, ${\mathit{\partial }}_{\mathit{\nu }}{u}_{2n}={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n-1}$ on ${\mathrm{\Gamma }}_1$ and $\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n}\right]+\mathit{\mu }{u}_{2n}=\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n-1}\right]+\mathit{\mu }{u}_{2n-1}$ on $\mathit{\gamma }$. From (10(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) ) and (11(11) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u,v)={\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}\text{for}u,v\in H^1(\mathrm{\Omega }).\end{array}$$(11) ), we have that$$\begin{array}{cc}\hfill a_{\mathit{\mu }}(u_{2n-1},u_{2n})& ={\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_{2n-1})u_{2n}\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n-1}\right]+\mathit{\mu }{u}_{2n-1})u_{2n}\mathit{dS}\hfill \\ \hfill & ={\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_{2n})u_{2n}\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n}\right]+\mathit{\mu }{u}_{2n})u_{2n}\mathit{dS}\hfill \\ \hfill & =a_{\mathit{\mu }}(u_{2n},u_{2n}).\hfill \end{array}$$Notice that $u_{2n+1}$ solves problem (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) with ${\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}=0$ on ${\mathrm{\Gamma }}_0$, $u_{2n+1}=u_{2n}$ on ${\mathrm{\Gamma }}_1$ and on $\mathit{\gamma }$. Again, it follows from (10(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) ) and (11(11) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u,v)={\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}\text{for}u,v\in H^1(\mathrm{\Omega }).\end{array}$$(11) ) that$$\begin{array}{cc}\hfill a_{\mathit{\mu }}(u_{2n},u_{2n+1})& ={\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_{2n})u_{2n+1}\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n}\right]+\mathit{\mu }{u}_{2n})u_{2n+1}\mathit{dS}\hfill \\ \hfill & ={\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1})u_{2n+1}\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}\right]+\mathit{\mu }{u}_{2n+1})u_{2n+1}\mathit{dS}\hfill \\ \hfill & =a_{\mathit{\mu }}(u_{2n+1},u_{2n+1}).\hfill \end{array}$$From these relations, we obtain that(25) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n+1}-u_{2n},u_{2n+1}-u_{2n})=a_{\mathit{\mu }}(u_{2n},u_{2n})-a_{\mathit{\mu }}(u_{2n+1},u_{2n+1})\end{array}$$(25) and(26) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n}-u_{2n-1},u_{2n}-u_{2n-1})=a_{\mathit{\mu }}(u_{2n-1},u_{2n-1})-a_{\mathit{\mu }}(u_{2n},u_{2n}).\end{array}$$(26) It thus follows from (25(25) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n+1}-u_{2n},u_{2n+1}-u_{2n})=a_{\mathit{\mu }}(u_{2n},u_{2n})-a_{\mathit{\mu }}(u_{2n+1},u_{2n+1})\end{array}$$(25) ) and (26(26) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n}-u_{2n-1},u_{2n}-u_{2n-1})=a_{\mathit{\mu }}(u_{2n-1},u_{2n-1})-a_{\mathit{\mu }}(u_{2n},u_{2n}).\end{array}$$(26) ) that the sequence ${(a_{\mathit{\mu }}(u_n,u_n))}_{n=0}^{\infty }$ is decreasing.

In the following, we denote the space $H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }\times H^{1/2}{(\mathit{\gamma })}^{\ast }$ by ${(H^{1/2})}^{\ast }$. Now for $\mathit{\chi }=(\mathit{\eta },\mathit{\xi })\in {(H^{1/2})}^{\ast }$, put $u_n(\mathit{\chi })=u_n(0,0,\mathit{\eta },\mathit{\xi })$. We will show that the set $\mathcal{R}$ of pairs $\mathit{\chi }\in {(H^{1/2})}^{\ast }$ such that ${(u_n(\mathit{\chi }))}_{n=0}^{\infty }$ converges to zero in $H^1(\mathrm{\Omega })$ is closed in ${(H^{1/2})}^{\ast }$. Suppose that ${\mathit{\chi }}_j\in \mathcal{R}$ and ${\mathit{\chi }}_j\to \mathit{\chi }\in {(H^{1/2})}^{\ast }$. Notice that$$\begin{array}{c}\hfill a_{\mathit{\mu }}{(u_n(\mathit{\chi }),u_n(\mathit{\chi }))}^{1/2}\le a_{\mathit{\mu }}{(u_n(\mathit{\chi }-{\mathit{\chi }}_j),u_n(\mathit{\chi }-{\mathit{\chi }}_j))}^{1/2}+a_{\mathit{\mu }}{(u_n({\mathit{\chi }}_j),u_n({\mathit{\chi }}_j))}^{1/2}.\end{array}$$Squaring both sides, we obtain that(27) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_n(\mathit{\chi }),u_n(\mathit{\chi }))\le 2a_{\mathit{\mu }}(u_n(\mathit{\chi }-{\mathit{\chi }}_j),u_n(\mathit{\chi }-{\mathit{\chi }}_j))+2a_{\mathit{\mu }}(u_n({\mathit{\chi }}_j),u_n({\mathit{\chi }}_j)).\end{array}$$(27) Since ${(a_{\mathit{\mu }}(u_n,u_n))}_{n=0}^{\infty }$ is decreasing, we have that$$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_n(\mathit{\chi }-{\mathit{\chi }}_j),u_n(\mathit{\chi }-{\mathit{\chi }}_j))\le a_{\mathit{\mu }}(u_0(\mathit{\chi }-{\mathit{\chi }}_j),u_0(\mathit{\chi }-{\mathit{\chi }}_j)).\end{array}$$Using the fact that $u_0$ is a solution to problem (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ), we obtain that$$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_n(\mathit{\chi }-{\mathit{\chi }}_j),u_n(\mathit{\chi }-{\mathit{\chi }}_j))\le C\parallel \mathit{\chi }-{\mathit{\chi }}_j{\parallel }_{{(H^{1/2})}^{\ast }}.\end{array}$$Now consider the second term in the right–hand side of (27(27) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_n(\mathit{\chi }),u_n(\mathit{\chi }))\le 2a_{\mathit{\mu }}(u_n(\mathit{\chi }-{\mathit{\chi }}_j),u_n(\mathit{\chi }-{\mathit{\chi }}_j))+2a_{\mathit{\mu }}(u_n({\mathit{\chi }}_j),u_n({\mathit{\chi }}_j)).\end{array}$$(27) ). Since we have assumed that ${\mathit{\chi }}_j\in \mathcal{R}$, $a_{\mathit{\mu }}(u_n({\mathit{\chi }}_j),u_n({\mathit{\chi }}_j))$ tends to zero as $n\to \infty$. This shows that ${(u_n(\mathit{\chi }))}_{n=0}^{\infty }$ converges to zero in $H^1(\mathrm{\Omega })$ and thus that $\mathit{\chi }\in \mathcal{R}$.

To show that $\mathcal{R}={(H^{1/2})}^{\ast }$, it suffices to prove that $\mathcal{R}$ is dense in ${(H^{1/2})}^{\ast }$. Assume that $\mathit{\phi }\in H^{1/2}({\mathrm{\Gamma }}_1)$ and ${\mathit{\phi }}^{\prime }\in H^{1/2}(\mathit{\gamma })$ satisfy(28) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_1({\mathit{\eta }}^{\prime })-{\mathit{\eta }}^{\prime })\mathit{\phi }\mathit{dS}+{\int }_{\mathit{\gamma }}([{\mathit{\partial }}_{\mathit{\nu }}{u}_1({\mathit{\xi }}^{\prime })]+\mathit{\mu }{u}_1({\mathit{\xi }}^{\prime })-{\mathit{\xi }}^{\prime }){\mathit{\phi }}^{\prime }\mathit{dS}=0\end{array}$$(28) for every ${\mathit{\eta }}^{\prime }\in H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }$ and ${\mathit{\xi }}^{\prime }\in H^{1/2}{(\mathit{\gamma })}^{\ast }$. We shall prove that $\mathit{\phi }=0$ on ${\mathrm{\Gamma }}_1$ and ${\mathit{\phi }}^{\prime }=0$ on $\mathit{\gamma }$.

Consider a function $v\in H^1(\mathrm{\Omega })$ that satisfies (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) with ${\mathit{\partial }}_{\mathit{\nu }}v=0$ on ${\mathrm{\Gamma }}_0$, $v=\mathit{\phi }$ on ${\mathrm{\Gamma }}_1$ and $v={\mathit{\phi }}^{\prime }$ on $\mathit{\gamma }$. The relation (10(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) ) and the expression (28(28) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}({\mathit{\partial }}_{\mathit{\nu }}{u}_1({\mathit{\eta }}^{\prime })-{\mathit{\eta }}^{\prime })\mathit{\phi }\mathit{dS}+{\int }_{\mathit{\gamma }}([{\mathit{\partial }}_{\mathit{\nu }}{u}_1({\mathit{\xi }}^{\prime })]+\mathit{\mu }{u}_1({\mathit{\xi }}^{\prime })-{\mathit{\xi }}^{\prime }){\mathit{\phi }}^{\prime }\mathit{dS}=0\end{array}$$(28) ) and using the fact that $v=\mathit{\phi }$ on ${\mathrm{\Gamma }}_1$ and $v={\mathit{\phi }}^{\prime }$ on $\mathit{\gamma }$, we obtain that$$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}(-{\mathit{\eta }}^{\prime }\mathit{\phi }+({\mathit{\partial }}_{\mathit{\nu }}v)u_1)\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}v\right]+\mathit{\mu }v)u_1\mathit{dS}-{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }{\mathit{\phi }}^{\prime }\mathit{dS}=0.\end{array}$$Let $u_1\in H^1(\mathrm{\Omega })$ be a solution to (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) with ${\mathit{\partial }}_{\mathit{\nu }}{u}_1=0$ on ${\mathrm{\Gamma }}_0$ and $u_1=u_0$ on ${\mathrm{\Gamma }}_1$ and on $\mathit{\gamma }$. The above expression thus gives(29) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}(-{\mathit{\eta }}^{\prime }\mathit{\phi }+({\mathit{\partial }}_{\mathit{\nu }}v)u_0)\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}v\right]+\mathit{\mu }v)u_0\mathit{dS}-{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }{\mathit{\phi }}^{\prime }\mathit{dS}=0.\end{array}$$(29) Now let $w\in H^1(\mathrm{\Omega })$ be a function that satisfies (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) with $w=0$ on ${\mathrm{\Gamma }}_0$, ${\mathit{\partial }}_{\mathit{\nu }}w={\mathit{\partial }}_{\mathit{\nu }}v$ on ${\mathrm{\Gamma }}_1$ and $\left[{\mathit{\partial }}_{\mathit{\nu }}w\right]+\mathit{\mu }w=\left[{\mathit{\partial }}_{\mathit{\nu }}v\right]+\mathit{\mu }v$ on $\mathit{\gamma }$. From (29(29) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}(-{\mathit{\eta }}^{\prime }\mathit{\phi }+({\mathit{\partial }}_{\mathit{\nu }}v)u_0)\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}v\right]+\mathit{\mu }v)u_0\mathit{dS}-{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }{\mathit{\phi }}^{\prime }\mathit{dS}=0.\end{array}$$(29) ), we obtain that$$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}(-{\mathit{\eta }}^{\prime }\mathit{\phi }+({\mathit{\partial }}_{\mathit{\nu }}w)u_0)\mathit{dS}+{\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}w\right]+\mathit{\mu }w)u_0\mathit{dS}-{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }{\mathit{\phi }}^{\prime }\mathit{dS}=0.\end{array}$$The relation (10(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) ) yields that$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla w·\nabla u_0-k^{2}w{u}_0)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}w{u}_0\mathit{dS}-{\int }_{{\mathrm{\Gamma }}_1}{\mathit{\eta }}^{\prime }\mathit{\phi }\mathit{dx}-{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }{\mathit{\phi }}^{\prime }\mathit{dS}=0.\end{array}$$Using again the relation (10(10) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(\nabla u·\nabla v-k^{2}uv)\mathit{dx}+\mathit{\mu }{\int }_{\mathit{\gamma }}\mathit{uv}\mathit{dS}={\int }_{\mathit{\gamma }}(\left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u)v\mathit{dS}+{\int }_{\mathrm{\Gamma }}({\mathit{\partial }}_{\mathit{\nu }}u)v\mathit{dS}\end{array}$$(10) ) and since the function $u_0\in H^1(\mathrm{\Omega })$ satisfies (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) with $u_0=0$ on ${\mathrm{\Gamma }}_0$, ${\mathit{\partial }}_{\mathit{\nu }}{u}_0={\mathit{\eta }}^{\prime }$ on ${\mathrm{\Gamma }}_1$ and $[{\mathit{\partial }}_{\mathit{\nu }}{u}_0]+\mathit{\mu }{u}_0={\mathit{\xi }}^{\prime }$ on $\mathit{\gamma }$, we arrive at$$\begin{array}{c}\hfill {\int }_{{\mathrm{\Gamma }}_1}{\mathit{\eta }}^{\prime }(w-\mathit{\phi })\mathit{dS}+{\int }_{\mathit{\gamma }}{\mathit{\xi }}^{\prime }(w-{\mathit{\phi }}^{\prime })\mathit{dS}=0.\end{array}$$Since ${\mathit{\eta }}^{\prime }\in H^{1/2}{({\mathrm{\Gamma }}_1)}^{\ast }$ and ${\mathit{\xi }}^{\prime }\in H^{1/2}{(\mathit{\gamma })}^{\ast }$ are arbitrary functions, we have $w=\mathit{\phi }$ on ${\mathrm{\Gamma }}_1$ and $w={\mathit{\phi }}^{\prime }$ on $\mathit{\gamma }$. On the other hand, since $v=\mathit{\phi }$ on ${\mathrm{\Gamma }}_1$, $v={\mathit{\phi }}^{\prime }$ on $\mathit{\gamma }$, and ${\mathit{\partial }}_{\mathit{\nu }}w={\mathit{\partial }}_{\mathit{\nu }}v$ on ${\mathrm{\Gamma }}_1$, we obtain that $w-v={\mathit{\partial }}_{\mathit{\nu }}(w-v)=0$ on ${\mathrm{\Gamma }}_1$. Now, using the fact that $w-v$ solves the Helmholtz equation in $\mathrm{\Omega }$, it follows that $w=v$. From the fact that $w={\mathit{\partial }}_{\mathit{\nu }}v=0$ on ${\mathrm{\Gamma }}_0$, it follows that $w=v=0$ in $\mathrm{\Omega }$. Thus, $\mathit{\phi }=0$ on ${\mathrm{\Gamma }}_1$ and ${\mathit{\phi }}^{\prime }=0$ on $\mathit{\gamma }$. This shows that $\mathcal{R}$ is dense in ${(H^{1/2})}^{\ast }$. Since $\mathcal{R}$ is closed and dense in ${(H^{1/2})}^{\ast }$, we have $\mathcal{R}={(H^{1/2})}^{\ast }$. That means that for any $\mathit{\chi }\in {(H^{1/2})}^{\ast }$, the sequence $u_n(\mathit{\chi })$ converges to zero in $H^1(\mathrm{\Omega })$. Since we assumed that $f=g=0$, the theorem is thus proved.$\square$

Remark

1. The boundary value problem (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) can be replaced by$$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\sigma }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$ where $\mathit{\sigma }$ is a positive constant. The alternating iterative algorithm described above thus runs the same way, where, for any even step, the boundary condition ${\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\sigma }u$ on ${\mathrm{\Gamma }}_1$ is used instead of the boundary condition ${\mathit{\partial }}_{\mathit{\nu }}u$ on ${\mathrm{\Gamma }}_1$. This case is considered in the numerical experiments in the next section.

2. The alternating iterative method described here does not converge if the boundary value problem (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) is given by$$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$ In that case, the even steps of the algorithm in Section 1.4 are kept the same and for any odd step, one wants to find $u_{2n+1}$ by solving the above problem with $\mathit{\varphi }=u_{2n}$ on ${\mathrm{\Gamma }}_1$ and $\mathit{\phi }=[{\mathit{\partial }}_{\mathit{\nu }}{u}_{2n}]+\mathit{\mu }{u}_{2n}$. The proof of the main theorem thus does not hold since the sequence ${(a_{\mathit{\mu }}(u_n,u_n))}_{n=0}^{\infty }$ is not monotonic. In fact, the Equations (25(25) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n+1}-u_{2n},u_{2n+1}-u_{2n})=a_{\mathit{\mu }}(u_{2n},u_{2n})-a_{\mathit{\mu }}(u_{2n+1},u_{2n+1})\end{array}$$(25) ) and (26(26) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n}-u_{2n-1},u_{2n}-u_{2n-1})=a_{\mathit{\mu }}(u_{2n-1},u_{2n-1})-a_{\mathit{\mu }}(u_{2n},u_{2n}).\end{array}$$(26) ) become$$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n+1}-u_{2n},u_{2n+1}-u_{2n})=a_{\mathit{\mu }}(u_{2n},u_{2n})-a_{\mathit{\mu }}(u_{2n+1},u_{2n+1})\end{array}$$ and $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u_{2n}-u_{2n-1},u_{2n}-u_{2n-1})=a_{\mathit{\mu }}(u_{2n},u_{2n})-a_{\mathit{\mu }}(u_{2n-1},u_{2n-1}),\end{array}$$from which we conclude that the sequence ${(a_{\mathit{\mu }}(u_n,u_n))}_{n=0}^{\infty }$ is neither decreasing nor increasing.

3. We also have the same convergent result, if we replace the Laplacian operator $\mathrm{\Delta }u$ by an elliptic operator $\nabla ·(A(x)\nabla u)$, where $A(x)$ is a symmetric matrix whose elements are bounded and measurable real–valued functions and the normal derivative ${\mathit{\partial }}_{\mathit{\nu }}$ replaced by the conormal derivative $\mathit{\nu }·(A(x)\nabla u)$.

4. We do not discuss the stopping rule here but one can use the same stopping rule as in [19, Section 7].

Numerical results

In this section, we present some numerical experiments. The results are obtained using the modified alternating algorithm presented in the previous sections, where the well–posed boundary value problems (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) and (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) are solved using the finite difference method (FDM). We also verify the non–convergence result for the standard alternating algorithm. We let $\mathrm{\Omega }=(0,1)\times (0,L)$, where $L>0$, be the domain and consider the following problem:$$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u(x,y)+k^{2}u(x,y)=0,\hfill & 0<x<1,0<y<L,\hfill \\ u(x,0)=f(x),\hfill & 0\le x\le 1,\hfill \\ u_y(x,0)=g(x),\hfill & 0\le x\le 1,\hfill \\ u(0,y)=u(1,y)=0,\hfill & 0\le y\le L.\hfill \end{array}\end{array}$$We put ${\mathrm{\Gamma }}_0=(0,1)\times \{0\}$ and ${\mathrm{\Gamma }}_1=(0,1)\times \{L\}$. Our aim is to compare the numerical and exact solutions at $y=L$.

For the implementation of the modified algorithm, the interior boundary $\mathit{\gamma }$ discussed in Section 1.4 is chosen so that the eigenvalue for the problem inside $\mathit{\gamma }$ and the eigenvalue for the problem outside $\mathit{\gamma }$ are approximately equal so that the relation (14(14) $$\begin{array}{c}\hfill \mathrm{\Lambda }-{\mathrm{\Lambda }}_{\mathit{\mu }}\le C{\left(\frac{{\mathrm{\Lambda }}^3}{\mathit{\mu }}\right)}^{1/2}.\end{array}$$(14) ) in Section 2.2 is satisfied. Different choices of $\mathit{\gamma }$ are discussed in Examples 4.1 and 4.2. We first provide details about the FDM. We discretize the domain by choosing an equidistant grid:$$\begin{array}{c}\hfill \{(x_i,y_j):x_i=\mathit{ih},y_j=\mathit{jh},0\le i\le N,0\le j\le M\}\end{array}$$with the grid size $h=N^{-1}$. Note that, since we want the grid size to be equal in the $x$- and $y$-directions, we use $M=\mathit{round}({\mathit{Lh}}^{-1})$. In that case, $N^{-1}={\mathit{LM}}^{-1}$ and the same step size is used in the $x$- and $y$-directions. Let $u_{i,j}$ denote the discrete approximation to $u(x_i,y_j)$. The finite difference approximation for the Helmholtz equation at each interior point $(x_i,y_j)$ simplifies to$$\begin{array}{c}\hfill (4-k^2{h}^2)u_{i,j}-u_{i-1,j}-u_{i+1,j}-u_{i,j-1}-u_{i,j+1}=0.\end{array}$$At the boundaries corresponding to $x=0$, and $x=1$, the value of the function $u$ is zero and the corresponding variables $u_{i,j}$ are explicitly set to zero. However, at the boundaries corresponding to $y=0$, and $y=L$ we get different equations depending on the type of the boundary condition. For the Dirichlet boundary conditions, we get the discretization of the form$$\begin{array}{c}\hfill u_{i,j}=d_i^j,i=0,\dots ,N,j=1\text{or}j=M,\end{array}$$where $d_i^j$ is the prescribed Dirichlet data at $y=0$ or $y=L$. The discretization of the Neumann boundary conditions is given by$$\begin{array}{c}\hfill (-3u_{i,j}+4u_{i,j+1}-u_{i,j+2}){(2h)}^{-1}=n_i^j,i=0,\dots ,N,j=1\text{or}j=M-2,\end{array}$$and $n_i^j$ is the prescribed Neumann data at $y=0$ or $y=L$. This particular choice means that we approximate the Neumann condition with accuracy $\mathcal{O}(h^2)$.

According to the type of the boundary data at $y=0$ and $y=L$, the discretization of the two well–posed boundary value problems (6(6) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ \left[{\mathit{\partial }}_{\mathit{\nu }}u\right]+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \\ \left[u\right]=0\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\end{array}$$(6) ) and (7(7) $$\begin{array}{c}\hfill \{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega }\setminus \mathit{\gamma },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\phi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\end{array}$$(7) ) using the finite difference approximation discussed above leads to two different types of linear systems $A_{i}u=b_i$, $i=1,2$, where each $A_i$ is a large sparse matrix of size $\mathit{MN}\times \mathit{MN}$, and each $b_i$ is a vector that contains the boundary data values. These systems are solved in an alternating way using the LU factorization of the matrix $A_i$. Since each matrix $A_i$ depends only on the size of the domain, the parameter $k^2$ and the parameter $\mathit{\mu }$, but not on the actual boundary data values, we can save the matrix $A_i$ and its sparse LU factorization between iterations. This significantly improves the computational speed.

Fig. 2 Numerical solution $u_e(x,y)$ obtained by solving the direct problem with boundary conditions $u(x,0)$ and $u_e(x,L)$ is displayed to the left. On the right we plot $u_y(x,0)$ (dashed line) and $u_y(x,L)$ (solid line) for $k^2=15$.

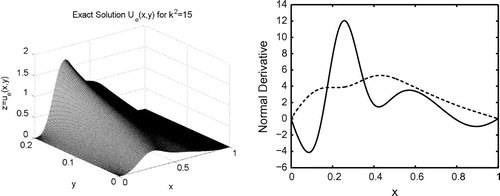
Fig. 3 On the left, we show the value of the exact solution at $y=L$ (solid line) and the reconstructed function (dashed line) for $k^2=15$. The divergence of the algorithm for $k^2=25.5$ is shown on the right where we plot the error $e_n$ for 1500 iterations.

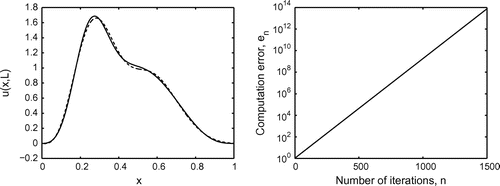
Fig. 4 The solid lines represent the exact solution $u_e(x,L)$ and the dashed lines the numerical solution $u_n(x,L)$. On the left, we present the results when no noise is added to the data. The corresponding results when a normally distributed random noise of variance $\mathit{ϵ}=2.5·{10}^{-2}$ is added to the data are presented on the right.

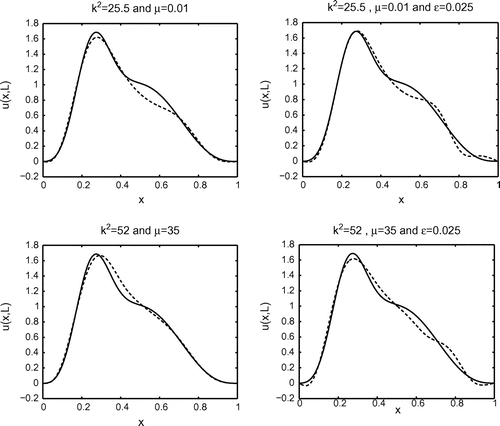
Fig. 5 The boundary condition $u_y(x,L)$ is replaced by the boundary condition $u_y(x,L)+\mathit{\sigma }u(x,L)$ in the modified alternating algorithm. The solid lines represent the exact solution $u_e(x,L)$ and the dashed lines the numerical solution $u_n(x,L)$. On the right a normally distributed random noise of variance $\mathit{ϵ}=2.5·{10}^{-2}$ is added to the data.

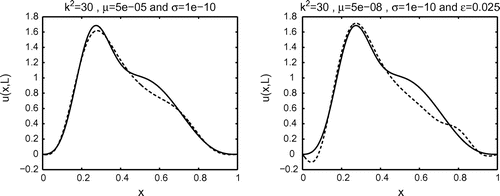
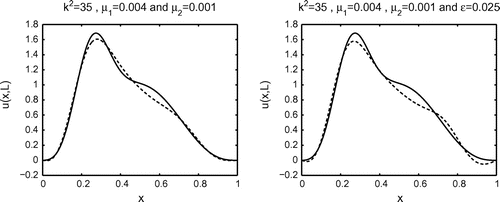
Fig. 6 Two interior boundaries described in Example 4.2 are chosen. The solid lines represent the exact solution $u_e(x,L)$ and the dashed lines the numerical solution $u_n(x,L)$. On the right a normally distributed random noise of variance $\mathit{ϵ}=2.5·{10}^{-2}$ is added to the data.

For the numerical computations, we particularly choose $L=0.2$, $N=400$ and $M=80$, and select the boundary data $f(x)=u(x,0)$ on ${\mathrm{\Gamma }}_0$ as$$\begin{array}{c}\hfill u(x,0)=(3\sin (\mathit{\pi }x)+\frac{\sin (3\mathit{\pi }x)}{19}+9\exp (-30{(x-L)}^2))x^2{(1-x)}^2.\end{array}$$The exact boundary data on ${\mathrm{\Gamma }}_1$, used to test the performance of the algorithm, is given by$$\begin{array}{c}\hfill u_e(x,L)=2(8\sin (\mathit{\pi }x)+\frac{\sin (3\mathit{\pi }x)}{17}+20\exp (-50{(x-L)}^2))x^2{(1-x)}^2.\end{array}$$The boundary data $g(x)=u_y(x,0)$ is obtained numerically after solving the direct problem for the Helmholtz equation with boundary data $u(x,0)$ and $u_e(x,L)$ given above and $u(0,y)=u(1,y)=0$. The numerical solution is displayed in Figure 2. To start the algorithm, we chose an arbitray initial guess $u_y(x,L)=0$ on ${\mathrm{\Gamma }}_1$. In order to test the convergence of the algorithm, we compute the following norm$$\begin{array}{c}\hfill e_n=\underset{0\le x\le 1}{\max }|u_e(x,L)-u_n(x,L)|,\end{array}$$where $u_n(x,L)$ is the numerical solution at $y=L$ and $n$ the iteration number. For all tests, the results are displayed after 1500 iterations. In Figure 3, we display the convergence of the standard alternating iterative algorithm, described in Section 1.2, for $k^2=15$ and its divergence for $k^2=25.5$. Notice that the algorithm diverges for $k^2>25.29$ according to the results in Section 1.3. This confirms the fact that the standard algorithm does not always converge. We can now implement the modified alternating iterative algorithm. For this, we need to choose the interior boundary $\mathit{\gamma }$.

Example 4.1

We choose the interior boundary as follows: we first choose the centre of gravity of the rectangle $\mathrm{\Omega }=(0,1)\times (0,L)$. We pick the interior boundary as a rectangle with the same centre of gravity as $\mathrm{\Omega }$, and side lengths $L_1$ and $L_2$. The interior domain is ${\mathrm{\Omega }}_1=4^{-1}(1-L_1,1+L_1)\times (L-L_2,L+L_2)$ with boundary $\mathit{\gamma }$. For the test, we chose $L=0.2$, $L_1=0.20$ and $L_2=0.08$. The boundary data values on $\mathit{\gamma }$ are chosen numerically so that they will be different from the values of the exact solution on $\mathit{\gamma }$.

Figure 4 shows the exact and numerical results for $u(x,L)$ for different values of $k^2$ and $\mathit{\mu }$. We also present the corresponding results when a normally distributed random noise of variance $\mathit{ϵ}=2.5·{10}^{-2}$ is added on the data $u(x,0)$ and $u_y(x,0)$.

For the results in Figure 5, it can be seen that when the boundary condition $u_y(x,L)$ is replaced by the boundary condition $u_y(x,L)+\mathit{\sigma }u(x,L)$ with the initial guess given by $u_y(x,L)+\mathit{\sigma }u(x,L)=0$, the algorithm converges. In this case, we have observed the improvement of the numerical results for the values of $\mathit{\mu }$ and $\mathit{\sigma }$ relatively small.

Example 4.2

We now choose two interior boundaries ${\mathit{\gamma }}_1$ and ${\mathit{\gamma }}_2$. The first rectangle is ${\mathrm{\Omega }}_1=4^{-1}(1-L_1,1+L_1)\times (L-L_2,L+L_2)$ with boundary ${\mathit{\gamma }}_1$ and the second rectangle ${\mathrm{\Omega }}_2=4^{-1}(1-L_3,1+L_3)\times L-L_4,L+L_4)$ inside ${\mathrm{\Omega }}_1$ has boundary ${\mathit{\gamma }}_2$. For the test, we chose $L_1=0.22$, $L_2=0.08$, $L_3=0.12$ and $L_4=0.04$. As above, the boundary data values on ${\mathit{\gamma }}_1$ and ${\mathit{\gamma }}_2$ are chosen numerically. The numerical results are shown in Figure 6 and it can be observed that accurate and stable results are obtained.

Acknowledgments

The work of Lydie Mpinganzima is supported by the Swedish Development International Agency (SIDA) and the National University of Rwanda (NUR).