Simultaneous determination of time-varying strength and location of a heating source in a three-dimensional domain

Abstract

In this article, identification of heating source location and time-dependent surface heat flux is investigated considering point temperature measurements on a boundary of the studied three-dimensional geometry. Such Inverse Heat Conduction Problems are ill-posed, since solution stability is not satisfied when observations are noisy/disturbed. We propose a robust algorithm for a simultaneous estimation of location and time-varying strength of a plane heat source. This iterative regularization method based on the conjugate gradient method is tested in several numerical configurations.

Keywords:

• inverse heat conduction problem
• parametric identification
• conjugate gradient method
• partial differential equations
• 3-D thermal model

1. Introduction

Inverse problems resolution for parametric identification in thermal context is widely investigated. In the specific framework of surface heat flux estimation, numerous studies can be mentioned and among recent references, one can cite [1] for boundary estimation in a falling film experiment using infrared radiometer (in a three-dimensional domain) [2] for the identification of an unknown heat flux applied to the interior surface of a cylinder using infrared camera (in a cylindrical geometry) or [3] devoted to unknown time- and space-dependent frictional heat flux identification (a non-linear system is considered in an axial-symmetric domain). Concurrently, determination of fixed heat sources location, or moving heat sources trajectories is less investigated. In [4], source locations are identified in a two-dimensional geometry, while heat sources number is unknown (and has also to be determined). The proposed method is extended in [5] considering measurement errors, point sources and sensors (numerical applications are shown in two- and three-dimensional domains). In [6], heat source locations identification is performed in a parallelepiped (heat fluxes are applied on several discs on one plate face while point measurements are obtained on the opposite face). Simultaneous identification of heat flux and location induce a greater complexity. The study presented in [7] is devoted to the estimation of the time-varying heat flux and the location of a single point source in a one-dimensional domain (temperatures are measured on both boundaries). A finite difference scheme is implemented for numerical simulation and measurement noise effect is analysed. In [8], the conjugate gradient method (CGM) is implemented in order to estimate simultaneously the strength and the position of heating source in a one-dimensional geometry. An experimental study is proposed in [9] for simultaneous estimation of a source heating flux (strength and location) in two-dimensional heat diffusion problem by implementing the boundary element method (BEM). Heat flux and location of line heat sources are identified in steady state in [10] and [11], while sources number is assumed to be known (a two-dimensional experimental situation is proposed). Another approach has been proposed in [12], where both strength and location of two moving sources are investigated considering measurement errors and 32 sensors located on the boundary of a square domain. In [13], identification of strength and location of heating in a two-dimensional geometry is successfully performed. More recently, in [14], an approach based on the implementation of the CGM is used for estimating a heating source (which this latter depends simultaneously on time and space) in one-dimensional geometry. In addition, in [15], heat flux and location of a single fixed source in a one-dimensional IHCP are estimated considering the temperature measured at the final time by using the CGM. Various numerical examples (with and without the presence of noisy data) have been presented to examine the robustness and the accuracy of the proposed approach.

Let us briefly present the common methods for IHCP resolution. Among the most common methods for ill-posed problem resolution in thermal context, classical minimization algorithm such as steepest descent method in [2] or BFGS (quasi-Newton) [16] are quite relevant. A method based on a boundary integral formulation combined with Green functions is presented in [8]. In [17], the mollification method is proposed for the identification of source term in one-dimensional IHCP. An example of the well-known Beck’s sequential function specification is presented in [18]. More recently, modal methods (such as Branch Eigen-modes Reduction Method, in [19]) are developed (see [20] for example). Minimization algorithms based on CGM are widely presented in [1,3,6], [21–28]. For example, in a three-dimensional domain, such approach is used for the identification of heat source locations in [6] and for time-varying strength identification in [28].

In the present work, simultaneous estimation of both the unknown parameters (time-varying strength of a heat flux and fixed heat source location) is investigated in a three-dimensional domain. In the studied geometry, the temperature evolution is described by a set of partial differential equations (parabolic equation in the domain subject to adequate boundary and initial conditions). The paper is organized as follows: in the next section, the thermal phenomenon is described by a set of partial differential equations (PDEs) and presented as a direct problem. Numerical simulations are performed using a finite element method (FEM) from the Comsol-Multiphysics^TM software. In the third section, the inverse problem is formulated and the main steps of the conjugate gradient algorithm are briefly exposed. In order to simultaneously identify the time-varying strength of a heat flux and location of a source, the formulation of a sensitivity problem and an adjoint problem and the admissible level of minimization value are addressed in the following three sections. In the sixth section, numerical results are provided and effects of disturbances on measurements are discussed through different cases. Finally, several concluding remarks and different outlooks are proposed.

2 Direct problem

Temperature evolution in the studied domain is described by a parabolic PDE with initial and boundary conditions. In the following Equation (1), the space variable is $(x\text{,}y\text{,}z)\in \mathrm{\Omega }\subset {\mathbb{R}}^3$ $\partial \mathrm{\Omega }$ is the boundary of domain $\mathrm{\Omega }$, the time variable is $t\in T=[0\text{,}{t}_f]$ in seconds and the temperature is denoted by $\theta (x\text{,}y\text{,}z\text{;}t)$ in $[\text{K}]$:(1) $\left.\begin{array}{ccc}\hfill C\frac{\partial \theta (x\text{,}y\text{,}z\text{;}t)}{\partial t}-\lambda \mathrm{\Delta }\theta (x\text{,}y\text{,}z\text{;}t)=0\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \mathrm{\Omega }\times T\text{,}\hfill \\ \hfill \theta (x\text{,}y\text{,}z\text{;}0)={\theta }_0\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z)\in \mathrm{\Omega }\text{,}\hfill \\ \hfill -\lambda \frac{\partial \theta (x\text{,}y\text{,}z\text{;}t)}{\partial n}=h(\theta (x\text{,}y\text{,}z\text{;}t)-{\theta }_0)-\mathrm{\Phi }(x\text{,}y\text{,}z\text{;}t)\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \partial \mathrm{\Omega }\times T.\hfill \\ \hfill \hfill \end{array}\right\}$(1)

Main parameters are defined in Table 1. Vector $n$ is the outward-pointing unit normal vector to $\partial \mathrm{\Omega }$.

Table 1. Notations and parameters.

Initial and ambient temperature θ0	Thermal conductivity, λ	Final instant, tf
293 K	21.9 W m^−1 K^−1	100 s
Volumic heat, C	Natural convection coefficient h	Disk radius r
2.35 10^6 J m^−3 K^−1	20 W m^−2 K^−1	2 × 10^−3 m

Let us consider in the following that the domain geometry is a parallelepipedic plate with known thermal properties (titanium plate in the present study). Unknown input is $\mathrm{\Phi }(x\text{,}y\text{,}z\text{;}t)$ in $[\text{W}{\text{m}}^{-2}]$ which depends on source location and time-varying strength. For example, for a single fixed source (located on the lower plate face $y=0$), a uniform heat flux spatial distribution on a disc $D$ (centre $I=(X\text{,}0\text{,}Z)$ and radius $r$) is described by:(2) $\mathrm{\Phi }(x\text{,}0\text{,}z\text{,}t)=\left\{\begin{array}{cc}0\hfill & \text{if}(x\text{,}z)\notin D\text{,}\hfill \\ \varphi (t)\hfill & \text{if}(x\text{,}z)\in D.\hfill \\ \hfill \end{array}\right.$(2)

For numerical reasons, it is obvious that such discontinuous function is quite difficult to deal with. Then, the following definition is considered:(3) ${\mathrm{\Phi }}_{\mu }(x\text{,}0\text{,}z\text{,}t)=-\frac{\varphi (t)}{\pi }\left(\arctan \left(\mu \sqrt{(x-X{)}^2+(z-Z{)}^2}-\mu r\right)+\frac{\pi }{2}\right)\text{.}$(3)

Parameter $\mu$ is used to describe the discontinuity in the neighbourhood of the disc boundary. For example, for $\mu \to +\infty$ then ${\mathrm{\Phi }}_{\mu }(x\text{,}0\text{,}z\text{,}t)\to \mathrm{\Phi }(x\text{,}0\text{,}z\text{,}t)$. Considering the mesh used for FEM, $\mu ={10}^4$ is a correct approximation; numerical simulation are not dramatically affected by this modelization of the spatial distribution of the heating flux. A discrete formulation of $\varphi (t)$ can be considered:(4) $\varphi (t)=\sum _{i=1}^N{\varphi }_i{s}_i(t)$(4)

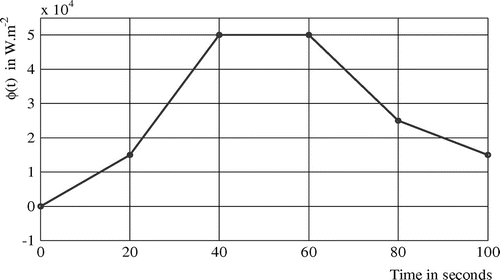
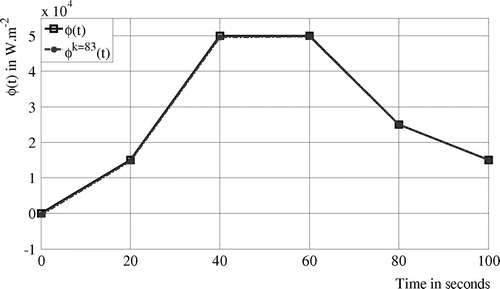
according to $N$ time steps and the basis of hat function $s_i(t)$, see Figure 1. Thus, for example, if $N=6$ and $\underline{\varphi }=({\varphi }_i{)}_{i=1\text{,}\cdots \text{,}6}=(0\text{,}15\text{,}50\text{,}50\text{,}25\text{,}15)$ $\text{kW}{\text{m}}^{-2}$, boundary heat flux $\varphi (t)$ is drawn in Figure 2.

Figure 1 Basis functions s_i (t).

Figure 2 Heat flux.

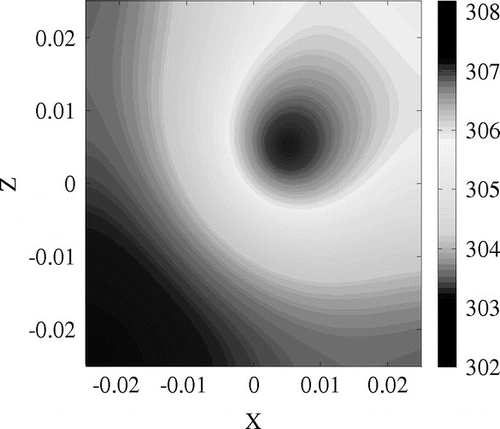
Considering the previous parameters, the direct problem described by the set of Equations (1) can be numerically solved using Comsol-Multiphyisics^TM interfaced with Matlab^®. An example of temperature evolution and spatial distribution (at $t=100\text{s}$) obtained with a single heating source on a square plate $(0.05\times 0.002\times 0.05)\text{m}$ is proposed. The fixed heat source location is $(0.005\text{,}0\text{,}0.005)\text{m}$; sensors coordinates are $C_1(0\text{,}0.002\text{,}0.006)$, $C_2(-0.0052\text{,}0.002\text{,}0.003)$ and $C_3(0.0052\text{,}0.002\text{,}0.003)$ in $\text{m}$, see Figure 3. Numerical simulations are shown in Figures45. Considering that both disc location $I=(X\text{,}0\text{,}Z)$ and heat flux $\underline{\varphi }=({\varphi }_i{)}_{i=1\text{,}\cdots \text{,}N}$ are unknown, an iterative regularization method based on the CGM (29, 30) is implemented for the three-dimensional IHCP resolution. Such algorithm is implemented for the minimizarion of a cost function describing the quadratic errors between the simulated temperature and observed temperature $\widehat{\theta }$. For the investigated configuration, three sensors $C_{m=1\text{,}2\text{,}3}$ are located on the non-heated face (number of sensors is $n_C=3$) and the temperature is measured with a proper time sample. The ill-posed and inverse problem is solved thanks to an iterative resolution of three well-posed problems: direct problem (for cost function calculus), adjoint problem (issued from Lagrangian formulation in order to estimate cost function gradient) and sensitivity problem (for descent depth determination). The CGM will be implemented in order to identify the unknown time-varying heat flux $\varphi (t)$ and the unknown source location $I(X\text{,}0\text{,}Z)$.

Figure 3 Source and sensors location.

Figure 4 Temperature evolution.

Figure 5 Spatial temperature distribution at t = t_f.

3 Inverse Heat Conduction Problem (IHCP)

Simultaneous identification of unknown parameters $\overline{\mathrm{\Phi }}=(X\text{,}Z\text{,}{\varphi }_{i=1\text{,}\cdots \text{,}N})$ is performed considering the minimization of cost function $J$ by an iterative descent method:(5) $J(\overline{\varphi }\text{,}X\text{,}Z)=\frac{1}{2}{\int }_0^{t_f}\sum _{m=1}^{n_C=3}(\theta (C_m\text{;}t\text{;}\overline{\varphi }\text{;}X\text{,}Z)-{\widehat{\theta }}_m(t){)}^2\mathit{dt}\approx \frac{1}{2}\sum _{j=1}^{n_f}\sum _{m=1}^{n_C=3}(\theta (C_m\text{;}j\text{;}\overline{\varphi }\text{;}X\text{,}Z)-{\widehat{\theta }}_m(j){)}^2\text{,}$(5)

where ${\widehat{\theta }}_m$ is the temperature measured by sensor $C_m$ and $n_f=100$ is the number of measurements provided by each sensor (sampling time is 1 s). A sequential approach is proposed. In the following, heat flux identification is denoted by HF, while source location identification is denoted by SL. The modified CGM is presented in the next section.

3.1 Conjugate gradient method (CGM)

1. Initialization: iteration number is $k=0$, intern counter is $n=0$ and arbitrary initial flux ${\overline{\varphi }}^{k=0}$ and initial source location $I^{k=0}=(X^{k=0}\text{,}0\text{,}{Z}^{k=0})$ are fixed. The first identification problem is, for example, heat flux identification $(\text{HF}=1\text{;}\text{SL}=0)$.

2. Solve the direct problem and calculate $J({\overline{\varphi }}^k\text{,}{I}^k)$.

   1. If $J({\overline{\varphi }}^k\text{,}{I}^k)⩽J_{\text{stop}}$, then the iterative procedure is halted and the current values of $({\overline{\varphi }}^k\text{,}{I}^k)$ are considered as relevant estimators.

   2. Else, the iterative procedure is continued.

3. Solve the adjoint problem.

   1. If $(\text{HF}=1\text{;}\text{SL}=0)$, determine the cost function gradient $\overline{\nabla J^k}=(\nabla J_{{\varphi }_i^k}{)}_{i=1\text{,}\cdots \text{,}N}$, while $\overline{\nabla J_I^k}=0\iff \nabla J_X^k=\nabla J_Z^k=0\text{and}\delta I=0\iff \delta X=\delta Z=0$.

   2. If $(\mathit{HF}=0\text{;}\text{SL}=1)$, determine the cost function gradient $\overline{\nabla J^k}=\overline{\nabla J_I^k}=(\nabla J_X^k\text{,}\nabla J_Z^k)$, and $(\nabla J_{{\varphi }_i^k}{)}_{i=1\text{,}\cdots \text{,}N}=0\text{and}\delta \varphi (t)=0$.

   3. Calculate the descent direction $\overline{d^{k+1}}=\overline{\nabla J^k}+{\beta }^k\overline{d^k}$ where ${\beta }^k=\Vert \overline{\nabla J^k}{\Vert }^2/\Vert \overline{\nabla J^{k-1}}{\Vert }^2$ (cf. [31]), except for ${\beta }^{k=0}=0$,

4. Solve the sensitivity problem in the descent direction

   1. Calculate the temperature variation $\delta \theta (x\text{,}y\text{,}z\text{;}t)$ in the descent direction $\overline{d^{k+1}}$.

   2. Calculate the descent depth ${\gamma }^{k+1}=\underset{\gamma \in {\mathbb{R}}^{\ast }}{\text{Arg}\min }J(\overline{{\mathrm{\Phi }}^k}-\gamma \overline{d^{k+1}})$.

5. Calculate

   1. if $(\text{HF}=1\text{;}\text{SL}=0)$ the new heat flux: ${\varphi }^{k+1}(t)={\varphi }^k(t)-{\gamma }^{k+1}\overline{d_{\varphi }^{k+1}}$.

   2. if $(\text{HF}=0\text{;}\text{SL}=1)$ the new source location: $I^{k+1}=I^k-{\gamma }^{k+1}\overline{d_I^{k+1}}$.

6. $n\leftarrow n+1\text{,}$

   1. If $(\text{HF}=1\text{;}\text{SL}=0)$ and $n=n_{\text{HF}}$: then $(\text{HF}=0\text{;}\text{SL}=1)$; $n=0$; ${\beta }^{k+1}=0$.

   2. If $(\text{HF}=0\text{;}\text{SL}=1)$ and $n=n_{\text{SL}}$: then $(\text{HF}=1\text{;}\text{SL}=0)$; $n=0$; ${\beta }^{k+1}=0$.

7. $k\leftarrow k+1$ and go to step (2).

Remarks In order to select $n_{\text{HF}}$ and $n_{\text{SL}}$ values (the maximum numbers of successive iteration dedicated to each problem HF or SL), the approach presented in [32] is adopted for restarting the descent direction procedures. In the proposed example, $n_{\text{HF}}$ is equal to the dimension of vector $\overline{\varphi }$ $(n_{\text{HF}}=6)$ and $n_{\text{SL}}=2$ is equal to the dimension of vector source coordinates $(X\text{,}Z)$.

3.2 Sensitivity problem

This problem consists in the determination of temperature variation $\delta \theta (x\text{,}y\text{,}z\text{;}t)$ induced by a variation of the heating flux strength $\delta \varphi (t)$ and the source location $\delta I(\delta X\text{,}0\text{,}\delta Z)$. Considering the partial differential equations system satisfied by the varied temperature $\theta (x\text{,}y\text{,}z\text{;}t)+\epsilon \delta \theta (x\text{,}y\text{,}z\text{;}t)$ (see direct problem given by Equation $(1)$ with a heating flux $\varphi (t)+\epsilon \delta \varphi (t)$ and a source location $\delta I=I+\epsilon \delta I=(X+\epsilon \delta X\text{,}Z+\epsilon \delta Z)$) then, while $\epsilon \to 0$, the sensitivity problem becomes:(6) $\left.\begin{array}{ccc}\hfill C\frac{\partial \delta \theta (x\text{,}y\text{,}z\text{;}t)}{\partial t}-\lambda \mathrm{\Delta }\delta \theta (x\text{,}y\text{,}z\text{;}t)=0\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \mathrm{\Omega }\times T\text{,}\hfill \\ \hfill \delta \theta (x\text{,}y\text{,}z\text{;}0)=0\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z)\in \mathrm{\Omega }\text{,}\hfill \\ \hfill -\lambda \frac{\partial \delta \theta (x\text{,}y\text{,}z\text{;}t)}{\partial \overrightarrow{n}}=h\delta \theta (x\text{,}y\text{,}z\text{;}t)-\delta \mathrm{\Phi }(x\text{,}y\text{,}z\text{;}t)\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \partial \mathrm{\Omega }\times T.\hfill \\ \hfill \hfill \end{array}\right\}$(6)

with $\delta \varphi (x\text{,}y\text{,}z\text{;}t)$ is the heating flux variation induced by $\delta \varphi (t)$ and $\delta I(\delta X\text{,}0\text{,}\delta Z)$:(7) $\delta \mathrm{\Phi }(x\text{,}y\text{,}z\text{;}t)=\frac{-1}{\pi }\left(\frac{\mu \varphi (t)((\delta X)(X-x)+(\delta Z)(Z-z))}{\xi (1+{\mu }^2(\xi -r{)}^2)}+\delta \varphi (t)\left(\arctan (\mu (\xi -r))+\frac{\pi }{2}\right)\right)\text{,}$(7)

where $\xi =\sqrt{(x-X{)}^2+(z-Z{)}^2}$.

Then, the descent depth is calculated using the following definition at each iteration:(8) ${\gamma }^{k+1}=\underset{\gamma \in {\mathbb{R}}^{\ast }}{\text{Arg}\min }J({\overline{\mathrm{\Phi }}}^k-{\gamma }^{k+1}\overline{d^{k+1}})=\underset{\gamma \in {\mathbb{R}}^{\ast }}{\text{Arg}\min }\left(\frac{1}{2}{\int }_0^{t_f}\sum _{m=1}^{n_C=3}(\theta (C_m\text{;}t\text{;}{\overline{\mathrm{\Phi }}}^k-{\gamma }^{k+1}\overline{d^{k+1}})-{\widehat{\theta }}_m(t){)}^2\mathit{dt}\right)\text{.}$(8)

After several developments (see examples in [7], [22]), the Equation (8) becomes:(9) ${\gamma }^{k+1}=\frac{{\int }_0^{t_f}\sum _{m=1}^{n_C=3}(\theta \left(C_m\text{;}t\text{;}{\overline{\mathrm{\Phi }}}^k\right)-{\widehat{\theta }}_m(t))\delta {\theta }_{\overline{d^{k+1}}}\left(C_m\text{;}t\text{;}{\overline{\mathrm{\Phi }}}^k\right)\mathit{dt}}{{\int }_0^{t_f}\sum _{m=1}^{n_C=3}{\left(\delta {\theta }_{\overline{d^{k+1}}}(C_m\text{;}t\text{;}{\overline{\mathrm{\Phi }}}^k)\right)}^2\mathit{dt}}\text{.}$(9)

The descent depth ${\gamma }^{k+1}$ is calculated at each iteration considering the sensitivity problem solution $\delta \theta (x\text{,}y\text{,}z\text{;}t)$ in the descent direction $\overline{d^{k+1}}$ .

3.3 Adjoint problem

The adjoint function $\psi (x\text{,}y\text{,}z\text{;}t)$ is introduced in order to determine the gradient function $\overline{\nabla J}=(\frac{\partial J}{\partial X}\text{,}\frac{\partial J}{\partial Z}\text{,}(\frac{\partial J}{\partial {\varphi }_i}{)}_{i=1\text{,}\cdots \text{,}N})$. Let $\ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )$ be the Lagrangian associated to the direct problem (see Equation $(1)$) defined by:(10) $\ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=J(\overline{\varphi }\text{,}I)+{\int }_0^{t_f}{\int }_{\mathrm{\Omega }}\left(C\frac{\partial \theta (.)}{\partial t}-\lambda \mathrm{\Delta }\theta (.)\right)\psi (.)\mathit{dt}d\mathrm{\Omega }\text{.}$(10)

Considering: $\delta \ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=\frac{\partial \ell }{\partial \theta }\delta \theta +{\sum }_{i=1}^N\frac{\partial \ell }{\partial {\varphi }_i}\delta {\varphi }_i+\frac{\partial \ell }{\partial X}\delta X+\frac{\partial \ell }{\partial Z}\delta Z+\frac{\partial \ell }{\partial \psi }\delta \psi$,

• if $\theta$ is a solution of the Equation (1), then: $\ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=J(\overline{\varphi }\text{,}I)$ and $\delta \ell (\theta \text{,}\overline{\mathrm{\varphi }}\text{,}I\text{,}\psi )=\delta J(\overline{\varphi }\text{,}I)$.

• if $\psi$ is fixed, then $\frac{\partial \ell }{\partial \psi }\delta \psi =0$ and $\delta \ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=\frac{\partial \ell }{\partial \theta }\delta \theta +{\sum }_{i=1}^N\frac{\partial \ell }{\partial {\varphi }_i}\delta {\varphi }_i+\frac{\partial \ell }{\partial X}\delta X+\frac{\partial \ell }{\partial Z}\delta Z$.

• moreover, $\psi$ is fixed in order to satisfy $\frac{\partial \ell }{\partial \theta }\delta \theta =0\text{,}\forall \delta \theta$.

The Lagrangian variation is:(11) $\begin{array}{c}\hfill \delta \ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=\hfill \\ \hfill {\int }_0^{t_f}{\int }_{\mathrm{\Omega }}\sum _{m=1}^{n_C=3}((\theta (C_m\text{;}t)-{\widehat{\theta }}_m(t)){\delta }_D(.\text{,}{C}_m))\delta \theta d\mathrm{\Omega }\mathit{dt}+{\int }_0^{t_f}{\int }_{\mathrm{\Omega }}\left(C\frac{\partial \delta \theta }{\partial t}-\lambda \mathrm{\Delta }\delta \theta \right)\psi \mathit{dt}d\mathrm{\Omega }\text{,}\hfill \end{array}$(11)

where ${\delta }_D$ is the Dirac distribution. Let $E(\theta )$ be the error function defined by: $E(\theta )={\sum }_{m=1}^{n_C=3}(\theta (C_m\text{;}t)-{\widehat{\theta }}_m(t)){\delta }_D(.\text{,}{C}_m)$. Then, the previous equation of Lagrangian (11) becomes:(12) $\delta \ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )={\int }_0^{t_f}{\int }_{\mathrm{\Omega }}E(\theta )\delta \theta (.)d\mathrm{\Omega }\mathit{dt}+{\int }_0^{t_f}{\int }_{\mathrm{\Omega }}\left(C\frac{\partial \delta \theta (.)}{\partial t}-\lambda \mathrm{\Delta }\delta \theta (.)\right)\psi (.)\mathit{dt}d\mathrm{\Omega }\text{.}$(12)

Considering Green theorem and sensitivity equations, adjoint problem can be formulated as:(13) $\left.\begin{array}{ccc}\hfill C\frac{\partial \psi (x\text{,}y\text{,}z\text{;}t)}{\partial t}+\lambda \mathrm{\Delta }\psi (x\text{,}y\text{,}z\text{;}t)=E(\theta )\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \mathrm{\Omega }\times T\text{,}\hfill \\ \hfill \psi (x\text{,}y\text{,}z\text{;}{t}_f)=0\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z)\in \mathrm{\Omega }\text{,}\hfill \\ \hfill -\lambda \frac{\partial \psi (x\text{,}y\text{,}z\text{;}t)}{\partial \overline{n}}=h\psi (x\text{,}y\text{,}z\text{;}t)\hfill & \hfill \hfill & \hfill (x\text{,}y\text{,}z\text{;}t)\in \partial \mathrm{\Omega }\times T.\hfill \\ \hfill \hfill \end{array}\right\}$(13)

Then, the Lagrangian variation expression given by (12) becomes:(14) $\delta \ell (\theta \text{,}\overline{\varphi }\text{,}I\text{,}\psi )=-{\int }_0^{t_f}{\int }_{{\mathrm{\Gamma }}_{\text{heated}}}\delta \mathrm{\Phi }(.)\psi (.)d\partial \mathrm{\Omega }\mathit{dt}=\delta J(\mathrm{\Phi }(.)\text{,}\psi )\text{.}$(14)

This previous equation leads to the following equations for gradient estimation:(15) $\left\{\begin{array}{c}\nabla J_{{\varphi }_i}=\frac{\partial J}{\partial {\varphi }_i}=\frac{1}{\pi }{\int }_0^{t_f}{\int }_{{\mathrm{\Gamma }}_{\text{heated}}}(\arctan (\mu (\xi -r))+\frac{\pi }{2})\psi (x\text{,}y\text{,}z\text{;}t)s_i(t)d\partial \mathrm{\Omega }\mathit{dt}\hfill \\ \nabla J_X=\frac{\partial J}{\partial X}=-\frac{1}{\pi }{\int }_0^{t_f}{\int }_{{\mathrm{\Gamma }}_{\text{heated}}}\varphi (t)(X-x)A(x\text{,}z)\psi (x\text{,}y\text{,}z\text{;}t)d\partial \mathrm{\Omega }\mathit{dt}\hfill \\ \nabla J_Z=\frac{\partial J}{\partial Z}=-\frac{1}{\pi }{\int }_0^{t_f}{\int }_{{\mathrm{\Gamma }}_{\text{heated}}}\varphi (t)(Z-z)A(x\text{,}z)\psi (x\text{,}y\text{,}z\text{;}t)d\partial \mathrm{\Omega }\mathit{dt}\hfill \end{array}\right.$(15) $\text{with}A(x\text{,}z)=\frac{\mu }{\xi (1+{\mu }^2(\xi -r{)}^2)}\text{.}$

In the two previous sections, it has been shown how to calculate descent depth and descent direction (which depends on cost function gradient).

3.4 Admissible level of minimization $J_{\text{stop}}$

In the ideal case where model errors, measurement errors and numerical errors are negligible, the halt criterion $J_{\text{stop}}$ can be chosen close to zero. In the investigated thermal process context $J_{\text{stop}}\approx 0.1$ has been considered. However, in practical experimentations, errors have to be taken into account and it is meaningless to obtain a cost function close to zero. In this study, considering a Gaussian additive noise on the measured temperature $\widehat{\theta }(x\text{,}y\text{,}z\text{;}t)$ the usual threshold (cf. [33]) the $J_{\text{stop}}=\frac{1}{2}{n}_C{n}_f{\sigma }^2$ can be proposed, where $n_C$ is the number of sensors ($n_C=3$ in the present study), $n_f$ is the number of measurements provided by each sensor ($n_f=100$ in the studied configuration, since time interval is $T=[0\text{,}{t}_f]=[0\text{,}100]\text{seconds}$ and time sampling is 1 s) and $\sigma$ is the standard deviation (Gaussian noise).The proposed threshold $J_{\text{stop}}$ arises from the iterative regularization CGM. Thus, it avoids estimated parameters convergence toward erroneous values taking into account noisy measurements.

4 Results for numerical implementation

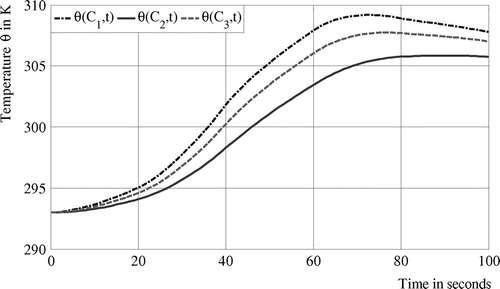
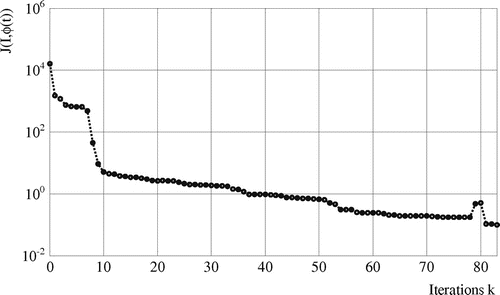
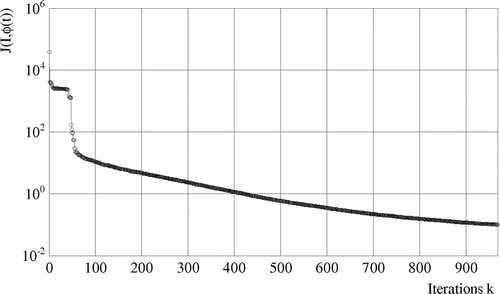
• Case 1: Let us consider that the unknown heat flux initial value is ${\overline{\varphi }}^{k=0}=0$ and the source position $I^{k=0}=(X^{k=0}\text{,}0\text{,}{Z}^{k=0})=(0\text{,}0\text{,}-0.005)\text{m}$, see Figure 3. Resolution of inverse problem is performed considering CGM and theoretical measured temperatures without noise, Figure 4. Cost-function evolution is shown in Figure 6 and Table 2. The estimated time strength of the heat flux is presented in Figure 7. Cost function values and source location versus iteration are presented in the Tables 2 and 3. In Figure 7, it is shown that the strength of the heat flux is accurately determined. Simultaneous identification is successful and source location is determined $(0.005\text{,}0\text{,}0.005)\text{m}$ with a reasonable accuracy, see Table 3.

• Case 2: Let us consider the same configuration as in Case 1, but with a Gaussian noise $\text{N}(0\text{,}0.5)$ added to observed temperature, see Figure 8. The cost function evolution is shown in Table 4. Considering the admissible level of minimization given in section 3.4 (cf. [33]) and the noise standard deviation, $J_{\text{stop}}$ is fixed at 37.5. The heat flux obtained after $k=10$ iterations is ${\overline{\varphi }}^{k=10}=(-0.2\text{,}17.4\text{,}46.3\text{,}47.9\text{,}29.3\text{,}6.2)$ $\text{kW}{\text{m}}^{-2}$. In few iterations, source coordinates are obtained (a small error due to noisy measurement is observed), see Table 5. Heat flux is correctly determined. Therefore, the proposed approach is quite attractive even with noisy observations.

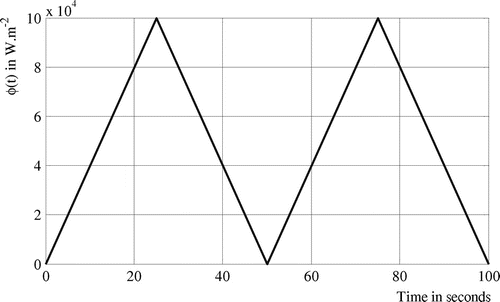
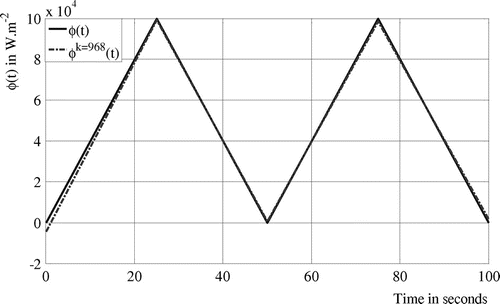
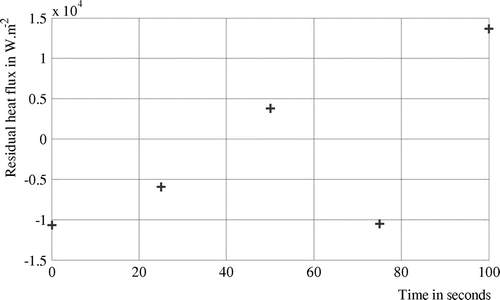
• Case 3: In this case, the exact source location is fixed at $I=(X\text{,}0\text{,}Z)=(0.01\text{,}0\text{,}0)\text{m}$ and the time-varying strength of the heat flux is presented in Figure 9. The heat flux is modelled as a piecewise linear continuous function on four time intervals (25 s each). Then, five basis functions are considered $(n_{\mathit{HF}}=5)$ and $\overline{\varphi }\in {\mathbb{R}}^{\mathbb{5}}$. 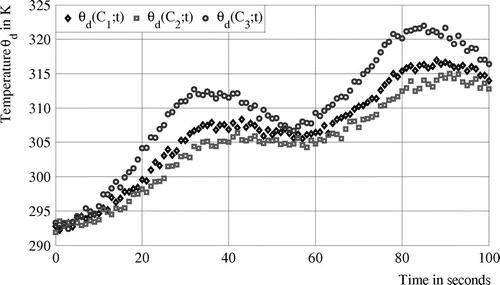Temperatures provided by the set of sensors after solving the direct problem are shown in Figure 10. The initial strength heat flux is similar to the previous cases ${\overline{\varphi }}^{k=0}=0$, and the initial source position is $I^{k=0}=(X^{k=0}\text{,}0\text{,}{Z}^{k=0})=(-0.01\text{,}0\text{,}0)\text{m}$. 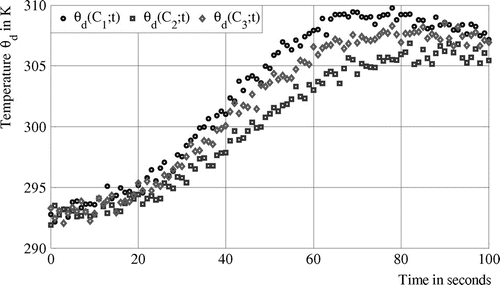The obtained results are shown in the Figures ^{Figure 11Figure 12Figure 13Figure 14} and Tables67. 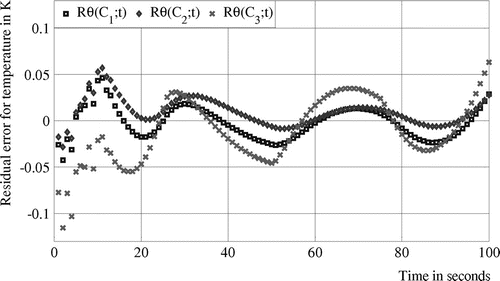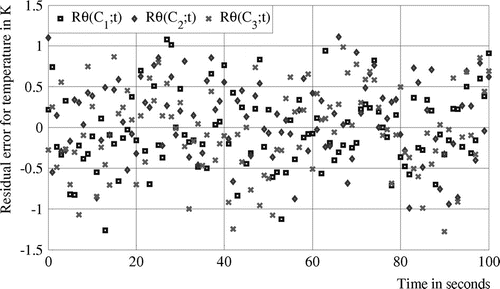Average values of the temperatures residuals issued by each sensor $C_1\text{,}{C}_2$ and $C_3$ are, respectively, equal to −0.002 K, 0.009 K and −0.011 K. The obtained results confirm the robustness of the CGM for identifying simultaneously the source position and the time-varying strength of the heat flux.

• Case 4: This last case is devoted to solve the same IHCP as Case 3, but with an additive Gaussian noise $\mathcal{N}(0\text{,}0.5)$ disturbing the observed temperature, see Figure 15. As previously mentioned, the stopping criterion (admissible level of minimization) is $J_{\text{stop}}=37.5$. The obtained results are presented in Figures 1617 and Tables89. The average values of the temperature residues obtained for each sensor ($C_1\text{,}{C}_2$ and $C_3$) are, respectively, about −0.06 K, 0.11 K and −0.05 K. It is important to notice that standard deviation between measured and simulated temperature for each temperature sensor has the same order of the Gaussian measurement noise magnitude $\mathcal{N}(0\text{,}0.5)$.

Figure 6 Cost function evolution, case 1.

Table 2. Criterion values vs. iteration, case 1.

Iteration k	0	1	…	3	…	7	8	9	…	39	…	83
J	16081.29	1522.68	…	737.23	…	482.49	44.86	9.32	…	0.95	…	0.009

Figure 7 Identified and exact heat flux, case 1.

Table 3. Coordinates vs. iteration, case 1.

Iteration k	0	…	7	8	…	15	16	…	83
X	0	…	0.0029	0.0046	…	0.0046	0.0046	…	0.0047
Z	−0.005	…	−0.0027	0.0045	…	0.0046	0.0047	…	0.0047

Figure 8 Evolution of the disturbed noisy temperature measurements, case 2.

Table 4. Criterion values vs. iteration, case 2.

Iteration k	0	1	2	3	4	5	6	7	8	9	10
J	16060	1531	1212	780.5	725.3	699.4	697.7	526.5	67.8	40.1	35.6

Table 5. Coordinates vs. iteration, case 2.

Iteration k	0	…	7	8	…	10
X	0	…	0.0028	0.0046	…	0.0046
Z	−0.005	…	−0.0027	0.0045	…	0.0045

Figure 9 Strength heat flux, case 3.

Figure 10 Temperature evolution, case 3.

Figure 11 Cost function evolution, case 3.

Figure 12 Identified and exact heat flux, case 3.

Figure 13 Residual temperature error, case 3.

Figure 14 Residual Heat flux error, case 3.

Table 6. Criterion values vs. iteration, case 3.

Iteration k	0	1	…	49	50	51	52	…	100	…	192	…
J	39039.8	4112.8	…	1324.6	186.3	123.4	97.6	…	10.7	…	4.85	…
Iteration k	…	260	…	418	419	…	968
J	…	2.98	…	1.02	0.99	…	0.09

Table 7. Coordinates vs. iteration, case 3.

Iteration k	0	…	48	…	192	…	273	…	…	318
X	−0.01	…	0.006	…	0.0077	…	0.00825	…	…	0.00848
Z	0	…	−0.002	…	0.00005	…	0.00008	…	…	0.00007
Iteration k	511	…	705	…	850	…	900	…	…	968
X	0.0092	…	0.00952	…	0.00964	…	0.00968	…	…	0.00969
Z	0.00005	…	0.00003	…	0.00002	…	0.00002	…	…	0.00001

Figure 15 Evolution of the disturbed noisy temperature measurements, case 4.

Figure 16 Residual temperature error, case 4.

Figure 17 Residual heat flux error, case 4.

Table 8. Criterion evolution vs. iteration, case 4.

Iteration k	0	1	…	8	…	40	41	…	43	44	45	…
J	39045	4200	…	2709	…	2156	954	…	137	95	90	…
Iteration k	…	60	…	80	…	120	…	150	…	154	155
J	…	52.9	…	45.5	…	39.8	…	37.8	…	37.5	37.4

Table 9. Coordinates vs. iteration, case 4

Iteration k	0	…	7	8	…	15	16	…	41	42	…
X	−0.01	…	−0.011	−0.0076	…	−0.006	−0.006	…	0.005	0.0050	…
Z	0	…	0.053	0.0051	…	0.006	0.006	…	0.001	−0.0014	…
Iteration k	68	69	70	…	117
X	0.0060	0.0062	0.0062	…	0.0069
Z	−0.0002	−0.00013	−0.00016	…	1.7 × 10^−5

Considering the previous results with and without noisy measurements, it is shown that the CGM algorithm is robust and efficient in order to simultaneously estimate the source location $I(X\text{,}0\text{,}Z)$, and the time-varying strength $\varphi (t)$ of the heat flux.

5 Conclusions

Considering temperature measurements at only three sensors, a three-dimensional inverse heat conduction problem (3-D IHCP) is solved by minimizing a quadratic criterion. It is shown that the CGM can be successfully adapted in order to identify both location and time-varying strength of the heat flux with the same data-set (see Cases 1 and 3). Effect of noise is also investigated through Cases 2 and 4 in order to assess the stability of the identification methodology.

Several outlooks can be considered for further works: the simultaneous identification of several sources (location and time-varying strength of the heat fluxes) and even their number. Last but not least, we are also interested in the identification of both heat flux and trajectory of heating mobile source using the CGM.