To solve the inverse Cauchy problem in linear elasticity by a novel Lie-group integrator

Abstract

In this paper, we propose a simple, iteration free and easy-to-implement numerical algorithm for the solution of inverse Cauchy problem in linear or nonlinear elasticity. The bottom of a finite rectangular plate is imposed by overspecified boundary data, and we seek unknown data on the top side. A spring-damping transform method (SDTM) is introduced to the Navier equations, such that after a discretization by the differential quadrature method, we can apply a novel Lie-group integrator, namely the mixed group-preserving scheme (MGPS), to solve them as an initial value problem. Several numerical examples including nonlinear ones are examined to show that the MGPS can overcome the ill-posed behaviour of the inverse Cauchy problem in elasticity, which has good efficiency and stability against the noisy disturbance, even with an intensity large up to $10\%$ and $20\%$.

Keywords:

• inverse Cauchy problem
• linear elasticity
• nonlinear elasticity
• spring-damping transform method
• mixed group-preserving scheme
• differential quadrature

1 Introduction

There are many important issues in the reconstruction of deformed shape for the purposes of structural health monitoring (SHM), damage detection, real-time shape control and shape modification. The shape reconstruction techniques from discrete position data have been under development for numerous years and there is a multitude of publications in the literature, especially with regard to the polynomial and spline reconstructions. Research on the reconstruction of displaced shape from strain measurements is less frequently encountered.[1] Indeed, a real-time reconstruction of the deformed shape of structure is a key technology for SHM. This sort problem is commonly referred to as a shape sensing problem, which is one class of the general inverse Cauchy problem in elasticity, if the deformation is restricted in the elastic range. For a real-time reconstruction of the deformed shape, it is necessary to develop a fast and stable algorithm for solving the resultant inverse Cauchy problems.

During the past several years, the science and engineering communities have paid much attention to the inverse Cauchy problem in linear elasticity, which is a noncharacteristic initial value problem of the elliptic type partial differential equations (PDEs). According to the Cauchy–Kowalewski theorem, the solution of an analytic Cauchy problem for PDEs exists and is unique. However, the inverse Cauchy problem is quite difficult to be solved numerically, since the solution does not depend continuously on the given data, that is, a small error in the specified data may result in an incorrect solution. Therefore, we must treat this type inverse problem with a suitable numerical algorithm, which compromises stability and accuracy.

The inverse Cauchy problem in linear elasticity was studied theoretically by Yeih et al. [2], who analyzed its existence, uniqueness and continuous dependence on the data, and proposed an alternative regularization procedure, namely the fictitious boundary indirect method, based on simple and double layer potential theory. Its numerical implementation was undertaken by Koya et al. [3], who employed the boundary element method (BEM) and the Nystr$\ddot{\text{o}}$m method for discretizing the boundary integrals.

The inverse Cauchy problem in linear elasticity is to solve the boundary value problem of Navier partial differential equations given by some overspecified Cauchy data on a partial portion of the boundary and other portion given no data, which is proved to have a unique solution if the solution exists. However, the problem of numerical instability lends the researchers a great challenge, because the inverse of the original forward operator is not obtainable. It means that the continuous dependence of the solution on the given data is not satisfied in the Hardmard sense. To treat this kind inverse problem, many techniques were proposed. The most famous one is the Tikhonov regularization method, which perturbs the original ill-posed problem into a constrained minimization problem. The Lagrangian multiplier, i.e. the regularization parameter, is not known in advance, which can be determined by the L-curve concept or some discrepancy principles. Except for this method, the truncated singular value decomposition method (SVD) had also been used. All of those methods try to improve the ill-conditioning behaviour of the resultant linear equations system.

The iterative algorithm of Kozlov et al. [4], which reduces the inverse Cauchy problem to solve a sequence of well-posed boundary value problems, was implemented using the BEM for linear elastic materials by Marin et al. [5], Marin and Lesnic,[6] and Comino et al. [7]. Ellabib and Nachaoui [8] have numerically investigated the relaxation of the alternating iterative algorithm of Kozlov et al. [4], while further investigations were carried out by Marin and Johansson,[9] who also proposed an alternative way of relaxation of both the prescribed displacements and tractions on the overspecified boundary. Moreover, Marin and Johansson [9] have proved the convergence of these schemes, and introduced appropriate optimal stopping rules to implement these algorithms with relaxation using the BEM. Andrieux and Baranger [10], and Baranger and Andrieux [11] have reformulated the inverse Cauchy problem for elastic material as an energy error minimization problem, with the unknowns given by the surface displacement and traction vectors on the underspecified boundary of the solid.

Four regularization methods for stably solving the inverse Cauchy problem in linear elasticity, namely the Tikhonov regularization method, the SVD, the conjugate gradient method (CGM) and the alternating iterative algorithm of Kozlov et al. [4], were compared by Marin and Lesnic,[12] and they found that the truncated SVD outperforms the Tikhonov regularization method, whilst the latter outperforms the CGM. Marin [13] has used the above alternating iterative algorithm of Kozlov et al. [4] together with the method of fundamental solutions (MFS) to solve the two-dimensional inverse Cauchy problem in linear elasticity. The inverse Cauchy problem in linear elasticity with the $L_2$-boundary data was approached by Marin and Lesnic [14] and Marin [15] by combining the BEM with the Landweber–Fridman method and the minimal error method.

Recently, Chen and his coworkers have used several alternating regularization techniques in conjunction with the singular boundary method (SBM) and the MFS to solve the inverse Cauchy problems.[16–19]

In contrast to those methods, the present paper aims to provide a simple numerical computation method based on a novel Lie-group integrator, directly integrating the inverse Cauchy problem as an initial value problem without needing of any iteration. In order to express the new method simpler and clearer, we first restrict ourself to the inverse Cauchy problem for a rectangular plate, because in this domain a numerical method of lines can be easily developed for the discretization of the Navier equations into a linear system of ODEs. An extension to arbitrary plane domain is possible. As mentioned above, the inverse Cauchy problem is a noncharacteristic problem, and there were only rare papers to develop a direct numerical integration method to solve it.[20–22] After a suitable and mathematically equivalent transformation technique by introducing the spring/damping terms into the Navier equations for an enhancement of the numerical stability in Section2, we develop a numerical method in Section 3 to solve the inverse Cauchy problem in linear elasticity for a rectangular plate, which is discretized into a linear ODEs system by using the numerical method of lines and differential quadrature method. In Section 4, we introduce three different group-preserving schemes, of which the last, as a combination of the previous two methods, is a novel Lie-group integrator named the mixed group-preserving scheme (MGPS), which is used in the numerical integration of the Cauchy problem in linear elasticity. The numerical results are given in Section 5. While Section 6 devotes to extend the Cauchy problem for a linear elliptic equation into that defined in an arbitrary plane domain, Section 7 extends the MGPS to nonlinear inverse Cauchy problems. Finally, the conclusions are drawn in Section 8.

2 A spring-damping transform method for the Cauchy problem of elasticity

2.1 Mathematical formulation

Consider an isotropic linear elastic material which occupies a bounded domain $\mathrm{\Omega }\in {\mathbb{R}}^2$ and assume that $\mathrm{\Omega }=[0,a]\times [0,b]$. ${\mathrm{\Gamma }}_1=[0,a]\times \{y=0\}$ denotes the bottom of the plate $\mathrm{\Omega }$, and ${\mathrm{\Gamma }}_2=[0,a]\times \{y=b\}$ denotes the top side. In the absence of body force, the equilibrium equations written with respect to the displacement vector $\mathbf{u}(\mathbf{x})=(u_1(\mathbf{x}),u_2(\mathbf{x}))$, known as the Navier equations, are given by [23]:1 $$\begin{array}{c}\hfill G\frac{{\mathit{\partial }}^2{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j\mathit{\partial }{x}_j}+\frac{G}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^2{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=0,\mathbf{x}\in \mathrm{\Omega },i=1,2,\end{array}$$1 where the repeated index is summed from 1 to 2, and $G$ and $\mathit{\nu }$ are, respectively, the shear modulus and the Poisson ratio of elastic material.

The strains ${\mathit{\epsilon }}_{ij}(\mathbf{x}),i,j=1,2$, are related to the displacement gradients by the small deformation kinematic relations:2 $$\begin{array}{c}\hfill {\mathit{\epsilon }}_{ij}(\mathbf{x})=\frac{1}{2}\left(\frac{\mathit{\partial }{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j},+,\frac{\mathit{\partial }{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i}\right),\mathbf{x}\in \overline{\mathrm{\Omega }},i,j=1,2,\end{array}$$2 while the stresses ${\mathit{\sigma }}_{ij}(\mathbf{x}),i,j=1,2$, are related to the strains through the Hooke constitutive law:3 $$\begin{array}{c}\hfill {\mathit{\sigma }}_{ij}(\mathbf{x})=2G\left({\mathit{\epsilon }}_{ij},(\mathbf{x}),+,\frac{\mathit{\nu }}{1-2\mathit{\nu }},{\mathit{\epsilon }}_{kk},(\mathbf{x}),{\mathit{\delta }}_{ij}\right),\mathbf{x}\in \overline{\mathrm{\Omega }},i,j=1,2,\end{array}$$3 where ${\mathit{\delta }}_{ij}$ is the Kronecker delta tensor. Let $\mathbf{n}(\mathbf{x})$ denote the outward normal vector on $\mathrm{\Gamma }$, and $\mathbf{t}(\mathbf{x})$ be the traction vector at a point $\mathbf{x}\in \mathrm{\Gamma }$ whose components are given by4 $$\begin{array}{c}\hfill t_i(\mathbf{x})={\mathit{\sigma }}_{ij}(\mathbf{x})n_j(\mathbf{x}),i=1,2.\end{array}$$4 As shown by Fung and Tong [23], in the direct problem of linear elasticity, the knowledge of the displacement and/or traction vectors on the whole boundary $\mathrm{\Gamma }$ gives the corresponding Dirichlet, Neumann or mixed boundary condition which enables us to determine the displacement vector in the whole domain $\mathrm{\Omega }$. Then, the strain tensor ${\mathit{\epsilon }}_{ij}$ can be calculated from the kinematic relations in Equation (22 $$\begin{array}{c}\hfill {\mathit{\epsilon }}_{ij}(\mathbf{x})=\frac{1}{2}\left(\frac{\mathit{\partial }{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j},+,\frac{\mathit{\partial }{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i}\right),\mathbf{x}\in \overline{\mathrm{\Omega }},i,j=1,2,\end{array}$$2 ) and the stress tensor ${\mathit{\sigma }}_{ij}$ is determined by using the constitutive law in Equation (33 $$\begin{array}{c}\hfill {\mathit{\sigma }}_{ij}(\mathbf{x})=2G\left({\mathit{\epsilon }}_{ij},(\mathbf{x}),+,\frac{\mathit{\nu }}{1-2\mathit{\nu }},{\mathit{\epsilon }}_{kk},(\mathbf{x}),{\mathit{\delta }}_{ij}\right),\mathbf{x}\in \overline{\mathrm{\Omega }},i,j=1,2,\end{array}$$3 ).

If it is possible to measure both the displacement and the displacement gradient vectors on a part of the boundary $\mathrm{\Gamma }$, say ${\mathrm{\Gamma }}_1$, and on another portion ${\mathrm{\Gamma }}_2$ it gives no data, then this leads to a mathematical formulation of an inverse Cauchy problem, which consists of Equation (11 $$\begin{array}{c}\hfill G\frac{{\mathit{\partial }}^2{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j\mathit{\partial }{x}_j}+\frac{G}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^2{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=0,\mathbf{x}\in \mathrm{\Omega },i=1,2,\end{array}$$1 ) and the following boundary conditions:5 $$\begin{array}{c}\hfill u_i(\mathbf{x})={\tilde{u}}_i(\mathbf{x}),u_{i,j}(\mathbf{x})={\tilde{u}}_{i,j}(\mathbf{x}),\mathbf{x}\in {\mathrm{\Gamma }}_1,i=1,2,j=2,\end{array}$$5 where $\tilde{\mathbf{u}}$ and ${\tilde{\mathbf{u}}}_{,j}$ are prescribed vector valued functions. In the above formulation of the boundary conditions in Equation (55 $$\begin{array}{c}\hfill u_i(\mathbf{x})={\tilde{u}}_i(\mathbf{x}),u_{i,j}(\mathbf{x})={\tilde{u}}_{i,j}(\mathbf{x}),\mathbf{x}\in {\mathrm{\Gamma }}_1,i=1,2,j=2,\end{array}$$5 ), it can be seen that the boundary ${\mathrm{\Gamma }}_1$ is overspecified by prescribing both the displacement ${\mathbf{u}|}_{{\mathrm{\Gamma }}_1}=\tilde{\mathbf{u}}$ and the $j$-th gradient ${\mathbf{u}}_{,j}{|}_{{\mathrm{\Gamma }}_1}={\tilde{\mathbf{u}}}_{,j}$ vector, whilst the boundary ${\mathrm{\Gamma }}_2$ is underspecified since both the displacement ${\mathbf{u}|}_{{\mathrm{\Gamma }}_2}$ and the traction ${\mathbf{t}|}_{{\mathrm{\Gamma }}_2}$ vectors are unknown and have to be determined for a completion of the boundary data. On the portion of $\mathrm{\Gamma }-({\mathrm{\Gamma }}_1\cup {\mathrm{\Gamma }}_2)$ we also have one type, not overspecified, boundary data for the uniqueness of solution. This problem, termed the inverse Cauchy problem, is much more difficult to be solved both analytically and numerically than the direct problem, since the solution does not satisfy the general conditions of well-posedness. Although the inverse Cauchy problem may have a unique solution, it is well known that this solution is unstable with respect to a small perturbation of the data on ${\mathrm{\Gamma }}_1$. Thus, the problem is ill-posed, and we cannot use a direct approach to solve the system of linear equations which arises from the discretization of Equation (11 $$\begin{array}{c}\hfill G\frac{{\mathit{\partial }}^2{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j\mathit{\partial }{x}_j}+\frac{G}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^2{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=0,\mathbf{x}\in \mathrm{\Omega },i=1,2,\end{array}$$1 ) and the boundary conditions in Equation (55 $$\begin{array}{c}\hfill u_i(\mathbf{x})={\tilde{u}}_i(\mathbf{x}),u_{i,j}(\mathbf{x})={\tilde{u}}_{i,j}(\mathbf{x}),\mathbf{x}\in {\mathrm{\Gamma }}_1,i=1,2,j=2,\end{array}$$5 ). Therefore, as mentioned above, some regularization methods are required in order to stably and accurately solve the inverse Cauchy problem in linear elasticity.

2.2 A spring-damping transform method

Before the introduction of our stabilization technique, we introduce the super-dashpot time-dependent stabilization technique developed by Essers.[24] For simplicity we only consider a one-dimensional steady $n$ equations system of fluid dynamics:6 $$\begin{array}{c}\hfill \mathbf{A}(\mathbf{u})\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }x}=\mathbf{0},\end{array}$$6 where $\mathbf{A}$ is an $n\times n$ matrix function and $\mathbf{u}$ is an $n$-dimensional unknown vector of variables.

Essers [24] has introduced his first DASH1 method by considering the $2n$ systems:7 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }t}=\mathbf{A}(\mathbf{u})\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }x},\hfill \end{array}$$7 8 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}+k\mathbf{u}={\mathbf{A}}^{\text{T}}\frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }x},\hfill \end{array}$$8 where $k>0$ is an internal damping factor, and $\mathbf{q}$ is a supplemental vector function. Eliminating $\mathbf{q}$ between Equations (77 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }t}=\mathbf{A}(\mathbf{u})\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }x},\hfill \end{array}$$7 ) and (88 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}+k\mathbf{u}={\mathbf{A}}^{\text{T}}\frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }x},\hfill \end{array}$$8 ) one obtains9 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{t}^2}+k\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}=\mathbf{D}\frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{x}^2},\end{array}$$9 where $\mathbf{D}={\mathbf{A}}^{\text{T}}\mathbf{A}$ is obviously a symmetric matrix with real positive eigenvalues $d_j^2,j=1,\dots ,n$. The above equations are actually similar to those of a vibrating string damped by dashpots. Essers [24] used this technique to stabilize and accelerate the iterative convergence of computational fluid algorithms.

Next, we consider a Cauchy problem of Laplace equation defined in a rectangle being studied by Liu and Kuo [20]:10 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}=0,0<x<\ell ,0<y<b,\hfill \end{array}$$10 11 $$\begin{array}{cc}& u(x,0)=f(x),0\le x\le \ell ,\hfill \end{array}$$11 12 $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }y}(x,0)=g(x),0\le x\le \ell ,\hfill \end{array}$$12 13 $$\begin{array}{cc}& u(0,y)=u_0(y),u(\ell ,y)=u_{\ell }(y),0\le y\le b,\hfill \end{array}$$13 where $f(x),g(x),u_0(y)$ and $u_{\ell }(y)$ are given functions. Here, we give a motivation to introduce a spring-damping method by using the following transformation:14 $$\begin{array}{c}\hfill u(x,y)=e^{\mathit{\alpha }y}U(x,y).\end{array}$$14 Such that Equations (1010 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}=0,0<x<\ell ,0<y<b,\hfill \end{array}$$10 )–(1313 $$\begin{array}{cc}& u(0,y)=u_0(y),u(\ell ,y)=u_{\ell }(y),0\le y\le b,\hfill \end{array}$$13 ) become15 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U=0,\hfill \end{array}$$15 16 $$\begin{array}{cc}& U(x,0)=f(x),0\le x\le \ell ,\hfill \end{array}$$16 17 $$\begin{array}{cc}& \frac{\mathit{\partial }U}{\mathit{\partial }y}(x,0)=g(x)-\mathit{\alpha }f(x),0\le x\le \ell ,\hfill \end{array}$$17 18 $$\begin{array}{cc}& U(0,y)=e^{-\mathit{\alpha }y}{u}_0(y),U(\ell ,y)=e^{-\mathit{\alpha }y}{u}_{\ell }(y),0\le y\le b.\hfill \end{array}$$18 Liu and Kuo [20] have proven that the introduction of the factor $\mathit{\alpha }$ can enhance the stability in the numerical integration of the above equations in the $y$-direction. For the purposes of comparison with Equation (99 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{t}^2}+k\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}=\mathbf{D}\frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{x}^2},\end{array}$$9 ), in Equation (1515 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U=0,\hfill \end{array}$$15 ) we replace $y$ by $t$:19 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{t}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }t}+{\mathit{\alpha }}^{2}U=-\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}.\end{array}$$19 Again, the left-hand side bears certain similarity to a vibrating string damped by dashpot and stabilized by spring. Unfortunately, the above equation is not a wave equation because a minus sign stands before ${\mathit{\partial }}^{2}U/\mathit{\partial }{x}^2$.

Now we can comment the methods proposed by Essers [24] and the one introduced in the above.

(i)	The method proposed by Essers [24] makes a perturbation from Equation (66 $$\begin{array}{c}\hfill \mathbf{A}(\mathbf{u})\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }x}=\mathbf{0},\end{array}$$6 ) to Equations (77 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }t}=\mathbf{A}(\mathbf{u})\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }x},\hfill \end{array}$$7 ) and (88 $$\begin{array}{cc}& \frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}+k\mathbf{u}={\mathbf{A}}^{\text{T}}\frac{\mathit{\partial }\mathbf{q}}{\mathit{\partial }x},\hfill \end{array}$$8 ) and then to Equation (99 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{t}^2}+k\frac{\mathit{\partial }\mathbf{u}}{\mathit{\partial }t}=\mathbf{D}\frac{{\mathit{\partial }}^2\mathbf{u}}{\mathit{\partial }{x}^2},\end{array}$$9 ). The present method makes a mathematical transformation from Equation (1010 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}=0,0<x<\ell ,0<y<b,\hfill \end{array}$$10 ) to Equation (1919 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{t}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }t}+{\mathit{\alpha }}^{2}U=-\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}.\end{array}$$19 ), which is not a perturbation.
(ii)	In the method proposed by Essers [24] there is only a dashpot; however, Equation (1919 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{t}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }t}+{\mathit{\alpha }}^{2}U=-\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}.\end{array}$$19 ) possesses a dashpot and a spring.
(iii)	The method proposed by Essers [24] modifies the type of the governing equations. The present method does not alter the type of the governing equations.
(iv)	Both methods posses the effect of ‘stabilization’ in the numerical algorithms.

The above process is called a spring-damping transform method (SDTM) in this paper. Although it is quite simple, as to be shown below the spring-damping method is effective for our inverse Cauchy problem of linear elasticity to increase the accuracy of numerical solutions. However, the essential ‘unstability’ of the inverse Cauchy problem must be further treated by a supplemental stabilization technique in Section 4.3.

2.3 The transformed equations

For our convenience, we rewrite Equation (11 $$\begin{array}{c}\hfill G\frac{{\mathit{\partial }}^2{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j\mathit{\partial }{x}_j}+\frac{G}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^2{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=0,\mathbf{x}\in \mathrm{\Omega },i=1,2,\end{array}$$1 ) into a componential form with $u(x,y):=u_1(x,y)$ and $v(x,y):=u_2(x,y)$:20 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }x\mathit{\partial }y}=0,0<x<a,0<y<b,\hfill \end{array}$$20 21 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }x\mathit{\partial }y}=0,0<x<a,0<y<b,\hfill \end{array}$$21 22 $$\begin{array}{cc}& u(x,0)=f_1(x),0\le x\le a,\hfill \end{array}$$22 23 $$\begin{array}{cc}& v(x,0)=f_2(x),0\le x\le a,\hfill \end{array}$$23 24 $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }y}(x,0)=g_1(x),0\le x\le a,\hfill \end{array}$$24 25 $$\begin{array}{cc}& \frac{\mathit{\partial }v}{\mathit{\partial }y}(x,0)=g_2(x),0\le x\le a,\hfill \end{array}$$25 26 $$\begin{array}{cc}& u(0,y)=h_1(y),u(a,y)=h_2(y),0\le y\le b,\hfill \end{array}$$26 27 $$\begin{array}{cc}& v(0,y)=h_3(y),v(a,y)=h_4(y),0\le y\le b,\hfill \end{array}$$27 where $f_1(x),f_2(x),g_1(x),g_2(x)$, $h_k(y),k=1,\dots ,4$ are given functions, and28 $$\begin{array}{c}\hfill {\mathit{\nu }}_1=\frac{2(1-\mathit{\nu })}{1-2\mathit{\nu }}.\end{array}$$28 We must emphasize that it is difficult to directly apply the numerical integration method to integrate the above equations as an initial value problem to obtain the solution $u(x,y)$ and $v(x,y)$.

In the present paper, we will develop a novel Lie-group integration method to directly solve the above inverse Cauchy problem by recovering the data on the top side $y=b$. However, before that we need to make the above equations ‘more stable’. The integration direction is along the $y$-axis, and thus as that done in Section 2.2 we consider the following transformations:29 $$\begin{array}{c}\hfill u(x,y)=e^{\mathit{\alpha }y}U(x,y),v(x,y)=e^{\mathit{\alpha }y}V(x,y).\end{array}$$29 From Equations (2020 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }x\mathit{\partial }y}=0,0<x<a,0<y<b,\hfill \end{array}$$20 )–(2727 $$\begin{array}{cc}& v(0,y)=h_3(y),v(a,y)=h_4(y),0\le y\le b,\hfill \end{array}$$27 ) and (2929 $$\begin{array}{c}\hfill u(x,y)=e^{\mathit{\alpha }y}U(x,y),v(x,y)=e^{\mathit{\alpha }y}V(x,y).\end{array}$$29 ) it follows that30 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$30 31 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{y}^2},+,2,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }y},+,{\mathit{\alpha }}^2,V\right]+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }U}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$31 32 $$\begin{array}{cc}& U(x,0)=f_1(x),0\le x\le a,\hfill \end{array}$$32 33 $$\begin{array}{cc}& V(x,0)=f_2(x),0\le x\le a,\hfill \end{array}$$33 34 $$\begin{array}{cc}& \frac{\mathit{\partial }U}{\mathit{\partial }y}(x,0)=g_1(x)-\mathit{\alpha }{f}_1(x),0\le x\le a,\hfill \end{array}$$34 35 $$\begin{array}{cc}& \frac{\mathit{\partial }V}{\mathit{\partial }y}(x,0)=g_2(x)-\mathit{\alpha }{f}_2(x),0\le x\le a,\hfill \end{array}$$35 36 $$\begin{array}{cc}& U(0,y)=e^{-\mathit{\alpha }y}{h}_1(y),U(a,y)=e^{-\mathit{\alpha }y}{h}_2(y),0\le y\le b,\hfill \end{array}$$36 37 $$\begin{array}{cc}& V(0,y)=e^{-\mathit{\alpha }y}{h}_3(y),V(a,y)=e^{-\mathit{\alpha }y}{h}_4(y),0\le y\le b.\hfill \end{array}$$37 It can been that in Equations (3030 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$30 ) and (3131 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{y}^2},+,2,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }y},+,{\mathit{\alpha }}^2,V\right]+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }U}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$31 ) we have introduced four extra terms: two spring terms ${\mathit{\alpha }}^{2}U$ and ${\mathit{\alpha }}^{2}V$ and two damping terms $2\mathit{\alpha }\mathit{\partial }U/\mathit{\partial }y$ and $2\mathit{\alpha }\mathit{\partial }V/\mathit{\partial }y$. In this regard, the present ‘stabilization technique’ is quite different from that of the Tikhonov regularization method.[25, 26] As mentioned in Section 1, the Tikhonov regularization method perturbs the original ill-posed problem into a ‘less ill-posed one’, not necessarily a well-posed one; however, the SDTM does not perturb the original ill-posed problem, which is merely a mathematical transformation. The ill-posedness still exists in the above equations. In Section 4.3, a new technique will be used to overcome the ill-posedness of the inverse Cauchy problem.

A similar regularization technique in the time domain has been first used by Liu [27] to stabilize the backward heat conduction problem, and then Liu and Kuo,[20] Liu et al. [21], and Liu and Chang [22] extended it to the spatial domain, and developed the spring and damping stabilization techniques to the inverse Cauchy problems of elliptic type PDEs.

Here we extend the spring-damping transform method (SDTM) as shown in Section2.2 for the Laplace equation to the inverse Cauchy problem in linear elasticity. However, we must emphasize that the above equations are also of the elliptic type systems, and the associated Cauchy problems are also ill-posed in nature, because the transformations in Equation (2929 $$\begin{array}{c}\hfill u(x,y)=e^{\mathit{\alpha }y}U(x,y),v(x,y)=e^{\mathit{\alpha }y}V(x,y).\end{array}$$29 ) do not alter the type of the governing equations. After the numerical of lines is used to discretize the governing equations, in Section 4.3 we will introduce a mixed-group preserving scheme to overcome the ill-posed behaviour of the inverse Cauchy problem.

Because the transformations invoked in Equation (2929 $$\begin{array}{c}\hfill u(x,y)=e^{\mathit{\alpha }y}U(x,y),v(x,y)=e^{\mathit{\alpha }y}V(x,y).\end{array}$$29 ) are purely mathematical, which do not change the inverse Cauchy problems which exhibit boundary singularities, e.g. an elastic solid with a crack/notch or jump/discontinuity in the available boundary conditions. However, those inverse Cauchy problems are much more complex than the present ones, and we do not treat them in this paper.

3 Numerical method of lines

The numerical method of lines is simple in concept that for a given system of PDEs discretize all but one of the independent variables. The semi-discrete procedure yields a coupled system of ODEs which are then being numerically integrated. For Equations (3030 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$30 ) and (3131 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{y}^2},+,2,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }y},+,{\mathit{\alpha }}^2,V\right]+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }U}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$31 ), we adopt the numerical method of lines to discretize the spatial coordinate $x$ and use the Differential Quadrature method (see the Appendix) to approximate the following differential terms:$$\begin{array}{cc}& \frac{\mathit{\partial }U(x,y)}{\mathit{\partial }x}\left|{}_{x=i\mathrm{\Delta }x},=,b_{ij},U_j,(y),,\right.\hfill \end{array}$$38 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},U_j,(y),,\right.\hfill \end{array}$$38 39 $$\begin{array}{cc}& \frac{\mathit{\partial }V(x,y)}{\mathit{\partial }x}\left|{}_{x=i\mathrm{\Delta }x},=,b_{ij},V_j,(y),,\right.\hfill \end{array}$$39 40 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},V_j,(y),,\right.\hfill \end{array}$$40 where $\mathrm{\Delta }x=a/(n+1)$ is a uniform discretization spacing length, $U_i(y)=U(i\mathrm{\Delta }x,y)$, $V_i(y)=V(i\mathrm{\Delta }x,y)$, and the coefficient matrices $b_{ij}$ and $a_{ij}=b_{ik}{b}_{kj}$ are introduced in the Appendix. Now Equations (3030 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2\mathit{\alpha }\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}^{2}U+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$30 ) and (3131 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{y}^2},+,2,\mathit{\alpha },\frac{\mathit{\partial }V}{\mathit{\partial }y},+,{\mathit{\alpha }}^2,V\right]+\frac{1}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }x\mathit{\partial }y},+,\mathit{\alpha },\frac{\mathit{\partial }U}{\mathit{\partial }x}\right]=0,\hfill \end{array}$$31 ) can be approximated by41 $$\begin{array}{cc}& \frac{\mathit{\partial }{U}_i(y)}{\mathit{\partial }y}=W_i(y),\hfill \end{array}$$41 42 $$\begin{array}{cc}& \frac{\mathit{\partial }{W}_i(y)}{\mathit{\partial }y}=-{\mathit{\nu }}_1{a}_{ij}{U}_j(y)-2\mathit{\alpha }{W}_i(y)-{\mathit{\alpha }}^2{U}_i(y)-\frac{1}{1-2\mathit{\nu }}[b_{ij}{Z}_j(y)+\mathit{\alpha }{b}_{ij}{V}_j(y)],\hfill \end{array}$$42 43 $$\begin{array}{cc}& \frac{\mathit{\partial }{V}_i(y)}{\mathit{\partial }y}=Z_i(y),\hfill \end{array}$$43 44 $$\begin{array}{cc}& \frac{\mathit{\partial }{Z}_i(y)}{\mathit{\partial }y}=-\frac{1}{{\mathit{\nu }}_1}{a}_{ij}{V}_j(y)-2\mathit{\alpha }{Z}_i(y)-{\mathit{\alpha }}^2{V}_i(y)-\frac{1}{2(1-\mathit{\nu })}[b_{ij}{W}_j(y)+\mathit{\alpha }{b}_{ij}{U}_j(y)].\hfill \end{array}$$44 The next step is to advance the solution from the initial conditions given at $y=0$ to a terminal position $y=b$. Really, Equations (3838 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},U_j,(y),,\right.\hfill \end{array}$$38 )–(4141 $$\begin{array}{cc}& \frac{\mathit{\partial }{U}_i(y)}{\mathit{\partial }y}=W_i(y),\hfill \end{array}$$41 ) have totally $4n$ coupled linear differential equations for the $4n$ variables $U_i(y),W_i(y),V_i(y),Z_i(y),i=1,2,\dots ,n$, which can be numerically integrated to obtain the solutions. However, we cannot directly apply the conventional numerical integration methods to integrate the above ODEs; the essentially numerical instability may cause a terribly incorrect solution. A numerical example will be given in Section 5 to show that the above equations are still highly ill-posed, which do not allow a direct numerical integration to obtain the solution, and thus we will develop a mixed group-preserving scheme to solve this ill-posed problem.

4 Group-preserving schemes

Liu [28] has derived a Lie-group transformation for the augmented dynamics on the future cone, and developed a group-preserving scheme for an effective numerical solution of nonlinear ordinary differential equations (ODEs).

4.1 Forward group-preserving scheme

Liu [28] has embedded the differential equations system into an augmented dynamical system, which concerns with not only the evolution of state variables but also the evolution of the magnitude of state variables vector. That is, for an $n$ ODEs system:45 $$\begin{array}{c}\hfill \dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t),\mathbf{x}\in {\mathbb{R}}^n,t\in \mathbb{R},\end{array}$$45 we can embed it into the following $n+1$-dimensional augmented dynamical system:46 $$\begin{array}{c}\hfill \frac{d}{dt}\left[\begin{array}{c}\mathbf{x}\\ \Vert \mathbf{x}\Vert \end{array}\right]=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& \frac{\mathbf{f}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }\\ \frac{{\mathbf{f}}^{\text{T}}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }& 0\end{array}\right]\left[\begin{array}{c}\mathbf{x}\\ \Vert \mathbf{x}\Vert \end{array}\right].\end{array}$$46 Here we assume $\Vert \mathbf{x}\Vert >0$, and hence the above system is well defined.

It is obvious that the first row in Equation (4343 $$\begin{array}{cc}& \frac{\mathit{\partial }{V}_i(y)}{\mathit{\partial }y}=Z_i(y),\hfill \end{array}$$43 ) is the same as the original Equation (4242 $$\begin{array}{cc}& \frac{\mathit{\partial }{W}_i(y)}{\mathit{\partial }y}=-{\mathit{\nu }}_1{a}_{ij}{U}_j(y)-2\mathit{\alpha }{W}_i(y)-{\mathit{\alpha }}^2{U}_i(y)-\frac{1}{1-2\mathit{\nu }}[b_{ij}{Z}_j(y)+\mathit{\alpha }{b}_{ij}{V}_j(y)],\hfill \end{array}$$42 ), but the inclusion of the second row in Equation (4343 $$\begin{array}{cc}& \frac{\mathit{\partial }{V}_i(y)}{\mathit{\partial }y}=Z_i(y),\hfill \end{array}$$43 ) gives us a Minkowskian structure of the augmented state variables of $\mathbf{X}:=({\mathbf{x}}^{\text{T}}{,\Vert \mathbf{x}\Vert )}^{\text{T}}$, satisfying a future cone condition:47 $$\begin{array}{c}\hfill {\mathbf{X}}^{\text{T}}\mathbf{g}\mathbf{X}=0,\end{array}$$47 where48 $$\begin{array}{c}\hfill \mathbf{g}=\left[\begin{array}{cc}{\mathbf{I}}_n& {\mathbf{0}}_{n\times 1}\\ {\mathbf{0}}_{1\times n}& -1\end{array}\right]\end{array}$$48 is a Minkowski metric, ${\mathbf{I}}_n$ is the identity matrix of order $n$ and the superscript $\text{T}$ stands for the transpose. In terms of $(\mathbf{x},\Vert \mathbf{x}\Vert )$, Equation (4444 $$\begin{array}{cc}& \frac{\mathit{\partial }{Z}_i(y)}{\mathit{\partial }y}=-\frac{1}{{\mathit{\nu }}_1}{a}_{ij}{V}_j(y)-2\mathit{\alpha }{Z}_i(y)-{\mathit{\alpha }}^2{V}_i(y)-\frac{1}{2(1-\mathit{\nu })}[b_{ij}{W}_j(y)+\mathit{\alpha }{b}_{ij}{U}_j(y)].\hfill \end{array}$$44 ) becomes49 $$\begin{array}{c}\hfill {\mathbf{X}}^{\text{T}}\mathbf{g}\mathbf{X}=\mathbf{x}·\mathbf{x}-{\Vert \mathbf{x}\Vert }^2={\Vert \mathbf{x}\Vert }^2-{\Vert \mathbf{x}\Vert }^2=0,\end{array}$$49 where the dot between two $n$-dimensional vectors denotes their Euclidean inner product. The cone condition is thus the most natural constraint that we can impose on the dynamical system (4343 $$\begin{array}{cc}& \frac{\mathit{\partial }{V}_i(y)}{\mathit{\partial }y}=Z_i(y),\hfill \end{array}$$43 ).

Consequently, we have an $n+1$-dimensional augmented differential equations system:50 $$\begin{array}{c}\hfill \dot{\mathbf{X}}=\mathbf{A}\mathbf{X}\end{array}$$50 with a constraint in Equation (4444 $$\begin{array}{cc}& \frac{\mathit{\partial }{Z}_i(y)}{\mathit{\partial }y}=-\frac{1}{{\mathit{\nu }}_1}{a}_{ij}{V}_j(y)-2\mathit{\alpha }{Z}_i(y)-{\mathit{\alpha }}^2{V}_i(y)-\frac{1}{2(1-\mathit{\nu })}[b_{ij}{W}_j(y)+\mathit{\alpha }{b}_{ij}{U}_j(y)].\hfill \end{array}$$44 ), where51 $$\begin{array}{c}\hfill \mathbf{A}:=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& \frac{\mathbf{f}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }\\ \frac{{\mathbf{f}}^{\text{T}}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }& 0\end{array}\right],\end{array}$$51 satisfying52 $$\begin{array}{c}\hfill {\mathbf{A}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{A}=\mathbf{0},\end{array}$$52 is a Lie algebra $so(n,1)$ of the proper orthochronous Lorentz group $S{O}_o(n,1)$. This fact prompts us to devise the so-called group-preserving scheme, whose discretized mapping $\mathbf{G}$ exactly preserves the following properties:53 $$\begin{array}{cc}& {\mathbf{G}}^{\text{T}}\mathbf{g}\mathbf{G}=\mathbf{g},\hfill \end{array}$$53 54 $$\begin{array}{cc}& det\mathbf{G}=1,\hfill \end{array}$$54 55 $$\begin{array}{cc}& G_0^0>0,\hfill \end{array}$$55 where $G_0^0$ is the 00th component of $\mathbf{G}$.

We assume that the value of $\mathbf{A}$ at the $k$-th time step is denoted by $\mathbf{A}(k)$, which is viewed as a constant matrix. An exponential mapping of $\mathbf{A}(k)$ admits a closed-form representation:56 $$\begin{array}{c}\hfill exp[h\mathbf{A}(k)]=\left[\begin{array}{cc}{\mathbf{I}}_n+\frac{(a_k-1)}{\Vert {\mathbf{f}}_k{\Vert }^2}{\mathbf{f}}_k{\mathbf{f}}_k^{\text{T}}& \frac{b_k{\mathbf{f}}_k}{\Vert {\mathbf{f}}_k\Vert }\\ \frac{b_k{\mathbf{f}}_k^{\text{T}}}{\Vert {\mathbf{f}}_k\Vert }& a_k\end{array}\right],\end{array}$$56 where57 $$\begin{array}{c}\hfill a_k:=cosh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right),b_k:=sinh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right).\end{array}$$57 Consequently, we can derive58 $$\begin{array}{cc}& {\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\mathit{\eta }}_1(k){\mathbf{f}}_k,\hfill \end{array}$$58 59 $$\begin{array}{cc}& {\mathit{\eta }}_1(k):=\frac{(a_k-1){\mathbf{f}}_k·{\mathbf{x}}_k+b_k\Vert {\mathbf{x}}_k\Vert \Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{f}}_k{\Vert }^2}.\hfill \end{array}$$59 This scheme preserves all the group properties in Equations (5050 $$\begin{array}{c}\hfill \dot{\mathbf{X}}=\mathbf{A}\mathbf{X}\end{array}$$50 )–(5252 $$\begin{array}{c}\hfill {\mathbf{A}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{A}=\mathbf{0},\end{array}$$52 ) for all $h>0$, which is called a forward group-preserving scheme.

4.2 Backward group-preserving scheme

We can also embed Equation (4242 $$\begin{array}{cc}& \frac{\mathit{\partial }{W}_i(y)}{\mathit{\partial }y}=-{\mathit{\nu }}_1{a}_{ij}{U}_j(y)-2\mathit{\alpha }{W}_i(y)-{\mathit{\alpha }}^2{U}_i(y)-\frac{1}{1-2\mathit{\nu }}[b_{ij}{Z}_j(y)+\mathit{\alpha }{b}_{ij}{V}_j(y)],\hfill \end{array}$$42 ) into the following $n+1$-dimensional augmented dynamical system:60 $$\begin{array}{c}\hfill \frac{d}{dt}\left[\begin{array}{c}\mathbf{x}\\ -\Vert \mathbf{x}\Vert \end{array}\right]=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& -\frac{\mathbf{f}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }\\ -\frac{{\mathbf{f}}^{\text{T}}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }& 0\end{array}\right]\left[\begin{array}{c}\mathbf{x}\\ -\Vert \mathbf{x}\Vert \end{array}\right].\end{array}$$60 It is obvious that the first equation in Equation (5757 $$\begin{array}{c}\hfill a_k:=cosh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right),b_k:=sinh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right).\end{array}$$57 ) is the same as the original Equation (4242 $$\begin{array}{cc}& \frac{\mathit{\partial }{W}_i(y)}{\mathit{\partial }y}=-{\mathit{\nu }}_1{a}_{ij}{U}_j(y)-2\mathit{\alpha }{W}_i(y)-{\mathit{\alpha }}^2{U}_i(y)-\frac{1}{1-2\mathit{\nu }}[b_{ij}{Z}_j(y)+\mathit{\alpha }{b}_{ij}{V}_j(y)],\hfill \end{array}$$42 ), but the inclusion of the second equation gives us a Minkowskian structure of the augmented state variables of $\mathbf{X}:=({\mathbf{x}}^{\text{T}},-{\Vert \mathbf{x}\Vert )}^{\text{T}}$, satisfying a past cone condition:61 $$\begin{array}{c}\hfill {\mathbf{X}}^{\text{T}}\mathbf{g}\mathbf{X}=\mathbf{x}·\mathbf{x}-{(-\Vert \mathbf{x}\Vert )}^2={\Vert \mathbf{x}\Vert }^2-{\Vert \mathbf{x}\Vert }^2=0.\end{array}$$61 Here, we should stress that the cone condition being imposed on the dynamical system (4343 $$\begin{array}{cc}& \frac{\mathit{\partial }{V}_i(y)}{\mathit{\partial }y}=Z_i(y),\hfill \end{array}$$43 ) is a future cone, and that for the dynamical system (5757 $$\begin{array}{c}\hfill a_k:=cosh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right),b_k:=sinh\left(\frac{h\Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{x}}_k\Vert }\right).\end{array}$$57 ) the imposed cone condition (5858 $$\begin{array}{cc}& {\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\mathit{\eta }}_1(k){\mathbf{f}}_k,\hfill \end{array}$$58 ) is a past cone.

Similarly, we have an $n+1$-dimensional augmented differential equations system:62 $$\begin{array}{c}\hfill \dot{\mathbf{X}}=\mathbf{B}\mathbf{X}\end{array}$$62 with a constraint in Equation (5858 $$\begin{array}{cc}& {\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\mathit{\eta }}_1(k){\mathbf{f}}_k,\hfill \end{array}$$58 ), where63 $$\begin{array}{c}\hfill \mathbf{B}:=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& -\frac{\mathbf{f}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }\\ -\frac{{\mathbf{f}}^{\text{T}}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }& 0\end{array}\right]\end{array}$$63 satisfying64 $$\begin{array}{c}\hfill {\mathbf{B}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{B}=\mathbf{0},\end{array}$$64 is a Lie algebra $so(n,1)$ of the proper orthochronous Lorentz group $S{O}_o(n,1)$.

Similarly, we assume that the value of $\mathbf{B}$ at the $k$-th time step is denoted by $\mathbf{B}(k)$, which is viewed as a constant matrix. Accordingly, an exponential mapping of $\mathbf{B}(k)$ admits a closed-form representation:65 $$\begin{array}{c}\hfill exp[-h\mathbf{B}(k)]=\left[\begin{array}{cc}{\mathbf{I}}_n+\frac{(a_k-1)}{\Vert {\mathbf{f}}_k{\Vert }^2}{\mathbf{f}}_k{\mathbf{f}}_k^{\text{T}}& \frac{b_k{\mathbf{f}}_k}{\Vert {\mathbf{f}}_k\Vert }\\ \frac{b_k{\mathbf{f}}_k^{\text{T}}}{\Vert {\mathbf{f}}_k\Vert }& a_k\end{array}\right],\end{array}$$65 where $a_k$ and $b_k$ were defined by Equation (5454 $$\begin{array}{cc}& det\mathbf{G}=1,\hfill \end{array}$$54 ), and we have66 $$\begin{array}{cc}& {\mathbf{x}}_{k-1}={\mathbf{x}}_k+{\mathit{\eta }}_2(k){\mathbf{f}}_k,\hfill \end{array}$$66 67 $$\begin{array}{cc}& {\mathit{\eta }}_2(k):=\frac{(a_k-1){\mathbf{f}}_k·{\mathbf{x}}_k-b_k\Vert {\mathbf{x}}_k\Vert \Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{f}}_k{\Vert }^2}.\hfill \end{array}$$67 This scheme preserves the group properties in Equations (5050 $$\begin{array}{c}\hfill \dot{\mathbf{X}}=\mathbf{A}\mathbf{X}\end{array}$$50 )–(5252 $$\begin{array}{c}\hfill {\mathbf{A}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{A}=\mathbf{0},\end{array}$$52 ) for all $h>0$, which is called a backward group-preserving scheme by Liu et al. [29].

Comparing Equations (5656 $$\begin{array}{c}\hfill exp[h\mathbf{A}(k)]=\left[\begin{array}{cc}{\mathbf{I}}_n+\frac{(a_k-1)}{\Vert {\mathbf{f}}_k{\Vert }^2}{\mathbf{f}}_k{\mathbf{f}}_k^{\text{T}}& \frac{b_k{\mathbf{f}}_k}{\Vert {\mathbf{f}}_k\Vert }\\ \frac{b_k{\mathbf{f}}_k^{\text{T}}}{\Vert {\mathbf{f}}_k\Vert }& a_k\end{array}\right],\end{array}$$56 ) and (6464 $$\begin{array}{c}\hfill {\mathbf{B}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{B}=\mathbf{0},\end{array}$$64 ) it is interesting to note that these two numerical schemes have the same form in addition that the sign before $b_k\Vert {\mathbf{x}}_k\Vert \Vert {\mathbf{f}}_k\Vert$ in the numerators.

4.3 Mixed group-preserving scheme

Although the above two schemes, forward and backward group-preserving schemes, are very accurate, but we cannot directly apply them to obtain the solution, because the inverse Cauchy problems are sensitive to noisy disturbance, which is added on the data by68 $$\begin{array}{c}\hfill {\widehat{f}}_i=f(x_i)[1+sR(i)],{\widehat{g}}_i=g(x_i)[1+sR(i)],\end{array}$$68 where $R(i)$ are random numbers in $[-1,1]$. In order to overcome this instability we apply the following novel Lie-group integrator to solve Equations (3838 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},U_j,(y),,\right.\hfill \end{array}$$38 )–(4141 $$\begin{array}{cc}& \frac{\mathit{\partial }{U}_i(y)}{\mathit{\partial }y}=W_i(y),\hfill \end{array}$$41 ):69 $$\begin{array}{cc}& U_i(y_{j+1})=U_i(y_j)+{\mathit{\eta }}_1(j)W_i(y_j),\hfill \end{array}$$69 70 $$\begin{array}{cc}& W_i(y_{j+1})=W_i(y_j)+{\mathit{\eta }}_2(j)H_1^i(y_j),\hfill \end{array}$$70 71 $$\begin{array}{cc}& V_i(y_{j+1})=V_i(y_j)+{\mathit{\eta }}_1(j)Z_i(y_j),\hfill \end{array}$$71 72 $$\begin{array}{cc}& Z_i(y_{j+1})=Z_i(y_j)+{\mathit{\eta }}_2(j)H_2^i(y_j),\hfill \end{array}$$72 where73 $$\begin{array}{cc}& H_1^i(y):=-{\mathit{\nu }}_1{a}_{ij}{U}_j(y)-2\mathit{\alpha }{W}_i(y)-{\mathit{\alpha }}^2{U}_i(y)-\frac{1}{1-2\mathit{\nu }}[b_{ij}{Z}_j(y)+\mathit{\alpha }{b}_{ij}{V}_j(y)],\hfill \end{array}$$73 74 $$\begin{array}{cc}& H_2^i(y):=-\frac{1}{{\mathit{\nu }}_1}{a}_{ij}{V}_j(y)-2\mathit{\alpha }{Z}_i(y)-{\mathit{\alpha }}^2{V}_i(y)-\frac{1}{2(1-\mathit{\nu })}[b_{ij}{W}_j(y)+\mathit{\alpha }{b}_{ij}{U}_j(y)],\hfill \end{array}$$74 and ${\mathit{\eta }}_1(j)$ and ${\mathit{\eta }}_2(j)$ are defined in Equations (5656 $$\begin{array}{c}\hfill exp[h\mathbf{A}(k)]=\left[\begin{array}{cc}{\mathbf{I}}_n+\frac{(a_k-1)}{\Vert {\mathbf{f}}_k{\Vert }^2}{\mathbf{f}}_k{\mathbf{f}}_k^{\text{T}}& \frac{b_k{\mathbf{f}}_k}{\Vert {\mathbf{f}}_k\Vert }\\ \frac{b_k{\mathbf{f}}_k^{\text{T}}}{\Vert {\mathbf{f}}_k\Vert }& a_k\end{array}\right],\end{array}$$56 ) and (6464 $$\begin{array}{c}\hfill {\mathbf{B}}^{\text{T}}\mathbf{g}+\mathbf{g}\mathbf{B}=\mathbf{0},\end{array}$$64 ), respectively. Here, instead of ${\mathit{\eta }}_1(j)$ used in the forward group-preserving scheme (5555 $$\begin{array}{cc}& G_0^0>0,\hfill \end{array}$$55 ), the term ${\mathit{\eta }}_2(j)$ used in Equations (6767 $$\begin{array}{cc}& {\mathit{\eta }}_2(k):=\frac{(a_k-1){\mathbf{f}}_k·{\mathbf{x}}_k-b_k\Vert {\mathbf{x}}_k\Vert \Vert {\mathbf{f}}_k\Vert }{\Vert {\mathbf{f}}_k{\Vert }^2}.\hfill \end{array}$$67 ) and (6969 $$\begin{array}{cc}& U_i(y_{j+1})=U_i(y_j)+{\mathit{\eta }}_1(j)W_i(y_j),\hfill \end{array}$$69 ) can impress the instability of inverse Cauchy problem. The above scheme is a mixture of the forward group-preserving scheme (5555 $$\begin{array}{cc}& G_0^0>0,\hfill \end{array}$$55 ), which uses ${\mathit{\eta }}_1$, and the backward group-preserving scheme (6363 $$\begin{array}{c}\hfill \mathbf{B}:=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& -\frac{\mathbf{f}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }\\ -\frac{{\mathbf{f}}^{\text{T}}(\mathbf{x},t)}{\Vert \mathbf{x}\Vert }& 0\end{array}\right]\end{array}$$63 ), of which ${\mathit{\eta }}_2$ is used; hence, we may name the present novel Lie-group integrator in Equations (6666 $$\begin{array}{cc}& {\mathbf{x}}_{k-1}={\mathbf{x}}_k+{\mathit{\eta }}_2(k){\mathbf{f}}_k,\hfill \end{array}$$66 )–(6969 $$\begin{array}{cc}& U_i(y_{j+1})=U_i(y_j)+{\mathit{\eta }}_1(j)W_i(y_j),\hfill \end{array}$$69 ) as a mixed group-preserving scheme (MGPS). Equations (6666 $$\begin{array}{cc}& {\mathbf{x}}_{k-1}={\mathbf{x}}_k+{\mathit{\eta }}_2(k){\mathbf{f}}_k,\hfill \end{array}$$66 ) and (6868 $$\begin{array}{c}\hfill {\widehat{f}}_i=f(x_i)[1+sR(i)],{\widehat{g}}_i=g(x_i)[1+sR(i)],\end{array}$$68 ) are the integrations of Equations (3838 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},U_j,(y),,\right.\hfill \end{array}$$38 ) and (4040 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},V_j,(y),,\right.\hfill \end{array}$$40 ), which are just the equations for the definitions of $\mathit{\partial }U/\mathit{\partial }y$ and $\mathit{\partial }V/\mathit{\partial }y$; they are unimportant, and in their integrations we use ${\mathit{\eta }}_1(j)$.

5 Numerical examples

In order to present the performance of the MGPS, we consider an isotropic linear elastic plate characterized by the material constants $G=3.35\times {10}^{10}$ N/m${}^2$ and $\mathit{\nu }=0.34$ corresponding to a copper alloy, and we solve the inverse Cauchy problem in Equations (11 $$\begin{array}{c}\hfill G\frac{{\mathit{\partial }}^2{u}_i(\mathbf{x})}{\mathit{\partial }{x}_j\mathit{\partial }{x}_j}+\frac{G}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^2{u}_j(\mathbf{x})}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=0,\mathbf{x}\in \mathrm{\Omega },i=1,2,\end{array}$$1 ) and (55 $$\begin{array}{c}\hfill u_i(\mathbf{x})={\tilde{u}}_i(\mathbf{x}),u_{i,j}(\mathbf{x})={\tilde{u}}_{i,j}(\mathbf{x}),\mathbf{x}\in {\mathrm{\Gamma }}_1,i=1,2,j=2,\end{array}$$5 ) for four typical examples.

5.1 Example 1

We consider the following analytical solution for displacements:75 $$\begin{array}{cc}& u(x,y)=\frac{{\mathit{\sigma }}_0}{2G(1+\mathit{\nu })}xy,\hfill \end{array}$$75 76 $$\begin{array}{cc}& v(x,y)=-\frac{{\mathit{\sigma }}_0}{4G(1+\mathit{\nu })}\left[\left(1,+,\frac{2{\mathit{\nu }}^2}{1-2\mathit{\nu }}\right),x^2,-,2,+,\mathit{\nu },y^2\right],\hfill \end{array}$$76 where $-1<x<1,0<y<1$. Here we fix ${\mathit{\sigma }}_0=1.5\times {10}^{10}$ N/m${}^2$. It should be noted that for this example, the overspecified Cauchy data is available on a portion ${\mathrm{\Gamma }}_1$ of the boundary $\mathrm{\Gamma }$ such that measure(${\mathrm{\Gamma }}_1$) $=$ measure($\mathrm{\Gamma }$)/3.

First we use this simple example to demonstrate that although we have added a factor $\mathit{\alpha }=-2$ into the numerical method of lines Equations (3838 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}U(x,y)}{\mathit{\partial }{x}^2}\left|{}_{x=i\mathrm{\Delta }x},=,a_{ij},U_j,(y),,\right.\hfill \end{array}$$38 )–(4141 $$\begin{array}{cc}& \frac{\mathit{\partial }{U}_i(y)}{\mathit{\partial }y}=W_i(y),\hfill \end{array}$$41 ), we cannot obtain stable solutions by using the GPS in Section 4.1 to integrate the above equations. Under a zero noise and with $\mathrm{\Delta }x=2/50$, $\mathrm{\Delta }y=1/2000$ used in the GPS, the errors of $u$ and $v$ at $y=1$ are shown in Figures 1(a) and 1(b), respectively. The maximum errors of $u$ and $v$ are, respectively, $7.49\times {10}^{19}$ and $1.56\times {10}^{19}$. 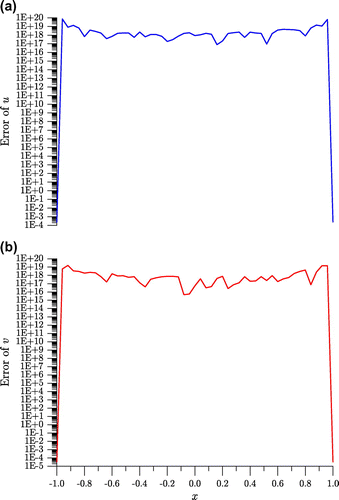It shows that the governing equations are highly ill-posed, which do not allow a direct numerical integration to obtain the solution, and thus we need to use the mixed group-preserving scheme (MGPS) developed in Section 4.3 to solve this ill-posed problem.

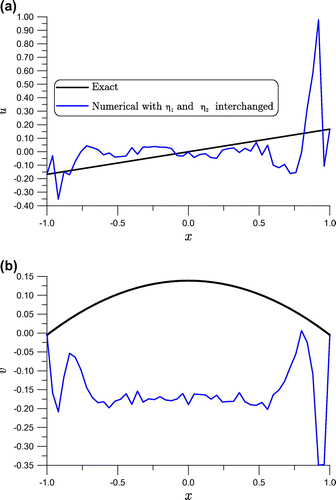
Figure 1. For example 1 by applying the GPS to integrate the governing equations with $\mathit{\alpha }=-2$ leads to unstable solutions.

The above computation shows that if we only consider the stabilizing effect by spring and dashpot, the resulting equations are also very ill-posed, which cannot be integrated by using the usual integration method, like as the GPS used in the above case. Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=2/50$, $\mathrm{\Delta }y=1/2000$ used in the MGPS, instead of GPS, the numerical solutions of displacements and tractions at $y=1$ are compared with the exact ones in Figure 2, where $\mathit{\alpha }=-2$ is used. In order to further prove that the algorithm is robust, we raise the noise intensity to $s=20\%$, and from Figure 2 we can observe that the two numerical solutions have little difference. It can be seen that the present algorithm is quite robust, which can recover the data on the top side very well, even under a large noise up to $s=10\%$ and $s=20\%$. 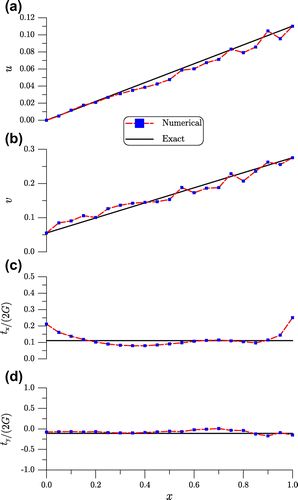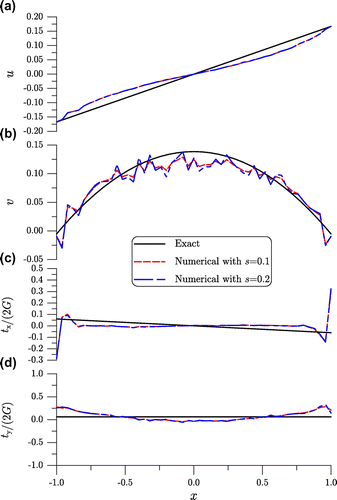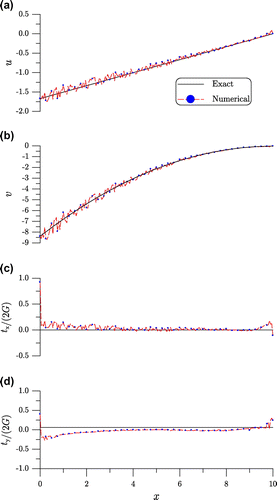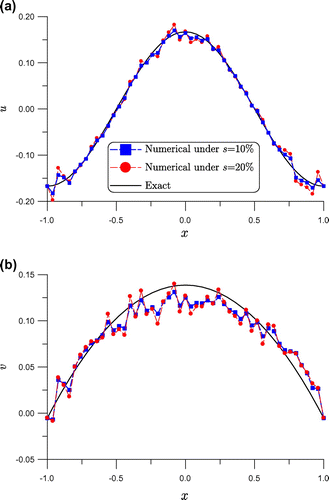The computational results are rather promising that one can apply the MGPS developed in Section 4.3 to solve the inverse Cauchy problems. Below we will employ the MGPS to solve all examples.

Figure 2. For example 1 comparing the recovered displacements and tractions with exact ones on the top side.

In Figure 3, we compare the numerical errors obtained by the MGPS with $\mathit{\alpha }=-1$ and $\mathit{\alpha }=0$ in the governing equations. The effect of $\mathit{\alpha }$ can be seen, which can largely increase the accuracy in the recovered solutions of $u$ and $v$. Although $\mathit{\alpha }=0$ is used, the MGPS itself can make a stable solution, however its accuracy is not so good.

Figure 3. For example 1 comparing the numerical errors of recovered displacements on the top side with $\mathit{\alpha }=-1$, and $\mathit{\alpha }=0$.

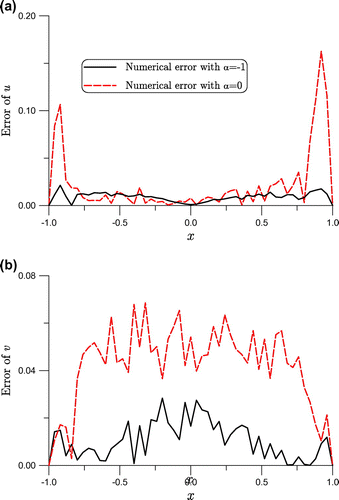
Figure 4. For example 1 comparing the numerical errors of displacements and the Neumann data on the top side with different $\mathit{\alpha }$.

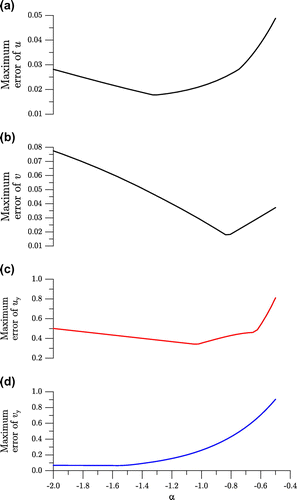
In Figure 4 we compare the numerical errors of displacements and the Neumann data of $u_y$ and $v_y$ on the top side obtained by the MGPS with different values of $\mathit{\alpha }$ in the range of $\mathit{\alpha }\in [-2,-0.5]$. It can be seen that all the $\mathit{\alpha }$ in the range of $\mathit{\alpha }\in [-2,-1]$ can cause rather small errors; however, when $\mathit{\alpha }$ is larger than $-1$ the errors of $u_y$ and $v_y$ increase rapidly. In the range of $\mathit{\alpha }\in [-2,-1]$ the algorithm is insensitive to the parameter. If we alternate the roles of ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$ in Equations (6666 $$\begin{array}{cc}& {\mathbf{x}}_{k-1}={\mathbf{x}}_k+{\mathit{\eta }}_2(k){\mathbf{f}}_k,\hfill \end{array}$$66 )–(6969 $$\begin{array}{cc}& U_i(y_{j+1})=U_i(y_j)+{\mathit{\eta }}_1(j)W_i(y_j),\hfill \end{array}$$69 ), it leads to an incorrect result as shown in Figure5.

Figure 5. For example 1 with ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$ alternating, comparing the numerical solutions with exact ones.

5.2 Example 2

We consider the following analytical solution for displacements:77 $$\begin{array}{c}\hfill u(x,y)=\frac{{\mathit{\sigma }}_0(1-\mathit{\nu })}{2G(1+\mathit{\nu })}x,v(x,y)=\frac{{\mathit{\sigma }}_0(1-\mathit{\nu })}{2G(1+\mathit{\nu })}(2-y+2x),0<x<1,0<y<1.\end{array}$$77 Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=1/20$, $\mathrm{\Delta }y=1/1000$ used in the MGPS, the numerical solutions of displacements and tractions at $y=1$ are compared with the exact ones in Figure 6, where $\mathit{\alpha }=-0.9$ 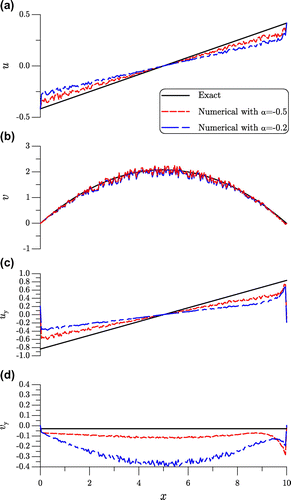is used. It can be seen that the present algorithm is quite robust, which can recover the data on the top side very well, even under a large noise.

Figure 6. For example 2 comparing the recovered displacements and tractions with exact ones on the top side.

5.3 Example 3

In this example, we consider a simply support beam with the following analytical solution for displacements:78 $$\begin{array}{cc}\hfill u(x,y)& =\frac{{\mathit{\sigma }}_0}{2G(1+\mathit{\nu })}(x-a/2)y,\hfill \\ \hfill v(x,y)& =\frac{{\mathit{\sigma }}_0}{4G(1+\mathit{\nu })}[(a-x)x-\mathit{\nu }{y}^2],0<x<a,0<y<0.5,\hfill \end{array}$$78 where $a=10$, and ${\mathit{\sigma }}_0=M/I$ with $I$ being the inertial moment and $M$ the applied moment. Here we fix ${\mathit{\sigma }}_0=1.5\times {10}^{10}$ N/m${}^2$. For this example, a body force $2{\mathit{\nu }}^2/(1-2\mathit{\nu })$ should be added on the right-hand side in Equation (2121 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }x\mathit{\partial }y}=0,0<x<a,0<y<b,\hfill \end{array}$$21 ).

Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=10/200$, $\mathrm{\Delta }y=0.5/1000$ used in the MGPS, the numerical solutions at $y=0.5$ are compared with the exact ones in Figure 7, where $\mathit{\alpha }=-0.2$ is used. It can be seen that the present algorithm is quite robust, which can recover the data on the top side very well, even under a large noise. In order to test the influence of $\mathit{\alpha }$, we compute the numerical solution under a different $\mathit{\alpha }=-0.5$, of which the recovered Cauchy data on the top side as shown in Figure 7 is less well. The errors of $u_y$ and $v_y$ are also acceptable. However, the accuracy of the recovered Neumann data of $u_y$ and $v_y$ was worse than that for the displacements.

Figure 7. For example 3 comparing the recovered displacements and the Neumann data with exact ones on the top side.

5.4 Example 4

In this example, we consider a cantilever beam with the following analytical solution for displacements:79 $$\begin{array}{cc}\hfill u(x,y)& =-\frac{{\mathit{\sigma }}_0}{2G(1+\mathit{\nu })}(a-x)y,\hfill \\ \hfill v(x,y)& =-\frac{{\mathit{\sigma }}_0}{4G(1+\mathit{\nu })}[{(a-x)}^2+\mathit{\nu }{y}^2],0<x<a,0<y<1,\hfill \end{array}$$79 where $a=10$. Similarly, a body force $2{\mathit{\nu }}^2/(1-2\mathit{\nu })$ should be added on the right-hand side in Equation (2121 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }x\mathit{\partial }y}=0,0<x<a,0<y<b,\hfill \end{array}$$21 ) for this example.

Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=10/200$, $\mathrm{\Delta }y=1/1000$, the numerical solutions at $y=0.5$ are compared with the exact ones in Figure 8, where $\mathit{\alpha }=-0.01$ is used. It can be seen that the numerical solutions are quite close to the exact ones.

Figure 8. For example 4 comparing the recovered displacements and tractions with exact ones on the top side.

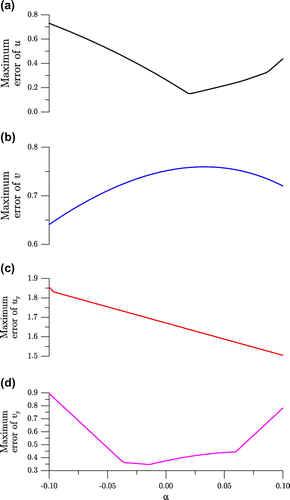
Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=10/100$, $\mathrm{\Delta }y=1/200$, in Figure 9 we plot the maximum numerical errors of displacements and the Neumann data of $u_y$ and $v_y$ on the top side with different values of $\mathit{\alpha }$ in the range of $\mathit{\alpha }\in [-0.1,0.1]$. It can be seen that all the $\mathit{\alpha }$ in the range of $\mathit{\alpha }\in [-0.1,0.1]$ can cause rather small errors.

Figure 9. For example 4 comparing the numerical errors of displacements and the Neumann data on the top side with different $\mathit{\alpha }$.

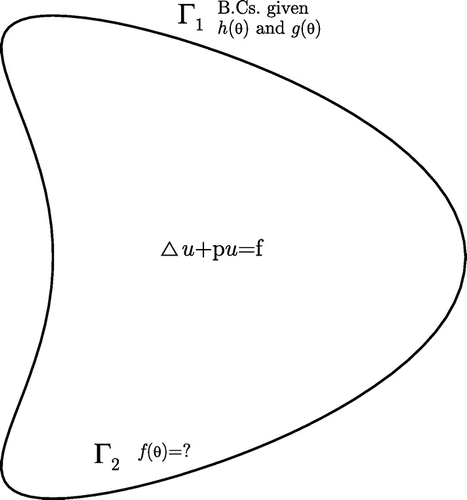
6 Extension to arbitrary plane domain

The extension of the MGPS to the inverse Cauchy problem defined in an arbitrary plane domain is possible. However, for the linear elasticity equations the process to derive the governing equations in terms of the new variables would be too lengthy, and it would be reported in other place. Here, we only consider the inverse Cauchy problem of a linear elliptic equation defined in an arbitrary plane domain as shown in Figure 10. We consider the following inverse Cauchy problem of the elliptic type equation:80 $$\begin{array}{cc}& \mathrm{\Delta }u+pu=f(x,y),(x,y)\in \mathrm{\Omega },\hfill \end{array}$$80 81 $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }n}=\tilde{\mathit{\varphi }}(x,y),(x,y)\in {\mathrm{\Gamma }}_1,\hfill \end{array}$$81 82 $$\begin{array}{cc}& u=\tilde{\mathit{\phi }}(x,y),(x,y)\in {\mathrm{\Gamma }}_1,\hfill \end{array}$$82 where $\mathrm{\Omega }=\{(x,y)|0<\sqrt{x^2+y^2}<\mathit{\rho }(\mathit{\theta })\}$, and ${\mathrm{\Gamma }}_1=\{(x,y)|\sqrt{x^2+y^2}=\mathit{\rho }(\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi }\}$. We suppose that in an arbitrary plane domain as shown in Figure 10, the boundary can be described by a contour curve with $\mathit{\rho }(\mathit{\theta })$ as its radius function. $p$ is a real constant, $f$, $\tilde{\mathit{\phi }}$ and $\tilde{\mathit{\varphi }}$ are given functions. If the boundary value ${u|}_{{\mathrm{\Gamma }}_2}$, ${\mathrm{\Gamma }}_2=\{(x,y)|\sqrt{x^2+y^2}=\mathit{\rho }(\mathit{\theta }),\mathit{\pi }\le \mathit{\theta }\le 2\mathit{\pi }\}$ can be made available, then the data are completed in the whole boundary, and the solution of elliptic equation can be obtained.

Figure 10. The inverse Cauchy problem to recover data on ${\mathrm{\Gamma }}_2$.

Here, it is convenient to consider the problem in the polar coordinates:83 $$\begin{array}{c}\hfill \left\{\begin{array}{c}x=rcos\mathit{\theta }\hfill \\ y=rsin\mathit{\theta }\hfill \end{array}\right.r\in [0,\mathit{\rho }],\mathit{\theta }\in [0,2\mathit{\pi }],\end{array}$$83 and write84 $$\begin{array}{c}\hfill u(r,\mathit{\theta }):=u(x=rcos\mathit{\theta },y=rsin\mathit{\theta }).\end{array}$$84 We consider the following transformation from $r$ to $R$:85 $$\begin{array}{c}\hfill R=\frac{r}{\mathit{\rho }}.\end{array}$$85 It is obvious that when $r=\mathit{\rho }$ we have $R=1$. So we can transform the arbitrary plane domain in terms of a small polar-coordinate $(r,\mathit{\theta })$ into a unit disk in terms of a large polar-coordinate $(R,\mathit{\theta })$

Next we transform the governing equation into the large polar-coordinate $(R,\mathit{\theta })$. Let86 $$\begin{array}{c}\hfill v(R,\mathit{\theta })=u(r,\mathit{\theta }).\end{array}$$86 Through some operations we can derive87 $$\begin{array}{cc}& {\displaystyle F_1\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{R}^2}+F_2\frac{\mathit{\partial }v}{\mathit{\partial }R}+F_3\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{\mathit{\theta }}^2}+F_4\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }R\mathit{\partial }\mathit{\theta }}+pv=f(R,\mathit{\theta }),(R,\mathit{\theta })\in {\mathrm{\Omega }}_0,}\hfill \end{array}$$87 88 $$\begin{array}{cc}& v=\mathit{\phi }(R,\mathit{\theta }),(R,\mathit{\theta })\in {\mathrm{\Gamma }}_1^0,\hfill \end{array}$$88 89 $$\begin{array}{cc}& {\displaystyle \frac{\mathit{\partial }v}{\mathit{\partial }n}=\mathit{\varphi }(R,\mathit{\theta }),(R,\mathit{\theta })\in {\mathrm{\Gamma }}_1^0,}\hfill \end{array}$$89 where ${\mathrm{\Omega }}_0=\{(R,\mathit{\theta })|R<1,0\le \mathit{\theta }\le 2\mathit{\pi }\}$, ${\mathrm{\Gamma }}_1^0=\{(R,\mathit{\theta })|R=1,0\le \mathit{\theta }\le \mathit{\pi }\}$, and90 $$\begin{array}{cc}& F_1:=\frac{1}{{\mathit{\rho }}^2}\left[1,+,{\left(\frac{{\mathit{\rho }}^{\prime }}{\mathit{\rho }}\right)}^2\right],\hfill \end{array}$$90 91 $$\begin{array}{cc}& F_2:=\frac{1}{{\mathit{\rho }}^{2}R}\left[1,-,\frac{\mathit{\rho }{\mathit{\rho }}^{″}-2{({\mathit{\rho }}^{\prime })}^2}{{\mathit{\rho }}^2}\right],\hfill \end{array}$$91 92 $$\begin{array}{cc}& F_3:=\frac{1}{{\mathit{\rho }}^2{R}^2},\hfill \end{array}$$92 93 $$\begin{array}{cc}& F_4:=-\frac{2{\mathit{\rho }}^{\prime }}{{\mathit{\rho }}^{3}R}.\hfill \end{array}$$93 The integration direction will be in the $R$-axis from $R=1$ to $R=-1$, and thus we consider the following variable transformation:94 $$\begin{array}{c}\hfill v(R,\mathit{\theta })=e^{\mathit{\alpha }R}U(R,\mathit{\theta }).\end{array}$$94 From Equations (8383 $$\begin{array}{c}\hfill \left\{\begin{array}{c}x=rcos\mathit{\theta }\hfill \\ y=rsin\mathit{\theta }\hfill \end{array}\right.r\in [0,\mathit{\rho }],\mathit{\theta }\in [0,2\mathit{\pi }],\end{array}$$83 )–(8585 $$\begin{array}{c}\hfill R=\frac{r}{\mathit{\rho }}.\end{array}$$85 ) it follows that95 $$\begin{array}{cc}& F_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{R}^2}+[2\mathit{\alpha }{F}_1+F_2+\mathit{\alpha }{F}_9]\frac{\mathit{\partial }U}{\mathit{\partial }R}+[{\mathit{\alpha }}^2{F}_1+\mathit{\alpha }{F}_2+{\mathit{\alpha }}^2{F}_9+p]U+F_3\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{\mathit{\theta }}^2}\hfill \end{array}$$95 96 $$\begin{array}{cc}& +\mathit{\alpha }{F}_4\frac{\mathit{\partial }U}{\mathit{\partial }\mathit{\theta }}+F_4\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }R\mathit{\partial }\mathit{\theta }}=e^{-\mathit{\alpha }R}f(R,\mathit{\theta }),\hfill \end{array}$$96 97 $$\begin{array}{cc}& U(1,\mathit{\theta })=e^{-\mathit{\alpha }}\mathit{\phi }(\mathit{\theta }),\mathit{\theta }\in [0,\mathit{\pi }],\hfill \end{array}$$97 98 $$\begin{array}{cc}& U_R(1,\mathit{\theta })=e^{-\mathit{\alpha }}[\mathit{\varphi }(\mathit{\theta })-\mathit{\alpha }\mathit{\phi }(\mathit{\theta })],\mathit{\theta }\in [0,\mathit{\pi }],\hfill \end{array}$$98 where99 $$\begin{array}{c}\hfill F_9:=-\frac{R{\mathit{\rho }}^{\prime }}{\mathit{\rho }}.\end{array}$$99 For simple notations we can write Equation (9191 $$\begin{array}{cc}& F_2:=\frac{1}{{\mathit{\rho }}^{2}R}\left[1,-,\frac{\mathit{\rho }{\mathit{\rho }}^{″}-2{({\mathit{\rho }}^{\prime })}^2}{{\mathit{\rho }}^2}\right],\hfill \end{array}$$91 ) as100 $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{R}^2}+F_5\frac{\mathit{\partial }U}{\mathit{\partial }R}+F_{6}U+F_7\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{\mathit{\theta }}^2}+\mathit{\alpha }{F}_8\frac{\mathit{\partial }U}{\mathit{\partial }\mathit{\theta }}+F_8\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }R\mathit{\partial }\mathit{\theta }}=\frac{e^{-\mathit{\alpha }R}f(R,\mathit{\theta })}{F_1},\end{array}$$100 where101 $$\begin{array}{c}\hfill F_5:=\frac{2\mathit{\alpha }{F}_1+F_2+\mathit{\alpha }{F}_9}{F_1},F_6:=\frac{{\mathit{\alpha }}^2{F}_1+\mathit{\alpha }{F}_2+{\mathit{\alpha }}^2{F}_9+p}{F_1},F_7:=\frac{F_3}{F_1},F_8:=\frac{F_4}{F_1}.\end{array}$$101 For Equation (9595 $$\begin{array}{cc}& F_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{R}^2}+[2\mathit{\alpha }{F}_1+F_2+\mathit{\alpha }{F}_9]\frac{\mathit{\partial }U}{\mathit{\partial }R}+[{\mathit{\alpha }}^2{F}_1+\mathit{\alpha }{F}_2+{\mathit{\alpha }}^2{F}_9+p]U+F_3\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{\mathit{\theta }}^2}\hfill \end{array}$$95 ) we adopt the numerical method of lines to discretize the angular coordinate $\mathit{\theta }$, and thus we have102 $$\begin{array}{cc}\hfill U_R^i(R)& =V^i(R),i=1,2,\cdots ,m,\hfill \end{array}$$102 103 $$\begin{array}{cc}& V_R^1(R)=-F_6^1\frac{5U^1(R)-11U^2(R)+7U^3(R)-U^4(R)}{{(2\mathrm{\Delta }\mathit{\theta })}^2}\hfill \\ & -F_4^1{V}^1(R)-F_5^1{U}^1(R)+\frac{e^{-\mathit{\alpha }R}{f}^1(R)}{F_1^1},i=1,\hfill \\ & V_r^i(R)=-F_6^i\frac{U^{i+1}(R)-2U^i(R)+U^{i-1}(R)}{{(\mathrm{\Delta }\mathit{\theta })}^2}-F_4^i{V}^i(R)-F_5^i{U}^i(R)\hfill \\ & +\frac{e^{-\mathit{\alpha }R}{f}^i(R)}{F_1^i},i=2,\dots ,n,\hfill \\ & V_r^m(R)=-F_6^m\frac{5U^m(R)-11U^{m-1}(R)+7U^{m-2}(R)-U^{m-3}(R)}{{(2\mathrm{\Delta }\mathit{\theta })}^2}\hfill \\ & -F_4^m{V}^m(R)-F_5^m{U}^m(R)+\frac{e^{-\mathit{\alpha }R}{f}^m(R)}{F_1^m},i=m,\hfill \end{array}$$103 where $m=n+1$, and for simplicity, we consider $\mathrm{\Delta }\mathit{\theta }=\frac{\mathit{\pi }}{n}$ to be a uniform increment of polar angle, and ${\mathit{\theta }}_i=(i-1)\mathrm{\Delta }\mathit{\theta }$. $U^i(R)=U(R,{\mathit{\theta }}_i)$, $V^i(R)=V(R,{\mathit{\theta }}_i)$, $f^i(R)=f(R,{\mathit{\theta }}_i)$, $F_j^i$ are the discretized quantities at the node of ${\mathit{\theta }}_i$. The above finite differences can maintain the same second-order accuracy.

The next step is to advance the solution from the initial conditions (at the upper boundary) to the desired position $R=-1$. Really, Equations (9797 $$\begin{array}{cc}& U(1,\mathit{\theta })=e^{-\mathit{\alpha }}\mathit{\phi }(\mathit{\theta }),\mathit{\theta }\in [0,\mathit{\pi }],\hfill \end{array}$$97 ) and (9898 $$\begin{array}{cc}& U_R(1,\mathit{\theta })=e^{-\mathit{\alpha }}[\mathit{\varphi }(\mathit{\theta })-\mathit{\alpha }\mathit{\phi }(\mathit{\theta })],\mathit{\theta }\in [0,\mathit{\pi }],\hfill \end{array}$$98 ) have totally $2m$ coupled differential equations for the $2m$ variables $U_i(R),V_i(R),i=1,2,\dots ,m$, which can be numerically integrated to obtain the solutions.

6.1 Example 5

In this example we apply the MGPS to104 $$\begin{array}{cc}& u_{xx}+u_{yy}=0,\hfill \end{array}$$104 105 $$\begin{array}{cc}& u(x,y)=x^2-y^2,\hfill \end{array}$$105 where the contour of the problem domain is$$\mathit{\rho }(\mathit{\theta })=2\sqrt{{(0.6cos(\mathit{\theta })+0.3cos(2\mathit{\theta })-0.2)}^2+{(0.6sin(\mathit{\theta }))}^2}.$$

Figure 11. For example 5 comparing numerical and exact solutions of the inverse Cauchy problem for Laplace equation.

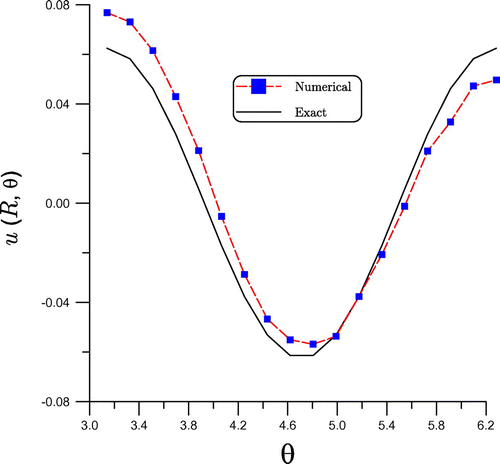
The required data can be obtained from the exact solution. By using the following parameters: $\mathrm{\Delta }\mathit{\theta }=\mathit{\pi }/17$, $h=0.5/2000$, and $\mathit{\alpha }=0.075$ for the noised case with $s=0.01$ we compare the numerical result obtained by the present Lie-group integration method with the exact one in Figure 11. The solution obtained is acceptable.

7 Extension to nonlinear inverse Cauchy problem

In order to extend the MGPS to the inverse Cauchy problem of nonlinear elasticity, we consider106 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }x\mathit{\partial }y}+G_1(u_x,u_y,v_x,v_y)=F_1(x,y),\hfill \\ & \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}+\frac{1}{1-2\mathit{\nu }}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }x\mathit{\partial }y}+G_2(u_x,u_y,v_x,v_y)=F_2(x,y),\hfill \end{array}$$106 and other conditions are the same as those in Equations (2222 $$\begin{array}{cc}& u(x,0)=f_1(x),0\le x\le a,\hfill \end{array}$$22 )–(2727 $$\begin{array}{cc}& v(0,y)=h_3(y),v(a,y)=h_4(y),0\le y\le b,\hfill \end{array}$$27 ).

Figure 12. For example 6 of a nonlinear inverse Cauchy problem of elasticity, comparing the recovered displacements and the Neumann data with exact ones on the top side.

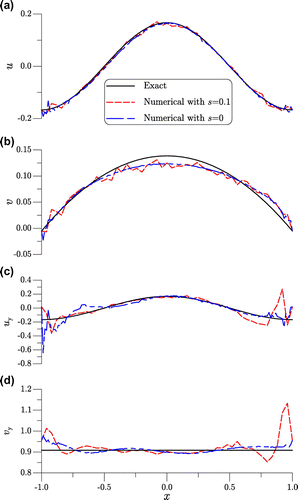
Figure 13. For example 7 of a nonlinear inverse Cauchy problem of elasticity, comparing the recovered displacements with exact ones on the top side.

Upon letting107 $$\begin{array}{c}\hfill u(x,y)=e^{{\mathit{\alpha }}_{1}y}U(x,y),v(x,y)=e^{{\mathit{\alpha }}_{2}y}V(x,y),\end{array}$$107 we can derive108 $$\begin{array}{cc}& {\mathit{\nu }}_1\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{y}^2}+2{\mathit{\alpha }}_1\frac{\mathit{\partial }U}{\mathit{\partial }y}+{\mathit{\alpha }}_1^{2}U+\frac{e^{({\mathit{\alpha }}_2-{\mathit{\alpha }}_1)y}}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }x\mathit{\partial }y},+,{\mathit{\alpha }}_2,\frac{\mathit{\partial }V}{\mathit{\partial }x}\right]\hfill \\ & =e^{-{\mathit{\alpha }}_{1}y}\left[F_1,(x,y),-,G_1,(e^{{\mathit{\alpha }}_{1}y}{U}_x,{\mathit{\alpha }}_1{e}^{{\mathit{\alpha }}_{1}y}U+e^{{\mathit{\alpha }}_{1}y}{U}_y,e^{{\mathit{\alpha }}_{2}y}{V}_x,{\mathit{\alpha }}_2{e}^{{\mathit{\alpha }}_{2}y}V+e^{{\mathit{\alpha }}_{2}y}{V}_y)\right],\hfill \end{array}$$108 109 $$\begin{array}{cc}& \frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}+{\mathit{\nu }}_1\left[\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{y}^2},+,2,{\mathit{\alpha }}_2,\frac{\mathit{\partial }V}{\mathit{\partial }y},+,{\mathit{\alpha }}_2^2,V\right]+\frac{e^{({\mathit{\alpha }}_1-{\mathit{\alpha }}_2)y}}{1-2\mathit{\nu }}\left[\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }x\mathit{\partial }y},+,{\mathit{\alpha }}_1,\frac{\mathit{\partial }U}{\mathit{\partial }x}\right]\hfill \\ & =e^{-{\mathit{\alpha }}_{2}y}\left[F_2,(x,y),-,G_2,(e^{{\mathit{\alpha }}_{1}y}{U}_x,{\mathit{\alpha }}_1{e}^{{\mathit{\alpha }}_{1}y}U+e^{{\mathit{\alpha }}_{1}y}{U}_y,e^{{\mathit{\alpha }}_{2}y}{V}_x,{\mathit{\alpha }}_2{e}^{{\mathit{\alpha }}_{2}y}V+e^{{\mathit{\alpha }}_{2}y}{V}_y)\right],\hfill \\ & U(x,0)=f_1(x),0\le x\le a,\hfill \\ & V(x,0)=f_2(x),0\le x\le a,\hfill \\ & \frac{\mathit{\partial }U}{\mathit{\partial }y}(x,0)=g_1(x)-{\mathit{\alpha }}_1{f}_1(x),0\le x\le a,\hfill \end{array}$$109 110 $$\begin{array}{cc}& \frac{\mathit{\partial }V}{\mathit{\partial }y}(x,0)=g_2(x)-{\mathit{\alpha }}_2{f}_2(x),0\le x\le a,\hfill \end{array}$$110 111 $$\begin{array}{cc}& U(0,y)=e^{-{\mathit{\alpha }}_{1}y}{h}_1(y),U(a,y)=e^{-{\mathit{\alpha }}_{1}y}{h}_2(y),0\le y\le b,\hfill \end{array}$$111 112 $$\begin{array}{cc}& V(0,y)=e^{-{\mathit{\alpha }}_{2}y}{h}_3(y),V(a,y)=e^{-{\mathit{\alpha }}_{2}y}{h}_4(y),0\le y\le b.\hfill \end{array}$$112 Now we can apply the DQ to discretize the above equations and then apply the MGPS to integrate them.

7.1 Example 6

We consider the following analytical solutions of displacements:113 $$\begin{array}{cc}& u(x,y)=\frac{{\mathit{\sigma }}_0}{2G(1+\mathit{\nu })}cos(\mathit{\pi }x)y,\hfill \end{array}$$113 114 $$\begin{array}{cc}& v(x,y)=-\frac{{\mathit{\sigma }}_0}{4G(1+\mathit{\nu })}\left[\left(1,+,\frac{2{\mathit{\nu }}^2}{1-2\mathit{\nu }}\right),x^2,-,2,+,\mathit{\nu },y^2\right],\hfill \end{array}$$114 and the nonlinear terms are115 $$\begin{array}{c}\hfill G_1=u_x^2(x,y),G_2=0.\end{array}$$115 The body forces $F_1(x,y)$ and $F_2(x,y)$ can be obtained by inserting the exact $u$ and $v$ into Equations (101101 $$\begin{array}{c}\hfill F_5:=\frac{2\mathit{\alpha }{F}_1+F_2+\mathit{\alpha }{F}_9}{F_1},F_6:=\frac{{\mathit{\alpha }}^2{F}_1+\mathit{\alpha }{F}_2+{\mathit{\alpha }}^2{F}_9+p}{F_1},F_7:=\frac{F_3}{F_1},F_8:=\frac{F_4}{F_1}.\end{array}$$101 ) and (102102 $$\begin{array}{cc}\hfill U_R^i(R)& =V^i(R),i=1,2,\cdots ,m,\hfill \end{array}$$102 ).

The parameters ${\mathit{\alpha }}_1=-0.1$ and ${\mathit{\alpha }}_2=-1$ are used. Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=2/50$, $\mathrm{\Delta }y=1/2000$ used in the MGPS, the numerical solutions at $y=1$ are compared with the exact ones in Figure 12. It can be seen that the present algorithm is quite robust, which can recover the data on the top side very well, even under a large noise, where the maximum errors of $u$ and $v$ are, respectively, 0.01926 and 0.02526. The errors of the Neumann data $u_y$ and $v_y$ are also acceptable. On the other hand, we also compute the solutions with $s=0$ as shown in Figure 12 by the dashed-dotted lines, which, as compared with the numerical results under a large noise with $s=10\%$, are more smooth without having highly oscillatory behaviour. The main reason to cause the highly oscillatory phenomenon of the noisy examples is the random noise with a large intensity we imposed in the numerical simulations.

7.2 Example 7

We use the same exact solutions as that in the above example; however, the nonlinear terms are more complex:116 $$\begin{array}{c}\hfill G_1=u_x^2(x,y),G_2=v_x^2(x,y)+v_y^2(x,y).\end{array}$$116 The body forces $F_1(x,y)$ and $F_2(x,y)$ can be obtained by inserting the exact $u$ and $v$ into Equations (101101 $$\begin{array}{c}\hfill F_5:=\frac{2\mathit{\alpha }{F}_1+F_2+\mathit{\alpha }{F}_9}{F_1},F_6:=\frac{{\mathit{\alpha }}^2{F}_1+\mathit{\alpha }{F}_2+{\mathit{\alpha }}^2{F}_9+p}{F_1},F_7:=\frac{F_3}{F_1},F_8:=\frac{F_4}{F_1}.\end{array}$$101 ) and (102102 $$\begin{array}{cc}\hfill U_R^i(R)& =V^i(R),i=1,2,\cdots ,m,\hfill \end{array}$$102 ).

The parameters ${\mathit{\alpha }}_1=-0.1$ and ${\mathit{\alpha }}_2=-1$ are used. Under a large noise with $s=10\%$, and with $\mathrm{\Delta }x=2/50$, $\mathrm{\Delta }y=1/2000$, the numerical solutions at $y=1$ are compared with the exact ones in Figure 13. It can be seen that the present algorithm is quite robust, which can recover the data on the top side very well, even under a large noise, where the maximum errors of $u$ and $v$ are, respectively, 0.01899 and 0.02526. For the purpose of comparison, we raise the noise intensity to $s=20\%$, and from Figure 13 we can observe that the numerical solutions also close to the exact ones, of which the maximum errors of $u$ and $v$ are, respectively, 0.034 and 0.036.

8 Conclusions

In this paper, we first transformed the two-dimensional Navier equations by using a spring-damping transform method (SDTM) through a parameter $\mathit{\alpha }$. Then, by using a novel Lie-group integrator of the mixed group-preserving scheme (MGPS) we can recover the missing data on the top side very well for the inverse Cauchy problem in linear elasticity. Indeed, $\mathit{\alpha }$ is not a regularization parameter and it plays both a spring and a damping constant, which can slightly stabilize the governing equations and hence increase the accuracy of the numerical solutions. In general, some tests can help us to choose the suitable values of $\mathit{\alpha }$ in a certain range. Several numerical examples of the inverse Cauchy problem in linear elasticity and in the Laplace equation for arbitrary plane domain were worked out, which showed that the new numerical integration methods are applicable to the inverse Cauchy problem in linear elasticity, even for the very severely ill-posed ones. Under the overspecified data with a quite large noise the MGPS together with the SDTM was also robust enough to recover other unknown boundary data. We have extended the present algorithm to nonlinear inverse Cauchy problems of elasticity, which is insensitive to the noise perturbation. The present approach of the SDTM plus the MGPS can be extended to solve the inverse Cauchy problem in large deformation elasticity defined in an arbitrary plane domain. These issues however will be pursued in the near future.

Acknowledgments

The author highly appreciates the constructive comments from anonymous referees, which improve the quality of this paper. Taiwan’s National Science Council project NSC-102-2221-E-002-125-MY3, granted to the author, is highly appreciated. The 2011 Outstanding Research Award from NSC, the 2011 Taiwan Research Front Award from Thomson Reuters, and the 2013 Lifetime Distinguished Professor Award from NTU cause a great encouragement to the author.

Appendix A

In this appendix, we provide some backgrounds of the Differential Quadrature (DQ) and the Integral Quadrature (IQ).

Bellman and Casti [30], and Bellman et al. [31] first proposed the Differential Quadrature (DQ) as an approximation of the derivatives of differentiable function to mimic the integral quadrature for integrable function. Here, we consider a scalar function $f(x)$ defined in a closed interval $x\in [a,b]$. It is supposed that there are $n$ grid points with coordinates $x_1=a,x_2,\dots ,x_n=b$. The function $f(x)$ is assumed to be differentiable at any grid point, so that its first-order derivative $f^{\prime }(x)$ at any grid point $x_i$ can be approximated byA.1 $$\begin{array}{c}\hfill f^{\prime }(x_i)=\sum _{j=1}^n{b}_{ij}f(x_j).\end{array}$$A.1 In the first approach by Bellman et al. [31], the test functions are chosen as:A.2 $$\begin{array}{c}\hfill g_k(x)=x^k,k=0,1,\dots ,n-1,\end{array}$$A.2 such that we have the following algebraic equations to determine the weighting coefficients $b_{ij}$:A.3 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\sum }_{j=1}^n{b}_{ij}=0,\hfill \\ {\sum }_{j=1}^n{b}_{ij}{x}_j=1,\hfill \\ {\sum }_{j=1}^n{b}_{ij}{x}_j^k=k{x}_i^{k-1},k=2,\dots ,n-1.\hfill \end{array}\right.\end{array}$$A.3 Similarly, for the integral quadrature:A.4 $$\begin{array}{c}\hfill {\int }_a^{b}f(x)dx=\sum _{i=1}^n{b}_{i}f(x_i),\end{array}$$A.4 we can deriveA.5 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\sum }_{i=1}^n{b}_i=b-a,\hfill \\ {\sum }_{i=1}^n{b}_i{x}_i^k=\frac{b^{k+1}-a^{k+1}}{k+1},k=1,\dots ,n-1.\hfill \end{array}\right.\end{array}$$A.5 By inspection, we can see that the above systems are with the Vandermonde matrix as the coefficient matrix. Therefore, we can apply the technique developed by Liu and Atluri [32] to solve the above system, i.e. we solveA.6 $$\begin{array}{c}\hfill \left[\begin{array}{ccccc}1& 1& \dots & 1& 1\\ \frac{x_1}{R_0}& \frac{x_2}{R_0}& \dots & \frac{x_{n-1}}{R_0}& \frac{x_n}{R_0}\\ {\left(\frac{x_1}{R_0}\right)}^2& {\left(\frac{x_2}{R_0}\right)}^2& \dots & {\left(\frac{x_{n-1}}{R_0}\right)}^2& {\left(\frac{x_n}{R_0}\right)}^2\\ ⋮& ⋮& \dots & ⋮& ⋮\\ {\left(\frac{x_1}{R_0}\right)}^{n-2}& {\left(\frac{x_2}{R_0}\right)}^{n-2}& \dots & {\left(\frac{x_{n-1}}{R_0}\right)}^{n-2}& {\left(\frac{x_n}{R_0}\right)}^{n-2}\\ {\left(\frac{x_1}{R_0}\right)}^{n-1}& {\left(\frac{x_2}{R_0}\right)}^{n-1}& \dots & {\left(\frac{x_{n-1}}{R_0}\right)}^{n-1}& {\left(\frac{x_n}{R_0}\right)}^{n-1}\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_k\\ ⋮\\ b_n\end{array}\right]=\left[\begin{array}{c}b-a\\ \frac{b^2-a^2}{2R_0}\\ ⋮\\ \frac{b^{k+1}-a^{k+1}}{(k+1)R_0^k}\\ ⋮\\ \frac{b^n-a^n}{n{R}_0^{n-1}}\end{array}\right],\end{array}$$A.6 where $R_0>0$ is a characteristic length with $[a,b]\subset [-R_0,R_0]$. Refer also Shen and Liu [33]. Indeed, the above formulation is equivalent to employ the followings as the new test functions:A.7 $$\begin{array}{c}\hfill g_k(x)={\left(\frac{x}{R_0}\right)}^k,k=0,1,\dots ,n-1.\end{array}$$A.7 By applying Equation (A1) twice we can obtain the DQ formula for the second-order differential:A.8 $$\begin{array}{c}\hfill f^{″}(x_i)=\sum _{j=1}^n{a}_{ij}f(x_j),\end{array}$$A.8 where $a_{ij}=b_{ik}{b}_{kj}$.