Localization of immersed obstacles from boundary measurements

Abstract

A direct method for the localization of obstacles in a Stokes system is presented and theoretically justified. The method is based on the so-called reciprocity gap functional and is illustrated with several numerical simulations.

Keywords:

• inverse obstacle problems
• Stokes system
• reciprocity functional
• Stokeslets

1 Introduction

In this work, we consider the following inverse problem: a rigid body (obstacle) occupies a region $\mathit{\omega }\subset {\mathbb{R}}^2$ and is immersed in an incompressible viscous fluid, occupying a bounded domain ${\mathrm{\Omega }}_c=\mathrm{\Omega }\backslash \overline{\mathit{\omega }}$. Inside this domain, Stokes system holds. At the boundary, Dirichlet conditions are considered: a prescribed velocity at the accessible part of the boundary, $\mathit{\partial }\mathrm{\Omega }$, and null velocity at the boundary of the obstacle, $\mathit{\partial }\mathit{\omega }$. On the other hand, the obstacle produces a stress tensor on $\mathit{\partial }\mathrm{\Omega }$ (measured data) from where we want to determine the location of the obstacle. This inverse problem is an example of an inverse obstacle problem in nondestructive testing. Such problems have many applications in several engineering areas (see, for instance, some examples in the book [1]). For the problem here considered we refer the work,[2] where theoretical results concerning obstacle identification from boundary measurements and local stability were established. In [3], an iterative method based on the topological derivative and the Kohn–Vogelius functional is proposed for the identification of multiple 3D small obstacles and their location. In [4], a numerical shape reconstruction method based on integral equations was presented and tested. In this case, the location of the obstacle was assumed to be known. In [5], an optimization method for the reconstruction of both obstacle shape and location was proposed and tested (see also the work [6]). In this case, both shape and location were retrieved simultaneously with an iterative method.

Here, we propose a direct method for the location of a single 2D obstacle based on Green’s formula for the Stokes equations. The method requires the computation of the so-called reciprocity functional at appropriate test functions (see [7] for an application to the determination of point forces in a Stokes system) and can be easily adapted for the 3D case. This type of approach was presented in [8] for the reconstruction of cavities or inclusions in a Laplace problem (see also [9] for the localization of several circular obstacles using the reciprocity gap functional in a transmission problem for the Laplace equation). This work was partially presented by the authors at a conference on the Portuguese Naval School (cf. [10]) and is organized as follows: In Section 2, we define the inverse problem here addressed and the associated direct problem. In Section 3, we present some theoretical results concerning the identification of obstacles from a pair of Cauchy boundary data. Section 4 addresses retrieving of the location using the reciprocity gap functional. We show that the proposed formulae for the location of the obstacle are related to the centre of mass coordinates, for some density functions. Moreover, we show that, for some prescribed boundary velocities, the retrieved centre of mass is related to the centre of the whole domain, $\mathrm{\Omega }$. We conclude the paper with a section containing several numerical simulations to illustrate the proposed method.

2 Direct and inverse problems

Let $\mathrm{\Omega }\subset {\mathbb{R}}^2$ be a simply connected, open and bounded domain with regular $C^1$ boundary $\mathrm{\Gamma }:=\mathit{\partial }\mathrm{\Omega }$, which we shall call a regular domain. Let $\mathit{\omega }$ be a regular domain such that $\mathit{\omega }\subset \subset \mathrm{\Omega }$, meaning that $\overline{\mathit{\omega }}\subset \mathrm{\Omega }$. Denote by $\mathit{\gamma }$ the boundary of $\mathit{\omega }$. Define the domain of propagation ${\mathrm{\Omega }}_c:=\mathrm{\Omega }\backslash \overline{\mathit{\omega }}$ and notice that $\mathit{\partial }{\mathrm{\Omega }}_c=\mathrm{\Gamma }\cup \mathit{\gamma }$. The domain ${\mathrm{\Omega }}_c$ will represent the region occupied by the fluid whereas $\mathit{\omega }$ is the region occupied by the obstacle.

Given a boundary velocity $\mathbf{g}=(g_1,g_2)$ of the fluid at $\mathrm{\Gamma }$, and the no-slip boundary condition at $\mathit{\gamma }$, the system of equations governing the fluid flow here considered is given by1 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 where $\mathbf{u}=(u_1,u_2)$ is the fluid velocity, $p$ the pressure and $\mathit{\mu }$ the dynamic viscosity, which we shall assume to be $\mathit{\mu }=1$. Recall that $\mathrm{\Delta }\mathbf{u}=\left(\mathrm{\Delta },u_1,,,\mathrm{\Delta },u_2\right)$ is the Laplacian and $\mathrm{\nabla }p$ the gradient of the pressure. The condition $\mathrm{\nabla }·\mathbf{u}=0$ means that $\mathbf{u}$ is solenoidal and represents the incompressibility of the fluid. This condition implies that the prescribed boundary velocity $\mathbf{g}$ must satisfy the no flux compatibility condition2 $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{g}·\mathbf{n}d\mathit{\sigma }=0,\end{array}$$2 where $\mathbf{n}$ is the normal field at $\mathrm{\Gamma }$, pointing outwards with respect to ${\mathrm{\Omega }}_c$. The stress tensor associated to the flux $(\mathbf{u},p)$ is$$T(\mathbf{u},p):=-pI+2\mathit{ϵ}(\mathbf{u})$$where$$\mathit{ϵ}(\mathbf{u})=\frac{1}{2}\left(\mathrm{\nabla },\mathbf{u},+,\mathrm{\nabla },{\mathbf{u}}^{\top }\right)$$is the stress strain tensor of $\mathbf{u}$. In particular, problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 ) can be written as$$\left\{\begin{array}{cc}\mathrm{\nabla }·T(\mathbf{u},p)=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right..$$The direct problem consists in, given a boundary velocity $\mathbf{g}$ at $\mathrm{\Gamma }$ (satisfying the no flux condition (22 $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{g}·\mathbf{n}d\mathit{\sigma }=0,\end{array}$$2 )), determine the generated traction at $\mathrm{\Gamma }$,3 $$\begin{array}{c}\hfill {\mathbf{g}}_{\mathbf{n}}{:=T(\mathbf{u},p)\mathbf{n}|}_{\mathrm{\Gamma }}\end{array}$$3 where $(\mathbf{u},p)$ satisfies Stokes system (11 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 ). It is well known that, taking $\mathbf{g}\in {\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })$, where$${\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma }):=\left\{,\mathbf{g},\in ,{\left(H^{1/2},(\mathrm{\Gamma })\right)}^2,:,{\int }_{\mathrm{\Gamma }},\mathbf{g},·,\mathbf{n},d,\mathit{\sigma },=,0\right\},$$problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 ) is well posed, with $(\mathbf{u},p)\in {\mathbf{H}}_{div}^1({\mathrm{\Omega }}_c)\times L^2({\mathrm{\Omega }}_c)/\mathbb{R}$. The space ${\mathbf{H}}_{div}^1({\mathrm{\Omega }}_c)$ is defined as the subspace of ${(H^1({\mathrm{\Omega }}_c))}^2$ such that $\mathrm{\nabla }·\mathbf{u}=0$ in ${\mathrm{\Omega }}_c$. Recall also that the pressure $p$ is unique up to an additive constant and that$$L^2({\mathrm{\Omega }}_c)/\mathbb{R}\cong L_0^2({\mathrm{\Omega }}_c),$$where$$L_0^2({\mathrm{\Omega }}_c):=\left\{p,\in ,L^2,({\mathrm{\Omega }}_c),:,{\int }_{{\mathrm{\Omega }}_c},p,=,0\right\}.$$In this functional setting, we have ${\mathbf{g}}_{\mathbf{n}}\in {\mathbf{H}}^{-1/2}(\mathrm{\Gamma })={\left({\mathbf{H}}^{1/2},(\mathrm{\Gamma })\right)}^{\prime }$.

The inverse problem consists in: given a pair of Cauchy data $\left(\mathbf{g},,,{\mathbf{g}}_{\mathbf{n}}\right){|}_{\mathrm{\Gamma }}$, where ${\mathbf{g}}_{\mathbf{n}}$ is defined by (33 $$\begin{array}{c}\hfill {\mathbf{g}}_{\mathbf{n}}{:=T(\mathbf{u},p)\mathbf{n}|}_{\mathrm{\Gamma }}\end{array}$$3 ), determine the location of $\mathit{\omega }$. Here, we are assuming only the knowledge of the exterior boundary $\mathrm{\Gamma }$ and that at the boundary of the obstacle, $\mathit{\gamma }$, we have a no-slip boundary condition (the geometry of $\mathit{\gamma }$ is, therefore, unknown).

3 Identification and reconstruction results

The following is a well-known identification result of obstacles from a single pair of Cauchy boundary data.

Proposition 3.1

([2, 4])   Let ${\mathit{\omega }}_1,{\mathit{\omega }}_2\subset \subset \mathrm{\Omega }$ be regular domains, $\mathbf{g}\in {\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })\backslash \left\{,\mathbf{0}\right\}$ and $({\mathbf{u}}^{(1)},p^{(1)})$, $({\mathbf{u}}^{(2)},p^{(2)})$ the corresponding solutions of (11 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 ). If$$T({\mathbf{u}}^{(1)},p^{(1)})\mathbf{n}{{|}_{\mathrm{\Gamma }}=T({\mathbf{u}}^{(2)},p^{(2)})\mathbf{n}|}_{\mathrm{\Gamma }}$$then$${\mathit{\omega }}_1={\mathit{\omega }}_2.$$

Using analytic continuation arguments, the previous identification result is also valid for Cauchy data in an open part of the boundary $\mathrm{\Gamma }$.

3.1 Reconstruction of circular shaped obstacles

As a consequence of the above result, let us see the following particular case of localization of circular-shaped obstacles. Let$$B_r(x_0,y_0):=\left\{(x,y),\in ,{\mathbb{R}}^2,:,\Vert (x,y)-(x_0,y_0)\Vert ,<,r\right\}$$and suppose, by simplicity, that $\mathrm{\Omega }=B_R(0,0)$. Define the set of admissible circular-shaped obstacles$${\mathcal{A}}_c=\left\{B_r,(x_0,y_0),:,B_r,(x_0,y_0),\subset ,\subset ,\mathrm{\Omega }\right\}.$$Given $\mathit{\omega }=B_r(x_0,y_0)\in {\mathcal{A}}_c$ consider the vector field4 $$\begin{array}{c}\hfill \mathbf{u}(x,y)=\left(\frac{r^2}{{(x-x_0)}^2+{(y-y_0)}^2},-,1\right)\left(y,-,y_0,,,x_0,-,x\right)\in {\mathbf{H}}_{div}^1(\mathrm{\Omega }\backslash \overline{\mathit{\omega }}).\end{array}$$4 It can be easily seen that the pair $(\mathbf{u},0)$ satisfies Stokes system in the domain of propagation ${\mathrm{\Omega }}_c=\mathrm{\Omega }\backslash \overline{\mathit{\omega }}$, considering the boundary velocity5 $$\begin{array}{c}\hfill {\mathbf{g}=\mathbf{u}|}_{\mathrm{\Gamma }}.\end{array}$$5 On the other hand,6 $$\begin{array}{c}\hfill {\mathbf{g}}_{\mathbf{n}}{=T(\mathbf{u},0)\mathbf{n}|}_{\mathrm{\Gamma }}=\frac{2r^2}{R{({(x-x_0)}^2+{(y-y_0)}^2)}^2}\left(R^2,{\mathbf{v}}_1,+,{\mathbf{v}}_2\right)\end{array}$$6 where$${\mathbf{v}}_1=(y_0-y,x-x_0)\text{and}{\mathbf{v}}_2=\left(x_0^2,y,-,y_0,(2x{x}_0+y{y}_0),,,-,y_0^2,x,+,x_0,(x{x}_0+2y{y}_0)\right).$$Thus, we can define the map$$\mathrm{\Lambda }:{\mathcal{A}}_c\ni B_r(x_0,y_0)\mapsto (\mathbf{g},{\mathbf{g}}_{\mathbf{n}})$$with $(\mathbf{g},{\mathbf{g}}_{\mathbf{n}})\in {\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })\times {\mathbf{H}}^{-1/2}(\mathrm{\Gamma })$ defined by (55 $$\begin{array}{c}\hfill {\mathbf{g}=\mathbf{u}|}_{\mathrm{\Gamma }}.\end{array}$$5 ) and (66 $$\begin{array}{c}\hfill {\mathbf{g}}_{\mathbf{n}}{=T(\mathbf{u},0)\mathbf{n}|}_{\mathrm{\Gamma }}=\frac{2r^2}{R{({(x-x_0)}^2+{(y-y_0)}^2)}^2}\left(R^2,{\mathbf{v}}_1,+,{\mathbf{v}}_2\right)\end{array}$$6 ), respectively. By Proposition 3.1, $\mathrm{\Lambda }$ is injective and, in particular, we have the following result.

Lemma 3.2

Let $(x_0,y_0,r)$ be such that $B_r(x_0,y_0)\in {\mathcal{A}}_c$. Then,$$(x_0,y_0,r)=\underset{\genfrac{}{}{0pt}{}{(x_0^{\ast },y_0^{\ast },r^{\ast })}{s.t.B_{r^{\ast }}(x_0^{\ast },y_0^{\ast })\in {\mathcal{A}}_c}}{argmin}\Vert {\mathbf{g}}_{\mathbf{n}}^{\ast }-{\mathit{\pi }}_2\circ \mathrm{\Lambda }(B_{r^{\ast }}(x_0^{\ast },y_0^{\ast }))\Vert ,$$where ${\mathbf{g}}_{\mathbf{n}}^{\ast }$ is the traction at $\mathrm{\Gamma }$ generated by the obstacle $B_r(x_0,y_0)$ and considering the boundary velocity ${\mathbf{g}}^{\ast }={\mathit{\pi }}_1\circ \mathrm{\Lambda }(B_{r^{\ast }}(x_0^{\ast },y_0^{\ast }))$.

Proof

The map ${\mathit{\pi }}_1$ (respectively ${\mathit{\pi }}_2$) denotes the projection of ${\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })\times {\mathbf{H}}^{-1/2}(\mathrm{\Gamma })$ onto ${\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })$ (respectively ${\mathbf{H}}^{-1/2}(\mathrm{\Gamma })$). Notice that$${\mathit{\pi }}_2\circ \mathrm{\Lambda }(B_r(x_0,y_0))={\mathbf{g}}_{\mathbf{n}}^{\ast }$$where ${\mathbf{g}}_{\mathbf{n}}^{\ast }$ is the traction at $\mathrm{\Gamma }$ generated by $B_r(x_0,y_0)$ and considering the velocity ${\mathbf{g}}^{\ast }={\mathit{\pi }}_1\circ \mathrm{\Lambda }(B_r(x_0,y_0))$. In particular,$$\Vert {\mathbf{g}}_{\mathbf{n}}^{\ast }-{\mathit{\pi }}_2\circ \mathrm{\Lambda }(B_r(x_0,y_0))\Vert =0$$and the triplet $(x_0,y_0,r)$ is a solution of the above minimization problem. We now prove that it is unique. Let $(x_0^{\ast },y_0^{\ast },r^{\ast })$ be such that$$\Vert {\mathbf{g}}_{\mathbf{n}}^{\ast }-{\mathit{\pi }}_2\circ \mathrm{\Lambda }(B_{r^{\ast }}(x_0^{\ast },y_0^{\ast }))\Vert =0.$$Then,$$\mathrm{\Lambda }(B_{r^{\ast }}(x_0^{\ast },y_0^{\ast })))=({\mathbf{g}}^{\ast },{\mathbf{g}}_{\mathbf{n}}^{\ast })=\mathrm{\Lambda }(B_r(x_0,y_0))$$and the result follows from the injectivity of $\mathrm{\Lambda }$. $\square$

This lemma shows that the reconstruction of circular-shaped obstacles can be obtained by solving the above minimization problem. However, it requires several boundary measurements which is a drawback when comparing with the iterative method proposed in [5]. Moreover, it relies on an explicit solution of Stokes system for circular-shaped obstacles and it cannot be generalized for other type of obstacles.

4 Recovering the location of an obstacle using the reciprocity functional

Here, we propose a method based on Green’s formula for the location of the obstacle. It requires only one boundary measurement and does not depend on the shape of the obstacle.

Given a regular domain $\mathit{\omega }\subset {\mathbb{R}}^2$ and a regular function $f:\mathit{\omega }\to \mathbb{R}$ with constant sign, the mass centre of $\mathit{\omega }$ with density $f$ is the pair $({\overline{x}}_f,{\overline{y}}_f)$ defined by$${\overline{x}}_f=\frac{{\displaystyle {\int }_{\mathit{\omega }}xf(x,y)dA}}{{\displaystyle {\int }_{\mathit{\omega }}f(x,y)dA}}\text{and}{\overline{y}}_f=\frac{{\displaystyle {\int }_{\mathit{\omega }}yf(x,y)dA}}{{\displaystyle {\int }_{\mathit{\omega }}f(x,y)dA}}.$$In particular, when the density is constant, we obtain the so-called centre of gravity $(\overline{x},\overline{y})$7 $$\begin{array}{c}\hfill \overline{x}=\frac{{\displaystyle {\int }_{\mathit{\omega }}xdA}}{|\mathit{\omega }|}\text{and}\overline{y}=\frac{{\displaystyle {\int }_{\mathit{\omega }}ydA}}{|\mathit{\omega }|},\end{array}$$7 where $|\mathit{\omega }|$ is the area of $\mathit{\omega }$. Suppose that $\mathit{\omega }$ has $C^2$ boundary. Since for a density function $f\in L^2(\mathit{\omega })$, there exists an unique $u\in H^2(\mathit{\omega })$ satisfying$$\left\{\begin{array}{cc}\mathrm{\Delta }u=f\hfill & \mathrm{in}\mathit{\omega }\hfill \\ u=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.$$then, second Green’s formula (e.g. [11]) yields, for a test function $v\in H^2(\mathit{\omega })$,$${\int }_{\mathit{\omega }}\left(\mathrm{\Delta },u,v,-,u,\mathrm{\Delta },v\right)dA={\int }_{\mathit{\gamma }}\left({\mathit{\partial }}_{\mathbf{n}},u,v,-,u,{\mathit{\partial }}_{\mathbf{n}},v\right)d\mathit{\sigma },$$where ${\mathit{\partial }}_{\mathbf{n}}{u:=\mathrm{\nabla }u·\mathbf{n}|}_{\mathit{\gamma }}$ is the normal derivative at $\mathit{\gamma }$. In particular, taking the harmonic test function $v(x,y)=x$ we have$${\int }_{\mathit{\omega }}f(x,y)xdA={\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}uxd\mathit{\sigma }.$$Therefore, we can also write the centre of mass $({\overline{x}}_f,{\overline{y}}_f)$ using only boundary integrals,8 $$\begin{array}{c}\hfill {\overline{x}}_f=\frac{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}uxd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}ud\mathit{\sigma }}}\text{and}{\overline{y}}_f=\frac{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}uyd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}ud\mathit{\sigma }}}.\end{array}$$8 In particular, for the centre of gravity, that is assuming $f\equiv 1$, we get9 $$\begin{array}{c}\hfill \overline{x}=\frac{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}{u}_{1}xd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}{u}_{1}d\mathit{\sigma }}}\text{and}\overline{y}=\frac{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}{u}_{1}yd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}{u}_{1}d\mathit{\sigma }}}\end{array}$$9 where $u_1$ is given by$$u_1=u_h+\frac{x^2}{2},$$and $u_h$ is the harmonic function in $\mathit{\omega }$ such that$$u_h{{|}_{\mathit{\gamma }}=-\frac{x^2}{2}|}_{\mathit{\gamma }}.$$

4.1 Centre of a circle

For the particular case of circular domains $\mathit{\omega }=B_r(x_0,y_0)$, it is well known that (e.g. [12])10 $$\begin{array}{c}\hfill u(x_0,y_0)=\frac{{\displaystyle {\int }_{\mathit{\gamma }}ud\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}d\mathit{\sigma }}},\end{array}$$10 for any harmonic function $u$ in $\mathit{\omega }$. Thus, considering the harmonic functions $u_1(x,y)=x$ and $u_2(x,y)=y$ we have, by (1010 $$\begin{array}{c}\hfill u(x_0,y_0)=\frac{{\displaystyle {\int }_{\mathit{\gamma }}ud\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}d\mathit{\sigma }}},\end{array}$$10 ), the following identity for the geometric centre of $\mathit{\omega }$,$$x_0=\frac{{\displaystyle {\int }_{\mathit{\gamma }}xd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}d\mathit{\sigma }}}\text{and}{y}_0=\frac{{\displaystyle {\int }_{\mathit{\gamma }}yd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}d\mathit{\sigma }}}.$$Notice that this formula coincides with (77 $$\begin{array}{c}\hfill \overline{x}=\frac{{\displaystyle {\int }_{\mathit{\omega }}xdA}}{|\mathit{\omega }|}\text{and}\overline{y}=\frac{{\displaystyle {\int }_{\mathit{\omega }}ydA}}{|\mathit{\omega }|},\end{array}$$7 ). In fact, for $f(x,y)\equiv 1$, the function$$u(x,y)=\frac{1}{4}{(x-x_0)}^2+\frac{1}{4}{(y-y_0)}^2-\frac{r^2}{4}$$satisfies$$\left\{\begin{array}{cc}\mathrm{\Delta }u=f\hfill & \mathrm{in}\mathit{\omega }=B_r(x_0,y_0)\hfill \\ u=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }{B}_r(x_0,y_0)\hfill \\ {\mathit{\partial }}_{\mathbf{n}}u=\frac{r}{2}\hfill & \mathrm{on}\mathit{\gamma }\hfill \\ \hfill \end{array}\right..$$Hence,$$\overline{x}=\frac{{\displaystyle {\int }_{\mathit{\omega }}xdA}}{{\displaystyle {\int }_{\mathit{\omega }}dA}}=\frac{{\displaystyle {\int }_{\mathit{\omega }}f(x,y)xdA}}{{\displaystyle {\int }_{\mathit{\omega }}f(x,y)dA}}=\frac{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}uxd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}{\mathit{\partial }}_{\mathbf{n}}ud\mathit{\sigma }}}=\frac{{\displaystyle {\int }_{\mathit{\gamma }}xd\mathit{\sigma }}}{{\displaystyle {\int }_{\mathit{\gamma }}d\mathit{\sigma }}}=x_0.$$

4.2 Reciprocity functional for Stokes equations

Let $(\mathbf{u},p)$ and $(\mathbf{v},q)\in \left({\mathbf{H}}^2,({\mathrm{\Omega }}_c),\cap ,{\mathbf{H}}_{div}^1,({\mathrm{\Omega }}_c)\right)\times H^1({\mathrm{\Omega }}_c)$, where ${\mathrm{\Omega }}_c=\mathrm{\Omega }\backslash \overline{\mathit{\omega }}$ and $\mathit{\omega },\mathrm{\Omega }$ are any $C^2$ regular domains. Assuming that the normal at $\mathit{\partial }{\mathrm{\Omega }}_c=\mathrm{\Gamma }\cup \mathit{\gamma }$ points outwards with respect to ${\mathrm{\Omega }}_c$, we have the following Gauss-Green formula11 $$\begin{array}{cc}\hfill {\int }_{{\mathrm{\Omega }}_c}\left(\left(\mathrm{\Delta },\mathbf{u},-,\mathrm{\nabla },p\right),·,\mathbf{v},-,\mathbf{u},·,\left(\mathrm{\Delta },\mathbf{v},-,\mathrm{\nabla },q\right)\right)dA& ={\int }_{\mathrm{\Gamma }}\left(T,(,\mathbf{u},,,p,),\mathbf{n},·,\mathbf{v},-,\mathbf{u},·,T,(,\mathbf{v},,,q,),\mathbf{n}\right)d\mathit{\sigma }\hfill \\ & +{\int }_{\mathit{\gamma }}\left(T,(,\mathbf{u},,,p,),\mathbf{n},·,\mathbf{v},-,\mathbf{u},·,T,(,\mathbf{v},,,q,),\mathbf{n}\right)d\mathit{\sigma }.\hfill \end{array}$$11 Given $(\mathbf{u},p)$, we define the reciprocity functional at $\mathrm{\Gamma }$12 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q):={\int }_{\mathrm{\Gamma }}\left(T,(,\mathbf{u},,,p,),\mathbf{n},·,\mathbf{v},-,\mathbf{u},·,T,(,\mathbf{v},,,q,),\mathbf{n}\right)d\mathit{\sigma }.\end{array}$$12 In the following, we shall assume that $(\mathbf{u},p)$ satisfies Stokes system (11 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathit{\mu }\mathrm{\Delta }\mathbf{u}-\mathrm{\nabla }p=\mathbf{0}\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathrm{\nabla }.\mathbf{u}=0\hfill & \mathrm{in}{\mathrm{\Omega }}_c\hfill \\ \mathbf{u}=g\hfill & \mathrm{on}\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }\hfill \\ \mathbf{u}=0\hfill & \mathrm{on}\mathit{\gamma }=\mathit{\partial }\mathit{\omega }\hfill \\ \hfill \end{array}\right.,\end{array}$$1 ). Hence,13 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q)={\int }_{\mathrm{\Gamma }}\left({\mathbf{g}}_{\mathbf{n}},·,\mathbf{v},-,\mathbf{g},·,T,(\mathbf{v},q),\mathbf{n}\right)d\mathit{\sigma }\end{array}$$13 where $(\mathbf{g},{\mathbf{g}}_{\mathbf{n}})$ is the pair of Cauchy data at $\mathrm{\Gamma }$ (recall that this data is assumed to be available in the inverse problem). Gauss-Green formula gives14 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q)=-{\int }_{{\mathrm{\Omega }}_c}\mathbf{u}·\left(\mathrm{\Delta },\mathbf{v},-,\mathrm{\nabla },q\right)dA-{\int }_{\mathit{\gamma }}T(\mathbf{u},p)\mathbf{n}·\mathbf{v}d\mathit{\sigma }.\end{array}$$14

4.3 Formulae for the centre of mass

Suppose that the pair of test functions $(\mathbf{v},q)$ satisfy$$\mathrm{\Delta }\mathbf{v}-\mathrm{\nabla }q=0\text{in}{\mathrm{\Omega }}_c.$$Then, using (1313 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q)={\int }_{\mathrm{\Gamma }}\left({\mathbf{g}}_{\mathbf{n}},·,\mathbf{v},-,\mathbf{g},·,T,(\mathbf{v},q),\mathbf{n}\right)d\mathit{\sigma }\end{array}$$13 ) we can write the identity$${\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q)=-{\int }_{\mathit{\gamma }}T(\mathbf{u},p)\mathbf{n}·\mathbf{v}d\mathit{\sigma }$$from where we can obtain the following reconstruction method for the centre of mass.

Take $q\equiv 0$ and15 $$\begin{array}{c}\hfill {\mathbf{v}}_1(x,y)=x{\overrightarrow{\mathbf{e}}}_2\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$15 where $({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2)$ is the standard basis in ${\mathbb{R}}^2$. We have,$${\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)=-{\int }_{\mathit{\gamma }}T(\mathbf{u},p)\mathbf{n}·{\overrightarrow{\mathbf{e}}}_{2}xd\mathit{\sigma }.$$On the other hand,$${\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)=-{\int }_{\mathit{\gamma }}T(\mathbf{u},p)\mathbf{n}·{\overrightarrow{\mathbf{e}}}_{2}d\mathit{\sigma }$$hence, assuming ${\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)\ne 0$, we get the approximation16 $$\begin{array}{c}\hfill \frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)}\end{array}$$16 for the first coordinate. For the second coordinate, we consider17 $$\begin{array}{c}\hfill {\mathbf{v}}_2(x,y)=y{\overrightarrow{\mathbf{e}}}_1\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$17 and obtain18 $$\begin{array}{c}\hfill \frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_2,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_1,0)}.\end{array}$$18

Remark 1

The above formulae (1515 $$\begin{array}{c}\hfill {\mathbf{v}}_1(x,y)=x{\overrightarrow{\mathbf{e}}}_2\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$15 ) and (1717 $$\begin{array}{c}\hfill {\mathbf{v}}_2(x,y)=y{\overrightarrow{\mathbf{e}}}_1\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$17 ) require only a single pair of Cauchy data $(\mathbf{g},{\mathbf{g}}_{\mathbf{n}})$ on $\mathrm{\Gamma }$. On the other hand, no information regarding the shape of $\mathit{\omega }$ is considered.

The following result shows that in certain cases, the formulae (1515 $$\begin{array}{c}\hfill {\mathbf{v}}_1(x,y)=x{\overrightarrow{\mathbf{e}}}_2\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$15 ) and (1717 $$\begin{array}{c}\hfill {\mathbf{v}}_2(x,y)=y{\overrightarrow{\mathbf{e}}}_1\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$17 ) provides the coordinates of the obstacle, for some density functions.

Proposition 4.1

Suppose that ${T(\mathbf{u},p)\mathbf{n}|}_{\mathit{\gamma }}\in {\mathbf{H}}^{1/2}(\mathit{\gamma })$. There exists $f_1,f_2\in L^2(\mathit{\omega })$ such that$$\frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)}=x_{f_1}\text{and}\frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_2,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_1,0)}=y_{f_2}.$$Moreover,19 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 where $(\overline{x},\overline{y})$ is the centre of gravity of $\mathit{\omega }$.

Proof

We show the above identities for the first coordinate (the second can be obtained in the same manner). Let $\tilde{g}=-T(\mathbf{u},p)\mathbf{n}·{\overrightarrow{\mathbf{e}}}_2\in H^{1/2}(\mathit{\gamma })$. Since the bilaplace problem$$\left\{\begin{array}{cc}{\mathrm{\Delta }}^{2}w=0\hfill & \mathrm{in}\mathit{\omega }\hfill \\ w=0\hfill & \mathrm{on}\mathit{\gamma }\hfill \\ {\mathit{\partial }}_{\mathbf{n}}w=\tilde{g}\hfill & \mathrm{on}\mathit{\gamma }\hfill \end{array}\right.$$is well posed in $H^2(\mathit{\omega })$ (e.g. [11]) then, for $f_1=\mathrm{\Delta }w\in L^2(\mathit{\omega })$ Green’s formula yields$${\int }_{\mathit{\omega }}{f}_{1}vdA={\int }_{\mathit{\omega }}(\mathrm{\Delta }wv-w\mathrm{\Delta }v)dA={\int }_{\mathit{\gamma }}\left({\mathit{\partial }}_{\mathbf{n}},w,v,-,w,{\mathit{\partial }}_{\mathbf{n}},v\right)d\mathit{\sigma }={\int }_{\mathit{\gamma }}\tilde{g}vd\mathit{\sigma },$$for every harmonic test function $v$. Therefore, taking $v=x$ we get$${\int }_{\mathit{\omega }}{f}_{1}xdA={\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0).$$Since we also have ${\int }_{\mathit{\omega }}{f}_{1}dA={\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)$ then,$$x_{f_1}=\frac{{\int }_{\mathit{\omega }}{f}_{1}xdA}{{\int }_{\mathit{\omega }}{f}_{1}dA}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)}.$$Identity (1818 $$\begin{array}{c}\hfill \frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_2,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_1,0)}.\end{array}$$18 ) follows from the linearity of ${\mathcal{R}}_{\mathrm{\Gamma }}$ since$$\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}=\frac{\frac{1}{{\int }_{\mathit{\omega }}xdA}{\mathcal{R}}_{\mathrm{\Gamma }}\left({\mathbf{v}}_1,,,0\right)}{{|\mathit{\omega }|}^{-1}{\mathcal{R}}_{\mathrm{\Gamma }}\left({\overrightarrow{\mathbf{e}}}_2,,,0\right)}=\frac{|\mathit{\omega }|}{{\int }_{\mathit{\omega }}xdA}\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left({\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left({\overrightarrow{\mathbf{e}}}_2,,,0\right)}=\frac{x_{f_1}}{\overline{x}}.$$$\square$

We now obtain a connection between centre of mass of the obstacle $\mathit{\omega }$ and centre of the whole domain $\mathrm{\Omega }$.

Corollary 4.2

Suppose that the prescribed velocity $\mathbf{g}$ at $\mathrm{\Gamma }$ satisfies the orthogonal conditions20 $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{g}·T({\mathbf{v}}_1,0)\mathbf{n}d\mathit{\sigma }={\int }_{\mathrm{\Gamma }}\mathbf{g}·T({\mathbf{v}}_2,0)\mathbf{n}d\mathit{\sigma }=0,\end{array}$$20 where ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are the fields defined in (1414 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q)=-{\int }_{{\mathrm{\Omega }}_c}\mathbf{u}·\left(\mathrm{\Delta },\mathbf{v},-,\mathrm{\nabla },q\right)dA-{\int }_{\mathit{\gamma }}T(\mathbf{u},p)\mathbf{n}·\mathbf{v}d\mathit{\sigma }.\end{array}$$14 ) and (1616 $$\begin{array}{c}\hfill \frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)}\end{array}$$16 ), respectively. Then, there exists ${\tilde{f}}_i\in L^2(\mathrm{\Omega })$ such that $\text{supp}{\tilde{f}}_i\subset \mathit{\omega }$ and21 $$\begin{array}{c}\hfill x_{{\tilde{f}}_1}=\frac{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{1}xdA}{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{1}dA}=\frac{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}xd\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}d\mathit{\sigma }}=x_{f_1},y_{{\tilde{f}}_2}=\frac{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{2}xdA}{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{2}dA}=\frac{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}yd\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}d\mathit{\sigma }}=y_{f_2}.\end{array}$$21

Proof

From (1212 $$\begin{array}{c}\hfill {\mathcal{R}}_{\mathrm{\Gamma }}(\mathbf{v},q):={\int }_{\mathrm{\Gamma }}\left(T,(,\mathbf{u},,,p,),\mathbf{n},·,\mathbf{v},-,\mathbf{u},·,T,(,\mathbf{v},,,q,),\mathbf{n}\right)d\mathit{\sigma }.\end{array}$$12 ), the identities (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ) imply$${\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)={\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}xd\mathit{\sigma }\text{and}{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_2,0)={\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}yd\mathit{\sigma }.$$Let ${\tilde{f}}_i\in L^2(\mathrm{\Omega })$ be the extension of $f_i\in L^2(\mathit{\omega })$ by zero to the whole $\mathrm{\Omega }$. Then,$$\frac{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{1}xdA}{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{1}dA}=\frac{{\int }_{\mathit{\omega }}{f}_{1}xdA}{{\int }_{\mathit{\omega }}{f}_{1}dA}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_1,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_2,0)}\text{and}\frac{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{2}xdA}{{\int }_{\mathrm{\Omega }}{\tilde{f}}_{2}dA}=\frac{{\int }_{\mathit{\omega }}{f}_{2}xdA}{{\int }_{\mathit{\omega }}{f}_{2}dA}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}({\mathbf{v}}_2,0)}{{\mathcal{R}}_{\mathrm{\Gamma }}({\overrightarrow{\mathbf{e}}}_1,0)}.$$$\square$

Remark 2

We can take, for instance, boundary velocities $\mathbf{g}\in {\mathbf{H}}_{\mathit{\sigma }}^{1/2}(\mathrm{\Gamma })$ such that $\mathbf{g}·{\overrightarrow{\mathbf{e}}}_1=\mathbf{g}·{\overrightarrow{\mathbf{e}}}_2$. In fact, since$$T({\mathbf{v}}_1,0)\mathbf{n}=T({\mathbf{v}}_2,0)\mathbf{n}=\left(\mathbf{n},·,{\overrightarrow{\mathbf{e}}}_2\right){\overrightarrow{\mathbf{e}}}_1+\left(\mathbf{n},·,{\overrightarrow{\mathbf{e}}}_1\right){\overrightarrow{\mathbf{e}}}_2$$then$$\mathbf{g}·T({\mathbf{v}}_1,0)\mathbf{n}=\mathbf{g}·T({\mathbf{v}}_2,0)\mathbf{n}=\mathbf{g}·\mathbf{n}.$$Since $\mathbf{g}$ satisfies the no flux condition (22 $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{g}·\mathbf{n}d\mathit{\sigma }=0,\end{array}$$2 ) it follows that $\mathbf{g}$ satisfies the hypothesis (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ).

Remark 3

Suppose that $\mathrm{\Omega }=B_r(x_0,y_0)$ is a circle. From the above result, if the traction data ${\mathbf{g}}_{\mathbf{n}}{|}_{\mathrm{\Gamma }}\approx c_1{\overrightarrow{\mathbf{e}}}_1+c_2{\overrightarrow{\mathbf{e}}}_2$, where $c_1$ and $c_2$ are constants then the obstacle $\mathit{\omega }$ should be centred with $\mathrm{\Omega }$, that is, $x_{f_1}\approx x_0$ and $y_{f_2}\approx y_0$.

5 Numerical examples

5.1 Numerical solution of the direct problem using Stokeslets

In this section, we will make a brief reference to the application of the Method of Fundamental Solutions (MFS) (e.g. [13]) to solve the direct Stokes problem. Such method was used in this work with the aim of generating stress data, ${\mathbf{g}}_{\mathbf{n}}(x_i)$, in a finite number of boundary points $x_i\in \mathrm{\Gamma }$.

A fundamental solution $(U,P)$ for the 2D Stokes system satisfies$$\left\{\begin{array}{cc}\mathrm{\Delta }{U}_i-\mathrm{\nabla }{P}_i=-\mathit{\delta }{\overrightarrow{\mathbf{e}}}_i\hfill & \mathrm{in}{\mathbb{R}}^2\hfill \\ \mathrm{\nabla }·U_i=0\hfill & \mathrm{in}{\mathbb{R}}^2\hfill \\ \hfill \end{array}\right.,$$where $\mathit{\delta }$ is the Dirac delta (distribution) centred at the origin. Here, we consider the Stokeslets$$\begin{array}{c}\hfill U(x)=-\frac{1}{4\mathit{\pi }}\left(I_2,log,\left(\frac{1}{|x|}\right),+,\frac{x\otimes x}{{|x|}^2}\right)\end{array}$$$$\begin{array}{c}\hfill P(x)=-\frac{1}{2\mathit{\pi }}\frac{x}{{|x|}^2}\end{array}$$where $\otimes$ stands for the tensor product. The MFS for the 2D Stokes flow consists in taking the approximations for the velocity and pressure (see [14]) as22 $$\begin{array}{c}\hfill \tilde{\mathbf{u}}(x)=\sum _{j=1}^2\sum _{k=1}^{N_1+M_1}{a}_{jk}{U}_j(x-y_k)\end{array}$$22 and23 $$\begin{array}{c}\hfill \tilde{p}(x)=\sum _{j=1}^2\sum _{k=1}^{N_1+M_1}{a}_{jk}{P}_j(x-y_k)\end{array}$$23 where $y_1,...,y_{N_1}$ are source points placed at an artificial boundary located outside the physical domain $\mathrm{\Omega }$ and $y_{N_1+1},...,y_{N_1+M_1}$ are sources on an interior artificial boundary contained in $\mathit{\omega }$. The basis functions $(U_j,P_j)$ are the canonical components $U_j=U·{\overrightarrow{\mathbf{e}}}_j$ and $P_j=P·{\overrightarrow{\mathbf{e}}}_j$.

The coefficients $a_{jk}$ that will determinate the approximation, can be computed by fitting the Dirichlet boundary conditions at some collocations points, that is, $\tilde{\mathbf{u}}(x_i)\approx \mathbf{g}(x_i)$ ($x_i\in \mathrm{\Gamma }$) and $\tilde{\mathbf{u}}(x_j)\approx 0$ ($x_j\in \mathit{\gamma }$).

Here, we considered a least squares fitting which leads to the following system of linear equations,$$\begin{array}{c}\hfill A^{T}Aa=A^{T}g\end{array}$$where $A$ is given by 2D blocks,$$\begin{array}{c}\hfill A=\left[\begin{array}{ccc}U(x_1-y_1)& ...& U(x_1-y_{N_1+M_1})\\ ⋮& & ⋮\\ U(x_{N_2+M_2}-y_1)& ...& U(x_{N_2+M_2}-y_{N_1+M_1})\end{array}\right]\end{array}$$and$$\begin{array}{c}\hfill g=\left[\begin{array}{c}{g}_1\\ ...\\ g_{N_2+M_2}\end{array}\right]\end{array}$$where$$\begin{array}{c}\hfill g_k=\left\{\begin{array}{cc}[g_1(x_k),g_2(x_k){]}^T\hfill & \mathrm{if}k=1,...,N_2\hfill \\ {[0,0]}^T\hfill & \mathrm{if}k=N_2+1,...,N_2+M_2\hfill \end{array}\right.\end{array}$$and $a={[\begin{array}{ccc}{a}_1& \cdots & a_{N_1+M_1}\end{array}]}^T$, with $a_k={[a_{1k},a_{2k}]}^T$.

5.2 Location reconstruction

In this section, we will present three examples in order to illustrate the feasibility and stability of the proposed method. The location of the obstacle is retrieved as $(\overline{x},\overline{y})$ where the coordinates are given by the formulae (1515 $$\begin{array}{c}\hfill {\mathbf{v}}_1(x,y)=x{\overrightarrow{\mathbf{e}}}_2\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$15 ) and (1717 $$\begin{array}{c}\hfill {\mathbf{v}}_2(x,y)=y{\overrightarrow{\mathbf{e}}}_1\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_{div}^1(\mathrm{\Omega })\end{array}$$17 ). In other words,$$\overline{x}=\frac{{\int }_{\mathrm{\Gamma }}\left({\mathbf{g}}_{\mathbf{n}},·,{\overrightarrow{\mathbf{e}}}_2,x,-,\mathbf{g},·,T,({\mathbf{v}}_1,0),\mathbf{n}\right)d\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}d\mathit{\sigma }},\overline{y}=\frac{{\int }_{\mathrm{\Gamma }}\left({\mathbf{g}}_{\mathbf{n}},·,{\overrightarrow{\mathbf{e}}}_1,y,-,\mathbf{g},·,T,({\mathbf{v}}_2,0),\mathbf{n}\right)d\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}d\mathit{\sigma }}.$$If the boundary velocity $\mathbf{g}$ satisfies the orthogonal conditions (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ) then the previous expressions can be written as$$\overline{x}=\frac{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}xd\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{2}d\mathit{\sigma }},\overline{y}=\frac{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}yd\mathit{\sigma }}{{\int }_{\mathrm{\Gamma }}{\mathbf{g}}_{\mathbf{n}}·{\overrightarrow{\mathbf{e}}}_{1}d\mathit{\sigma }}.$$We approximate the above line integrals using a trapezoidal rule. The observation points, that is, the points $x_i\in \mathrm{\Gamma }$ where we have the measured data ${\mathbf{g}}_{\mathbf{n}}(x_i)$ will be represented by (blue) dots. The shape of the obstacle will be represented by a full blue line and the retrieved location of the obstacle by a bold red dot.

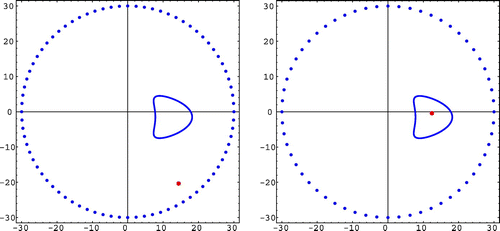
5.2.1 Example 1

We start by studying the influence of boundary velocity $\mathbf{g}$. We test two situations: One considering boundary velocity satisfying the orthogonal condition (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ) and other not satisfying this condition. The considered obstacle was the kite, defined by the parametrization$$\mathit{\gamma }(t)=\left(11.75,+,1.3,cos,(t),+,0.5,cos,(2t)\right){\overrightarrow{\mathbf{e}}}_1+\left(1.5,sin,(t),-,1.5\right){\overrightarrow{\mathbf{e}}}_2,t\in [0,2\mathit{\pi }].$$

Figure 1. Reconstruction results from two boundary velocities satisfying (right plot) and not satisfying (left plot) the orthogonal condition (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ).

Figure 2. The same as the previous figure when considered a different size for the kite.

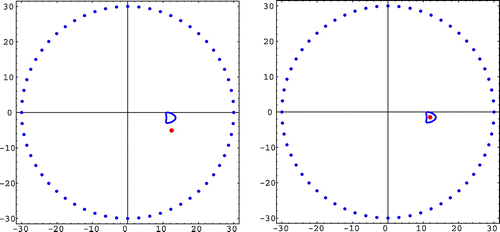
We considered $\mathrm{\Gamma }=\mathit{\partial }{B}_{30}(0,0)$ and the boundary velocities ${\mathbf{g}}_1(x,y)=y{\overrightarrow{\mathbf{e}}}_1+x{\overrightarrow{\mathbf{e}}}_2$ and ${\mathbf{g}}_2(x,y)={\overrightarrow{\mathbf{e}}}_1+{\overrightarrow{\mathbf{e}}}_2$. Notice that$${\int }_{\mathrm{\Gamma }}{\mathbf{g}}_1·T({\mathbf{v}}_1,0)\mathbf{n}d\mathit{\sigma }={\int }_{\mathrm{\Gamma }}{\mathbf{g}}_1·T({\mathbf{v}}_2,0)\mathbf{n}d\mathit{\sigma }=1800\mathit{\pi }$$and ${\mathbf{g}}_2$ satisfies the orthogonal condition (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ) (see remark 2). We took the measured data at 60 observation points uniformly distributed over $\mathrm{\Gamma }$, without adding noise. As we can see in Figure 1 (right plot) we were able to retrieve the location of the obstacle, when the boundary velocity satisfies the orthogonal condition (1919 $$\begin{array}{c}\hfill x_{f_1}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}xdA},{\mathbf{v}}_1,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_2,,,0\right)}\overline{x}\text{and}{y}_{f_2}=\frac{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,\frac{1}{{\int }_{\mathit{\omega }}ydA},{\mathbf{v}}_2,,,0\right)}{{\mathcal{R}}_{\mathrm{\Gamma }}\left(-,{|\mathit{\omega }|}^{-1},{\overrightarrow{\mathbf{e}}}_1,,,0\right)}\overline{y}\end{array}$$19 ). For this case, the retrieved location was $(12,-1.5)$. When we considered the boundary velocity ${\mathbf{g}}_1$ we obtained the location $(12.4,-5.1)$, which is a bad result (see the left plot of the mentioned figure). The results deteriorate by increasing the size of the obstacle (see Figure 2).

Table 1. Reconstruction of a small circular obstacle $\mathit{\omega }=B_{0.03}(4.2,0)$ immersed in $\mathrm{\Omega }=B_5(0,0)$.

Observations	without noise	$10\%$ noise	$20\%$ noise
10	$(3.02,-0.15)$	$(3.15,-0.06)$	$(5.33,0.17)$
30	$(4.18,-0.02)$	$(5.12,0.03)$	$(4.32,0.91)$
60	$(4.20007,0.00014)$	$(4.33,0.024)$	$(5.83,0.45)$

Table 2. The same as the previous Table but considering the domain $\mathrm{\Omega }=B_{30}(0,0)$.

Observations	without noise	$10\%$ noise	$20\%$ noise
10	$(4.19,0.004)$	$(3.97,0.23)$	$(4.74,0.66)$
30	$(4.19,0.0003)$	$(3.54,0.09)$	$(4.36,0.14)$
60	$(4.20,0.0003)$	$(4.26,0.19)$	$(4.201,0.06)$

5.2.2 Example 2

In this second example, we tested the sensibility of the method with respect to the size and location of the obstacle. We started by testing the effect of the size on the reconstruction results. We considered the circular obstacle bounded by $\mathit{\gamma }=\mathit{\partial }{B}_{0.03}(4.2,0)$ immersed in two regions: first, a region bounded by $\mathrm{\Gamma }=\mathit{\partial }{B}_5(0,0)$ and then bounded by $\mathrm{\Gamma }=\mathit{\partial }{B}_{30}(0,0)$. The velocity field prescribed at $\mathrm{\Gamma }$ was $\mathbf{g}(x,y)={\overrightarrow{\mathbf{e}}}_1+{\overrightarrow{\mathbf{e}}}_2$.

The centre was retrieved using 10, 30 and 60 observations on $\mathrm{\Gamma }$. The numerical results are summarized in Tables 1 and 2, respectively. Overall, we obtained good reconstruction results even in the presence of noisy data.

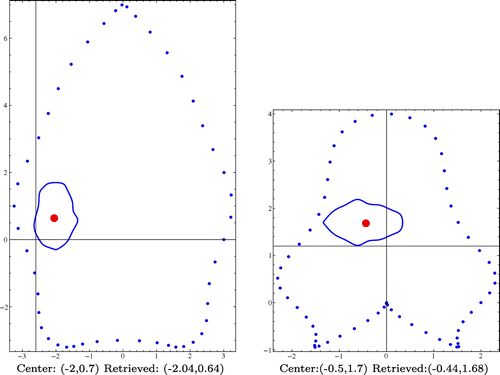
Figure 3. Reconstruction results considering 10 boundary observations and several obstacle shape and location.

Figure 4. Two different schemes for the observation points.

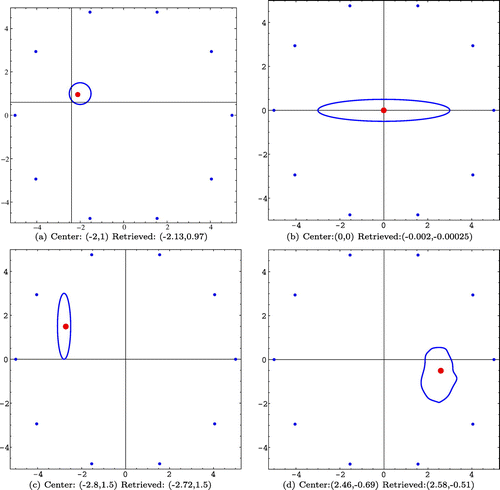
Next, we considered several star-shaped obstacles with different geometries and locations. The boundary velocity was $\mathbf{g}={\overrightarrow{\mathbf{e}}}_2$ for the first example and $\mathbf{g}={\overrightarrow{\mathbf{e}}}_1+{\overrightarrow{\mathbf{e}}}_2$ for the others. We took 10 noise-free boundary measurements and obtained the results presented in Figure 3. Notice that the last obstacle (plot (d) of Figure 3) is not symmetric. The parametrization of the corresponding boundary is$$\begin{array}{c}\hfill \mathit{\gamma }(t)=\left(0.4,(,1.5,-,sin,(t),cos,{(2t)}^3,),cos,(t),+,2\right){\overrightarrow{\mathbf{e}}}_1+\left((,2.5,-,cos,{(t)}^3,),sin,(t),-,0.7\right){\overrightarrow{\mathbf{e}}}_2.\end{array}$$

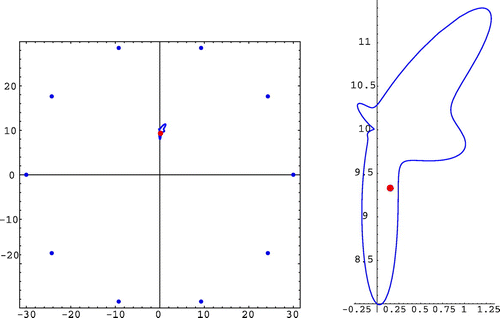
5.2.3 Example 3

In this example, we considered two different geometries for the enclosing domain $\mathrm{\Omega }$. In both cases, the domains are star shaped and nonconvex (see Figure 4). The boundary velocity was $\mathbf{g}={\overrightarrow{\mathbf{e}}}_1+{\overrightarrow{\mathbf{e}}}_2$ and the noise-free measured data were obtained at 50 observation points. As we can see in Figure 4, the location of the obstacle was retrieved accurately.

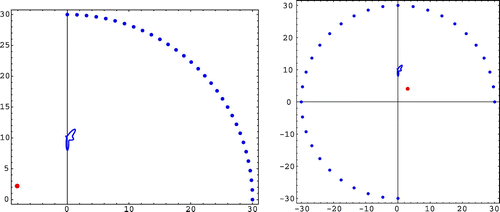
Last simulations concern a nonconvex shark-shaped obstacle. The boundary is given by the parametrization24 $$\begin{array}{cc}\hfill \mathit{\gamma }(t)=& \left(1.9,\frac{1+0.9cos(t)+0.1sin(2t)}{1+0.75sin(t)cos(4t)},cos,(t),-,5.5\right){\overrightarrow{\mathbf{e}}}_1\hfill \\ & +\left(1.9,\frac{1+0.9cos(t)+0.1sin(2t)}{1+0.75sin(t)cos(4t)},sin,(t),-,12.7\right){\overrightarrow{\mathbf{e}}}_2\hfill \end{array}$$24 and the enclosing domain $\mathrm{\Omega }$ is the open ball of radius 30 centred at the origin. The velocity considered was $\mathbf{g}(x,y)={\overrightarrow{\mathbf{e}}}_1+{\overrightarrow{\mathbf{e}}}_2$ and we obtained the corresponding (noise free) measurement and 10 observation points (see Figure 5 for the reconstruction results). Other location and dimension for the shark was also considered (Figure 6). Moreover, we tested for noisy data and obtained good reconstruction results.

Figure 5. Localization of a shark. On the left, a plot of the obstacle, observation points and detected location (red bold dot). On the right, a plot of the obstacle and the retrieved location, $(-5.1,-14.4)$.

Figure 6. Localization of a smaller shark. The retrieved location was $(0.15,9.33)$.

Figure 7. Reconstruction from partial data. The obtained points are $(3.03,4.07)$ on the right, and $(8.1,2.2)$ on the left.

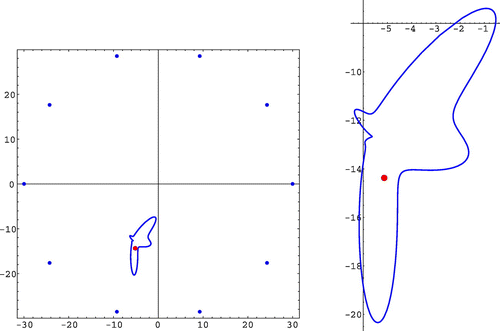
Last simulations are an attempt to recover the centre of the object from partial data. In one case, we took 30 observation points at the first quadrant (left plot of Figure 7). A second situation where the observations’ points were located on the first, second and third quadrants is illustrated by right plot of Figure 7. In both cases, the results were not good and an a priori data completion method is required.

6 Conclusions

In this paper, we proposed a reconstruction method for the location of a single 2D obstacle in a Stokes flow, using the so-called reciprocity gap functional. The method is sufficiently general and can be easily adapted for 3D problems and other type of inverse obstacle problems. It is very fast and the numerical simulations shows that is accurate and stable. The good performance of the method can be exploited in, for instance, inverse geometric problems, where the geometry of the obstacle is also the goal. These problems are usually tackled as an optimization problem for both shape and location (e.g. [5]). However, a more direct approach can be applied when the location of the obstacle is known (e.g. [15]).

As seen in the last couple simulations, it requires data on the whole $\mathrm{\Gamma }$, which can be a drawback.