Seismic data reconstruction via weighted nuclear-norm minimization

Abstract

The low-rank matrix completion theory based on nuclear-norm minimization is becoming increasingly popular in practice, and has been applied to seismic data reconstruction of missing traces. In this paper, we investigate the weighted nuclear-norm minimization model on low-rank seismic texture matrix which is obtained with a designed texture-patch pre-transformation. Unlike the previous nuclear-norm model that treats all singular values of the seismic data matrix equally, the weighted nuclear-norm model, based on the idea of iterative reweighting, makes a closer approximation to the ‘counting rank function’ and can promote the low-rank matrices. We apply weighted spectral soft-thresholding iterative scheme and weighted iterative supported detection method to solve the weighted model. Experimental study on synthetic and real seismic data shows that high-quality reconstruction can be obtained by the weighted low-rank methods.

Keywords:

• seismic data reconstruction
• matrix completion
• missing column
• weighted nuclear-norm minimization

1 Introduction

Seismic data are often irregularly or sparsely sampled along spatial coordinates, which is caused by the presence of surface obstacles, dead or severely contaminated traces, instrument, no permit area and economic constraints. Reconstruction and interpolation of missing data in seismic records is a critical element of the data processing chain, and has become a main issue in seismic research. The reconstruction quality may directly affect the subsequent processing steps such as migration, multiple suppression and amplitude vs. azimuth analysis.

Many different techniques have been proposed to reconstruct missing traces. In the last several years, sparsity-promoting $l_1$-norm minimization methods have been successfully applied to seismic data reconstruction of missing traces. They commonly require the sparse representation of the data in a transformation domain, such as Radon transform,[1] Fourier transform [2, 3] and Curvelet transform.[4, 5]

Besides the sparsity-promoting method, rank-reduction methods have been proposed for the seismic data reconstruction with missing traces. The rank-reduction methods mainly fail in two different categories: Cadzow filtering and nuclear-norm minimization. The Cadzow methods first transfer the data into frequency-space ( f-x) domain, then generate a Hankel matrix from the spatial samples for each frequency, then finally perform a rank-reduced eigen-decomposition of the Hankel matrix. This method guarantees that Hankel matrix is low rank for seismic data with linear events. However, the method pays huge computational cost because one has to repeatedly perform the Hankel matrix for every frequency. The Cadzow method was first used for seismic interpolation by Trickett et al. [6], and then extended to high dimensional [7] and de-aliased reconstruction.[8]

The low-rank matrix completion theory based on nuclear-norm minimization is becoming increasingly popular in practice, and has been applied to seismic data reconstruction with missing traces. Yang et al. [9] discovered the connection between seismic data reconstruction and the general matrix completion problem, and first formulated the seismic data reconstruction as a nuclear-norm minimization problem through building a pre-transformation. Recently, Ma [10] extended the low-rank matrix completion with a designed texture-patch pre-transformation to three-dimensional seismic data reconstruction. The matrix completion problem [11, 12] of finding a lowest rank matrix from a subset of its entries is one important special case for recovering a low-rank matrix in many applications. But the matrix completion model is generally NP-hard due to the combinational nature of the rank function. As known, the nuclear-norm minimization is a convex relaxation for the original problem of rank minimization.[13] Then, the matrix completion problem can be partially justified through a proper nuclear-norm minimization model. Nowadays, many efficient algorithms have been proposed to solve the nuclear-norm minimization, including singular value thresholding algorithm (IST or SVT) [14] using soft-thresholding operations on the singular values of a certain matrix at each iteration, accelerated proximal gradient method [15] based on a fast iterative shrinkage-thresholding algorithm for compressed sensing, the augmented Lagrangian and alternating direction methods [16] and fixed-point continuation with Bregman iteration.[17] All of these algorithms bear the computational cost required by singular value decompositions at each iteration, which is very expensive particularly for large-scale problems. Generally, we can apply the low-rank factorization model (low-rank matrix fitting [LMaFit]) [18] mainly based on the idea of non-linear successive over-relaxation algorithm, which avoids the singular value decomposition at each iteration. This method is usually much faster than the singular value decomposition based methods.[9]

From an algorithmic viewpoint, one central idea of the above mentioned most solution methods is the convex relaxation of the $l_0$-functional (the function giving the number of non-zero elements of a vector) and of the rank function. A weak point of the nuclear-norm minimization algorithms is that it treats all singular values of the sampled matrix equally. Our work is inspired by [19] that extended the principle of iterative weighting of $l_1$-norm into the matrix completion problem. Since the weighted nuclear-norm minimization model, based on the idea of iterative reweighting, makes a closer approximation to the ‘counting rank function’ when the chosen weights are close to the singular values of the matrix. Thus, it promotes lower rank matrices.

In this paper, we also consider two-dimensional seismic data reconstruction with missing traces. We follow Yang et al’s method [9] that uses the texture-patch mapping, but consider the weighted nuclear-norm minimization model to complete the low-rank texture-patch matrix in order to obtain the high-quality reconstruction. However, the weighted nuclear-norm is generally non-convex. We define a new approximate model formulation by adding a ridge term to the weighted nuclear-norm penalization. Algorithmically, we introduce weighted spectral soft-thresholding iterative scheme (WSST) and weighted iterative supported detection method (WISD) to approximate the minimizer of the resulting weighted model. It is compared numerically on seismic data reconstruction to the existing algorithms such as IST [14] and LMaFit.[18]

This paper is organized as follows. In Section 2, we give basic definition on the matrix completion and introduce a brief review on the construction of low-rank texture-patch matrix. Section 3 presents a weighted nuclear-norm minimization model and provides two efficient algorithms to approximate this weighted model. Numerical experiments are carried out to evaluate the performance of our proposed methods for seismic data reconstruction in Section 4. Finally, we draw conclusions in Section 5.

2 Matrix completion and pre-transformation

Matrix completion problem can be understood as a generalization of compressed sensing of vectors, which has been attracting a lot of researchers quite recently, see [11, 12, 20, 21]. The aim is to fill in the missing values of a matrix from sufficient number of known entries with the assumption that it is of low-rank. According to the matrix completion theory, one can recover the randomly missing data by solving the following rank-minimization model:2.1 $$\begin{array}{c}\hfill \underset{X}{min}rank(X),\text{s.t.}{X}_{ij}=M_{ij},\forall (i,j)\in \mathrm{\Omega },\end{array}$$2.1 where $X\in {\mathbb{R}}^{m\times n}$ is the original seismic data that we want to reconstruct, $M\in {\mathbb{R}}^{m\times n}$ is not fully observed/sampled seismic data with missing traces, $rank(X)$ stands for the rank of the matrix $X$ (i.e. the number of non-zero singular values of matrix $X$) and $\mathrm{\Omega }$ denotes an index subset corresponding to the observed entries with cardinality $k$.

We define the masking operator $P_{\mathrm{\Omega }}:{\mathbb{R}}^{m\times n}\to {\mathbb{R}}^{m\times n}$ as follows:$$\begin{array}{c}\hfill {[P_{\mathrm{\Omega }}(X)]}_{ij}=\left\{\begin{array}{cc}{X}_{ij},\hfill & (i,j)\in \mathrm{\Omega }\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$Here, $P_{\mathrm{\Omega }}$ stands for the projection on the observation subspace of matrices with non-zeros restricted to index subset $\mathrm{\Omega }$. Usually noise is unavoidable in the measurements, so the above model (2.12.1 $$\begin{array}{c}\hfill \underset{X}{min}rank(X),\text{s.t.}{X}_{ij}=M_{ij},\forall (i,j)\in \mathrm{\Omega },\end{array}$$2.1 ) is often relaxed to the nuclear-norm regularized unconstraint optimization problem:2.2 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }rank(X)+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$2.2 where $\Vert ·{\Vert }_F^2$ is the Frobenius norm, i.e. the square root of the sum of squares of the elements, $\mathit{\lambda }>0$ is a properly tuned parameter.

However, the above models are unfortunately NP-hard and known to be very hard to solve in practice even for small matrices, which can stem from non-convexity and discontinuity of the rank function. As known, the nuclear-norm (i.e. the $l_1$-norm of the singular values), which we denote by $\Vert ·{\Vert }_{\ast }$, is the convex envelope of the rank function over the unit ball of the operator norm, and is a widely used surrogate of the rank function to induce low-rank solutions for many optimization problems with matrix variables. Then, the above problems can be efficiently solved under suitable assumptions on $P_{\mathrm{\Omega }}$ by considering their convex relaxations:2.3 $$\begin{array}{c}\hfill \underset{X}{min}\Vert X{\Vert }_{\ast },\text{s.t.}{X}_{ij}=M_{ij},\forall (i,j)\in \mathrm{\Omega },\end{array}$$2.3 where $\Vert X{\Vert }_{\ast }={\sum }_{j=1}^{m\wedge n}{\mathit{\sigma }}_j(X)$, ${\mathit{\sigma }}_j(X)$ denotes the $j$th largest singular value of $X$ and ${\mathit{\sigma }}_1(X)\ge \cdots \ge {\mathit{\sigma }}_{m\wedge n}(X)$ are in decreasing order, or2.4 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }{\Vert X\Vert }_{\ast }+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2.\end{array}$$2.4 In the following, the vector of the singular values of the matrix $X$ is denoted by $\mathit{\sigma }(X)=({\mathit{\sigma }}_1(X),\cdots ,{\mathit{\sigma }}_{m\wedge n}(X))$, sorted in non-increasing order. It has been shown by Candes and Retch [11] that the above convex relaxations can exactly recover the original sparse and low-rank matrix under quite general conditions. It will be found that the relationship between the nuclear-norm and the rank function of a matrix is analogical to the relationship between $l_1$-norm and $l_0$-norm of a vector in the area of sparse signal recovery. The solution to the regularized version (2.42.4 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }{\Vert X\Vert }_{\ast }+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2.\end{array}$$2.4 ) is given by the iterative singular value soft-thresholding scheme (IST):2.5 $$\begin{array}{c}\hfill X^{k+1}=S_{\mathit{\lambda }}\left(X^k,-,P_{\mathrm{\Omega }},(X^k),+,P_{\mathrm{\Omega }},(M)\right),\end{array}$$2.5 where $S_{\mathit{\lambda }}$ is the soft-thresholding operator defined for every $B\in {\mathbb{R}}^{m\times n}$ by applying$$S_{\mathit{\lambda }}(t)=\text{sgn}(t)\text{max}(|t|-\mathit{\lambda },0),$$to the singular values of $B=U\mathrm{\Sigma }{V}^T$, i.e.$$S_{\mathit{\lambda }}(B)=U{\mathrm{\Sigma }}_{\mathit{\lambda }}{V}^T,$$with a diagonal matrix ${\mathrm{\Sigma }}_{\mathit{\lambda }}=\text{diag}(\text{max}({\mathit{\sigma }}_1(B)-\mathit{\lambda },0),\cdots ,\text{max}({\mathit{\sigma }}_{m\wedge n}(B)-\mathit{\lambda },0))$.

In the compressed sensing framework, it is known that one necessary condition for successfully applying the sparsity-promoting inversion method to improve the recovery is that the signal or image of interest is sparse or compressible in the transformation domain. Analogously, for the matrix completion framework, since we consider the case where a observed number $k$ of entries is comparably much smaller than the total number $mn$ of entries, the matrix completion problem is in general severely ill-posed. In order to obtain a meaningful result, one needs to impose a sparsity assumption on the original data $X$, which is done by assuming that $X$ is of low rank. If the original data is not of low rank, we should find a pre-transformation to organize the original data such that it leads to a low-rank presentation.

In this paper, we work with the original data using the so-called texture transformation, which is defined as base texture [22] and applied to seismic data recovery in [9]. Below two are the motivations to use the texture transformation. First, the seismic sampling matrix with missing traces results in some ‘zero’ columns, but according to the matrix completion theory, the entries must be sufficiently and uniformly distributed, that is to say, one needs at least one non-zero entry per column to have any hope of achieving successful reconstruction. The texture transformation can reshape the original data with missing traces to a new format with missing pixels, avoiding these ‘zero’ columns. Second, after texture transformation the new matrix has low rank. In the following, we briefly describe the texture transformation by defining a texture-patch matrix. For the given original data $X\in {\mathbb{R}}^{m\times n}$, we first construct its block matrix $H$ consisting of the sub-matrices $B_j\in {\mathbb{R}}^{r\times r}$ as follows.[22]$$\begin{array}{c}\hfill H=\left(\begin{array}{cccc}{B}_1& B_2& \cdots & B_{n/r}\\ B_{n/r+1}& B_{n/r+2}& \cdots & B_{2n/r}\\ ⋮& ⋮& \ddots & ⋮\\ B_{(\frac{m}{n})\frac{n}{r}+1}& B_{(\frac{m}{n})\frac{n}{r}+2}& \cdots & B_{\frac{mn}{r^2}}\end{array}\right).\end{array}$$Next, all columns of $B_j$ are rearranged into one column vector with the length $r^2$, denoted by $w_j$. Then, the texture-patch matrix is defined as follows$$\begin{array}{c}\hfill \tilde{X}:=P_H(X)=[w_1,w_2,\dots ,w_{mn/r^2}]\in {\mathbb{R}}^{r^2\times (mn/r^2)},\end{array}$$where the operator $P_H:{\mathbb{R}}^{m\times n}\to {\mathbb{R}}^{r^2\times (mn/r^2)}$ is called the patch mapping for recognizing a new matrix. The obtained texture-patch matrix $\tilde{X}$ is with lower rank than X itself.[22] We can reconstruct $X$ by recovering $\tilde{X}$ with the proper matrix completion algorithms.

We first reconstruct $\tilde{X}$ with the following matrix completion model:2.6 $$\begin{array}{c}\hfill \underset{\tilde{X}}{min}\mathit{\lambda }\Vert \tilde{X}{\Vert }_{\ast }+\frac{1}{2}\Vert P_H(P_{\mathrm{\Omega }}(X))-P_H(P_{\mathrm{\Omega }}(M)){\Vert }_F^2,\end{array}$$2.6 and then obtain the reconstructed original matrix $X$ by inverse transformation $X=P_H^{-1}(\tilde{X})$.

Denoting by ${\tilde{P}}_{\mathrm{\Omega }}(·)=P_H(P_{\mathrm{\Omega }}(·))$ the reorganized mapping, (2.62.6 $$\begin{array}{c}\hfill \underset{\tilde{X}}{min}\mathit{\lambda }\Vert \tilde{X}{\Vert }_{\ast }+\frac{1}{2}\Vert P_H(P_{\mathrm{\Omega }}(X))-P_H(P_{\mathrm{\Omega }}(M)){\Vert }_F^2,\end{array}$$2.6 ) can be formulated as2.7 $$\begin{array}{c}\hfill \underset{\tilde{X}}{min}\mathit{\lambda }\Vert \tilde{X}{\Vert }_{\ast }+\frac{1}{2}\Vert {\tilde{P}}_{\mathrm{\Omega }}(\tilde{X})-{\tilde{P}}_{\mathrm{\Omega }}(\tilde{M}){\Vert }_F^2.\end{array}$$2.7 For the sake of writing simplicity, in the next section we omit the blow.

3 The weighted model for matrix completion

In this section, we consider the weighted nuclear-norm minimization model: for a given weight vector $\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2,\dots ,{\mathit{\omega }}_{m\wedge n})$ with ${\mathit{\omega }}_1\ge \dots \ge {\mathit{\omega }}_{m\wedge n}>0$,3.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 where $\Vert X{\Vert }_{\ast ,\mathit{\omega }}$ denotes the weighted sum of singular values of $X$, e.g. $\Vert X{\Vert }_{\ast ,\mathit{\omega }}={\sum }_{j=1}^{m\wedge n}\frac{{\mathit{\sigma }}_j(X)}{{\mathit{\omega }}_j}$, here named by the weighted nuclear-norm.

Since the weighting aim is to promote low-rank matrices, the weight vector $\mathit{\omega }$ should be chosen non-increasingly. Assuming that $\widehat{X}$ is a solution of (2.42.4 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }{\Vert X\Vert }_{\ast }+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2.\end{array}$$2.4 ), now we would like to use the idea of reweighting with the weighting estimates for instance$${\mathit{\omega }}_j={\mathit{\sigma }}_j(\widehat{X}),$$and find a solution to the problem (3.13.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 ) for this choice of weights. We note that, when the weight vector $\mathit{\omega }$ is close to $\mathit{\sigma }(X)$, $\Vert X{\Vert }_{\ast ,\mathit{\omega }}$ is close to $rank(X)$. That is to say, this weighting makes a closer approximation to the ‘counting rank function’. So it can promote the low-rank matrices and will allow us to obtain better reconstructed results. Unfortunately, let us stress the fact that, while we call $\Vert ·{\Vert }_{\ast ,\mathit{\omega }}$ the weighted nuclear-norm, it is indeed not a norm since it is typically non-convex in general, leading that (3.13.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 ) cannot be used easily as an objective function. Consequently, (3.13.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 ) is not a convex minimization problem in general, and a minimization algorithm is very likely to admit several locally optimal solutions. Hence there are no efficient methods to solve it. In order to alleviate the problem of local minima and to obtain a meaningful solution, the first idea that may come to mind is to use a convex relaxation of non-convex function $\Vert ·{\Vert }_{\ast ,\mathit{\omega }}$ ( just as convex relaxation of the rank function to the nuclear-norm). Then a ridge term is added to the weighted nuclear-norm penalization, and a new approximate estimator model formulation is defined as follows:3.2 $$\begin{array}{c}\hfill \underset{X}{min}\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2+\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{\mathit{\tau }}{2}\Vert X{\Vert }_F^2,\end{array}$$3.2 for any $\mathit{\tau }\ge 0$. The minimizer of (3.23.2 $$\begin{array}{c}\hfill \underset{X}{min}\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2+\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{\mathit{\tau }}{2}\Vert X{\Vert }_F^2,\end{array}$$3.2 ) exists and is unique this time (more details see Proposition 2 of [19]), since the objective function is now strongly convex.

Proposition 2

[19]   Let $B\in {\mathbb{R}}^{m\times n}$, $\mathit{\lambda },\mathit{\tau }>0$ and $w_1\ge \dots \ge w_{m\wedge n}>0$. Then the minimization problem$$\begin{array}{c}\hfill \underset{A\in {\mathbb{R}}^{m\times n}}{min}\frac{1}{2}\Vert A-B{\Vert }_F^2+\mathit{\lambda }\sum _{j=1}^{m\wedge n}\frac{{\mathit{\sigma }}_j(A)}{w_j}+\frac{\mathit{\tau }}{2}\Vert A{\Vert }_F^2\end{array}$$has a unique solution, given by $\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(B)$, where $S_{\mathit{\lambda }}^{\mathit{\omega }}(B)=U{\mathrm{\Sigma }}_{\mathit{\lambda }}^{\mathit{\omega }}{V}^T$ denotes the weighted soft-shrinkage operator with$${\mathrm{\Sigma }}_{\mathit{\lambda }}^{\mathit{\omega }}=\text{diag}\left(,\text{max},\left({\mathit{\sigma }}_1,(B),-,\frac{\mathit{\lambda }}{{\mathit{\omega }}_j},,,0\right),,,\cdots ,,,,\text{max},\left({\mathit{\sigma }}_{rank(B)},(B),-,\frac{\mathit{\lambda }}{{\mathit{\omega }}_j},,,0\right)\right).$$

Hence the solution of (3.23.2 $$\begin{array}{c}\hfill \underset{X}{min}\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2+\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{\mathit{\tau }}{2}\Vert X{\Vert }_F^2,\end{array}$$3.2 ) can be formulated as the following iteration scheme:3.3 $$\begin{array}{c}\hfill X^{k+1}=\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(X^k-P_{\mathrm{\Omega }}(X^k)+P_{\mathrm{\Omega }}(M)).\end{array}$$3.3 The parameter $\mathit{\tau }>0$ can be arbitrarily small, which ensures the uniqueness and convergence of the iterative scheme (3.33.3 $$\begin{array}{c}\hfill X^{k+1}=\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(X^k-P_{\mathrm{\Omega }}(X^k)+P_{\mathrm{\Omega }}(M)).\end{array}$$3.3 ). It needs emphasizing the fact that the solution by the iterative scheme (3.33.3 $$\begin{array}{c}\hfill X^{k+1}=\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(X^k-P_{\mathrm{\Omega }}(X^k)+P_{\mathrm{\Omega }}(M)).\end{array}$$3.3 ) with $\mathit{\tau }=0$ is not equivalent to the solution of problem (3.13.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 ), since the weighted nuclear-norm $\Vert ·{\Vert }_{\ast ,\mathit{\omega }}$ is not convex.

In the following, two effective algorithms are described to solve this convex relaxation weighted model (3.23.2 $$\begin{array}{c}\hfill \underset{X}{min}\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2+\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{\mathit{\tau }}{2}\Vert X{\Vert }_F^2,\end{array}$$3.2 ) in details to approximate the solution of (3.13.1 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2,\end{array}$$3.1 ), starting from a given initial approximation. One is the WSST proposed by Gaiffas et al. [19]. The algorithm is outlined in Algorithm 1. We first obtain a solution of the nuclear-norm minimization problem (2.42.4 $$\begin{array}{c}\hfill \underset{X}{min}\mathit{\lambda }{\Vert X\Vert }_{\ast }+\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2.\end{array}$$2.4 ), denoted by $\widehat{X}$. Then we update the weights by taking $\mathit{\omega }=\mathit{\sigma }(\widehat{X})$, and we start all over. We use the iteration scheme (3.33.3 $$\begin{array}{c}\hfill X^{k+1}=\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(X^k-P_{\mathrm{\Omega }}(X^k)+P_{\mathrm{\Omega }}(M)).\end{array}$$3.3 ) to find the approximate solution with only repeating the process of updating the weights. Through this process, we are typically going to get the goal of decreasing the final rank of WSST algorithm, while keeping a good reconstruction accuracy.

The other one is the WISD algorithm outlined in Algorithm 2, which is regarded as an iterative weighted algorithm with a non-uniform weighting scheme for dealing with (3.23.2 $$\begin{array}{c}\hfill \underset{X}{min}\frac{1}{2}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(M){\Vert }_F^2+\mathit{\lambda }\Vert X{\Vert }_{\ast ,\mathit{\omega }}+\frac{\mathit{\tau }}{2}\Vert X{\Vert }_F^2,\end{array}$$3.2 ). It can be seen that the difference between WSST and WISD algorithms lies in the use of adaptively changed weights according to ‘the first jump rule’.[23] In fact, at iteration $k+1$, the singular values $\mathit{\sigma }(X^{k+1})$ are sorted in ascending order, and then we compute the difference between each two adjacent elements. The rule looks for the smallest $i$ such that$${\mathit{\sigma }}_{i+1}(X^{k+1})-{\mathit{\sigma }}_i(X^{k+1})>\mathit{\eta },$$with $\mathit{\eta }=\frac{\Vert \mathit{\sigma }(X^{k+1}){\Vert }_{\infty }}{rank(X)}$. This amounts to looking for the first jump larger than $\mathit{\eta }$. We update the thresholding $\mathit{\mu }={\mathit{\sigma }}_i(X^{k+1})$ with ‘the first jump rule’, and then update the detected support $\mathrm{\Lambda }=\{j:{\mathit{\sigma }}_j(X^{k+1})>\mathit{\mu }\}$. Moreover, we choose for the weights the simple relationship $1/\mathit{\mu }$ for the singular values in ${\mathrm{\Lambda }}^C$. This choice guarantees that the weights for those singular values in $\mathrm{\Lambda }$ are smaller than weights for singular values in ${\mathrm{\Lambda }}^C$. The advantage of this choice is that the weights for all singular values are adaptively changed.

Note that in Algorithms 1 and 2 the target value of $\mathit{\lambda }$ is simply taken as ${\mathit{\lambda }}_{\text{target}}=\mathit{\epsilon }{\Vert P(M)\Vert }_{\infty }$, with $\mathit{\epsilon }={10}^{-6}$ or $\mathit{\epsilon }={10}^{-3}$ depending on the problem. We use the iterations (3.33.3 $$\begin{array}{c}\hfill X^{k+1}=\frac{1}{1+\mathit{\tau }}{S}_{\mathit{\lambda }}^w(X^k-P_{\mathrm{\Omega }}(X^k)+P_{\mathrm{\Omega }}(M)).\end{array}$$3.3 ) with relatively smaller $\mathit{\tau }$, i.e. $\mathit{\tau }<{10}^{-6}$, otherwise the problem will drop into local minimum easily. We use a simple stopping rule $\Vert X^{k+1}-X^k{\Vert }_2/{\Vert X^k\Vert }_2\le \text{tol}$ with $\text{tol}={10}^{-5}$ or $\text{tol}={10}^{-3}$ also depending on the scaling of the problem.

4 Numerical results

In this section, we test the above proposed weighted model with WSST and WISD algorithms on one synthetic single-short prestack seismic data and two real poststack seismic data, in comparison with the nuclear-norm minimization model with the singular value soft-thresholding algorithm (IST) [24] and the LMaFit.[18] In this paper, we only consider random irregular missing traces on regular grids. The jittered sampling pattern [5] is used for the location of missing traces. The corrupted version with 50% randomly missing traces for seismic data-set is used. The computational parameters are taken empirically to achieve best results in all our tests.

We define the signal-to-noise ratio (SNR):$$\begin{array}{c}\hfill \text{SNR}=10·\text{log}(\frac{\Vert X{\Vert }_F^2}{\Vert X-X^{\ast }{\Vert }_F^2})\end{array}$$to estimate the reconstruction quality, where $X$ and $X^{\ast }$ denote the original data and its reconstruction, respectively. As another performance measure we also compare the reconstruction of one single trace, i.e. one column of the data matrix. Therefore, in the next we will present the single trace of the original data that is missed in observed data (in red dashed line) and the same trace of reconstruction by IST, LMaFit, WSST and WISD (in blue solid line).

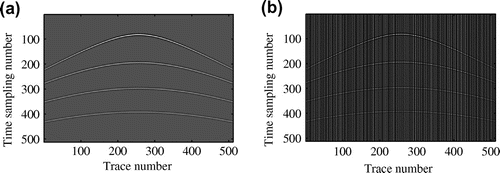
One synthetic single-short prestack seismic data with the size of $512\times 512$, denoted by $X_1$ and shown in Figure 1(a), is firstly tested to show the performance of our approach. The corrupted data with 50% randomly missing traces for $X_1$ is shown in Figure 1(b). And white Gaussian noise is considered to be added to the sampling data. Let $\mathit{\delta }$ denote the noise level. For $X_1$, we take $q=0.02$ for both WSST and WISD algorithms. Since the visual difference in the reconstructed images is not obvious, we omit presenting the reconstructed images. In the left-half part of Figure 2, we show the comparison of the 100th trace taken from the original data and the reconstructions for the noise-free case ($\mathit{\delta }=0$) by different algorithms. (a)–(d) are obtained via IST, LMaFit, WSST and WISD, respectively. To further illustrate the reconstructed results more clearly, the right-half part in each subfigure presents the corresponding single trace error, i.e. the difference between the 100th trace of the original data and the same trace of reconstruction. It is clear from the right-half part of Figure 2 that the improvement by the weighted low-rank methods (i.e. WSST and WISD) can be seen obviously.

Figure 1. (a) Original seismic data $X_1$. (b) Corrupted data with 50% missing traces.

Figure 2. Reconstructions for $X_1$ under $\mathit{\delta }=0$. (a)–(d): Reconstructed 100th single traces via IST, LMaFit, WSST and WISD, respectively. Left-half part is the 100th trace comparison, while the right-half part is the corresponding reconstruction error comparison.

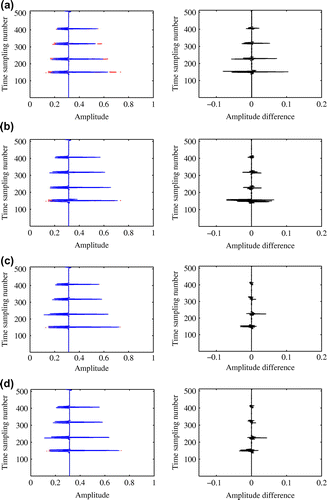
Table 1. The SNR and CPU times of reconstructions for $X_1$ by four different algorithms with three different noise levels.

Noise	SNR and CPU times for $X_1$
level	IST(CPU)	LMaFit(CPU)	WSST(CPU)	WISD(CPU)
$\mathit{\delta }=0$	14.4704(33.78s)	15.7683(4.08s)	17.2115(9.55s)	17.1280(2.44s)
$\mathit{\delta }=0.01$	13.5495(27.51s)	14.0634(2.82s)	15.4221(1.92s)	15.4270(1.39s)
$\mathit{\delta }=0.03$	11.3439(22.85s)	11.0226(2.82s)	12.3375(1.05s)	12.3395(0.67s)

Table 2. The SNR and CPU times of reconstructions for $X_2$ by four different algorithms with three different sampling ratios.

Sampling	SNR and CPU times for $X_2$
ratio (%)	IST(CPU)	LMaFit(CPU)	WSST(CPU)	WISD(CPU)
25	11.3900(251.4s)	15.5493(0.83s)	16.5086(15.32s)	16.5438(13.12s)
35	15.2804(77.28s)	15.5753(1.97s)	17.7437(24.34s)	17.7888(12.18s)
50	17.4351(34.73s)	17.6134(0.34s)	18.9050(11.14s)	18.9372(8.88s)

Table 3. The SNR and CPU times of reconstructions for $X_3$ by four different algorithms with three different sampling ratios.

Sampling	SNR and CPU times for $X_3$
ratio (%)	IST(CPU)	LMaFit(CPU)	WSST(CPU)	WISD(CPU)
25	9.8132(95.69s)	11.0437(1.02s)	11.9217(47.28s)	11.9793(18.00s)
35	11.5813(59.10s)	12.0613(1.09s)	13.1103(47.58s)	13.2361(17.35s)
50	13.7402(34.71s)	14.7511(1.19s)	16.7312(20.34s)	16.7332(18.64s)

Figure 3. The SNR change of reconstructions by four different algorithms for $X_1$ as the sampling ratio increases from 20 to 90%.

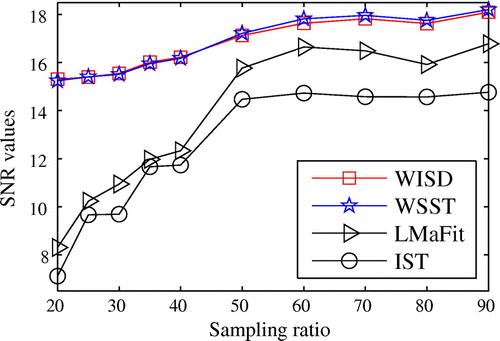
Figure 4. Left column: original data $X_2$ (a) and $X_3$ (c). Right column: (b) and (d) are the corresponding corrupted data with 50% traces missing for $X_2$ and $X_3$, respectively.

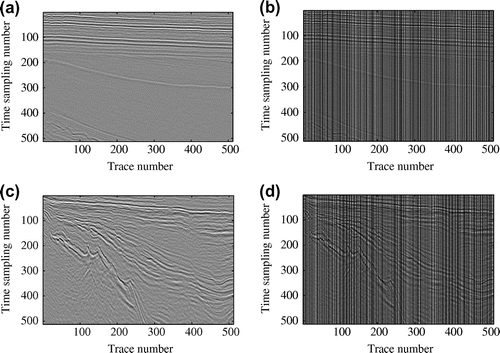
Figure 5. Reconstructions for $X_2$. (a)–(d): Reconstructed eighth single traces via IST, LMaFit, WSST and WISD, respectively. Left-half part is the eighth trace comparison, while the right-half part is the corresponding reconstruction error comparison.

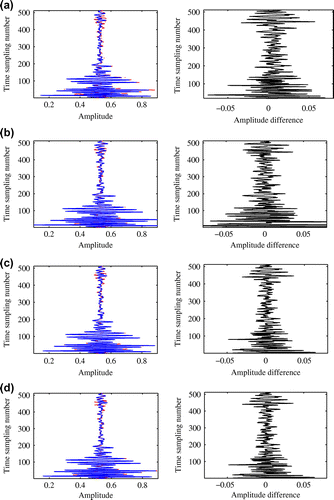
Figure 6. Reconstructions for $X_3$. (a)–(d): Reconstructed central single traces via IST, LMaFit, WSST and WISD, respectively. Left-half part is the central trace comparison, while the right-half part is the corresponding reconstruction error comparison.

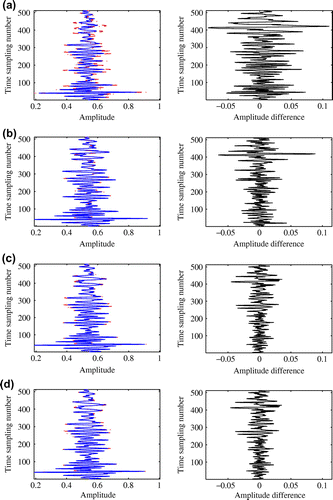
Figure 7. The SNR change of reconstructions by four different algorithms ((a) for $X_2$ and (b) for $X_3$) as the sampling ratio increases from 20 to 90%.

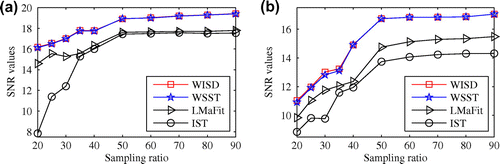
Table 1 reports the SNR values and CPU times of reconstructions by four different algorithms under three noise levels (i.e. $\mathit{\delta }=0$, $\mathit{\delta }=0.01$ and $\mathit{\delta }=0.03$). It can be found that the high-quality reconstruction can be achieved by the weighted low-rank methods, particularly in terms of higher SNR values, but paying the cost of computational time. And as an adaptively chosen weights, WISD is faster than WSST and offers more competitive reconstructions. Moreover, we can also see that the SNR decreases significantly for the higher noise level, in comparison with the noise-free case ($\mathit{\delta }=0$). Figure 3 displays the SNR change of reconstructions by four different algorithms under the noise level $\mathit{\delta }=0$ as the sampling ratio increases from 20 to 90%. The increasing sampling measurement indeed leads to improved performance. It is also obvious that the SNR values of reconstructions produced by the proposed weighted low-rank model are higher than those with the standard nuclear-norm minimization model.

In the next experiment, we test our proposed method on two real poststack seismic data. The first data referred to $X_2$ is a rather simple data with the size of $512\times 512$, shown in Figure 4(a). The second one referred to $X_3$ is a more complex data with the size of $512\times 512$, shown in Figure 4(c). The corrupted version with 50% randomly missing traces for data-set $X_2$ and $X_3$ are shown in Figure 4(b) and (d), respectively. For $X_2$, we take in all our computations $q=0.01$ with both WSST and WISD algorithms, while using $q=0.02$ for $X_3$. The reconstructed results by IST, LMaFit, WSST and WISD are depicted in Figures 5 and 6, respectively. It can be seen clearly from the right-half part of Figures 5 and 6 that the reconstructions by the weighted low-rank method have smaller single trace errors, which illustrates the good performance of the weighted low-rank methods.

In addition, we report the SNR values and CPU times of reconstructions from $X_2$ and $X_3$ with three different sampling ratios, which are summarized in Tables 2 and 3, respectively. The results also indicate that the weighted low-rank model indeed improves the SNR values of reconstructions but paying the cost of computational time. However, we find that the SNR values of the reconstructions for $X_3$ become worse than that for $X_2$ due to more complex structures.

Finally, Figure 7 displays the SNR change of reconstructions by four different algorithms for $X_2$ and $X_3$ as the sampling ratio increases from 20 to 90%. In (a), we plot the SNR change for $X_2$. In (b), we plot the SNR change for $X_3$.

5 Conclusion

In this paper, we study the reconstruction of the seismic data with randomly missing traces. We have presented a weighted nuclear-norm minimization model based on one texture-patch pre-transformation to improve the reconstruction. Due to its non-convexity, we define a new approximate estimator model formulation by adding a ridge term to the weighted nuclear-norm penalization. Algorithmically, we introduce two efficient algorithms (WSST and WISD) to approximate the minimizer of this weighted model. The performance of these two algorithms are first tested on a synthetic prestack seismic data for the noisy and corrupted case. In addition, we also test our proposed method to reconstruct two real post-stack seismic data. Results show that the proposed method works efficiently and performs better in comparison to a traditional algorithm and a state-of-the-art low-rank factorization algorithm. How to extend the weighted matrix completion methods for aliasing data with regularly missing traces is the next work.

Notes

This work is supported by NSFC [grant number 91330108], [grant number 41374121], [grant number 61327013], [grant number 91230119]; the Fundamental Research Funds for the Central Universities [grant number HIT.BRETIV.201314] and the Program for New Century Excellent Talents in University [grant number NCET-11-0804].