Optimal design of simultaneous source encoding

Abstract

A broad range of parameter estimation problems involve the collection of an excessively large number of observations N. Typically, each such observation involves excitation of the domain through injection of energy at some predefined sites and recording of the response of the domain at another set of locations. It has been observed that similar results can often be obtained by considering a far smaller number K of multiple linear superpositions of experiments with $K\ll N$. This allows the construction of the solution to the inverse problem in time $\mathcal{O}(K)$ instead of $\mathcal{O}(N)$. Given these considerations it should not be necessary to perform all the N experiments but only a much smaller number of K experiments with simultaneous sources in superpositions with certain weights. Devising such procedure would results in a drastic reduction in acquisition time. The question we attempt to rigorously investigate in this work is: what are the optimal weights? We formulate the problem as an optimal experimental design problem and show that by leveraging techniques from this field an answer is readily available. Designing optimal experiments requires some statistical framework and therefore the statistical framework that one chooses to work with plays a major role in the selection of the weights.

Keywords:

• helmhotlz
• seismic
• large scale
• design
• numeric

1 Introduction

We consider discrete parameter estimation problems with data vectors $d_j$ modelled as1 $$\begin{array}{c}\hfill d_j=A_{j}m+{\mathit{ϵ}}_j(j=1,\dots ,N),\end{array}$$1 where $A_j$ is an $s\times n$ linear observation matrix that corresponds, for example, to the $j$th configuration of an experiment, $m\in {\mathrm{I}\mathrm{R}}^n$ is the parameter vector to be recovered and ${\mathit{ϵ}}_j$ are zero-mean independent random vectors with covariance matrix ${\mathit{\sigma }}^{2}I$. In addition, we assume that there is a large set of observation matrices $A_j$, which is the case of interest in many geophysical and medical applications such as seismic and electromagnetic (EM) exploration, diffraction and electrical impedance tomography.[1–3]

The linear systems in (11 $$\begin{array}{c}\hfill d_j=A_{j}m+{\mathit{ϵ}}_j(j=1,\dots ,N),\end{array}$$1 ) can be aggregated into a single large system by defining2 $$\begin{array}{c}\hfill \widehat{A}\equiv \left(\begin{array}{c}{A}_1\\ ⋮\\ A_N\end{array}\right)\mathrm{and}\widehat{d}\equiv \left(\begin{array}{c}{d}_1\\ ⋮\\ d_N\end{array}\right).\end{array}$$2 In the well-posed case where ${\widehat{A}}^{}\top \widehat{A}$ has a stable inverse, the least-squares (maximum likelihood if ${\mathit{ϵ}}_j$ are Gaussian) estimate $\widehat{m}$ of $m$ is3 $$\begin{array}{c}\hfill \widehat{m}={({\widehat{A}}^{\top }\widehat{A})}^{-1}{\widehat{A}}^{\top }\widehat{d}.\end{array}$$3 When ${\widehat{A}}^{}\top \widehat{A}$ does not have a stable inverse, a penalized least-squares estimate of the form4 $$\begin{array}{c}\hfill \widehat{m}={({\widehat{A}}^{\top }\widehat{A}+{\mathit{\lambda }}^{2}M)}^{-1}{\widehat{A}}^{\top }\widehat{d},\end{array}$$4 is often used. Here $M$ is usually a symmetric positive semi-definite matrix and $\mathit{\lambda }$ is a positive regularization parameter. This choice will simplify analysis later on, although the proposed approach can be generalized for use of other regularizers of other functional forms.

We are particularly interested in large-scale problems where both the number of model parameters $n$ and the number of observations $N$ are large. For instance, in an electromagnetic or a seismic survey, the number of a such observations, $N$, can be of the order of ${10}^4$ or ${10}^5$. For such problems, solution of the system (44 $$\begin{array}{c}\hfill \widehat{m}={({\widehat{A}}^{\top }\widehat{A}+{\mathit{\lambda }}^{2}M)}^{-1}{\widehat{A}}^{\top }\widehat{d},\end{array}$$4 ) using direct methods is intractable computationally and instead iterative methods (typically, CGLS or LSQR [4]) are employed. The main computational bottleneck associated with such solvers is the computation of matrix vector products: When $N$ is very large, the computation of $\widehat{A}$ times a vector can be prohibitively intensive by itself. We thus need to devise some data reduction methodology to make computations feasible.

For example, return to the well-posed case and assume the matrices $A_j$ come from a parameter estimation problem where the observed phenomena can be described by a set of differential equations that are linear w.r.t. the source term. Such operators can be written as$$A_j=S{L}^{-1}{Q}_j,$$where $S$ and $Q_j$ are sparse selection matrices related to the sensors and the sources, respectively, but $L$ is a discretization of a partial differential equation on a mesh. Such problems arise in seismic and electromagnetic exploration as well as in impedance and diffraction tomography.[1–3] The least-squares estimate of the model $m$ is5 $$\begin{array}{c}\hfill \widehat{m}={\left(\sum _j{Q}_j^{}\top L^{-\top }{S}^{}\top S{L}^{-1}{Q}_j\right)}^{-1}\sum _j{Q}_j^{}\top L^{-\top }{S}^{}\top d_j,\end{array}$$5 which requires multiple applications of $L^{-1}$, thus, making the procedure computationally expensive. Alternatively, a far less-expensive procedure relies upon a recently developed data reduction technique based on the idea of ‘simultaneous sources’.[5–9] Here the estimate is based on a weighted combination of the form $d(w)=\sum w_j{d}_j$. The basic idea is to exploit the savings achieved by simultaneously collecting the data.

For example, if each experiment corresponds to a different source in seismic or electromagnetic exploration, it can be rather expensive both in terms of time and cost to record many different experiments. If, on the other hand, it is possible to ‘shoot’ simultaneously with all the sources, then the recording time can be significantly shortened as a collection of simultaneous sources enables direct measurement of linear combinations of the data. That is, for a fixed $w$ one conducts an experiment that measures $d(w)$ directly. This acquisition strategy is of course far more efficient than the conventional process in which each data vector is measured independently while later on combining them with the weights $w$.

The linear system corresponding to $d(w)$ is6 $$\begin{array}{c}\hfill d(w)=A(w)m+\mathit{ϵ}(w),\end{array}$$6 where $A(w)=\sum w_j{A}_j$ and $\mathit{ϵ}(w)=\sum w_j{\mathit{ϵ}}_j$. We assume the individual source noise levels ${\mathit{ϵ}}_j$ are known. The estimates (33 $$\begin{array}{c}\hfill \widehat{m}={({\widehat{A}}^{\top }\widehat{A})}^{-1}{\widehat{A}}^{\top }\widehat{d}.\end{array}$$3 ) and (44 $$\begin{array}{c}\hfill \widehat{m}={({\widehat{A}}^{\top }\widehat{A}+{\mathit{\lambda }}^{2}M)}^{-1}{\widehat{A}}^{\top }\widehat{d},\end{array}$$4 ) corresponding to $d(w)$ are7 $$\begin{array}{c}\hfill \widehat{m}{(w)=(A(w)}^{\top }A(w)/{\Vert w\Vert }^2{)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$7 if $A{(w)}^{}\top A(w)$ has a stable inverse, and8 $$\begin{array}{c}\hfill \widehat{m}(w)={\left(A{(w)}^{\top }A(w)/{\Vert w\Vert }^2+{\mathit{\lambda }}^{2}M\right)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$8 otherwise. Clearly, both solutions depend on $w$ only through its unit-norm normalization $w/\Vert w\Vert$.

For example, let us return to the well-posed parameter estimation example with $A_j=S{L}^{-1}{Q}_j$. The penalized least-squares estimate (88 $$\begin{array}{c}\hfill \widehat{m}(w)={\left(A{(w)}^{\top }A(w)/{\Vert w\Vert }^2+{\mathit{\lambda }}^{2}M\right)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$8 ) is$$\begin{array}{cc}\hfill \widehat{m}& ={\left[\left(\sum _j{w}_j{Q}_j^{}\top \right)L^{-\top }{S}^{}\top S{L}^{-\top }\left(\sum _k{w}_k{Q}_j\right)\right]}^{-1}\hfill \\ \hfill & \times \left(\sum _i{w}_i{Q}_i^{}\top \right)L^{-\top }{S}^{}\top \left(\sum _m{w}_m{d}_m\right),\hfill \end{array}$$which requires much fewer applications of $L^{-1}$ than (55 $$\begin{array}{c}\hfill \widehat{m}={\left(\sum _j{Q}_j^{}\top L^{-\top }{S}^{}\top S{L}^{-1}{Q}_j\right)}^{-1}\sum _j{Q}_j^{}\top L^{-\top }{S}^{}\top d_j,\end{array}$$5 ). Of course, some information may be lost as $(d_1,\dots ,d_N)$ is not, in general, a sufficient statistic for $m$. We return to this point in Section 2.2 but it should be clear that some information might be sacrificed for the sake of computational or data collection savings.

Although the advantages of using simultaneous sources have been previously explored, the question of selecting appropriate weights $w$ has not received sufficient attention. We are aware of two main conducts that have been utilized so far. In [10], the weights $w_j$ are independent zero-mean random variables of variance one and are used to define the Hutchinson randomized trace estimator.[11] More precisely, let $R$ be the residual matrix defined as$$R=\left(\begin{array}{ccc}{A}_{1}m-d_1& \cdots & A_{N}m-d_N\end{array}\right).$$Then,$$\begin{array}{cc}\hfill {\mathsf{E}\Vert A(w)m-d(w)\Vert }^2& =\mathsf{E}(w^{}\top R^{}\top Rw)=\mathsf{trace}(R^{}\top R)\hfill \\ \hfill & =\sum _j\Vert A_{j}m-d_j{\Vert }^2={\Vert R\Vert }_F^2,\hfill \end{array}$$where ${\Vert ·\Vert }_F$ denotes the Frobenius norm. If $w^{(1)},\dots ,w^{(b)}$ are independent random weight vectors, then by the law of large numbers$$\frac{1}{b}\sum _{k=1}^b\Vert A(w^{(k)})m-d(w^{(k)}){\Vert }^2\to {\Vert R\Vert }_F,$$as $b\to \infty$. Therefore, the finite sum on the left-hand side can be used to approximate ${\Vert R\Vert }_F$. It is easy to see that the uniform distribution on $\{-1,1\}$ minimizes the variance of the trace estimator (see e.g. [12]). Methods to select appropriate values of $b$ are discussed in [12].

In [13] the Frobenius norm of the residual matrix is replaced by the squared 2-norm and $w$ is then chosen so that$${\Vert A(w)m-d(w)\Vert }^2\approx {\Vert R\Vert }_2^2.$$The paper is structured as follows. In Section 2, we derive the mathematical framework. In Section 3, we discuss efficient numerical techniques for the solution of the weight design problem. In Section 4, we demonstrate the effectiveness of our approach by performing numerical experiments and finally, in Section 5 we summarize the study.

2 Optimal selection of weights

In this section, we consider statistical properties of the estimate $\widehat{m}$ to select optimal weights $w$. We also discuss methods to compensate for the information loss and to compare the loss achieved with different choices of weights $w$.

We begin our discussion with the well-posed problem and its solution (77 $$\begin{array}{c}\hfill \widehat{m}{(w)=(A(w)}^{\top }A(w)/{\Vert w\Vert }^2{)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$7 ). As can be observed, $\widehat{m}$ depends only on $w/\Vert w\Vert$; we may therefore assume that $\Vert w\Vert =1$. Since $\widehat{m}$ is an unbiased estimator and $\mathsf{Var}(\mathit{ϵ}(w))={\mathit{\sigma }}^{2}I$, it follows that its mean square error ($\mathsf{MSE}$) is$$\begin{array}{c}\hfill \mathsf{MSE}(\widehat{m})=\mathsf{E}{\Vert \widehat{m}(w)-m\Vert }^2={\mathit{\sigma }}^2\mathsf{trace}({(A{(w)}^{\top }A(w))}^{-1}).\end{array}$$To find an optimal $w$, in the sense of minimizing the $\mathsf{MSE}$, we need to solve the constrained optimization problem9 $$\begin{array}{cc}\hfill \underset{w}{min}& \mathsf{trace}({(A{(w)}^{\top }A(w))}^{-1})\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$9 Before discussing properties of the solutions, we consider the ill-posed problem.

2.1 The ill-posed case

Other than recent numerous exceptions (see [14–19] and references therein), optimal experimental design of ill-posed problems has been somewhat an under-researched topic. In the case of ill-posed problems, the selection of optimal weights for (88 $$\begin{array}{c}\hfill \widehat{m}(w)={\left(A{(w)}^{\top }A(w)/{\Vert w\Vert }^2+{\mathit{\lambda }}^{2}M\right)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$8 ) is more difficult because this estimate is biased and its bias depends on the unknown $m$: $\mathsf{bias}(\widehat{m})=-{\mathit{\lambda }}^{2}C{(w)}^{-1}Mm$, where the inverse Fisher matrix is given by$$C(w)=A{(w)}^{\top }A(w)+{\mathit{\lambda }}^{2}M$$(again, we may assume $\Vert w\Vert =1$). The $\mathsf{MSE}$ of $\widehat{m}$ is then10 $$\begin{array}{cc}\hfill \mathsf{MSE}(\widehat{m})& =\mathsf{E}\Vert \widehat{m}{-m\Vert }^2={\Vert \mathsf{bias}(\widehat{m})\Vert }^2+\mathsf{trace}(\mathsf{Var}(\widehat{m}))\hfill \\ \hfill & ={\mathit{\lambda }}^4{\Vert C{(w)}^{-1}Mm\Vert }^2+{\mathit{\sigma }}^2\mathsf{trace}(A(w)C{(w)}^{-2}A{(w)}^{\top }).\hfill \end{array}$$10 As in the well-posed case, the goal would be to find weights $w$ that minimize this $\mathsf{MSE}$ subject to the constraint $\Vert w\Vert =1$ but this is not possible because $m$ is unknown. We need information on $m$ to control the $\mathsf{MSE}$.

If $m$ is known to be in a convex set $S$, then we could consider a minmax approach where we minimize the worst $\mathsf{MSE}(\widehat{m})$ for $m\in S$. A less pessimistic approach is to minimize an average $\mathsf{MSE}(\widehat{m})$ over $S$. Of course, other choices are possible and may be useful as long as their interpretation can be rationalized. In this note, we minimize a weighted average of the $\mathsf{MSE}$. We model $m$ as random and since $\widehat{m}$ only depends linearly on $m$, it is enough to use prior second-order moment conditions. For example, if $\mathsf{E}(m)=0$ and $\mathsf{Var}(m)={\mathrm{\Sigma }}_m$, then the Bayes risk $R_{\mathrm{FB}}(w)$ under squared error loss of the frequentist estimate $\widehat{m}$ defined by the fixed $w$ is$$\begin{array}{cc}\hfill R_{\mathrm{FB}}(w)& =\mathsf{E}(\mathsf{MSE}(\widehat{m}))\hfill \\ \hfill & ={\mathit{\lambda }}^4\mathsf{trace}(C{(w)}^{-1}M{\mathrm{\Sigma }}_{m}MC{(w)}^{-1})+{\mathit{\sigma }}^2\mathsf{trace}(A(w)C{(w)}^{-2}A{(w)}^{}\top ),\hfill \end{array}$$and we solve the optimization problem11 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{FB}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$11 Finally, assume the distributions are Gaussian. That is, the conditional distribution of $d(w)$ given $m$ is $\mathcal{N}(A(w)m,{\mathit{\sigma }}^{2}I)$ and the prior distribution of $m$ is $\mathcal{N}(0,{\mathit{\tau }}^2{M}^{-1})$, with ${\mathit{\tau }}^2={\mathit{\sigma }}^2/{\mathit{\lambda }}^2$. In this case, (88 $$\begin{array}{c}\hfill \widehat{m}(w)={\left(A{(w)}^{\top }A(w)/{\Vert w\Vert }^2+{\mathit{\lambda }}^{2}M\right)}^{-1}A{(w)}^{\top }d(w)/{\Vert w\Vert }^2\end{array}$$8 ) is the posterior mean (and a maximum a posteriori or MAP estimator) and the posterior covariance matrix is $\mathsf{Var}(m\mid d(w))={\mathit{\sigma }}^{2}C{(w)}^{-1}$. For each fixed $w$ the Bayes risk of $\widehat{m}$ is therefore$$R_{\mathrm{B}}(w)={\mathit{\sigma }}^2\mathsf{trace}(C{(w)}^{-1}).$$The corresponding optimization problem is12 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12

Remark

So far we have only considered linear/affine reconstructions of the model, which of course do not include many recovering techniques based, for example, on total variation or sparsity control. However, if the reason for choosing one of these nonlinear procedures is the belief that its optimal Bayes risk is smaller than that of the linear reconstruction, then the optimal Bayes risk of the latter provides an upper bound for the optimal Bayes risk of the nonlinear procedure. Furthermore, if the upper bound is not too conservative then minimizing the Bayesian risk for an affine estimator can be a useful guide for other reconstruction techniques.

2.2 Compensating for the information loss

As we have explained, some information may be lost with the reduction to $d(w)$. If the loss is unacceptable, we may compensate by using more than a single reduction as follows. Let $k$ be the number of independent data reductions and $w^{(\ell )}={(w_1^{(\ell )},\dots ,w_N^{(\ell )})}^{}\top$. Define$$d_j^{(\ell )}=A_{j}m+{\mathit{ϵ}}_j^{(\ell )}(j=1,\dots ,N,\ell =1,\dots ,k),$$where the sequence ${\{{\mathit{ϵ}}_j^{(\ell )}\}}_{j,\ell }$ is assumed to be i.i.d. $\mathcal{N}(0,{\mathit{\sigma }}^2)$. The ${\ell }^{th}$ data reduction is $d(w^{(\ell )})={\sum }_j{w}_j^{(\ell )}{d}_j^{(\ell )}$. We solve for $m$ using the vector of $k$ reductions $d(W_k)$ and matrix $A(W_k)$ defined as$$d(W_k)=\left(\begin{array}{c}d(w^{(1)})\\ ⋮\\ d(w^{(k)})\end{array}\right)\text{and}A(W_k)=\left(\begin{array}{c}A(w^{(1)})\\ ⋮\\ A(w^{(k)})\end{array}\right).$$The associated Bayes risk is $R_{\mathrm{B}}(W_k)={\mathit{\sigma }}^2\mathsf{trace}(C{(W_k)}^{-1})$ with $C(W_k)=A{(W_k)}^{\top }A(W_k)+{\mathit{\lambda }}^{2}M$. The optimization problem is13 $$\begin{array}{cc}\hfill \underset{W_k}{min}& R_{\mathrm{B}}(W_k)\hfill \\ \hfill \text{s.t.}& \Vert w^{(1)}\Vert =1,\dots ,\Vert w^{(k)}\Vert =1.\hfill \end{array}$$13 There are some particular cases that may make this optimization easier and provide upper bounds for the optimal solution of (1313 $$\begin{array}{cc}\hfill \underset{W_k}{min}& R_{\mathrm{B}}(W_k)\hfill \\ \hfill \text{s.t.}& \Vert w^{(1)}\Vert =1,\dots ,\Vert w^{(k)}\Vert =1.\hfill \end{array}$$13 ). These bounds can be useful when we study the loss as a function of $k$. One particular case consists of using prior information about the experiments to classify the matrices $A_j$ into $k$ groups whose members are similar on a realistic set of models $m$. For example $d(w^{(1)})$ may include only $A_1$ and $A_2$ while $d(w^{(2)})$ uses only $A_3$, $A_4$ and $A_5$, etc. A second simplification consists of assuming $w^{(1)}=\dots =w^{(k)}$ so that there is only one constraint but $k$ independent experiments. The final and simplest approach is to find the optimal $w^{\ast }$ in (1212 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12 ) and then repeat the experiment $k$ times. This leads to the risk14 $$\begin{array}{c}\hfill R_{\mathrm{B}}(w^{\ast },k)={\mathit{\sigma }}^2\mathsf{trace}[{(kA{(w^{\ast })}^{\top }A(w^{\ast })+{\mathit{\lambda }}^{2}M)}^{-1}].\end{array}$$14

2.3 Quantifying the information loss

Although in general the optimization problem does not have a unique minimum, a local minimum may still provide a sufficient reduction of the risk achieved with the reduced data $d(w)$. This does not mean, however, that the data reduction is useful for much information may be lost. It is therefore important to assess whether the computational savings obtained through the data reduction justifies the information loss.

Figure 1. The loss as a function of the number of vectors.

To assess the information loss of the data reduction, we compare its associated risk to that of the complete data. The Bayes risk of the complete (i.e. exhaustive acquisition) problem is$$R_0=\mathsf{trace}\left({({\widehat{A}}^{\top }\widehat{A}+{\mathit{\lambda }}^{2}M)}^{-1}\right),$$while the risk associated with the reduced data $d(w)$ is15 $$\begin{array}{c}\hfill R_{\mathrm{B}}(w)=\mathsf{trace}\left({(A{(w)}^{\top }A(w)+{\mathit{\lambda }}^{2}M)}^{-1}\right).\end{array}$$15 We quantify the information loss using the risk ratio16 $$\begin{array}{c}\hfill \mathsf{Loss}(w)=\frac{R_{\mathrm{B}}(w)}{R_0}.\end{array}$$16 This loss indicates the degradation of the average recovery when using the reduction $d(w)$ instead of the full data. If the loss is much greater than $1$ then using a single set of weights may lead to significant deterioration in the recovery. In this case one may want to use a number of weights as explained in Section 2.2. The loss is then$$\mathsf{Loss}(W_k)=\frac{R_{\mathrm{B}}(W_k)}{R_0}.$$To determine an appropriate value of $k$, we may plot the loss as a function of $k$. The idea is to balance the trade-off between the cost of the experiment and the information loss. The following example illustrates this point.

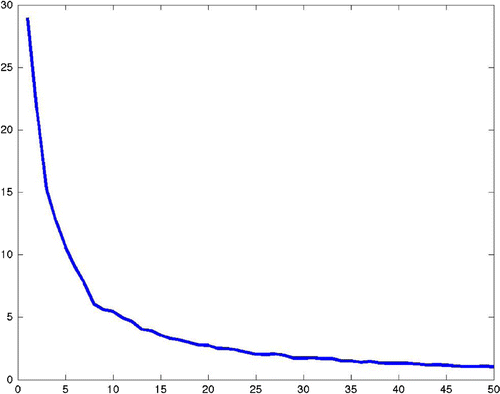
Example 1

We generate $N=50$ random matrices $A_j$ of sizes $100\times 200$ and use $k$ random unit vectors (not optimal) $w^{(1)},\dots ,w^{(k)}$. Figure 1 shows a plot of $R_{\mathrm{B}}(W_k)$ as a function of $k$. The curve has a classical L-shape and provides an upper bound for the optimal risks $R_{\mathrm{B}}(W_k^{\ast })$. The figure shows that using less than $10$ experiments will result in significant loss of information but using more than $30$ may be a waste of resources. Thus, the loss curve is important if we would like to design an effective and yet efficient experiment.

2.4 Numerical properties of the design function

We now study properties of the weights selected in the fully Bayesian framework; that is, solutions of (1212 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12 ). First, note that neither the constraint $\Vert w\Vert =1$ nor the objective functions $R_{\mathrm{B}}(w)$ and $R_{\mathrm{B}}(W_k)$ are convex and consequently there is no guarantee of a unique solution. In fact, if $w_{\ast }$ is a solution of (1212 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12 ), then so is ${\tilde{w}}_{\ast }=-w_{\ast }$. And any permutation of an optimal sequence $w_{\ast }^{(1)},\dots ,w_{\ast }^{(k)}$ is a solution of (1313 $$\begin{array}{cc}\hfill \underset{W_k}{min}& R_{\mathrm{B}}(W_k)\hfill \\ \hfill \text{s.t.}& \Vert w^{(1)}\Vert =1,\dots ,\Vert w^{(k)}\Vert =1.\hfill \end{array}$$13 ).

Example 2

Consider the following simple $2\times 2$ well-posed case:$$A_1=\left(\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right),A_2=\left(\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & -1\hfill \end{array}\right).$$It is easy to see that for $\Vert w\Vert =1$,$$\mathsf{trace}({(A{(w)}^{\top }A(w))}^{-1})=\frac{2}{1-4w_1^2{w}_2^2}=\frac{1}{2{(w_1^2-1/2)}^2},$$and the optimal solutions of (99 $$\begin{array}{cc}\hfill \underset{w}{min}& \mathsf{trace}({(A{(w)}^{\top }A(w))}^{-1})\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$9 ) are $w^{\ast }=\pm (1,0)$. That is, the optimal solution does not use the information provided by $d_2$. To see how much information is lost, we compare the risk of the full least-squares solution and the one based on $d(w^{\ast })$. The two optimal weights lead to the same estimate $\widehat{m}(w^{\ast })=d_1$ with $\mathsf{MSE}(w^{\ast })={\mathit{\sigma }}^2\mathsf{trace}(I)=2{\mathit{\sigma }}^2$. For the full least-squares solution, we have ${\widehat{A}}^{}\top \widehat{A}=2I$ and thus$${\widehat{m}}_{\mathrm{ls}}=\frac{1}{2}\left(\begin{array}{c}{d}_{1,1}+d_{2,1}\hfill \\ d_{1,2}-d_{2,2}\hfill \end{array}\right),$$with $\mathsf{MSE}(w_{\mathrm{ls}}^{\ast })={\mathit{\sigma }}^2$. Hence, in this case the information lost by the reduction to $d(w^{\ast })$ leads to a $\mathsf{MSE}$ that is twice as large as that of the full least-squares estimate. To compensate, we may conduct a single replication with the optimal $w^{\ast }$ to match the $\mathsf{MSE}$ obtained without the data reduction.

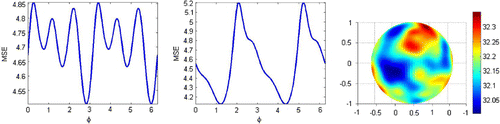
Example 3

Next, we consider the problem (1212 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12 ) for a the case $N=2$ and $N=3$. The matrices $A_i$ are random $7\times 10$ matrices with i.i.d. $N(0,1)$ entries, $M=I$ and $\mathit{\sigma }=1=\mathit{\lambda }$. We parameterize $w$ in terms of the angle $0\le \mathit{\varphi }\le 2\mathit{\pi }$ by $w=(cos\mathit{\varphi }sin\mathit{\varphi })$ for $N=2$ and by spherical coordinates for $N=3$. In Figure 2, the value of the objective function for two random realizations of the matrices $A_1$ and $A_2$ is plotted, and one realization for $N=3$. The problem has multiple minima for the first instance, but a unique minimum for the second instance, as the two minima are equivalent. For the case $N=3$ there are many more local minima at various places on the sphere. Local minima may not be too detrimental to our final goal. The value of $\mathsf{MSE}$ is not as important as long as we achieve a reduction of the risk. For the same reason, even if we do not have a global solution we may still find weights $w$ that substantially decrease the risk one would have achieved by using other more naive choices.

Figure 2. The objective function as a function of $\mathit{\varphi }$ for the weight $w=(cos\mathit{\varphi }sin\mathit{\varphi })$ for two realizations of the matrices $A_1$ and $A_2$ from example $3$. We also show the case $N=3$.

3 Numerical solution

3.1 Direct approach

To solve the problem (1212 $$\begin{array}{cc}\hfill \underset{w}{min}& R_{\mathrm{B}}(w)\hfill \\ \hfill \text{s.t.}& \Vert w\Vert =1.\hfill \end{array}$$12 ), we enforce the constraints by parameterizing $w$ in terms of $N-1$ spherical coordinate angles ${\mathit{\varphi }}_i$ on the unit $N$-sphere:17 $$\begin{array}{cc}& w_1=cos({\mathit{\varphi }}_1)\hfill \\ \hfill & w_2=sin({\mathit{\varphi }}_1)cos({\mathit{\varphi }}_2)\hfill \\ \hfill & w_3=sin({\mathit{\varphi }}_1)sin({\mathit{\varphi }}_2)cos({\mathit{\varphi }}_3)\hfill \\ \hfill & ⋮\hfill \\ \hfill & w_{N-1}=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})cos({\mathit{\varphi }}_{N-1})\hfill \\ \hfill & w_N=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})sin({\mathit{\varphi }}_{N-1}).\hfill \end{array}$$17 We then use the BFGS method to solve the minimization problem iteratively. This requires the computation of the derivatives of the objective function. Rewriting the objective function as$$\mathcal{J}(w)=\mathsf{trace}({(A{(w)}^{\top }A(w)+M)}^{-1})=\sum _j{e}_j^{\top }{(A{(w)}^{\top }A(w)+M)}^{-1}{e}_j$$and setting$$z_j={(A{(w)}^{\top }A(w)+M)}^{-1}{e}_j\leftrightarrow (A{(w)}^{\top }A(w)+M)z_j=e_j$$we have that$${\overrightarrow{\mathrm{\nabla }}}_w\mathcal{J}(w)={\left(\sum _j{e}_j^{\top }{\overrightarrow{\mathrm{\nabla }}}_w{z}_j(w)\right)}^{\top }$$To evaluate the derivative of $z_j$ we use implicit differentiation$$0={\overrightarrow{\mathrm{\nabla }}}_w((A{(w)}^{\top }A(w)+M)z_j)={\overrightarrow{\mathrm{\nabla }}}_w(A{(w)}^{\top }A(w)z_j^{\mathrm{fix}})+(A{(w)}^{\top }A(w)+M){\overrightarrow{\mathrm{\nabla }}}_w{z}_j$$We further define the matrices$$\begin{array}{cc}\hfill G_F(v)& :={\overrightarrow{\mathrm{\nabla }}}_w(A(w)v)=\left(\begin{array}{ccc}{A}_{1}v\hfill & \dots \hfill & A_{N}v\hfill \end{array}\right)\hfill \\ \hfill G_T(u)& :={\overrightarrow{\mathrm{\nabla }}}_w(A{(w)}^{\top }u)=\left(\begin{array}{ccc}{A}_1^{\top }u\hfill & \dots \hfill & A_N^{\top }u\hfill \end{array}\right)\hfill \end{array}$$which leads to the calculation$$G_j(w):={\overrightarrow{\mathrm{\nabla }}}_w(A{(w)}^{\top }A(w)z_j)=A{(w)}^{\top }{G}_F(z_j)+G_T(A(w)z_j)$$and finally18 $$\begin{array}{c}\hfill {\overrightarrow{\mathrm{\nabla }}}_w\mathcal{J}=-\sum _j{G}_j^{\top }(w){(A{(w)}^{\top }A(w)+M)}^{-1}{e}_j.\end{array}$$18 The gradient w.r.t. the angles $\mathit{\varphi }$ is then obtained by multiplication by the Jacobian of the transformation (1717 $$\begin{array}{cc}& w_1=cos({\mathit{\varphi }}_1)\hfill \\ \hfill & w_2=sin({\mathit{\varphi }}_1)cos({\mathit{\varphi }}_2)\hfill \\ \hfill & w_3=sin({\mathit{\varphi }}_1)sin({\mathit{\varphi }}_2)cos({\mathit{\varphi }}_3)\hfill \\ \hfill & ⋮\hfill \\ \hfill & w_{N-1}=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})cos({\mathit{\varphi }}_{N-1})\hfill \\ \hfill & w_N=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})sin({\mathit{\varphi }}_{N-1}).\hfill \end{array}$$17 ). We have used the BFGS [20] method to solve each optimization problem and we fix the termination tolerance of each problem, demanding that the norm of the gradient is reduced to ${10}^{-2}$ of its initial value. To address the problem of multiple minima, we repeat the optimization procedure for a number of random initial guesses for $w$ and select the solution with the smallest value of the objective function. The method to solve the problem (1313 $$\begin{array}{cc}\hfill \underset{W_k}{min}& R_{\mathrm{B}}(W_k)\hfill \\ \hfill \text{s.t.}& \Vert w^{(1)}\Vert =1,\dots ,\Vert w^{(k)}\Vert =1.\hfill \end{array}$$13 ) which involves multiple weights is completely analogous.

The techniques introduced in the previous sections work well for small-scale problems. However for large-scale problems, when $A_j$ is large the computation of the objective function and its derivatives can be rather expensive. Here, we can use a stochastic trace estimation [11] and substitute the problem with19a $$\begin{array}{cc}\hfill min{R}_{FB}(w;v)& =\mathbf{E}\hfill \end{array}$$19a v[ 2 v&#Xtop;(C(w)-1M mMC(w)-1)v

+   v&#Xtop; (A(w)&#Xtop;C(w)-2A(w)) v ]

s.t. w1 and19b $$\begin{array}{cc}\hfill min{R}_{FB}(w)& ={\mathit{\sigma }}^2{\mathbf{E}}_v[v^{\top }(A{(w)}^{\top }A(w)+{\mathit{\sigma }}^{2}M)v]\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \Vert w\Vert \le 1\hfill \end{array}$$19b where the expectation value over random vectors $v$ is approximated by sampling.

3.2 Heuristic weight selection

We can interpret minimization of (1515 $$\begin{array}{c}\hfill R_{\mathrm{B}}(w)=\mathsf{trace}\left({(A{(w)}^{\top }A(w)+{\mathit{\lambda }}^{2}M)}^{-1}\right).\end{array}$$15 ) as maximizing the operator $A{(w)}^{\top }A(w)$. However, in practice it only needs to be maximized over a set of ‘relevant’ models $m$. Let us now make the bold step of maximizing over a single reference model $m_0$, which can be, for example, a constant background model or a more sophisticated prior. (Note that we cannot use the data to obtain $m_0$ as we consider experimental design here.) We now obtain$$W=\underset{W}{\text{arg max}}{m}_0^{\top }A{(W)}^{\top }A(W)m_0.$$Now $A(W)m_0$ is just the reduced data that would result from the model $m_0$. Let us define and compute the $m_0$ data matrix $\tilde{d}$ as in (22 $$\begin{array}{c}\hfill \widehat{A}\equiv \left(\begin{array}{c}{A}_1\\ ⋮\\ A_N\end{array}\right)\mathrm{and}\widehat{d}\equiv \left(\begin{array}{c}{d}_1\\ ⋮\\ d_N\end{array}\right).\end{array}$$2 ) but with $d_i$ taken to be a row of $s$ data (so $\tilde{d}$ is $N\times s$) and denote by $W$ the $k\times N$ matrix of weights (with unit norm rows). We get$$W=\underset{W}{\text{arg max}}\mathsf{trace}{\tilde{d}}^{\top }{W}^{T}W\tilde{d}$$Let us now perform a singular value decomposition (SVD) upon $\tilde{d}=U\mathrm{\Sigma }{S}^{\top }$. We obtain$$W=\underset{W}{\text{arg max}}{\Vert WU\mathrm{\Sigma }\Vert }_2^2$$and the solution for $W$ (under appropriate constraints) is the sub matrix of $U^{\top }$ corresponding to the truncated SVD, which is equivalent to obtaining the first $k$ principal components from the data matrix $\tilde{d}$. For large-scale problems, the first $k$ left eigen vectors and the corresponding eigen values can be estimated effectively through Lanczos iteration. In the following sections, we shall refer to this heuristic choice for $W$ as the ‘SVD’ choice. This heuristic approach works almost as well as the more optimal $W$ in the numerical examples below while avoiding the intricate and expensive optimization process associated with the optimal weights problem. A similar approach using the SVD for faster data processing rather than experimental design was proposed in [21].

4 Numerical experiments

In this section, we test the methods developed on two-dimensional seismic tomography problems. First, we consider a simple toy model on a square domain to test and second we consider a more complicated reconstruction based on the Marmousi model.[22]

We consider a rectangular domain $\mathrm{\Omega }$ with the top boundary $\mathit{\partial }{\mathrm{\Omega }}_1$ representing a ground-air interface while the remaining boundary $\mathit{\partial }{\mathrm{\Omega }}_2$ represents an artificial boundary of the model.

The acoustic pressure field $u$ is determined by the Helmholtz equation with appropriate boundary conditions:20a $$\begin{array}{cc}\hfill (\mathrm{\nabla }·\mathrm{\nabla }+{\mathit{\omega }}^{2}m)u& =q\mathrm{in}\mathrm{\Omega }\hfill \end{array}$$20a 20b $$\begin{array}{cc}\hfill u& =0\mathrm{on}\mathit{\partial }{\mathrm{\Omega }}_1\hfill \end{array}$$20b 20c $$\begin{array}{cc}\hfill ({\mathit{\partial }}_{\overrightarrow{n}}+i\mathit{\omega }\sqrt{m})u& =0\mathrm{on}\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$20c where $m(x)$ is the slowness, i.e. $m=1/c^2$ with $c$ the propagation velocity and $q(x)$ represents sources of angular frequency $\mathit{\omega }$. The Sommerfeld boundary condition (20c20c $$\begin{array}{cc}\hfill ({\mathit{\partial }}_{\overrightarrow{n}}+i\mathit{\omega }\sqrt{m})u& =0\mathrm{on}\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$20c ) prevents artificial reflections from the synthetic domain boundary $\mathit{\partial }{\mathrm{\Omega }}_2$. We discretize (20) on a rectangular grid using a five-point stencil for the Laplacian which is sufficient for numerical experiments and obtain$$\begin{array}{c}\hfill A^{\mathit{\omega }}\mathbf{u}=(-L^{\mathit{\omega }}(m)+{\mathit{\omega }}^2\mathrm{diag}(\mathbf{m}))\mathbf{u}=\mathbf{q},\end{array}$$where the Laplace operator $L^{\mathit{\omega }}$ depends upon $m$ and $\mathit{\omega }$ through the Sommerfeld boundary condition. Note that $\mathbf{u}$ is a complex-valued vector.

Figure 3. Reconstructions with their corresponding relative error ${\mathit{ϵ}}_r=\frac{\Vert m-m_{true}{\Vert }_2}{\Vert m_{true}{|}_2}$.

Figure 4. Reconstructions with a single combined source using various weight choices (left). On the right, the fields generated by the sources are displayed.

The inverse problem is to determine $\mathbf{m}$ from measurements of $\mathbf{u}$ for several given sources ${\mathbf{q}}_i$, where $i=1,\dots N$ labels the experiments which can involve several frequencies. We assume further that all experiments measure $\mathbf{u}$ at the same locations which are described by the linear sampling operator $S$, i.e. we measure ${\mathbf{d}}_i=S{\mathbf{u}}_i$. The predicted data for a given slowness model $\mathbf{m}$ is ${\mathbf{F}}_i(\mathbf{m})=S{A}^{-1}{\mathbf{q}}_i$ (suppressing implicit $\mathit{\omega }$ dependence) and the least-squares error is21 $$\begin{array}{c}\hfill {\mathit{\varphi }}_e(\mathbf{m})=\frac{1}{2}\sum _{i=1}^N{({\mathbf{F}}_i-{\mathbf{d}}_i)}^{†}({\mathbf{F}}_i-{\mathbf{d}}_i).\end{array}$$21 We add a Tikhonov regularization term to ${\mathit{\varphi }}_e$ and solve the inverse problem as22 $$\begin{array}{c}\hfill {\mathbf{m}}^{\ast }=\underset{\mathbf{m}}{\text{arg min}}{\mathit{\varphi }}_e+\frac{1}{2}{\mathit{\lambda }}^2{\Vert \mathbf{m}\Vert }_{\mathrm{\Delta }}^2\end{array}$$22 where ${\Vert ·\Vert }_{\mathrm{\Delta }}$ denotes the Laplacian weighted ${\ell }_2$ norm.

We can apply the formalism developed above and consider instead of (2121 $$\begin{array}{c}\hfill {\mathit{\varphi }}_e(\mathbf{m})=\frac{1}{2}\sum _{i=1}^N{({\mathbf{F}}_i-{\mathbf{d}}_i)}^{†}({\mathbf{F}}_i-{\mathbf{d}}_i).\end{array}$$21 )23 $$\begin{array}{c}\hfill {\widehat{\mathit{\varphi }}}_e(\mathbf{m})=\frac{1}{2}\sum _{k=1}^K{\left(\sum _{i=1}^N{w}_i^{(k)}({\mathbf{F}}_i-{\mathbf{d}}_i)\right)}^{†}\left(\sum _{j=1}^N{w}_j^{(k)}({\mathbf{F}}_j-{\mathbf{d}}_j)\right)\end{array}$$23 for various choices of weights. The Bayes risk function (1313 $$\begin{array}{cc}\hfill \underset{W_k}{min}& R_{\mathrm{B}}(W_k)\hfill \\ \hfill \text{s.t.}& \Vert w^{(1)}\Vert =1,\dots ,\Vert w^{(k)}\Vert =1.\hfill \end{array}$$13 ) is defined by linearization around a reference model ${\mathbf{m}}_0$. Because we are dealing with complex variables, the weight vectors are now complex valued and satisfy ${\mathbf{w}}^{†}\mathbf{w}=1$ and there is an additional complex phase factor $e^{i{\mathit{\rho }}_k}$ for each component in (1717 $$\begin{array}{cc}& w_1=cos({\mathit{\varphi }}_1)\hfill \\ \hfill & w_2=sin({\mathit{\varphi }}_1)cos({\mathit{\varphi }}_2)\hfill \\ \hfill & w_3=sin({\mathit{\varphi }}_1)sin({\mathit{\varphi }}_2)cos({\mathit{\varphi }}_3)\hfill \\ \hfill & ⋮\hfill \\ \hfill & w_{N-1}=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})cos({\mathit{\varphi }}_{N-1})\hfill \\ \hfill & w_N=sin({\mathit{\varphi }}_1)\dots sin({\mathit{\varphi }}_{N-2})sin({\mathit{\varphi }}_{N-1}).\hfill \end{array}$$17 ).

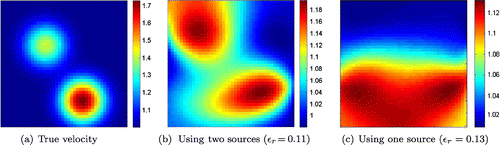
4.1 A simple toy model

For the first problem, we consider we take $\mathrm{\Omega }$ to be the square domain ${[-11]}^2$ which we discretize by a uniform ${42}^2$ grid. Absorbing boundary conditions are assumed except at the top where we impose Dirichlet boundary conditions. Sources are placed on the left boundary and $20$ uniformly spaced detectors are placed on the right. In Figure 3(a), we depict the synthetic velocity model which we use to compute simulated data to which we add $2\%$ Gaussian noise. Sources of $f=0.5$ (i.e. one wavelength in domain) are placed on the left in two configurations. First we consider $N=2$ experiments with a source at $1/3$ depth and at $2/3$ depth. Second one source is placed in the middle. The inversion is performed as described in Section 3 and the regularization parameter $\mathit{\lambda }$ was chosen by the Morozov discrepancy principle.[23] We solved the optimization problem (2222 $$\begin{array}{c}\hfill {\mathbf{m}}^{\ast }=\underset{\mathbf{m}}{\text{arg min}}{\mathit{\varphi }}_e+\frac{1}{2}{\mathit{\lambda }}^2{\Vert \mathbf{m}\Vert }_{\mathrm{\Delta }}^2\end{array}$$22 ) using limited memory BFGS. We depict the resulting reconstructions in Figure 3(b) and (c) along with a relative error measure defined as follows:24 $$\begin{array}{c}\hfill {\mathit{ϵ}}_r=\frac{\Vert m-m_{true}{\Vert }_2}{\Vert m_{true}{\Vert }_2}\end{array}$$24 It is clear that for $N=2$ we capture the basic structure of the model, whereas $N=1$ is insufficient.

Figure 5. Reconstructions of the Marmousi velocity model using only the low frequency $f=0.2$ data with all and with $2$ simultaneous sources. We also indicate the relative reconstruction error ${\mathit{ϵ}}_r=\frac{\Vert m_{rec}-m_{true}{\Vert }_2}{m_{true}{\Vert }_2}$.

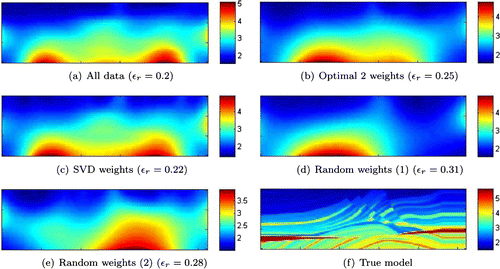
Figure 6. Fields for the $2$ simultaneous sources for the case $f=0.2$ using the various weight selection methods. Notice how the good weights cover the domain more or less uniformly.

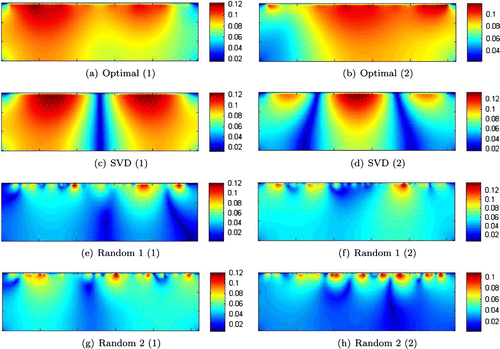
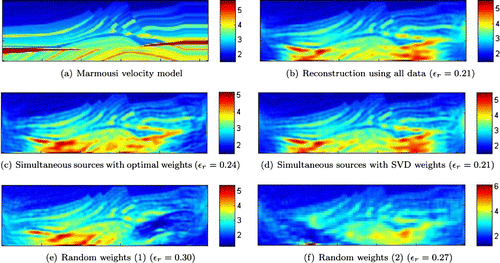
Figure 7. Reconstructions of the Marmousi velocity model using the protocol described. We compare the final result using all the data, and a simultaneous sources protocol with optimal, SVD and random weights.

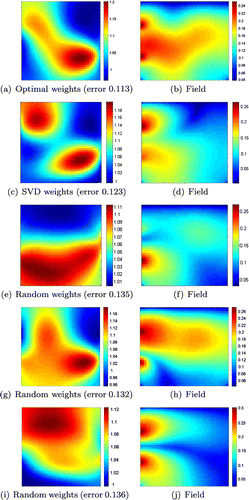
Next we consider using a single simultaneous source by superposition of the two sources with a unit norm weight vector. In Figure 4, we show reconstructions using various methods for selection of the weights (left column). The right column shows the absolute value of the pressure field $u$ generated by the corresponding simultaneous source. We computed the optimal weight vector as described in Section 3 using $32$ different random initial guesses for $w$, and selecting the one with lowest risk. Second, we used the method described in Section 3.2 and finally we generated three random phase weight vectors. It is evident that the optimal weights yield the best reconstruction both visually and in terms of relative error as defined in (2424 $$\begin{array}{c}\hfill {\mathit{ϵ}}_r=\frac{\Vert m-m_{true}{\Vert }_2}{\Vert m_{true}{\Vert }_2}\end{array}$$24 ). These optimal results were followed closely by those of the SVD method 3.2. The random weights offered a reasonable reconstruction in (g) but not in (e) and (i). By inspecting the fields in the rightmost column seems that the optimal choice has selected the source combination to provide the best possible domain coverage. The source of the SVD-based approach did so to a lesser extent and the random choices essentially cover the domain randomly, as expected.

4.2 Marmousi model

As a second numerical experiment, we consider the true velocity model depicted in Figure 5(f) of the Marmousi model. The domain is 3 km by 10 km and velocity is given in km ${\mathrm{s}}^{-1}$ units. We use a $208\times 60$ grid for the discretization. Forty emitters are placed at uniform distances on the surface and $39$ receivers are placed in between the emitters. We generate data for five distinct frequencies $f=0.2,1.5,3,4.5,6$ (in Hz), with a total of $5\times 40=200$ experiments. We note that the low frequencies are needed to avoid local minima, but are not quite realistic. We added $3\%$ Gaussian noise to the synthetic data. Optimal weights were precomputed before the inversion by linearization around a constant $m_0=2$ km ${\mathrm{s}}^{-1}$ background model which was also used for the SVD method for selection weights.

First of all we present the reconstructions for a single frequency of $0.2$ Hz using all $40$ experiments and with $K=2$ weight vectors, each a combination of the $40$ sources. For the latter we show the results for the optimal weights, SVD-based weight selection, and random phase weights in two realizations. It is clear from Figure 5 that the random weight selection performs much worse that the other methods. In this case the SVD reconstruction is even better than using the optimal weights.

In Figure 6, we depict the resulting pressure field from the two simultaneous sources. We observe again that the optimal and SVD weights result in a more or less uniform and balanced coverage of the domain whereas the random choices do no share this virtue.

To obtain more accurate reconstructions, higher frequencies must be included. Because of the nonconvexity of the problem we perform a frequency continuation by which we first solve (to full convergence) for the lowest frequency, then use the result as initial guess for the next stage where we add an additional frequency, etc. Because accuracy of the reconstruction increases we can expect to require more simultaneous sources as well as more and more frequencies are included. In this example, we use $K=2,6,12,20,30,$ simultaneous sources corresponding to frequencies $f=0.2,1.5,3,4.5,6$, again for the aforementioned three methods for weights selection. In Figure 7, we depict the resulted reconstructions. Remarkably, the reconstructions with the SVD or optimal weights are no worse visually than the reconstruction using all the data, whereas the random weights do not offer comparable results. We note that the advantage of using simultaneous sources decreases with higher frequencies.

5 Summary and conclusions

We have introduced a novel methodology for optimal experimental design of acquisitions involving simultaneous sources. Based on an optimal Bayesian risk statistical framework and the assumption of a linear inverse problem we have formulated an optimality criterion for selection of the weights in which individual observations should be combined. We derived a heuristic guess for the optimal weights based upon the SVD and we performed numerical experiments to test the efficacy of the method. In all cases, it was found that an informed choice of the weights generally outperforms a random weight choice. This is because our statistical framework incorporates information about the domain under consideration and the experimental setup.

Even though for most realistic applications the numerical models lead to nonlinear inverse problems, both weight selection based on a linearized version of the model was still found to perform quite well. Development of computationally viable optimal simultaneous source experimental design that accounts for the nonlinear nature of the observation model is a subject for future work.

In this study, Gaussian assumptions were taken for the noise model and Tikhonov regularization was considered for the ill-posed case. These choices are by no mean exclusive, and in principle, derivation of optimal experimental design for simultaneous sources can be performed for other alternative noise models as well as for other forms of regularization.

So far incorporation of constraints was not considered (other than such that can be introduced in the form of exact penalty). Future research would be to generalize the proposed formulation to account for such.

Additional information

Funding

This work was supported in part by IBM Research and MITACS Open Collaborative Research project for Design in Inversion http://ocrdesign.wix.com/home.