?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
We consider the problem of estimating the 2D vector displacement field in a heterogeneous elastic solid deforming under plane stress conditions. The problem is motivated by applications in quasistatic elastography. From precise and accurate measurements of one component of the 2D vector displacement field and very limited information of the second component, the method reconstructs the second component quite accurately. No a priori knowledge of the heterogeneous distribution of material properties is required. This method relies on using a special form of the momentum equations to filter ultrasound displacement measurements to produce more precise estimates. We verify the method with applications to simulated displacement data. We validate the method with applications to displacement data measured from a tissue mimicking phantom, and in-vivo data; significant improvements are noticed in the filtered displacements recovered from all the tests. In verification studies, error in lateral displacement estimates decreased from about 50% to about 2%, and strain error decreased from more than 250% to below 2%.
1. Introduction
Ultrasound elasticity imaging (UEI), or elastography, is a rapidly growing field, primarily due to the increasing interest in the non-invasive quantification of the mechanical properties of soft tissues.[Citation1–Citation6] A crucial step in UEI is the estimation of a tissue’s motion. This motion is typically generated by a quasistatic compression, and the deformation of the tissue is measured with ultrasound. The measured deformation and an appropriate mathematical model can then be used to infer the mechanical properties of the soft tissue.
Ultrasound measurements of tissue deformation are typically much more precise in the ‘axial’ direction (i.e. the direction of the ultrasound beam), than in the so-called ‘lateral’ direction, the image direction transverse to the direction of the ultrasound beam.
The origin of the difference in precision is due to the anisotropy of the ultrasound point spread function (PSF). The width of the peak of the radio frequency (RF) PSF in the axial direction (the direction of sound propagation) is roughly an order of magnitude smaller than that in the lateral direction.[Citation7]
With only one component of the displacement field measured precisely, it is impossible to compute precise estimates of the full strain tensor field, which would otherwise be useful information to researchers who do strain imaging. Furthermore, one goal of measuring the displacement field is as input to an inverse problem to estimate material property distributions.[Citation6,Citation8] Computing the material properties from only one component of the displacement field is computationally intensive.[Citation6,Citation8] In that situation, an iterative inversion approach is required, which may take hundreds to thousands of iterations to converge. Such an iterative inversion code usually needs displacement boundary conditions to drive the forward problem, and using the noisy measurements as boundary conditions can corrupt the material property estimates.[Citation9–Citation11] On the other hand, efficient direct methods to compute material properties from full vector displacement field measurements exist.[Citation12–Citation14] The present contribution uses an inverse problem approach that aims to improve lateral displacement estimates from ultrasound measurements.
Much research has been performed in order to recover better lateral displacements both in the UEI and the ultrasound blood flow imaging field. There are four main approaches that dominate the literature. In [Citation15–Citation25], the authors use various forms of interpolation within standard or modified block-matching algorithms to estimate subsample lateral displacements. These approaches try to make the best use of available data as is, but do not overcome the fundamental difficulty posed by the anisotropic PSF. An alternative approach is to use beam steering to measure displacements at arbitrary angles, and then use the arbitrary angled displacement estimates to determine the axial and lateral displacements as described in [Citation26–Citation31]. This method uses additional image data to overcome the limitations of a single PSF. A third approach, pursued by [Citation32–Citation35], is to use novel beam forming techniques to modulate the RF signal in the lateral direction so that it contains more phase information. This approach tries to reduce the anisotropy of the PSF. A fourth approach, pursued by [Citation11,Citation36–Citation38], is to constrain the displacements to satisfy the incompressibility condition. Many different types of soft tissues can be assumed to be incompressible because they are mostly composed of water. A fifth approach, pursued in [Citation39], is to constrain the displacements to satisfy the momentum equations.
Among the existing approaches, the incompressibility processing method introduced in [Citation36], and the momentum equation based processing method [Citation39] are arguably the most similar in spirit to the method presented here to reconstruct better lateral displacements. In [Citation36], the authors assumed that the deformation is linear, incompressible and plane strain in character. With these assumptions, they formulated a minimization problem where the objective was to find lateral displacements that minimized the error between the measurements and predicted lateral displacements that satisfied the modelling assumptions. The incompressibility processing described in [Citation38] is basically the same as the method developed in [Citation36], with the addition of weighting functions to the lateral displacement reconstruction equations. These weighting functions are based on the absolute value and the gradient of the cross-correlation function. In [Citation37], the method developed in [Citation36] is extended to accommodate large plane strain deformations. Finally, in [Citation11], the incompressibility constraint is used to improve the lateral and elevational displacements for a 3D deformation.
In [Citation39], the authors constrain the measured displacements to satisfy the plane strain elasticity equations. Using only the measured axial displacements, and an filtering strategy, they are able to reconstruct the full displacement field. The drawback of this approach is that it requires a priori knowledge of the material parameters’ distribution.
In this paper, we also use the momentum equation to reconstruct the lateral displacements. The approach assumes only that the material property distribution is well-represented as piecewise constant. We will be using a spatial regularization term within an inverse problem formulation to adaptively enforce, and locally relax, a special form of the momentum conservation equation on the measured displacement field. Special weighting functions will be used to place more emphasis on the axial component of the displacement field.
The rest of the paper is arranged as follows: Section 2 describes the new formulation to estimate better lateral displacements; we refer to this method as ‘SPREME’, which stands for SParse RElaxation of the Momentum Equation. Section 3 describes the simulation experiments used to test and verify the displacement filtering algorithm. Section 4 describes the phantom experiments used to validate the performance of the displacement filtering algorithm on ultrasound measured data. Section 5 describes the in-vivo experiments used to further test the performance of the displacement filtering algorithm on patient data. Finally, a brief summary and conclusion is given in Section 6 along with possible future directions of the work. The appendix describes a simpler formulation that produces apparently improved displacement and strain fields. Despite appearances, however, the resulting strain and displacement fields are non-physical.
2. Formulation
We suppose we are given a measured displacements in a 2D region . We further suppose the measurements of the axial displacement,
, are significantly more precise and accurate than the measurements of the lateral displacement. We make use of the assumption that within the observed plane, the body’s deformation may be well approximated by the plane stress approximation. These assumptions lead to the following problem statement:
Problem 2.1:
Given 2D measured displacement , for all
, find the 2D displacement vector
, and the 2D linearized strain tensor
such that:
(1)
(1)
is minimized, and:(2)
(2)
and:(3)
(3)
where:(4)
(4)
and:(5)
(5)
With diagonal , Equation (Equation1
(1)
(1) ) may be written explicitly as:
(6)
(6)
In Equation (Equation6(6)
(6) ), the weights (T
, T
) allow more importance to be placed on the accurate component of the displacement field while calculating the predicted displacement field. In Equation (Equation3
(3)
(3) ), a.e. means almost everywhere, and implies that the constraint is enforced everywhere in the domain except on a set of measure zero (i.e. along curves and at isolated points).
To motivate constraint (Equation3(3)
(3) ), we consider a thin sheet in the (x, y) plane made of solid material that is linearly elastic, isotropic, incompressible and simply connected. We further assume that the deformation of the material is small, quasistatic and approximately plane stress in character. These modelling assumptions are justified because our application of interest is in the ultrasound elastography field, where the goal is to determine the linear elastic properties of soft tissue, typically modelled as incompressible because of their usually large water content, from small displacement measurements. The assumptions lead to the following definitions for the linear strain
, and the Cauchy stress
[Citation40,Citation41]:
(7)
(7)
(8)
(8)
where ,
is the shear modulus distribution, and p(x, y) is the hydrostatic pressure field. For a plane stress deformation:
(9)
(9)
For an incompressible material:(10)
(10)
Substituting (Equation10(10)
(10) ) into (Equation9
(9)
(9) ) gives:
(11)
(11)
Using (Equation11(11)
(11) ) in (Equation8
(8)
(8) ) yields:
(12)
(12)
The equilibrium equation, with no body force, is , or using (Equation12
(12)
(12) ):
(13)
(13)
If is piecewise constant, then
a.e. in
.
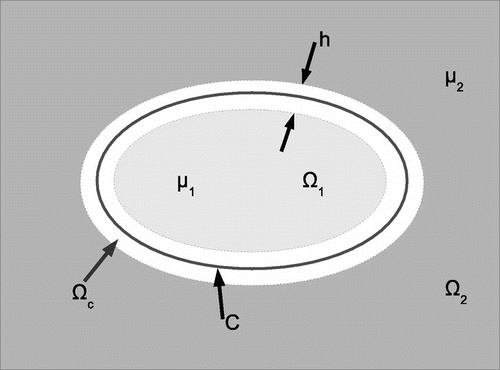
2.1. Uniqueness of solution
Given an axial displacement measurement , the conditions necessary to guarantee the uniqueness of the lateral displacements computed using the equilibrium equation constraints will be derived in this section. This derivation begins with the assumption that the material has a piecewise homogeneous shear modulus distribution. This means that the material’s domain,
, can be divided into n different subdomains,
, and the shear modulus in each subdomain is constant. The shear modulus is not constant on the interface between the subdomains, however. An illustration of this type of domain, for a special case when
, is shown in Figure . The conditions necessary for uniqueness of the lateral displacements in each subdomain will be derived next.
2.1.1. Solution in a single subdomain
Lemma 2.1:
Given in subdomain
, in which
constant, then the general solution of Equations (Equation2
(2)
(2) )–(Equation5
(5)
(5) ) for
, with
is:
(14)
(14)
Proof:
Since in
, we may expand Equation (Equation3
(3)
(3) ) in terms of displacements via Equations (Equation4
(4)
(4) ) and (Equation2
(2)
(2) ), resulting in the following equations:
(15)
(15)
(16)
(16)
All the terms on the right-hand side of both these equations are supposed to be known since by assumption here, is known precisely. The terms on the left-hand side involving the lateral displacements,
, are unknowns. We now show that these equations lead to a solution for
that has at most four unknown constants. We begin by splitting the total solution into homogeneous and particular parts. To that end, we let:
(17)
(17)
Here, is any particular solution of (Equation15
(15)
(15) ) and (Equation16
(16)
(16) ), which, by assumption, has no free constants or undetermined functions. If they appear in the process of solving (Equation15
(15)
(15) ) and (Equation16
(16)
(16) ), then they shall be set to arbitrary values (e.g. zero) without loss of generality. Any part of the general solution (Equation17
(17)
(17) ) that is undetermined by
is thus contained in
, the homogeneous solution of (Equation15
(15)
(15) ) and (Equation16
(16)
(16) ).
The homogeneous solution satisfies:(18)
(18)
(19)
(19)
Integrating (Equation19(19)
(19) ) twice yields:
(20)
(20)
Substituting (Equation20(20)
(20) ) into (Equation18
(18)
(18) ) gives:
(21)
(21)
Equation (Equation21(21)
(21) ) implies:
(22)
(22)
Integrating (Equation22(22)
(22) ) for f(x) and g(y) yields:
(23)
(23)
(24)
(24)
Combining (Equation23(23)
(23) ), (Equation24
(24)
(24) ), in (Equation20
(20)
(20) ) gives:
(25)
(25)
where . Therefore, the total solution is of the form (Equation14
(14)
(14) ).
Equation (Equation14(14)
(14) ) shows that within any homogeneous subregion of the body, given the axial displacement
, the lateral displacement
has at most four undetermined constants.
2.1.2. Solution in connected subdomains covering entire domain of interest
Interestingly, the form of the homogeneous solution is completely independent of the given . Thus, we may conclude almost immediately:
Lemma 2.2:
Given in
, in which
is piecewise constant, such that
(26)
(26)
then the general solution of Equations (Equation2(2)
(2) )–(Equation5
(5)
(5) ) for
with
is:
(27)
(27)
Here, is determined entirely by
, while
are undetermined constants.
Proof:
We consider several contiguous subregions, each of which is homogeneous. From Lemma 2.1, the solution within subregion n is given by:(28)
(28)
If we consider the displacement to be continuous at a non-special interfaceFootnote1 between subregion n and adjacent subregion m, and we assume that
is continuous on the interface, then we conclude:
(29)
(29)
To see this, note that , and
leads to the equation:
(30)
(30)
with . We note that (Equation30
(30)
(30) ) holds at every point on the interface. Provided that the functions
, x, y, 1 are linearly independent on the interfaces, then the only solution of (Equation30
(30)
(30) ) is
. Interfaces on which these functions are linearly dependent are special cases, and we call them ‘special interfaces’.
Since the ’s take the same value in every subregion, we may consider the homogeneous functions to be defined globally. Thus, the global solution is:
(31)
(31)
Lemma 2.2 and Equation (Equation31(31)
(31) ) imply that by knowing the axial displacement throughout the domain in a piecewise homogeneous material, the lateral displacement may be determined up to four coefficients. Hence, if sufficient information exists in the measurements to determine these four coefficients accurately, then the lateral displacement field may be determined accurately throughout the domain.
In the next section, we derive a variational formulation that permits this estimation in a natural way.
2.2. SPREME variational formulation
In practice, we shall enforce constraint (Equation3(3)
(3) ) approximately as a penalty, in the form of a regularization term. To determine the appropriate form of that term, we refer to Figure and consider a continuous
of the form:
(32)
(32)
Figure 1. A piecewise continuous distribution of elastic modulus represented as the limit of a continuous distribution. The function has the constant value
for
, has the constant value
for
and is continuous and monotone in a narrow intermediate region,
.
where is the set of all points within
from curve C. We assume there is a constant
so that
for all
Suppose everywhere in
, then:
(33)
(33)
In order to form the penalty term, we assume (Equation33(33)
(33) ) is satisfied and consider:
(34)
(34)
where min
is the minimum value of
in
,
,
is the largest eigenvalue of
and
is the perimeter of curve C; see Figure .
We see in (Equation34(34)
(34) ) that for piecewise constant
(i.e. when
),
(35)
(35)
Equation (Equation35(35)
(35) ) shows that we may enforce the constraint
by choosing to enforce the integral condition (Equation35
(35)
(35) ) with
.
The derivative of the absolute value function is undefined at the origin, so in practice, we introduce a small positive constant, , and approximate (Equation35
(35)
(35) ) as:
(36)
(36)
where:(37)
(37)
Note that .
In Equation (Equation36(36)
(36) ), k denotes an iteration counter. As k approaches infinity, we expect
to approach
. In this limit, for
, the approximation in (Equation36
(36)
(36) ) is then exact. The
in the denominator is a small numerical constant that prevents the denominator from being zero when
Using (Equation36(36)
(36) ) instead of (Equation3
(3)
(3) ), we reformulate the problem as:
Problem 2.2:
Given ,
and
, find
and
that minimize:
(38)
(38)
where:(39)
(39)
and:(40)
(40)
and:(41)
(41)
and:(42)
(42)
This yields a quadratic minimization problem at each iteration for and
(Note that the shear modulus
is not required in the formulation). We initialize iterations using
. Equation (Equation38
(38)
(38) ) contains a displacement data matching term (
), a compatibility term (
) and a regularization term (
).
minimizes the mismatch between the measured displacement field and the filtered displacement field and
constrains the calculated strains to satisfy the compatibility equation.
is a constant that is used to regulate how strongly the compatibility condition is enforced.
is used to constrain the strains to satisfy the equilibrium equations almost everywhere in the domain.
is a constant used to regulate how strongly the equilibrium is enforced globally, and
may be interpreted as a spatially varying regularization constant that regulates how strongly the equilibrium equation is enforced locally.
The way the regularization, , works can be best explained with Figure . In this figure, where
is constant (i.e. in the background (
) and in the inclusion (
)),
will be small, meaning that
will be large, so the equilibrium equation will be strongly enforced in these regions. Therefore,
can be confidently determined there up to the homogeneous solution. Where
is not constant (i.e. in
, a thin region along the interface between the inclusion and the background),
will be large, meaning that
will be small, so the equilibrium equation will not be strongly enforced. Thus, the strains are permitted to change rapidly there. Continuity of the lateral displacements is enforced there through the
term. This ‘spatially adaptive’ regularization thus allows us to enforce the equilibrium equation everywhere in the domain, except near material interfaces.
We note that if the goal is to evaluate the strain tensor only, then it is tempting to reformulate the problem without the displacement variable, . Such a formulation is presented in Appendix 1. There, it is shown that the strains obtained from the formulation are not compatible, and hence not physical, for some simulation experiments.
Equation (Equation38(38)
(38) ) is the SPREME functional. Our implementation minimizes
by the Galerkin finite element method (FEM) discretization. The weak form is derived first by computing the following directional derivatives:
(43)
(43)
(44)
(44)
where and
are admissible variations of
and
, respectively, and
. We drop the k’s for the rest of the presentation to simplify notation. Taking the directional derivatives yields the following system of equations:
(45)
(45)
(46)
(46)
Equations (Equation45(45)
(45) ) and (Equation46
(46)
(46) ) are discretized following standard FE methods, (e.g. [Citation41]) with bilinear shape functions
defined on quadrilateral elements. The shape functions have the special property that
at node a and
at all other nodes. This gives the following discrete approximations of the functions on each element:
(47)
(47)
Here, ,
represent the values of
and
at node b.
This discretization of the variational equations results in an algebraic equation of the form , in which
is a vector containing the unknown nodal values of
and
. A new finite element within an in-house FEM code was created to build and solve the system of linear equations. See [Citation42] for more details on the finite element discretization.
3. Verification of computational implementation
The purpose of verification is to confirm that, given data that satisfy the modelling assumptions, a computational implementation produces the correct solution that is consistent with the assumed model. In this section, therefore, the results of two different simulation experiments conducted to test the implementation of the SPREME formulation will be described. For the two experiments performed, reference analytical displacement and strain fields are available, and they were used to evaluate the quality of reconstructed displacements and strains from the SPREME formulation.
3.1. Reference analytical solution
An exact analytical solution of the elasticity equations is used to generate reference displacement data. The solution corresponds to that of an infinite elastic sheet with a perfectly bonded circular inclusion. The sheet is subject to uniform stress at infinity. The problem was non-dimensionalized using the region of interest size as the reference length, and the background shear modulus as the reference stress. The shear modulus of the inclusion and background was , and
, respectively. Poisson’s ratio was taken to be
, consistent with the incompressibility assumption. The radius of the inclusion was
. The solution to the elasticity equation was obtained using the methods described in [Citation43].
3.2. Uniaxial tension test
Figure 2. Uniaxial and biaxial tension tests: The exact analytical solution for far-field tension applied to an infinite sheet with a bonded circular inclusion is used for verification of the computational implementation. In the figure, ROI indicates the region of interest over which displacement fields are assumed to have been ‘measured’.
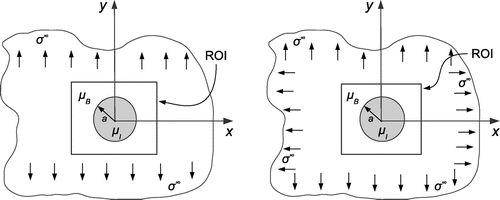
Figure 3. Uniaxial tension test. Upper row: Exact noiseless displacement field for uniaxial tension experiment. These represent the target displacement fields. Lower row: Noise-corrupted displacement fields used for verification. The noise level in the lateral displacements is similar to that seen in physically measured displacement fields shown in Figure .
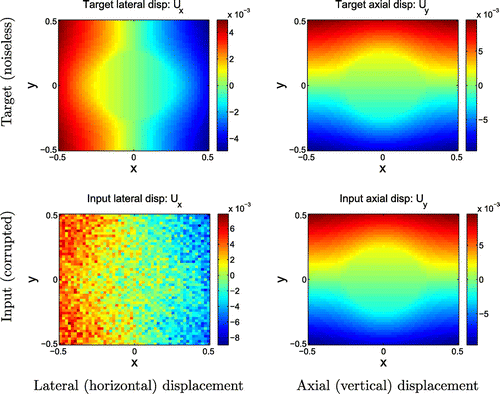
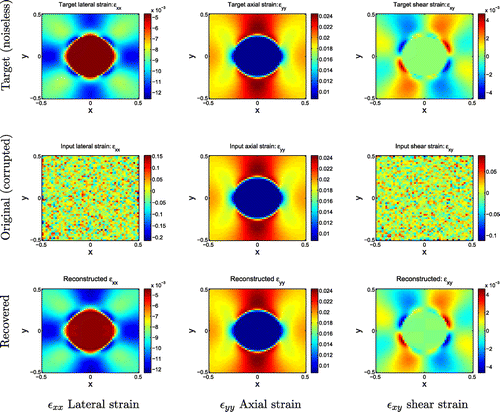
Figure 4. Uniaxial tension test results. Top row: Target noiseless strain fields from uniaxial tension test. Middle row: Strain fields calculated from noise-corrupted input displacement fields. Bottom row: Strain fields recovered from SPREME.
For the first experiment, the sheet was subject to uniaxial tension in the y direction as depicted in Figure . The stress at infinity was taken to be . The displacement field corresponding to this deformation was evaluated in a subregion around the inclusion. This subregion was discretized into
square elements in the x and y directions, and the axial and lateral displacements were evaluated at each of the 2601 nodes. This reference displacement field is shown in Figure . This target displacement field was differentiated by finite differences to calculate the target strains shown in Figure . Since the analytical expressions for the displacements are available, the target strains can be differentiated exactly rather than using finite differences. There is no analytical expression for the noise-corrupted displacement fields, however, and therefore we have chosen to treat both noisy and reference fields in the identical manner. These target fields will be used as a reference to benchmark the accuracy of the fields reconstructed with SPREME.
Our problem assumptions include that we are given accurate axial displacements and noisy lateral displacements. Therefore, Gaussian noise was added to the lateral displacement () in order to simulate ultrasound displacement measurements, and the axial displacement (
) was left unchanged. The corrupted displacement field is shown in Figure .
The corrupted displacement field was differentiated by finite differences to obtain the strains displayed in Figure . The strain component was unchanged. The features in the other strain components, however, were completely obscured by noise.
The corrupted displacement field was processed with SPREME using the following parameter values: ,
,
,
,
,
. These parameters were chosen by trial and error from extensive computational testing. This same trial and error method was used to choose the best parameters for all the other computational experiments performed. Six iterations were performed to allow the strains to converge. The strains from SPREME are displayed in the bottom row of Figure . The reconstructed strains are very smooth because of the regularization on the momentum equation. This regularization term is very similar to a total variation (TV) regularization which tends to penalize reconstructions with high oscillations, but allows reconstructions to have jumps that need to be present to fit the data.[Citation44]
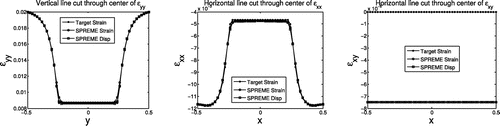
Accuracy of reconstructed strains and displacements may be seen qualitatively in line plots passing through the centre of the inclusion region, Figure . These plots show excellent agreement between the target strains and the reconstructed strains (referred to as SPREME Strain in the legend) in every component of the strain. We recall that the SPREME formulation has independent variables for both displacements and strains, and therefore we also use this figure to evaluate consistency of the SPREME displacements and strains. To see this, we use a finite difference approximation of the derivative of the reconstructed displacements to obtain another estimate of computed strains; these are labelled SPREME Disp in the legend, and are also in excellent agreement with the other quantities.
Figure 5. Uniaxial tension: Line plots through the axial, lateral and shear strain fields. The SPREME method produces independent estimates of displacement and strain. Thus, each graph shows three curves. One is the target strain. The second is the strain output from SPREME labelled ‘SPREME Strain’. The third is the derivative of the output SPREME displacement, labelled ‘SPREME Disp’. Comparing the latter two provides a test for consistency between these fields.
Overall quantitative accuracy of the displacements (strains) computed with SPREME were evaluated for both individual components and for the total vector (tensor). The component error is defined as:(48)
(48)
(49)
(49)
Here, and
are the target displacement and strain components, respectively, and the
and
go from 1–2 with 1 representing the x direction, and 2 representing the y direction. The counter a runs over all nodes in the mesh.
The norms calculated with these formulas were plotted as a function of iteration number in Figure . For iteration zero, was the displacement field corrupted by noise, and
was initialized to zero strain. The plots in the figure demonstrate that the errors reduce significantly with iteration number. The exact values of the errors in the field variables after the sixth iteration are displayed in Table . From the table, we see that the error in
(resp.
) reduced from about 50% (resp.
) to about 2%.
Figure 6. Uniaxial tension test: Error in each component of the field variables as a function of iteration number.
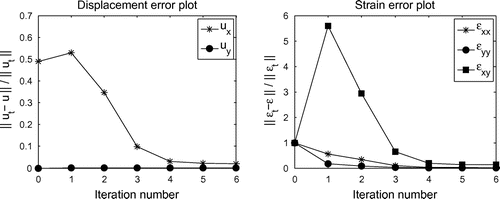
Figure 7. Uniaxial tension test: Total error in the field variables as a function of iteration number.
The total error in strain and displacement was computed with the following formulas:(50)
(50)
(51)
(51)
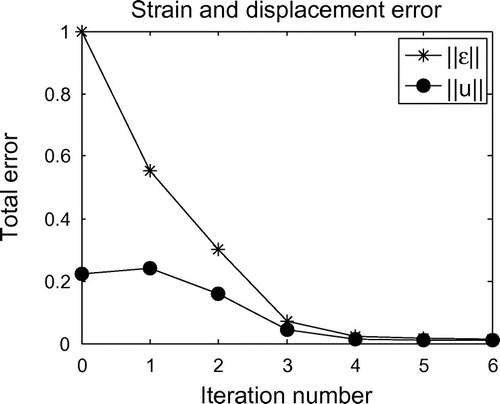
Here, and
. A plot of these total errors as a function of iteration number is shown in Figure , which shows that the total errors decrease with iteration.
Table 1. Uniaxial tension test: Errors in the recovered field variables after the sixth iteration, and initial errors in the input field variables.
3.3. Biaxial tension test
For the second verification test, we consider the same body, this time under biaxial tension; c.f. Figure . The stress at infinity was . Next, Gaussian noise was added to the lateral displacement field, and reconstructions were performed using the following parameters:
,
,
,
,
,
. These are approximately the same parameters as the last experiment, except with
significantly increased to accommodate the applied horizontal stress.
Figure 8. Biaxial tension test results. Upper row: Target noiseless strain fields from uniaxial tension test. Lower row: Strain fields recovered from SPREME. Relatively large weights on noisy lateral displacement increase the error in the recovered strains relative to those in Figure .
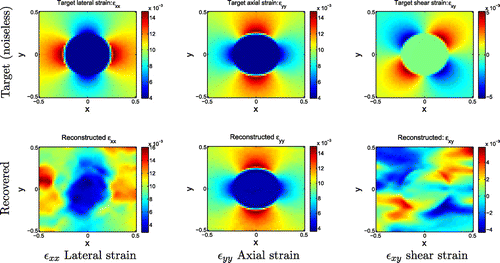
The target and reconstructed strains at the sixth iteration are shown in Figure . The features in the lateral and shear strains are recovered, but we see significantly more error in this test case than in Figure . That error is quantified in Table . The table shows clearly that the errors in the lateral displacement, and lateral and shear strains reduced significantly from the errors in the input field. This means that the method is able to work also for this type of deformation. The method did not work as well as it did for the case when the domain was under uniaxial tension, however. This is most likely due to the need to use relatively large weights on the noisy lateral displacements to capture the effect of significant lateral normal stress applied at infinity. Thus, the effect of the noise in that displacement component was amplified. Nevertheless, the error in reduced from about
to about
, a very significant reduction.
Table 2. Biaxial tension test: Errors in the recovered field variables after the sixth iteration, and in the input field variables for the biaxial tension experiment with noise.
4. Validation
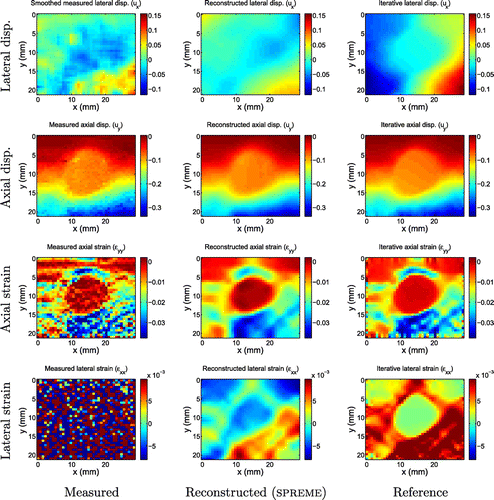
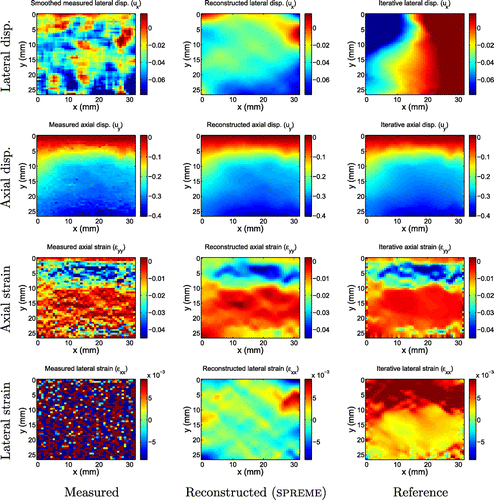
In the verification section, we demonstrated that SPREME correctly reconstructs plane stress displacement fields. Here, in the validation section, we demonstrate that the SPREME implementation of the plane stress model applies to physical systems of interest. The displacement data used for the test were measured within a gelatin phantom under uniaxial compression as described in [Citation9]. This displacement data were analysed previously by an iterative elastic modulus inversion algorithm.[Citation9] The results from that study, and a smoothed version of the measured displacements, will be used as a reference to compare to the results produced by SPREME.
Figure 9. Axial displacement fields. First row: Measured displacement field; second row: Displacements reconstructed by SPREME; third row: Reference displacements from an iterative inversion algorithm.
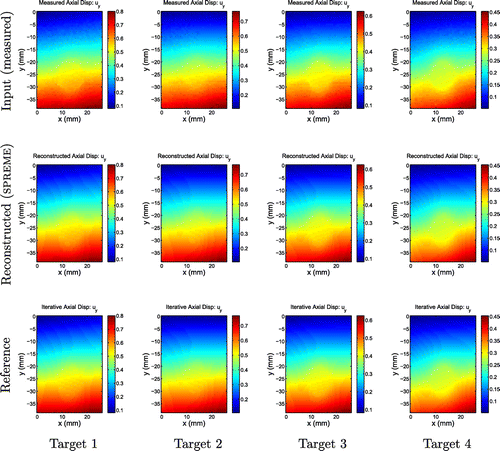
Figure 10. Lateral displacement fields. First row: Measured displacements; second row: A smoothed version of the measured displacements; third row: Displacements reconstructed by SPREME; fourth row: Reference results from an iterative inversion algorithm. We note general agreement in gross features between all rows for targets 1 and 2. For targets 3 and 4, there is disagreement between the reference and the other fields, which we attribute to inaccuracies in assumed boundary conditions used to create the reference solution.
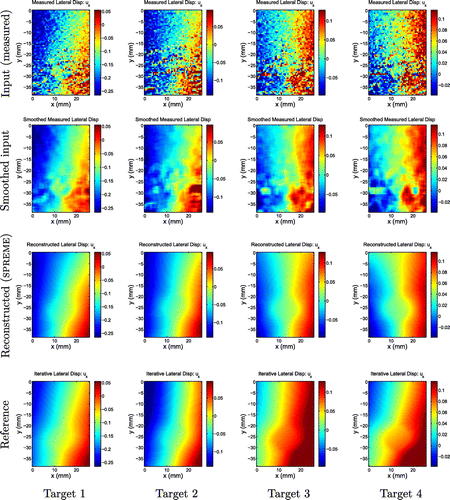
Figure 11. Axial strain fields. First row: Measured strains; second row: Strains reconstructed by SPREME; third row: Reference results from an iterative inversion algorithm. We note qualitative and quantitative agreements between the rows; we note also the presence of boundary artefacts in the reference fields that are not present in the SPREME fields.
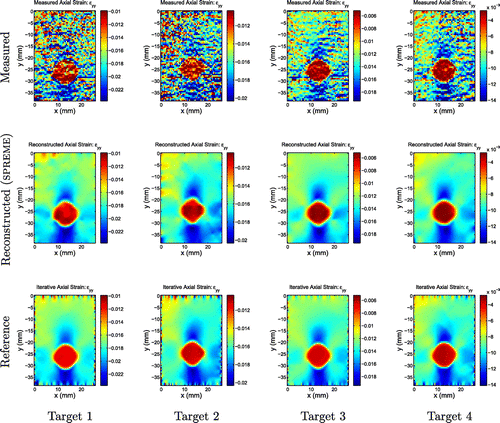
Figure 12. Lateral strain fields. First row: Measured strains; second row: Strains reconstructed by SPREME; third row: Reference results from an iterative inversion algorithm. We note general agreement of the main features between the SPREME and reference results; boundary noise present in reference results is not apparent in SPREME results; SPREME fields show higher dynamic range than reference fields.
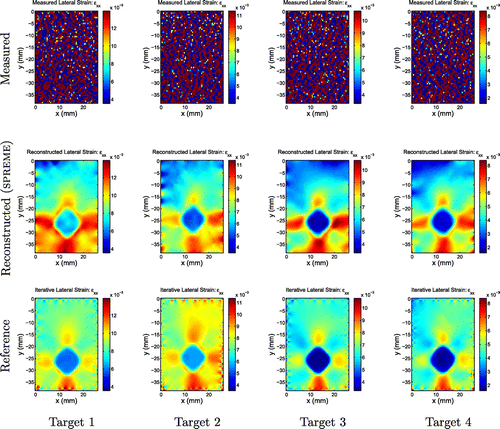
Figure 13. Shear strain fields. First row: Measured strains; second row: Strains reconstructed by SPREME; third row: Reference results from an iterative inversion algorithm. We note general agreement of the main features between the SPREME and reference results; boundary noise present in reference results is not apparent in SPREME results; SPREME fields show higher dynamic range than reference fields.
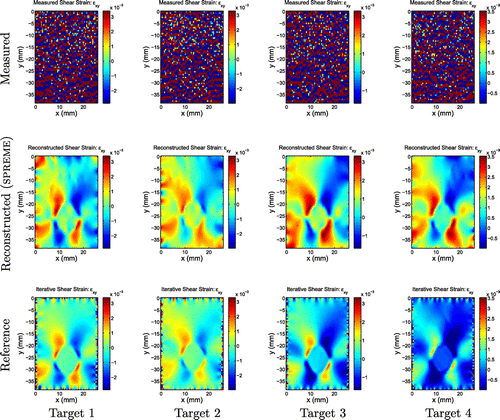
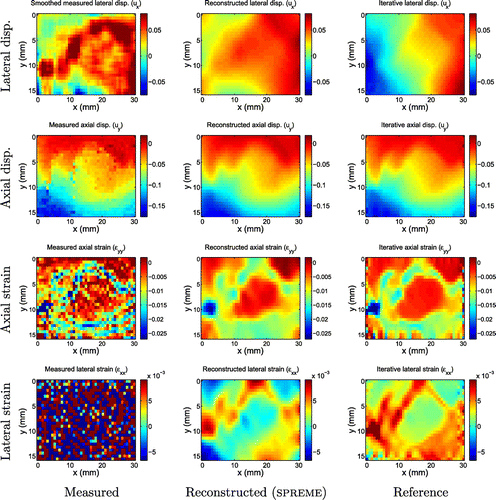
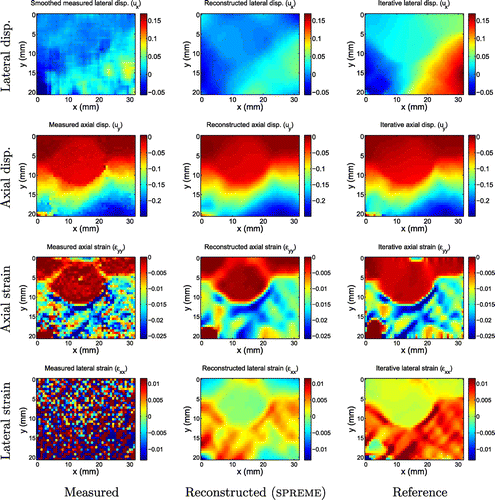
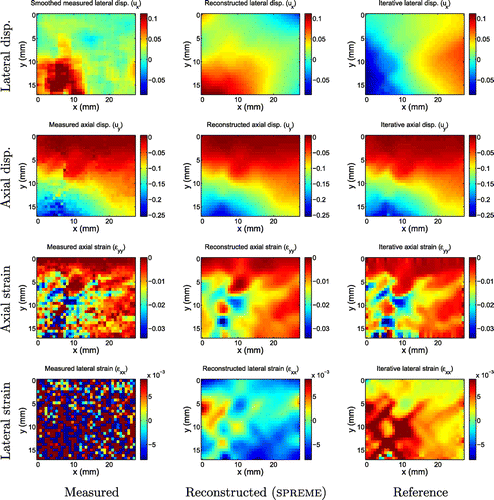
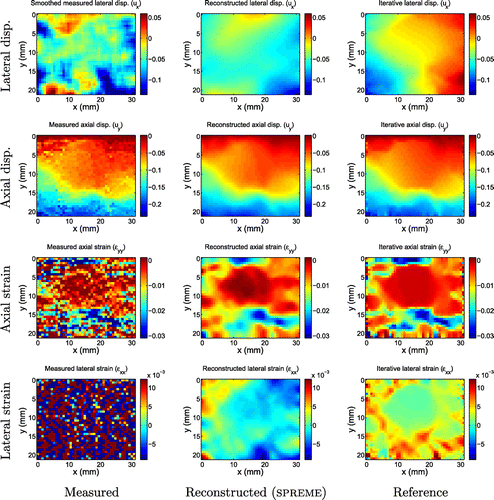
Figure 14. Displacement fields measured in-vivo in the breast as described in [Citation10]. Upper row: Fibroadenoma, a benign breast tumour (FA 3) Lower row: Invasive Ductal Carcinoma, a malignant breast tumour (IDC 2).
![Figure 14. Displacement fields measured in-vivo in the breast as described in [Citation10]. Upper row: Fibroadenoma, a benign breast tumour (FA 3) Lower row: Invasive Ductal Carcinoma, a malignant breast tumour (IDC 2).](/cms/asset/1aca1ed9-4d1d-4f5b-9220-f7c4e2510cd6/gipe_a_1161034_f0014_oc.gif)
Figure 15. Displacement and strain images for fibroadenoma 3. We note that the reconstructed SPREME lateral displacements reproduce the gross features seen in the smoothed measurements, while the reference method does not.
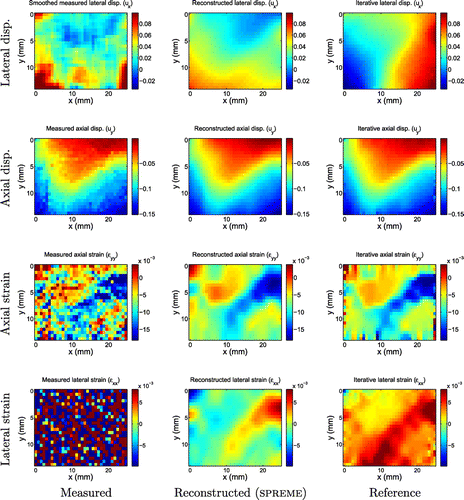
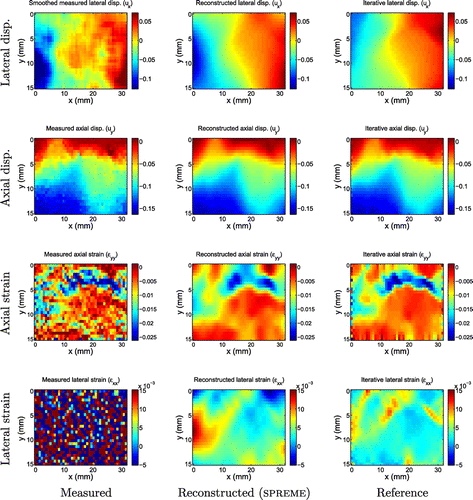
Figure 16. Displacement and strain images for invasive ductal carcinoma 2. In this example, we see more consensus between the gross features of the smoothed measurements, the reconstructed SPREME lateral displacements and the reference lateral displacements.
4.1. Phantom tests
The displacement data used for the test were measured within a gelatin phantom under uniaxial compression as described in [Citation9]. Here, for completeness of presentation, we briefly describe the data collection procedure. An agar and gelatin phantom was manufactured to have the acoustic and mechanical properties of soft tissue using methods described in [Citation45]. The phantom was a 100-mm cube containing four spherical inclusions of diameter 10 mm. The inclusion centres are coplanar in a horizontal plane separated by 30 mm centre-to-centre distance. Each of the inclusions has a different material Young’s modulus.[Citation9]
4.1.1. Ultrasound imaging and displacement estimation
The phantom was imaged with a Siemens SONOLINE Antares (Siemens Medical Solutions USA, Inc, Malvern, PA) clinical ultrasound system, with a linear ultrasound transducer array (Siemens VFX9-4) which was pulsed at 8.89MHz.[Citation9] A 15- cm 15- cm compression plate, much larger than the phantom surface, was attached to the ultrasound transducer to help generate approximately uniaxial deformation of the phantom. The phantom was first imaged before any deformation was applied, and it was imaged after every 0.5% strain up until a total strain of 20% with respect to the phantom’s height.[Citation9] During the imaging, RF data, representing the spatial distribution of the backscattered pressure field, were recorded. A modified block matching algorithm was used to estimate the displacement field from the RF data.[Citation46] Because the models used in this paper depend on the small strain assumption, we use only the measured deformation fields corresponding to small strain; specifically, we choose
overall strain.
4.1.2. Reference results
We compare our reconstructed displacement fields to two reference fields.
The first reference displacement is simply the spatially smoothed version of the measured lateral displacement field. This smoothing is achieved by performing a local spatial average with corrections at the boundaries. A smoothed displacement field reveals its main features, but, of course, obscures detail.
A second reference displacement field is computed as the result of a second inverse problem to reconstruct the linear elastic shear modulus, as described in [Citation10]. To that end, given a current guess of the modulus field, a forward elasticity problem is solved driven by assumed boundary conditions. The modulus field is updated to minimize the difference between measured and predicted displacements. Only axial displacements are used in the minimization.
4.1.3. Phantom results and discussion
The displacement for each target was downsampled to a 63 54 grid, which is the same grid that was used to generate the reference results.[Citation9] Images of the measured, smoothed, reconstructed and reference displacements are shown in Figures and . The parameters used for SPREME processing were:
. Eleven iterations were performed for each target, though it was observed that the strains typically converged by the 5th iteration.
We note that the reconstructed axial displacements match the measured and reference axial displacements very closely. The reconstructed lateral displacements, however, were less similar to the reference displacements. This difference is most noticeable in targets 3 and 4. It is interesting to note that the general features in the SPREME displacement images for both these targets are more similar to the smoothed measurements than are the general features in the reference displacement images. This indicates that the reference lateral displacements are in error, and this is likely due to errors in the assumed boundary conditions used to compute the reference results.Footnote2
Axial strain images () for each target are shown in Figure , while the lateral strain fields (
) are in Figure . The measured (resp. reference) strains were computed by differentiating the measured (resp. reference) displacement fields using a finite difference approximation. Three observations may be made. First, except for the lateral measured strain, all strain fields show clearly the presence of a stiff inclusion of the same size and shape, and with similar strain contrasts. The high noise level in the measured lateral displacement fields, however, is magnified through differentiation to a point where it obscures all features that might be present in the data. Second, we note boundary artefacts in the reference strain fields; these are caused by the assumed boundary conditions in the reference reconstruction method. The SPREME strain fields are relatively free of such artefacts. Third, strain contrast or dynamic range is slightly (resp. significantly) higher in the SPREME axial (resp. lateral) strain reconstructions than in the reference fields. This is perhaps due to deleterious effects of regularization used in the reference method, which tends to diminish modulus, and thus reconstructed strain, contrast. Similar observations may be made when comparing shear strains, Figure .
We compare the measured and reconstructed strains by estimating the contrast, and the contrast-to-noise (CNR) ratio. For the CNR, we define contrast as , where
is the average strain over a representative region in the inclusion, and
is the average strain over a representative region in the background. The noise is estimated as the standard deviation of the strain values in the background region. For target 1, the axial strain contrast in the measured strain field is estimated to be
, while that in the recovered strain field is
. The CNR is estimated to be 2.3 for the measured strain field, and 10.4 for the recovered strain field. This confirms that the strain contrast is preserved through the processing, but the CNR is significantly improved, as clearly evident in Figure .
5. Application to in-vivo image data
In this section, we test SPREME with in-vivo displacement data measured from patients with breast masses. The main goal of this test is to evaluate whether SPREME is sufficiently robust to provide useful results with clinical data. The in-vivo displacement data used for the tests have been processed with an iterative inversion code in a different study described in [Citation10]. The results from that study will be used as a reference to benchmark the results produced by SPREME. These results contain displacement fields from five biopsy-proven fibroadenomas and five biopsy proven invasive ductal carcinomas, which represent the most common forms of benign and malignant breast tumours. For the present purposes of demonstration, in this section, we present results from one of each; the reconstructed displacement and strains for the other eight cases are shown in Appendix 2. For all the cases treated, we work on the same mesh as used in [Citation10], and focus on displacement fields corresponding to roughly 1% overall strain in order to stay in the linear range. The input measured displacement fields used are shown in Figure .
5.1. In-vivo results and discussion
The parameters used for SPREME processing of the clinical data were: . The reconstructed displacement and strain fields obtained after the 11th iteration are shown in Figures and , along with the reference fields. As with the validation study, we compare to two reference fields: the smoothed measured lateral displacement fields, and the results obtained by an iterative inversion algorithm published in [Citation10]. Generally speaking, we see excellent agreement between all three fields in the axial displacement and strain components.
In the lateral displacement and strain fields, however, there is less consistency. The SPREME lateral displacement fields tend to reproduce the gross features seen in the smoothed lateral displacement measurements; the reference results, however, sometimes agree (c.f. Figure ), and sometimes disagree (c.f. Figure ) with the other two. The reference displacements seem to indicate an outward motion at the left and right side of the imaged domain in all the tumour cases (even in the eight other cases shown in Appendix 2). The smoothed measurements and the predicted displacements from SPREME, however, do not indicate this type of motion in all the tumour cases. This outward motion predicted by an iterative inversion code is probably an artefact due to the assumed boundary condition of traction free sides on the left and right sides of the imaged domain, and an implied symmetry. These assumptions may not be always valid in practice.
In contrast to the lateral displacement fields, the lateral strain fields recovered from SPREME were remarkably similar to the reference strains in all cases. This is surprising because the reconstructed lateral displacements were not always similar to the reference lateral displacements. This implies that the dominant difference between the SPREME and reference lateral displacement may be a rigid body mode.
6. Summary and conclusions
In this paper, we consider the problem of reconstructing both components of a 2D vector displacement field in a heterogenous elastic medium, given a precise measurement of one of the two components and a noisy measurement of the other. This problem is motivated by applications in quasistatic ultrasound elastography, in which technological limitations allow the very precise measurement of one component of displacement, but impede the measurement of others.
Under the assumption that the material is piecewise homogenous, we proved that the momentum equations and knowledge of one component of the displacement field determine the other displacement component up to four undetermined coefficients. We then went on to derive a variational formulation that can exploit the condition of piecewise homogeneity without other a priori knowledge of modulus distribution.
We then showed verification, validation and application of a finite element implementation from this variational formulation. The verification was performed on simulated data and showed that the method described here converges quickly, and dramatically reduces error in the noisy (uncertain) displacement component. This came at the expense of a slight increase in noise in the precise components. Nevertheless, in the verification studies conducted, the overall strain error reduced from roughly O(1) (several hundred percent) to (a few percent). The validation studies showed that this method produces realistic displacement fields from measurements in tissue mimicking phantoms. The predicted displacements tend to be more consistent with measurements than those of a reference method in the literature. Finally, the application of SPREME to data collected in-vivo demonstrates that SPREME is sufficiently robust to work in the application domain that originally motivated its development.
Further improvements in lateral displacement estimation with SPREME are possible. Since SPREME is a post-processing method, it can be used in conjunction with the other lateral displacement estimation techniques outlined in the introduction to obtain more precise estimates of the displacement field. Since these methods produce improved measurements of the lateral displacements, relatively large weights can potentially be used on the lateral displacements when processing them with SPREME. This processing can be done efficiently because SPREME converges in very few iterations.
An area that needs further work is finding a systematic method to identify good choices of the algorithmic parameters in SPREME. Regularization parameter selection is an open and active area of research in inverse problems, and is not addressed in the present study.
The SPREME approach may be generalized to other applications, as described in [Citation42]. The idea is that one identifies the form of the momentum equation that results for a homogeneous material property distribution. This equation is then enforced almost everywhere, as indicated in Equation (Equation3(3)
(3) ). See [Citation42] for details.
Acknowledgements
The authors will like to thank Prof. Timothy J. Hall and members of his lab at the University of Wisconsin for sharing the phantom and in-vivo displacement data.
Additional information
Funding
Notes
No potential conflict of interest was reported by the authors.
1 A ‘special interface’ would be one for which there exists s.t.
for all (x, y) on the interface.
2 We recall that the iterative inversion code performs a forward elasticity solve at every iteration. This solve requires displacement and traction boundary conditions. The lateral direction is assumed to be traction free. The measured axial displacements were fixed as boundary conditions on all four edges of the phantom.
References
- Gao L, Parker K, Lerner R, et al. Imaging of the elastic properties of tissue -- a review. Ultrasound Med. Biol. 1996;22:959–977.
- Ophir J, Alam S, Garra B, et al. Elastography: ultrasonic estimation and imaging of the elastic properties of tissues. Proc. Inst. Mech. Eng. Part H: J. Eng. Med. 1999;213:203–233.
- Parker KJ, Taylor LS, Gracewski S, et al. A unified view of imaging the elastic properties of tissue. J. Acoust. Soc. Am. 2005;117:2705–2712.
- Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annu. Rev. Biomed. Eng. 2003;5:57–78.
- Parker KJ, Doyley M, Rubens D. Imaging the elastic properties of tissue: the 20 year perspective. Phys. Med. Biol. 2011;56:R1–R29.
- Doyley M. Model-based elastography: a survey of approaches to the inverse elasticity problem. Phys. Med. Biol. 2012;57:R35–R73.
- Szabo TL. Diagnostic ultrasound imaging: inside out. Kidlington: Elsevier Academic Press; 2004.
- Barbone PE, Oberai AA. A review of the mathematical and computational foundations of biomechanical imaging. In: Suvranu D, Farshid G, Mohammad M,editors. Computational modeling in biomechanics. Dordrecht: Springer; 2010. p. 375–408.
- Dord J, Goenezen S, Oberai A, et al. Validation of quantitative linear and nonlinear compression elastography. In: Nenadic IZ, Urban MW, Greenleaf JF, editors. Ultrasound elastography for biomedical applications and medicine. Elsevier; 2016.
- Goenezen S, Dord J, Sink Z, et al. Linear and nonlinear elastic modulus imaging: An application to breast cancer diagnosis. IEEE Trans. Med. Imaging. 2012;31:1628–1637.
- Richards M, Barbone P, Oberai A. Quantitative three-dimensional elasticity imaging from quasi-sta tic deformation: a phantom study. Phys. Med. Biol. 2009;54:757–779.
- Albocher U, Oberai A, Barbone P, et al. Adjoint-weighted equation for inverse problems of incompressible plane-stress elasticity. Comput. Methods Appl. Mech. Eng. 2009;198:2412–2420.
- Barbone P, Rivas C, Harari I, et al. Adjoint-weighted variational formulation for the direct solution of inverse problems of general linear elasticity with full interior data. Int. J. Numer. Methods Eng. 2010;81:1713–1736.
- Albocher U, Barbone P, Richards M, et al. Approaches to accommodate noisy data in the direct solution of inverse problems in incompressible plane strain elasticity. Inverse Probl. Sci. Eng. 2014;22:1307–1328.
- Konofagou E, Ophir J. A new elastographic method for estimation and imaging of lateral displacements, lateral strains, corrected axial strains and poissons ratios in tissues. Ultrasound Med. Biol. 1998;24:1183–1199.
- Geiman BJ, Bohs LN, Anderson ME, et al. A novel interpolation strategy for estimating subsample speckle motion. Phys. Med. Biol. 2000;45:1541–1552.
- Konofagou EE, Ophir J. Precision estimation and imaging of normal and shear components of the 3d strain tensor in elastography. Phys. Med. Biol. 2000;45:1553–1563.
- Chen X, Zohdy M, Emelianov S, et al. Lateral speckle tracking using synthetic lateral phase. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004;51:540–550.
- Ebbini E. Phase-coupled two-dimensional speckle tracking algorithm. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2006;53:972–990.
- Brusseau E, Kybic J, Deprez J-F, et al. 2-D locally regularized tissue strain estimation from radio-frequency ultrasound images: theoretical developments and results on experimental data. IEEE Trans. Med. Imaging. 2008;27:145–160.
- Deprez J-F, Brusseau E, Schmitt C, et al. 3D estimation of soft biological tissue deformation from radio-frequency ultrasound volume acquisitions. Med. Image Anal. 2009;13:116–127.
- Kim S, Aglyamov SR, Park S, et al. An autocorrelation-based method for improvement of sub-pixel displacement estimation in ultrasound strain imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011;58:838–843.
- Rivaz H, Boctor EM, Choti MA, et al. Real-time regularized ultrasound elastography. IEEE Trans. Med. Imaging. 2011;30:928–945.
- Mailloux GE, Bleau A, Bertrand M, et al. Computer analysis of heart motion from two-dimensional echocardiograms. IEEE Trans. Biomed. Eng. 1987;BME-34:356–364.
- Basarab A, Liebgott H, Morestin F, et al. A method for vector displacement estimation with ultrasound imaging and its application for thyroid nodular disease. Med. Image Anal. 2008;12:259–274.
- Tanter M, Bercoff J, Sandrin L, et al. Ultrafast compound imaging for 2-d motion vector estimation: application to transient elastography. IEEE Trans Ultrason. Ferroelectr. Freq. Control. 2002;49:1363–1374.
- Techavipoo U, Chen Q, Varghese T, et al. Estimation of displacement vectors and strain tensors in elastography using angular insonifications. IEEE Trans. Med. Imaging. 2004;23:1479–1489.
- Rao M, Chen Q, Shi H, et al. Normal and shear strain estimation using beam steering on linear-array transducers. Ultrasound Med. Biol. 2007;33:57–66.
- Hansen H, Lopata R, Idzenga T, et al. Full 2d displacement vector and strain tensor estimation for superficial tissue using beam-steered ultrasound imaging. Phys. Med. Biol. 2010;55:3201–3218.
- Xu H, Varghese T. Normal and shear strain imaging using 2d deformation tracking on beam steered linear array datasets. Med. Phys. 2013;40:012902. 13 p.
- Abeysekera JM, Zahiri Azar R, Goksel O, et al. Analysis of 2-d motion tracking in ultrasound with dual transducers. Ultrasonics. 2012;52:156–168.
- Korukonda S, Doyley MM. Estimating axial and lateral strain using a synthetic aperture elastographic imaging system. Ultrasound Med. Biol. 2011;37:1893–1908.
- Korukonda S, Doyley MM. Visualizing the radial and circumferential strain distribution within vessel phantoms using synthetic-aperture ultrasound elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012;59:1639–1653.
- Jensen JA, Munk P. A new method for estimation of velocity vectors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998;45:837–851.
- Liebgott H, Wilhjehm J, Jensen JA, et al. Psf dedicated to estimation of displacement vectors for tissue elasticity imaging with ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007;54:746–756.
- Lubinski M, Emelianov S, Raghavan K, et al. Lateral displacement estimation using tissue incompressibility. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1996;43:247–256.
- Skovoroda AR, Lubinski MA, Emelianov SY, et al. Nonlinear estimation of the lateral displacement using tissue incompressibility. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998;45:491–503.
- O’Donnell M, Chen X, Kaluzynski K, et al. Strain magnitude estimation based on adaptive incompressibility processing. In: 2001 IEEE Ultrasonics Symposium. Vol. 2; Atlanta, GA: IEEE; 2001. p. 1643–1646.
- Hu Z, Zhang H, Yuan J, et al. An H∞ strategy for strain estimation in ultrasound elastography using biomechanical modeling constraint. PloS One. 2013;8:1–15.
- Atkin RJ, Fox N. An introduction to the theory of elasticity. Mineola, NY: Dover Publications; 2005.
- Hughes TJR. The finite element method: linear static and dynamic finite element analysis. Dover Publications; 2000.
- Babaniyi O. Direct elastic modulus reconstruction via sparse relaxation of physical constraints [Master’s thesis]. Boston, MA: Boston University; 2012.
- Honein T. On heterogenization in elasticity [PhD dissertation]. Stanford, CA: Stanford University; 1990.
- Vogel CR. Computational methods for inverse problems. Vol. 10. Philadelphia: SIAM; 2002.
- Pavan T, Madsen E, Frank G, et al. Nonlinear elastic behavior of phantom materials for elastography. Phys. Med. Biol. 2010;55:2679–2692.
- Jiang J, Hall T. A fast hybrid algorithm combining regularized motion tracking and predictive search for reducing the occurrence of large displacement errors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011;58:730–736.
Appendix 1
Formulation without compatibility
Given ,
and
, find
that minimizes:
(A1)
(A1)
where:(A2)
(A2)
and:(A3)
(A3)
In Equation (EquationA2(A2)
(A2) ),
is a fourth-order weighting tensor that allows more importance to be placed on the more accurate strain component. So in ultrasound measurements, where the axial strains (
) are typically more accurate than the lateral and shear strains (
), the
weights will be larger than
and
.
Equation (EquationA1(A1)
(A1) ) was minimized with respect to
to get the weak form using the same method outlined in Section 2.2. The weak form was then discretized with finite element bilinear shape functions to get a linear system of equations. A finite element within an in-house FEM code was created to solve the linear system of equations.
This formulation was tested with the perfect input displacements shown in Figure . The following parameters were used to run the code: ,
,
,
,
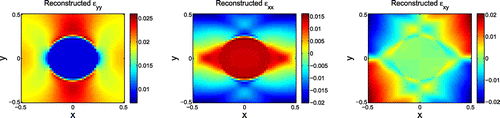
. These weights were chosen in order to simulate ultrasound measurements where the lateral and shear strains are not well known. Five iterations were performed, and the reconstructions obtained at the fifth iteration are shown in Figure . The lateral and shear strains look very different from the target distributions shown in Figure .
Table A1. Errors in the recovered strains after the fifth iteration.
To quantitatively determine how accurate the reconstructions were, the errors between the reconstructed strains at the fifth iteration and target strains were computed using the formula shown in Equation (Equation48(48)
(48) ). The results of this computation are displayed in Table . These results show that the lateral and shear strains are not accurate.
Another method used to check the output strains from the FE code is the compatibility equations which are shown below [Citation40]:(A4)
(A4)
The equation used to check the compatibility condition is slightly different from the equation shown in (EquationA4(A4)
(A4) ). The derivation of the equation used is shown below:
(A5)
(A5)
(A6)
(A6)
(A7)
(A7)
(A8)
(A8)
In (EquationA8(A8)
(A8) ),
is introduced as a measure of incompatibility. Setting
in (EquationA8
(A8)
(A8) ), and taking its derivative with respect to x, we see that it is the same as Equation (EquationA4
(A4)
(A4) ). Therefore, by knowing
and
, we can use Equation (EquationA8
(A8)
(A8) ) to check that the strains from the FE code satisfy the compatibility equation.
was evaluated pointwise within the domain for each of the experiments performed. To get a sense of how well the compatibility equation is satisfied for each experiment, we calculate the
norm. The formula used to evaluate the
norm is defined below:
(A9)
(A9)
The norm of
was computed for a large range of experiments where the weights were varied, and the parameters
,
and n were fixed to
,
and 0.5, respectively. The results from these experiments are shown in Table . The results on the table demonstrate that the compatibility equation becomes increasingly violated as
and
are reduced, and the level of violation is maximum when
. The mesh size for the experiment is 0.02; therefore, any value of
smaller than this mesh size can be neglected as discretization error. When
and
become smaller than
, then the compatibility equation becomes violated for the experiment. This means that this alternate formulation cannot be used to calculate correct strains when the weights for the lateral and shear strain components are too small. When the weights for some of the strain components are small, the FE code constrains the corresponding strains with small weights to satisfy the equilibrium equations, but the strains are not forced to come from a single-valued continuous displacement field. This formulation will therefore not work on real measured data where we would wish to use small weights to exclude the strain components calculated from the imprecisely measured displacement component.
Table A2. Compatibility results using various weights.
By way of comparison, the SPREME formulation yields .
Appendix 2
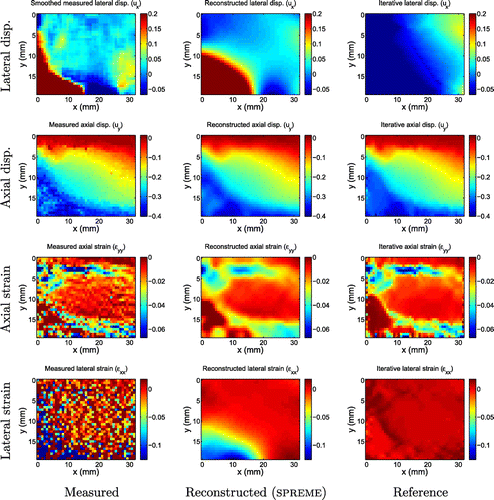
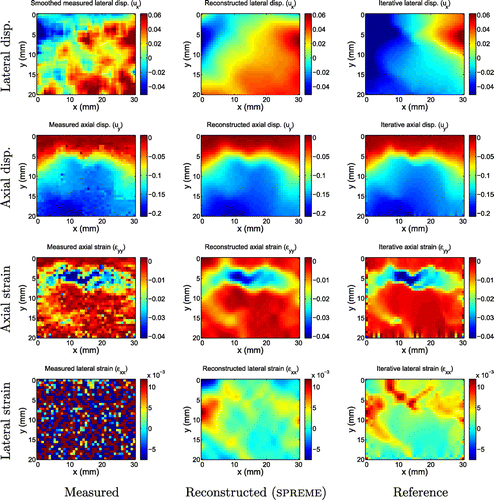
Clinical data reconstructions
In this section, for completeness, we show the reconstructions obtained from processing the rest of the in-vivo data from [Citation10]. The observations made earlier apply to these results as well. 0