Inverse problem of fracture mechanics for a circular disc under mixed boundary conditions

Abstract

Solution method for the problem of prevention of early brittle fracture of a circular disc with mixed boundary conditions was proposed. Theoretical analysis on determination of normal displacement of points on the boundary of a circular disc weakened by arbitrarily allocated rectilinear cracks was carried out. A closed system of algebraic equations permitting to provide minimization of fracture parameters (stress intensity factors) subject to geometrical and mechanical characteristics of a disc was constructed. Minimization of the stress intensity factors in a circular disc was carried out. They found normal displacement of points on the boundary of the circular disc increases carrying capacity of the disc.

Keywords:

• Circular disc
• mixed boundary conditions
• cracks
• function of displacement of points of disc’s boundary
• minimization of fracture parameters

Introduction

Circular discs are widely used in modern mechanisms. Discs strength problems are very urgent and undoubtedly, the interest to these problems will increase in connection with the existing tendency of machine-building and power development. To analyse the reliability of discs, it is necessary to research their stress–strain state and fracture. Simulation and analysis of stress–strain state in discs has a special applied value first of all for right choice of their construction, optimal sizes and permissible value of workloads. Discs often work under very intensive conditions. There is voluminous literature on strength analysis of discs (see review in the monographs [1,2]).

In the papers [3–6], the model of nucleation and propagation of cohesive cracks in circular discs under mixed boundary conditions was constructed. On the design stage of new constructions, it is necessary to take into account the cases when in the elements of the details of machines there may arise cracks, and to carry out limit analysis to establish that the would-be initial cracks will not grow to critical sizes and will not cause fracture in the course of estimated service life. The size of initial minimal crack should be considered as the design characteristics of material. On the contemporary stage of development of engineering, optimal design of machine elements, providing their serviceability, is of great value. Therefore, optimal design of circular discs has a significant value. Using design-technological methods, in particular the geometry of a disc (displacements of the points of the boundary), one can reasonably control the serviceability increase of a disc.

The solution of a mechanics problem for determining such a function of displacements of the points of a circular disc boundary under which the stress created by these displacements could retard the crack growth in a disc is of significant interest.

Formulation of the problem

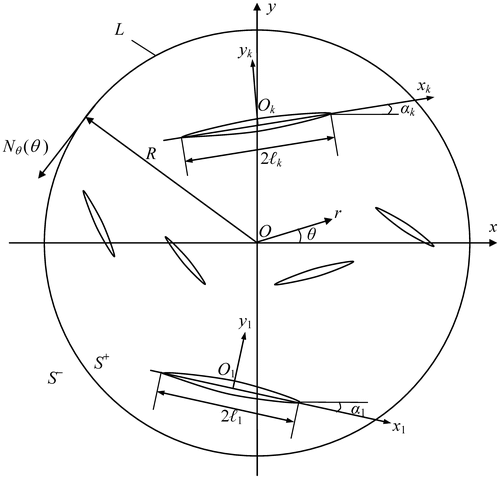
We assume that the disc has N rectilinear cracks of length 2ℓ_k (k = 1, 2, …, N). At the centres of the cracks, allocate the origin of local systems of coordinates x_kO_ky_k whose axes x_k coincide with the crack lines and form the angles α_k with the axis x (Figure 1). The crack faces are free from external loads. The normal displacement ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$ and tangential component of surface forces $N_{\mathit{\theta }}\left(\mathit{\theta }\right)$ hold on the boundary of the circular disc. The function ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$ is assumed to be a sought-for function. It is required to determine the normal displacement ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$ on the disc’s boundary so that the stress field created by it prevents the crack propagation.

Figure 1. Calculation scheme of inverse problem of fracture mechanics for a disc.

In the problem under consideration, the boundary conditions have the form:(1) $${\mathit{\tau }}_{r\mathit{\theta }}=N_{\mathit{\theta }}\left(\mathit{\theta }\right);{\mathit{\upsilon }}_r=f_r\left(\mathit{\theta }\right)\text{on}L,$$(1) (2) $${\mathit{\sigma }}_{y_k}=0;{\mathit{\tau }}_{x_k{y}_k}=0\text{on}{L}_k(k=1,2,\dots ,N)$$(2)

where L is the disc’s circular boundary and L_k are the faces of the k-th crack.

Case of a single crack

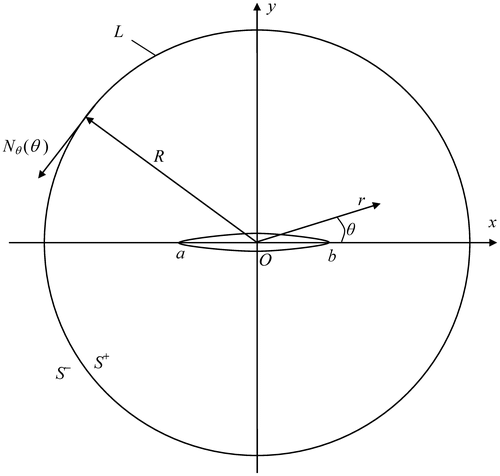
We denote the considered domain contained between the circle L of radius R and the rectilinear crack $L_1=\left[a,b\right]$ (α₁ = 0) along the abscissa axis by S⁺, the domain to be complemented to the complete complex plane by S⁻ (Figure 2).

Figure 2. Calculation scheme of inverse problem of fracture mechanics for case of a single crack.

Under the conditions of a plane problem, the disc’s stress–strain state is described by two analytic functions $\mathrm{\Phi }\left(z\right)$ and $\mathrm{\Omega }\left(z\right)$ of complex variable(3) $${\mathit{\sigma }}_x+{\mathit{\sigma }}_y=4\text{Re}\mathrm{\Phi }\left(z\right);$$(3) $${\mathit{\sigma }}_y-i{\mathit{\tau }}_{xy}=\mathrm{\Phi }\left(z\right)+\mathrm{\Omega }\left(\overline{z}\right)+\left(z-\overline{z}\right)\overline{{\mathrm{\Phi }}^{\prime }\left(z\right)};$$(4) $$2\mathit{\mu }\frac{\mathit{\partial }}{\mathit{\partial }x}\left(u+i\mathit{\upsilon }\right)=\mathit{\kappa }\mathrm{\Phi }\left(z\right)-\mathrm{\Omega }\left(\overline{z}\right)-\left(z-\overline{z}\right)\overline{{\mathrm{\Phi }}^{\prime }\left(z\right)};$$(4) $$\mathrm{\Omega }(z)=\overline{\mathrm{\Phi }}(z)+z{\overline{\mathrm{\Phi }}}^{\prime }(z)+\overline{\mathrm{\Psi }}(z),$$

where $\mathit{\kappa }=\left(3-v\right)/\left(1+v\right)$; v is the Poisson ratio of the disc’s material; μ is the shear modulus of the material.

Under these assumptions, the problem is reduced to determination of two analytic functions of complex variable $\mathrm{\Phi }\left(z\right)$ and $\mathrm{\Omega }\left(z\right)$ analytic in the domain S⁺ and satisfying the following boundary conditions on the contour L:(5) $$\text{Re}\left\{\mathit{\kappa }\mathrm{\Phi }\left(t\right)-\overline{\mathrm{\Phi }\left(t\right)}+\frac{R^2}{t^2}\left[t\overline{{\mathrm{\Phi }}^{\prime }\left(t\right)}+\overline{\mathrm{\Psi }\left(t\right)}\right]\right\}=2\mathit{\mu }{f}_r^{\prime }\left(t\right),$$(5) (6) $$\text{Im}\left\{\mathrm{\Phi }\left(t\right)+\overline{\mathrm{\Phi }\left(t\right)}-\frac{t^2}{R^2}\left[\overline{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right]\right\}=-N_{\mathit{\theta }}\left(t\right).$$(6)

The loading conditions on the crack faces $L_1^{+}$ and $L_1^{-}$ and will be:(7) $${\mathrm{\Phi }}^{+}\left(x\right)+{\overline{\mathrm{\Phi }}}^{-}\left(x\right)+x{\overline{\mathrm{\Phi }}}^{-\prime }\left(x\right)+{\overline{\mathrm{\Psi }}}^{-}\left(x\right)=0\text{on}{L}_1^{+},$$(7)

$${\mathrm{\Phi }}^{-}\left(x\right)+{\overline{\mathrm{\Phi }}}^{+}\left(x\right)+x{\overline{\mathrm{\Phi }}}^{+\prime }\left(x\right)+{\overline{\mathrm{\Psi }}}^{+}\left(x\right)=0\text{on}{L}_1^{-}.$$

For finding the normal displacement function ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$ on L, the problem statement should be complemented by the condition (criterion) of determination of the sought-for normal displacement function. According to the Irwin-Orowan’s theory of quasi-brittle fracture, the stress intensity factor is a parameter characterizing the stress state in the vicinity of the crack tip. Thus, the quantity of maximum value of the stress intensity factor in the vicinity of the crack tip may be considered responsible for fracture of the disc’s material.

Studying the main fracture parameters and influence of the normal displacement ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$ on the disc’s boundary, properties of the material and other factors on them, one can reasonably control the fracture by design-technological methods, in particular by the displacements on the disc’s boundary. As a criterion of determination of the normal displacement ${\mathit{\upsilon }}_r\left(\mathit{\theta }\right)$, we take the minimization (equality to zero) of stress intensity factors in the vicinity of the crack tip. This minimization promotes serviceability increase in the circular disc.

Without loss of generality of the stated problem, it is accepted that the sought-for function of normal displacement $f_r\left(\mathit{\theta }\right)$ may be represented in the form of the Fourier series. Therefore, we should order the coefficients V_k of expansion of the sought-for function of normal displacement so that the minimization (equality to zero) of stress intensity factors is provided. This additional condition admits to determine the sought-for normal displacement function of $f_r\left(\mathit{\theta }\right)$ on the disc’s boundary. Passing in relations (5) and (6) to conjugated values, after some transformations on the contour L, we get boundary conditions in the form(8) $$\begin{array}{c}\left(\mathit{\kappa }-1\right)\left[\mathrm{\Phi }\left(t\right)+\overline{\mathrm{\Phi }\left(t\right)}\right]+\frac{R^2}{t^2}\left[t\overline{{\mathrm{\Phi }}^{\prime }\left(t\right)}+\overline{\mathrm{\Psi }\left(t\right)}\right]\hfill \\ +\frac{t^2}{R^2}\left[\frac{R^2}{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right]=4\mathit{\mu }{f}_r^{\prime }\left(t\right)\text{on}L,\hfill \end{array}$$(8) (9) $$-\frac{R^2}{t^2}\left[t\overline{{\mathrm{\Phi }}^{\prime }\left(t\right)}+\overline{\mathrm{\Psi }\left(t\right)}\right]+\frac{t^2}{R^2}\left[\frac{R^2}{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right]=2i{N}_{\mathit{\theta }}\left(t\right)\text{on}L.$$(9)

Based upon (8) and (9), on the circle L we have(10) $$\left(\mathit{\kappa }-1\right)\left[\mathrm{\Phi }\left(t\right)+\overline{\mathrm{\Phi }\left(t\right)}\right]+\frac{2t^2}{R^2}\left[\frac{R^2}{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right]=2\left[2\mathit{\mu }{f}_r^{\prime }\left(t\right)+i{N}_{\mathit{\theta }}\left(t\right)\right].$$(10)

To this equality (10), we substitute the functions $f_r\left(t\right)$ and $N_{\mathit{\theta }}\left(t\right)$ in the form of the Fourier series(11) $$f_r\left(t\right)=\sum _{v=-\infty }^{\infty }{V_v\left(\frac{t}{R}\right)}^v,i{N}_{\mathit{\theta }}\left(t\right)=\sum _{v=-\infty }^{\infty }{T_v\left(\frac{t}{R}\right)}^v,$$(11)

where T_v (v = 0, ±1, ±2, …) are the known complex coefficients; V_k are the sought-for coefficients to be determined. As a result, we get(12) $$\begin{array}{c}\left(\mathit{\kappa }-1\right)\left[\mathrm{\Phi }\left(t\right)+\overline{\mathrm{\Phi }\left(t\right)}\right]+2\frac{t^2}{R^2}\left[\frac{R^2}{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right]\hfill \\ =2\left\{\sum _{v=0}^{\infty }\left[T_v+\frac{2\mathit{\mu }\left(v+1\right)}{R}{V}_{v+1}\right]{\left(\frac{t}{R}\right)}^v+\sum _{v=1}^{\infty }\left[T_{-v}-\frac{2\mathit{\mu }\left(v-1\right)}{R}{V}_{-v+1}\right]{\left(\frac{R}{t}\right)}^v\right\}.\hfill \end{array}$$(12)

Introducing on L a new unknown auxiliary function $\mathit{\omega }\left(t\right)\in H$ (the Holder condition) in the form(13) $$2\mathit{\omega }\left(t\right)=\left(\mathit{\kappa }-1\right)\left[\mathrm{\Phi }\left(t\right)+\overline{\mathrm{\Phi }\left(t\right)}\right]-\frac{2t^2}{R^2}\left[\frac{R^2}{t}{\mathrm{\Phi }}^{\prime }\left(t\right)+\mathrm{\Psi }\left(t\right)\right].$$(13)

Putting together relations (12) and (13), we have(14) $$\begin{array}{c}\mathrm{\Phi }\left(t\right)=\frac{\mathit{\omega }\left(t\right)}{\mathit{\kappa }-1}+\frac{1}{\mathit{\kappa }-1}\sum _{v=0}^{\infty }\left[\frac{2\mathit{\mu }\left(v+1\right)}{R}{V}_{v+1}+T_v\right]{\left(\frac{t}{R}\right)}^v\hfill \\ +\frac{1}{\mathit{\kappa }-1}\sum _{v=1}^{\infty }\left[T_{-v}-\frac{2\mathit{\mu }\left(v-1\right)}{R}{V}_{-v+1}\right]{\left(\frac{R}{t}\right)}^v\text{on}L.\hfill \end{array}$$(14)

Having substituted (14) in (13), we get(15) $$\mathrm{\Psi }\left(t\right)=Q\left(t\right)+R_1\left(t\right)+R_2\left(t\right)\text{on}L,$$(15)

where(16) $$Q\left(t\right)=-\frac{R^2}{2t^2}\left[\mathit{\omega }\left(t\right)+\overline{\mathit{\omega }\left(t\right)}\right]-\frac{R^2}{\left(\mathit{\kappa }-1\right)t}{\mathit{\omega }}^{\prime }\left(t\right),$$(16) (17) $$\begin{array}{c}{R}_1\left(t\right)=\sum _{v=0}^{\infty }\left[\frac{1}{2}\left(1-\frac{v-2}{\mathit{\kappa }-1}\right)T_{v+2}-\frac{1}{2}{\overline{T}}_{-v-2}+\frac{\mathit{\mu }\left(v+1\right)}{R}{V}_{-v-1}\right.\hfill \\ +\left.\frac{\mathit{\mu }\left(v+3\right)}{R}\left(1-\frac{v-2}{\mathit{\kappa }-1}\right)V_{v+3}\right]{\left(\frac{t}{R}\right)}^v,\hfill \end{array}$$(17) $$\begin{array}{c}{R}_2\left(t\right)=-\sum _{v=2}^{\infty }\left[\left.\frac{\mathit{\mu }\left(v-1\right)}{R}{\overline{V}}_{v-1}+\frac{1}{2}{\overline{T}}_{v-2}\right]{\left(\frac{R}{t}\right)}^v+\sum _{v=3}^{\infty }\left[\frac{1}{2}\left(1+\frac{v-2}{\mathit{\kappa }-1}\right)T_{-v+2}\right.\right.\hfill \\ -\left.\frac{\mathit{\mu }\left(v-3\right)}{R}\left(1+\frac{v-2}{\mathit{\kappa }-1}\right)V_{-v+3}\right]{\left(\frac{R}{t}\right)}^v+\left[\frac{\mathit{\mu }}{R}{V}_1+\frac{1}{2}{T}_0\right]\frac{R^2}{t^2}\hfill \\ +\left[\frac{1}{2}\left(1-\frac{1}{\mathit{\kappa }-1}\right)T_1-\right.\frac{1}{2}{\overline{T}}_{-1}\left.-\frac{\mathit{\mu }}{\left(\mathit{\kappa }-1\right)R}{V}_1+\frac{2\mathit{\mu }}{R}{V}_2\right]\frac{R}{t}.\hfill \end{array}$$

From relations (14) and (15), based upon the theorem on analytic continuation and the properties of the Cauchy-type integral, we have(18) $${\mathrm{\Phi }}_{\ast }\left(z\right)=\left\{\begin{array}{c}\begin{array}{c}\mathrm{\Phi }\left(z\right)-\frac{1}{\mathit{\kappa }-1}\frac{1}{2\mathit{\pi }i}\underset{L}{\int }\frac{\mathit{\omega }\left(t\right)}{t-z}\text{d}t-\frac{1}{\mathit{\kappa }-1}\sum _{v=0}^{\infty }\left[\frac{2\mathit{\mu }\left(v+1\right)}{R}{V}_{v+1}+T_v\right]{\left(\frac{z}{R}\right)}^{v}z\in S^{+},\hfill \\ \hfill \end{array}\hfill \\ -\frac{1}{\mathit{\kappa }-1}\frac{1}{2\mathit{\pi }i}\underset{L}{\int }\frac{\mathit{\omega }\left(t\right)\text{d}t}{t-z}+\frac{1}{\mathit{\kappa }-1}\sum _{v=1}^{\infty }\left[T_{-v}-\frac{2\mathit{\mu }\left(v-1\right)}{R}{V}_{-v+1}\right]{\left(\frac{R}{z}\right)}^{v}z\in S^{-},\hfill \end{array}\right.$$(18) (19) $${\mathrm{\Psi }}_{\ast }\left(z\right)=\left\{\begin{array}{c}\begin{array}{c}\mathrm{\Psi }\left(z\right)-\frac{1}{2\mathit{\pi }i}\underset{L}{\int }\frac{Q\left(t\right)}{t-z}\text{d}t-R_2\left(z\right)z\in S^{+},\hfill \\ \hfill \end{array}\hfill \\ -\frac{1}{2\mathit{\pi }i}\underset{L}{\int }\frac{Q\left(t\right)}{t-z}\text{d}t+R_2\left(z\right)z\in S^{-}.\hfill \end{array}\right.$$(19)

In relations (18)–(19), the functions ${\mathrm{\Phi }}_{\ast }\left(z\right)$ and ${\mathrm{\Psi }}_{\ast }\left(z\right)$ are analytic in the complete complex plane cut along the section $L_1=\left[a,b\right]$ (of the crack) and vanish at infinity, i.e. ${\mathrm{\Phi }}_{\ast }\left(\infty \right)=0$, ${\mathrm{\Psi }}_{\ast }\left(\infty \right)=0$.

We will look for the auxiliary unknown function $\mathit{\omega }\left(t\right)\in H$ on L in the form of the Fourier series(20) $$\mathit{\omega }\left(t\right)={\mathit{\alpha }}_0^{\ast }+\sum _{v=1}^{\infty }\left[{\mathit{\alpha }}_v^{\ast }{\left(\frac{t}{R}\right)}^v+{\mathit{\alpha }}_{-v}^{\ast }{\left(\frac{R}{t}\right)}^v\right],$$(20)

where ${\mathit{\alpha }}_v^{\ast }$ $\left(v=0,\pm 1,\pm 2,\dots \right)$ are unknown complex coefficients.

Substituting relation (20) into the first formulas of (18), (19) and using the Cauchy integral theorem, we get general formulas for the sought-for functions:(21) $$\mathrm{\Phi }\left(z\right)={\mathrm{\Phi }}_{\ast }\left(z\right)+\sum _{v=0}^{\infty }{B}_v{\left(\frac{z}{R}\right)}^{v}z\in S^{+},$$(21) $$\mathrm{\Psi }\left(z\right)={\mathrm{\Psi }}_{\ast }\left(z\right)+\sum _{v=0}^{\infty }{D}_v{\left(\frac{z}{R}\right)}^{v}z\in S^{+}$$

Here(22) $$B_v=\frac{1}{\mathit{\kappa }-1}\left[{\mathit{\alpha }}_v^{\ast }+T_v+\frac{2\mathit{\mu }\left(v+1\right)}{R}{V}_{v+1}\right],$$(22) $$\begin{array}{c}{D}_v=-\left(\frac{1}{2}+\frac{v+2}{\mathit{\kappa }-1}\right){\mathit{\alpha }}_{v+2}^{\ast }-\frac{1}{2}{\overline{\mathit{\alpha }}}_{-v-2}^{\ast }+\frac{1}{2}\left(1-\frac{v+2}{\mathit{\kappa }-1}\right)T_{v+2}\hfill \\ -\frac{1}{2}{\overline{T}}_{-v-2}+\frac{\mathit{\mu }\left(v+3\right)}{R}\left(1-\frac{v+2}{\mathit{\kappa }-1}\right)V_{v+3}+\frac{\mathit{\mu }\left(v+1\right)}{R}{\overline{V}}_{-v-1}.\hfill \end{array}$$

For determining the function ${\mathrm{\Phi }}_{\ast }\left(z\right)$ and consequently the function ${\mathrm{\Psi }}_{\ast }\left(z\right)$, by the known method [7] we arrive at a linear conjugation problem(23) $${\left[{\mathrm{\Phi }}_{\ast }\left(t\right)-{\mathrm{\Omega }}_{\ast }\left(t\right)\right]}^{+}-{\left[{\mathrm{\Phi }}_{\ast }\left(t\right)-{\mathrm{\Omega }}_{\ast }\left(t\right)\right]}^{-}=0;$$(23) $${\left[{\mathrm{\Phi }}_{\ast }\left(t\right)+{\mathrm{\Omega }}_{\ast }\left(t\right)\right]}^{+}+{\left[{\mathrm{\Phi }}_{\ast }\left(t\right)+{\mathrm{\Omega }}_{\ast }\left(t\right)\right]}^{-}=f\left(t\right).$$

Here$${\mathrm{\Omega }}_{\ast }\left(z\right)={\overline{\mathrm{\Phi }}}_{\ast }\left(z\right)+z{\overline{{\mathrm{\Phi }}^{\prime }}}_{\ast }\left(z\right)+{\overline{\mathrm{\Psi }}}_{\ast }\left(z\right);$$$$f\left(t\right)=\sum _{k=0}^{\infty }\left({\mathit{\beta }}_k+p_k\right){\left(\frac{t}{R}\right)}^k;$$

(24) $${\mathit{\beta }}_k=-2\left[\frac{1}{\mathit{\kappa }-1}{\mathit{\alpha }}_k^{\ast }+\frac{k+1}{\mathit{\kappa }-1}{\overline{\mathit{\alpha }}}_k^{\ast }-\frac{1}{2}{\mathit{\alpha }}_{-k-2}^{\ast }-\left(\frac{1}{2}+\frac{k+2}{\mathit{\kappa }-1}\right){\overline{\mathit{\alpha }}}_{k+2}^{\ast }\right];$$(24) $$\begin{array}{c}{p}_k=-2\left[\frac{1}{\mathit{\kappa }-1}{T}_k+\frac{k+1}{\mathit{\kappa }-1}{\overline{T}}_k-\frac{1}{2}{T}_{-k-2}+\left(\frac{1}{2}-\frac{k+2}{\mathit{\kappa }-1}\right){\overline{T}}_{k+2}\right.\hfill \\ \left.+\frac{2\mathit{\mu }\left(k+1\right)}{\left(\mathit{\kappa }-1\right)R}{V}_{k+1}+\frac{2\mathit{\mu }{\left(k+1\right)}^2}{\left(\mathit{\kappa }-1\right)R}{\overline{V}}_{k+1}+\frac{\mathit{\mu }\left(k+1\right)}{R}{V}_{-k-1}+\frac{\mathit{\mu }\left(k+3\right)}{R}\left(1+\frac{k+2}{\mathit{\kappa }-1}\right){\overline{V}}_{k+3}\right].\hfill \end{array}$$

The sought-for solution of boundary value problem (23) is written in the form(25) $${\mathrm{\Phi }}_{\ast }\left(z\right)={\mathrm{\Omega }}_{\ast }\left(z\right)=\frac{1}{2\mathit{\pi }i\sqrt{\left(z-a\right)\left(z-b\right)}}\underset{a}{\overset{b}{\int }}\frac{\sqrt{\left(t-a\right)\left(t-b\right)}f\left(t\right)\text{d}t}{\left(t-z\right)}.$$(25)

Here as(26) $$z\to \infty \sqrt{(z-a)(z-b)}=z+\mathrm{O}\left(1/z\right).$$(26)

The root under the integration sign is the value of the branch of appropriate analytic function distinguished by condition (26) on the upper crack face. Using solution (25), for the stress intensity factors, we have(27) $$K_I^a+i{K}_{II}^a=\frac{\sqrt{2}}{\sqrt{\mathit{\pi }{\left(b-a\right)}^{}}}\underset{a}{\overset{b}{\int }}f(x)\sqrt{\frac{b-x}{x-a}}\text{d}x,$$(27) $$K_I^b+i{K}_{II}^b=\frac{\sqrt{2}}{\sqrt{\mathit{\pi }{\left(b-a\right)}^{}}}\underset{a}{\overset{b}{\int }}f(x)\sqrt{\frac{x-a}{b-x}}\text{d}x.$$

Through the function f(x), the sought-for coefficients ${\mathit{\alpha }}_k^{\ast }$, V_k enter into the obtained relation.

For composing the systems of infinite linear algebraic equations with respect to unknowns ${\mathit{\alpha }}_k^{\ast }$ $\left(k=0,\pm 1,\pm 2,\dots \right)$, we substitute (21), (22) allowing for (25) and expansions$$\sqrt{\left(t-a\right)\left(t-b\right)}=t\sum _{r=0}^{\infty }{M}_r{\left(\frac{R}{t}\right)}^r;\frac{1}{\sqrt{\left(t-a\right)\left(t-b\right)}}=\sum _{r=0}^{\infty }{M}_r^{\ast }{\left(\frac{R}{t}\right)}^{r+1}$$

into condition (13). After some transformations, condition (13) is reduced to the form(28) $$\sum _{m=0}^{\infty }{A}_m^{}{\left(\frac{t}{R}\right)}^m+\sum _{m=0}^{\infty }{A}_m^{\ast }{\left(\frac{R}{t}\right)}^m=\sum _{m=0}^{\infty }{C}_m^{}{\left(\frac{t}{R}\right)}^m+\sum _{m=0}^{\infty }{C}_m^{\ast }{\left(\frac{R}{t}\right)}^m.$$(28)

Comparing in the both sides of the obtained relation the coefficients with identical powers $t/R$ and $R/t$, we find two infinite systems of linear algebraic equations with respect to ${\mathit{\alpha }}_k^{\ast }$(29) $$A_0+A_0^{\ast }=C_0+C_0^{\ast }\left(m=0\right),A_m=C_m,A_m^{\ast }=C_m^{\ast }\left(m=1,2,\dots \right).$$(29)

The expressions for A_m, $A_m^{\ast }$, C_m, $C_m^{\ast }$ $\left(m=0,1,2,\dots \right)$ are not cited because of their bulky form.

In the state of optimal design problem, the coefficients V_k = a_k + ib_k should be defined. For constructing missing equations, we require the stress intensity factors in the vicinity of the crack tip to be equal to zero. Adding(30) $$K_{\text{I}}^a+i{K}_{\text{II}}^a=0,K_{\text{I}}^b+i{K}_{\text{II}}^b=0.$$(30)

two complex linear algebraic equations to remaining equations, we get a closed algebraic system for determining all unknowns including the coefficients V_k of expansion of the function of normal displacement.

Case of arbitrary number of cracks

Now let the disc have N rectilinear cracks of length 2ℓ_k (k = 1, 2, … , N) (Figure 1).

Let us consider an optimal design problem, more exactly, a problem on determination of the function of normal displacement of the points of the disc’s boundary that provide the minimization (equality to zero) of stress intensity factors in the vicinity of all crack tips.

The solution of the problem for this case is similar to the case of a single crack with a difference that for finding the functions ${\mathrm{\Phi }}_{\ast }\left(z\right)$ and ${\mathrm{\Psi }}_{\ast }\left(z\right)$, the method for construction of Kolosov–Muskhelishvili formulas in the explicit form, corresponding to unknown displacements along the cracks lines, is used. The problem is reduced to determination of two analytic functions of complex variable $\mathrm{\Phi }\left(z\right)$, $\mathrm{\Psi }\left(z\right)$ satisfying boundary conditions (5), (6) and(31) $$\mathrm{\Phi }\left(x_k\right)+\overline{\mathrm{\Phi }\left(x_k\right)}+x_k\overline{{\mathrm{\Phi }}^{\prime }\left(x_k\right)}+\overline{\mathrm{\Psi }\left(x_k\right)}=0\left(k=1,2,\dots ,N\right),$$(31)

We look for the functions ${\mathrm{\Phi }}_{\ast }\left(z\right)$ and ${\mathrm{\Psi }}_{\ast }\left(z\right)$ in the form [1,3](32) $${\mathrm{\Phi }}_{\ast }\left(z\right)=\frac{1}{2\mathit{\pi }}\sum _{k=1}^N\underset{-{\ell }_k}{\overset{{\ell }_k}{\int }}\frac{g_k(t)}{t-z_k}\text{d}t;$$(32) $${\mathrm{\Psi }}_{\ast }\left(z\right)=\frac{1}{2\mathit{\pi }}\sum _{k=1}^N{e}^{-2i{\mathit{\alpha }}_k}\underset{-{\ell }_k}{\overset{{\ell }_k}{\int }}\left[\frac{\overline{g_k(t)}}{t-z_k}-\frac{\overline{{\mathrm{T}}_k}{e}^{i{\mathit{\alpha }}_k}}{{\left(t-z_k\right)}^2}{g}_k(t)\right]\text{d}t;$$$${\mathrm{T}}_k=t{e}^{i{\mathit{\alpha }}_k}+z_k^0;z_k^0=x_k^0+i{y}_k^0;z_k=e^{-i{\mathit{\alpha }}_k}\left(z-z_k^0\right).$$

Here g_k(x_k) are the sought-for functions what characterize the opening of crack faces(33) $$g_k(x_k)=\frac{2\mathit{\mu }}{i\left(1+\mathit{\kappa }\right)}\frac{\mathit{\partial }}{\mathit{\partial }x}\left[u_k^{+}(x_k,0)-u_k{}^{-}(x_k,0)+i\left({\mathit{\upsilon }}_k^{+}(x_k,0)-{\mathit{\upsilon }}_k^{-}(x_k,0)\right)\right]\left(k=1,2,\dots ,N\right).$$(33)

Boundary conditions (31) help to determine the unknown functions g_k(x_k) on the segments y_k = 0, −ℓ_k ≤ x_k ≤ ℓ_k $\left(k=1,2,\dots ,N\right)$.

Satisfying by functions (21), (32) boundary conditions (31) on the crack faces, we get a system of N singular integral equations with respect to the unknown functions g_k(x_k) $\left(k=1,2,\dots ,N\right)$:(34) $$\sum _{k-1}^N\underset{-{\ell }_k}{\overset{{\ell }_k}{\int }}\left[K_{nk}\left(t,x\right)g_k\left(t\right)+L_{nk}\left(t,x\right)\overline{g_k\left(t\right)}\right]\text{d}t=\mathit{\pi }{F}^{\ast }\left(x\right)$$(34)

$$\left|x\right|\le {\ell }_{n}n=1,2,\dots ,N.$$

Here$$K_{nk}(t,x)=\frac{e^{i{\mathit{\alpha }}_k}}{2}\left[\frac{1}{T_k-X_n}+\frac{e^{-2i{\mathit{\alpha }}_n}}{{\overline{T}}_k-{\overline{X}}_n}\right],$$$$L_{nk}(t,x)=\frac{e^{-i{\mathit{\alpha }}_k}}{2}\left[\frac{1}{{\overline{T}}_k-{\overline{X}}_n}-\frac{T_k-X_n}{{\left({\overline{T}}_k-{\overline{X}}_n\right)}^2}{e}^{-2i{\mathit{\alpha }}_n}\right],$$$$F^{\ast }\left(x\right)=-\left[{\mathrm{\Phi }}_0\left(x\right)+\overline{{\mathrm{\Phi }}_0\left(x\right)}+x\overline{{\mathrm{\Phi }}_0^{\prime }\left(x\right)}+\overline{{\mathrm{\Psi }}_0\left(x\right)}\right],$$$${\mathrm{\Phi }}_0\left(z\right)=\sum _{v=0}^{\infty }{B}_v{\left(\frac{z}{R}\right)}^v,{\mathrm{\Psi }}_0\left(z\right)=\sum _{v=0}^{\infty }{D}_v{\left(\frac{z}{R}\right)}^v.$$

To the system of singular integral equations (34) for internal cracks we should add additional equalities expressing the condition of uniqueness of displacements in tracing the crack contours(35) $$\underset{-{\ell }_k}{\overset{{\ell }_k}{\int }}{g}_k^{}\left(t\right)\text{d}t=0k=1,2,\dots ,N.$$(35)

Singular integral equations (34) under additional conditions (35) by means of the procedure for converting a system to an algebraic system [8–10] are reduced to the system of N × M algebraic equations for determining N × M unknown values(36) $$\begin{array}{c}\frac{1}{M}\sum _{m=1}^M\sum _{k=1}^N{\ell }_k\left[g_k(t_m)K_{nk}\left({\ell }_k{t}_m,{\ell }_n{x}_r\right)+\overline{g_k(t_m)}{L}_{nk}\left({\ell }_k{t}_m,{\ell }_n{x}_r\right)\right]\hfill \\ =F^{\ast }(x_r^{})n=1,2,\dots ,N;r=1,2,\dots ,M-1,\hfill \end{array}$$(36) $$\sum _{m=1}^M{g}_n^{}(t_m)=0,$$

where $t_m=cos\frac{2m-1}{2M}\mathit{\pi }$, m = 1, 2, …, M, $x_r^{}=cos\frac{\mathit{\pi }r}{M}$.

If in algebraic equations (36), we pass to complex conjugated values, we get another N × M algebraic equations. The right hand sides of algebraic equations (36) by the function F^*(x_r) contain the unknown values of the coefficients ${\mathit{\alpha }}_k^{\ast }$ and V_k.

The obtained relations (21), (22), (32), (36) admit to get final solution of the problem if the coefficients ${\mathit{\alpha }}_k^{\ast }$, V_k $(k=0,\pm 1,\dots )$ are determined. For composing an infinite system of linear algebraic equations with respect to unknowns ${\mathit{\alpha }}_k^{\ast }$, we behave as in the case of single crack. As a result, we get infinite linear algebraic systems of type (29).

The obtained systems of equations with respect to g_k(t_m) (k = 1, 2, …, N; m = 1, 2, …, M), ${\mathit{\alpha }}_v^{\ast }$ $(v=0,\pm 1,\dots )$ admit at the given displacement of the points on the disc’s boundary to determine stress–strain state of the disc involving arbitrary number of cracks in the disc’s material. By solving algebraic systems and formulas$$K_{\text{I}n}^{}-i{K}_{\text{II}n}^{}=\sqrt{\mathit{\pi }{\ell }_n}\frac{1}{M}\sum _{m=1}^M{\left(-1\right)}^m{g}_n^0\left(t_m\right)cot\frac{2m-1}{4M}\mathit{\pi }$$

at the right tip of the crack $(n=1,2,\dots ,N)$ and$$K_{\text{I}n}^{}-i{K}_{\text{II}n}^{}=\sqrt{\mathit{\pi }{\ell }_n}\frac{1}{M}\sum _{m=1}^M{\left(-1\right)}^{M+m}{g}_n^0\left(t_m\right)tan\frac{2m-1}{4M}\mathit{\pi }$$

at the left tip of the crack, one can calculate the stress intensity factors.

As before, we restrict oneself in expansion the sought-for function of normal displacement of the points of the boundary in Fourier series with the amount of members that coincides with the amount of crack tips.

In the case of N internal cracks in the disc, we will be restricted with 2 N coefficients of expansions of the function of normal displacement of the points of the disc’s boundary in Fourier series. We require the stress intensity factors in the vicinity of crack tips be equal to zero(37) $$\sum _{m=1}^M{(-1)}^m{g}_n^0\left(t_m\right)cot\frac{2m-1}{2M}\mathit{\pi }=0(n=1,2,\dots ,N),$$(37) $$\sum _{m=1}^M{(-1)}^{M+m}{g}_n^0\left(t_m\right)tan\frac{2m-1}{2M}\mathit{\pi }=0.$$

Adding 2 N complex linear algebraic equations to main resolving equations (about of which we spoke above), we get a closed algebraic system for determining all unknowns, including the V_k = a_k + ib_k coefficients of expansion of the sought-for function of normal displacement of points of the disc boundary in Fourier series.

Let a part of the crack N₁ reach with one end the external surface of the circular disc. Then the amount of cracks will be $\left(2N-N_1\right)$. In this case, when a part of the cracks are surface, in expansion of the sought-for function of normal displacement of the points of the disc boundary in Fourier series, we are restricted with $\left(2N-N_1\right)$ coefficients. Require the stress intensity factors in the vicinity of tips to be equal to zero. Adding these $\left(2N-N_1\right)$ linear algebraic equations to the main resolving equations, we get in this case also a closed algebraic system of equations for determining all unknowns. For numerical solution of the obtained systems of equations we use the Gauss method with the choice of the principle element. By varying the values of the parameters α_k and $z_k^0$ (k = 1, 2, …, N) it is possible to investigate different cases of crack arrangement in the circular disc and to estimate their effect on the optimum values of the function of normal displacement of the points of the disc boundary.

Numerical examples

(a) case of single crack

Numerical calculations were carried out applied to steel (grade 20X23H18 (ЭИ417)) disc. It was accepted that the disc radius R = 0.47 m; surface load N_θ = 300 MPa; Poisson ratio of disc material ν = 0.33; Young’s modulus E = 2.04·10⁵ MPa. The results of calculations of the function of normal displacement of the points of the disc boundary (the coefficients are given in mm) are cited in the Table 1. It was assumed that the disc was weakened with single internal crack with orientation angles: α₁ = 60°; $z_1^0=0.1R{e}^{i\mathit{\pi }/6}$ and the dimensionless crack length ${\ell }_1/R=0.02$.

Table 1. The values of Fourier coefficients of optimal normal displacement of the points of the disc boundary for case of single crack in the disc.

a0	a1	b0	b1
0.1123	0.0791	0	0.0714

(b) case of several crack

The results of calculations of the function of normal displacement of the points of the disc boundary (the coefficients are given in mm) are cited in the Table 2. It was assumed that the disc was weakened with three internal cracks with different orientation angles: α₁ = 15°; α₂ = 30°; α₃ = 45°; ${\ell }_1/R=0.05$; ${\ell }_2/R=0.02$; ${\ell }_3/R=0.01$; $z_1^0=0.2R{e}^{i\mathit{\pi }/18}$; $z_2^0=0.25R{e}^{i\mathit{\pi }/12}$; $z_3^0=0.15R{e}^{i\mathit{\pi }/10}$. The disc material and the external load were the same.

Table 2. The values of Fourier coefficients of optimal normal displacement of the points of the disc boundary for case of three cracks in the disc.

a0	a1	a2	a3	a4	a5
0.1216	0.0879	0.0718	0.0653	0.0561	0.0487
b0	b1	b2	b3	b4	b5
0	0.0742	0.0679	0.0539	0.0473	0.0365

The convergence of the procedure of singular equations numerical solution is discussed in many papers (see [8–10]). Numerous studies show that the number of collocations M should not be less than 20. Since M = 20 values of coefficients of the function of normal displacement are not significantly change. In calculations, this number was equal to 30.

The optimal solutions, i.e. the found coefficients serve to increase the carrying capacity of the disc.

(c) numerical case (direct problem)

As already mentioned above, for the given displacement of points and surface tangent loading on the disc boundary by means of solution of linear algebraic systems (29) and formulas (27) the stress intensity factors are found for a centre cracked circular disc. The obtained algebraic system (29) and formulas (27) to calculate the stress intensity factors in the vicinity of the crack ends with any preserved accuracy. In the paper [11,12], the stress intensity factors are found for the centre-cracked classic Brazilian disc. However, in the paper [11,12], the boundary conditions of the problem on the disc contour differ from conditions (1), (2). Apparently, the direct problem under mixed conditions (1)-(2) has not be considered up to now. The numerical example was performed for the case: the tangential force N_θ = 0 and normal displacement is identical at all the points of the disc contour f_r = const. The following values of the problem parameters were taken for calculations: ν = 0.5; a = −0.5R; b = 0.5R; f_r = −δ; δ = const. Stress distribution at the disc points along the diameter containing a crack is given in Table 3.

Table 3. The values of circumferential and radial stresses at the disc points along the diameter.

z	R	0.9R	0.8R	0.7R	0.6R	0.52R
${\mathit{\delta }}_{\mathit{\theta }}/\mathit{\mu }{R}^{-1}\mathit{\delta }$	2.96567	2.65376	2.43285	2.44356	3.02565	3.85462
${\mathit{\delta }}_r/\mathit{\mu }{R}^{-1}\mathit{\delta }$	1.65632	1.24687	1.11641	0.95374	1.23465	2.05634

Analysis of numerical data of the example under consideration showes that:

(1)	The points of the cracked diameters are in the compression area;
(2)	By absolute value, the circumferential stresses σθ in average twice exceeds the radial stress σr;
(3)	For circumferential and radial stresses along the crack line there exist unique minimum points not coinciding between themselves.

Sufficiency of reduction in the series for the expressions of complex potentials was verified with the error in satisfaction of the obtained solutions the boundary conditions.

Conclusions

The main resolving equations found in the paper admit at the given function of normal displacement of the points of the boundary of a circular disc, by determining the stress intensity factors to predict the growth of existing cracks in the disc, to establish admissible level of damages and maximum value of workloads providing sufficient safety factor. The solution of optimal design problem on determination of normal displacement of the points of the disc boundary permits on the design stage to choose optimal geometrical parameters of the disc providing increase of carrying capacity.

Thus, the results obtained in the present theoretical study open new possibilities in the optimum design of circular disc by choosing the function of normal displacement of the points of the disc boundary.

Disclosure statement

No potential conflict of interest was reported by the authors.