Numerical solution of two-dimensional inverse force function in the wave equation with nonlocal boundary conditions

Abstract

In this paper, the spectral meshless radial point interpolation (SMRPI) technique is applied to the inverse time-dependent force function in the wave equation on regular and irregular domains. The SMRPI is developed for identifying the force function which satisfies in the wave equation subject to the integral overspecification over a portion of the spatial domain or to the overspecification at a point in the spatial domain. This method is based on erudite combination of meshless methods and spectral collocation techniques. The point interpolation method with the help of radial basis functions is used to construct shape functions which play as basis functions in the frame of SMRPI. Since the problem is known to be ill-posed, Thikhonov regularization strategy is employed to solve effectively the discrete ill-posed resultant linear system. Three numerical examples are tested to show that numerical results are accurate for exact data and stable with noisy data.

Keywords:

• Spectral meshless radial point interpolation (SMRPI) method
• radial basis function
• inverse force problem
• regularization
• wave equation

AMS Subject Classifications:

• 65M32
• 65N21

1. Introduction

Inverse problems appear in various applications, when a phenomenon can not be observed directly, but only through indirect measurements. They are generally ill-posed problems in the Hadamard sense, since the existence or uniqueness or the continuous dependence on the data of their solutions may not be ensured. The third criteria have the effect that the observation noise can be arbitrarily amplified and so special cares are required to deal with the inverse problems [1–4]. The classical way to solve the inverse problems, in general, is to minimize a suitable cost function which is solved using optimization techniques, see e.g. [5,6]. Inverse problems arise in geophysical field such as seismic imaging [7], in image processing like medical imaging [8], in physical sciences as in deconvolution problems for ground-based telescopes [9].

Wave equation is a certain hyperbolic partial differential equation that occurred early to describe the motion of vibrating strings and membranes. It is a basis in many areas such as seismic imaging and imaging steep dipping structures. In most application, the wave speed, the initial state or the force function need to be estimated. Force estimation can be practised in some areas of engineering such as wave, wind, seismic, explosion or noise excitations [10]. The present paper considers the following inverse wave equation:(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1)

with initial conditions(2) $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),u_t(\mathbf{x},0)=v_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$(2)

and Dirichlet boundary condition(3) $$\begin{array}{c}\hfill u(\mathbf{x},t)=h(\mathbf{x},t),\mathbf{x}\in \mathit{\partial }\mathrm{\Omega },t>0,\end{array}$$(3)

subject to either the integral overspecification over the spatial domain(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4)

or to an overspecification at a point in the spatial domain(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5)

where $u_0(\mathbf{x})$ and $v_0(\mathbf{x})$ are the initial displacement and velocity, respectively. Also m(t) is a known time variable function, $w(\mathbf{x})$ is a given weight function, and further assume that $F(\mathbf{x},t)=f(\mathbf{x},t)r(t)+g(\mathbf{x},t)$ where $f(\mathbf{x},t)$ and $g(\mathbf{x},t)$ are known forcing function components and r(t) is an unknown time-dependent coefficient to be determined. In addition $\mathit{\partial }\mathrm{\Omega }$ is the closed curve bounding the region and $\overline{\mathrm{\Omega }}=\mathrm{\Omega }\bigcup \mathit{\partial }\mathrm{\Omega }$ denotes the spatial domain. If the force $F(\mathbf{x},t)$ is given, then Equations (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathbf{x},t)=h(\mathbf{x},t),\mathbf{x}\in \mathit{\partial }\mathrm{\Omega },t>0,\end{array}$$(3) ) form a direct well-posed problem. Physically, Equation (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ) represents a space average measurement of the displacement. Also, if we set $w(\mathbf{x})=\mathit{\delta }(\mathbf{x}-{\mathbf{x}}^{\ast })$, for fixed ${\mathbf{x}}^{\ast }\in \mathrm{\Omega }$, then Equation (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ) becomes a pointwise measurement of the displacement i.e. Equation (5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ), where $\mathit{\delta }(·)$ is Dirac delta function. Many researchers have investigated the identification of a space-dependent forcing function, for instance [11–18]. Also, references [19,20] concerning two-dimensional force identification and improved regularization method. For the definition and notation of the functional spaces involved in the sequel and related concepts, see Chapter 1 of [16]. Indeed, the theoretical basis for our numerical investigation is given in [16], Section 9.2, where the existence and uniqueness of solution of the inverse time-dependent force function for the wave equation have been established.

Meshless methods have attracted much attention in recent years [21,22]. There are various types of meshless techniques, for example, meshless techniques based on weak forms such as the element-free Galerkin method [23–25], diffuse element method [26], meshless local radial point interpolation method (RPIM) [27,28], meshless local Petrov–Galerkin method [29–31] and including their developments; meshless techniques based on collocation techniques (strong forms) such as the meshless collocation technique based on radial basis functions (RBFs) and finally meshless techniques based on the combination of weak forms and collocation technique [32–39].

Shivanian [40,41] proposed a new kind of SMRPI method which is based on meshless methods and benefits from spectral collocation ideas. In SMRPI technique, the point interpolation method with the help of those RBFs, which were free of shape parameter, has been proposed to construct shape functions which have Kronecker delta function property.

The authors of [42], for one-dimensional case, are discretized Equations (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) )–(4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ) numerically using the finite-difference method (FDM), and in order to stabilize the solution, the Tikhonov regularization method of various orders has been employed. The main deficiency of mesh-based techniques such as the FDM, the finite-element method is that these numerical techniques are dependent on mesh or elements. The SMRPI method do not require extensive mesh generation and elements, also it is flexible in dealing with problems by irregular domains or multi-dimensional. The localization property of SMRPI method reduces the ill-conditioning of the problem and makes it efficient for inverse problems such as inverse force function in the wave equation. In comparison with [42] the computational cost of the method is the modest due to the usage of strong form equation, collocation approach and that the matrix operations require only the inversion of matrices of small size. Based on spectral methods, evaluation of high-order derivatives of given differential equation is not difficult by constructing and using operational matrices. In addition, we conjecture that there is a relation between the operational matrices or how to choose nodes distribution so that there exists a relation between them, then it would be a great advantage for SMRPI. Overall, these conjectures would be challenge opportunity for the researchers and it also will be our next works.

Indeed, the innovation and mainspring of this article is to solve the inverse time-dependent force function in wave equation on irregular and regular domains in the case of two-dimensional that has not been researched in earlier literature. Therefore, the SMRPI is developed for such an inverse force problem of the hyperbolic wave equation on regular and irregular domains. The force function satisfies in the two-dimensional wave equation subject to the integral overspecification over a portion of the spatial domain or to the overspecification at a point in the spatial domain.

The outline of this paper is as follows: In Section 2, we introduce the SMRPI scheme briefly so that the high-order operational matrices are obtained. In Section 3, we obtain a time discrete scheme to the mentioned equation. Time discretization approximation for implementation of the SMRPI is given in Section 4. In this section, we briefly mention the Tikhonov regularization and the choice of the regularization parameter. In Section 5, we report the numerical experiments of solving Equation (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) ) for three test problems. Finally a conclusion is given in Section 6.

Figure 1. Local support domains for an arbitrary nodal point ${\mathbf{x}}_i$ for two-dimensional hypothesis domain.

Figure 2. Considered domains in the current paper.

Figure 3. $u_{approx}$ and ${\mathit{\epsilon }}_{\infty }(u)$ profiles for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$ for Example 1.

Figure 4. The exact solutions $\{r(t),u(x,0.5,T)\}$ in comparison with the regularized numerical solutions for $N=625$, $\mathit{\delta }t=0.01$, $\mathit{\sigma }\in \{1,2,3\}\%$ and $T=1$ on ${[0,1]}^2$ for Example 1.

Figure 5. Condition number and regularization parameter values for $k=\overline{1:T/\mathit{\delta }t}$ with $N=121$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$ for Example 1.

2. Proposed method

In this section, our purpose is to obtain shape function in SMRPI approach. Since we use the RBF of conditionally positive definite to build the shape functions, remember the following definition and theorem from [43].

Definition 1:

A continuous function $\mathit{\phi }:{\mathbb{R}}^d\to \mathbb{C}$ is said to be conditionally positive semi-definite of order m (i.e. to have conditional positive definiteness of order m) if, for all $N\in \mathbb{N}$, all pairwise distinct centers $x_1,\dots ,x_N\in {\mathbb{R}}^d$, and all $\mathbf{c}={[c_1,\dots ,c_N]}^{tr}\in {\mathbb{C}}^N$ satisfying$$\sum _{j=1}^N{c}_{j}p(x_j)=0,$$

for all complex-valued polynomials of degree less than m, the quadratic form$$\sum _{j=1}^N\sum _{k=1}^N{c}_j{\overline{c}}_k\mathit{\phi }(x_j-x_k)$$

is nonnegative. $\mathit{\phi }$ is said to be conditionally positive definite of order m if the quadratic form is positive, unless $\mathbf{c}$ is zero.

Theorem 1 (Micchelli):

Suppose that $\mathit{\phi }\in C[0,\infty )\cap C^{\infty }(0,\infty )$ is given. Then the function $\mathit{\varphi }=\mathit{\phi }(\Vert .{\Vert }_2^2)$ is conditionally positive semi-definite of order $m\in {\mathbb{N}}_0$ on every ${\mathbb{R}}^d$ if and only if ${(-1)}^m{\mathit{\phi }}^{(m)}$ is completely monotone on $(0,\infty )$.

Now, one can find many conditionally positive definite functions using this theorem. For an example, the thin-plate or surface splines $\mathit{\phi }(r)={(-1)}^{k+1}{r}^{2k}log(r)$ are conditionally positive definite of order $m=k+1$ on every ${\mathbb{R}}^d$. Consider a continuous function $u(\mathbf{x})$ defined in a domain $\mathrm{\Omega }$, which is represented by a set of field nodes. The $u(\mathbf{x})$ at a point of interest $\mathbf{x}$ is approximated in the form of(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6)

where $R_i(\mathbf{x})$ is a RBF, n is the number of RBFs, $P_j(\mathbf{x})$ is monomial in the space coordinate x, and np is the number of polynomial basis functions. Coefficients $a_i$ and $b_j$ are unknown which should be determined. 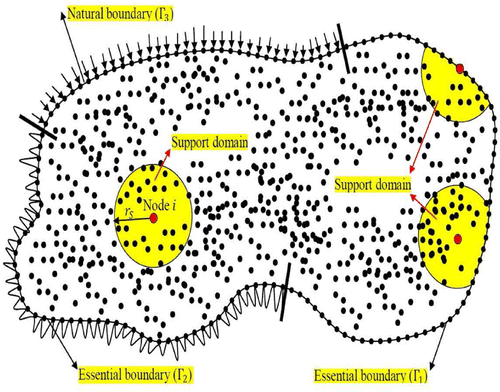In order to determine $a_i$ and $b_j$ in Equation (6(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6) ), a support domain is formed for the point of interest at x, and n field nodes are included in the support domain (see Figure 1) (support domain is usually a disc with radius $r_s$). Coefficients $a_i$ and $b_j$ can be determined by enforcing Equation (6(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6) ) to be satisfied at these n nodes surrounding the point of interest $\mathbf{x}$. Therefore, by the idea of interpolation Equation (6(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6) ) is converted to the following form:(7) $$\begin{array}{c}\hfill u(\mathbf{x})={\mathrm{\Phi }}^{tr}(\mathbf{x}){\mathbf{U}}_s=\sum _{i=1}^n{\mathit{\varphi }}_i(\mathbf{x})u_i.\end{array}$$(7)

where ${\mathit{\varphi }}_i(\mathbf{x})$’s are called the RPIM shape functions which have the Kronecker delta function property, that is(8) $$\begin{array}{c}\hfill {\mathit{\varphi }}_i({\mathbf{x}}_j)=\left\{\begin{array}{cc}1\hfill & \text{for}i=j,j=1,2,\dots ,n,\hfill \\ 0\hfill & \text{for}i\ne j,i,j=1,2,\dots ,n.\hfill \end{array}\right.\end{array}$$(8)

This is because the RPIM shape functions are created to pass through nodal values. Moreover, the shape functions are the partitions of unity, i.e.(9) $$\begin{array}{c}\hfill \sum _{i=1}^n{\mathit{\varphi }}_i(\mathbf{x})=1\end{array}$$(9)

for more details about RPIM shape functions and the way they are constructed, the readers are referred to [40]. Now, we construct operational matrices which are essential tools of present approach. Operational matrices make the technique more appropriate to handle partial differential equations with higher order derivatives. Suppose that the number of total nodes covering the domain of the problem i.e. $\overline{\mathrm{\Omega }}=\mathrm{\Omega }\bigcup \mathit{\partial }\mathrm{\Omega }$ is N. On the other hand, we know that n is dependent on point of interest $\mathbf{x}$ (so, after that we call it $n_{\mathbf{x}}$ ) in Equation (7(7) $$\begin{array}{c}\hfill u(\mathbf{x})={\mathrm{\Phi }}^{tr}(\mathbf{x}){\mathbf{U}}_s=\sum _{i=1}^n{\mathit{\varphi }}_i(\mathbf{x})u_i.\end{array}$$(7) ) which is the number of nodes included in support domain ${\mathrm{\Omega }}_{\mathbf{x}}$ corresponding to the point of interest $\mathbf{x}$ (for example ${\mathrm{\Omega }}_{\mathbf{x}}$ can be a disc centred at $\mathbf{x}$ with radius $r_s$, see Figure 1). Therefore, we have $n_{\mathbf{x}}\le N$ and Equation (7(7) $$\begin{array}{c}\hfill u(\mathbf{x})={\mathrm{\Phi }}^{tr}(\mathbf{x}){\mathbf{U}}_s=\sum _{i=1}^n{\mathit{\varphi }}_i(\mathbf{x})u_i.\end{array}$$(7) ) can be modified as(10) $$\begin{array}{c}\hfill u(\mathbf{x})={\mathrm{\Phi }}^{tr}(\mathbf{x}){\mathbf{U}}_s=\sum _{j=1}^N{\mathit{\varphi }}_j(\mathbf{x})u_j.\end{array}$$(10)

In fact, corresponding to node ${\mathbf{x}}_j$ there is a shape function ${\mathit{\varphi }}_j(\mathbf{x}),j=1,2,\dots ,N$, we define ${\mathrm{\Omega }}_{\mathbf{x}}^c=\}{\mathbf{x}}_j:{\mathbf{x}}_j\notin \mathrm{\Omega }\{$ then obviously from Equation (8(8) $$\begin{array}{c}\hfill {\mathit{\varphi }}_i({\mathbf{x}}_j)=\left\{\begin{array}{cc}1\hfill & \text{for}i=j,j=1,2,\dots ,n,\hfill \\ 0\hfill & \text{for}i\ne j,i,j=1,2,\dots ,n.\hfill \end{array}\right.\end{array}$$(8) )(11) $$\begin{array}{c}\hfill \forall {\mathbf{x}}_j\in {\mathrm{\Omega }}_{\mathbf{x}}^c:{\mathit{\varphi }}_j(\mathbf{x})=0.\end{array}$$(11)

The derivatives of $u(\mathbf{x})$ are easily obtained as(12) $$\begin{array}{c}\hfill {\displaystyle \frac{\mathit{\partial }u(\mathbf{x})}{\mathit{\partial }x}}=\sum _{j=1}^N{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }x}}{u}_j,{\displaystyle \frac{\mathit{\partial }u(\mathbf{x})}{\mathit{\partial }y}}=\sum _{j=1}^N{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }y}}{u}_j,\end{array}$$(12)

and for high derivatives of $u(\mathbf{x})$(13) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{s}u(\mathbf{x})}{\mathit{\partial }{x}^s}}=\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{x}^s}}{u}_j,{\displaystyle \frac{{\mathit{\partial }}^{s}u(\mathbf{x})}{\mathit{\partial }{y}^s}}=\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{y}^s}}{u}_j,\end{array}$$(13)

where ${\displaystyle \frac{{\mathit{\partial }}^s(.)}{\mathit{\partial }{x}^s}}$ and ${\displaystyle \frac{{\mathit{\partial }}^s(.)}{\mathit{\partial }{y}^s}}$ are s’th derivatives with respect to x and y. Denoting $u_x^{(s)}(.)={\displaystyle \frac{{\mathit{\partial }}^s(.)}{\mathit{\partial }{x}^s}}$, $u_y^{(s)}(.)={\displaystyle \frac{{\mathit{\partial }}^s(.)}{\mathit{\partial }{y}^s}}$ and setting $\mathbf{x}={\mathbf{x}}_i$ in Equation (12(12) $$\begin{array}{c}\hfill {\displaystyle \frac{\mathit{\partial }u(\mathbf{x})}{\mathit{\partial }x}}=\sum _{j=1}^N{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }x}}{u}_j,{\displaystyle \frac{\mathit{\partial }u(\mathbf{x})}{\mathit{\partial }y}}=\sum _{j=1}^N{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }y}}{u}_j,\end{array}$$(12) ) then the following matrix form is given(14) $$\begin{array}{cc}\hfill \left(\begin{array}{c}{u}_{x_1}^{\prime }\\ u_{x_2}^{\prime }\\ ⋮\\ u_{x_N}^{\prime }\end{array}\right)& =\left(\begin{array}{cccc}{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_1)}{\mathit{\partial }x}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_1)}{\mathit{\partial }x}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_1)}{\mathit{\partial }x}}\\ {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_2)}{\mathit{\partial }x}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_2)}{\mathit{\partial }x}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_2)}{\mathit{\partial }x}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_N)}{\mathit{\partial }x}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_N)}{\mathit{\partial }x}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_N)}{\mathit{\partial }x}}\end{array}\right)\left(\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_N\end{array}\right),\hfill \end{array}$$(14) (15) $$\begin{array}{cc}\hfill \left(\begin{array}{c}{u}_{y_1}^{\prime }\\ u_{y_2}^{\prime }\\ ⋮\\ u_{y_N}^{\prime }\end{array}\right)& =\left(\begin{array}{cccc}{\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_1)}{\mathit{\partial }y}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_1)}{\mathit{\partial }y}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_1)}{\mathit{\partial }y}}\\ {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_2)}{\mathit{\partial }y}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_2)}{\mathit{\partial }y}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_2)}{\mathit{\partial }y}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_1({\mathbf{x}}_N)}{\mathit{\partial }y}}& {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_2({\mathbf{x}}_N)}{\mathit{\partial }y}}& \cdots & {\displaystyle \frac{\mathit{\partial }{\mathit{\varphi }}_N({\mathbf{x}}_N)}{\mathit{\partial }y}}\end{array}\right)\left(\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_N\end{array}\right).\hfill \end{array}$$(15) We denote the above coefficients matrices as Dx, Dy and also for high-order derivatives we have the following matrix-vector multiplications:(16) $$\begin{array}{c}\hfill U_x^{(s)}=D^{(s)}xU,U_y^{(s)}=D^{(s)}yU\end{array}$$(16)

where(17) $$\begin{array}{cc}\hfill U_x^{(s)}& =(u_{x_1}^{(s)},u_{x_2}^{(s)},\dots ,u_{x_N}^{(s)}{)}^{tr},U_y^{(s)}=(u_{y_1}^{(s)},u_{y_2}^{(s)},\dots ,u_{y_N}^{(s)}{)}^{tr}\hfill \end{array}$$(17) (18) $$\begin{array}{cc}\hfill D_{x_{ij}}^{(s)}& ={\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j({\mathbf{x}}_i)}{\mathit{\partial }{x}^s}},\hfill \end{array}$$(18) (19) $$\begin{array}{cc}\hfill D_{y_{ij}}^{(s)}& ={\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j({\mathbf{x}}_i)}{\mathit{\partial }{y}^s}},\hfill \end{array}$$(19) (20) $$\begin{array}{cc}\hfill U& ={(u_1,u_2,\dots ,u_N)}^{tr}.\hfill \end{array}$$(20)

3. The time discretization approximation

In this section, we employ a time-stepping scheme to overcome the time derivatives. For this purpose, the following finite-difference approximations for the time derivative operators are used:(21) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}\cong {\displaystyle \frac{u^{k+1}(\mathbf{x})-2u^k(\mathbf{x})+u^{k-1}(\mathbf{x})}{\mathit{\delta }{t}^2}},\end{array}$$(21)

also, according to the following $\mathit{\theta }$-weighted scheme(22) $$\begin{array}{c}\hfill \mathrm{\Delta }u(\mathbf{x},t)\cong \mathit{\theta }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})+(1-\mathit{\theta })\mathrm{\Delta }{u}^k(\mathbf{x}),\end{array}$$(22)

and(23) $$\begin{array}{c}\hfill F(\mathbf{x},t)\cong \mathit{\theta }{F}^{k+1}(\mathbf{x})+(1-\mathit{\theta })F^k(\mathbf{x}),\end{array}$$(23)

where $u^k(\mathbf{x},t)=u(\mathbf{x},k\mathit{\delta }t)$, $r^k=r(k\mathit{\delta }t)$, $\mathbf{x}=(x,y)$, $0\le \mathit{\theta }\le 1$ and $\mathit{\delta }t=t^{k+1}-t^k$ is the time step size. Using the above discussion and as for $F(\mathbf{x},t)=f(\mathbf{x},t)r(t)+g(\mathbf{x},t)$, Equation (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) ) can be written as(24) $$\begin{array}{cc}\hfill {\displaystyle \frac{u^{k+1}(\mathbf{x})-2u^k(\mathbf{x})+u^{k-1}(\mathbf{x})}{\mathit{\delta }{t}^2}}& =\mathit{\theta }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})+(1-\mathit{\theta })\mathrm{\Delta }{u}^k(\mathbf{x})\hfill \\ \hfill & +\mathit{\theta }(f^{k+1}(\mathbf{x})r^{k+1}+g^{k+1}(\mathbf{x}))+(1-\mathit{\theta })(f^k(\mathbf{x})r^k+g^k(\mathbf{x})).\hfill \end{array}$$(24)

By rearranging of Equation (24(24) $$\begin{array}{cc}\hfill {\displaystyle \frac{u^{k+1}(\mathbf{x})-2u^k(\mathbf{x})+u^{k-1}(\mathbf{x})}{\mathit{\delta }{t}^2}}& =\mathit{\theta }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})+(1-\mathit{\theta })\mathrm{\Delta }{u}^k(\mathbf{x})\hfill \\ \hfill & +\mathit{\theta }(f^{k+1}(\mathbf{x})r^{k+1}+g^{k+1}(\mathbf{x}))+(1-\mathit{\theta })(f^k(\mathbf{x})r^k+g^k(\mathbf{x})).\hfill \end{array}$$(24) ), we obtain(25) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\delta }{t}^2\mathit{\theta }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})-\mathit{\delta }{t}^2\mathit{\theta }{f}^{k+1}(\mathbf{x})r^{k+1}=2u^k(\mathbf{x})+\mathit{\delta }{t}^2(1-\mathit{\theta })\mathrm{\Delta }{u}^k(\mathbf{x})-u^{k-1}(\mathbf{x})\hfill \\ \hfill & +\mathit{\delta }{t}^2(1-\mathit{\theta })f^k(\mathbf{x})r^k+\mathit{\delta }{t}^2(\mathit{\theta }{g}^{k+1}(\mathbf{x})+(1-\mathit{\theta })g^k(\mathbf{x})).\hfill \end{array}$$(25)

This is a fairly general implicit formula when $\mathit{\theta }=1$. When $\mathit{\theta }=1/2$, becomes the Crank–Nicolson formula. Finally, if $\mathit{\theta }=0$, this implicit difference equation reduces to the explicit equation.

Remark 1:

Although Equation (25(25) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\delta }{t}^2\mathit{\theta }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})-\mathit{\delta }{t}^2\mathit{\theta }{f}^{k+1}(\mathbf{x})r^{k+1}=2u^k(\mathbf{x})+\mathit{\delta }{t}^2(1-\mathit{\theta })\mathrm{\Delta }{u}^k(\mathbf{x})-u^{k-1}(\mathbf{x})\hfill \\ \hfill & +\mathit{\delta }{t}^2(1-\mathit{\theta })f^k(\mathbf{x})r^k+\mathit{\delta }{t}^2(\mathit{\theta }{g}^{k+1}(\mathbf{x})+(1-\mathit{\theta })g^k(\mathbf{x})).\hfill \end{array}$$(25) ) is valid for any value of $0\le \mathit{\theta }\le 1$, we will use $\mathit{\theta }=1/2$ (the famous Crank–Nicholson scheme). This choice of $\mathit{\theta }$ produces more accurate approximation [44].

Suppose that $\mathit{\lambda }=\mathit{\delta }{t}^2/2$, then we obtain(26) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }\mathrm{\Delta }{u}^k(\mathbf{x})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k),\hfill \end{array}$$(26)

where $G(\mathbf{x};k)=\mathit{\lambda }(g^{k+1}(\mathbf{x})+g^k(\mathbf{x})).$

4. Discretization and numerical implementation for SMRPI method

In this section, we consider Equation (26(26) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }\mathrm{\Delta }{u}^k(\mathbf{x})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k),\hfill \end{array}$$(26) ) and explain how to implement SMRPI method to obtain discrete equations. Equation (26(26) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }\mathrm{\Delta }{u}^{k+1}(\mathbf{x})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }\mathrm{\Delta }{u}^k(\mathbf{x})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k),\hfill \end{array}$$(26) ) can be rewritten as(27) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{y}^2}})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{y}^2}})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k).\hfill \end{array}$$(27)

Consider N nodes with arbitrary distribution on the boundary and domain of the problem. Assuming that $\{u({\mathbf{x}}_i,k\mathit{\delta }t),r(k\mathit{\delta }t)\}$, $i=1,2,\dots ,N$ are known, our aim is to compute $\{u({\mathbf{x}}_i,(k+1)\mathit{\delta }t),r((k+1)\mathit{\delta }t)\}$, $i=1,2,\dots ,N$. So, we have $N+1$ unknowns and to compute these unknowns we need $N+1$ equations. As it will be described, corresponding to each node we obtain one equation. For nodes which are located in the interior of the domain i.e. for ${\mathbf{x}}_i\in \mathrm{\Omega }$, to obtain the discrete equations from Equation (27(27) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{y}^2}})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{y}^2}})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k).\hfill \end{array}$$(27) ), substituting approximation formulas (10(10) $$\begin{array}{c}\hfill u(\mathbf{x})={\mathrm{\Phi }}^{tr}(\mathbf{x}){\mathbf{U}}_s=\sum _{j=1}^N{\mathit{\varphi }}_j(\mathbf{x})u_j.\end{array}$$(10) ) and (13(13) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{s}u(\mathbf{x})}{\mathit{\partial }{x}^s}}=\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{x}^s}}{u}_j,{\displaystyle \frac{{\mathit{\partial }}^{s}u(\mathbf{x})}{\mathit{\partial }{y}^s}}=\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^s{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{y}^s}}{u}_j,\end{array}$$(13) ) into Equation (27(27) $$\begin{array}{cc}& u^{k+1}(\mathbf{x})-\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^{k+1}(\mathbf{x})}{\mathit{\partial }{y}^2}})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2u^k(\mathbf{x})+\mathit{\lambda }({\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{x}^2}}+{\displaystyle \frac{{\mathit{\partial }}^2{u}^k(\mathbf{x})}{\mathit{\partial }{y}^2}})-u^{k-1}(\mathbf{x})+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k).\hfill \end{array}$$(27) ) yields(28) $$\begin{array}{cc}& \sum _{j=1}^N{\mathit{\varphi }}_j(\mathbf{x})u_j^{k+1}-\mathit{\lambda }(\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^2{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{x}^2}}{u}_j^{k+1}+\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^2{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{y}^2}}{u}_j^{k+1})-\mathit{\lambda }{f}^{k+1}(\mathbf{x})r^{k+1}\hfill \\ \hfill & =2\sum _{j=1}^N{\mathit{\varphi }}_j(\mathbf{x})u_j^k+\mathit{\lambda }(\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^2{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{x}^2}}{u}_j^k+\sum _{j=1}^N{\displaystyle \frac{{\mathit{\partial }}^2{\mathit{\varphi }}_j(\mathbf{x})}{\mathit{\partial }{y}^2}}{u}_j^k)\hfill \\ \hfill & -\sum _{j=1}^N{\mathit{\varphi }}_j(\mathbf{x})u_j^{k-1}+\mathit{\lambda }{f}^k(\mathbf{x})r^k+G(\mathbf{x};k).\hfill \end{array}$$(28)

Now, setting $\mathbf{x}={\mathbf{x}}_i$, $i=1,2,\dots ,N_{\mathrm{\Omega }}$ ( $N_{\mathrm{\Omega }}$ is the number of nodes in $\mathrm{\Omega }$) in the above equation and applying notations (16(16) $$\begin{array}{c}\hfill U_x^{(s)}=D^{(s)}xU,U_y^{(s)}=D^{(s)}yU\end{array}$$(16) )–(20(20) $$\begin{array}{cc}\hfill U& ={(u_1,u_2,\dots ,u_N)}^{tr}.\hfill \end{array}$$(20) ) implies(29) $$\begin{array}{cc}& u_i^{k+1}-\mathit{\lambda }\sum _{j=1}^N(D_{x_{ij}}^{(2)}+D_{y_{ij}}^{(2)})u_j^{k+1}-\mathit{\lambda }{f}^{k+1}({\mathbf{x}}_i)r^{k+1}\hfill \\ \hfill & =2u_i^k+\mathit{\lambda }\sum _{j=1}^N(D_{x_{ij}}^{(2)}+D_{y_{ij}}^{(2)})u_j^k-u_i^{k-1}+\mathit{\lambda }{f}^k({\mathbf{x}}_i)r^k+G({\mathbf{x}}_i;k),i=1,2,\dots ,N_{\mathrm{\Omega }}.\hfill \end{array}$$(29)

For nodes which are located on the boundary $\mathrm{\Gamma }$ using Equation (3(3) $$\begin{array}{c}\hfill u(\mathbf{x},t)=h(\mathbf{x},t),\mathbf{x}\in \mathit{\partial }\mathrm{\Omega },t>0,\end{array}$$(3) ) we have the following relation(30) $$\begin{array}{c}\hfill u_i^{k+1}=h({\mathbf{x}}_i,(k+1)\mathit{\delta }t),i=1,2,\dots ,N_{\mathrm{\Gamma }}.\end{array}$$(30)

For the non-classical condition (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ), use the following approximation:(31) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},(k+1)\mathit{\delta }t)\mathrm{d}\mathbf{x}\cong \sum _{j=1}^N{d}_{j}w({\mathbf{x}}_j)u_j^{k+1},\end{array}$$(31)

where $d_j$’s are the coefficients in an appropriate numerical integration rule and N is the total number of nodes covering $\overline{\mathrm{\Omega }}$, i.e. $N=N_{\mathrm{\Omega }}+N_{\mathrm{\Gamma }}.$ Therefore, we have the following equation to impose non-classical condition (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) )(32) $$\begin{array}{c}\hfill \sum _{j=1}^N{d}_{j}w({\mathbf{x}}_j)u_j^{k+1}=m((k+1)\mathit{\delta }t),\end{array}$$(32)

or from (5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) we have(33) $$\begin{array}{c}\hfill u_{n_0}^{k+1}=m((k+1)\mathit{\delta }t),\end{array}$$(33)

where $n_0$ is the index of ${\mathbf{x}}^{\ast }$. Therefore, we have $N_{\mathrm{\Omega }}+N_{\mathrm{\Gamma }}+1$, i.e. $N+1$ equations and $N+1$ unknowns. If we show the sparse system as the following matrix form(34) $$\begin{array}{c}\hfill \mathbf{A}\left(\begin{array}{c}{\mathbf{U}}^{k+1}\\ r^{k+1}\end{array}\right)=\mathbf{B}\left(\begin{array}{c}{\mathbf{U}}^k\\ r^k\end{array}\right)+\mathbf{C}\left(\begin{array}{c}{\mathbf{U}}^{k-1}\\ r^{k-1}\end{array}\right)+\widehat{\mathbf{b}},\end{array}$$(34)

then matrixes $\mathbf{A},\mathbf{B}$, $\mathbf{C}$ and $\widehat{\mathbf{b}}$ are defined as follows:(35) $$\begin{array}{c}\hfill {\mathbf{A}}_{ij}=\left\{\begin{array}{cc}{\mathit{\delta }}_{ij}-\mathit{\lambda }(D_{x_{ij}}^{(2)}+D_{y_{ij}}^{(2)}),\hfill & i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ {\mathit{\delta }}_{ij},\hfill & i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ d_{j}w({\mathbf{x}}_j),\hfill & i=N+1\hfill \\ OR\hfill \\ 1_{n_0},\hfill & i=N+1\hfill \end{array}\right.,\text{for}j=1,2,\dots ,N,\end{array}$$(35)

where $1_{n_0}$ indicates the coefficient of $u^{k+1}({\mathbf{x}}^{\ast })$ is 1 and others are zero.(36) $$\begin{array}{cc}\hfill {\mathbf{A}}_{ij}& =\left\{\begin{array}{cc}-\mathit{\lambda }{f}^{k+1}({\mathbf{x}}_i),\hfill & i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ 0,\hfill & i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ 0,\hfill & i=N+1\hfill \end{array}\right.,\text{for}j=N+1.\hfill \end{array}$$(36) (37) $$\begin{array}{cc}\hfill {\mathbf{B}}_{ij}& =\left\{\begin{array}{cc}2{\mathit{\delta }}_{ij}+\mathit{\lambda }(D_{x_{ij}}^{(2)}+D_{y_{ij}}^{(2)})\hfill & ,i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ 0\hfill & ,i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ 0\hfill & ,i=N+1\hfill \end{array}\right.,\text{for}j=1,2,\dots ,N,\hfill \end{array}$$(37) (38) $$\begin{array}{cc}\hfill {\mathbf{B}}_{ij}& =\left\{\begin{array}{cc}\mathit{\lambda }{f}^k({\mathbf{x}}_i)\hfill & ,i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ 0\hfill & ,i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ 0\hfill & ,i=N+1\hfill \end{array}\right.,\text{for}j=N+1.\hfill \end{array}$$(38) (39) $$\begin{array}{cc}\hfill {\mathbf{C}}_{ij}& =\left\{\begin{array}{cc}-{\mathit{\delta }}_{ij}\hfill & ,i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ 0\hfill & ,i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ 0\hfill & ,i=N+1\hfill \end{array}\right.,\text{for}j=1,2,\dots ,N,\hfill \end{array}$$(39)

and ${\mathbf{C}}_{ij}=0$ for $i=1,2,\dots ,N+1$ and $j=N+1$.(40) $$\begin{array}{c}\hfill {\widehat{\mathbf{b}}}_i=\left\{\begin{array}{cc}G({\mathbf{x}}_i;k),\hfill & i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ h^{k+1}({\mathbf{x}}_i),\hfill & i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ m((k+1)\mathit{\delta }t),\hfill & i=N+1\hfill \end{array}\right..\end{array}$$(40)

In Equations (35(35) $$\begin{array}{c}\hfill {\mathbf{A}}_{ij}=\left\{\begin{array}{cc}{\mathit{\delta }}_{ij}-\mathit{\lambda }(D_{x_{ij}}^{(2)}+D_{y_{ij}}^{(2)}),\hfill & i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ {\mathit{\delta }}_{ij},\hfill & i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ d_{j}w({\mathbf{x}}_j),\hfill & i=N+1\hfill \\ OR\hfill \\ 1_{n_0},\hfill & i=N+1\hfill \end{array}\right.,\text{for}j=1,2,\dots ,N,\end{array}$$(35) )–(39(39) $$\begin{array}{cc}\hfill {\mathbf{C}}_{ij}& =\left\{\begin{array}{cc}-{\mathit{\delta }}_{ij}\hfill & ,i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ 0\hfill & ,i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ 0\hfill & ,i=N+1\hfill \end{array}\right.,\text{for}j=1,2,\dots ,N,\hfill \end{array}$$(39) ), ${\mathit{\delta }}_{ij}$ is the Kronecker delta function, i.e.(41) $$\begin{array}{c}\hfill {\mathit{\delta }}_{ij}=\left\{\begin{array}{cc}1,\hfill & i=j\hfill \\ 0,\hfill & i\ne j\hfill \end{array}\right..\end{array}$$(41)

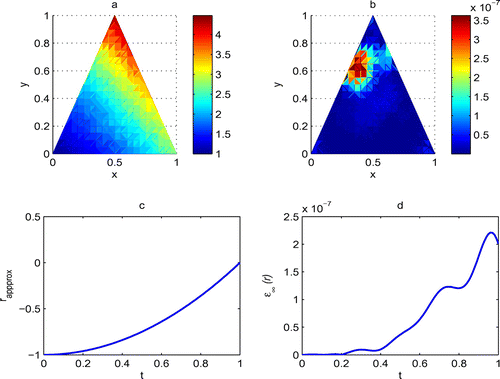
Figure 6. Graphs of approximate solution and absolute error of $u(\mathbf{x},t)$ (a) and (b) with approximate solution and absolute error of r(t) (c) and (d) in the case of no regularization and $N=441$, $\mathit{\delta }t=0.01$ and $T=1$ on domain ${\mathrm{\Omega }}_2$ for Example 1.

Figure 7. $u_{approx}$ (left) and ${\mathit{\epsilon }}_{\infty }(u)$ (right) profiles for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$ for Example 2.

At the first time level, when $k=0$, according to the initial conditions that were introduced in Equation (2(2) $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),u_t(\mathbf{x},0)=v_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$(2) ), we apply the following assumptions:(42) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathbf{U}}^0\\ r^0\end{array}\right)={\left(\begin{array}{c}{[{\mathbf{u}}_0]}_{N\times 1}\\ r(0)\end{array}\right)}_{(N+1)\times 1},\end{array}$$(42)

and(43) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathbf{U}}^{-1}\\ r^{-1}\end{array}\right)=\left(\begin{array}{c}{\mathbf{U}}^1\\ r^1\end{array}\right)-2\mathit{\delta }t{\left(\begin{array}{c}{[{\mathbf{v}}_0]}_{N\times 1}\\ 0\end{array}\right)}_{(N+1)\times 1},\end{array}$$(43)

where$${\mathbf{u}}_0=(u_0({\mathbf{x}}_1),u_0({\mathbf{x}}_2),\dots ,u_0({\mathbf{x}}_N){)}^{tr},$$

and$${\mathbf{v}}_0=(v_0({\mathbf{x}}_1),v_0({\mathbf{x}}_2),\dots ,v_0({\mathbf{x}}_N){)}^{tr}.$$

Roughly speaking, r(0) in Equation (42(42) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathbf{U}}^0\\ r^0\end{array}\right)={\left(\begin{array}{c}{[{\mathbf{u}}_0]}_{N\times 1}\\ r(0)\end{array}\right)}_{(N+1)\times 1},\end{array}$$(42) ) can be obtianed as follows:

From Equation (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ), we have(44) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x}){\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(44)

or(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45)

Now, it is enough to substitute $t=0$ in Equation (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) ) that gives the only unknown of Equation (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) ), i.e, r(0). Similarly, r(0) can be obtained from Equation (5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ).

4.1. Regularization

It seems useful to recall first the singular value decomposition (SVD) here. Let $A\in {\mathbb{R}}^{m\times n}$ be a rectangular matrix with $m\ge n$. Then the SVD of A is a decomposition of the form(46) $$\begin{array}{c}\hfill A=U\mathrm{\Sigma }{V}^{tr}=\sum _{i=1}^n{u}_i{\mathit{\sigma }}_i{v}_i^{tr},\end{array}$$(46)

where $U=(u_1,u_2,\dots ,u_n)$ and $V=(v_1,v_2,\dots ,v_n)$ are matrices with orthonormal columns, $U{U}^{tr}=V{V}^{tr}=I_n$, and where $\mathrm{\Sigma }=diag({\mathit{\sigma }}_1,{\mathit{\sigma }}_2,\dots ,{\mathit{\sigma }}_n)$ has non-negative diagonal elements appearing in non-increasing order such that ${\mathit{\sigma }}_1\ge {\mathit{\sigma }}_2\ge \cdots \ge {\mathit{\sigma }}_n\ge 0.$ The numbers ${\mathit{\sigma }}_i$ are the singular values of A while the vectors $u_i$ and $v_i$ are the left and right singular vectors of A, respectively. The condition number of A is equal to the ratio ${\mathit{\sigma }}_1/{\mathit{\sigma }}_n.$

In practical applications, the given Equation (32(32) $$\begin{array}{c}\hfill \sum _{j=1}^N{d}_{j}w({\mathbf{x}}_j)u_j^{k+1}=m((k+1)\mathit{\delta }t),\end{array}$$(32) ) or Equation (33(33) $$\begin{array}{c}\hfill u_{n_0}^{k+1}=m((k+1)\mathit{\delta }t),\end{array}$$(33) ) usually contain certain noise. Instead of the exact data $m((k+1)\mathit{\delta }t)$, we only have(47) $$\begin{array}{c}\hfill m^{\mathit{ϵ}}((k+1)\mathit{\delta }t)=m((k+1)\mathit{\delta }t)+\mathit{\sigma }\mathit{\epsilon },\end{array}$$(47)

where $\mathit{\epsilon }$ is a random number whose range is $[-1,1]$. $\mathit{\sigma }$ is a user-defined parameter to denote the percentage of the noise. Now, we can rewrite the system (34(34) $$\begin{array}{c}\hfill \mathbf{A}\left(\begin{array}{c}{\mathbf{U}}^{k+1}\\ r^{k+1}\end{array}\right)=\mathbf{B}\left(\begin{array}{c}{\mathbf{U}}^k\\ r^k\end{array}\right)+\mathbf{C}\left(\begin{array}{c}{\mathbf{U}}^{k-1}\\ r^{k-1}\end{array}\right)+\widehat{\mathbf{b}},\end{array}$$(34) ) as(48) $$\begin{array}{c}\hfill \mathbf{A}\tilde{\mathbf{U}}={\tilde{\mathbf{b}}}^{\mathit{ϵ}},\end{array}$$(48)

where $\tilde{\mathbf{U}}={\{{\mathbf{U}}^{k+1},r^{k+1}\}}^{tr}$, also the right-hand side ${\tilde{\mathbf{b}}}^{\mathit{ϵ}}$ includes the noisy data and$${\tilde{\mathbf{b}}}^{\mathit{ϵ}}=\mathbf{B}\left(\begin{array}{c}{\mathbf{U}}^k\\ r^k\end{array}\right)+\mathbf{C}\left(\begin{array}{c}{\mathbf{U}}^{k-1}\\ r^{k-1}\end{array}\right)+{\widehat{\mathbf{b}}}^{\mathit{ϵ}},$$

where(49) $$\begin{array}{c}\hfill {\widehat{\mathbf{b}}}_i^{\mathit{ϵ}}=\left\{\begin{array}{cc}G({\mathbf{x}}_i;k),\hfill & i=1,2,\dots ,N_{\mathrm{\Omega }}\hfill \\ h^{k+1}({\mathbf{x}}_i),\hfill & i=N_{\mathrm{\Omega }}+1,\dots ,N\hfill \\ m^{\mathit{ϵ}}((k+1)\mathit{\delta }t),\hfill & i=N+1\hfill \end{array}\right..\end{array}$$(49)

As previously mentioned, this linear inverse problem has a unique solution, but it is ill-posed which means small errors in the input data cause large errors in the output solution. To see an example of instability this problem refer to [42]. In order to deal with this instability we employ the Tikhonov regularization [45] which gives the regularized solution [46]. The purpose of numerical regularization theory is to provide efficient and numerically stable methods for including proper side constraints that lead to useful stabilized solutions, and to provide robust methods for choosing the optimal weight given to these side constraints such that the regularized solution is a good approximation to the desired unknown solution [47]. The Tikhonov regularized solution of the final linear system (48(48) $$\begin{array}{c}\hfill \mathbf{A}\tilde{\mathbf{U}}={\tilde{\mathbf{b}}}^{\mathit{ϵ}},\end{array}$$(48) ), say ${\tilde{\mathbf{U}}}_{\mathit{\alpha }}$ , is defined to be the solution to the following least-squares problem:(50) $$\begin{array}{c}\hfill \underset{\tilde{\mathbf{U}}}{min}\{\Vert \mathbf{A}\tilde{\mathbf{U}}-{\tilde{\mathbf{b}}}^{\mathit{ϵ}}{\Vert }^2+{\mathit{\alpha }}^2{\Vert \tilde{\mathbf{U}}\Vert }^2\},\end{array}$$(50)

where $\Vert .\Vert$ denotes the usual Euclidean norm and $\mathit{\alpha }$ is the regularization parameter. The interpretation of Tikhonov regularization indicates that it keeps the residual $\Vert \mathbf{A}\tilde{\mathbf{U}}-{\tilde{\mathbf{b}}}^{\mathit{ϵ}}{\Vert }^2$ small and stabilizes by preventing ${\tilde{\mathbf{U}}}_{\mathit{\alpha }}$ from becoming large through the penalty term ${\mathit{\alpha }}^2{\Vert \tilde{\mathbf{U}}\Vert }^2$. We use the quasi-optimality criterion [48] to find the regularization parameter $\mathit{\alpha }$. This method chooses the optimal regularization parameters by minimizing the following function:(51) $$\begin{array}{c}\hfill Q(\mathit{\alpha })=(\sum _{i=1}^{N+1}(f_i(1-f_i){\displaystyle \frac{u_i^{tr}{\tilde{\mathbf{b}}}^{\mathit{ϵ}}}{{\mathit{\sigma }}_i}}{)}^2{)}^{1/2},\end{array}$$(51)

where $f_i={\mathit{\sigma }}_i^2/({\mathit{\sigma }}_i^2+{\mathit{\alpha }}^2)$, so called the filter factors, $u_i$ and ${\mathit{\sigma }}_i$ obtain from SVD of $\mathbf{A}$. In our computation, we use the Matlab code developed by Hansen [47] for solving the ill-conditioned system (48(48) $$\begin{array}{c}\hfill \mathbf{A}\tilde{\mathbf{U}}={\tilde{\mathbf{b}}}^{\mathit{ϵ}},\end{array}$$(48) ).

5. Numerical results

In this section, we present the numerical results of the proposed method on three test problems. We test the accuracy and stability of the method described in this paper by performing the mentioned scheme for different values of $\mathit{\sigma },h$ ( the distance between the nodes in x or y direction) and $\mathit{\delta }t$. To show the accuracy and convergence of the method, two kinds of error measures, maximum absolute error ${\mathit{\epsilon }}_{\infty }$ and relative error ${\mathit{\epsilon }}_R$ defined by:(52) $$\begin{array}{cc}\hfill {\mathit{\epsilon }}_{\infty }(r)& =\Vert r_{exact}-r_{approx}{\Vert }_{\infty }=max\}|r_{exact}(t_k)-r_{approx}(t_k)|:k=1,2,\dots ,T/\mathit{\delta }t\{,\hfill \end{array}$$(52) (53) $$\begin{array}{cc}\hfill {\mathit{\epsilon }}_R(r)& ={\displaystyle \frac{\Vert r_{exact}-r_{approx}{\Vert }_{\infty }}{\Vert r_{exact}{\Vert }_{\infty }}},\hfill \end{array}$$(53) (54) $$\begin{array}{cc}\hfill {\mathit{\epsilon }}_{\infty }(u)& =\Vert u_{exact}-u_{approx}{\Vert }_{\infty }=max\}|u_{exact}({\mathbf{x}}_i,T)-u_{approx}({\mathbf{x}}_i,T)|:i=1,2,\dots ,N\{,\hfill \end{array}$$(54) (55) $$\begin{array}{cc}\hfill {\mathit{\epsilon }}_R(u)& =\sqrt{{\displaystyle \frac{\sum _{i=1}^N{(u_{exact}({\mathbf{x}}_i,T)-u_{approx}({\mathbf{x}}_i,T))}^2}{\sum _{i=1}^N{(u_{exact}({\mathbf{x}}_i,T))}^2}}},\hfill \end{array}$$(55)

are used, where $\}{u}_{exact},r_{exact}\{$ and $\}{u}_{approx},r_{approx}\{$ are exact and approximate solutions, respectively. There are a number of types of RBFs, and the characteristics of RBFs have been widely investigated. In the current work, we have chosen the thin plate spline (TPS) as radial basis functions in Equation (6(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6) ) as follows:(56) $$\begin{array}{c}\hfill R(\mathbf{x})=r^{2\mathit{\beta }}ln(r),r=\Vert \mathbf{x}-{\mathbf{x}}_i\Vert ,\mathit{\beta }=1,2,\dots ,\end{array}$$(56)

corresponding to the support domain at central point ${\mathbf{x}}_i$, $i=1,2,\dots ,N$. For the second-order partial differential Equation (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) ), $\mathit{\beta }=2$ is used for TPSs and also in test problems, we let $r_s=4.2h$. In Equation (6(6) $$\begin{array}{c}\hfill u(\mathbf{x})=\sum _{i=1}^n{R}_i(\mathbf{x})a_i+\sum _{j=1}^{np}{P}_j(\mathbf{x})b_j={\mathbf{R}}^{tr}(\mathbf{x})\mathbf{a}+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{b},\end{array}$$(6) ) set $np=28$ that results polynomial basis functions as follows:$$\begin{array}{cc}\hfill P^{tr}(\mathbf{x})=\{1,x,& y,x^2,xy,y^2,x^3,x^{2}y,x{y}^2,y^3,x^4,x^{3}y,x^2{y}^2,x{y}^3,\hfill \\ \hfill & y^4,x^5,x^{4}y,x^3{y}^2,x^2{y}^3,x{y}^4,y^5,x^6,x^{5}y,x^4{y}^2,x^3{y}^3,x^2{y}^4,x{y}^5,y^6\}.\hfill \end{array}$$

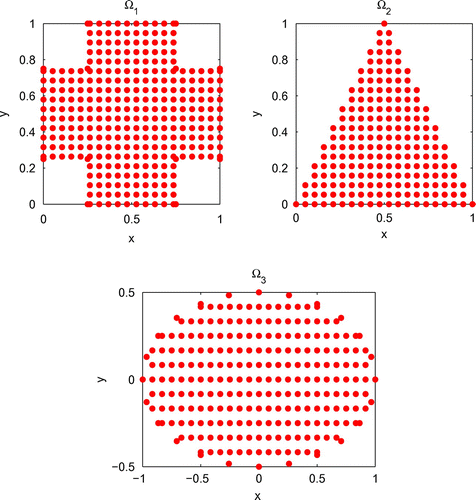
Also, in Equation (31(31) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},(k+1)\mathit{\delta }t)\mathrm{d}\mathbf{x}\cong \sum _{j=1}^N{d}_{j}w({\mathbf{x}}_j)u_j^{k+1},\end{array}$$(31) ), Simpson’s composite numerical integration rule is used and let $w(\mathbf{x})\equiv 1.$ Furthermore, Figure 2 presents the irregular domains considered in test problems and the irregular domain ${\mathrm{\Omega }}_3$ is defined by$${\mathrm{\Omega }}_3=\{(x,y):x^2+4y^2\le 1\}.$$

Remark 2:

In three test problems that will come, we use an agreement, this means that, if Equations (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) )–(3(3) $$\begin{array}{c}\hfill u(\mathbf{x},t)=h(\mathbf{x},t),\mathbf{x}\in \mathit{\partial }\mathrm{\Omega },t>0,\end{array}$$(3) ) with (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ) are satisfied, then we consider the problem on ${[0,1]}^2$. If Equations (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathbf{x},t)=h(\mathbf{x},t),\mathbf{x}\in \mathit{\partial }\mathrm{\Omega },t>0,\end{array}$$(3) ) with (5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) are governed, in this case, we solve the problem on the irregular domains that will be mentioned in every test problem. For second case, we set ${\mathbf{x}}^{\ast }={\mathbf{x}}_{20}$, i.e. 20 is the index of node, in three test problems, that results different ${\mathbf{x}}^{\ast }$ depending on different h.

Example 1:

As the first test problem, consider Equations (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) on the ${[0,1]}^2$ and irregular domain ${\mathrm{\Omega }}_2$ with exact solutions of the following form(57) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t^{2}exp(x+y),t^2-1\}.\end{array}$$(57)

Then, the other functions in (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) are obtained using the above exact solutions. To investigate the stability of the SMRPI, the artificial noisy data have been generated in this study by Equation (47(47) $$\begin{array}{c}\hfill m^{\mathit{ϵ}}((k+1)\mathit{\delta }t)=m((k+1)\mathit{\delta }t)+\mathit{\sigma }\mathit{\epsilon },\end{array}$$(47) ). Numerical results of ${\mathit{\epsilon }}_{\infty }$ and ${\mathit{\epsilon }}_R$ on ${[0,1]}^2$ for $N=529$, $\mathit{\delta }t=0.02$ and $T=1$ with percentage of the noises $\mathit{\sigma }\in \{1,3,5\}\%$ are listed in Table 1. Obviously, under different levels of noises being imposed on the Equation (4(4) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})u(\mathbf{x},t)\mathrm{d}\mathbf{x}=m(t),t>0,\end{array}$$(4) ) or Equation (5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) up to 1–5%, the proposed method is stable. Also in Table 2, the numerical results of ${\mathit{\epsilon }}_{\infty }$ and ${\mathit{\epsilon }}_R$ are given for r(t) and u(x, y, T) in cases of different N and $\mathit{\delta }t$ with percentage of the noise $\mathit{\sigma }=1\%$. It is apparent, The SMRPI accuracy improves with increasing number of nodes and iterations. Also, it can be seen that the condition number of the global matrix increasing by increasing the number of nodes and iterations. In Figure 3, the approximate solutions and absolute errors of u(x, y, T) are shown for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$ which again implies that the stability of the proposed method because by increasing the noise, the absolute errors do not have significant difference. Figure 4 shows the exact solutions $\{r(t),u(x,0.5,T)\}$ in comparison to numerical solutions for $N=625$, $\mathit{\delta }t=0.01$ and percentage of the noises $\mathit{\sigma }\in \{1,3,5\}\%$ on ${[0,1]}^2$. Both of graphs in Figure 4, show the high accuracy of present method in this Example. Condition number and regularization parameter values for iteration $k=1:100$ with $N=121$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$, are plotted in Figure 5. One can see that condition number for fixed N is constant that is because function f(x, y, t) in Equation (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) ) is independent of time variable. Indeed using Equation (57(57) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t^{2}exp(x+y),t^2-1\}.\end{array}$$(57) ) we obtain(58) $$\begin{array}{c}\hfill f(x,y,t)=-2e^{(x+y)},g(x,y,t)=0.\end{array}$$(58)

Graphs of approximate solutions and absolute errors of u(x, y, T) and r(t) with free noise on ${\mathrm{\Omega }}_2$ for $N=441$, $\mathit{\delta }t=0.01$ and $T=1$, are shown in Figure 6. It is visible that SMRPI is flexible in dealing with problems by irregular domains.

 

Table 1. Numerical results of absolute errors and relative errors on ${[0,1]}^2$ with $N=529$, $\mathit{\delta }t=0.02$, $T=1$ and condition number $5.5427\times {10}^3$ for Example 1.

$\mathit{\sigma }$ (%)	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_R(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_R(u)$
1	5.9904e$-$002	5.9904e$-$002	2.5846e$-$002	3.0563e$-$003
3	6.2430e$-$002	6.2430e$-$002	2.6260e$-$002	3.0864e$-$003
5	7.6729e$-$002	7.6729e$-$002	3.8895e$-$002	5.0006e$-$003

Table 2. Numerical results of absolute errors, relative errors and condition numbers on ${[0,1]}^2$ with $\mathit{\sigma }=1\%$ and $T=1$ for Example 1.

	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_R(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_R(u)$	cond
$h=\mathit{\delta }t=1/10$	9.1063e$-$001	9.1063e$-$001	6.6331e$-$00	9.4847e$-$001	3.0202e$-$002
$h=1/14,\mathit{\delta }t=1/20$	7.6473e$-$001	7.6473e$-$001	4.7625e$-$001	7.3015e$-$002	5.8425e$-$002
$h=1/20,\mathit{\delta }t=1/50$	6.8627e$-$002	6.8627e$-$002	1.0667e$-$002	1.2570e$-$003	1.7197e$-$003
$h=1/24,\mathit{\delta }t=1/100$	5.7520e$-$002	5.7520e$-$002	2.7169e$-$003	3.2620e$-$004	4.7351e$-$003

Figure 8. Graphs of absolute errors r(t) and u(x, y, T) using the SMRPI with $\mathit{\sigma }\in \{0,3,5\}\%$, $N\in \{121,225,441,625,1089,1849,2209\}$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$ for Example 2.

Figure 9. Condition number and regularization parameter values for $k=\overline{1:T/\mathit{\delta }t}$ with $N=2209$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$ for Example 2.

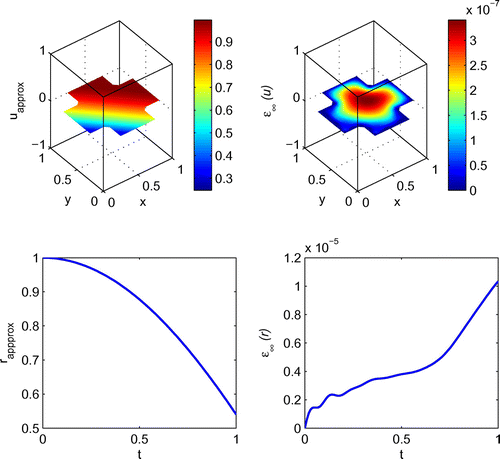
Figure 10. Graphs of approximate solution and absolute error of $u(\mathbf{x},t)$ (a,b) with approximate solution and absolute error of r(t) (c,d) in the case of no regularization and $N=441$, $\mathit{\delta }t=0.01$ and $T=1$ on domain ${\mathrm{\Omega }}_1$ for Example 2.

Example 2:

Consider Equations (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) on the ${[0,1]}^2$ and irregular domains ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_3$ with exact solutions of the following form(59) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t\sin (x+y),\cos (t)\}.\end{array}$$(59)

Then, the other functions in (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) are obtained using Equation (59(59) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t\sin (x+y),\cos (t)\}.\end{array}$$(59) ). In this Example, we enter the noise to investigate the stability of the SMRPI as Equation (2(2) $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),u_t(\mathbf{x},0)=v_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$(2) ). Table 3 presents the numerical results of ${\mathit{\epsilon }}_{\infty }$ and ${\mathit{\epsilon }}_R$ on ${[0,1]}^2$ for $N=1849$, $\mathit{\delta }t=0.02$ and $T=1$ with percentage of the noises $\mathit{\sigma }\in \{1,3,5\}\%$. Clearly from Table 3 we can conclude the stability of proposed method because errors do not have much difference with increased noises. To prove that the SMRPI does not depend on the shape of an irregular area, we have collected the numerical results of ${\mathit{\epsilon }}_{\infty }$ for r(t) and u(x, y, T) in cases of different N and $\mathit{\delta }t$ with no regularization on irregular domains ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_3$ in Table 4. It is understandable from Table 4 that the SMRPI accuracy is perfect by increasing the number of nodes and iterations. Graphs of approximate solutions and absolute errors of u(x, y, T) for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$, have been shown in Figure 7 which leads to the stability of the proposed method. In Figure 8, the graphs of absolute errors r(t) and u(x, y, T) have been depicted vs. $N\in \{121,225,441,625,1089,1849,2209\}$, $\mathit{\delta }t=0.02$ and percentage of the noises $\mathit{\sigma }\in \{0,3,5\}\%$ on ${[0,1]}^2$. It is observed from Figure 8 that errors decay with the decreasing noisy data, and the numerical solutions achieved best accuracy with noise-free measurement data. Also, one can see by increasing the collocation points, in every level of noises, the errors have been improved. Figure 9 shows the condition number and regularization parameter values for iteration $k=1:50$ with $N=2209$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$. As in Example 1, one can see that condition number for fixed N is constant that is because function $f(\mathbf{x},t)$ in Equation (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) ) is independent of time variable that is from Equation (59(59) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t\sin (x+y),\cos (t)\}.\end{array}$$(59) ) we have(60) $$\begin{array}{c}\hfill f(x,y,t)=x+y,g(x,y,t)=2t\sin (x+y)-(x+y)\cos (t).\end{array}$$(60)

Graphs of approximate solutions and absolute errors of u(x, y, T) and r(t) with free noise on ${\mathrm{\Omega }}_1$ for $N=441$, $\mathit{\delta }t=0.01$ and $T=1$, have been drawn in Figure 10. Once again the ability of the proposed method to deal with irregular domains is evident from Figure 10.

 

Table 3. Numerical results of absolute errors and relative errors on ${[0,1]}^2$ with $N=1849$, $\mathit{\delta }t=0.02$, $T=1$ and condition number $4.7605\times {10}^4$ for Example 2.

$\mathit{\sigma }$ (%)	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_R(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_R(u)$
1	1.7999e$-$001	1.7999e$-$001	1.1730e$-$002	7.4711e$-$003
3	1.8026e$-$001	1.8026e$-$001	1.1737e$-$002	7.4766e$-$003
5	1.8212e$-$001	1.8212e$-$001	1.2048e$-$002	7.6859e$-$003

Figure 11. $u_{approx}$ (left) and ${\mathit{\epsilon }}_{\infty }(u)$ (right) profiles for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$ for Example 3.

Figure 12. Graphs of relative errors r(t) and u(x, y, T) using the SMRPI with $\mathit{\sigma }\in \{0,3,5\}\%$, $N\in \{121,225,441,625,1089,1681\}$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$ for Example 3.

Figure 13. Condition number and regularization parameter values for $k=\overline{1:T/\mathit{\delta }t}$ with $N=441$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$ for Example 3.

Figure 14. Graphs of approximate solution and absolute error of $u(\mathbf{x},t)$ (a,b) with approximate solution and absolute error of r(t) (c,d) in the case of no regularization and $N=2209$, $\mathit{\delta }t=0.01$ and $T=1$ on domain ${\mathrm{\Omega }}_3$ for Example 3.

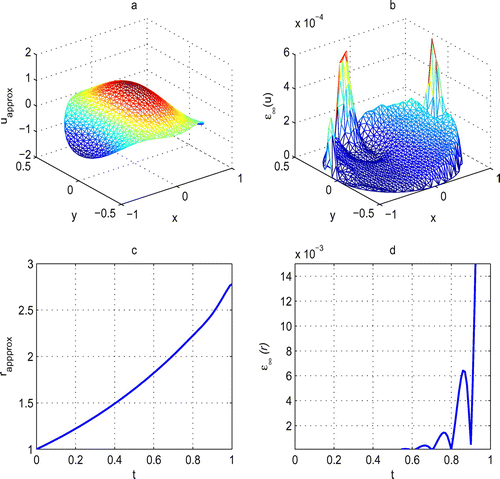
Table 4. Numerical results of absolute errors with no regularization and $T=1$, on irregular domains ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_3$ for Example 2.

	${\mathrm{\Omega }}_1$		${\mathrm{\Omega }}_2$		${\mathrm{\Omega }}_3$
	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_{\infty }(u)$
$N=225$, $\mathit{\delta }t=1/10$	3.4436e$-$004	8.9253e$-$006	3.2252e$-$004	5.6662e$-$004	5.4894e$-$003	1.0634e$-$003
$N=441$, $\mathit{\delta }t=1/50$	8.2893e$-$005	2.3996e$-$006	4.8099e$-$006	1.1507e$-$006	1.7490e$-$003	7.3119e$-$004
$N=729$ , $\mathit{\delta }t=1/80$	5.4471e$-$005	1.1960e$-$006	2.6571e$-$006	1.8344e$-$007	1.3912e$-$003	2.1163e$-$004
$N=1089$ , $\mathit{\delta }t=1/100$	1.0076e$-$005	3.5422e$-$007	1.5345e$-$006	4.7612e$-$008	2.0823e$-$004	4.0857e$-$005
$N=1225$ , $\mathit{\delta }t=1/150$	5.5202e$-$006	1.5043e$-$007	1.4544e$-$006	3.5298e$-$008	1.3900e$-$005	2.9496e$-$005

Table 5. Numerical results of absolute errors and relative errors on ${[0,1]}^2$ with $N=2209$, $\mathit{\delta }t=0.02$, $T=1$ and condition number $2.8050\times {10}^4$ for Example 3.

$\mathit{\sigma }$ (%)	${\mathit{\epsilon }}_{\infty }(r)$	${\mathit{\epsilon }}_R(r)$	${\mathit{\epsilon }}_{\infty }(u)$	${\mathit{\epsilon }}_R(u)$
0	1.3175e$-$009	4.8467e$-$010	1.6392e$-$007	1.6617e$-$007
1	1.2140e$-$000	4.4659e$-$001	1.7974e$-$001	1.9101e$-$001
3	1.2179e$-$000	4.48060e$-$001	1.8048e$-$001	1.9180e$-$001
5	1.2168e$-$000	4.4762e$-$001	1.8026e$-$001	1.9156e$-$001

Example 3:

We consider Equations (45(45) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}w(\mathbf{x})(\mathrm{\Delta }u(\mathbf{x},t)+f(\mathbf{x},t)r(t)+g(\mathbf{x},t))\mathrm{d}\mathbf{x}=m^{″}(t),\end{array}$$(45) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) on the ${[0,1]}^2$ and irregular domain ${\mathrm{\Omega }}_3$ with exact solutions of the following form(61) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t^{2}cos(\mathit{\pi }x)cos(\mathit{\pi }y),exp(t)\},\end{array}$$(61)

where the other functions in (1(1) $$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{\partial }}^{2}u(\mathbf{x},t)}{\mathit{\partial }{t}^2}}=\mathrm{\Delta }u(\mathbf{x},t)+F(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$(1) )–(5(5) $$\begin{array}{c}\hfill u({\mathbf{x}}^{\ast },t)=m(t),t>0,\end{array}$$(5) ) are obtained using Equation (61(61) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t^{2}cos(\mathit{\pi }x)cos(\mathit{\pi }y),exp(t)\},\end{array}$$(61) ). Table 5 lists the numerical results of ${\mathit{\epsilon }}_{\infty }$ and ${\mathit{\epsilon }}_R$ on ${[0,1]}^2$ for $N=2209$, $\mathit{\delta }t=0.02$ and $T=1$ with percentage of the noises $\mathit{\sigma }\in \{0,1,3,5\}\%$. In this table, we perform a sensitivity analysis with respect to the percentage of the noises that is in the case of no regularization the results are very close to the exact solutions. However for the levels of noise $\mathit{\sigma }\in \{1,3,5\}\%$, the results have been heavily influenced by noise, still the results are stable. That means errors do not have significant difference with increased noises. Figure 11 shows graphs of approximate solutions and absolute errors of u(x, y, T) for different noise levels with $N=625$, $\mathit{\delta }t=0.01$ and $T=1$ on ${[0,1]}^2$. In Figure 12, the graphs of relative errors r(t) and u(x, y, T) are shown vs. $N\in \{121,225,441,625,1089,1681\}$ with $\mathit{\delta }t=0.02$ and percentage of the noises $\mathit{\sigma }\in \{0,3,5\}\%$ on ${[0,1]}^2$. Evidently, we conclude from Figure 12 that errors decay with the decreasing noisy data, and the numerical solutions have earned best accuracy with noise-free measurement data. Also it is observed that increasing the number of nodes reduces errors. Figure 13 presents the condition number and regularization parameter values for iteration $k=1:50$ with $N=441$, $\mathit{\delta }t=0.02$ and $T=1$ on ${[0,1]}^2$. In this Example, from Equation (61(61) $$\begin{array}{c}\hfill \{u(x,y,t),r(t)\}=\{t^{2}cos(\mathit{\pi }x)cos(\mathit{\pi }y),exp(t)\},\end{array}$$(61) ) we obtain(62) $$\begin{array}{c}\hfill f(x,y,t)=x+y+t,g(x,y,t)=-e^t(x+y+t)+2(1+{\mathit{\pi }}^2{t}^2)\cos (\mathit{\pi }x)\cos (\mathit{\pi }y).\end{array}$$(62)

In Figure 14, the graphs of approximate solutions and absolute errors of u(x, y, T) and r(t) have been depicted with free noise on ${\mathrm{\Omega }}_3$ for $N=2209$, $\mathit{\delta }t=0.01$ and $T=1$. The trivial result of Figure 14 is that SMRPI is a suitable method for general shaped domains.

6. Conclusion

In this article, the SMRPI has been applied to identify the time-dependent force function which satisfies in the wave equation subject to the integral overspecification over a portion of the spatial domain or to the overspecification at a point in the spatial domain. Since the problem is known to be ill-posed, in order to stabilise the solution, Thikhonov regularization strategy has been employed to solve effectively the discrete ill-posed resultant linear system so that the choice of the regularization parameter was based on the quasi-optimality criterion. To investigate the stability of the SMRPI, the artificial noisy data have been generated in this study by Equation (47(47) $$\begin{array}{c}\hfill m^{\mathit{ϵ}}((k+1)\mathit{\delta }t)=m((k+1)\mathit{\delta }t)+\mathit{\sigma }\mathit{\epsilon },\end{array}$$(47) ). The numerical examples of linear inverse force function have been worked out which show that the SMRPI method is simple and stable to solve the inverse force function in the wave equation with noisy data. Also, numerical results have been presented for both regular and irregular domains. Obviously SMRPI is flexible in dealing with problems by irregular domains.

Acknowledgements

The authors are grateful to three anonymous reviewers for carefully reading this paper and for their comments and suggestions which have improved the paper.

Additional information

Funding

This work was supported by the Imam Khomeini International University [6617].

Notes

No potential conflict of interest was reported by the authors.