Uncertainty quantification using probabilistic numerics: application to models in mathematical epidemiology

Abstract

Probabilistic numerics (PN) is a framework for analysing numerical algorithms accounting for all sources of numerical errors, including errors due to both round off and the choice of numerical scheme. The goal of this work is to use a Bayesian-based PN method to illustrate the quantification of uncertainty in mathematical epidemiology modelling. We simultaneously account for the uncertainty in data, parameters, as well as numerical discretization in applying this framework to the data from an ongoing community-acquired Methicillin-resistant Staphylococcus aureus epidemic in Chicago.

Keywords:

• Probabilistic numerics
• MRSA
• Bayesian inference
• uncertainty quantification
• mathematical epidemiology

AMS Subject Classifications:

• 62F15
• 92D30

1. Introduction

Probabilistic numerics (PN) is a framework for analysing numerical algorithms in a probabilistic context. The main objectives are to account for all sources of numerical errors, including errors due to both round off and the choice of numerical scheme. Moreover, a probabilistic framework allows for quantification and control of computational precision, i.e. of how these computational errors jointly propagate through the algorithm.

A natural way to cast this problem in the probabilistic context is to posit the following. Broadly speaking, we first consider an unknown function u. We wish to estimate u or some functional of it, such as an integral. One could assume a prior measure over an appropriate space of functions, to describe what we know about u a priori. Upon choosing and implementing a candidate numerical scheme, we can evaluate the numerical approximation $u^N(t)$ at a set of grid points $t_1,t_2,\dots t_N$. This allows us to compute the posterior measure of u, using the Bayes theorem, treating the numerical approximation $u^N(t)$ as data. One could then estimate u and the desired functionals based on this posterior measure. As noted by Diaconis in [1], this approach was originally proposed by Poincar in 1896 [2].

In the recent decades, PN methods have experienced a resurgence of interest, starting with the seminal works by Wahba [3] and O’Hagan [4]. Indeed, many classic quadrature and interpolation rules can be interpreted as Bayesian estimators arising from certain families of stochastic process priors placed on the integrand. We direct the interested reader to the recent overview article by Hennig et al. [5] and to a more in-depth discussion applied to uncertainty quantification in differential equations within a formal Bayesian context in Chkrebtii et al. [6].

Regarding the example application in this work, there is a long history of epidemiologists using mathematics to study the spread of infectious diseases in populations. At the turn of the twentieth century, Sir Ronald Ross created a simple mathematical model of malaria transmission [7]. In the early 1900s Kermack and McKendrick [8] began developing compartmental models to describe groups of infectious individuals. For a more recent overview of compartmental modelling in mathematical epidemiology, we refer the interested reader to the review by Hethcote [9].

In this paper, we investigate mathematical epidemiology models by focusing on the uncertainty quantification, while simultaneously accounting for multiple sources of uncertainty including data, parameters, as well as numerical approximation. Using a simple mathematical epidemiology model (the susceptible-infectious-recovered (SIR) model) we illustrate how PN can provide insight into how numerical uncertainty propagates to solutions and can lead to incorrect inference. We then use the susceptible-infectious-susceptible (SIS) model to describe the current community-acquired Methicillin-resistant Staphylococcus aureus (CA-MRSA) epidemic in Chicago. This model has a known analytical solution, which facilitates transparency in uncertainty quantification under different approaches. We consider an inverse problem for inference about parameters in the SIS model and to illustrate how all sources of error play a part in the overall uncertainty, using maximum likelihood (ML) and a Bayesian-based PN framework.

2. Methods

In this section, we provide overviews of the two main methods we employ in this work, maximum likelihood (Section 2.1) and a Bayesian-based probabilistic numerics uncertainty quantification (Section 2.2).

2.1. Maximum Likelihood

At the core of the ML technique is an assumption that there is a probability distribution associated with each data point. The most often utilized distribution is normal, which we will also use here. Under this assumption, each observation is assumed to be normally distributed with the mean equal to the postulated model output and an additive observational variance (usually unknown) as follows$$y(t)=u(t,\mathrm{\Theta })+\mathit{\epsilon }(t).$$

Here, y(t) is the data (observation) at time t, $u(t,\mathrm{\Theta })$ is the model output, $\mathrm{\Theta }$ is the vector of unknown model parameters and $\mathit{\epsilon }(t)$ is the discrepancy between the data and the model at time t. Assuming normal i.i.d. (independent and identically distributed) discrepancies with mean zero and time-independent variance ${\mathit{\sigma }}^2$, i.e. $\mathit{\epsilon }(t)\sim \mathcal{N}(0,{\mathit{\sigma }}^2),\forall t$, the likelihood function of the parameters for a given data set is then given as follows$$\mathcal{L}(\mathrm{\Theta },\mathit{\sigma }|\mathit{y})=\prod _{t=1}^T\frac{1}{\mathit{\sigma }}{e}^{-\frac{{\left(y(t)-u(t,\mathrm{\Theta })\right)}^2}{2{\mathit{\sigma }}^2}},$$

where $\mathit{y}$ is the vector of T observations. Inference about $\mathrm{\Theta }$ can be based asymptotically on the Fisher information matrix whose entries are given by$${\mathrm{\Phi }}_{ij}=\frac{{\mathit{\partial }}^2}{\mathit{\partial }{\mathrm{\Theta }}_i{\mathrm{\Theta }}_j}log\mathcal{L}(\mathrm{\Theta },\mathit{\sigma }|\mathit{y}).$$

In the case of the SIS model (with an analytical solution), u is a function of $\mathrm{\Theta }=(\mathit{\beta },\mathit{\gamma },I_0)$, with infection rate $\mathit{\beta }$, recovery rate $\mathit{\gamma }$ and initial number of infectious $I_0$. This makes the computation of $\mathrm{\Phi }$ relatively straightforward.

2.2. Bayesian approach

Inference under the Bayesian framework is based on the posterior distribution P of the model parameters, given the data. It builds on the likelihood function as follows:$$P(\mathrm{\Theta },\mathit{\sigma }|\mathit{y})=\mathcal{L}(\mathrm{\Theta },\mathit{\sigma }|\mathit{y}){\mathit{\pi }}_1(\mathrm{\Theta }){\mathit{\pi }}_2(\mathit{\sigma }),$$

where $\mathit{\sigma }$ is defined above, ${\mathit{\pi }}_1$ is the prior distribution on $\mathrm{\Theta }$, reflecting a priori knowledge and uncertainty about these parameters. Similarly ${\mathit{\pi }}_2$ is the prior distribution on $\mathit{\sigma }$, reflecting our uncertainty about the noise in the data. Unlike in the ML approach, inference is based on the entire distribution P and not just the curvature at its maximum. This allows asymmetric, long-tailed and possibly disjoint uncertainty intervals, known as the credible intervals in Bayesian statistics. Through the combination of priors and likelihoods, the Bayesian approach is able to reflect the joint uncertainty in the parameters and the data. This is in contrast to the ML approach which only translates the uncertainty in the data to the uncertainty in the parameters.

2.2.1. Probabilistic numerics

To establish the basic notation and approach, we denote N as the degree of numerical discretization, u as the analytical solution, and $u^N$ as the computational output. Thus the posterior distribution on two quantities of interest ($\mathrm{\Theta }$ and u) is(1) $$\begin{array}{c}\hfill P(\mathrm{\Theta },u(\mathbf{t},\mathrm{\Theta })|u^N(\mathbf{t},\mathrm{\Theta }))\propto \mathcal{L}(u^N(\mathbf{t},\mathrm{\Theta })|u(\mathit{t},\mathrm{\Theta }),\mathrm{\Theta })\times {\mathit{\pi }}_1(u(\mathbf{t},\mathrm{\Theta })|\mathrm{\Theta })\times {\mathit{\pi }}_2(\mathrm{\Theta }),\end{array}$$(1)

where $\mathbf{t}$ is a vector of timepoints. The function $\mathcal{L}$ is the likelihood of the computational output $u^N$, given the analytical solution u, parameters $\mathrm{\Theta }$ and discretization order N. The distribution ${\mathit{\pi }}_1$ is the prior measure over the space of solutions u for a specific value of parameter $\mathrm{\Theta }$. Note that the classical non-Bayesian applications such as ML, ${\mathit{\pi }}_1$ would correspond to a point measure with all mass at u. Lastly, the distribution ${\mathit{\pi }}_2$ is the prior on the parameters $\mathrm{\Theta }$.

According to Stuart in [10], a Gaussian distribution is the natural probability measure for a differential equation solution. That is to say, the numerical error structure is a Gaussian Process ($\mathcal{G}P$) from one timepoint to the next. Thus, the prior ${\mathit{\pi }}_1$ on the unknown solution function $u(t,\mathrm{\Theta })$ is usually modelled as a $\mathcal{G}P$ [4,10]. $\mathcal{G}P$s are a flexible class of stochastic processes defined through the mean function of time and a covariance function between two arbitrary times $t_j$, $t_k$. This implies that the true solution u(t) is a priori believed to be normally distributed with prespecified mean and variance at every timepoint t.

Similarly, one can use a $\mathcal{G}P$ to describe the derivatives of the true solution u, specifying prior belief about the smoothness of u. For the case of simple ODEs, it will usually suffice to specify a joint Gaussian Process prior on the true solution $u(t,\mathrm{\Theta })$ and its first derivative $u_t(t,\mathrm{\Theta })$, especially when the Forward Euler scheme is considered. Note that in Equation (1(1) $$\begin{array}{c}\hfill P(\mathrm{\Theta },u(\mathbf{t},\mathrm{\Theta })|u^N(\mathbf{t},\mathrm{\Theta }))\propto \mathcal{L}(u^N(\mathbf{t},\mathrm{\Theta })|u(\mathit{t},\mathrm{\Theta }),\mathrm{\Theta })\times {\mathit{\pi }}_1(u(\mathbf{t},\mathrm{\Theta })|\mathrm{\Theta })\times {\mathit{\pi }}_2(\mathrm{\Theta }),\end{array}$$(1) ), the variable $u_t$ does not appear because it is integrated out as ultimately we only care about the true solution u. More precisely, the $\mathcal{G}P$ prior structure is formulated via$$\begin{array}{c}\left[\begin{array}{c}{u}_t\hfill \\ u\hfill \end{array}\right]\sim \mathcal{G}P\left(\left[\begin{array}{c}{m}_t\hfill \\ m\hfill \end{array}\right],\left[\begin{array}{cc}C(R_{\mathit{\lambda }},R_{\mathit{\lambda }})& C(Q_{\mathit{\lambda }},R_{\mathit{\lambda }})\\ C(Q_{\mathit{\lambda }},R_{\mathit{\lambda }})& C(Q_{\mathit{\lambda }},Q_{\mathit{\lambda }})\end{array}\right]\right)\hfill \end{array},$$

where $R_{\mathit{\lambda }}\in L^2$ is a kernel function, $Q_{\mathit{\lambda }}$ is defined as$$Q_{\mathit{\lambda }}(t_1,t_2)={\int }_0^{t_1}{R}_{\mathit{\lambda }}(s,t_2)\mathrm{d}s$$

and m, $m_t$ are mean functions of u, $u_t$, respectively. For example, m(0) is the mean value of the true solution at the initial time $t=0$, i.e. the initial condition for u. The covariance function is defined as$$C({\mathit{\psi }}_1,{\mathit{\psi }}_2)={\mathit{\alpha }}^{-1}{\int }_{\mathbb{R}}{\mathit{\psi }}_1(t_1,s){\mathit{\psi }}_2(t_2,s)\mathrm{d}s,$$

for length scale $\mathit{\lambda }\in (0,\infty )$, prior precision $\mathit{\alpha }$, and arbitrary integrable functions ${\mathit{\psi }}_1$, ${\mathit{\psi }}_2$ on ${\mathbb{R}}^2$. Note that this formulation ensures that $C(0,0)=0$, i.e. the variance at time zero equals zero, thus enforcing the initial condition $u(0,\mathrm{\Theta })=m(0).$

2.2.2. Example

To illustrate this $\mathcal{G}P$ applied to a simple model from mathematical epidemiology, we consider the traditional SIR model$$\begin{array}{cc}\hfill \text{ODE:}\left\{\begin{array}{c}{S}_t(t)=-\mathit{\beta }S(t)I(t)\hfill \\ I_t(t)=\mathit{\beta }S(t)I(t)-\mathit{\gamma }I(t)\hfill \\ R_t(t)=\mathit{\gamma }I(t)\hfill \end{array}\right.& \text{IC:}\left\{\begin{array}{c}S(0)=499\hfill \\ I(0)=1\hfill \\ R(0)=0\hfill \end{array}\right.\hfill \end{array}$$

with a population of 499 susceptibles and one infectious individual. The states and the first derivatives are all assumed a priori to follow a Gaussian Process, implying that all states and their derivatives are random variables. Moreover, if a Forward Euler method is used, the distribution of each variable at each step can be derived explicitly as another Gaussian Process as a direct consequence of the initial $\mathcal{G}P$-prior on u and $u_t$. Note that Chkrebtii et al. [6] present an illustration of this mapping.

Furthermore, it is important to note that any numerical scheme (and not just Forward Euler) can be viewed as a transformation of the Gaussian process, with every step in that numerical scheme having its own distribution derived from the original Gaussian Process on u and $u_t$. However, while the Forward Euler method is not typically encountered outside a classroom, it has been the workhorse in the PN literature. The reason for this is that computing how the distributions map from one time step to the next for higher-order numerical methods can be challenging.¹

To illustrate the PN approach, an SIR model solved with the Forward Euler method is presented in Figure 1. The red dashed curves are the high accuracy numerical solutions, solved using the variable order, variable stepsize Runge–Kutta method as implemented in Matlab’s ode15s. The green dotted curves are the non-$\mathcal{G}P$-based Forward Euler with $N=40$ and $N=80$ in Figure 1(a) and (b), respectively. The faint grey solid curves reflect the posterior uncertainty about u and they are a random sample from the posterior distribution (the posterior Gaussian process) of u where the solid cyan curve is the pointwise average of the ensemble. What appears to be a ‘black’ curve is actually a thick cluster of grey curves. The spread of the grey curves represents the uncertainty in the solution u due to the parameter uncertainty and data uncertainty as well as numerical discretization uncertainty.

Figure 1. SIR simulations for $\mathit{\beta }=0.001$, $\mathit{\gamma }=0.1$ and with $N=40$ and $N=80$ grid points. The red dashed curve is the high accuracy numerical solution, solved using the variable order, variable stepsize Runge–Kutta method as implemented in Matlab’s ode15s. The green dotted curve is the non-$\mathcal{G}P$-based Forward Euler. The grey curves are all the realizations of the $\mathcal{G}P$-based ensemble and the cyan curve is the pointwise average of the ensemble.

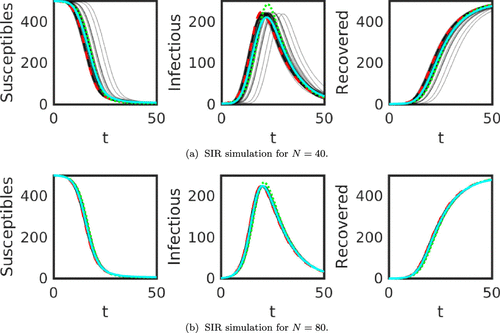
In particular, we draw attention to how the majority of the posterior sample of grey solid curves is to the right of the red dashed curve, meaning that the posterior is slightly biased. Indeed, the cyan solid curve is entirely to the right of the red dashed curve, thus estimating the peak of the epidemic to be later. We also note that the PN-based Forward Euler does not overshoot the peak of the epidemic as is done with the green dotted ‘deterministic’ Forward Euler solve.

3. Inverse problem application: SIS model for CA-MRSA

Staphylococcus aureus is a bacterium commonly found in the human nasal mucosa or on the skin [11]. Although generally harmless to healthy individuals, this bacterium can cause a range of infections in its hosts, from benign skin and soft tissue infections to endocarditis and sepsis [12]. It is, in fact, the most common bacterial pathogen isolated from human infections [12,13]. When treating S. aureus infections, the strains which show resistance to the first-line defence of antibiotic treatments present a considerable burden to the patient as well as to the health care system. Since the start of a widespread use of antibiotics in the second half of the twentieth century, antibiotic resistant S. aureus strains have become widespread. Of particular concern has been the Methicillin-resistant Staphylococcus aureus (MRSA), which is resistant to penicillin and all of its derivatives.

Over the past two decades MRSA, has become widespread in the general community in the US and around the world [13]. The new community-associated MRSA (CA-MRSA) strains have been isolated from populations without relation to a health care or nursing home environments. Since two decades ago, MRSA infections in the community have been on the rise [13,14]. A recent report from The Centers for Disease Control report stated that more people had died from MRSA than AIDS in 2005 [15] and it is now understood that CA-MRSA is the main source of this increased prevalence and mortality [13,16]. A better understanding of the CA-MRSA epidemic is thus critical for public health.

A deterministic SIS model for CA-MRSA was described and implemented in a meta-analytic framework for a set of cities in [14]. The CA-MRSA dynamics in this model is governed by a set of two differential equations, describing the trade-off between susceptible and infectious fraction in a population over time:(2) $$\begin{array}{cc}\hfill \text{ODE:}\left\{\begin{array}{cc}{S}_t(t)\hfill & =-\mathit{\beta }S(t)I(t)/n+\mathit{\gamma }I\hfill \\ I_t(t)\hfill & =\mathit{\beta }S(t)I(t)/n-\mathit{\gamma }I(t)\hfill \end{array}\right.& \text{IC:}\left\{\begin{array}{cc}S(0)\hfill & =n-I_0\hfill \\ I(0)\hfill & =I_0\hfill \end{array}\right.\hfill \end{array}$$(2)

where $I_0$ is the initial infectious population, n is the total population size, and the parameters $\mathit{\beta }$ and $\mathit{\gamma }$ describe the transition rates between disease stages. This model is well known in mathematical epidemiology and has been extensively studied over the years. For example, the system of Equation (2(2) $$\begin{array}{cc}\hfill \text{ODE:}\left\{\begin{array}{cc}{S}_t(t)\hfill & =-\mathit{\beta }S(t)I(t)/n+\mathit{\gamma }I\hfill \\ I_t(t)\hfill & =\mathit{\beta }S(t)I(t)/n-\mathit{\gamma }I(t)\hfill \end{array}\right.& \text{IC:}\left\{\begin{array}{cc}S(0)\hfill & =n-I_0\hfill \\ I(0)\hfill & =I_0\hfill \end{array}\right.\hfill \end{array}$$(2) ) can be solved analytically via substituting $S=n-I$ into the second equation and then separating variables to solve for I. The solution is the logistic curve [17,18](3) $$\begin{array}{c}\hfill I(t)=\frac{n\left(1-\frac{\mathit{\gamma }}{\mathit{\beta }}\right)}{1+\left(\left(\frac{n\left(1-\frac{\mathit{\gamma }}{\mathit{\beta }}\right)}{I_0}-1\right)e^{(\mathit{\beta }-\mathit{\gamma })}\right)e^{-(\mathit{\beta }-\mathit{\gamma })t}}.\end{array}$$(3)

Alternatively, this system of equations can be solved numerically using modern discretization techniques for ordinary differential equations. In the case of both analytical and numerical solutions, however, parameter estimation can be carried out in multiple ways: ML and Bayesian. The Bayesian framework allows for additional parameter information to be incorporated into the inference. This additional information is incorporated into the prior information and can include information, such as previous outbreaks, experimental data and expert opinions. ML, however, can only capture the uncertainty due to the data explicitly under consideration. In the case of the numerical solution, the Bayesian framework can be extended to account for the uncertainty due to the discretization scheme and the solver itself. In the next section, we present likelihood and Bayesian (including PN) approaches to quantifying uncertainty in SIS parameters for the MRSA epidemic.

4. Inverse problem applied to CA-MRSA

The previous section describes three sources of uncertainties: parameters, data and numerical schemes. The natural next question is how do these types of uncertainties impact inference in inverse problems. To illustrate this, we discuss an inverse problem in the context of MRSA.

Figure 2 depicts the results from applying the ML to the model in equation (3(3) $$\begin{array}{c}\hfill I(t)=\frac{n\left(1-\frac{\mathit{\gamma }}{\mathit{\beta }}\right)}{1+\left(\left(\frac{n\left(1-\frac{\mathit{\gamma }}{\mathit{\beta }}\right)}{I_0}-1\right)e^{(\mathit{\beta }-\mathit{\gamma })}\right)e^{-(\mathit{\beta }-\mathit{\gamma })t}}.\end{array}$$(3) ). The circles are the CA-MRSA data for each year, the solid curve is the ML estimated number of infected over time and the dashed lines are the prediction intervals. The ML parameter estimates and their 95% confidence intervals are reported in the upper left. Note that the confidence intervals are computed using the Fisher Information matrix and thus the asymptotic arguments are likely to be suspect (given that there are only nine data points). Note that these results are comparable to those reported in [14].

Figure 2. ML fit for SIS model to Chicago data. Note the ‘CI’ in this figure denotes 95% confidence intervals for SIS parameters.

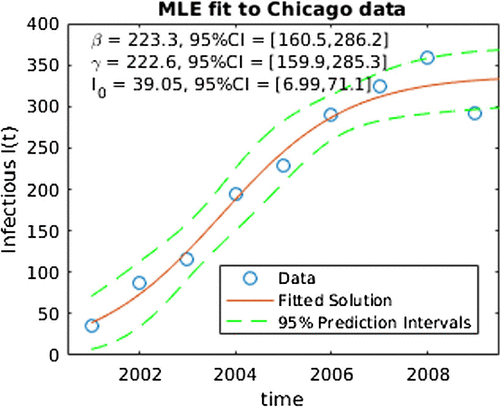
Table 1. Central 95% credible intervals for SIS parameters.

Percentile	$\mathit{\beta }$	$\mathit{\gamma }$	$I_0$	$\mathit{\lambda }$	$\mathit{\alpha }$
2.5%	186.72	186.04	38.66	3867.2	1.38
97.5%	248.95	248.1	49.08	104202.7	3.07

Figure 3. PN fit for SIS model to data. Note the ‘CI’ in this figure denotes central 95% credible intervals for SIS parameters.

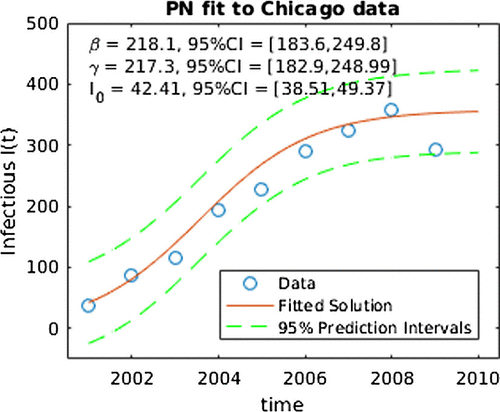
The Bayesian-based PN approach uses a Markov chain Monte Carlo algorithm to generate a sample from the approximate joint posterior distribution. The approximate joint distribution was generated using a chain 1,000,000 steps long with a burn-in of 20% and pruned to 100,000 steps. There were $N=50$ gridpoints and the priors were $\mathit{\beta }\sim \text{Exp}(250)$, $\mathit{\gamma }\sim \text{Exp}(249.16)$, $I_0\sim \mathcal{N}(41,{16}^2)$, $\mathit{\alpha }\sim log\mathcal{N}(10,1)$, and $\mathit{\lambda }\sim {\mathit{\chi }}^2(1)$. Note that these priors were made relatively flat to make the results comparable with the likelihood results. Similarly, the Gaussian process priors are very vague, with key parameters in those priors to be estimated from the data. The 2.5% and 97.5% percentiles as lower and upper bounds of 95% credible intervals are reported in Table 1. Depicted in Figure 3 is the prediction interval for the number of infected I(t) over time as well as the parameter fits and their credible intervals. As expected, the prediction interval in the PN result is larger than the ML one. We note that the MLE and posterior mean point estimates are quite similar in the two approaches and the confidence intervals from the MLE overlap with the credible intervals for the PN. However, the PN credible intervals for $\mathit{\beta }$ and $\mathit{\gamma }$ are notably smaller than the MLE confidence intervals, which is unexpected. We note that the parameter vector in the PN case is larger and includes two parameters ($\mathit{\alpha }$, $\mathit{\lambda }$) which relate to the numerical precision and the length scale, respectively. This result suggests that accounting properly for the numerical uncertainty may have impact on parameter inference in inverse problems, increasing uncertainty in some parameters (or states) and decreasing in others. Accordingly, this is a topic we plan to address in our future efforts.

5. Concluding remarks

This paper presents a comparison between ML and PN methods in terms of mathematical epidemiology models. In this simple setting of SIS and SIR models, we are able to illustrate how numerical uncertainty can impact inference in parameter inverse problems.

The PN-based method generates estimates for uncertainty which account for numerical discretization. However, the computation time needed to compute the PN-based inference is substantially longer than that needed for the ML. This increased time is due to the fact that PN-based inference relies on the use of an MCMC method. In the results for both ML- and PN- based methods, it’s also clear that the PN methods results in larger prediction intervals as a result of the inclusion of the uncertainty due to the numerical discretization. MCMC-based methods also require careful calibration and convergence diagnostics and themselves present an addition source of error and uncertainty in the results (which is currently ignored).

For future research directions, the most obvious need is to fully investigate the impact of higher-order (more accurate) methods for solving ODEs. In particular, our future work plans involve studying classes of explicit and implicit Runge–Kutta algorithms and how they could be investigated in a probabilistic context. Preliminary results indicate that this $\mathcal{G}P$-based analysis approach could be useful in explaining how some RK methods are more stable for a wider range of ODE systems. However, it is also important to note that there are other interesting directions such as relaxing the $\mathcal{G}P$-assumption on the transitions from one time step to the next.

Acknowledgements

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. These funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Additional information

Funding

This work was partially supported by the National Science Foundation [grant number DMS-1127914] to the Statistical and Applied Mathematical Sciences institute and the NIH - National Institute of General Medical Sciences [grant number U01GM087729].

Notes

No potential conflict of interest was reported by the authors.

1 A natural topic for future research is to consider higher-order ODE methods in the PN context.