Bayesian model calibration and uncertainty quantification for an HIV model using adaptive Metropolis algorithms

Abstract

In this paper, we discuss Bayesian model calibration and use adaptive Metropolis algorithms to construct densities for input parameters in a previously developed HIV model. To quantify the uncertainty in the parameters, we employ two MCMC algorithms: Delayed Rejection Adaptive Metropolis (DRAM) and Differential Evolution Adaptive Metropolis (DREAM). The densities obtained using these methods are compared to those obtained through direct evaluation of Bayes formula. We also employ uncertainties in input parameters and observation errors to construct prediction intervals for a model response. We verify the accuracy of the Metropolis algorithms by comparing chains, densities and correlations obtained using DRAM, DREAM and direct numerical evaluation of Bayes’ formula. We also perform similar analysis for credible and prediction intervals for responses.

Keywords:

• Bayesian model calibration
• uncertainty quantification
• HIV model

1. Introduction

Uncertainty quantification plays an important role in the modelling of biological processes that involve complex phenomena. Input parameters are often correlated and cannot be directly measured from data, so these parameters must be estimated. Additionally, available data may be noisy due to measurement noise or limitations in sensor capabilities. The difficulty in parameter estimation can be exacerbated in biological applications since measurements are taken in groups rather than individual state variables as discussed in [1]. For these reasons, it is essential to quantify uncertainties in the model response due to uncertainties in the parameters, errors in the measurement data and model discrepancy.

Development of models for viral infection processes is critical to understand the disease spread of HIV, and quantified uncertainties are required when constructing optimized treatment regimes. To illustrate these issues, we employ the HIV model(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1)

developed in [2,3]. Here, $T_1$ and $T_1^{\ast }$ represent the uninfected and infected type 1 target cells, respectively. Similarly, $T_2$ and $T_2^{\ast }$ represent uninfected and infected type 2 target cells. Note that $T_1$ and $T_2$ cells could represent, for instance, CD4 T-lymphocytes and macrophages. Here, V is the total number of infectious and non-infectious free viruses, and E represents the immune effector cells. Whereas, this model is quite simplified, it provides a framework to investigate control strategies for HIV [2]. Studying the HIV infection dynamics using mathematical models can contribute to understanding of fundamental features of infection and to improved disease monitoring and treatment. Though we perform our verification using model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ), there are more comprehensive models such as the one found in [4].

The description of the parameters in model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) are summarized in Table 1. Examples of parameters that can be measured are $\mathit{\delta }$, the death rate of infected cells, and c, the death rate of free virus. Values of parameters that can be directly measured are provided in [5–8]. On the other hand, immune response parameters such as $m_1$ and $m_2$ are not well known and must be inferred through a fit to data. The authors of [9] determine the parameter values involved in their model by applying physical constraints and using the expressions for the steady states.

In this paper, we employ a Bayesian framework to infer probability density functions (pdf) for model parameters. We subsequently propagate these uncertainties through the model to construct credible and prediction intervals for a quantity of interest. We focus on the performance of two adaptive Metropolis algorithms – Delayed Rejection Adaptive Metropolis (DRAM) [10] and DiffeRential Evolution Adaptive Metropolis (DREAM) [11,12] – due to their capability to infer highly correlated posterior densities.

We note that the use of DRAM and DREAM for dynamic models is well established. The contribution of this paper is to illustrate a framework for verifying the accuracy of these algorithms when inferring distributions for highly correlated parameters and constructing credible and prediction intervals for quantities of interest. We illustrate this verification process using two techniques. In the first, we employ energy statistics to test the null hypothesis that posterior samples, computed using DRAM and DREAM, are from the distributions obtained by directly approximating Bayes’ relation using quadrature techniques for a 3-parameter example. Secondly, we employ energy statistics to compare posterior samples from DRAM and DREAM for a moderate dimensional example having 12 parameters. For this case, we also verify the accuracy of both algorithms by comparing posterior means with the true parameters used to generate synthetic data. By establishing this verification procedure, we significantly extend initial analysis of the model using DRAM for a 6-parameter case as presented in [13].

In Section 2, we summarize the process of model calibration using Bayesian inference. Synthetic measurement data are used to infer probability density functions (pdf) for the parameters in the model. We then discuss different algorithms that one can employ to compute the posterior distributions in Section 3. Once parameter densities are constructed, the uncertainties in the input parameters and observation errors are propagated through the model to construct uncertainty bounds. More specifically, credible and prediction intervals allow us to bound the model response distributions in terms of parameter uncertainties and the observations errors. The process of constructing these estimates is described in Section 4. Finally, in Section 5, we demonstrate the model calibration process and the construction of prediction intervals using DRAM and DREAM for the HIV model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ). We verify the accuracy of the two methods by constructing densities for three parameters and comparing the results to densities that are computed by solving the Bayes’ formula directly. The accuracy of DRAM and DREAM is also verified by estimating the densities for a larger set of parameters, which vary greatly in their orders of magnitude.

Table 1. Parameters in the HIV model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ).

${\mathit{\lambda }}_1$	Target cell 1 production rate	${\mathit{\rho }}_1$	Ave. virions infecting type 1 cells
${\mathit{\lambda }}_2$	Target cell 2 production rate	${\mathit{\rho }}_2$	Ave. virions infecting type 2 cells
$d_1$	Target cell 1 death rate	$b_E$	Max. birth rate immune effectors
$d_2$	Target cell 2 death rate	$d_E$	Max. death rate immune effectors
$k_1$	Population 1 infection rate	$K_b$	Birth constant, immune effectors
$k_2$	Population 2 infection rate	$K_d$	Death constant, immune effectors
c	Virus natural death rate	${\mathit{\lambda }}_E$	Immune effector production rate
$\mathit{\delta }$	Infected cell death rate	${\mathit{\delta }}_E$	Natural death rate, immune effectors
$\mathit{ϵ}$	Population 1 treatment efficacy	$N_T$	Virions produced per infected cell
$m_1$	Population 1 clearance rate	f	Treatment efficacy reduction
$m_2$	Population 2 clearance rate

2. Bayesian inference

In [2], where the model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) is developed, the authors estimate parameter values using frequentist techniques. The authors use an iterative generalized least squares method and obtain uncertainty in the estimation process. Here, we perform Bayesian inference to estimate densities for model parameters. The Bayesian framework is also natural for uncertainty quantification since one can propagate the parameter densities through the model.

Bayesian techniques have been applied to models arising in bioscience, including an HIV model [14]. In the field outside of HIV modelling, the importance of parameter estimation and uncertainty quantification of pharmacokinetics models is illustrated in [15]. Smoothing using Gaussian processes on chemical reaction dynamics of producing nylon involving 6 to 24 parameters is discussed in [16], and [17] discusses accelerated sampling procedures of Bayesian inference with applications in systems biology and nonlinear dynamic systems. The estimation of rate constants for a continuous-time Markov ion channel model is discussed in [18]. Other applications of Bayesian inference include deformable neuronanotomical atlases [19] and several other models in Systems Biology Markup Language [20].

For $N_t$ observations, we employ the statistical model(2) $$\begin{array}{c}\hfill Y_i=f(t_i,Q)+{\mathit{\epsilon }}_i,i=1,\dots ,N_t,\end{array}$$(2)

where $Y_i,{\mathit{\epsilon }}_i$ and Q are random variables, respectively, denoting measurements at time $t_i$, observation errors, and parameters. The response of model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) at time $t_i$ is defined to be $f(t_i,Q)$.

For the comparisons between DRAM and DREAM, we employ synthetic data for which we specify the structure of the observation errors ${\mathit{\epsilon }}_i$. We assume they are independent and identically distributed (iid) and ${\mathit{\epsilon }}_i\sim \mathcal{N}(0,{\mathit{\sigma }}^2)$, where ${\mathit{\sigma }}^2$ is an unknown value that we infer. For measured data, the assumption of iid data is often violated, thus necessitating consideration of a statistical model(3) $$\begin{array}{c}\hfill Y_i=f(t_i,Q)+\mathit{\delta }(t_i,\tilde{Q})+{\mathit{\epsilon }}_i,\end{array}$$(3)

where $\mathit{\delta }(t_i,\tilde{Q})$ is a model discrepancy term with hyperparameters $\tilde{Q}$ that are also inferred.

Let y be the realization of the random variable Y such that(4) $$\begin{array}{c}\hfill y_i=f(t_i,q)+{\mathit{ϵ}}_i,\end{array}$$(4)

where f is the model response with realized parameters q evaluated at time $t=t_i$ for $i=1,\dots ,N_t$ and ${\mathit{ϵ}}_i$ is a realization of the observation error. We assume that models may have multiple responses. In a model with multiple responses, we let $N_r$ be the number of responses. For example, $N_r=6$ in model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ).

For the statistical model (2(2) $$\begin{array}{c}\hfill Y_i=f(t_i,Q)+{\mathit{\epsilon }}_i,i=1,\dots ,N_t,\end{array}$$(2) ), our objective is to construct the posterior density that best reflects the distribution of parameter values based on the sampled observations.

2.1. Bayesian estimation formula

The Bayesian estimation formula(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5)

states that a posterior distribution $\mathit{\pi }(q|y)$ is specified in terms of a likelihood function $\mathit{\pi }(y|q)$ and prior distribution ${\mathit{\pi }}_0(q)$. Here, p is the dimension of input parameters. With the assumption that the model errors are iid and ${\mathit{\epsilon }}_i\sim \mathcal{N}(0,{\mathit{\sigma }}^2)$, the likelihood for a model with a single response is given by(6) $$\begin{array}{c}\hfill \mathit{\pi }(y|q)={(2\mathit{\pi }{\mathit{\sigma }}^2)}^{-N_t/2}exp\left(-\frac{S{S}_q}{2{\mathit{\sigma }}^2}\right)\end{array}$$(6)

where(7) $$\begin{array}{c}\hfill S{S}_q=\sum _{i=1}^{N_t}{\left[y_i-f(t_i,q)\right]}^2.\end{array}$$(7)

We employ flat priors chosen to ensure that solutions to the model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) remain positive and well posed. For several parameters, such as $\mathit{\lambda }$ and $d_1$, we employ improper flat priors defined on $[0,\infty )$. We note that for such improper priors, one must employ likelihoods that ensure proper posteriors.

The likelihood function for a model with multiple responses and iid observation errors is given by(8) $$\begin{array}{c}\hfill \mathit{\pi }(y|q)=\left[\prod _{j=1}^{N_r}\frac{1}{{(2\mathit{\pi }{\mathit{\sigma }}_j^2)}^{N_t/2}}\right]exp\left(-\sum _{j=1}^{N_r}\frac{S{S}_q^j}{2{\mathit{\sigma }}_j^2}\right)\end{array}$$(8)

where(9) $$\begin{array}{c}\hfill {\displaystyle S{S}_q^j=\sum _{i=1}^{N_t}{\left[y_i^j-f^j(t_i,q)\right]}^2\text{for}j=1,\dots ,N_r.}\end{array}$$(9)

3. Posterior distributions

The goal for model calibration is to construct the posterior distribution $\mathit{\pi }(q|y)$ for parameters q using (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ). However, evaluation of the right-hand side of (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ) and computation of marginal densities require multidimensional integration, where the dimension of integration depends on the number of input parameters to be estimated. When this dimension is high, it becomes impossible to compute the integral analytically, and even quadrature via Monte Carlo sampling becomes prohibitively expensive. To avoid approximating high-dimensional integrals, we employ sampling-based Markov Chain Monte Carlo (MCMC) methods. We employ two MCMC algorithms: Delayed Rejection Adaptive Metropolis (DRAM) and DiffeRential Evolution Adaptive Metropolis (DREAM). We also consider a direct method, where the integral is approximated using a numerical quadrature, to compute the posterior. For low-dimensional parameter spaces, comparison with these direct solutions provides a way to verify the accuracy of densities constructed using sampling-based Metropolis methods.

3.1. Direct method

We start by computing the density using the formula in (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ) with numerical approximation, which we term the direct method. We note that the likelihood functions that appear in the numerator and denominator of (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ) can be very small. For the case of a flat prior, we avoid numerical evaluation of $\frac{0}{0}$ by reformulating the posterior so that (10a) $$\begin{array}{cc}\hfill \mathit{\pi }(q|y)& =\frac{e^{-\frac{1}{2{\mathit{\sigma }}^2}S{S}_q}}{{\int }_{{\mathbb{R}}^p}{e}^{-\frac{1}{2{\mathit{\sigma }}^2}S{S}_{\mathit{\zeta }}}\mathrm{d}\mathit{\zeta }}\hfill \\ \hfill & =\frac{1}{{\int }_{{\mathbb{R}}^p}{e}^{-\frac{1}{2{\mathit{\sigma }}^2}(S{S}_{\mathit{\zeta }}-S{S}_q)}\mathrm{d}\mathit{\zeta }}.\hfill \end{array}$$(10a)

Since the integral in (10b) cannot be computed analytically, we use a trapezoid rule with a uniform grid to approximate the integral. For one-dimensional integration with a uniform grid on $x\in [a,b]$ with n grid points, we let(11) $$\begin{array}{c}\hfill {\displaystyle x_i=a+(i-1)h\text{with}h=\frac{b-a}{n-1}\text{for}i=1,\dots ,n.}\end{array}$$(11)

The one-dimensional trapezoid rule is then(12) $$\begin{array}{c}\hfill {\int }_a^{b}f(x)\mathrm{d}x\approx \frac{h}{2}\sum _{i=1}^{n-1}\left[f(x_i)+f(x_{i+1})\right].\end{array}$$(12)

We employ a tensored trapezoid rule to approximate higher dimensional integrals. We verified the accuracy of these techniques by performing convergence tests with increasing values of n. The solution obtained in the direct method is regarded as the true solution when verifying the accuracy of sampling-based methods.

3.2. Delayed rejection adaptive metropolis (DRAM)

We first summarize DRAM as discussed in [10] and detailed in [13]. The adaptive Metropolis (AM) step allows the algorithm to update the chain covariance matrix as chain samples are accepted. This way, information learned about the posterior distribution through the accepted chain candidate is used to update the proposal. The sample covariance matrix, which determines the variance and correlation of the proposal distribution, is given by(13) $$\begin{array}{c}\hfill V_k=s_p\text{cov}(q^0,q^1,\dots ,q^{k-1})+e{I}_p.\end{array}$$(13)

Here, $s_p$ is a design parameter that depends on the parameter dimension p. A common choice is $s_p=2.{38}^2/p$ as detailed in [10]. The term $e{I}_p$ ensures that $V_k$ is positive definite with $e>0$. The covariance matrix is updated every $k_0$ steps, often specified as $k_0\approx 100$ in practice. Also, the covariance is computed recursively to improve the efficiency so that(14) $$\begin{array}{c}\hfill V_{k+1}=\frac{k-1}{k}{V}_k+\frac{s_p}{j}\left[k{\overline{q}}^{k-1}{({\overline{q}}^{k-1})}^T-(k+1){\overline{q}}^k{({\overline{q}}^k)}^T+q^k{(q^k)}^T+\mathit{\epsilon }{I}_p\right],\end{array}$$(14)

where the sample mean is also computed recursively(15) $$\begin{array}{c}\hfill {\overline{q}}^k=\frac{1}{k+1}\sum _{i=0}^k{q}^i=q^k+\frac{k}{k+1}({\overline{q}}^{k-1}-q^k).\end{array}$$(15)

Secondly, Delayed Rejection (DR) provides a mechanism for constructing alternative candidates when the current candidate is rejected. A second-stage candidate is chosen using the proposal function(16) $$\begin{array}{c}\hfill q^{\ast 2}\sim J_2(q^{\ast 2}|q^{k-1},q^{\ast })=N(q^{k-1},{\mathit{\gamma }}_2^2{V}_k),\end{array}$$(16)

where $J_2(q^{\ast 2}|q^{k-1},q^{\ast })$ is the notation for proposing $q^{\ast 2}$ having started at $q^{k-1}$ and rejected $q^{\ast }$, and ${\mathit{\gamma }}_2<1$ ensures that the second-stage proposal function is narrower than the original. The second-stage step improves the chance that the next candidate will be accepted and increases mixing. We take ${\mathit{\gamma }}_2=\frac{1}{5}$ and employ second-stage DR in our examples in Section 5, though different values of ${\mathit{\gamma }}_2$ and numbers of delayed rejection stages can be employed.

The DRAM algorithm with a flat prior is summarized in the following algorithm. To simplify notation, we suppress time dependence and multiple responses and consider the statistical model $Y_i=f_i(Q)+{\mathit{\epsilon }}_i$ with realizations $y_i=f_i(q)+{\mathit{ϵ}}_i$ for $i=1,\dots ,N_t$.

(1)	Set the design parameters $n_s,{\mathit{\sigma }}_s^2,k_0,s_p$ and number of chain iterates M.
(2)	Determine $q^0=\text{arg}{min}_q{\sum }_{i=1}^{N_t}{[y_i-f_i(q)]}^2$.
(3)	Set $S{S}_{q^0}={\sum }_{i=1}^{N_t}{[y_i-f_i(q^0)]}^2$.
(4)	Compute the observation error variance estimate $s_0^2=\frac{S{S}_{q^0}}{N_t-p}$.
(5)	Construct the covariance estimate $V_0=s_0^2{[{\mathit{\chi }}^T(q^0)\mathit{\chi }(q^0)]}^{-1}$ and $R_0=\text{chol}(V_0)$, where the sensitivity matrix has components ${\mathit{\chi }}_{ik}(q^0)=\frac{\mathit{\partial }{f}_i(q^0)}{\mathit{\partial }{q}_k}$.
(6)	For $k=1,\dots ,M$ (a) Sample $z_k\sim \mathcal{N}(0,I)$. (b) If $u_{\mathit{\alpha }}\sim \mathcal{U}(0,1)$. (c) Construct the candidate $q^{\ast }=q^{k-1}+R_{k-1}^T{z}_k$ where $R_{k-1}^T{R}_{k-1}=V_{k-1}$. (d) Compute $S{S}_{q^{\ast }}={\sum }_{i=1}^{N_t}{[y_i-f_i(q^{\ast })]}^2$. (e) Compute the ratio $$\mathit{\alpha }(q^{\ast }|q^{k-1})=\text{min}\left(1,e^{-[S{S}_{q^{\ast }}-S{S}_{q^{k-1}}]/2s_{k-1}^2}\right).$$ (f) If $u_{\mathit{\alpha }}<\mathit{\alpha }$ $$\text{Set}{q}^k=q^{\ast },S{S}_{q^k}=S{S}_{q^{\ast }}$$ Else $$\text{Enter DR Algorithm}$$ (g) Update $s_k\sim \text{Inv-gamma}(a_{val},b_{val})$, where $$a_{val}=0.5(1+N_t),b_{val}=0.5({\mathit{\sigma }}_s^2+S{S}_{q^k})$$ (h) If $\text{mod}(k,k_0)=1$ $$\text{Update}{V}_k=s_p\text{cov}(q^0,q^1,\dots ,q^{k-1})+e{I}_p\text{and}{R}_k=\text{chol}(V_k)$$ Else $$V_k=V_{k-1}\text{and}{R}_k=R_{k-1}$$

The Delayed Rejection (DR) algorithm in Step 6(f) is the following:

(1)	Set the design parameter ${\mathit{\gamma }}_2=\frac{1}{5}$.
(2)	Sample $z_k\sim \mathcal{N}(0,I)$.
(3)	Construct second-state candidate $q^{\ast 2}=q^{k-1}+{\mathit{\gamma }}_2{R}_{k-1}^T{z}_k$.
(4)	Sample $u_{{\mathit{\alpha }}_2}\sim \mathcal{U}(0,1)$.
(5)	Compute $S{S}_{q^{\ast 2}}={\sum }_{i=1}^N{[y_i-f_i(q^{\ast 2})]}^2$.
(6)	Compute $${\mathit{\alpha }}_2(q^{\ast 2}|q^{k-1},q^{\ast })=min\left({\displaystyle 1,\frac{\mathit{\pi }(q^{\ast 2}|y)J_1(q^{\ast }|q^{\ast 2})[1-\mathit{\alpha }(q^{\ast }|q^{\ast 2})}{\mathit{\pi }(q^{k-1}|y)J_1(q^{\ast }|q^{k-1})[1-\mathit{\alpha }(q^{\ast }|q^{k-1})]}}\right)$$ where $J_1(q_p|q_d)$ is the first stage proposal distribution from (6c).
(7)	If $u_{{\mathit{\alpha }}_2}<{\mathit{\alpha }}_2$ $$\text{Set}{q}^k=q^{\ast 2},S{S}_{q^k}=S{S}_{q^{\ast 2}}$$
	Else $$\text{Set}{q}^k=q^{k-1},S{S}_{q^k}=S{S}_{q^{k-1}}.$$

These two mechanisms DR and AM together provide an efficient algorithm to modify and update a proposal function. The software for DRAM implementation in MATLAB is available at [21,22].

3.2.1. Chain mixing and convergence

There exist a variety of diagnostic tests to assess the mixing and convergence of chains.

To assess mixing, one often computes the acceptance ratio, which is defined as the percentage of accepted candidates. Whereas, the optimal value of acceptance ratio varies depending on the geometry of the posterior, values between 0.1 and 0.5 are often considered desirable. Alternatively, one can check the autocorrelation(17) $$\begin{array}{c}\hfill R(k)=\frac{{\sum }_{i=1}^{M-k}(q_i-\overline{q})(q_{i+k}-\overline{q})}{{\sum }_{i=1}^M{(q_i-\overline{q})}^2}\end{array}$$(17)

to establish that the chain is producing uncorrelated samples from the posterior.

Qualitative and quantitative convergence tests generally establish the lack of convergence rather than convergence. Qualitatively, one can visually examine chains to assess both mixing and convergence. However, a visually burned-in chain does not necessarily guarantee convergence since it may later jump – e.g., to another mode in a multi-modal distribution. Quantitatively, DRAM uses Geweke’s convergence diagnostics based on [23]. This tests for equality of the mean of the first 10% and last 50% of the chain. However, Geweke diagnostics provide a necessary but not a sufficient condition for convergence. Hence the Geweke values indicate when the chain is not converged rather than when it is converged. Finally, one can run independent parallel chains with over-dispersed starting values, relative to the posterior distribution and monitor Gelman–Rubin convergence diagnostics. Due to its inherently parallel nature, we employ this strategy when monitoring the convergence of DREAM chains.

3.3. Differential evolution adaptive metropolis (DREAM)

The second MCMC method we employ is DREAM, which is developed in [11,24]. DREAM is an adaptive Metropolis algorithm, which can prove advantageous for problems having multimodal or heavy tailed posterior densities. Because it employs differential evolution to provide chain mixing, it can locate regions containing global minima more effectively than DRAM can with single chains.

The candidate parameters are proposed based on differential evolution(18) $$\begin{array}{c}\hfill z^i=x^i+(I_p+e)\mathit{\gamma }(d,p)\left[\sum _{j=1}^d{x}^{r_1(j)}-\sum _{n=1}^d{x}^{r_2(n)}\right]+\mathit{ϵ},\end{array}$$(18)

where $z^i$ is the candidate point in chain i, $x^i$ is the current population, $\mathit{\gamma }$ is the value of the jump size and d denotes the number of randomly sampled pairs. Furthermore, p is the number of parameters, $N_c$ denotes the number of chains, and $r_1(j),r_2(n)\in \{1,\dots ,N_c\}$ satisfy $r_1(j)\ne r_2(n)$ for $j,n=1,\cdots ,\mathit{\delta }$. Finally, we take $e\sim {\mathcal{U}}_p(-b,b)$ with $|b|<1$ and $\mathit{ϵ}\sim {\mathcal{N}}_p(0,b^{\ast })$, where b and $b^{\ast }$ are small compared to the width of the target distribution.

DREAM runs multiple chains simultaneously, and the chain values are used to adapt the proposal distribution, which in turn affects the mixing. The communication between chains occurs at given intervals, and the cost of communication between chains is much lower compared to the cost of model evaluations. Hence, the method is inherently parallel and can be advantageous for parameters having multimodal, heavy-tailed densities.

The algorithm, assuming a flat prior, is summarized as follows:

(1)	Draw a current population $\{x^i\},i=1\dots ,N_c$, from the prior distribution.
(2)	Compute the likelihood $\mathit{\pi }(y|x^i)$.
(3)	Construct the candidate $z^i=x^i+(I_p+e)\mathit{\gamma }(d,p)\left[{\sum }_{j=1}^d{x}^{r_1(j)}-{\sum }_{n=1}^d{x}^{r_2(n)}\right]+\mathit{ϵ}$ for $i=1,\cdots ,N_c$.
(4)	For $j=1,\dots ,p$, replace each element of $z_j^i$ with $x_j^i$ using a binomial scheme with probably $1-CR$, where CR is the crossover probability.
(5)	Compute the likelihood $\mathit{\pi }(y|z^i)$ and accept the candidate point with Metropolis acceptance probability $$\mathit{\alpha }(z^i|x^i)=\left\{\begin{array}{cc}min\left(\frac{\mathit{\pi }(y|z^i)}{\mathit{\pi }(y|x^i)},1\right)\hfill & \text{if}\mathit{\pi }(y|x^i)>0\hfill \\ 1\hfill & \text{if}\mathit{\pi }(y|x^i)=0.\hfill \end{array}\right.$$
(6)	If accepted, update the chain $x^i=z^i$, otherwise remain at the old location $x^i$.
(7)	Remove potential outlier chains using the interquartile range statistics during the burn-in process as explained in the next subsection.
(8)	Compute the Gelman and Rubin convergence diagnostic R [25] for each dimension $j=1,\dots ,p$ using the last 50% of samples in each chain.
(9)	If $R\le 1.2$ for all j, stop, otherwise go to chain evolution (steps 3-6).

To compute the acceptance probability, DREAM computes the log likelihood. For models with a single response, the log likelihood function is given by(19) $$\begin{array}{c}\hfill log(\mathit{\pi }(y|q))=-\frac{N_t}{2}log(2\mathit{\pi }{\mathit{\sigma }}^2)-\frac{1}{2{\mathit{\sigma }}^2}\sum _{i=1}^{N_t}{[y_i-f_i(q)]}^2.\end{array}$$(19)

In the DREAM software, which can be requested at [26], DREAM can accommodate both homoscedastic and heteroscedastic types of observation errors. For models with homoscedastic errors, the code can easily be modified to accommodate models with multiple responses, once one accommodates potentially differing error variances. Details regarding extensions to the basic DREAM algorithm to improve the search efficiency are provided in [24].

3.3.1. Burn-in and convergence

The convergence of sequences of chain elements is monitored using R-statistics, which is a factor by which the scale of the sequences shrink to the posterior distribution as one takes more samples. As detailed in [25], R-statistics uses the mean and variance between sequences as well as the variance of samples within a single sequence, referred to as ‘within sequence variance’. The R-statistics are quantitative and can be used to assess convergence without visually inspecting chains. It is important to note that the first assumption of R-statistics is that the seed values of the multiple chains be over-dispersed relative to the posterior distribution. The second assumption is that the chains are independent. Although the DREAM chains are not independent during burn-in due to crossover, the states of individual chains are independent after they become independent of initialization. More details can be found in [11,24].

To compute the R-statistic, take a sample of the last 50% of the chain values. Let $N_s$ be the number of samples and $N_c$ be the number of chains. The steps for computing the factor are the following.

(1)	Compute the sequence means.
(2)	Compute the sample variance B of the sequence means.
(3)	Compute the sample variance of each sequence.
(4)	Compute the average of within sequences variances, W.
(5)	Estimate the variance of posterior distribution by $${\displaystyle S^2=\frac{N_s-1}{N_s}W+\frac{1}{N_s}B.}$$
(6)	Compute the R-statistic $${\displaystyle R=\sqrt{\frac{N_c+1}{N_c}\frac{S^2}{W}-\frac{N_s-1}{N_c{N}_s}}.}$$

The scale reduction near 1 indicates that each set of the $N_c$ chains of $N_s$ simulated values is close to the target density. We take $R\le 1.2$ as the cut-off for convergence. The chain evolution is continued until $R\le 1.2$ is achieved. The convergence is also confirmed by computing the autocorrelation time [11].

4. Credible and prediction intervals

4.1. Intervals computed using DRAM

To construct credible and prediction intervals using DRAM, N parameter values specified by the user are sampled and the model responses are computed at these parameter values. For example, the 95% credible interval for an expected response is constructed by sorting the computed responses and determining the upper 2.5% and 97.5% quartiles. To compute the 95% prediction interval, for future observations, the observation error is added to the computed responses before determining the 95% interval. The observation error is generated by a normally distributed random variable with mean 0 and variance ${\mathit{\sigma }}^2$. In DRAM, one has the option of inferring ${\mathit{\sigma }}^2$ based on the conjugacy between the prior and likelihood. If ${\mathit{\sigma }}^2$ is not inferred during model calibration, we use the OLS estimate of the observation error to construct the prediction intervals. Readers are directed to [13] for more details regarding the computation and interpretation of credible and prediction intervals in the context of Bayesian inference.

4.2. Intervals computed using DREAM

In DREAM, the values from all of the chains are combined in a matrix so that the $i^{th}$ column contains all the chain values for the parameter $q_i$. The number of columns thus corresponds to the number of parameters that are estimated. The model response is computed for the last 25% of the values from each column. It is noted that 25% is chosen to ensure that the parameter values in the chains have converged. The generated responses are sorted, and the appropriate interval of the response is stored. For example, the responses at upper 2.5% and 97.5% are stored to compute the 95% credible interval. For prediction intervals, observation error is added to the response. The error is generated from a distribution $\mathit{\epsilon }\sim N(0,{\text{RMSE}}^2)$, where(20) $$\begin{array}{c}\hfill \text{RMSE}=\sqrt{{\displaystyle \frac{1}{N_t-p}\sum _{i=1}^{N_t}{(f(t_i;q_{OLS})-y_i)}^2}}\end{array}$$(20)

and $q_{OLS}$ denotes the parameters determined through the ordinary least squares Step 2 in the DRAM algorithm. Once the noise is added to the model responses, they are sorted and the responses at the upper 2.5% and 97.5% are stored, for example, to construct the 95% prediction interval. Since the DREAM package does not come with the feature to update observation error, we added this feature using the prior conjugate in the similar manner it is implemented in DRAM. If the observation error is updated during the chain evolutions, sampled ${\mathit{\sigma }}^2$ values are used when constructing the prediction interval.

Table 2. Nominal parameter values.

${\mathit{\lambda }}_1=$1.0e+4	${\mathit{\lambda }}_2=31.98$	$d_1=0.01$	$d_2=0.01$	$k_1=$8.0e-7	$k_2=$1.0e-4
$c=13$	$\mathit{\delta }=0.7$	$m_1=$1.0e-5	$m_2=$1.0e-5	${\mathit{\rho }}_1=1$	${\mathit{\rho }}_2=1$
$b_E=0.3$	$d_E=0.25$	$K_b=100$	$K_d=500$	${\mathit{\lambda }}_E=1$	${\mathit{\delta }}_E=0.1$
$N_T=100$	$f=0.34$	$\mathit{ϵ}=0$

5. Metropolis algorithm performance

We demonstrate here the performance of the two adaptive Metropolis methods for the HIV model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) for two cases. In the first, we consider three parameters $q=[b_E,\mathit{\delta },d_1]$ to permit verification of DRAM and DREAM through direct numerical approximation of (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ). We also illustrate the construction of credible and prediction intervals for the model response and demonstrate that DRAM and DREAM provide comparable results. Secondly, we consider the construction of posterior densities for 12 parameters to illustrate the feasibility of DRAM and DREAM for a problem with moderate dimensionality.

To generate the synthetic data, we solve the model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ) with the initial condition(21) $$\begin{array}{c}\hfill y_0=\left[\begin{array}{cccccc}9\text{e+5},& 4000,& 1,& 1,& 1,& 12\end{array}\right],\end{array}$$(21)

for the states $[T_1,T_2,T_1^{\ast },T_2^{\ast },V,E]$, and the parameter values summarized in Table 2, which are reported in [3]. Once the solution to the model is computed, we add iid normally distributed observation errors. Here, ${\mathit{\epsilon }}_j\sim \mathcal{N}(0,{\mathit{\sigma }}_j^2)\text{for}j=1,\dots ,6$, where(22) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{cccc}{\mathit{\sigma }}_1,& {\mathit{\sigma }}_2,& \dots ,& {\mathit{\sigma }}_6\end{array}\right]& =\left[\begin{array}{cccccc}{\mathit{\sigma }}_{T_1},& {\mathit{\sigma }}_{T_2},& {\mathit{\sigma }}_{T_1^{\ast }},& {\mathit{\sigma }}_{T_2^{\ast }},& {\mathit{\sigma }}_V,& {\mathit{\sigma }}_E\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccccc}2\text{e+4},& 10,& 3\text{e+3},& 10,& 10\text{e+4},& 2.5\end{array}\right].\hfill \end{array}\end{array}$$(22)

For verification, we employ the direct method to compute the parameter densities for $q=[b_E,\mathit{\delta },d_1]$. In this example, we use a uniform grid with 101 grid points in each dimension. We restricted the region of integration to $[0.292,0.305]\times [0.62,0.8]\times [0.002,0.022]$ for our computations to decrease the run time since the magnitude of the likelihood function outside the specified region is negligible. The accuracy of numerical approximation of the direct method is illustrated by a convergence test summarized in Table 3. The means and standard deviations of the three parameters remain unchanged between $n=81$ and $n=101$ quadrature points in the trapezoid rule (12(12) $$\begin{array}{c}\hfill {\int }_a^{b}f(x)\mathrm{d}x\approx \frac{h}{2}\sum _{i=1}^{n-1}\left[f(x_i)+f(x_{i+1})\right].\end{array}$$(12) ). This indicates that the numerical approximation of integrals in (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ) has converged and hence the direct method can provide a baseline for the verification of the sampling methods.

For the three parameter case, we first perform numerical experiments assuming that the observation error is fixed. In this case, we employed the OLS estimate of the observation error. The chains, marginal densities, correlations and prediction intervals are compared with this setting. We then perform additional experiments, where the observation error is updated as the chains evolve. For the second case, we compare the credible and prediction intervals of DRAM and DREAM. We do not include Direct here since we have not incorporated observation error. In principle, it is possible to do so by integrating with respect to the noise parameters. However, for the considered example with six responses, this would add six dimensions to the integration, which is infeasible.

Table 3. Mean and standard deviation of $b_E$, $\mathit{\delta }$ and $d_1$ using $n=61,81,101$ quadrature points.

	$b_E$ Mean	$b_E$ Sigma	$\mathit{\delta }$ Mean	$\mathit{\delta }$ Sigma	$d_1$ Mean	$d_1$ Sigma
$n=61$	2.9990e-1	7.5089e-4	7.0558e-1	3.0448e-3	9.5777e-3	7.5642e-4
$n=81$	2.9990e-1	7.5090e-4	7.0558e-1	3.0448e-3	9.5777e-3	7.5644e-4
$n=101$	2.9990e-1	7.5090e-4	7.0558e-1	3.0448e-3	9.5777e-3	7.5645e-4

5.1. Three parameter case

5.1.1. Chains and marginal densities

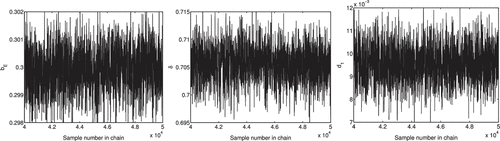
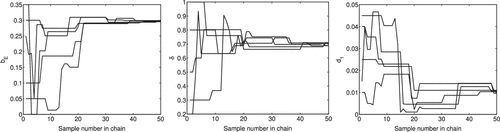
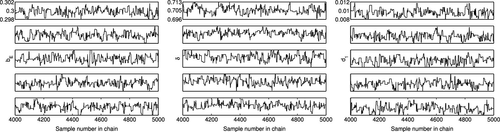
Whereas DRAM and DREAM each have criteria to assess the convergence of parameters, the chains can also be used to examine the convergence visually for both DRAM and DREAM. It is noted that DRAM contains a single chain, from which means and variances of the parameters are computed. In Figure 1, we observe that the DRAM chains have visually converged in probability to a stationary distribution. On the other hand, DREAM is comprised of multiple chains, which evolve to fluctuate around the mean value as the iteration number increases. The initial iterations are plotted in Figure 2 to illustrate the mixing between chains. The last 1000 iterations of five chains are plotted in Figure 3 and we see that the chains have converged.

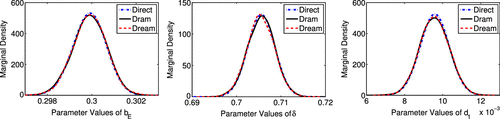
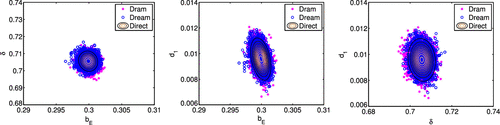
We see from the results summarized in Table 4 that the means and the standard deviations for the three parameters are qualitatively comparable among the three methods. In Figure 4, we illustrate that the marginal densities obtained with the three methods are in agreement. The densities shown in Figure 4 are obtained using a smoothed kernel density estimate (KDE). Typically, DREAM requires more KDE smoothing than DRAM. This is one aspect of DREAM that must be addressed by the users. In Figure 5, we show the contour plots of the marginal posterior distributions for each pair of parameters, computed with the Direct method, along with joint sample points produced by DRAM and DREAM. We note that qualitatively the variability and correlation are in agreement for the three methods.

Figure 1. DRAM chains for $b_E$, $\mathit{\delta }$ and $d_1$.

Figure 2. Initial DREAM chains for $b_E$, $\mathit{\delta }$ and $d_1$.

Figure 3. Burned-in DREAM chains for $b_E$, $\mathit{\delta }$ and $d_1$.

Table 4. Mean and standard deviation for $b_E$, $\mathit{\delta }$ and $d_1$.

Method	$b_E$ Mean	$b_E$ Sigma	$\mathit{\delta }$ Mean	$\mathit{\delta }$ Sigma	$d_1$ Mean	$d_1$ Sigma
Direct	2.999e-1	7.509e-4	7.056e-1	3.045e-3	9.577e-3	7.564e-4
DRAM	2.999e-1	7.416e-4	7.056e-1	3.041e-3	9.565e-3	7.676e-4
DREAM	3.000e-1	7.486e-4	7.055e-1	2.989e-3	9.567e-3	7.476e-4

Both the marginal densities and correlations appear to be qualitatively comparable, thus visually confirming the accuracy of the sampling-based Metropolis algorithms. Moreover, the scatter plots constructed using DRAM and DREAM coincide with the contour plots constructed using the Direct method. The contour plots represent the values of joint density functions. We note that the parameters $d_1$ and $b_E$ are slightly negatively correlated, while $d_1$ and $\mathit{\delta }$, as well as $\mathit{\delta }$ and $b_E$, exhibit minimal correlation.

Figure 4. Marginal densities for $b_E$, $\mathit{\delta }$ and $d_1$ obtained using Direct evaluation, DRAM and DREAM.

Figure 5. Contour plots from the Direct method plotted with joint sample points from DRAM and DREAM showing the correlations between $b_E$, $\mathit{\delta }$ and $d_1$.

5.1.2. Energy statistics

Visual verification, based on the examination of Figure 4, is qualitative and subject to the degree to which smoothing is employed when constructing KDE. To quantify the hypothesis that DRAM and DREAM are sampling from the same distribution as the posterior distribution that is directly computed via the Direct method, we employ the energy statistics detailed in [27,28].

To determine whether two sets of samples are drawn from the same distribution, we let $X_1,\dots ,X_{n_1}$ and $Y_1,\dots ,Y_{n_2}$ be independent random samples. To test the null hypothesis $H_0:F_X=F_Y$, we compute the energy distance(23) $$\begin{array}{c}\hfill {\mathit{ϵ}}_{n_1,n_2}=\frac{2}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{m=1}^{n_2}|X_i-Y_m|-\frac{1}{n_1^2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_1}|X_i-X_j|-\frac{1}{n_2^2}\sum _{k=1}^{n_2}\sum _{m=1}^{n_2}|Y_k-Y_m|\end{array}$$(23)

and test statistics(24) $$\begin{array}{c}\hfill T_{n_1,n_2}=\frac{n_1{n}_2}{n_1+n_2}{\mathit{ϵ}}_{n_1,n_2}.\end{array}$$(24)

Here $F_X$ and $F_Y$ denote the distributions of X and Y and $|·|$ is the Euclidean norm. By summing the absolute difference between samples from two distributions, the test statistics indicate the distance between two sets of samples. Smaller test values indicate that samples from two distributions are closer than those samples with larger test values, indicating greater consistency with $H_0$.

Suppose that two sets of samples X and Y are under consideration. Let $F_{\mathit{\alpha }}$ be the test statistic of the pooled sample $W=[X,Y]$, and $F_{\mathit{\alpha }}^{(r)}$ be the test statistic of the $r^{th}$ permutation of the elements in W. Intuitively, the statistics of random permutations of a set [X , Y] should be identically distributed under the null hypothesis. For hypothesis testing, we compute the p-value(25) $$\begin{array}{c}\hfill {\displaystyle p=\frac{1+{\sum }_{r=1}^{R}I(F_{\mathit{\alpha }}^{(r)}\ge F_{\mathit{\alpha }})}{R+1}}\end{array}$$(25)

as detailed in [29]. Here, R is the number of replicates, which is the number of times the test statistics are computed. The null hypothesis is rejected if the p-value is less than a specified significance level.

Table 5. Energy test performed for 3 parameters using samples via Direct, DRAM and DREAM.

Methods	Parameter	E-statistic	p-value
	$b_E$	0.00076725	0.418
Direct & DRAM	$\mathit{\delta }$	0.0014563	0.83
	$d_1$	0.0030468	0.01
	$b_E$	0.0020542	0.054
Direct & DREAM	$\mathit{\delta }$	0.015674	0.01
	$d_1$	0.0021053	0.064
	$b_E$	0.00078297	0.384
DRAM & DREAM	$\mathit{\delta }$	0.018046	0.004
	$d_1$	0.0009867	0.29
Direct & DRAM	joint	0.0066912	0.128
Direct & DREAM	joint	0.016778	0.002
DRAM & DREAM	joint	0.016828	0.006

To test the null hypothesis that DRAM and DREAM chains come from the same distribution as the samples from the Direct method, we use 2500 samples for each method with $R=499$ replicates. For the Direct samples, we obtain random samples using the inverse cumulative distribution functions. For DRAM and DREAM, we sampled every tenth value in a chain after burn-into ensure approximately uncorrelated samples. The test statistics and p-values for the energy test are summarized in Table 5.

For the significance level $\mathit{\alpha }=0.01$, the null hypothesis that the samples are from the same distribution is not rejected when the test is performed for individual parameters using Direct and DRAM, as well as Direct and DREAM. However, for both cases there is a p-value of 0.01 that is at the threshold for $\mathit{\alpha }=0.01$. For the DRAM and DREAM comparison, we reject the null hypothesis for the individual parameter $\mathit{\delta }$.

For joint samples, the energy test indicates that samples from DRAM are from the true posterior distribution numerically approximated by Direct. However, we reject the null hypothesis that DREAM is sampling from the true distribution at the considered levels. This likely reflects the rougher DREAM chains observed in Figure 3. As future work, we will also investigate the degree to which DREAM can be further tuned to improve its efficiency and convergence to the posterior distribution. Similarly, we reject the null hypothesis that the joint samples from DRAM and DREAM are from the same distributions.

We emphasize that we performed these tests with the chain samples, rather than kernel density estimates, to avoid introducing an additional estimation procedure into the results.

5.1.3. Convergence diagnostics

In this section, we examine the convergence diagnostics for DRAM and DREAM. The default diagnostics used in DRAM are summarized in Table 6.

Table 6. Convergence diagnostics for DRAM.

Parameter	$\mathit{\tau }$	Geweke
$d_1$	8.9863	0.99971
$\mathit{\delta }$	10.055	0.99941
$b_E$	9.447	0.98654

We let $\mathit{\tau }$ denote the autocorrelation time, which is the ratio of covariance and variance of samples. The covariance is computed using samples that are 10 iterations apart, unless otherwise specified by a user. The autocorrelation time is used to establish that the samples are uncorrelated. More details are documented in [22].

The Geweke diagnostic near 1 indicates that the mean from the first 10% and last 50% samples are very close. The acceptance ratio without the delayed rejection stage is 0.310 and the ratio combined with 2nd stage delayed rejection is 0.527.

On the other hand, we look at R-statistics and autocorrelation time for DREAM. The R values for all three parameters are below 1.2 after $1\times {10}^4$ iterations. The acceptance ratio for DREAM is 0.343.

5.1.4. Prediction Intervals

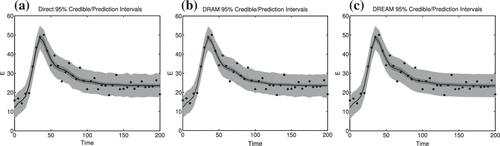
Finally, we consider the credible and prediction intervals shown in Figure 6. The inner intervals represent the credible intervals, which incorporate parameter uncertainties. The outer intervals in lighter grey represent the prediction intervals. The results obtained using Direct evaluation, DRAM and DREAM are nearly identical. One can observe that about 95 out of the 100 data points fall in the prediction intervals, suggesting that they have good frequentist coverage properties in this application.

Figure 6. Credible and prediction intervals for the response E using (a) Direct evaluation, (b) DRAM and (c) DREAM.

5.2. 12 Parameter case

Here we illustrate the performance of the DRAM and DREAM algorithms to infer parameter densities for a moderate number of parameters. We estimate the densities for $Q_{12}=[b_E,\mathit{\delta },d_1,k_2,{\mathit{\lambda }}_1,K_b,K_d,k_1,{\mathit{\lambda }}_2,c,{\mathit{\rho }}_1,{\mathit{\rho }}_2]$. We note that the smallest and the largest parameter values among $Q_{12}$, which are used to generate the synthetic data, are $k_1=8$e-7 and ${\mathit{\lambda }}_1=$ 1e+4, respectively. Hence the orders of magnitude among these parameters vary greatly.

We use the generated data to perform model calibration using DRAM and DREAM. We take a total of 1,000,000 chain evaluations including burn-in for DRAM. In DREAM, we set the maximum number of function evaluations to be 1,000,000 and use 10 chains. The prior for both DRAM and DREAM is a uniform distribution $q_i\sim U(a_i,b_i)$ for $i=1,\dots ,12$ where $a_i$ and $b_i$ are summarized in Table 7.

Table 7. Lower and upper bounds for the prior distributions $q_i\sim U(a_i,b_i)$ for $i=1,\dots ,12$.

	$b_E$	$\mathit{\delta }$	$d_1$	$k_2$	${\mathit{\lambda }}_1$	$K_b$	$K_d$	$k_1$	${\mathit{\lambda }}_2$	c	${\mathit{\rho }}_1$	${\mathit{\rho }}_2$
$a_i$	0	0	0	0	0	0	0	0	0	0	0	0
$b_i$	0.5	1	0.05	1e-3	1e+5	1e3	1e+3	1e-6	50	50	10	10

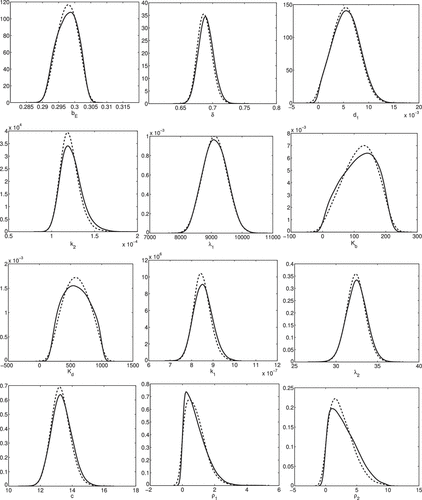
The estimated densities are plotted in Figure 7 and the pairwise plots are shown in Figures 8 and 9. The Direct method is not applicable in this case due to the larger dimension of input parameters. The mean values are summarized in Table 8, where the values listed as TRUE represent the parameter values used to generate the synthetic data. We note that the convergence of the posterior means to the TRUE values is an asymptotic result and may not be achieved for the limited considered data. As we will detail in later discussion, the discrepancy in ${\mathit{\rho }}_2$ is likely due to the fact the fact that it may not be identifiable in the sense that it is uniquely determined by the data.

Figure 7. Estimated densities for 12 parameters with DRAM (solid line) and DREAM (dashed line).

Figure 8. Parameter pairwise plots computed using DRAM.

Figure 9. Parameter pairwise plots computed using DREAM.

Table 8. Mean values obtained using DRAM and DREAM for 12 parameters.

	$b_E$	$\mathit{\delta }$	$d_1$	$k_2$	${\mathit{\lambda }}_1$	$K_b$
TRUE	3.00e-1	7.00e-1	1.00e-2	1.00e-4	1.00e+4	1.00e+2
DRAM	2.98e-1	6.90e-1	5.55e-3	1.23e-4	9.12e+3	1.16e+2
DREAM	2.98e-1	6.88e-1	5.36e-3	1.21e-4	9.11e+3	1.18e+2
	$K_d$	$k_1$	${\mathit{\lambda }}_2$	c	${\mathit{\rho }}_1$	${\mathit{\rho }}_2$
TRUE	5.00e+2	8.00e-7	3.20e+1	1.30e+1	1.00	1.00
DRAM	5.91e+2	8.54e-7	3.25e+1	1.33e+1	8.33e-1	2.96
DREAM	5.95e+2	8.49e-7	3.24e+1	1.33e+1	8.08e-1	2.63

The acceptance ratios for DRAM and DREAM are 0.201 and 0.147, respectively. The convergence diagnostics for DRAM are summarized in Table 9. Larger values of $\mathit{\tau }$ compared to the three parameter case indicate slower convergence for the 12 parameter case. The Geweke values near 1 for most parameters indicates that the means have remained the same over iterations. The R-statistics and autocorrelations are employed as convergence diagnostics for DREAM. R-statistics values are below the threshold after $1\times {10}^5$ iterations; however, the autocorrelation values are not near zero for some parameters. Again, the lack of samples from the analytically derived posterior indicates the necessity for performing a verification test through comparison of DRAM and DREAM.

Table 9. Convergence diagnostics with DRAM for 12 parameters.

Parameter	$\mathit{\tau }$	Geweke
$b_E$	83.45	0.9992
$\mathit{\delta }$	59.92	0.9993
$d_1$	57.80	0.9988
$k_2$	83.78	0.9927
${\mathit{\lambda }}_1$	57.24	0.9996
$K_b$	81.52	0.9678
$K_d$	81.91	0.9684
$k_1$	61.40	0.9970
${\mathit{\lambda }}_2$	57.78	0.9971
c	59.86	0.9984
${\mathit{\rho }}_1$	64.68	0.9563
${\mathit{\rho }}_2$	75.96	0.9937

Figures 7–9 indicate that the two methods qualitatively yield similar marginal densities and pairwise plots for all 12 parameters. To quantitatively ascertain whether DRAM and DREAM are sampling from the same posterior distribution, we compute the energy statistics (24(24) $$\begin{array}{c}\hfill T_{n_1,n_2}=\frac{n_1{n}_2}{n_1+n_2}{\mathit{ϵ}}_{n_1,n_2}.\end{array}$$(24) ) detailed in Section 5.1.2. For this test, we use 2500 samples from each DRAM and DREAM and $R=499$ replicates. Again, every tenth sample of a chain is recorded to obtain approximately uncorrelated samples.

The test statistics and p-values are presented in Table 10. We note here that whereas the smoothed KDE plots in Figure 7 are qualitatively similar, the null hypothesis is rejected for all parameters except for ${\mathit{\lambda }}_1$ and c at the $\mathit{\alpha }=0.01$ level. In the 12-parameter case, statistical tests indicate that the samples from DRAM and DREAM are not from the same distributions. This may be due, in part, to the property that DREAM chains are often rougher than DRAM chains due to the differential evolution component used to explore the posterior.

Table 10. Energy test performed for 12 parameters using DRAM and DREAM samples with the null hypothesis that DRAM and DREAM chains are drawn from the same distribution.

Parameter	E-statistic	p-value
$b_E$	0.17683	0.002
$\mathit{\delta }$	0.19762	0.002
$d_1$	0.023338	0.002
$k_2$	0.00067553	0.002
${\mathit{\lambda }}_1$	1363	0.044
$K_b$	1877.3	0.002
$K_d$	8882.3	0.002
$k_1$	6.2494e-7	0.002
${\mathit{\lambda }}_2$	0.7872	0.002
c	2.4344	0.022
${\mathit{\rho }}_1$	41.298	0.002
${\mathit{\rho }}_2$	46.425	0.002
joint	0.17682	0.002

The mean values are also not in agreement among TRUE, DRAM and DREAM for some parameters. We note that convergence of the posterior means to the true values is expected in the asymptotic limit and discrepancies are likely due to the limited amount of data. In some cases, the disagreement may also be due to the observation errors. In the absence of observation errors, the mean values of DRAM and DREAM are much closer to the true values. The disagreement may also be caused by parameter non-identifiability issues. For example, single-valued correlated parameters may not be estimated uniquely. In our example, $d_1$ and ${\mathit{\lambda }}_1$ as well as $k_1$ and c appear linearly correlated with nearly single-valued pairwise plots which could be a consequence of parameter non-identifiability or an inability of the available data to distinguish their effects. The posterior distributions for $K_b,K_d$ and ${\mathit{\rho }}_2$ are similar to the priors, thus indicating that the model and data are not informing the inference procedure for these parameters and hence they are likely not identifiable.

There are methods to eliminate parameter non-identifiability. Though they perform frequentist inference, the authors of [30] present methods for detecting non-identifiable parameters prior to estimation. Also, issues with over-parameterization are discussed in [18], where the ion channel model with superfluous states results in parameters that spread over a wide range of values, are multi-modal or are uniformly distributed. Detection of non-identifiable parameters results not only in accurate parameter estimation, but also reduction of parameter dimensions. An example is illustrated in [31], which demonstrates the reduction of 61 model parameters to 26 parameters through successful isolation of non-identifiable parameters. Alternatively, one could perform parameter selection to eliminate non-identifiable parameters prior to model calibration. Some parameter selection techniques include variance-based methods and screening methods based on global sensitivity analysis. Details on this topic can be found in [13] and the use of global sensitivity analysis to isolate influential parameters in an analogous HIV model is presented in [32].

Alternatively, one can employ active subspace techniques to determine subspaces of identifiable parameters [33–35]. This approach has the advantage that it can accommodate linear combinations of parameters rather than focusing solely on parameter subsets as is the case for global sensitivity analysis and parameter subset selection algorithms.

6. Conclusions

We described Bayesian techniques for model calibration and used them to construct prediction intervals for the HIV model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ). We first constructed posterior densities for three parameters using DRAM and DREAM. A single chain for each parameter evolves to the posterior distribution using delayed rejection and adaptation features in DRAM, whereas multiple chains are run to increase efficiency in DREAM.

We showed that DRAM and DREAM can be used to construct parameter densities even when individual parameters differ by many orders of magnitudes. One of the major differences between DRAM and DREAM is the single-chain in DRAM as opposed to the simultaneous multiple chains in DREAM. Running multiple chains of DRAM is an option for convergence assessment based on Gelman–Rubin diagnostics. In the case of the HIV model (1(1) $$\begin{array}{cc}\hfill \dot{T_1}& ={\mathit{\lambda }}_1-d_1{T}_1-(1-\mathit{ϵ})k_{1}V{T}_1\hfill \\ \hfill \dot{T_2}& ={\mathit{\lambda }}_2-d_2{T}_2-(1-\mathit{ϵ})k_{2}V{T}_2\hfill \\ \hfill \dot{T_1^{\ast }}& =(1-\mathit{ϵ})k_{1}V{T}_1-\mathit{\delta }{T}_1^{\ast }-m_{1}E{T}_1^{\ast }\hfill \\ \hfill \dot{T_2^{\ast }}& =(1-f\mathit{ϵ})k_{2}V{T}_2-\mathit{\delta }{T}_2^{\ast }-m_{2}E{T}_2^{\ast }\hfill \\ \hfill \dot{V}& =N_T\mathit{\delta }(T_1^{\ast }+T_2^{\ast })-cV-[(1-\mathit{ϵ}){\mathit{\rho }}_1{k}_1{T}_1+(1-f\mathit{ϵ}){\mathit{\rho }}_2{k}_2{T}_2]V\hfill \\ \hfill \dot{E}& ={\mathit{\lambda }}_E+\frac{b_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_b}E-\frac{d_E(T_1^{\ast }+T_2^{\ast })}{T_1^{\ast }+T_2^{\ast }+K_d}E-{\mathit{\delta }}_{E}E\hfill \end{array}$$(1) ), a single-chain DRAM is sufficient to efficiently sample from the posterior distribution.

To verify the accuracy of the DRAM and DREAM methods, we compared the posterior densities and pairwise plots obtained via DRAM and DREAM to the true values computed directly from (5(5) $$\begin{array}{c}\hfill \mathit{\pi }(q|y)=\frac{\mathit{\pi }(y|q){\mathit{\pi }}_0(q)}{{\int }_{{\mathbb{R}}^p}\mathit{\pi }(y|q){\mathit{\pi }}_0(q)dq}\end{array}$$(5) ) for a three parameter case. Through the use of energy statistics, we showed that DRAM and DREAM are sampling from the true posterior density for the three parameter case. For a twelve parameter case, we showed that although DRAM and DREAM yielded qualitatively similar posterior densities, they differed somewhat for various parameters. This difference was quantitatively illustrated through the use of energy statistics. This may be due, in part, to the property that DREAM produces rougher chains due the differential evolution aspect of the algorithm. We note that the primary contribution of the paper is the illustration of this verification framework. As future work, we will also investigate the degree to which DREAM can be further tuned to improve its efficiency and convergence to the posterior distribution.

We also discussed credible and prediction intervals, which are constructed by propagating the input uncertainties through the model. The credible intervals quantify uncertainties in the model responses due to the parameter uncertainties, whereas the prediction intervals quantify uncertainties in the responses due to both the parameter uncertainties and the observation error. In the HIV example, credible and prediction intervals were constructed for the immune effector cells, E, using DRAM and DREAM as a part of a verification exercise.

The Metropolis methods discussed here can be used to perform parameter estimation and to obtain predictive estimates in other models, and can be extended to a larger number of parameters. These methods have been successfully applied to models involving gene transcription activity [36,37], cellular signaling pathways [38], and an algae model [31]. Moreover, the application of DRAM and DREAM to models with higher parameter dimensions has also been documented. Models with input parameter dimensions of 25, 50 and 100, are examined in [11]. Also, a hydrology model in [12], calibrated using DREAM, has 63 to 65 parameters. Recently, [39] presented the use of MCMC methods, including DRAM and DREAM, as a part of uncertainty quantification for a groundwater flow problem, in addition to a 10-dimensional multimodal mathematical function and 100-dimensional Gaussian functions. In their examples, it is reported that DREAM is more efficient than DRAM. These applications indicate the efficiency of DRAM and DREAM in model calibration for models arising in bioscience with a wide range of parameter dimensions.

Acknowledgements

The authors thank Kayla Coleman for performing energy tests and providing insights regarding their interpretation. The authors also thank Tom Banks for input and discussion regarding the HIV model.

Additional information

Funding

This research was supported in part by DOE Consortium for Advanced Simulation of LWR (CASL) through the [grant number DE-AC05-00OR22725]. It was also supported in part by the Air Force Office of Scientific Research through the [grant number AFOSR FA9550-11-1-0152].

Notes

No potential conflict of interest was reported by the authors.