Effects of a priori parameter selection in minimum relative entropy method on inverse electrocardiography problem

Abstract

The goal in inverse electrocardiography (ECG) is to reconstruct cardiac electrical sources from body surface measurements and a mathematical model of torso–heart geometry that relates the sources to the measurements. This problem is ill-posed due to attenuation and smoothing that occur inside the thorax, and small errors in the measurements yield large reconstruction errors. To overcome this, ill-posedness, traditional regularization methods such as Tikhonov regularization and truncated singular value decomposition and statistical approaches such as Bayesian Maximum A Posteriori estimation and Kalman filter have been applied. Statistical methods have yielded accurate inverse solutions; however, they require knowledge of a good a priori probability density function, or state transition definition. Minimum relative entropy (MRE) is an approach for inferring probability density function from a set of constraints and prior information, and may be an alternative to those statistical methods since it operates with more simple prior information definitions. However, success of the MRE method also depends on good choice of prior parameters in the form of upper and lower bound values, expected uncertainty in the model and the prior mean. In this paper, we explore the effects of each of these parameters on the solution of inverse ECG problem and discuss the limitations of the method. Our results show that the prior expected value is the most influential of the three MRE parameters.

Keywords:

• Inverse problems
• inverse electrocardiography
• minimum relative entropy
• parameter estimation
• regularization

AMS Subject Classification:

• 65R32

1. Introduction

Normal heart function is based on a sequence of propagating electrical pulses, in other words electrical potentials, through the heart muscle cells. Organized propagation of this electrical activity yields efficient pumping of the heart. However, if there is a pathological condition, propagation of electrical activity deviates from its normal course, causing arrhythmias that lead to heart diseases or, in more severe cases, heart attack and even death. Thus, monitoring of electrical activity of the heart is crucial to assess its well-being. Electrocardiography (ECG) is a graphical tool used to record the potentials generated on the body surface due to electrical activity of the heart. Clinicians have been using classical 12-lead ECG for over a century to diagnose heart-related diseases.

However, in the 12-lead ECG system, it is often difficult to understand and characterize the cardiac electrical activity due to sparse spatial sampling on the body surface and attenuation and smoothing within the torso. One alternative to overcome these shortcomings is estimating the cardiac electrical sources from body surface potential measurements using mathematical models that relate these sources to the measurements [1]. This estimation problem is called the inverse problem of ECG. Solution of the inverse ECG problem, which is also called as Electrocardiographic Imaging (ECGI), has a potential that could fill the gap between low-resolution 12-lead ECG and high-resolution invasive methods and possibly effectively reflect the underlying cardiac activity. Lately, ECGI has received a renewed academic and commercial attention due to this potential to be used in clinical applications. Researchers working on ECGI came together and formed the Consortium for Electrocardiographic Imaging (CEI) [2], with the goal of building strong interactions and collaborations among the people contributing to this area. Besides the continuing academic research, a non-invasive commercial ECGI set-up developed by CardioInsight, which was recently acquired by Medtronic, has become available for clinical use [3,4].

Many different cardiac source models are available to characterize the electrical activity of the heart. Epicardial potential and transmembrane potential-based models are the most widely used models. Among the two, epicardial potential-based models have been used more extensively due to their simple clinical interpretation and experimental availability, which makes it easy to evaluate the solutions. In this study, we also use epicardial potentials as the cardiac source model. In this model, body surface potential measurements are linearly related to the epicardial potentials. However, due to attenuation, spatial smoothing and discretization effects, the inverse problem has an ill-posed nature; i.e. small perturbations in the measured data or the geometric model can lead to unstable solutions and unacceptably large errors if the problem is solved by standard linear least squares minimization approach. In order to resolve this stability problem, regularization methods or statistical inversion approaches have been utilized. One of the most popular regularization methods is Tikhonov regularization, which is a modification of the standard linear least squares solution [5]. Other approaches are truncated singular value decomposition (TSVD) [6], truncated total least squares (TSVD) [7], least squares QR (LSQR) factorization [8] and hybrid approaches that combine traditional approaches such as Tikhonov regularization and the LSQR method with genetic algorithms [8]. In addition to these more traditional regularization methods, partial differential equation (PDE)-constrained optimization has been used in [9], in which the whole PDE model is used as a constraint rather than only the source constraints. In another study by Potyagaylo et al., the authors formulate the problem as an unconstrained binary quadratic optimization problem using the step-like behaviour of the transmembrane potentials in the depolarization phase [10].

However, standard regularization solutions to the inverse problem of electrocardiography have achieved only limited success; although the main features of epicardial potential distributions are roughly reconstructed, there is often considerable loss of accuracy with respect to location and amplitude of extrema and wavefronts [11]. Some alternatives to overcome these shortcomings were proposed in the form of multiple constraints approaches, in which more than one type of prior information is included in the cost function definition [11–13]. Statistical approaches are also applied to solve the inverse ECG problem and they proved to be very effective in finding an accurate solution. In statistical approaches, it is assumed that the unknowns, in this case the epicardial potentials that we would like to estimate, are random variables. The prior information on these solutions is then incorporated into the model via probabilistic models. In Bayesian Maximum A Posteriori (MAP) estimation, prior information about the epicardial potentials is used to generate a priori probability density function (pdf), and the solution is the potential distribution that maximizes the posterior pdf [14,15]. Bayesian MAP estimation can also be extended to include spatial and temporal correlations of the epicardial potentials simultaneously [16,17]. More recently, Bayesian estimation has been used for estimating transmembrane potential distribution within the heart; in [18], transmembrane potentials are modelled using an $L_p$-norm prior, and the value of p is estimated using hierarchical Bayesian estimation. State-space models such as the Kalman filter, Kalman smoother and the extended Kalman filter have been applied to the inverse ECG problem [19,20], in which the epicardial potentials are the states to be estimated. These statistical methods provide a natural way of including spatio-temporal correlations through state transitions. Another study presented by Corrado et al. defines both the electrical and the mechanical measurements as the state variables and uses unscented Kalman filter to estimate these state variables [21].

Both the Kalman filter and Bayesian MAP estimation methods were successful in accurately reconstructing the epicardial potential distributions. However, performance of the Bayesian MAP estimation method relies on a good a priori pdf, which is not usually available. Even with simple Gaussian assumption, prior expected value (mean) vector and covariance matrix are necessary to fully represent the epicardial potentials. Similarly, forming an appropriate state transition rule for the Kalman filter approach to yield accurate and robust results is still an unresolved problem.

Minimum relative entropy (MRE) is another statistical approach for inferring a pdf from a set of constraints and prior information. There have been several inverse problem applications of the MRE method. In [22], MRE method was used for estimating pharmacokinetic parameters. In hydrology, it was used for estimating the contaminant source location in drinking water systems, and for recovering release history of groundwater contaminant [23–26]. In geology, it was used for detecting $C{O}_2$ leakage history and location(s) [27]. In atmospheric science, MRE was used in order to identify the source term of gas emission in atmosphere, in combination with particle swarm optimization (PSO) method [28]. Another application was an estimation problem for finite dimensional quantum systems [29] for reconstructing the behaviour of a quantum channel or in retrieving information at the receiver of a communication system.

In this paper, we investigate how the parameters of the MRE method could change the solution of the inverse ECG problem and discuss the limitations of the method. These MRE parameters are the lower and upper bounds and the expected value of the solution, and the expected uncertainty in the model. Using these parameters, first an a priori pdf is constructed, and using this pdf, an a posteriori pdf is estimated, which is then used to define a solution estimate. This method is more flexible compared to the Bayesian MAP estimation technique, in which a full covariance matrix is required in addition to a mean vector, even with the simplified Gaussian assumption. We also explore various approaches for defining the prior mean, which turns out to be the most influential MRE parameter.

In this study, we use true epicardial potentials recorded from dog hearts, and we simulate body surface potentials from these true recordings by multiplying the epicardial potential data matrix with the forward transfer matrix and then adding simulated Gaussian distributed noise. Forward problem to obtain the forward transfer matrix is solved using the boundary element method [30].

This paper is organized as follows. In Section 2, we present our problem definition, MRE method and its application to linear inverse ECG problem. In Section 3, we present results of our MRE studies. Finally, in Section 4, we include our concluding remarks along with future work plans.

2. Methods

In the geometrical model we used in this work, the heart and body surfaces are represented in terms of triangular surface elements, and the vertices of these triangles correspond to nodes (or leads) at which body surface and epicardial potentials are measured and estimated, respectively. Thus, after discretization, epicardial potential and body surface potential vectors at a single time instant are obtained from these potential distributions by writing the potential values at the nodes into column vectors of length equal to the number of nodes on respective surfaces. If there are N nodes on the heart surface and M nodes on the body surface, the epicardial potential vector at time instant k is defined as ${\mathbf{x}}_k\in {\mathbb{R}}^{N\times 1}$, and the corresponding body surface potential measurement vector is defined as ${\mathbf{y}}_k\in {\mathbb{R}}^{M\times 1}$.

In order to establish a mathematical relationship between the epicardial potentials and the body surface potential measurements, forward problem of ECG is solved using the geometry and the electrical properties of the torso. Surface methods such as the boundary element method (BEM) [30] are commonly preferred to solve the forward ECG problem in terms of epicardial potentials. Approximation of BEM results to a linear relationship yields:(1) $$\begin{array}{c}\hfill {\mathbf{y}}_k=\mathbf{A}{x}_k+{\mathbf{n}}_k,k=1,\dots ,T,\end{array}$$(1)

where $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ is the forward transfer matrix. Here, ${\mathbf{n}}_k\in {\mathbb{R}}^{M\times 1}$ is also added to the model to represent discretization errors and noise in the measurements. In most of the applications, ${\mathbf{n}}_k$ is assumed to be normally distributed, and uncorrelated with the epicardial potentials.

The goal in inverse ECG problem is then to estimate the epicardial potentials ${\mathbf{x}}_k$, using the body surface potential measurements ${\mathbf{y}}_k$ and the forward model $\mathbf{A}$. The problem posed in Equation (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_k=\mathbf{A}{x}_k+{\mathbf{n}}_k,k=1,\dots ,T,\end{array}$$(1) ) is frequently solved at each time instant (k) independently, thus we can drop the time subscript from the vectors for ease of representation, keeping in mind that a solution should be obtained at every time instant. Thus, in the following section, when we define parameters such as the mean vector, upper and lower bounds and expected uncertainty, they are specific to a single time instant. In the application, they may or may not change at different time instants. In Section 3, we give a more detailed explanation on how we define these parameters at different time instants.

2.1. Minimum relative entropy method

The relative entropy principle is a general information theoretic method for deducing unknown probability density function (pdf) when there exists a prior estimate of the density function and information in the form of constraints on expected values [31].

Suppose that the random vector $\mathbf{x}$ has an unknown multivariate density function (pdf) ${\mathbf{q}}^{†}(\mathbf{x})$, which has an initial estimate $\mathbf{p}(\mathbf{x})$ and there exist some additional constraints that restrict ${\mathbf{q}}^{†}(\mathbf{x})$. Typical constraint information includes:(2) $$\begin{array}{cc}& {\mathbf{q}}^{†}(\mathbf{x})\ge 0,\hfill \end{array}$$(2) (3) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}=1,\hfill \end{array}$$(3) (4) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}=\widehat{f_j}(j=1,2,\dots ,M).\hfill \end{array}$$(4)

The functions $f_j(\mathbf{x})$ and data $\widehat{f_j}$ defined in Equation (4(4) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}=\widehat{f_j}(j=1,2,\dots ,M).\hfill \end{array}$$(4) ) are known. The constraints given in Equations (2(2) $$\begin{array}{cc}& {\mathbf{q}}^{†}(\mathbf{x})\ge 0,\hfill \end{array}$$(2) ) and (3(3) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}=1,\hfill \end{array}$$(3) ) are required for ${\mathbf{q}}^{†}(\mathbf{x})$ to be a valid pdf and Equation (4(4) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}=\widehat{f_j}(j=1,2,\dots ,M).\hfill \end{array}$$(4) ) represents existing information in the form of expected value constraint. The problem presented here is to determine pdf $\mathbf{q}(\mathbf{x})$, which is an estimate of ${\mathbf{q}}^{†}(\mathbf{x})$, based on the provided information. Then, the relative entropy principle states that the estimate $\mathbf{q}(\mathbf{x})$ of the probability density function ${\mathbf{q}}^{†}(\mathbf{x})$ minimizes the function:(5) $$\begin{array}{c}\hfill H(\mathbf{q},\mathbf{p})=\underset{{\mathbf{q}}^{†}}{min}H({\mathbf{q}}^{†},\mathbf{p}),\end{array}$$(5)

subject to constraints given in Equations (2(2) $$\begin{array}{cc}& {\mathbf{q}}^{†}(\mathbf{x})\ge 0,\hfill \end{array}$$(2) )–(4(4) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}=\widehat{f_j}(j=1,2,\dots ,M).\hfill \end{array}$$(4) ). Here, $H({\mathbf{q}}^{†},\mathbf{p})$ is the entropy of ${\mathbf{q}}^{†}(\mathbf{x})$ relative to $\mathbf{p}(\mathbf{x})$, also known as the Kullback-Leibler divergence [32,33], defined as:(6) $$\begin{array}{c}\hfill H({\mathbf{q}}^{†},\mathbf{p})={\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}.\end{array}$$(6)

One of the standard methods to solve the minimization problem defined in Equation (5(5) $$\begin{array}{c}\hfill H(\mathbf{q},\mathbf{p})=\underset{{\mathbf{q}}^{†}}{min}H({\mathbf{q}}^{†},\mathbf{p}),\end{array}$$(5) ) is to introduce Lagrange multipliers $\mathit{\mu }$ and ${\mathit{\gamma }}_j$, $j=(1,2,\dots ,M)$ corresponding to the constraints [31]. By introducing the Lagrange multipliers, optimization problem can be stated as:(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7)

Note that constraint in Equation (2(2) $$\begin{array}{cc}& {\mathbf{q}}^{†}(\mathbf{x})\ge 0,\hfill \end{array}$$(2) ) is indirectly included in Equation (7(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7) ) since ${\mathbf{q}}^{†}(\mathbf{x})$ appears in the integral of the logarithmic term (Kullback-Leibler divergence), which forces ${\mathbf{q}}^{†}(\mathbf{x})$ to be larger than or equal to zero in order for Equation (7(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7) ) to be a valid mathematical definition.

The solution of Equation (7(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7) ) is obtained by computing its variation (derivative) relative to ${\mathbf{q}}^{†}(\mathbf{x})$. Therefore, $\mathbf{q}(\mathbf{x})$ satisfies:(8) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=\mathbf{p}(\mathbf{x})exp\left(-1-\mathit{\mu }-\sum _{j=1}^M{\mathit{\gamma }}_j{f}_j(\mathbf{x})\right).\end{array}$$(8)

The constraint given in Equation (4(4) $$\begin{array}{cc}& {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}=\widehat{f_j}(j=1,2,\dots ,M).\hfill \end{array}$$(4) ) can be extended to incorporate uncertainty about the values of $\widehat{f_j}$ to fit the solution within a specified tolerance:(9) $$\begin{array}{c}\hfill \sum _{j=1}^M{\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)}^2\le {\mathit{ϵ}}^2.\end{array}$$(9)

Then, Equation (7(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7) ) can be stated as:(10) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\mathit{\gamma }\left[\sum _{j=1}^M{\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)}^2-{\mathit{ϵ}}^2\right]\end{array}\right).\end{array}$$(10)

Since $\widehat{f_j}$ is a constant term, it can be carried into the integral equation. If we define a function $g_j(\mathbf{x})$ such that(11) $$\begin{array}{c}\hfill g_j(\mathbf{x})=f_j(\mathbf{x})-\widehat{f_j},\end{array}$$(11)

the last integral term of Equation (10(10) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\mathit{\gamma }\left[\sum _{j=1}^M{\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)}^2-{\mathit{ϵ}}^2\right]\end{array}\right).\end{array}$$(10) ) can be stated as:(12) $$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}={\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\left(f_j(\mathbf{x})-\widehat{f_j}\right)\mathrm{d}\mathbf{x}={\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})g_j(\mathbf{x})\mathrm{d}\mathbf{x}.\end{array}$$(12)

We can obtain the solution of Equation (10(10) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\mathit{\gamma }\left[\sum _{j=1}^M{\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)}^2-{\mathit{ϵ}}^2\right]\end{array}\right).\end{array}$$(10) ) by computing its variation relative to ${\mathbf{q}}^{†}(\mathbf{x})$. Therefore, $\mathbf{q}(\mathbf{x})$ satisfies:(13) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=\mathbf{p}(\mathbf{x})exp\left(-1-\mathit{\mu }-\sum _{j=1}^M{\mathit{\lambda }}_j{g}_j(\mathbf{x})\right),\end{array}$$(13)

where(14) $$\begin{array}{c}\hfill {\mathit{\lambda }}_j=2\mathit{\gamma }{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})g_j(\mathbf{x})\mathrm{d}\mathbf{x}(j=1,2,\dots ,M),\end{array}$$(14)

where $\mathit{\gamma }$ and ${\mathit{\lambda }}_j$ are again the Lagrange multipliers to be determined.

One essential piece of the minimum relative entropy method is defining a prior pdf, $\mathbf{p}(\mathbf{x})$. For many estimation problems, a reasonable upper and lower bound for the unknowns can be obtained. Then, the base level of information about the unknown random vector $\mathbf{x}$ is a multivariate uniform distribution between these bounds [25]:(15) $$\begin{array}{c}\hfill \mathbf{b}(\mathbf{x})=\left\{\begin{array}{cc}\prod _{i=1}^N\frac{1}{U_i-L_i},& \mathrm{i}f{L}_i\le x_i\le U_i,\hfill \\ 0,& \mathrm{o}therwise,\hfill \end{array}\right.\end{array}$$(15)

where $U_i$ and $L_i$ are the upper and lower bounds of $x_i$ (ith element of $\mathbf{x}$), respectively. An estimate of the prior pdf (we will call this estimate $\widehat{\mathbf{p}}(\mathbf{x})$) can be obtained by minimizing entropy of $\mathbf{p}(\mathbf{x})$ relative to the boxcar pdf $\mathbf{b}(\mathbf{x})$, subject to the expected value constraint:(16) $$\begin{array}{c}\hfill {\overline{x}}_j={\int }_{{\mathbb{R}}^N}{x}_j\mathbf{p}(\mathbf{x})\mathrm{d}\mathbf{x}(j=1,2,\dots ,N),\end{array}$$(16)

where $\overline{\mathbf{x}}={[{\overline{x}}_1,{\overline{x}}_2,\dots ,{\overline{x}}_N]}^T$ is the prior expected value (mean) vector, and ${\overline{x}}_i$ is the expected value of $x_i$. The optimization problem is similar to Equation (7(7) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=arg\underset{{\mathbf{q}}^{†}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})ln\frac{{\mathbf{q}}^{†}(\mathbf{x})}{\mathbf{p}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\mu }\left[{\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{j=1}^M{\mathit{\gamma }}_j\left({\int }_{{\mathbb{R}}^N}{\mathbf{q}}^{†}(\mathbf{x})f_j(\mathbf{x})\mathrm{d}\mathbf{x}-\widehat{f_j}\right)\end{array}\right).\end{array}$$(7) ), and estimate of $\mathbf{p}(\mathbf{x})$ is given as:(17) $$\begin{array}{c}\hfill \widehat{\mathbf{p}}(\mathbf{x})=arg\underset{\mathbf{p}}{min}\left(\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}\mathbf{p}(\mathbf{x})ln\frac{\mathbf{p}(\mathbf{x})}{\mathbf{b}(\mathbf{x})}\mathrm{d}\mathbf{x}+\mathit{\eta }\left[{\int }_{{\mathbb{R}}^N}\mathbf{p}(\mathbf{x})\mathrm{d}\mathbf{x}-1\right]\\ \hfill +\sum _{i=1}^N{\mathit{\beta }}_i\left({\int }_{{\mathbb{R}}^N}{x}_i\mathbf{p}(\mathbf{x})\mathrm{d}\mathbf{x}-{\overline{x}}_i\right)\end{array}\right).\end{array}$$(17)

Solving the minimization problem yields:(18) $$\begin{array}{c}\hfill \mathbf{p}(\mathbf{x})=\mathbf{b}(\mathbf{x})exp\left(-1-\mathit{\eta }-\sum _{i=1}^N{\mathit{\beta }}_i{x}_i\right),\end{array}$$(18)

where $\mathit{\eta }$ and ${\mathit{\beta }}_i$ are the Lagrange multipliers, where each ${\mathit{\beta }}_i$ is determined by the definition from Equation (16(16) $$\begin{array}{c}\hfill {\overline{x}}_j={\int }_{{\mathbb{R}}^N}{x}_j\mathbf{p}(\mathbf{x})\mathrm{d}\mathbf{x}(j=1,2,\dots ,N),\end{array}$$(16) ) and $\mathit{\eta }$ by the normalization requirement:(19) $$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^N}\mathbf{p}(\mathbf{x})\mathrm{d}\mathbf{x}=1.\end{array}$$(19)

More detailed derivation of the MRE method for posterior and prior pdfs and also computation methods of Lagrange multipliers can be found in [23–25,34–36].

2.1.1. Application to discrete linear inverse problem

In this part, we present how minimum relative entropy method can be applied to discrete linear inverse problems. Consider the discrete linear inverse problem defined in Equation (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_k=\mathbf{A}{x}_k+{\mathbf{n}}_k,k=1,\dots ,T,\end{array}$$(1) ) at a single time instant, without the time index:(20) $$\begin{array}{c}\hfill \mathbf{y}=\mathbf{A}x+\mathbf{n}.\end{array}$$(20)

Our aim is to estimate $\mathbf{x}$. The known function $f_j(\mathbf{x})$ and its expected value in discrete linear case can be defined as:(21) $$\begin{array}{c}\hfill f_j(\mathbf{x})=\sum _{i=1}^N{A}_{ji}{x}_i,\end{array}$$(21) (22) $$\begin{array}{c}\hfill \widehat{f_j}={\int }_{{\mathbb{R}}^N}\mathbf{q}(\mathbf{x})\left[\sum _{i=1}^N{A}_{ji}{x}_i\right]\mathrm{d}\mathbf{x},\end{array}$$(22)

where $A_{ji}$ is the element located at jth row and ith column of matrix $\mathbf{A}$. Here, the known expected value $\widehat{f_j}$ corresponds to physical measurement, $y_j$. If we assume that the upper and lower bound of $\mathbf{x}$ defined in Equation (15(15) $$\begin{array}{c}\hfill \mathbf{b}(\mathbf{x})=\left\{\begin{array}{cc}\prod _{i=1}^N\frac{1}{U_i-L_i},& \mathrm{i}f{L}_i\le x_i\le U_i,\hfill \\ 0,& \mathrm{o}therwise,\hfill \end{array}\right.\end{array}$$(15) ) is allowed in the range (0, U), we obtain the probability density function $\mathbf{q}(\mathbf{x})$ as:(23) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=\prod _{i=1}^N\frac{-a_i}{exp(-a_{i}U)-1}exp(-a_i{x}_i),\end{array}$$(23)

where(24) $$\begin{array}{c}\hfill a_i={\mathit{\beta }}_i+\sum _{j=1}^M{\mathit{\lambda }}_j{A}_{ji}.\end{array}$$(24)

The estimate $\widehat{\mathbf{x}}$ is then the expected value of Equation (23(23) $$\begin{array}{c}\hfill \mathbf{q}(\mathbf{x})=\prod _{i=1}^N\frac{-a_i}{exp(-a_{i}U)-1}exp(-a_i{x}_i),\end{array}$$(23) ), and the ith element of this estimate is:(25) $$\begin{array}{c}\hfill {\widehat{x}}_i=\frac{exp(-a_{i}U)a_{i}U+exp(-a_{i}U)-1}{a_i[exp(-a_{i}U)-1]}.\end{array}$$(25)

For non-zero lower bounds, the problem can be re-scaled by defining $\widehat{\mathbf{x}}={\widehat{\mathbf{x}}}_0+\mathbf{l}$, where $\widehat{\mathbf{x}}$ is the true solution, ${\widehat{\mathbf{x}}}_0$ is the corresponding model solution for zero lower bound and $\mathbf{l}$ is the vector of lower bounds. Zero lower bound solution ${\widehat{\mathbf{x}}}_0$ can be calculated using modified data ${\mathbf{y}}_m=\mathbf{y}-\mathbf{A}l$. The upper bounds and expected values must be replaced by $U_i-L_i$ and ${\overline{x}}_i-L_i$, respectively. After ${\widehat{\mathbf{x}}}_0$ is computed with the MRE method, the true solution is obtained from $\widehat{\mathbf{x}}={\widehat{\mathbf{x}}}_0+\mathbf{l}$ [23].

2.2. Tikhonov regularization

Tikhonov regularization is the most frequently used method to solve the inverse problem of ECG. Thus, we include this method here for comparison. In this method, in addition to a good fit to the available data, a physiologically meaningful constraint is also imposed on the solution. The resulting cost function to be minimized becomes [5]:(26) $$\begin{array}{c}\hfill L(\mathbf{x})={∥\mathbf{A}x-\mathbf{y}∥}_2^2+{\mathit{\lambda }}^2{∥\mathbf{R}x∥}_2^2.\end{array}$$(26)

Here, $\mathit{\lambda }$ stands for the regularization parameter, and $\mathbf{R}$ is the regularization matrix that imposes the constraint on the solution. If $\mathbf{R}$ is the identity matrix, the problem is termed as the zero-order regularization; if it is the surface gradient operator and the surface Laplacian operator, the problem is called the first-order and the second-order regularization, respectively. The solution can be stated in compact form as:(27) $$\begin{array}{c}\hfill \widehat{\mathbf{x}}={\left({\mathbf{A}}^T\mathbf{A}+{\mathit{\lambda }}^2{\mathbf{R}}^T\mathbf{R}\right)}^{-1}{\mathbf{A}}^T\mathbf{y}.\end{array}$$(27)

The choice of an appropriate $\mathit{\lambda }$ is an important issue to obtain accurate and yet regular results. It provides a trade-off between a good fit to the measured data and the physiological constraint imposed on the solution. In this study, an appropriate value of $\mathit{\lambda }$ is chosen using the L-curve method [37].

3. Results

In order to assess the success of each method, we simulated body surface potential measurements from known epicardial potential distributions; hence, we have the ground truth (i.e. the real epicardial potentials) to compare our solutions with.

We used epicardial potentials measured from a canine heart by Robert S. MacLeod and his co-workers at the University of Utah [38]. In their experiments, the heart was suspended in a human-shaped electrolytic tank, and potentials from the heart surface were recorded via a sock that was placed around the heart, with 490 electrodes sewn into it. Electrical stimulation was applied at one of the ventricular electrodes. The measurements at each time instant are modelled as ${\mathbf{x}}_k$ in Equation (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_k=\mathbf{A}{x}_k+{\mathbf{n}}_k,k=1,\dots ,T,\end{array}$$(1) ). The BSPMs were simulated from these measured epicardial potentials first by multiplying them by a previously calculated forward transfer matrix ($\mathbf{A}$), then by adding white Gaussian noise at 30 dB signal-to-noise ratio (SNR) value. This noise is represented by ${\mathbf{n}}_k$ in Equation (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_k=\mathbf{A}{x}_k+{\mathbf{n}}_k,k=1,\dots ,T,\end{array}$$(1) ). Boundary element method [30] was used for solving the forward problem. The forward matrix $\mathbf{A}$ that is used for simulating the data was found by including some inhomogeneity (lungs) within the torso, and the forward matrix used for solving the inverse problem was generated using a homogeneous torso to avoid inverse crime to some extent [39]. In recent years, there has been renewed interest in studying the effects of inhomogeneities on forward and inverse ECG solutions [40–44]. Although we used a homogeneous model here to solve the inverse problem as many other studies have done before, these new studies indicate that the ECGI studies will favour more detailed models in the future. We have included a brief assessment of these studies in Section 4 for the interested reader.

The results were compared quantitatively using the well-known correlation coefficient (CC) metric. In this study, CC is calculated at each time instant by comparing the true epicardial potential vector ${\mathbf{x}}_k$ with the solution vector ${\widehat{\mathbf{x}}}_k$ as:(28) $$\begin{array}{c}\hfill CC(k)=\frac{{\displaystyle N{\sum }_{j=1}^N{\mathbf{x}}_k(j){\widehat{\mathbf{x}}}_k(j)-\left({\sum }_{j=1}^N{\mathbf{x}}_k(j)\right)\left({\sum }_{j=1}^N{\widehat{\mathbf{x}}}_k(j)\right)}}{\sqrt{\left[{\displaystyle N{\sum }_{j=1}^N{\mathbf{x}}_k^2(j)-{\left({\sum }_{j=1}^N{\mathbf{x}}_k(j)\right)}^2}\right]\left[{\displaystyle N{\sum }_{j=1}^N{\widehat{\mathbf{x}}}_k^2(j)-{\left({\sum }_{j=1}^N{\widehat{\mathbf{x}}}_k(j)\right)}^2}\right]}}.\end{array}$$(28)

Then, mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values are obtained over time for comparison of results. Qualitative assessments were made by visual inspection of the real and the estimated epicardial potential maps using the Map3d software developed in University of Utah [45].

The results are presented in two parts. In the first part, effects of deviations of the MRE parameters (i.e. the prior mean, upper and lower bounds, expected uncertainty value) from their true values are evaluated. In the second part, we present different approaches for defining the prior mean, which turns out to be the most influential of the three prior parameters. Note that in the following sections, all simulations that require noise to be added to the measurements and/or parameters are run with a single noise realization per case.

3.1. Effects of MRE parameters

In this study, we have adapted MRE implementation given in [24] to our problem. To achieve this, knowledge about the lower and upper bounds, prior mean of the unknown variable $\mathbf{x}$ and the expected uncertainty value, ${\mathit{ϵ}}^2$, is required. In this section, we investigate the effects of each MRE parameter by changing only one parameter at a time and keeping the others fixed at their true values. True values of these parameters are defined as follows:

• Prior mean vector: The true prior mean vector at the kth time instant is equal to the true epicardial potential vector at that time instant, i.e. ${\overline{\mathbf{x}}}_k={\mathbf{x}}_k$.

• Upper and lower bounds: We use upper and lower bounds that are fixed with respect to time, but different for each lead. In order to find the true upper and lower bound vectors at time instant k, we first obtain an epicardial potential matrix $\mathbf{X}\in {\mathbb{R}}^{N\times T}$, whose kth column consists of the true epicardial potential vector at the kth time instant ($k=1,\dots ,T$): (29) $$\begin{array}{c}\hfill \mathbf{X}=\left[\begin{array}{cccccc}{\mathbf{x}}_1& {\mathbf{x}}_2& \cdots & {\mathbf{x}}_k& \cdots & {\mathbf{x}}_T\end{array}\right].\end{array}$$(29) Next, we find the maximum and minimum values of the epicardial potentials at lead j ($j=1,\dots ,N$) over all time instants: (30) $$\begin{array}{cc}\hfill x_{max}(j)& =max(\mathbf{X}(j,:)),\hfill \end{array}$$(30) (31) $$\begin{array}{cc}\hfill x_{min}(j)& =min(\mathbf{X}(j,:)).\hfill \end{array}$$(31) Then, for all time instants k, we use the same true upper and lower value vectors: (32) $$\begin{array}{c}\hfill {\mathbf{u}}_k={\left[\begin{array}{cccc}{x}_{max}(1)& x_{max}(2)& \cdots & x_{max}(N)\end{array}\right]}^T,\end{array}$$(32) (33) $$\begin{array}{c}\hfill {\mathbf{l}}_k={\left[\begin{array}{cccc}{x}_{min}(1)& x_{min}(2)& \cdots & x_{min}(N)\end{array}\right]}^T.\end{array}$$(33) This means that the true values of the upper and lower bounds for the jth lead at the kth time instant are equal to ${\mathbf{u}}_k(j)$ and ${\mathbf{l}}_k(j)$, respectively.

• Expected uncertainty: True value of the expected uncertainty, ${\mathit{ϵ}}^2$, is the same for all leads and over all time instants, and is assumed to be equal to the variance of the noise in the body surface measurements.

3.1.1. Effects of upper and lower bounds

For this case, we explored the effects of over and underestimating the upper and lower values. We modified the upper and lower bound vectors in Equations (32(32) $$\begin{array}{c}\hfill {\mathbf{u}}_k={\left[\begin{array}{cccc}{x}_{max}(1)& x_{max}(2)& \cdots & x_{max}(N)\end{array}\right]}^T,\end{array}$$(32) ) and (33(33) $$\begin{array}{c}\hfill {\mathbf{l}}_k={\left[\begin{array}{cccc}{x}_{min}(1)& x_{min}(2)& \cdots & x_{min}(N)\end{array}\right]}^T.\end{array}$$(33) ) by multiplying them by a scalar, $\mathit{\alpha }$ as:(34) $$\begin{array}{c}\hfill {\widehat{\mathbf{u}}}_k=\mathit{\alpha }{\mathbf{u}}_k,{\widehat{\mathbf{l}}}_k=\mathit{\alpha }{\mathbf{l}}_k.\end{array}$$(34)

and then by varying $\mathit{\alpha }$ in the range 0.4–2.0. In this study, we fixed the expected uncertainty to its true value. Using only the true mean vector was highly unrealistic since one does not have access to the true potentials in practice; thus, in addition to the true mean vector, we also included results for noisy mean vectors at 5 and 15 dB SNR.

The results are presented in Table 1 as mean and standard deviation values of CC over time. These results show that if prior bounds are large enough such that the maximum and minimum values of true epicardial potentials can lie between these values, then high CC values can be achieved. This condition is satisfied for $\mathit{\alpha }\ge 1$. On the other hand, estimation performance degrades if $\mathit{\alpha }<0.9$, even in the noise-free case. Furthermore, using noisier (lower SNR) prior mean values drops the estimation quality, especially if $\mathit{\alpha }<1$. In this case, using larger upper and lower bound values compensates for this performance drop to some degree; for prior mean at 5 dB SNR, CC value increases as $\mathit{\alpha }$ increases from 1 to 2. This suggests that it is better to overestimate the upper and lower bound values rather than using the true values or underestimating them.

Table 1. Mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values for CC obtained for various upper and lower bounds. Results are presented for the true prior mean vector, and noisy prior mean vectors at 15 and 5 dB SNR values.

	True prior mean	Prior mean at 15 dB SNR	Prior mean at 5 dB SNR
$\mathit{\alpha }$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$
0.4	0.7976 $\pm$ 0.1130	0.7766 $\pm$ 0.1128	0.5278 $\pm$ 0.3163
0.5	0.8761 $\pm$ 0.1371	0.8490 $\pm$ 0.1298	0.6644 $\pm$ 0.1417
0.6	0.8944 $\pm$ 0.1944	0.8787 $\pm$ 0.1864	0.6918 $\pm$ 0.1404
0.7	0.8911 $\pm$ 0.2270	0.8681 $\pm$ 0.2337	0.7125 $\pm$ 0.1221
0.8	0.9237 $\pm$ 0.1915	0.8852 $\pm$ 0.2323	0.6904 $\pm$ 0.0955
0.9	0.9922 $\pm$ 0.0281	0.9540 $\pm$ 0.0674	0.7109 $\pm$ 0.0877
1.0	0.9993 $\pm$ 0.0035	0.9819 $\pm$ 0.0064	0.7367 $\pm$ 0.0894
1.5	0.9999 $\pm$ 0.0003	0.9823 $\pm$ 0.0057	0.8295 $\pm$ 0.0479
2.0	0.9996 $\pm$ 0.0016	0.9820 $\pm$ 0.0065	0.8536 $\pm$ 0.0313

3.1.2. Effects of prior mean

In this test, upper and lower bounds of epicardial potentials were fixed as given by Equation (34(34) $$\begin{array}{c}\hfill {\widehat{\mathbf{u}}}_k=\mathit{\alpha }{\mathbf{u}}_k,{\widehat{\mathbf{l}}}_k=\mathit{\alpha }{\mathbf{l}}_k.\end{array}$$(34) ) with $\mathit{\alpha }=2$, and the true value of the expected uncertainty was used, but the prior mean vector was varied. To alter the true prior mean vector, Gaussian white noise was added to the true prior mean at various SNR values (SNR = 1, 5, 10, 15 and 20 dBs). Then, CC was calculated at all time instants to compare the MRE solution and the real epicardial potentials. Table 2 displays the mean and standard deviation values of these CCs over time for the true and noisy prior mean vectors.

Table 2. Mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values for CC obtained for various prior mean vectors. Upper and lower bounds, and expected uncertainty in the error are fixed; the true prior mean vector is disturbed by Gaussian white noise at different SNR values.

SNR	$E\{CC\}\pm \mathit{\sigma }\{CC\}$
1	0.7331 $\pm$ 0.0328
5	0.8595 $\pm$ 0.0270
10	0.9476 $\pm$ 0.0158
15	0.9819 $\pm$ 0.0073
20	0.9939 $\pm$ 0.0037
True	0.9996 $\pm$ 0.0016

These results show that as one deviates from the true mean, performance of MRE result degrades. It is tolerable for down to 10 dB SNR; the average CC values are still above 90%. However, for lower SNR values, average CC value drops severely.

3.1.3. Effects of expected uncertainty

For this case, we explored the effects of over and underestimating the expected uncertainty value. We modified the expected uncertainty value by multiplying its true value by a scalar, $\mathit{\beta }$ in the range 0.4–1.6. The upper and lower values are fixed as given by Equation (34(34) $$\begin{array}{c}\hfill {\widehat{\mathbf{u}}}_k=\mathit{\alpha }{\mathbf{u}}_k,{\widehat{\mathbf{l}}}_k=\mathit{\alpha }{\mathbf{l}}_k.\end{array}$$(34) ) with $\mathit{\alpha }=2$. Again, in addition to the true mean value, we also included results for noisy mean values at 5 and 15 dB SNR.

The results are presented in Table 3 as mean and standard deviation values of CC. If $\mathit{\beta }$ is larger than 1 (overestimation of the expected uncertainty value), even with the noisy mean values, high CC values can be achieved (larger than 0.8). On the other hand, if $\mathit{\beta }$ is smaller than 1 (underestimation of the expected uncertainty value), even with the true mean values, CC values suffer significantly.

Table 3. Mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values for CC obtained for various expected uncertainty values. Results are presented for the true prior mean vector, and noisy prior mean vectors at 15 and 5 dB SNR values.

	True prior mean	Prior mean at 15 dB SNR	Prior mean at 5 dB SNR
$\mathit{\beta }$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$	$E\{CC\}\pm \mathit{\sigma }\{CC\}$
0.4	0.6593 $\pm$ 0.2673	0.8013 $\pm$ 0.1923	0.7225 $\pm$ 0.1638
0.6	0.9945 $\pm$ 0.0105	0.9400 $\pm$ 0.1230	0.8283 $\pm$ 0.1021
0.8	0.9972 $\pm$ 0.0136	0.9821 $\pm$ 0.0060	0.8557 $\pm$ 0.0315
1.0	0.9996 $\pm$ 0.0016	0.9817 $\pm$ 0.0062	0.8531 $\pm$ 0.0298
1.2	0.9997 $\pm$ 0.0009	0.9819 $\pm$ 0.0063	0.8541 $\pm$ 0.0331
1.4	0.9988 $\pm$ 0.0048	0.9819 $\pm$ 0.0061	0.8555 $\pm$ 0.0340
1.6	0.9997 $\pm$ 0.0009	0.9808 $\pm$ 0.0070	0.8503 $\pm$ 0.0405

3.2. Determining MRE parameters

The results obtained in the previous section show that the most important parameter of the MRE method is the prior expected value; more realistic prior mean yields better estimation. The upper and lower bounds might be deduced easily from experimental data available from animal studies or mathematical models, and the expected uncertainty can be estimated based on our information about the measurement system and its possible noise sources. However, defining the prior mean is more complicated and requires more attention. Thus, in this section, we present two simple approaches to define prior mean value. Upper and lower bounds of epicardial potentials are defined as in Equations (32(32) $$\begin{array}{c}\hfill {\mathbf{u}}_k={\left[\begin{array}{cccc}{x}_{max}(1)& x_{max}(2)& \cdots & x_{max}(N)\end{array}\right]}^T,\end{array}$$(32) ) and (33(33) $$\begin{array}{c}\hfill {\mathbf{l}}_k={\left[\begin{array}{cccc}{x}_{min}(1)& x_{min}(2)& \cdots & x_{min}(N)\end{array}\right]}^T.\end{array}$$(33) ) with $\mathit{\alpha }=2$, and the true expected uncertainty value was used.

In the first approach, solution in the previous time instant (${\widehat{\mathbf{x}}}_{k-1}$) multiplied by a constant ($\mathit{\mu }$) was used as the prior mean parameter for the current time instant (${\overline{\mathbf{x}}}_k$):(35) $$\begin{array}{c}\hfill {\overline{\mathbf{x}}}_k={\mathit{\mu }\widehat{\mathbf{x}}}_{k-1}.\end{array}$$(35)

This is a simple assumption that relates the epicardial potentials at a certain lead with only the epicardial potential at the same lead in the previous time instant, and it is referred to as Random Walk model, which is used to define state transitions in the Kalman filtering literature [46]. Prior mean at the initial time instant (${\overline{\mathbf{x}}}_0$) is set to zero vector.

We applied three different scalar coefficients, $\mathit{\mu }=0.9,1.0,1.1$. The results are presented in Table 4 as average and standard deviation values of CC. We obtained the best results for $\mathit{\mu }=0.9$.

Table 4. Mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values for CC obtained for previous time instant solution multiplied by a constant.

	MRE	MRE	MRE
	$\mathit{\mu }=0.9$ from prev. sol.	$\mathit{\mu }=1.0$ from prev. sol.	$\mathit{\mu }=1.1$ from prev. sol.
$E\{CC\}$	0.7496	0.7251	0.6798
$\mathit{\sigma }\{CC\}$	0.2005	0.2014	0.2038

In the second approach, we used a constant prior mean value for all leads. Three different cases have been examined:

• Case 1: Different prior mean values at every time instant (time varying (TV) mean): (36) $$\begin{array}{cc}\hfill {\overline{x}}_k& =\frac{1}{N}\sum _{j=1}^N{x}_k(j),\hfill \end{array}$$(36) (37) $$\begin{array}{cc}\hfill {\overline{\mathbf{x}}}_k& ={\overline{x}}_k\mathbf{1},\hfill \end{array}$$(37) where $\mathbf{1}={[1,1,\cdots ,1]}^T$, and $x_k(j)$ is the epicardial potential value of lead j at the kth time instant. True epicardial potentials were used to obtain ${\overline{x}}_k$.

• Case 2: Fixed prior mean value for all leads and all times, where the averaging is over all times and leads: (38) $$\begin{array}{cc}\hfill \overline{x}& =\frac{1}{NT}\sum _{k=1}^T\sum _{j=1}^N{x}_k(j),\hfill \end{array}$$(38) (39) $$\begin{array}{cc}\hfill {\overline{\mathbf{x}}}_k& =\overline{x}\mathbf{1}.\hfill \end{array}$$(39) Similar to Case 1, true epicardial potentials were used to obtain $\overline{x}$ in this solution.

• Case 3: This case is very similar to Case 2; an average $\overline{x}$ value was used to obtain the mean vector at all time instants. However, unlike Case 2, here epicardial potentials obtained from other experiments (i.e. from what we call a ‘training set’) were used to define $\overline{x}$, as well as upper and lower bounds. We have included 22 different ectopic beats (specifically, recordings during the QRS cycle of the ECG, when the initial stimulation site is on the ventricles) in this training set, and each recording has been initiated from a different part of the heart surface. For each of these 22 recordings, an upper bound, a lower bound and a mean value have been calculated as explained in Case 2. Then, averages of these parameters were used in the MRE solution.

Table 5. Mean ($E\{CC\}$) and standard deviation ($\mathit{\sigma }\{CC\}$) values for CC obtained for various prior expected value determination methods.

		MRE	MRE	MRE	MRE
	Tikhonov	$\mathit{\mu }=0.9$ from prev. sol.	Case 1	Case 2	Case 3
$E\{CC\}$	0.7695	0.7496	0.7584	0.7581	0.7713
$\mathit{\sigma }\{CC\}$	0.1826	0.2005	0.2168	0.2077	0.1659

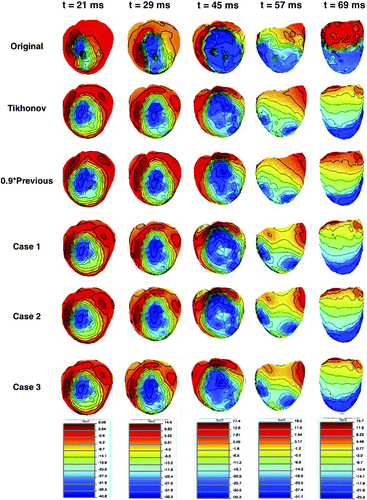
We compared the performances of three MRE solutions, i.e. the case when the prior mean is set to 0.9 times the previous time solution, and the two cases for constant mean over all leads (time varying and fixed). Tikhonov regularization is also included here to form a comparison basis. The average and standard deviation values of CC for these four types of solutions are presented in Table 5. According to the results in this table, we observe no significant difference between the methods in terms of average CC values.

However, these CC values can only give us a general idea about how these solutions vary, and in cases like this when the CC values are very close to each other, it is necessary to examine the solutions in more detail. To achieve this, we plotted original and reconstructed epicardial potential maps for five different time instants in Figure 1. In these epicardial potential maps, blue regions represent the activated regions, and red regions represent the regions that have not been activated yet (rest regions). The high gradient transition region between those two, where there are closely spaced contour lines, is the activation wavefront, which gives information about activation times of tissue at different locations on the heart and conduction velocities. While visually comparing these maps, we mainly consider whether the wavefront reconstructed by the inverse solution is a good representation of the original wavefront. Secondly, we expect to have a good match between the activated and rest regions. When we examine these maps, we observe that at most of the time instants, there is no clear advantage of using the MRE approach over the traditional Tikhonov regularization method with our simple prior mean definitions. However, at $t=57$ ms, wavefronts reconstructed by the MRE approach (Case 1, Case 2 and Case 3) show better fidelity to the wavefront in the original map. In these maps, the contour lines are more tightly packed compared to Tikhonov regularization and random-walk approach (with $\mathit{\mu }=0.9$) solutions. Sharp turns in the original wavefront around the 10 o’clock direction cannot be observed with the latter two approaches, but visible in Case 1, Case 2 and Case 3 results. It is also observed that there is no clear advantage of using a different mean value for different times compared to using a fixed value for all times; both yield similar results. Using a training set rather than the true epicardial potentials to estimate the mean value yields similar results in this study. This is not surprising since we only use a single constant value for all times and leads, and this constant value is calculated from all available epicardial potential values. Under different stimulation scenarios, propagation patterns over the heart surface and epicardial waveform shapes with respect to time may vary significantly, but the average values more or less stay constant.

Figure 1. Original and reconstructed epicardial potential maps at five different time instants during the QRS region.

4. Discussion and conclusion

In this study, we explored applicability of the MRE method for solving the inverse ECG problem. Specifically, we were interested in understanding the effect of each parameter required for using the MRE method on the inverse solutions. Towards this goal, we carried out numerical simulations in which we changed only one parameter of the MRE method at a time and kept the remaining parameters fixed. Based on these simulation results, we concluded that:

• When the prior mean is close to the true value, upper and lower bounds do not have a significant effect on the estimation performance unless they were underestimated. However, when the prior mean deviates from its true value, overestimating the upper and lower bound values improves performance of the MRE method.

• Underestimated expected uncertainty also causes a reduction in estimation quality. It should be equal to or larger than the true value for better performance.

• The most important parameter is the prior mean; if it deviates from the true value, performance of the MRE method degrades.

Upper and lower bounds and the expected uncertainty can be deduced from previously recorded experimental data, mathematical models of cardiac electrical activity, measurement system properties and possible noise sources. However, in order to successfully solve the inverse ECG problem, one needs a good prior estimate for the expected mean. In this study, we applied two simple methods to obtain the expected mean: random-walk and using a constant mean. Random-walk yielded results similar to Tikhonov regularization, but even with the simple approach using a constant mean for all leads and all times, we improved the wavefront reconstruction at some time instants compared to Tikhonov regularization. Still, the approaches that we used in this paper to use MRE in practical applications do not outperform conventional regularization methods. However, the results in Section 3.1 suggest that with a more careful definition of the MRE parameters, this approach has promise for real data applications. Comparing the results of Sections 3.1 and 3.2, we believe that there is room for improvement that will make MRE a good method to solve the inverse ECG problem more accurately than the traditional regularization methods. However, more work has to be done to find a good prior expected mean so that we can obtain a performance that approaches the high performance of the results with accurate prior expected mean.

There have been studies on defining an appropriate prior pdf for the epicardial potentials and other types of electrical activity of the heart. Previous work on Bayesian estimation of epicardial potentials [14,15] assumed that prior pdf is multivariate Gaussian distribution. This definition was based on empirical study of the epicardial potential distributions, and it was not proven that Gaussian prior is the best way to represent the epicardial potentials. Furthermore, even though the potentials are assumed to have a Gaussian distribution, depending on the initial stimulation site or in general the pathology of the heart that produces the corresponding epicardial potentials, it was still a challenge to define an appropriate mean and covariance matrix that best represent the data. In previous studies, the prior pdf model parameters were either obtained from training sets of previously recorded potentials [15] or from simulated potentials that result from mathematical modelling of cardiac electrical activity [47]. More recently, Rahimi et al. applied hierarchical Bayesian estimation to estimate the 3D distribution of transmembrane potentials in the heart [18], and they observed that depending on the current time within the cardiac cycle, $L_1$-norm prior (Laplacian), $L_2$-norm prior (Gaussian) or $L_p$-norm prior ($1<p<2$) should be chosen, and value of p should be one of the estimated parameters as well. In the light of these studies, it is clear that the prior pdf should be chosen carefully. In this study, we wanted to keep the simple uniform (box-car) pdf definition for the epicardial potentials; however, we did not want to use it directly as the prior pdf in the Bayesian estimation procedure. Thus, we used a two-step definition of the prior pdf of the epicardial potentials; in the first step, we used the box-car pdf in terms of upper and lower bounds only, then in the second step, we used this simple pdf definition to estimate the prior pdf that will be used with the Bayesian estimation.

In this study, following original work on MRE studies, we defined the prior pdf to be an exponential distribution and starting from the box-car pdf, we estimated the parameters of this exponential distribution. It is of course possible to define the prior pdf for the epicardial potentials as a Gaussian distribution as in [15], or as an $L_p$-norm prior as in [18], and starting from the box-car pdf, estimate the parameters of these representations. It is even possible to skip the box-car pdf step and directly specify the prior pdf and use it in the Bayesian estimation of epicardial potentials. This was our first effort in applying the MRE method to inverse ECG problem; thus, we wanted to follow the same steps of MRE implementation presented in most of the studies in the literature [24,25]. Our studies will continue on inferring prior expected value from experimental data and mathematical models of epicardial potentials. We will also explore the applicability of the MRE method assuming its prior pdf is Gaussian, or any other structured on non-structured function.

Simultaneously recorded body surface potentials and the corresponding epicardial potentials were not available at the time that this study was carried out; therefore, we could not use true body surface potential measurements in this study. However, in order for this (or any other) inverse ECG solution method to be valuable in clinical studies, these methods need to be tested with real data, in addition to simulated data. On the other hand, using simulated body surface potentials has its own advantages. Evaluation of inverse problem solutions with true body surface potential measurements still involves an ongoing discussion in the inverse ECG community. In this study, our purpose was to assess the applicability of the MRE method to the solution of inverse ECG problem, and using simulated data based on true epicardial potential measurements enabled numerical comparison of our MRE inverse solutions with these true potentials. Recently, as part of CEI, researchers have released their data-sets for use by others working on ECGI [2]. These data-sets include simulated data, experimental data and data from human subjects. Our goal in the near future is to apply our methods to these data-sets and compare the performances of our algorithms with the results of other groups using the same data-sets.

Another limitation of our study was the type of inhomogeneities that we included in solving the forward problem. There have been studies in the literature to understand how much detail should go into modelling of the torso inhomogeneities for solving the forward and inverse ECG problems [30,40,43,48,52]. Forward solution studies included simulation studies and comparisons involving simultaneous recordings of heart and body surface potential measurements. In the first group, researchers have compared the performances of using a homogeneous torso model versus a more complete inhomogeneous torso model in their simulations [49,50,53]. These studies in general concluded that the amplitudes of the torso potentials were affected by the inhomogeneities; however, their general distributions were similar. In [50], it was argued that as far as 12-lead ECG recordings were concerned, these amplitude variations were within acceptable inter-patient variations. Klepfer et al. concluded that subcutaneous fat, anisotropic skeletal muscle and lungs should be included in simulating the torso potentials [49]. Keller et al. discussed that lungs are more important for atrial signals, whereas heart conductivities were more influential for ventricular signals; however, blood and anisotropic skeletal muscle showed the most significant effect on both types of signals [53]. The goal in the second group of studies was to compare simulated potentials using torso models in varying detail to measure torso potentials [30,40,48]. General conclusion in these studies was also that potential maps were similar, whereas amplitudes were different for simulated and measured potentials. In the most recent and most comprehensive of these studies by Bear et al. [40], it was shown that both the homogeneous and the inhomogeneous torso models yielded potential amplitudes that were different from the true measured torso potentials, but the inhomogeneous torso produced potential amplitudes closer to the true potentials compared to the homogeneous case. How these torso inhomogeneities affect the inverse solutions is still an open question. In an earlier study by Ramanathan et al. in 2001, it was concluded that there is no significant difference in inverse solutions when the homogeneous torso model was used [51]. On the other hand, van Oosterom has argued that inverse solutions improved when the lungs were included in the model [52]. However, this was not an extensive study on the effects of torso inhomogeneities, and the forward model used for simulating the body surface potentials also included only lungs between the heart and torso surfaces. In a later study by Zemzemi et al. [41], it was shown that the effects of using a homogeneous torso model for solving the inverse ECG problem were more influential when the measurement errors were small, but when the noise in the measurements was higher, homogeneous or inhomogeneous models had smaller differences. The most recent and comprehensive study was carried out by Punshchykova et al. [42] in 2016 using data from 5 patients with ectopic beats, using a homogeneous model and two inhomogeneous models with different complexity levels. They reported obtaining most stable results using the homogeneous model (smaller standard deviation of ectopic foci locations); however, their most complex inhomogeneous model yielded localization of ectopic foci with best fidelity to measured data. They concluded that theirs was a limited study with data from a few patients, and more validation with more patient recordings was necessary to generalize these findings. In an editorial on the current state of research on forward problem of ECG, Rudy concluded that, even though using a more complete (inhomogeneous) torso model has its advantages, as far as many clinical ECGI applications are concerned, using a homogeneous torso model would be adequate [43]. Cluitmans et al. [44] in a recent review on the other hand argued that more in-vivo studies should be conducted to determine the level of complexity that should be included in the forward model for clinical applications of ECGI. Clearly, this is still an open discussion among the community; therefore, we believe that there is still work to do to improve the forward ECG solution, with the hope to further improve the inverse ECG solutions. Our research efforts in the near future will include solving the forward ECG problem using the finite element method, by taking into account the torso inhomogeneities.

We will also pursue other optimization and inverse problem solution approaches appropriate for the inverse ECG problem. Markov chain Monte Carlo (MCMC) integration is one such approach that has been successfully applied in the fields of electrical imaging of the brain [54] and electrical impedance tomography [55]. We believe that MCMC would perform well in our problem as well especially with non-structured probability density function assumptions.

In recent years, methods such as Multivariate Adaptive Regression Splines (MARS), Conic MARS (CMARS) and its robust version RCMARS [56,57] have been successfully applied to many areas of science and technology such as satellite data reconstruction [58,59], image processing in meteorology [60] and ground motion prediction [61]. These methods are examples of nonparametric regression modelling techniques that make no assumption about the underlying functional relationship between the dependent and independent variables. We plan to use (C)MARS techniques to solve inverse ECG problem to overcome the sensitivity of the MRE method to the model parameters.

Acknowledgements

The authors would like to thank Dr. Robert S. MacLeod from University of Utah for the data used in this study. This work was made possible in part by software, Map3d (this project (Map3d) was supported by the National Institute of General Medical Sciences of the National Institutes of Health under grant number P41 GM103545-18).

Notes

No potential conflict of interest was reported by the authors.