The integrated acceleration of the Chambolle-Pock algorithm applied to constrained TV minimization in CT image reconstruction

ABSTRACT

Background and Objective: The constrained, total variation (TV) minimization algorithm has been applied in computed tomography (CT) for more than 10 years to reconstruct images accurately from sparse-view projections. Chambolle-Pock (CP) algorithm framework has been used to derive the algorithm instance for the constrained TV minimization programme. However, the ordinary CP (OCP) algorithm has slower convergence rate and each iteration is also time-consuming. Thus, we investigate the acceleration approaches for achieving fast convergence and high-speed reconstruction. Methods: To achieve fast convergence rate, we propose a new algorithm parameters setting approach for OCP. To achieve high-speed reconstruction in each iteration, we use graphics processing unit (GPU) to speed-up the two time-consuming operations, projection and backprojection. Results: We evaluate and validate our acceleration approaches via two-dimensional (2D) reconstructions of a low-resolution Shepp–Logan phantom from noise-free data and a high-resolution Shepp–Logan phantom from noise-free and noisy data. For the three-specific imaging cases considered here, the convergence process are speeded up for 89, 9 and 81 times, and the reconstruction in each iteration maybe speeded up for 120, 340 and 340 times, respectively. Totally, the whole reconstructions for the three cases are speeded up for about 10,000, 3060 and 27,540 times, respectively. Conclusions: The OCP algorithm maybe tremendously accelerated by use of the improved algorithm parameters setting and use of GPU. The integrated acceleration techniques make the OCP algorithm more practical in the CT reconstruction area.

KEYWORDS:

• TV minimization
• Chambolle-Pock algorithm
• acceleration
• GPU
• image reconstruction

1. Introduction

Optimization-based image reconstruction in computed tomography (CT) has received much attention in the recent 10 years because it may accurately reconstruct image from sparse-view projections, achieving low-dose illumination to the scanned patients [1–3]. In fact, the ability of optimization programmes to achieve accurate sparse reconstruction is coming from the fact that the optimization programmes embody the thought of compressed sensing (CS) [4]. CS thinks that a signal maybe accurately restored from sparse data if the signal has a sparse transform, i.e. the majorities of the values of the transform are zero or close to zero [4]. The accurate solver (restored signal) maybe obtained by solving an optimization programme whose objective function is the ℓ ₁ norm of the sparse transform subject to the corresponding data constraint. Total variation (TV) norm has been known to be a powerful tool for performing edge-preserving regularization [1]. In fact, TV minimization-based image reconstruction algorithm is a simple, classic and effective CS-based algorithm for TV norm is the ℓ ₁ norm of the gradient-magnitude transform (GMT) of the image. From 2006, TV algorithm has been heavily studied from theory to application, from medical area to industrial district for it has potential to achieve accurate reconstruction from sparse-view, limited-angle and other non-ideal projections [5–9].

TV norm is difficult to handle for it is not linear, quadratic ore even everywhere differentiable. These features preclude the use of some existing optimization algorithms, for example, the gradient-based algorithms [10]. In these algorithms to solve the TV minimization programme, there are three frequently used algorithms: adaptive-steepest-descent-projection-onto-convex-sets (ASD-POCS) [2], alternating direction method of multipliers (ADMM) [11,12] based and Chambolle-Pock algorithms [10,13].

ASD-POCS is designed according to the physical meaning of the optimization programme. It may not always guarantee convergence for the algorithm parameters are physically designed rather than mathematically derived though an appropriate parameters setting may arrive at convergence in most cases. Another potential disadvantage is that the convergence speed will be very slow when the image-solver has moved to the boundary of the data-tolerance-error-ball [2]. ADMM algorithm simplifies the process of the non-smooth ℓ ₁ norm by introducing a new variable, then use shrinkage operation to solve the ℓ ₁ norm minimization problem. The main disadvantage of ADMM is that there is a sub-optimization problem which has not close form. Chambolle-Pock algorithm framework is a powerful algorithm tool to solve various convex optimization programmes even if they are non-smooth [13].

There are two types of CP algorithms, the ordinary CP (OCP) and the pre-conditioned CP (PCP) [10] for solving the constrained TV minimization which has some advantages over OCP. Actually, PCP has faster convergence speed [6,10,14]. People have verified the high efficiency of PCP in unconstrained TV minimization algorithm for 2D CT reconstruction [10], linear programming, TV-ℓ ₁ image denoizing, graph cuts and minimal partitions [14]. However, deriving the proximal mapping may become more involved for PCP, so it has important meaning for us to explore the acceleration approaches to improve the convergence rate of OCP. Also, we know that the reconstruction in each iteration is time-consuming because of the two computing-intensive operations: projection and backprojection. Thus, we need to search approaches to speed-up the whole reconstruction.

In the work, we propose a new algorithm parameters setting approach for OCP and refer the corresponding algorithm to as n-OCP, achieving fast convergence rate. We use GPU to speed-up the time-consuming projection and backprojection in each iteration, achieving fast reconstruction. The integrated acceleration approach may speed-up the whole reconstruction process of the TV minimization programme.

In Section 2, we introduce the OCP algorithm and design an implementation method based on pixel-driven projection and backprojection. In Section 3, we propose the integrated acceleration method. In Section 4, we validate and evaluate the method via low-resolution and high-resolution phantom and using noise-free and noisy projection data. Finally, we give a brief discussion and conclusion in Section 5.

2. The OCP algorithm for constrained TV minimization and its implementation

In CT, measurement of each detector cell is the line integral of the image function by the ray-line no matter the scanning configuration is parallel, fan or cone beam. So the discrete-to-discrete (D2D) imaging models are the same for any imaging configuration since the D2D model is a system of linear equations with every equation describing the relation between a measurement and all the image pixels, i.e. the line integral. Just because of the uniformity and for the specific description, we focus on the 2D parallel beam CT configuration. But note that, it is without loss of generality and the whole method chain maybe extended or transplanted to other imaging configuration.

Suppose the imaging configuration is: (1) the size of the image is n × n with n being even; (2) the pixel is unit square; (3) the origin of the imaging ordinate system and the rotation centre are both located at $\left[\frac{n}{2},\frac{n}{2}\right]$; (4) the length of the projection is n and the sampling interval of the projection, i.e. the length of the detector cell is unit length; (5) the origin of the detector axis is located at cell $\frac{n}{2}+1$; (6) number of the projections are n _p ; (7) the projections are angularly sampled evenly in the angular range $\left[0,\pi \right]$; and (8) the ray beam is parallel.

2.1. D2D imaging model

The 2D D2D imaging model considered here, maybe modelled as a system of linear equations,

(1) $$g=Au$$(1)

where g is a column vector with M elements, representing the projection data, u is a column vector with N elements, representing the image and A is the system matrix whose size is M × N, representing the 2D Radon transform. A _ij is the contribution of the $j\text{th}$ pixel to the $i\text{th}$ data. The computation method of A _ij is, in fact, the so-called projection method, including pixel-driven [15], ray-driven [16,17]and distance-driven projection [15,18] methods, etc. In the imaging configuration here, $M=n\times n_{p}andN=n^2$.

We define three vector spaces: I the space of the discrete image; D the space of the projection data; and V the space of spatial-vector-valued image, where V = I ² for 2D reconstruction here, i.e.

(2) $$I=R^N;D=R^M;V=R^{2N}$$(2)

for (1), $g\in D;u\in I\text{and}A\in R^{M\times N}$.

2.2. The constrained TV minimization program

The imaging model shown in (1) is a system of linear equations. Usually, the system is large scale, ill-posed and possible under-conditioned. To solve it accurately, the optimization technique maybe employed. Here, we design a constrained, TV minimization programme as follows:

(3) $$u^{\ast }={argmin\Vert u\Vert }_{\mathit{TV}},\text{s.t}.{\Vert g-Au\Vert }_2\le \epsilon$$(3)

where u ^* is the solver of the optimization programme, i.e. the minimal of the objective function; ε is the data-tolerance-error; and u _TV is the TV norm of image u, expressed in (4).

(4) $${\Vert u\Vert }_{\mathit{TV}}={∥\left({\left|\mathrm{\nabla }u\right|}_g\right)∥}_1$$(4)

Where the right-hand term means the ℓ ₁ norm of the GMT of u. ∇is the gradient transform matrix with ∇ ∊ R ^2N×N , which is the combination of ∇₁ and ∇₂ with ∇₁, ∇₂ ∊ R ^N×N , expressed in (5).

(5) $$\mathrm{\nabla }=\left(\begin{array}{c}{\mathrm{\nabla }}_1\hfill \\ {\mathrm{\nabla }}_2\hfill \end{array}\right)$$(5)

Where ∇₁ and ∇₂ are the horizontal and vertical gradient transform matrix (see Appendix D of [10]), respectively.

Clearly, ∇u ∊ V. But ${\left|\mathrm{\nabla }u\right|}_g\in I$ is the GMT image, which is either isotropic or anisotropic according to the specific gradient-magnitude definition, ${\left|·\right|}_g$.

The isotropic gradient-magnitude transform is:

(6) $${\left|\begin{array}{c}a\hfill \\ b\hfill \end{array}\right|}_g=\sqrt{a^2+b^2}$$(6)

and the anisotropic one is:

(7) $${\left|\begin{array}{c}a\hfill \\ b\hfill \end{array}\right|}_g=\left|a\right|+\left|b\right|$$(7)

${\left|·\right|}_g$ may convert every scalar-pair into one scalar, i.e. convert the gradient image into a gradient-magnitude image, so ${\left|\mathrm{\nabla }u\right|}_g\in I$, whereas ∇u ∊ V.

2.3. The OCP algorithm for TV minimization and its parameter setting

The CP algorithm instance for TV minimization programme shown in 2.2 maybe mathematically derived, so it may guarantee convergence. Every sub-optimization has a close form. Here, we just list the algorithm for OCP in Algorithm 1 without derivation [10].

Table

Algorithm 1. Pseudocode for K steps of the OCP algorithm to solve the constrained, TV minimization
1: $L={∥\begin{array}{c}A\hfill \\ \mathrm{\nabla }\hfill \end{array}∥}_2$; ${\sigma }_1=\frac{1}{L},{\sigma }_2=\frac{1}{L},\tau =\frac{1}{L}$, $\theta =1,n=0$
2: $u_0=0;p_0=0;q_0=0;{\overline{u}}_0=0;g$ is known
3: repeat
4: $p_{n+1}=max(\Vert p_n+{\sigma }_1\left(A{\overline{u}}_n-g\right){\Vert }_2-{\sigma }_1\epsilon ,0)\left(p_n+{\sigma }_1\left(A{\overline{u}}_n-g\right)\right)/{\Vert p_n+{\sigma }_1\left(A{\overline{u}}_n-g\right)\Vert }_2$
5: $q_{n+1}=\left(q_n+{\sigma }_2\mathrm{\nabla }{\overline{u}}_n\right)/\text{max}\left(1_I,{\left|q_n+{\sigma }_2\mathrm{\nabla }{\overline{u}}_n\right|}_g\right)$
6: u n+1 = u n − τA ^T p n+1 − τ∇^T q n+1
7: ${\overline{u}}_{n+1}=u_{n+1}+\theta \left(u_{n+1}-u_n\right)$
8: n = n + 1
9: until n = K
10: u K is the designed solution.

Line 1 is for the initialization of the algorithm parameters, $\sigma ,\tau ,\theta \text{and}n$. The calculation method of constant L is shown in Algorithm 2. Line 2 is to initialize the variables. It is important to make the structure of every variable clear. Here, $u\in I;\overline{u}\in I$. They correspond to the image vector which is a column vector with N elements. p ∊ D; g ∊ D. They correspond to the projection-data vector which is a column vector with M elements. q ∊ V. it corresponds to the gradient-image vector (spatial-vector-valued image), which is a column vector with 2N elements. Line 4 is a Shrinkage operation, which may let the length of the M dimensional vector $p_n+\sigma \left(A{\overline{u}}_n-g\right)$ shrink to 0 or shorten length of $\sigma \epsilon$ if its length is less than or greater than the threshold $\sigma \epsilon$, respectively. Line 5 is a hard-threshold-Shrinkage operator which may let each 2D space vector corresponding to a pixel shrink to 1 or maintain the original length. It maybe confusing for the numerator is in V and the denominator is in I. ‘/’ in line 5 means component-wise division. But it should be also noted that the component here in the numerator-vector and the denominator-vector are different: the component of the numerator-vector is a 2D vector which corresponds to a pixel-gradient at a specific pixel while the component of the denominator-vector is a scalar which corresponds to a pixel-gradient magnitude. Thus, every component operation is a division of a 2D vector by a scalar which represents a 2D vector magnitude. Vector in V has double elements of that in I, hence we know why the dimensions of the vectors at numerator and denominator are different. Line 6 is for the update of the reconstructed image.

The constant L in algorithm 1 maybe computed by Algorithm 2 [10].

Table

Algorithm 2. Pseudocode for K steps of the generic power algorithm to calculate L
1: x 0 = 1; n = 0
2: repeat
3: x n+1 = A ^T Ax n
4: $x_{n+1}=x_{n+1}/{\Vert x_{n+1}\Vert }_2$
5: L = ${∥\begin{array}{c}A{x}_{n+1}\hfill \\ \mathrm{\nabla }{x}_{n+1}\hfill \end{array}∥}_2$
6: n = n + 1
7: until $\mathbf{n}=\mathbf{K}$

In line 1 of Algorithm 2, x ₀ = 1 means the initial image is a 1-image meaning that the value of every pixel is 1.

2.4. The implementation of OCP

The implementation of an algorithm is also very important for it may decide the final efficiency and reconstruction accuracy. The OCP algorithm maybe implemented explicitly if the matrixes are represented using the true matrix form. However, it would be impractical if the matrix size is too huge to store in computer memory. For example, the system matrix of a 2D image of size 1024 × 1024 would need a huge matrix of size 8 TB, if the projection set also has 1024 × 1024 elements and every element is represented by a double precision float number, which is impossible to be stored in micro-computer. Thus, it is practical and potentially efficient to regard the matrix shown in Algorithm 1 as an operator. The implementation method is on how to implement every matrix-operation via operator-operation.

(1)	The computing of ∇

∇ is the gradient transform matrix and maybe implemented by the definition of the horizontal and vertical gradient transform . If ∇₁ u and ∇₂ u are the horizontal and vertical gradient images, respectively, their transform equations maybe expressed in (8) and (9).

(8) $${\mathrm{\nabla }}_{1}u\left(i,j\right)=u\left(i,j\right)-u\left(i,j-1\right)$$(8)

(9) $${\mathrm{\nabla }}_{2}u\left(i,j\right)=u\left(i,j\right)-u\left(i-1,j\right)$$(9)

(2)	The computing of ${\mathrm{\nabla }}^T$

The operator ∇ ^T is the opposite operator of ∇ but note that it is not the inverse operator. For ∇:I → V, so ∇ ^T :V → I. If $f={\mathrm{\nabla }}^T\left(\begin{array}{c}{h}_1\hfill \\ h_2\hfill \end{array}\right)\text{with}f,h_1,h_2\in I$, then the operation maybe implemented by:(10) $$f\left(i,j\right)=h^1\left(i,j\right)-h^1\left(i,j+1\right)+h^2\left(i,j\right)-h^2\left(i+1,j\right)i,j\in [1,n]$$(10)

(3)	The computing of A

A is the system matrix converting the image into projection data, so, in fact, we may regard the matrix as a projection operator $A:R^{n\times n}\to R^{n\times n_p}$, i.e. from image to projection. Here, we use pixel-driven projection method to implement the operation. For the traditional pixel-driven projection method may introduce high-frequency artefacts, we design an accurate method by virtually dividing each pixel into four sub-pixels. The pseudocode of the operation is shown in Algorithm 3.

Table

Algorithm 3: The pseudocode for the accurate pixel-driven projection algorithm. Suppose f is an image with size n × n and p is a 1D projection signal of length n under a specific angle $\theta$. The code may generate p from f.
1: for i = 1: n
2: for j = 1: n
3: Divide the pixel at $\left(i,j\right)$ into 4 small pixels, whose values are f 1, f 2, f 3, f 4 with the same value f(i, j)
4: for k = 1:4
5: Calculate the coordinates(x, y)of pixel f k in the imaging coordinate system
6: Calculate the projection address t using the equation: t = xcosθ + ysinθ
7: Linearly anterpolate the pixel value f k to the two adjacent detector cells of the projection address in p, then weight these detector-cell-values by factor 0.25.
8: end for k
9: end for j
10: end for i

(4)	The computing on $A^T$

The CP algorithm demands that A ^T is the exact transpose of the matrix A. Usually, it may not always be correct that A ^T can be represented by the opposite operation of the operation corresponding to A. For example, A ^T is not ray-driven backprojection while A is the ray-driven projection. Fortunately, pixel-driven projection and backprojection are strictly mutual-transpose, so we may implement A ^T via the classic pixel-driven backprojection shown in Algorithm 4, regarding A ^T as a backprojection operator, $A^T:R^{n\times n_p}\to R^{n\times n}$, i.e. from projection to image.

Table

Algorithm 4: The pseudocode for the pixel-driven backprojection algorithm. Suppose f is an image with size n × n and p is a 1D projection signal of length n under a specific angle $\theta$. The code may generate f from p.
1: for i = 1: n
2: for j = 1: n
3: Calculate the coordinates (x, y) of pixel (i, j) in the imaging coordinate system
4: Calculate the projection address t using the equation: t = xcosθ + ysinθ
5: Do a linear interpolation operator with the two adjacent detector cells of the projection address to get the value at the projection address and assign it to f(i, j).
6: end for j
7: end for i

3. Integrated acceleration of OCP algorithm

We may accelerate the whole iteration process of OCP by two approaches: improve the convergence rate by use of a new algorithm-parameters determination approach and speedup the reconstruction process in each iteration by use of GPU parallel computing. The first one is soft acceleration pattern and the second one is hardware acceleration pattern. Thus, the combined use of the two approaches is referred to as integrated acceleration.

3.1. n-OCP: an approach to improve the convergence rate of OCP

The convergence rate of OCP is slow which has been verified by Refs. [10,19] and our reconstruction practices. In the section, we propose a method named n-OCP which may improve the convergence rate by new initialization determination of the algorithm parameters.

The pseudocode of PCP to solve the constrained TV minimization programme maybe obtained by performing the replacement: ${\mathrm{\Sigma }}_1\leftarrow {\sigma }_1,{\mathrm{\Sigma }}_2\leftarrow {\sigma }_2,T\leftarrow \tau$ (see Appendix E of [10]). The PCP has been demonstrated that it may achieve much faster convergence rate than OCP [10,19]. For the difference of the two algorithms is only on the selection of the algorithm parameters, we think the slow convergence of OCP suffers from the low-efficiency of the algorithm parameters. It is possible to design a faster OCP algorithm by improving the parameter setting.

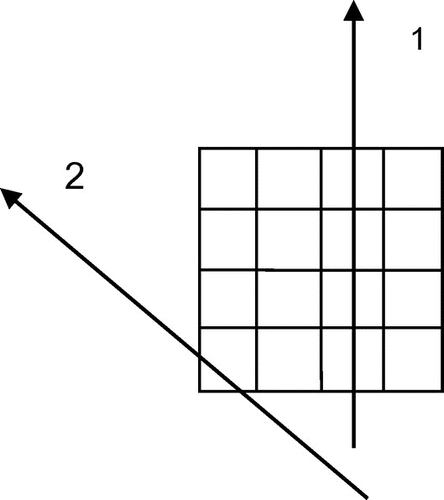
${\mathrm{\Sigma }}_1=\frac{1_D}{A{1}_I}$ is a algorithm parameter of PCP. Its function is to normalize the data error, i.e. the subtraction of the guessed data and the measured data. ${\mathrm{\Sigma }}_1$ is a matrix of size $\left[n,n_p\right]$. 1 _I is a 1-image, thus A1 _I may get a projection-set of the 1-image. Clearly, every measurement of the projection-set is the summation of the weighting factors of the pixels of contribution to the measurement. For example, the weighting-factor summation for ray 1 and 2 are 4 and 1, respectively, (see Figure 1). Then ¼ and 1 are the ${\mathrm{\Sigma }}_1$-value for ray 1 and 2 by performing the calculation ${\mathrm{\Sigma }}_1=\frac{1_D}{A{1}_I}$. Clearly, the actual function of ${\mathrm{\Sigma }}_1$ is to normalize the data error. For the corresponding parameter in OCP of ${\mathrm{\Sigma }}_1$ in PCP is σ ₁, a scalar, we set-up a scalar normalization factor, i.e. ${\sigma }_1=\frac{1}{n}$., which is the normalization factor for every measurement at angle 0 ^o (see ray 1, Figure 1). The new determination of σ ₁ has potential to achieve better performance for it comes from the physical meaning of the parameter and is motivated by the setting method of PCP.

Figure 1. The schematic diagram to illuminate the physical meaning of ${\mathrm{\Sigma }}_1$ in PCP.

${\mathrm{\Sigma }}_2=\frac{1_V}{\left|\mathrm{\nabla }\right|1_I}$, an algorithm parameter in PCP, is, in fact, a 0.5-vector in vector space V, so we set σ ₂ in OCP, corresponding to ${\mathrm{\Sigma }}_2$ in PCP, to be scalar 0.5. Thus, the new determination method for σ ₂ is the same with that of PCP and has potential to achieve better acceleration performance.

$T=\frac{1_I}{A^T{1}_D+\left|{\mathrm{\nabla }}^T\right|1_V}$ is the third algorithm parameter of PCP to control the update strength of the reconstructed image. A ^T 1 _D means a backprojection operation of the 1-projection. In fact, its value is the number of the projections for the pixels in the region covered by the parallel beam. For example, the corresponding value of the pixels in the recovered region is 180 if the number of projections is 180. $\left|{\mathrm{\nabla }}^T\right|1_V$ is a 4-image. So, we may set τ to be $\frac{1}{n_p+4}$ to expect it has similar property with $T$ in PCP.

Thus, we get the new version of OCP algorithm with the new parameter setting that ${\sigma }_1=\frac{1}{n},{\sigma }_2=0.5\text{and}\tau =\frac{1}{n_p+4}$. We name the algorithm n-OCP for the parameters are relative to n and n _p and ‘n’ may mean that the parameter determination method is new.

3.2. The GPU acceleration of the reconstruction process in each iteration

We have known that the reconstruction process in each iteration is also time-consuming because of the two computation-intensive operations, projection and backprojection. In Section 2.4, we design the pixel-driven projection and backprojection algorithms and show their pseudocode.

GPU (Graphics Processing Unit) is a powerful tool to speed-up computation if its pattern is single instruction multiple data (SIMD) [20]. If the operation for each data are the same, then the kind of programme maybe converted into CUDA (Compute Unified Device Architecture) C kernel function. When the kernel is loaded into the GPU device, each thread may process the corresponding data via the corresponding thread according to the definition of the thread structure and the relation of thread ID and the data index. All the threads will be executed by GPU device parallelly, i.e. all the data will be processed by GPU parallelly, the whole operation is accelerated. Pixel-driven projection and backprojection are both suitable for use of GPU [8,9]. Pixel-driven projection is performed pixel by pixel with each pixel projected to the detector and then linearly anterpolated to the projection. Pixel-driven backprojection is also performed pixel by pixel with each pixel projected to the detector an then getting its value from the projection by performing linear interpolation on the two cells which are neighbours of the projection address. Clearly, projection and backprojection are both MDSP (Multi Data Single Programme), it is feasible to re-write the codes into CUDA version. Below, we list the GPU version of the projection and backprojection operations in algorithms 5 and 6, respectively.

Table

Algorithm 5: The GPU version of pixel-driven projection operation
Main programme part for setting up the logical structure of the Threads in GPU
M1: Create a kernel k from the .cu and .ptx files
M2: Setup the structure of Block. k.ThreadBlockSize=n;
M3: Setup the structure of Grid. k.GridSize=n;
M4: Execute the kernel.
CUDA kernel part
C1: Setup the pixel index via the Thread index. i = threadIdx.x; j = blockIdx.x;
C2: Divide the pixel at $\left(i,j\right)$ into 4 small pixels, whose values are f 1, f 2, f 3, f 4 with the same value f(i, j)
C3: for k = 1:4
C4: Calculate the coordinates(x, y)of pixel f k in the imaging coordinate system
C5: Calculate the projection address t using the equation: t = x cos θ + y sin θ
C6: Linearly anterpolate the pixel value f k to the two adjacent detector cells of the projection address in p, then weight these detector-cell-values by factor 0.25.
C7: end for k

Table

Algorithm 6: The GPU version of pixel-driven backprojection operation
Main programme part for setting up the logical structure of the Threads in GPU
M1: Create a kernel k from the .cu and .ptx files
M2: Setup the structure of Block. k.ThreadBlockSize = n;
M3: Setup the structure of Grid. k.GridSize = n;
M4: Execute the kernel.
CUDA kernel part
C1: Setup the pixel index via the Thread index. i = threadIdx.x; j = blockIdx.x;
C2: Calculate the coordinates(x, y)of pixel(i, j) in the imaging coordinate system
C3: Calculate the projection address t using the equation: t = x cos θ + y sin θ
C4: Do a linear interpolation operator with the two adjacent detector cells to get the value at the projection address and assign it to f(i, j).

In both algorithms 5 and 6, the size of the Grid and Block are both n, so the index (ID) for Thread and Block are both 1:n. In Line C1 of algorithms 5 and 6, the pixel index is determined by the Thread ID and Block ID. Clearly, the pixels maybe traversed by this determination method. The corresponding relation between pixel index and Thread and Block IDs is shown in Figure 2.

Figure 2. The relation between pixel index and Thread and Block IDs. Note: The pixel-operation tasks are submitted to SM column by column for one column corresponds to one Block.

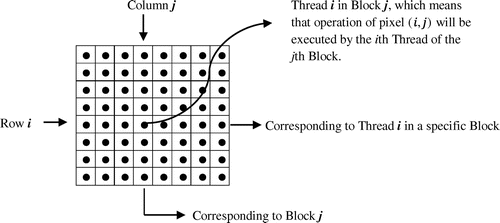
The execution unit of GPU is streaming multiprocessors (SM), which is loaded in terms of the granularity of Blocks. The pixel-operations will be loaded into SM one column by one column in the Thread configuration here. Since the structure of Threads and the usage of register and local memory of each parallel computing may impact the acceleration performance, we should also analyse the specific configuration in terms of specific imaging condition to evaluate the acceleration potential and check if it may make some bottlenecks for acceleration.

The GPU we used is NVIADA GeForce GTX 760, whose parameters are shown in Table 1 (from the whitepaper for NVIDIA Kepler architecture and the parameters list of the Matlab function gpuDevice).

Table 1. The key parameters of GeForce GTX 760.

GPU card	GeForce GTX 760	Architecture	Kepler GK104
Max threads per block	1024	Compute capability	3.0
Number of SMs	6	Total memory	4 GB
Max blocks per SM	16	Number of cores on card	1152
Max threads per SM	2048	Number of 32bit registers Per SM	64 K
Number of cores in SM	192	Max shared memory per block	48 KB

When we set-up the Thread structure for a GPU computing task, it is necessary to evaluate the potential acceleration effect according to the designed Thread structure and the parameters specified for the used GPU. The calculation and validation method will be illuminated according to specific cases in next section.

4. Results

In the section, we will validate the proposed acceleration approaches via 2D parallel-beam CT reconstructions. Two Shepp–Logan phantoms of size 64 × 64 and of size 256 × 256 are used as low-resolution and high-resolution images to generate projection sets by use of Equation (1(1) $$g=Au$$(1) ), respectively. For the 256 × 256 high-resolution phantom, we generate noise-free data and noisy data. Then, we may reconstruct the images between OCP and n-OCP algorithms to compare their speeds. We design a practical convergence condition that the RMSE (root-mean-square error) between the reconstructed image and the truth image is lower than or equal to a given small enough number.

4.1. Integrated acceleration validation on a low-resolution phantom

The simulation phantom is the Shepp–Logan phantom of size 64 × 64. The imaging geometry is based on parallel beam scanning. We sample 64 projections uniformly distributed in the range $[0,\pi ]$ and sample 64 measurements on each projection evenly. Thus, the projection set is of size 64 × 64. The D2D model of form of Equation (1(1) $$g=Au$$(1) ) for the imaging case is a linear system of equations with 64 × 64 unknown and 64 × 64 equations. By the additional use of TV minimization technique, it is possible to construct the image accurately. We will focus on the acceleration effect under specific convergence condition.

4.1.1. Soft acceleration effect

For the case here, we set $\epsilon =0$ for Equation (3(3) $$u^{\ast }={argmin\Vert u\Vert }_{\mathit{TV}},\text{s.t}.{\Vert g-Au\Vert }_2\le \epsilon$$(3) ) and the convergence condition that the RMSE between the reconstructed image and the truth-image is less than or equal to 10⁻⁶. Then we use the OCP and n-OCP algorithm to perform reconstructions.

Figure 3 shows the reconstructed images by OCP and n-OCP at iteration 1000. Figures 4 and 5 show the convergence behaviours of image-error and image-TV of the two algorithms during iteration 1–1000 and the whole convergence process, respectively.

Figure 3. The comparison of the reconstructed images at iteration 1000 of the OCP (b) and n-OCP (c) algorithms (a) is the truth-image of the Shepp–Logan phantom of size 64 × 64.

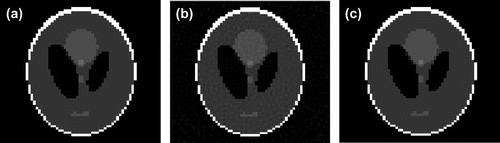
Figure 4. The iteration behaviours of image-error (a) and TV (b) of OCP and n-OCP during iteration 1–1000 for reconstructing the Shepp–Logan phantom of size 64 × 64. Note: The metric of the image-error is root-mean-square-error (RMSE) (the same below).

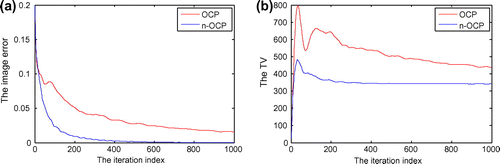
Figure 5. The iteration behaviours of image-error (a) and TV (b) during the whole convergence process for reconstructing the Shepp–Logan phantom of size 64 × 64.

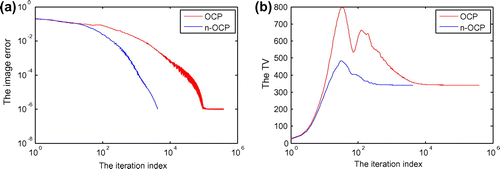
From Figure 3, it maybe seen that the reconstructed image by OCP at iteration 1000 has clear artefacts compared to that by n-OCP, which is almost the same with the truth-image as per the visual evaluation. Observing the iteration behaviours of the two algorithms during iteration 1–1000 from Figure 4, we may see that the convergence speed of n-OCP is much faster than that of OCP. At iteration 1000, the image-error has dropped to about 1.8 × 10⁻⁴ for n-OCP while OCP may just reach 1.6 × 10⁻². At iteration 1000, the TV of n-OCP is 341.9 which is very close to the truth-TV, 341.6, while the TV of OCP is 436.3 which is far away from the truth.

From Figure 5(a), it is seen that n-OCP is much faster than OCP. To achieve the defined convergence condition that $\text{RMSE}\le {10}^{-6}$, n-OCP needs 4311 iterations while OCP needs 385,660 iterations. The same conclusion maybe drawn by analysis of the TV trends of the two algorithms (see Figure 5(b)).

In conclusion, n-OCP may speed-up the convergence process for $\frac{385,660}{4311}\approx 89$ times in terms of the imaging case here. The improved algorithm-parameters setting method may immensely improve the convergence rate.

4.1.2. Hard acceleration effect

In the specific GPU configuration of backprojection operation for 64 × 64 reconstruction, there are 64 Blocks and each Block has 64 Threads. Each SM may contain up to 16 Blocks and 2048 Threads, so each SM here will be loaded 16 Blocks with each Block including 64 Threads, i.e. be loaded 1024 Threads. All the 64 × 64 = 4096 Threads maybe loaded into the GPU card one time, for there are 6 SM which maybe loaded 1024 × 6 = 6144 Threads in terms of the Thread structure here.

Also, we should test the confine of the register and local memory in a SM and evaluate if the SM maybe loaded so many Blocks determined by the calculation above. In the CUDA kernel function, we define four int-type variables and six float-type variables. Each int-type variable needs 4 bytes and each float-type variable also needs 4 bytes, so every thread will need 40 bytes. Each SM will need 40 KB space to store the variables for the loaded 1024 Threads. For the GPU card used, each SM has 64 K 32bit registers (equivalent to 256 KB space). Clearly, the registers are enough to load the variables for each loaded Thread.

By the evaluation according to the confines of SM, we know that our design for the Thread structure is reasonable and the Threads maybe loaded into SMs efficiently.

Similar analysis for projection operation maybe performed. The Thread structure is the same.

The reconstruction in each iteration with the projection and backprojection operations both using GPU acceleration needs only 0.02s for the imaging case here. However, CPU implementation of each iteration needs 2.4 s. In the case, the reconstruction in each iteration maybe speeded up for $\frac{2.4}{0.02}=120$ times.

4.1.3 Integrated acceleration effect

In the case, the soft acceleration factor is 89 and the hard acceleration factor is 120, so the integrated acceleration factor is 120 × 89 = 10,680, i.e. the reconstruction speed achieving a designed solution of GPU-based n-OCP is 10,679 times faster than that of CPU-based OCP.

4.2. Integrated acceleration validation on a high-resolution phantom

The simulation phantom is the Shepp–Logan phantom of size 256 × 256. The imaging geometry is based on parallel beam scanning. We sample 256 projections uniformly distributed in the range $[0,\pi ]$ and sample 256 measurements on each projection evenly. Thus, the projection set is of size 256 × 256. The D2D model of form of Equation (1(1) $$g=Au$$(1) ) for the imaging case is a linear system of equations with 256 × 256 unknown and 256 × 256 equations. By the additional use of TV minimization technique, it is possible to construct the image accurately. We will focus on the acceleration effect under specific convergence condition.

4.2.1. Soft acceleration effect

For the case here, we set $\epsilon =0$ for Equation (3(3) $$u^{\ast }={argmin\Vert u\Vert }_{\mathit{TV}},\text{s.t}.{\Vert g-Au\Vert }_2\le \epsilon$$(3) ) and the convergence condition that the RMSE between the reconstructed image and the truth-image is less than or equal to 10⁻⁵. Then, we use the OCP and n-OCP algorithm to perform reconstructions.

Figure 6 shows the reconstructed images by OCP and n-OCP at iteration 1000. Figures 7 and 8 show the convergence behaviours of image-error and image-TV of the two algorithms during iteration 1–1000 and the whole convergence process, respectively.

Figure 6. The comparison of the reconstructed images at iteration 1000 of the OCP (b) and n-OCP (c) algorithms (a) is the truth-image of the Shepp–Logan phantom of size 256 × 256.

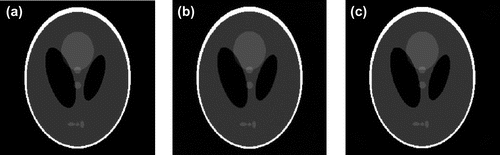
Figure 7. The iteration behaviours of image-error (a) and TV (b) of OCP and n-OCP during iteration 1–1000 for reconstructing the Shepp–Logan phantom of size 256 × 256. Note: The metric of the image-error is RMSE.

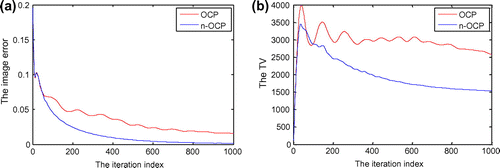
Figure 8. The iteration behaviours of image-error (a) and TV (b) during the whole convergence process for reconstructing the Shepp–Logan phantom of size 256 × 256.

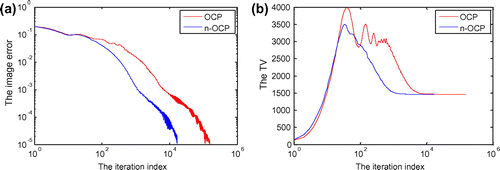
From Figure 6, it maybe seen that the reconstructed image by OCP at iteration 1000 has ring artefacts compared to that by n-OCP, which is almost the same with the truth-image as per the visual evaluation. Observing the iteration behaviours of the two algorithms during iteration 1–1000 from Figure 7, we may see that the convergence speed of n-OCP is much faster than that of OCP. At iteration 1000, the image-error has dropped to about 1.5 × 10⁻³ for n-OCP while OCP may just reach 1.57 × 10⁻². At iteration 1000, the TV of n-OCP is 1536 which is close to the truth-TV, 1460.5, while the TV of OCP is 2586, which is far away from the truth.

From Figure 8(a), it is seen that n-OCP is much faster than OCP. To achieve the defined convergence condition that $\text{RMSE}\le {10}^{-5}$, n-OCP needs 16,827 iterations while OCP needs 153,484 iterations. The same conclusion maybe drawn by analysis of the TV trends of the two algorithms (see Figure 8(b)).

In conclusion, n-OCP may speed-up the convergence process for $\frac{153,484}{16,827}\approx 9$ times in terms of the imaging case here. The improved algorithm-parameters setting method may improve the convergence rate.

4.2.2. Hard acceleration effect

In the specific GPU configuration of backprojection operation for 256 × 256 reconstruction, there are 256 Blocks and each Block has 256 Threads. Each SM may contain up to 16 Blocks and 2048 Threads, so each SM here, will be loaded up to 8 Blocks with each Block including 256 Threads, i.e. be loaded 2048 Threads. All the 256 × 256 = 65,536 Threads maybe loaded into the GPU card $\frac{65,536}{12,288}\approx 6$times, for there are 6 SM which maybe loaded 2048 × 6 = 12,288 Threads.

Also, we should test the confine of the register and local memory in a SM and evaluate if the SM maybe loaded so many Blocks determined by the calculation above. In the CUDA kernel function, we define four int-type variables and six float-type variables. Each int-type variable needs 4 bytes and each float-type variable also needs 4 bytes, so every thread will need 40 bytes. Each SM will need 80 KB space to store the variables for the loaded 2048 Threads. For the GPU card used, each SM has 64 K 32bit registers (equivalent to 256 KB space). Clearly, the registers are enough to load the variables for each loaded Thread.

By the evaluation according to the confines of SM, we know that our design for the Thread structure is reasonable and the Threads maybe loaded into SMs efficiently.

Similar analysis for projection operation maybe performed. The Thread structure is the same.

The reconstruction in each iteration with the projection and backprojection operations both using GPU acceleration needs only 0.12s for the imaging case here. However, CPU implementation of each iteration needs about 41s. In the case, the reconstruction in each iteration maybe speeded up for $\frac{41}{0.12}\approx 340$ times.

4.2.3. Integrated acceleration effect

In the case, the soft acceleration factor is 9 and the hard acceleration factor is 340, so the integrated acceleration factor is 9 × 340 = 3060, i.e. the reconstruction speed achieving the designed solution of GPU-based n-OCP is 3060 times faster than that of CPU-based OCP.

4.3. Integrated acceleration validation on a high-resolution phantom via noisy projection data

The simulation phantom is the Shepp–Logan phantom of size 256 × 256. The imaging configurations are the same with that in Section 4.2 except that the projection set is contaminated by Gaussian noise whose SNR (Signal-to-Noise Ratio) is 45db.

4.3.1. Soft acceleration effect

For the truth projection set is known, we set $\epsilon =51.3452$ for Equation (3(3) $$u^{\ast }={argmin\Vert u\Vert }_{\mathit{TV}},\text{s.t}.{\Vert g-Au\Vert }_2\le \epsilon$$(3) ), which is the ℓ ₂ norm of the subtraction vector of the noisy projection and the truth projection. The convergence condition is that the RMSE between the reconstructed image and the truth-image is less than or equal to 8 × 10⁻³. Then, we use the OCP and n-OCP algorithm to perform reconstructions.

Figure 9 shows the reconstructed images by OCP and n-OCP at iteration 1000. Figures 10 and 11 show the convergence behaviours of image-error and image-TV of the two algorithms during iteration 1–1000 and the whole convergence process, respectively.

Figure 9. The comparison of the reconstructed images at iteration 1000 of the OCP (b) and n-OCP (c) algorithms via noisy projection data (a) is the truth-image of the Shepp–Logan phantom of size 256 × 256.

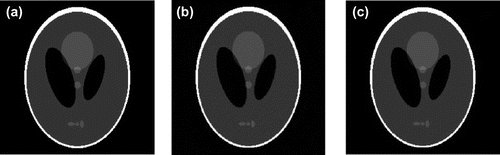
Figure 10. The iteration behaviours of image-error (a) and TV (b) of OCP and n-OCP during iteration 1–1000 via noisy projection data. Note: The metric of the image-error is RMSE.

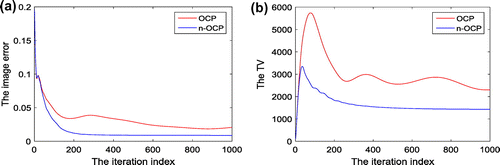
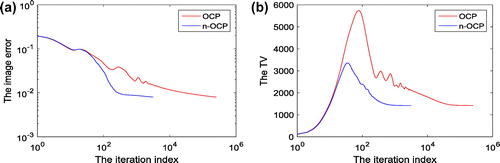
Figure 11. The iteration behaviours of image-error (a) and TV (b) during the whole convergence process via noisy projection data.

From Figure 9, it maybe seen that the reconstructed image by OCP at iteration 1000 has obvious noise compared to that by n-OCP, which is almost the same with the truth-image as per the visual evaluation. Observing the iteration behaviours of the two algorithms during iteration 1–1000 from Figure 10, we may see that the convergence speed of n-OCP is much faster than that of OCP. At iteration 1000, the image-error has dropped to about 8.7 × 10⁻³ for n-OCP while OCP may just reach 2.1 × 10⁻². At iteration 1000, the TV of n-OCP is 1431 which is close to the truth-TV, 1460.5, while the TV of OCP is 2303, which is far away from the truth.

From Figure 11(a), it is seen that n-OCP is much faster than OCP. To achieve the defined convergence condition that $\text{RMSE}\le 8\times {10}^{-3}$, n-OCP needs 3123 iterations while OCP needs 253,628 iterations. The same conclusion maybe drawn by analysis of the TV trends of the two algorithms (see Figure 11(b)).

In conclusion, n-OCP may speed-up the convergence process for $\frac{253,628}{3123}\approx 81$ times in terms of the imaging case here. The improved algorithm-parameters setting method may improve the convergence rate.

4.3.2. Hard acceleration effect

The reconstruction in each iteration maybe speeded up for $\frac{41}{0.12}\approx 340$ times, which is the same as the acceleration factor of the noise-free case shown in Section 4.2.

4.3.3. Integrated acceleration effect

In the case, the soft acceleration factor is 81 and the hard acceleration factor is 340, so the integrated acceleration factor is 81 × 340 = 27,540, i.e. the reconstruction speed achieving the designed solution of GPU-based n-OCP is 27,540 times faster than that of CPU-based OCP.

5. Discussions

In the work, we design an integrated acceleration approach for the OCP algorithm for solving the constrained, TV minimization programme in CT reconstruction. The OCP algorithm is too slow to be practical for the real-data reconstruction whether for industrial or for medical applications. The PCP algorithm has faster convergence speed, but its algorithm parameters are vectors rather than scalars, which may make the derivation of the proximal operator complex. So it is valuable to design a faster OCP algorithm whose parameters are scalars. Motivated by the physical meaning of the parameters of PCP, we proposed a new OCP algorithm, named n-OCP, which has much faster convergence rate than OCP. For the imaging cases in the work, n-OCP may speed-up the convergence process for 89, 9 and 81 times, respectively. However, the whole reconstruction for n-OCP is still slow for the projection and backprojection operations in each iteration are time-consuming. Based on the fact that the pixel-driven projection and backprojection is pixel-operation-parallel, we design two GPU-based parallel computing functions for implementing projection and backprojection. For the three cases, each iteration maybe speeded up for 120, 340 and 340 times by use of GPU, respectively. Totally, the integrated acceleration factor for the OCP algorithm may arrive at about 10,000, 3060 and 27,540 times, respectively.

In fact, the acceleration factor achieved by GPU maybe higher if the Thread structure maybe optimally designed. For the reconstruction of the high-resolution image of size 256 × 256, the acceleration factor goes up to 340 times, whereas the acceleration factor is just 120 times for reconstruction of the low-resolution image of size 64 × 64. The reason is that SM will be fully and optimally used for the 256 × 256-image reconstruction, i.e. 2048 Threads will be loaded into SM, however SM may not be used optimally for the 64 × 64-image reconstruction for only 1024 Threads maybe loaded into SM, theoretically losing half efficiency.

Though it is impossible to quantitatively figure out the total acceleration factor because of the non-linear acceleration of GPU and the different performances for different GPUs, we may conclude that the GPU-based n-OCP algorithm may achieve faster convergence and high-speed reconstruction in each iteration. The integrated acceleration may promote the application of the CP-based algorithms in image reconstructions.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Shaanxi Provincial Natural Science Foundation of China [grant number 2016JM8034]; the Natural Science Foundation of China [grant number 61501310]; Shanxi Provincial Natural Science Foundation of China [grant number 201601D011041].