An inverse problem for Sturm–Liouville operators with nodal data on arbitrarily-half intervals

Abstract

Inverse nodal problems for the Sturm–Liouville operator are to reconstruct this operator from the given nodal points(zeros) of its eigenfunctions. In this paper, the potential $q(x)$ up to its mean value on the whole interval is uniquely determined by two adjacent twin-dense nodal subsets on arbitrarily-half subintervals corresponding to eigenvalues with various boundary conditions and an example on numerical solutions for reconstructing $q(x)$ from a nodal subset on $[0,1]$ is presented.

Keywords:

• Inverse nodal problem
• Sturm–Liouville operator
• potential function
• twin-dense nodal subset
• arbitrarily-half interval

2010 Mathematics Subject Classifications:

• 34A55
• 34B24
• 47E05

1. Introduction

Consider an inverse nodal problem of Sturm–Liouville operators $L_{\xi }:=L(q,h,H_{\xi })$, and denote (1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) together with boundary conditions (2) $\begin{array}{rl}& U_0(u):=u^{\prime }(0,\lambda )-hu(0,\lambda )=0,\end{array}$(2) (3) $\begin{array}{rl}& V_{\xi }(u):=u^{\prime }(1,\lambda )+H_{\xi }u(1,\lambda )=0,\end{array}$(3) for $\xi =0,1,$ where $h,H_0,H_1\in \mathbb{R}$, $H_0\ne H_1$, $q(x)$ is a real-valued and integrable function on $[0,1]$. The inverse nodal problem for the Sturm–Liouville operator, first posed by McLaughlin [1], is to reconstruct this operator from the given nodal points (zeros) of its eigenfunctions. Subsequently, the inverse nodal problem has been widely studied by many scholars. There are many results on inverse nodal problems in the available literature by using the theory of differential operator (e.g. see [2–11]).

In addition, the work related to the inverse nodal problems for the Sturm–Liouville operator is involved in nonlinear differential equation [12,13] and in numerical solution of differential equation[14,15]. Yang [16] presented an interesting theorem for (1(1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) )-(3(3) $\begin{array}{rl}& V_{\xi }(u):=u^{\prime }(1,\lambda )+H_{\xi }u(1,\lambda )=0,\end{array}$(3) ) in the case of $\xi =0,$ and showed that the s-dense nodal subset on the interval $[0,b]$ with $1/2<b\le 1$ is sufficient to determine the potential $q(x)$ up to its mean value and coefficients $h,H_0$ of boundary conditions by the Gesztesy-Simon theorem [17]. For the results on the theory concerning densities of zeros of entire functions, the readers may refer to the references [17–19]. Keskin et al. [20,21] studied the inverse nodal problems for Dirac type integro-differential operator and obtained a lot of helpful and interesting results. Later on, the Yang's result was improved by many authors (see [22–25]). Yang [24] gave a counterexample to illustrate that there exists two different potentials on the interval $(1-{\epsilon }_0/2,1+{\epsilon }_0/2),0<{\epsilon }_0<1$ with the assumption that two Sturm–Liouville operators have the same spectrum and same nodal points on arbitrary subinterval $[0,1-{\epsilon }_0/2]\cup [1+{\epsilon }_0/2,1]$. That is to say that in general the twin-dense nodal subset on the arbitrary interval $[a,b]$ which does not contain the midpoint $\frac{1}{2}$ is not sufficient to recover the potential $q(x)$ up to its mean value on $[0,1]$. In order to determine the uniqueness of the potential $q(x)$, one needs the nodal subset on subinterval of the right(or left) half domain together with some additional information.

Recently, Guo and Wei [25] studied inverse nodal problems for the Sturm–Liouville problems defined on interval $[0,1]$ with separated boundary conditions, and obtained some interesting results. It is worth mentioning that Theorem 2.2 in [25] not only shows us that the potential $q(x)$ can be uniquely determined by a twin dense subset of the nodal set on $(a_1,a_2)$ with $1/2\in (a_1,a_2)$, but also the length $a_2-a_1$ of subinterval $(a_2,a_1)$ can be arbitrarily small. Meanwhile, we also realize that there are probably too much conditions in Theorem 2.6 which is treated to recover the potential on [0,1] in the case of $1/2\notin [a_1,a_2]$. More precisely, it may be sufficient that only one pair of nodal point has the same derivative, instead of each of nodal points with the same derivative. In view of this fact, we have the motivation to improve Theorem 2.6 in [25].

The aim of this paper is to solved the inverse nodal problem for Sturm–Liouville problems on interval $[0,1]$ with some boundary conditions. Based on the Weyl m-function, we reconstruct the potential $q(x)$ of (1(1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) ) from given twin-dense nodal subsets on any subinterval $[a,b]$ of the right half domain, i.e. $\frac{1}{2}<a<b\le 1$, and prove that the potential $q(x)$ up to its mean value on the whole interval can be reconstructed by two adjacent twin-dense nodal subsets on any subinterval $[a,b]$ of the right half domain corresponding to eigenvalues with various boundary conditions. Actually, the interval $[a,b]$ could be an arbitrary subinterval of $[0,1]$ and the interval length b−a can be arbitrarily small. We also present an example on numerical solutions for reconstructing the coefficients from a nodal subset on $[0,1]$.

2. Preliminaries

Let $S(x,\lambda ),C(x,\lambda ),u_{-}(x,\lambda )$ and $u_{+,\xi }(x,\lambda )$ be solutions of Equation (1(1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) ) with the initial conditions: $\begin{array}{rl}& S(0,\lambda )=0,S^{\prime }(0,\lambda )=1,C(0,\lambda )=1,C^{\prime }(0,\lambda )=0,\\ & u_{-}(0,\lambda )=1,u_{-}^{\prime }(0,\lambda )=h,u_{+,\xi }(1,\lambda )=1,u_{+,\xi }^{\prime }(1,\lambda )=-H_{\xi }\end{array}$ for $\xi =0,1.$ Clearly, $U_0(u_{-})=V_{\xi }(u_{+,\xi })=0$. Denote $\lambda ={\rho }^2$ and $\tau =|\mathrm{Im}\rho |$. For $|\rho |\to \mathrm{\infty }$, the following asymptotic formulae (4) $\begin{array}{rl}& u_{-}(x,\lambda )=\cos \rho x+(h+\frac{1}{2}{\int }_0^{x}q(t)\mathrm{d}t)\frac{\sin \rho x}{\rho }+o\left(\frac{{\mathrm{e}}^{\tau x}}{\rho }\right),\end{array}$(4) (5) $\begin{array}{rl}& u_{-}^{\prime }(x,\lambda )=-\rho \sin \rho x+O({\mathrm{e}}^{\tau x}),\end{array}$(5) (6) $\begin{array}{rl}& u_{+,\xi }(x,\lambda )=\cos \rho (1-x)+(H_{\xi }+\frac{1}{2}{\int }_x^{1}q(t)\mathrm{d}t)\frac{\sin \rho (1-x)}{\rho }+o\left(\frac{{\mathrm{e}}^{\tau (1-x)}}{\rho }\right),\end{array}$(6) (7) $\begin{array}{rl}& u_{+,\xi }^{\prime }(x,\lambda )=\rho \sin \rho (1-x)+O({\mathrm{e}}^{\tau (1-x)})\end{array}$(7) hold uniformly with respect to $x\in [0,1]$ (see [26]). The following formula is called the Green's formula ${\int }_0^1(yl(z)-zl(y))\mathrm{d}x=⟨y,z⟩(1)-⟨y,z⟩(0),$ where $⟨y,z⟩(x):=y(x)z^{\prime }(x)-y^{\prime }(x)z(x)$ is the Wronskian of y and z. The characteristic function of $L_{\xi }$ is ${\mathrm{\Delta }}_{\xi }(\lambda ):=⟨u_{+,\xi },u_{-}⟩(x,\lambda ).$ Obviously, ${\mathrm{\Delta }}_{\xi }(\lambda )=V_{\xi }(u_{-})=-U_0(u_{+,\xi })=-\rho \sin \rho +O({\mathrm{e}}^{\tau }).$ Let ${\sigma }_{\xi }(L_{\xi }):=\{{\lambda }_{n\xi }{\}}_{n=0}^{\mathrm{\infty }}$ be the set of all eigenvalues of $L_{\xi }$. Then all zeros ${\lambda }_{n\xi }$ of ${\mathrm{\Delta }}_{\xi }(\lambda )$ are real and simple, and (8) ${\rho }_{n\xi }:=\sqrt{{\lambda }_{n\xi }}=n\pi +\frac{{\omega }_{\xi }}{n\pi }+o\left(\frac{1}{n}\right)\mathrm{as}n\to \mathrm{\infty }$(8) for $\xi =0,1,$ where ${\omega }_{\xi }=2h+2H_{\xi }+{\int }_0^{1}q(t)\mathrm{d}t$. Since both $u_{-}(x,{\lambda }_{n\xi })$ and $u_{+,\xi }(x,{\lambda }_{n\xi })$ are the eigenfunction corresponding to the eigenvalue ${\lambda }_{n\xi }$, there exists a constant $\beta ({\lambda }_{n\xi })\ne 0$ such that (9) $u_{+,\xi }(x,{\lambda }_{n\xi })=\beta ({\lambda }_{n\xi })u_{-}(x,{\lambda }_{n\xi })\mathrm{for}\mathrm{all}x\in [0,1],\xi =0,1.$(9) Define the Weyl m-functions as follow, $m_{+,\xi }(x,\lambda )=\frac{u_{+,\xi }^{\prime }(x,\lambda )}{u_{+,\xi }(x,\lambda )}\mathrm{and}{m}_{-}(x,\lambda )=-\frac{u_{-}^{\prime }(x,\lambda )}{u_{-}(x,\lambda )}.$ By the results in [27], the following asymptotic formulae (10) $\begin{array}{rl}& m_{+,\xi }(x,\lambda )=i\rho +o(1),\\ & \frac{1}{m_{+,\xi }(x,\lambda )}=-\frac{i}{\rho }+o\left(\frac{1}{{\rho }^2}\right)\end{array}$(10) hold uniformly in $x\in [0,1-\delta ]$, $\delta >0$, as $|\lambda |\to \mathrm{\infty }$ in any sector ${\epsilon }_0<\arg \lambda <\pi -{\epsilon }_0$ for some ${\epsilon }_0>0$, and (11) $\begin{array}{rl}& m_{-,\xi }(x,\lambda )=i\rho +o(1),\\ & \frac{1}{m_{-,\xi }(x,\lambda )}=-\frac{i}{\rho }+o\left(\frac{1}{{\rho }^2}\right)\end{array}$(11) uniformly in $x\in [\delta ,1]$, as $|\lambda |\to \mathrm{\infty }$ in any sector ${\epsilon }_1<\arg \lambda <\pi -{\epsilon }_1$ for some ${\epsilon }_1>0$.

Since the potential can not be uniquely determined by the twin-dense nodal subset on $[a,b]$ without midpoint corresponding to partial eigenvalues of $\{{\lambda }_{n0}\}$ and condition (13(13) $\mathrm{♯}\{n_k\in S_{\xi }:n_k\le n\}\ge 2{\alpha }_{\xi }n+1-3{\alpha }_{\xi },\xi =0,1$(13) ) (see [24,25,28], we still need some other nodal information corresponding to partial eigenvalues of $\{{\lambda }_{n1}\}$. Let $u_{-}(x,{\lambda }_{n\xi })$ be the eigenfunction corresponding to the n-th eigenvalue ${\lambda }_{n\xi }$ of $L_{\xi }$ and $x_{n\xi }^j$ be the nodal points of the eigenfunction $u_{-}(x,{\lambda }_{n\xi })$, where $0<x_{n\xi }^1<x_{n\xi }^2<\cdots <x_{n\xi }^j<\cdots <x_{n\xi }^n<1,n\ge 1$. Let $X_{\xi }:=\{x_{n\xi }^j\}$ be the set of nodal points of $L_{\xi }$. Then we have (see [29]) (12) $x_{n\xi }^j={\beta }_{n\xi }^j+\frac{1}{2(n\pi {)}^2}(2h+{\int }_0^{{\beta }_{n\xi }^j}q(t)\mathrm{d}t)-\frac{2{\omega }_{\xi }{\beta }_{n\xi }^j}{2(n\pi {)}^2}+o\left(\frac{1}{n^2}\right),$(12) where ${\beta }_{n\xi }^j=\frac{j-\frac{1}{2}}{n}.$ Write ${\mathbb{N}}_0=\mathbb{N}\cup \{0\}$, ${\mathbb{N}}_2=\mathbb{N}\mathrm{\setminus }\{1\}$, and $S_{\xi }:=\{n_{k,\xi }\in {\mathbb{N}}_2:n_{k,\xi }<n_{k+1,\xi },k\in \mathbb{N}\}$ for $\xi =0$ or 1. Denote $W_{S_{\xi }}([a,b]):=\{x_{n_k,\xi }^j:n_{k,\xi }\in S_{\xi }\}\bigcap [a,b]$ twin-dense nodal subset (see [13,22]). The following result on the Weyl m-function follows from [27].

Lemma 2.1

[27]

Let $m_{+,\xi }(b_0,\lambda )$ with $b_0\in [0,1)$ $(\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{p}\mathbf{.},m_{-}(a_0,\lambda )$ with $a_0\in (0,1])$ be the Weyl m-function. Then $m_{+,\xi }(b_0,\lambda )$ $(\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{p}\mathbf{.},m_{-}(a_0,\lambda ))$ uniquely determines the coefficient $H_{\xi }(\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{p}\mathbf{.},h)$ of the boundary condition as well as $q(x)$ on the interval $[b_0,1](\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{p}\mathbf{.},[0,a_0])$.

To prove our main results, we need the following result in [17]:

Lemma 2.2

$([17,PropositionB.6])$ Let $f(z)$ be an entire function such that

1. $\underset{|z|=R_k}{sup}|f(z)|\le C_1\exp (C_2{R}_k^{\alpha })$ for some $0<\alpha <1,$ some sequence $R_k\to \mathrm{\infty }$ as $k\to \mathrm{\infty }$ and $C_1,C_2>0$.

2. $\underset{|x|\to \mathrm{\infty }}{lim}|f(ix)|=0,x\in \mathbb{R}$.

Then $f\equiv 0.$

3. Main results and proofs

We consider boundary value problems $L_{\xi }$ and ${\tilde{L}}_{\xi }=L_{\xi }(\tilde{q},\tilde{h},{\tilde{H}}_{\xi })$, and suppose here and in the sequel that they have the same form except for different coefficients. If a certain symbol γ denotes an object related to $L_{\xi }$, then the corresponding symbol $\tilde{\gamma }$ with tilde denotes the analogous object related to ${\tilde{L}}_{\xi }$, and $\hat{\gamma }=\gamma -\tilde{\gamma }$.

The so-called $W_{S_{\xi }}([a,b])={\tilde{W}}_{{\tilde{S}}_{\xi }}([a,b])$ means that for any $x_{n_{k,\xi }}^{j_k}\in W_{S_{\xi }}([a,b])$, $x_{n_{k,\xi }}^{j_k}={\tilde{x}}_{{\tilde{n}}_{k,\xi }}^{{\tilde{j}}_k}\mathrm{and}{x}_{n_{k,\xi }}^{j_k+1}={\tilde{x}}_{{\tilde{n}}_{k,\xi }}^{{\tilde{j}}_k+1},\mathrm{or}{x}_{n_{k,\xi }}^{j_k}={\tilde{x}}_{{\tilde{n}}_{k,\xi }}^{{\tilde{j}}_k}\mathrm{and}{x}_{n_{k,\xi }}^{j_k-1}={\tilde{x}}_{{\tilde{n}}_{k,\xi }}^{{\tilde{j}}_k-1}$ hold, where $x_{n_{k,\xi }}^{j_k+j}\in W_{S_{\xi }}([a,b])$ and ${\tilde{x}}_{{\tilde{n}}_{k,\xi }}^{{\tilde{j}}_k+j}\in {\tilde{W}}_{{\tilde{S}}_{\xi }}([a,b]).$ Since the twin-dense nodal subset $W_{S_0}([a,c])$ on the right arbitrary interval for any $S_0$ cannot uniquely determine the potential $q(x)$ on the whole interval $[0,1]$ (see [16]), we add another adjacent twin-dense nodal subset $W_{S_1}([c,b])$ corresponding to the eigenvalues in $M_1$ on the right arbitrary interval to sufficiently guarantee the uniqueness of the potential $q(x)$. Thus the uniqueness theorem can be determined by two adjacent twin-dense nodal subsets $W_{S_0}([a,c])$ and $W_{S_1}([c,b])$.

Theorem 3.1

Let $\frac{1}{2}<a<c<b\le 1$. Suppose that $H_0={\tilde{H}}_0$ and $h=\tilde{h},$ $W_{S_0}([a,c])={\tilde{W}}_{{\tilde{S}}_0}([a,c])$ and $W_{S_1}([c,b])={\tilde{W}}_{{\tilde{S}}_1}([c,b])$. If (13) $\mathrm{♯}\{n_k\in S_{\xi }:n_k\le n\}\ge 2{\alpha }_{\xi }n+1-3{\alpha }_{\xi },\xi =0,1$(13) for sufficiently large $n>0,$ where ${\alpha }_1=1-b,$ ${\alpha }_0+{\alpha }_1\ge a,$ then $q(x)-{\int }_0^{1}q(t)\mathrm{d}t\stackrel{a.e.}{=}\tilde{q}(x)-{\int }_0^1\tilde{q}(t)\mathrm{d}ton[0,1],and{H}_1={\tilde{H}}_1.$

Remark 3.1

By symmetry, one can obtain an analogy of Theorem 3.1 for the case $0\le a<b<1/2.$ We omit the details here. Actually, the interval $[a,b]$ could be any subinterval of $[0,1]$ and the interval length b−a can be arbitrarily small.

Substitutng the condition “$H_0={\tilde{H}}_0$ and $h=\tilde{h}$” by “$q(x)-\tilde{q}(x)$ is continuous at x = c” in Theorem 3.1, we obtain

Theorem 3.2

Let $\frac{1}{2}<a<c<b\le 1$. Suppose that $W_{S_0}([a,c])={\tilde{W}}_{{\tilde{S}}_0}([a,c])$ and $W_{S_1}([c,b])={\tilde{W}}_{{\tilde{S}}_1}([c,b])$. If the function $q(x)-\tilde{q}(x)$ is continuous at x = c and (13(13) $\mathrm{♯}\{n_k\in S_{\xi }:n_k\le n\}\ge 2{\alpha }_{\xi }n+1-3{\alpha }_{\xi },\xi =0,1$(13) ) holds for each $\xi =0,1,$ then (14) $q(x)-{\int }_0^{1}q(t)\mathrm{d}t\stackrel{a.e.}{=}\tilde{q}(x)-{\int }_0^1\tilde{q}(t)\mathrm{d}ton[0,1],h=\tilde{h}and{H}_{\xi }={\tilde{H}}_{\xi },\xi =0,1.$(14)

Next we prove our main results.

Proof of Theorem 3.1.

Without loss of generality, we assume ${\alpha }_1\ge {\alpha }_0$. It is easy to prove the formula (15(15) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_0\mathrm{on}[a,c],\end{array}$(15) )–(18(18) $\begin{array}{rl}& n_{k,\xi }={\tilde{n}}_{k,\xi }\mathrm{except}\mathrm{for}\mathrm{a}\mathrm{finite}\mathrm{number}\mathrm{of}{n}_{k,\xi }\in S_{\xi },\xi =0,1.\end{array}$(18) ) from (12(12) $x_{n\xi }^j={\beta }_{n\xi }^j+\frac{1}{2(n\pi {)}^2}(2h+{\int }_0^{{\beta }_{n\xi }^j}q(t)\mathrm{d}t)-\frac{2{\omega }_{\xi }{\beta }_{n\xi }^j}{2(n\pi {)}^2}+o\left(\frac{1}{n^2}\right),$(12) ) (see Lemma 3.1 in [23]) (15) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_0\mathrm{on}[a,c],\end{array}$(15) (16) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_1\mathrm{on}[c,b],\end{array}$(16) (17) $\begin{array}{rl}& {\lambda }_{\xi ,n_{k,\xi }}-{\tilde{\lambda }}_{\xi ,{\tilde{n}}_{k,\xi }}=2{\hat{\omega }}_{\xi }\mathrm{for}\mathrm{all}{n}_{k,\xi }\in S_{\xi },\xi =0,1\end{array}$(17) (18) $\begin{array}{rl}& n_{k,\xi }={\tilde{n}}_{k,\xi }\mathrm{except}\mathrm{for}\mathrm{a}\mathrm{finite}\mathrm{number}\mathrm{of}{n}_{k,\xi }\in S_{\xi },\xi =0,1.\end{array}$(18)

Let ${\tilde{q}}_1(x):=\tilde{q}(x)+2{\hat{\omega }}_1,x\in [0,1],M_{\xi }:=\{{\lambda }_{n_k,\xi }:{\lambda }_{n_k,\xi }\in \sigma (L_{\xi }),n_{k,\xi }\in S_{\xi }\},\xi =0,1.$ Consider the new Sturm–Liouville operator $L_1({\tilde{q}}_1)$ defined by (19) $lu=-u^{″}+{\tilde{q}}_1(x)u=\lambda u,0<x<1,$(19) associated with boundary conditions (2(2) $\begin{array}{rl}& U_0(u):=u^{\prime }(0,\lambda )-hu(0,\lambda )=0,\end{array}$(2) ) and (3(3) $\begin{array}{rl}& V_{\xi }(u):=u^{\prime }(1,\lambda )+H_{\xi }u(1,\lambda )=0,\end{array}$(3) ). Then the new Sturm–Liouville operator $L_1({\tilde{q}}_1)$ has the same eigenvalues ${\lambda }_{n_{k,1}}$ for all $n_{k,1}\in S_1$ as $L_1(q)$ and $q(x)-{\tilde{q}}_1(x)\stackrel{a.e.}{=}0\mathrm{on}[c,b].$ Next we prove Theorem 3.1 by the following two steps.

Step 1. We now shall prove that (20) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[b,1],\mathrm{and}{H}_1={\tilde{H}}_1.$(20) For any $x_{n_k,1}^{j_k}\in W_{S_1}([c,b])$, by Green formula for (1(1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) ) and (19(19) $lu=-u^{″}+{\tilde{q}}_1(x)u=\lambda u,0<x<1,$(19) ) together with $u_{-}(x_{n_k,1}^{j_k},{\lambda }_{n_k,1})=0$ and ${\tilde{u}}_{-}(x_{n_k,1}^{j_k},{\lambda }_{n_k,1})=0$, we can (21) $\begin{array}{rl}& {\int }_{x_{n_k,1}^{j_k}}^b(q(x)-{\tilde{q}}_1(x))u_{-}(x,{\lambda }_{n_k,1}){\tilde{u}}_{-}(x,{\lambda }_{n_k,1})\mathrm{d}x\\ & =⟨u_{-},{\tilde{u}}_{-}⟩(b,{\lambda }_{n_k,1})-⟨u_{-},{\tilde{u}}_{-}⟩(x_{n_k,1}^{j_k},{\lambda }_{n_k,1}),\end{array}$(21) where $⟨u_{-},{\tilde{u}}_{-}⟩(x,\lambda ):=u_{-}(x,\lambda ){\tilde{u}}_{-}^{\prime }(x,\lambda )-u_{-}^{\prime }(x,\lambda ){\tilde{u}}_{-}(x,\lambda ).$ Since $q(x)-{\tilde{q}}_1(x)\stackrel{a.e.}{=}0$ on $[c,b]$, (21(21) $\begin{array}{rl}& {\int }_{x_{n_k,1}^{j_k}}^b(q(x)-{\tilde{q}}_1(x))u_{-}(x,{\lambda }_{n_k,1}){\tilde{u}}_{-}(x,{\lambda }_{n_k,1})\mathrm{d}x\\ & =⟨u_{-},{\tilde{u}}_{-}⟩(b,{\lambda }_{n_k,1})-⟨u_{-},{\tilde{u}}_{-}⟩(x_{n_k,1}^{j_k},{\lambda }_{n_k,1}),\end{array}$(21) ) implies (22) $⟨u_{-},{\tilde{u}}_{-}⟩(b,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(22) By (9(9) $u_{+,\xi }(x,{\lambda }_{n\xi })=\beta ({\lambda }_{n\xi })u_{-}(x,{\lambda }_{n\xi })\mathrm{for}\mathrm{all}x\in [0,1],\xi =0,1.$(9) ) and (22(22) $⟨u_{-},{\tilde{u}}_{-}⟩(b,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(22) ), we obtain (23) $⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(23) By (6(6) $\begin{array}{rl}& u_{+,\xi }(x,\lambda )=\cos \rho (1-x)+(H_{\xi }+\frac{1}{2}{\int }_x^{1}q(t)\mathrm{d}t)\frac{\sin \rho (1-x)}{\rho }+o\left(\frac{{\mathrm{e}}^{\tau (1-x)}}{\rho }\right),\end{array}$(6) ), (7(7) $\begin{array}{rl}& u_{+,\xi }^{\prime }(x,\lambda )=\rho \sin \rho (1-x)+O({\mathrm{e}}^{\tau (1-x)})\end{array}$(7) ) and (10(10) $\begin{array}{rl}& m_{+,\xi }(x,\lambda )=i\rho +o(1),\\ & \frac{1}{m_{+,\xi }(x,\lambda )}=-\frac{i}{\rho }+o\left(\frac{1}{{\rho }^2}\right)\end{array}$(10) ), we have that (24) $\begin{array}{rl}|⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,\lambda )|& =u_{+,1}^{\prime }(b,\lambda ){\tilde{u}}_{+,1}^{\prime }(b,\lambda )(\frac{1}{{\tilde{m}}_{+,1}(b,\lambda )}-\frac{1}{m_{+,1}(b,\lambda )})\\ & =o({\mathrm{e}}^{2(1-b)\tau }).\end{array}$(24) as $|\lambda |\to \mathrm{\infty }$ in any sector ${\epsilon }_1<\arg \lambda <\pi -{\epsilon }_1$ for ${\epsilon }_1>0$ and $|⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,\lambda )|=O({\mathrm{e}}^{2(1-b)\tau })$ for all $\lambda \in \mathbb{C}$. Define the function $K_1(\lambda )$ by $K_1(\lambda ):=\frac{⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,\lambda )}{G_1(\rho )},$ where $G_{\xi }(\lambda ):=\prod _{{\lambda }_{n_k,\xi }\in M_{\xi }}(1-\frac{\lambda }{{\lambda }_{n_k,\xi }}),\xi =0,1.$ We may substitute $1-(\lambda /{\lambda }_{n_k,\xi })$ by λ in case ${\lambda }_{n_k,\xi }=0$. Let $N_{{\sigma }_{\xi }}(t):=\mathrm{♯}\{{\lambda }_{n\xi }:{\lambda }_{n\xi }\le t,{\lambda }_{n\xi }\in {\sigma }_{\xi }(L_{\xi })\}\mathrm{and}{N}_{M_{\xi }}(t):=\mathrm{♯}\{{\lambda }_{n\xi }:{\lambda }_{n\xi }\le t,{\lambda }_{n\xi }\in M_{\xi }\}.$ By (13(13) $\mathrm{♯}\{n_k\in S_{\xi }:n_k\le n\}\ge 2{\alpha }_{\xi }n+1-3{\alpha }_{\xi },\xi =0,1$(13) ), we can conclude that (25) $N_{M_{\xi }}(t)\ge 2{\alpha }_{\xi }{N}_{{\sigma }_{\xi }}(t)-{\alpha }_{\xi }$(25) for sufficiently large $t\in {\mathbb{R}}^{+}$. By the same arguments in the proof of Proposition B.5 in [17], there exists some sequence $R_{1k}\to \mathrm{\infty }$ as $k\to \mathrm{\infty }$ such that (26) $\underset{|\lambda |=R_{1k}}{sup}|K_1(\lambda )|\le C_{11}\exp (C_{12}{R}_{1k}^{r_1})$(26) for some $0\le r_1<1$, $C_{11},C_{12}>0$. Since ${\mathrm{\Delta }}_1(\lambda )$ is an entire function in λ of order $\frac{1}{2}$, there exists a positive constant C such that $N_{M_1}(t)\le N_{{\sigma }_1}(t)\le C{t}^{1/2}.$ Then $N_{G_1}(t_0)=N_{{\sigma }_1}(t_0)=0$ for some real number $t_0$. For a fixed $y\in \mathbb{R}$ with sufficiently large $|y|$, we have (27) $\begin{array}{rl}\ln |G_1(\mathrm{i}y)|& =\frac{1}{2}\ln G_1(\mathrm{i}y)\overline{G_1(\mathrm{i}y)}\\ & =\frac{1}{2}\sum _{{\lambda }_{n_k,1}\in M_1}\ln (1+\frac{y^2}{({\lambda }_{n_k,1}{)}^2})=\frac{1}{2}{\int }_{t_0}^{\mathrm{\infty }}\ln (1+\frac{y^2}{t^2})\mathrm{d}{N}_{G_1}(t)\\ & =\frac{1}{2}\ln (1+\frac{y^2}{t^2})N_{G_1}(t){|}_{t_0}^{\mathrm{\infty }}-\frac{1}{2}{\int }_{t_0}^{\mathrm{\infty }}{N}_{G_1}(t)\mathrm{d}[\ln (1+\frac{y^2}{t^2})].\end{array}$(27) Notice that $\ln (1+\frac{y^2}{t^2})=O\left(\frac{1}{t^2}\right)$ for sufficiently large t, we have that $\underset{t\to \mathrm{\infty }}{lim}\ln (1+\frac{y^2}{t^2})N_{G_1}(t)=0\mathrm{and}\underset{t\to \mathrm{\infty }}{lim}\ln (1+\frac{y^2}{t^2})N_{{\sigma }_1}(t)=0.$ Therefore, it follows from (25(25) $N_{M_{\xi }}(t)\ge 2{\alpha }_{\xi }{N}_{{\sigma }_{\xi }}(t)-{\alpha }_{\xi }$(25) ) that there exists a constant $t_1\ge t_0$ and $C_1$ such that $\begin{array}{rl}& N_{G_1}(t)\ge 2{\alpha }_1{N}_{{\sigma }_1}(t)-{\alpha }_1,t\ge t_1,\\ & N_{G_1}(t)\ge 2{\alpha }_1{N}_{{\sigma }_1}(t)-C_1,t<t_1.\end{array}$ By (27(27) $\begin{array}{rl}\ln |G_1(\mathrm{i}y)|& =\frac{1}{2}\ln G_1(\mathrm{i}y)\overline{G_1(\mathrm{i}y)}\\ & =\frac{1}{2}\sum _{{\lambda }_{n_k,1}\in M_1}\ln (1+\frac{y^2}{({\lambda }_{n_k,1}{)}^2})=\frac{1}{2}{\int }_{t_0}^{\mathrm{\infty }}\ln (1+\frac{y^2}{t^2})\mathrm{d}{N}_{G_1}(t)\\ & =\frac{1}{2}\ln (1+\frac{y^2}{t^2})N_{G_1}(t){|}_{t_0}^{\mathrm{\infty }}-\frac{1}{2}{\int }_{t_0}^{\mathrm{\infty }}{N}_{G_1}(t)\mathrm{d}[\ln (1+\frac{y^2}{t^2})].\end{array}$(27) ) together with the following relation $\frac{y^2}{t^3+t{y}^2}=-\frac{\mathrm{d}}{\mathrm{d}t}(\frac{1}{2}\ln (1+\frac{y^2}{t^2})),$ we obtain (28) $\begin{array}{rl}\ln |G_1(\mathrm{i}y)|& ={\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t\\ & ={\int }_{t_0}^{t_1}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t+{\int }_{t_1}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t\\ & \ge 2{\alpha }_1{\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{{\sigma }_1}(t)\mathrm{d}t-{\alpha }_1{\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}\mathrm{d}t+({\alpha }_1-C_1){\int }_{t_0}^{t_1}\frac{y^2}{{}^{t^3+t{y}^2}}\mathrm{d}t\\ & =2{\alpha }_1\ln |{\mathrm{\Delta }}_1(\mathrm{i}y)|-{\alpha }_1\ln (1+y^2)+\frac{{\alpha }_1-C_1}{2}\ln \frac{t_0^2(t_1^2+y^2)}{t_1^2(t_0^2+y^2)}.\end{array}$(28) Thus, by (28(28) $\begin{array}{rl}\ln |G_1(\mathrm{i}y)|& ={\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t\\ & ={\int }_{t_0}^{t_1}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t+{\int }_{t_1}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{G_1}(t)\mathrm{d}t\\ & \ge 2{\alpha }_1{\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}{N}_{{\sigma }_1}(t)\mathrm{d}t-{\alpha }_1{\int }_{t_0}^{\mathrm{\infty }}\frac{y^2}{{}^{t^3+t{y}^2}}\mathrm{d}t+({\alpha }_1-C_1){\int }_{t_0}^{t_1}\frac{y^2}{{}^{t^3+t{y}^2}}\mathrm{d}t\\ & =2{\alpha }_1\ln |{\mathrm{\Delta }}_1(\mathrm{i}y)|-{\alpha }_1\ln (1+y^2)+\frac{{\alpha }_1-C_1}{2}\ln \frac{t_0^2(t_1^2+y^2)}{t_1^2(t_0^2+y^2)}.\end{array}$(28) ), (29) $|G_1(\mathrm{i}y)|\ge c_{11}|{\mathrm{\Delta }}_1(iy){|}^{2{\alpha }_1}|y{|}^{2{\alpha }_1}$(29) for sufficiently large $|y|$, where $c_{11}$ is constant. By (24(24) $\begin{array}{rl}|⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,\lambda )|& =u_{+,1}^{\prime }(b,\lambda ){\tilde{u}}_{+,1}^{\prime }(b,\lambda )(\frac{1}{{\tilde{m}}_{+,1}(b,\lambda )}-\frac{1}{m_{+,1}(b,\lambda )})\\ & =o({\mathrm{e}}^{2(1-b)\tau }).\end{array}$(24) ) and (29(29) $|G_1(\mathrm{i}y)|\ge c_{11}|{\mathrm{\Delta }}_1(iy){|}^{2{\alpha }_1}|y{|}^{2{\alpha }_1}$(29) ), (30) $|K_1(iy)|=o({\mathrm{e}}^{2(1-b-{\alpha }_1)|y|})=o(1)$(30) as $y\to \mathrm{\infty }$. By Lemma 2.2 together with (26(26) $\underset{|\lambda |=R_{1k}}{sup}|K_1(\lambda )|\le C_{11}\exp (C_{12}{R}_{1k}^{r_1})$(26) ) and (30(30) $|K_1(iy)|=o({\mathrm{e}}^{2(1-b-{\alpha }_1)|y|})=o(1)$(30) ), we have $K_1(\lambda )\equiv 0,\lambda \in \mathbb{C}.$ Then $⟨u_{+,1},{\tilde{u}}_{+,1}⟩(b,\lambda )=0,\mathrm{\forall }\lambda \in \mathbb{C}.$ Consequently (31) $m_{+,1}(b,\lambda )={\tilde{m}}_{+,1}(b,\lambda ),\mathrm{\forall }\lambda \in \mathbb{C}.$(31) By Lemma 2.1 and (31(31) $m_{+,1}(b,\lambda )={\tilde{m}}_{+,1}(b,\lambda ),\mathrm{\forall }\lambda \in \mathbb{C}.$(31) ), (20(20) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[b,1],\mathrm{and}{H}_1={\tilde{H}}_1.$(20) ) is valid.

Step 2. We shall prove that (32) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[0,a].$(32) Since $h=\tilde{h}$, $H_0={\tilde{H}}_0$ and $H_1={\tilde{H}}_1$, by (8(8) ${\rho }_{n\xi }:=\sqrt{{\lambda }_{n\xi }}=n\pi +\frac{{\omega }_{\xi }}{n\pi }+o\left(\frac{1}{n}\right)\mathrm{as}n\to \mathrm{\infty }$(8) ) we have that (33) ${\hat{\omega }}_0={\hat{\omega }}_1.$(33) From (15(15) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_0\mathrm{on}[a,c],\end{array}$(15) ), (16(16) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_1\mathrm{on}[c,b],\end{array}$(16) ), (20(20) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[b,1],\mathrm{and}{H}_1={\tilde{H}}_1.$(20) ) and (33(33) ${\hat{\omega }}_0={\hat{\omega }}_1.$(33) ), it follows that (34) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[a,1].$(34) and the new Sturm–Liouville operator $L_0({\tilde{q}}_1)$ has the same eigenvalues ${\lambda }_{n_k,0}$ for all $n_{k,0}\in S_0$ as $L_0(q)$. Similarly we can prove (35) $⟨u_{-},{\tilde{u}}_{-}⟩(a,{\lambda }_{n_k,0})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,0}\in M_0.$(35) By Green formula for (1(1) $lu:=-u^{″}+q(x)u=\lambda u,x\in (0,1)$(1) ) and (19(19) $lu=-u^{″}+{\tilde{q}}_1(x)u=\lambda u,0<x<1,$(19) ) on $[a,c]$ together with (22(22) $⟨u_{-},{\tilde{u}}_{-}⟩(b,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(22) ) and $q(x)-{\tilde{q}}_1(x)\stackrel{a.e.}{=}0$ on $[a,c]$, we obtain (36) $⟨u_{-},{\tilde{u}}_{-}⟩(a,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(36) By (4(4) $\begin{array}{rl}& u_{-}(x,\lambda )=\cos \rho x+(h+\frac{1}{2}{\int }_0^{x}q(t)\mathrm{d}t)\frac{\sin \rho x}{\rho }+o\left(\frac{{\mathrm{e}}^{\tau x}}{\rho }\right),\end{array}$(4) ), (5(5) $\begin{array}{rl}& u_{-}^{\prime }(x,\lambda )=-\rho \sin \rho x+O({\mathrm{e}}^{\tau x}),\end{array}$(5) ) and (11(11) $\begin{array}{rl}& m_{-,\xi }(x,\lambda )=i\rho +o(1),\\ & \frac{1}{m_{-,\xi }(x,\lambda )}=-\frac{i}{\rho }+o\left(\frac{1}{{\rho }^2}\right)\end{array}$(11) ), (37) $\begin{array}{rl}|⟨u_{-},{\tilde{u}}_{-}⟩(a,\lambda )|& =u_{-}^{\prime }(a,\lambda ){\tilde{u}}_{-}^{\prime }(a,\lambda )(\frac{1}{{\tilde{m}}_{-}(a,\lambda )}-\frac{1}{m_{-}(a,\lambda )})\\ & =o({\mathrm{e}}^{2a\tau })\end{array}$(37) as $|\lambda |\to \mathrm{\infty }$ in any sector ${\epsilon }_1<\arg \lambda <\pi -{\epsilon }_1$ for ${\epsilon }_1>0$, and $|⟨u_{-},{\tilde{u}}_{-}⟩(a,\lambda )|=O({\mathrm{e}}^{2a\tau })$ for all $\lambda \in \mathbb{C}$. Denote $K_2(\lambda ):=\frac{⟨u_{-},{\tilde{u}}_{-}⟩(a,\lambda )}{G_0(\lambda )G_1(\lambda )}.$ We notice that all eigenvalues of $L_0$ and $L_1$ are simple and distinct. Therefore, by (35(35) $⟨u_{-},{\tilde{u}}_{-}⟩(a,{\lambda }_{n_k,0})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,0}\in M_0.$(35) ) and (36(36) $⟨u_{-},{\tilde{u}}_{-}⟩(a,{\lambda }_{n_k,1})=0\mathrm{for}\mathrm{all}{\lambda }_{n_k,1}\in M_1.$(36) ), it is clear that $K_2(\lambda )$ is an entire function in λ. By the same arguments as in the proof of (26(26) $\underset{|\lambda |=R_{1k}}{sup}|K_1(\lambda )|\le C_{11}\exp (C_{12}{R}_{1k}^{r_1})$(26) ) and (29(29) $|G_1(\mathrm{i}y)|\ge c_{11}|{\mathrm{\Delta }}_1(iy){|}^{2{\alpha }_1}|y{|}^{2{\alpha }_1}$(29) ), there exists some sequence $R_{2k}\to \mathrm{\infty }$ as $k\to \mathrm{\infty }$ such that (38) $\underset{|\lambda |=R_{2k}}{sup}|K_2(\lambda )|\le C_{21}\exp (C_{22}{R}_{2k}^{r_2})$(38) for some $0\le r_2<1$, $C_{21},C_{22}>0$ and (39) $|G_0(iy)G_1(iy)|\ge c{\mathrm{e}}^{2({\alpha }_0+{\alpha }_1)|y|},$(39) where c is constant. By (37(37) $\begin{array}{rl}|⟨u_{-},{\tilde{u}}_{-}⟩(a,\lambda )|& =u_{-}^{\prime }(a,\lambda ){\tilde{u}}_{-}^{\prime }(a,\lambda )(\frac{1}{{\tilde{m}}_{-}(a,\lambda )}-\frac{1}{m_{-}(a,\lambda )})\\ & =o({\mathrm{e}}^{2a\tau })\end{array}$(37) ) and (39(39) $|G_0(iy)G_1(iy)|\ge c{\mathrm{e}}^{2({\alpha }_0+{\alpha }_1)|y|},$(39) ), we have that (40) $|K_2(iy)|=o({\mathrm{e}}^{2(a-{\alpha }_0-{\alpha }_1)|y|})$(40) as $|y|\to \mathrm{\infty }$. By Lemma 2.2 together with (38(38) $\underset{|\lambda |=R_{2k}}{sup}|K_2(\lambda )|\le C_{21}\exp (C_{22}{R}_{2k}^{r_2})$(38) ), (40(40) $|K_2(iy)|=o({\mathrm{e}}^{2(a-{\alpha }_0-{\alpha }_1)|y|})$(40) ) and ${\alpha }_0+{\alpha }_1\ge a$, we obtain $K_2(\lambda )\equiv 0,\lambda \in \mathbb{C}.$ Then $⟨u_{-},{\tilde{u}}_{-}⟩(a,\lambda )=0,\mathrm{\forall }\lambda \in \mathbb{C}.$ Consequently, (41) $m_{-}(a,\lambda )={\tilde{m}}_{-}(a,\lambda ),\mathrm{\forall }\lambda \in \mathbb{C}.$(41) Hence, (32(32) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[0,a].$(32) ) is valid by Lemma 2.1 and (41(41) $m_{-}(a,\lambda )={\tilde{m}}_{-}(a,\lambda ),\mathrm{\forall }\lambda \in \mathbb{C}.$(41) ). It follows from (32(32) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[0,a].$(32) ) and (34(34) $q(x)\stackrel{a.e.}{=}{\tilde{q}}_1(x)\mathrm{on}[a,1].$(34) ) that $q(x)-{\int }_0^{1}q(t)\mathrm{d}t\stackrel{a.e.}{=}\tilde{q}(x)-{\int }_0^1\tilde{q}(t)\mathrm{d}t\mathrm{on}[0,1],\mathrm{and}{H}_1={\tilde{H}}_1.$ Thus, the proof of Theorem 3.1 is completed.

Proof of Theorem 3.2.

By (15(15) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_0\mathrm{on}[a,c],\end{array}$(15) ) and (16(16) $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_1\mathrm{on}[c,b],\end{array}$(16) ) and noticing that the function $q(x)-\tilde{q}(x)$ is continuous at x = c, ${\hat{\omega }}_0={\hat{\omega }}_1.$ This implies $\begin{array}{rl}& q(x)-\tilde{q}(x)\stackrel{a.e.}{=}2{\hat{\omega }}_1\mathrm{on}[a,b],\\ & {\lambda }_{n_k,\xi }-{\tilde{\lambda }}_{{\tilde{n}}_k,\xi }=2{\hat{\omega }}_1\mathrm{for}\mathrm{all}{n}_{k,\xi }\in S_{\xi },\xi =0,1.\end{array}$ By the same arguments as in proof of Theorem 3.1, we have (14(14) $q(x)-{\int }_0^{1}q(t)\mathrm{d}t\stackrel{a.e.}{=}\tilde{q}(x)-{\int }_0^1\tilde{q}(t)\mathrm{d}ton[0,1],h=\tilde{h}and{H}_{\xi }={\tilde{H}}_{\xi },\xi =0,1.$(14) ).

4. An example

In this section we study a numerical solution of the inverse nodal problem for the Sturm–Liouville operator $L_0(q;h;H_0)$ by an example. 

Example 4.1

Let $W_{S_0}([0,1])=\{x_{n_{k,0}}^j\}$ be the nearest neighbour dense nodal subset of the Sturm–Liouville operator $L_0(q;h;H_0)$ such that (42) $x_{n_{k,0}}^j={\beta }_{n_{k,0}}^j+\frac{1}{2(\pi n_k{)}^2}(2+\frac{1-\cos (\pi {\beta }_{n_{k,0}}^j)}{\pi }-2(2+\frac{1}{\pi }){\beta }_{n_{k,0}}^j)+o\left(\frac{1}{n_k^2}\right).$(42) Denote $Q(x)={\int }_0^{x}q(t)\mathrm{d}x$ and let $Q(1)={\int }_0^{1}q(t)\mathrm{d}x=2/\pi$, Then $q(x)$ on $[0,1]$ can be reconstructed.

We may find $q(x)$ by the following steps.

Step 1. Choose $x_{n_{k,0}}^j\in W_{S_0}([0,1])$ such that $\underset{k\to \mathrm{\infty }}{lim}{x}_{n_{k,0}}^j=x$ for a fixed $x\in [0,1]$, i.e. $\underset{k\to \mathrm{\infty }}{lim}{\beta }_{n_{k,0}}^j=x,$ By (42(42) $x_{n_{k,0}}^j={\beta }_{n_{k,0}}^j+\frac{1}{2(\pi n_k{)}^2}(2+\frac{1-\cos (\pi {\beta }_{n_{k,0}}^j)}{\pi }-2(2+\frac{1}{\pi }){\beta }_{n_{k,0}}^j)+o\left(\frac{1}{n_k^2}\right).$(42) ) and (12(12) $x_{n\xi }^j={\beta }_{n\xi }^j+\frac{1}{2(n\pi {)}^2}(2h+{\int }_0^{{\beta }_{n\xi }^j}q(t)\mathrm{d}t)-\frac{2{\omega }_{\xi }{\beta }_{n\xi }^j}{2(n\pi {)}^2}+o\left(\frac{1}{n^2}\right),$(12) ), we find (43) $\begin{array}{rl}{f}_0(x)& :=\underset{k\to \mathrm{\infty }}{lim}2{\left(n_k\pi \right)}^2(x_{n_{k,0}}^j-{\beta }_{n_{k,0}}^j)\\ & =2h+{\int }_0^{x}q(t)\mathrm{d}t-{\omega }_{0}x\end{array}$(43) (44) $\begin{array}{rl}& =2+\frac{1-\cos (\pi x)}{\pi }-2(2+\frac{1}{\pi })xx\in [0,1]\end{array}$(44) Step 2. Let $x_0=0$ in (44(44) $\begin{array}{rl}& =2+\frac{1-\cos (\pi x)}{\pi }-2(2+\frac{1}{\pi })xx\in [0,1]\end{array}$(44) ), we obtain $f_0(0)=2$. Reconstruct $h=f_0(0)/2=1.$

Step 3. Let x = 1 in (43(43) $\begin{array}{rl}{f}_0(x)& :=\underset{k\to \mathrm{\infty }}{lim}2{\left(n_k\pi \right)}^2(x_{n_{k,0}}^j-{\beta }_{n_{k,0}}^j)\\ & =2h+{\int }_0^{x}q(t)\mathrm{d}t-{\omega }_{0}x\end{array}$(43) ) and (44(44) $\begin{array}{rl}& =2+\frac{1-\cos (\pi x)}{\pi }-2(2+\frac{1}{\pi })xx\in [0,1]\end{array}$(44) ), noticing that ${\omega }_0=2h+2H_0+{\int }_0^{1}q(t)\mathrm{d}t$ and $Q(1)=2/\pi$, we get $H_0=f_0(1)/2=1.$

Step 4. From (43(43) $\begin{array}{rl}{f}_0(x)& :=\underset{k\to \mathrm{\infty }}{lim}2{\left(n_k\pi \right)}^2(x_{n_{k,0}}^j-{\beta }_{n_{k,0}}^j)\\ & =2h+{\int }_0^{x}q(t)\mathrm{d}t-{\omega }_{0}x\end{array}$(43) ) and (44(44) $\begin{array}{rl}& =2+\frac{1-\cos (\pi x)}{\pi }-2(2+\frac{1}{\pi })xx\in [0,1]\end{array}$(44) ) it follows that (45) $q(x)\stackrel{a.e.}{=}\sin (\pi x),x\in [0,1]$(45) which is called the accurate solution of $q(x)$. 

By Example 4.1, we reconstruct the accurate solution $q(x)=\sin (\pi x)$ from the nearest neighbour dense nodal subset $W_{S_0}([0,1])$ with (42(42) $x_{n_{k,0}}^j={\beta }_{n_{k,0}}^j+\frac{1}{2(\pi n_k{)}^2}(2+\frac{1-\cos (\pi {\beta }_{n_{k,0}}^j)}{\pi }-2(2+\frac{1}{\pi }){\beta }_{n_{k,0}}^j)+o\left(\frac{1}{n_k^2}\right).$(42) ) and $Q(1)=2/\pi$. Next we present a numerical solution of the above inverse nodal problem (refer to [30]). We choose a subset of $W_{S_0}([0,1])$ such that $x_{N_0,0}^j$ satisfy (42(42) $x_{n_{k,0}}^j={\beta }_{n_{k,0}}^j+\frac{1}{2(\pi n_k{)}^2}(2+\frac{1-\cos (\pi {\beta }_{n_{k,0}}^j)}{\pi }-2(2+\frac{1}{\pi }){\beta }_{n_{k,0}}^j)+o\left(\frac{1}{n_k^2}\right).$(42) ), where $N_0$ sufficiently large. Let xk = kh, where h>0 is called a step length, $k=1,2,\dots ,[1/h]$. For each $x_k$, we find a number $j(x_k,N_0)$, $1\le j(x_k,N_0)\le N_0$, such that $j(x_k,N_0):=\underset{1\le j\le N_0}{min}\{|x_k-x_{N_0,0}^j|\}.$ The corresponding approximate solution $q_{\mathrm{est}}(x)$ is defined by (46) $q_{\mathrm{est}}(x_k):=\sin \left(\pi x_{N_0,0}^{j(x_k,N_0)}\right)\mathrm{for}\mathrm{all}k=1,2,\dots ,\left[\frac{1}{h}\right].$(46) By (45(45) $q(x)\stackrel{a.e.}{=}\sin (\pi x),x\in [0,1]$(45) ) and (46(46) $q_{\mathrm{est}}(x_k):=\sin \left(\pi x_{N_0,0}^{j(x_k,N_0)}\right)\mathrm{for}\mathrm{all}k=1,2,\dots ,\left[\frac{1}{h}\right].$(46) ), $\begin{array}{rl}|q(x_k)-q_{\mathrm{est}}(x_k)|& =|\sin (\pi x_k)-\sin \left(\pi x_{N_0,0}^{j(x_k,N_0)}\right)|\\ & =2\left|\sin \frac{\pi (x_k-x_{N_0,0}^{j(x_k,N_0)})}{2}\cos \frac{\pi (x_k+x_{N_0,0}^{j(x_k,N_0)})}{2}\right|\\ & ⩽\pi |x_k-x_{N_0,0}^{j(x_k,N_0)}|\\ & ⩽\pi \underset{0⩽k⩽N_0}{max}\{|x_{N_0,0}^{j(x_k,N_0)+1}-x_{N_0,0}^{j(x_k,N_0)}|,|x_{N_0,0}^{j(x_k,N_0)}-x_{N_0,0}^{j(x_k,N_0)-1}|\}\\ & ⩽{\displaystyle \frac{\pi }{N_0}}\end{array}$ for all $k=1,2,\dots ,[1/h]$. Thus the difference of $q(x)$ and $q_{\mathrm{est}}(x)$ is (47) $|q(x_k)-q_{\mathrm{est}}(x_k)|⩽\frac{\pi }{N_0}$(47) for all $x_k$. Consequently the positive number $\pi /N_0$ in (47(47) $|q(x_k)-q_{\mathrm{est}}(x_k)|⩽\frac{\pi }{N_0}$(47) ) is called an error for the accurate solution $q(x)$ and the corresponding approximate solution $q_{\mathrm{est}}(x)$. 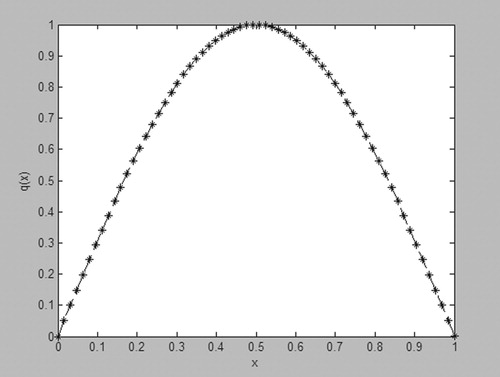Figure  1 is a comparison of $q(x)$ and $q_{\mathrm{est}}(x)$ with the error 0.05.

Figure 1. Comparison of the accurate solution $q(x)$ and the corresponding approximate solution $q_{\mathrm{est}}(x)$ for h = 0.0159 and $N_0=63$ with the nodal subset $\{x_{N_0,0}^{j(x_k,N_0)}{\}}_{j=1}^{63}:(\ast \ast \ast )$ for $q(x)$ and $(---)$ for $q_{\mathrm{est}}(x)$.

Acknowledgments

The authors are very grateful to the referees for their valuable suggestions and useful comments.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The first author is supported by the NNSF of China [11771409] and the open project of Research Insititute for Building Energy-Saving, Anhui Jianzhu University [K02580].