Inverse singular value problem for nonsymmetric ahead arrow matrix

ABSTRACT

Constructing a matrix by its spectral information including singular values is called inverse singular value problem (ISVP). In this paper, an ISVP for nonsymmetric ahead arrow matrix by two eigenpairs of the required matrix and one singular value of each leading principal submatrices is investigated. To solve the problem, the recurrence relation of characteristic polynomial of the block Jordan–Weilant matrix associated with the aim matrix is obtained. The conditions of solvability of the problem are derived. Finally a numerical algorithm and an example are given.

Keywords:

• Inverse singular value problem
• nonsymmetric ahead arrow matrices
• principal submatrices
• Jordan–Weilant matrix
• spectral information

2010 Mathematics Subject Classifications:

• 65F15
• 65F18

1. Introduction

An inverse eigenvalue problem (IEP) is the problem of generating a matrix using its total or partial spectral information. In some practical applications, the system in hand is modelled as a matrix. The spectral information of such matrices will contain some intrinsic properties of the system, hence by applying the desired conditions on the matrix entries and its spectral information, we will be able to generate a matrix that represents a system with the desired properties. There are many different types of IEPs. Chu and Golub in [1] presented an elaborate classification of IEPs. Some IEPs include singular values information, which are called inverse singular value problems (ISVPs). IEPs have been considered by many researchers because of their applications in various sciences. Control issues [2], finite element [3,4], mechanic [5] and perturbation [6] are examples of practical applications of IEPs in mathematics and engineering. The level of difficulty of an IEP depends on the available eigen information and the structure of the matrix to be constructed. Graph theory is another practical field in which the IEP of matrices corresponding to a graph is studied. It has been of interest for many years and been studied in many works [7–18].

An ahead arrow matrix $A_n$, defined as follows: (1) $A_n=\left[\begin{array}{ccccc}{a}_1& b_1& b_2& \cdots & b_{n-1}\\ c_1& a_2& 0& \cdots & 0\\ c_2& 0& \ddots & \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & 0\\ c_{n-1}& 0& \cdots & 0& a_n\end{array}\right],$(1) such that the diagonal entries are real and $b_i,c_i\in \mathbb{R}-\left\{0\right\},i=1,\dots ,n-1$. The IEPs of the graph corresponding to this matrix are studied by O. Boyko in [19] and J. Eckhardt in [20] in order to solve an inverse spectral problem for a star graph of Stieltjes strings and Krein strings, respectively. In 2006, Peng in [21] studied an application of the ahead arrow matrix $A_n$ in control theory and showed that it is equivalent to an IEP of it. Pickman et al. in [22] in 2007 studied an IEP of this matrix by the minimal and maximal eigenvalues of its all leading principal submatrices. After that Sharma et al. in [15,16] and Xu et al. in [17] also investigated recursive construction of the symmetric case of this matrix with different eigen information of the submatrices of the required matrix. Recently, Pickmann et al. in [23] studied an IEP, and some spectral properties, of this matrix in the nonsymmetric case.

In this paper, we solve the ISVP stated below, denoted by ISVPNA¹, consisting in constructing a matrix of form $A_n$ with partial eigendata and singular value information.

Problem 1.1

ISVPNA

n + 1 real distinct numbers $s^{\left(1\right)},\dots ,s^{(n-1)},{\lambda }_1^{\left(n\right)},{\lambda }_2^{\left(n\right)}$, two vectors $X_n=(x_1,\dots ,x_n{)}^T$ and ${X_n}^{\mathrm{\prime }}=({x_1}^{\mathrm{\prime }},\dots ,{x_n}^{\mathrm{\prime }}{)}^T$,$s^{\left(i\right)}>0,i=1,\dots ,n-1$, are given. Find matrix $A_n$ such that $s^{\left(i\right)},i=1,\dots ,n-1$ is singular value of leading principal submatrices $A_i$, $({\lambda }_1^{\left(n\right)},X_n)$ and $({\lambda }_2^{\left(n\right)},X_n^{\mathrm{\prime }})$ are two eigenpairs of $A_n$.

The paper is organized as follows. In Section 2, we introduce the problem statement and some of the preliminary concepts that will be used throughout the paper. In Section 3, main results are discussed and an algorithm is given. In Section 4, we present an example to illustrate the efficiency of the proposed method, and finally, in Section 5 is some concluding remarks and future perspectives.

2. Preliminaries

Every $m\times n$ matrix A can be decomposed into $A=U\mathrm{\Sigma }{V}^T$ where $U_{m\times m}$ and $V_{n\times n}$ are orthogonal and Σ is a $m\times n$ diagonal matrix [24]. This decomposition is called the singular value decomposition (SVD).

We define the Jordan–Weilant matrix $B_{2i},i=1,\dots ,n$ as (2) $B_{2i}=\left[\begin{array}{cc}0& A_i\\ A_i^t& 0\end{array}\right],$(2) $A_i$ to denote the $i\times i$ leading principal submatrix of $A_n$.The matrix $B_{2i}$ is symmetric and hence all of its eigenvalues are real. The singular values of $A_i$ are absolute value of eigenvalues of $B_{2i}$ [24]. Throughout the paper let (3) $\begin{array}{rl}{G}_i& =\left[\begin{array}{ccccc}-b_1& -b_2& \cdots & \cdots & -b_i\\ -a_2& 0& & \cdots & 0\\ 0& \ddots & & \ddots & ⋮\\ ⋮& \ddots & & & 0\\ 0& \cdots & 0& & -a_{i+1}\end{array}\right],\end{array}$(3) (4) $\begin{array}{rl}{H}_i& =\left[\begin{array}{ccccc}-c_1& -a_2& 0& \cdots & 0\\ -c_2& 0& -a_3& \ddots & ⋮\\ ⋮& ⋮& 0& \ddots & 0\\ ⋮& ⋮& & \ddots & -a_i\\ -c_i& 0& \cdots & \cdots & 0\end{array}\right].\end{array}$(4) In the next section, the main results and numerical algorithm of the solution are given.

3. Main idea

In this section, we will present necessary proofs to obtain the solution of ISVPNA.

Lemma 3.1

If s is a scalar and (5) $\begin{array}{rl}{R}_{2i-3}& =\left[\begin{array}{cc}s{I}_{i-1}& G_{i-2}\\ G_{i-2}^t& s{I}_{i-2}\end{array}\right],\end{array}$(5) (6) $M_{2i-2}=p>bmatrixs{I}_{i-1}{H}_{i-1}{H}_{i-1}^{t}s{I}_{i-1}$(6) (7) $\begin{array}{r}{N}_{2i-2}=\left[\begin{array}{cccc}0& \cdots & 0& \\ & s{I}_{i-2}& ⋮& -A_{i-1}\\ & & 0& \\ & H_{i-1}^t& & s{I}_{i-1}\end{array}\right]\end{array}$(7) for $i\ge 3$ then $\begin{array}{rl}\left(a\right)det\left(M_{2i-2}\right)& =s^2\left(\sum _{j=1}^{i-2}{(-1)}^{i+j}{c}_j^2\prod _{k=2,k\ne j+1}^{i-1}(s^2-a_k^2)\right)+(s^2-c_i^2)\prod _{k=2}^{i-1}(s^2-a_k^2),\\ \left(b\right)det\left(N_{2i-2}\right)& =c_{i-1}\left({(-1)}^{i+1}{a}_1\prod _{j=2}^{i-1}(s^2-a_j^2)\right.\\ & \left.+\sum _{j=1}^{i-2}\left({(-1)}^{i+j}{b}_j{c}_j{a}_{j+1}\prod _{k=2}^j{a}_k^2\prod _{k=j+1}^{i-1}(s^2-a_k^2)\right)\right),\\ \left(c\right)det\left(R_{2i-3}\right)& =s\left[\prod _{k=2}^{i-1}(s^2-a_k^2)+\sum _{j=1}^{i-2}\left({(-1)}^{i+j}{b}_j^2\prod _{k=2,j\ne j+1}^{i-1}(s^2-a_k^2)\right)\right].\end{array}$

Proof.

It is achieved by expanding the determinant. To compute $det\left(M_{2i-2}\right)$ we have

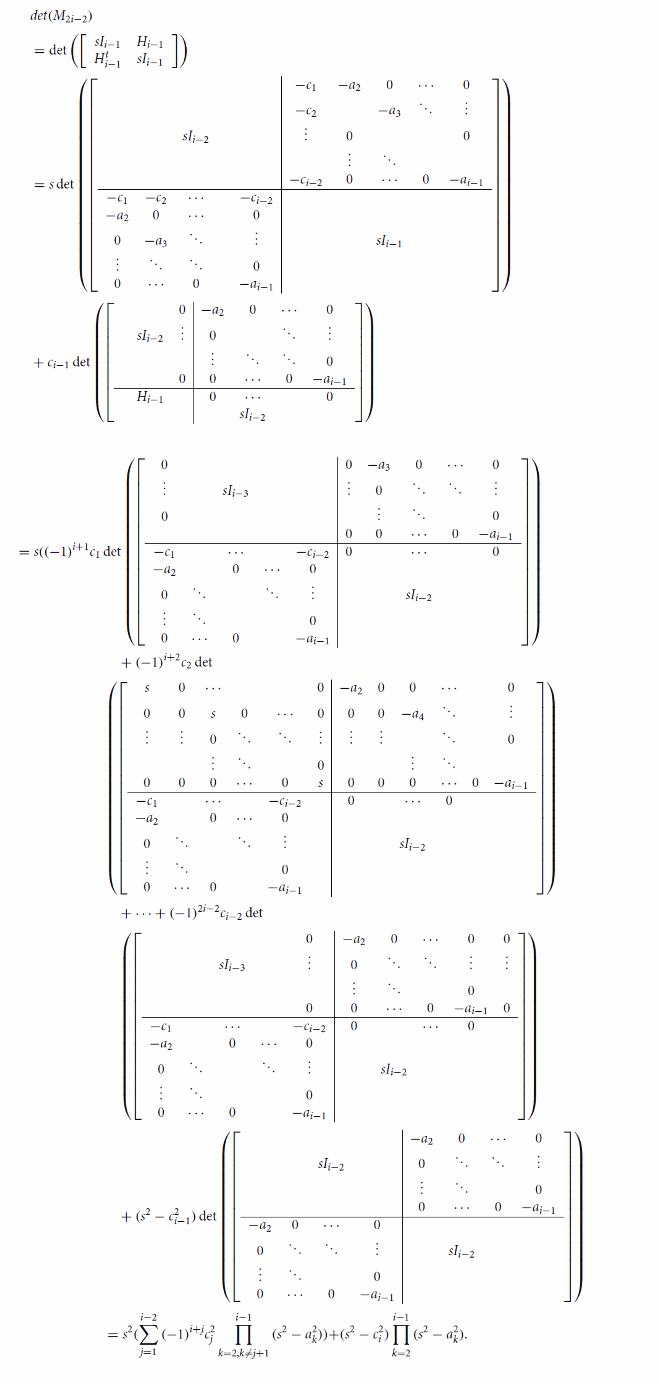
$det\left(N_{2i-2}\right)$ and $det\left(R_{2i-3}\right)$ can be obtained by similar way.

In the following Lemma, the recurrence relations of characteristic polynomial of $B_{2i},i=1,\dots ,n$ are given.

Lemma 3.2

The sequence $\left\{P_{2i}\right(s)=det(s{I}_{2i}-B_{2i}){\}}_{i=1}^{2n}$ of characteristic polynomials of $B_{2i}$ satisfies the following recurrence relations: (8) $\begin{array}{rl}{P}_2\left(s\right)& =s^2-a_1^2,\\ P_4\left(s\right)& =s^4-(a_1^2+a_2^2+b_1^2+c_1^2)s^2+(a_1{a}_2-b_1{c}_1{)}^2,\\ P_{2i}\left(s\right)& =(s^2-a_i^2)P_{2i-2}\left(s\right)-s{c}_{i-1}^{2}det\left(R_{2i-3}\right)-b_{i-1}^{2}det\left(M_{2i-2}\right)\\ & +(-1{)}^{i}2a_i{b}_{i-1}det(N_{2i-2}),i=3,\dots ,n.\end{array}$(8)

Proof.

$P_2\left(s\right)$ and $P_4\left(s\right)$ are clearly obtained by expanding the determinant. For $P_{2i}\left(s\right)$, we have

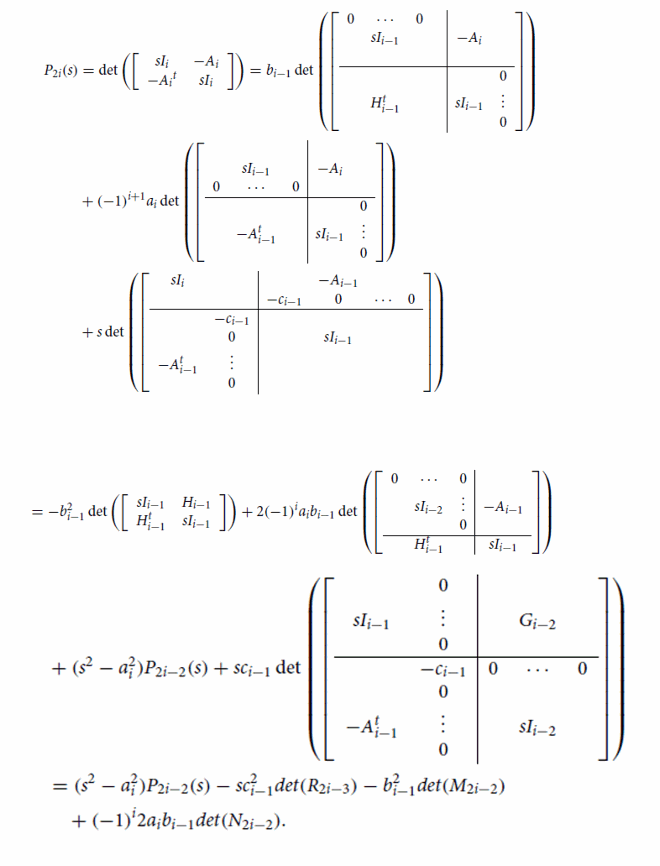
and the proof is completed.

In the following Lemma, we show that every component $x_i$ of $X_n,i=2,\dots ,n$ is a multiple of $x_1$.

Lemma 3.3

If $X_n=(x_1,x_2,\dots ,x_n{)}^T$ and $({\lambda }^{\left(n\right)},X_n)$ is an eigenpair of $A_n$, then $x_1\ne 0$ and the entries of $X_n$ are obtained as: (9) $x_i=\frac{c_{i-1}}{{\lambda }^{\left(n\right)}-a_i}{x}_1,i=2,\dots ,n.$(9)

Proof.

Since $({\lambda }^{\left(n\right)},X_n)$ is an eigenpair of $A_n$, so $A_n{X}_n={\lambda }^{\left(n\right)}{X}_n$. By expanding this relation one obtains: (10) $\begin{array}{rl}& a_1{x}_1+\sum _{i=1}^{n-1}{b}_i{x}_{i+1}={\lambda }^{\left(n\right)}{x}_1,\end{array}$(10) (11) $\begin{array}{rl}& c_{i-1}{x}_1+a_i{x}_i={\lambda }^{\left(n\right)}{x}_i,i=2,\dots ,n,\end{array}$(11) therefore (12) $x_i=\frac{c_{i-1}}{{\lambda }^{\left(n\right)}-a_i}{x}_1,i=2,\dots n.$(12) We note that the denominator is nonzero, because if not, from Equation (11(11) $\begin{array}{rl}& c_{i-1}{x}_1+a_i{x}_i={\lambda }^{\left(n\right)}{x}_i,i=2,\dots ,n,\end{array}$(11) ) $c_{i-1}{x}_1=0$, hence it follows $c_{i-1}=0$ which contradicts the conditions of matrix $A_n$. Since $X_n$ is an eigenvector, hence $X_n\ne 0$, if $x_1=0$ then from Equation (12(12) $x_i=\frac{c_{i-1}}{{\lambda }^{\left(n\right)}-a_i}{x}_1,i=2,\dots n.$(12) ) all the other entries of $X_n$ become zero. Thus $x_1\ne 0$ and the proof is completed.

3.1. The solution of ISVPNA

Now, we will present the conditions under which there is solution to ISVPNA. Let ${\mathrm{\Delta }}_1=4{s^{\left(2\right)}}^2({s^{\left(2\right)}}^2-(c_1^2+a_1^2\left)\right)({s^{\left(2\right)}}^2-(c_1^2+a_2^2\left)\right),$ $\begin{array}{rl}{\mathrm{\Delta }}_{i-1}& =4a_i^2(det(N_{2i-2}){)}^2+4det\left(M_{2i-2}\right)\left(\right({s^{\left(i\right)}}^2-a_i^2\left)P_{2i-2}\right(s)-s^{\left(i\right)}{c}_{i-1}^{2}det(R_{2i-3}\left)\right)),\\ & i=3,\dots ,n-1,\end{array}$and $M_2=\left[\begin{array}{cc}s& -c_1\\ -c_1& s\end{array}\right],N_2=\left[\begin{array}{cc}0& -a_1\\ -c_1& s\end{array}\right],R_1=\left[\begin{array}{c}1\end{array}\right].$

Theorem 3.4

If

1. $x_i{x}_i^{\prime }\ne 0,i=1,\dots ,n,w_i=x_1{x_i}^{\mathrm{\prime }}-x_i{x_1}^{\mathrm{\prime }}\ne 0,i=2,\dots ,n$,

2. ${\mathrm{\Delta }}_{i-1}\ge 0,i=2,\dots ,n-1$,

3. $\left|a_{i}det\left(N_{2i-2}\right)\right|+\left|({s^{\left(i\right)}}^2-a_i^2)P_{2i-2}\left(s^{\left(i\right)}\right)-s^{\left(i\right)}{c}_{i-1}^{2}det\left(R_{2i-3}\right)\right|>0,i=2,\dots ,n-1$,

4. $\left({\lambda }_1^{\left(n\right)}-a_1\right)x_1\ne \sum _{i=1}^{n-2}{b}_i{x}_{i+1}$,

then ISVPNA has solution.

Proof.

Let the conditions 1–4 hold. It is easy to see that $a_1=\pm s^{\left(1\right)}$. We set $a_1=s^{\left(1\right)}$. Since $({\lambda }_1^{\left(n\right)},X_n)$ and $({\lambda }_2^{\left(n\right)},X_n^{\mathrm{\prime }})$ are two eigenpairs of $A_n$, so by Lemma (3.3) for $i=2,\dots ,n,$ (13) $\left\{\begin{array}{l}{c}_{i-1}{x}_1+a_i{x}_i={\lambda }_1^{\left(n\right)}{x}_i\\ c_{i-1}{x_1}^{\mathrm{\prime }}+a_i{x_i}^{\mathrm{\prime }}={\lambda }_2^{\left(n\right)}{x_i}^{\mathrm{\prime }}\end{array}\right.,$(13)

From condition 1, $w_i=x_1{x_i}^{\mathrm{\prime }}-x_i{x_1}^{\mathrm{\prime }},i=2,\dots ,n$ is nonzero, therefore (14) $\begin{array}{rl}{a}_i& =\frac{x_1{x_i}^{\mathrm{\prime }}{\lambda }_2^{\left(n\right)}-x_i{x_1}^{\mathrm{\prime }}{\lambda }_1^{\left(n\right)}}{w_i},\end{array}$(14) (15) $\begin{array}{rl}{c}_{i-1}& =\frac{({\lambda }_1^{\left(n\right)}-{\lambda }_2^{\left(n\right)})x_i{x_i}^{\mathrm{\prime }}}{w_i}.\end{array}$(15) Now to obtain $b_i$, we use the Jordan-Weilant matrix $B_{2i},i=2,\dots ,n-1$. The singular values of $A_i,i=2,\dots ,n-1$ are equal to the absolute value of eigenvalues of $B_{2i}$, therefore, $det(s^{\left(i\right)}I-B_{2i})=0,i=2,\dots ,n-1$. In matrix $B_4$: $det(s^{\left(2\right)}I-B_4)=s^{\left(2\right)4}-(a_1^2+a_2^2+b_1^2+c_1^2)s^{\left(2\right)2}+(a_1^2{a}_2^2-2a_1{a}_2{b}_1{c}_1+b_1^2{c}_1^2)=0,$by rewriting this equation, we get $b_1$ as (16) $\begin{array}{rl}& (c_1^2-{s^{\left(2\right)}}^2)b_1^2-2a_1{a}_2{c}_1{b}_1+({s^{\left(2\right)}}^4-(c_1^2+a_1^2+a_2^2){s^{\left(2\right)}}^2+a_1^2{a}_2^2)=0,\\ & {\mathrm{\Delta }}_1=4{s^{\left(2\right)}}^2({s^{\left(2\right)}}^2-(c_1^2+a_1^2\left)\right)({s^{\left(2\right)}}^2-(c_1^2+a_1^2\left)\right),\\ & b_1=\frac{a_1{a}_2{c}_1\pm s^{\left(2\right)}\sqrt{({s^{\left(2\right)}}^2-(c_1^2+a_1^2\left)\right)({s^{\left(2\right)}}^2-(c_1^2+a_2^2\left)\right)}}{c_1^2-s^{\left(2\right)2}}.\end{array}$(16) From condition 2, ${\mathrm{\Delta }}_1\ge 0$ and so these two solutions are real. Without loss of generality, we take the one with smallest magnitude as $b_1$. This issue is also evident in higher dimensions of the matrix. From Lemma (3.2), $P_{2i}\left(s^{\left(i\right)}\right)=0$ is a quadratic equation in $b_{i-1}$, by rewriting this equation and substituting $s^{\left(i\right)}$ in $M_{2i-2},N_{2i-2}$ and $R_{2i-3}$ for $i=3,\dots ,n-1$, we obtain (17) $\begin{array}{rl}& -b_{i-1}^{2}det\left(M_{2i-2}\right)+(-1{)}^{i}2a_i{b}_{i-1}det(N_{2i-2})\\ & +({s^{\left(i\right)}}^2-a_i^2)P_{2i-2}\left(s^{\left(i\right)}\right)-s^{\left(i\right)}{c}_{i-1}^{2}det\left(R_{2i-3}\right)=0.\end{array}$(17) From condition 2, ${\mathrm{\Delta }}_{i-1}=4a_i^2(det(N_{2i-2}){)}^2+4det\left(M_{2i-2}\right)\left(\right({s^{\left(i\right)}}^2-a_i^2\left)P_{2i-2}\right(s^{\left(i\right)})-s^{\left(i\right)}{c}_{i-1}^{2}det(R_{2i-3}\left)\right)),$is nonnegative, so $b_{i-1}=\frac{{(-1)}^{i+1}2a_{i}det\left(N_{2i-2}\right)\pm \sqrt{{\mathrm{\Delta }}_{i-1}}}{-2det\left(M_{2i-2}\right)}.$By similar way, we take the one with smallest magnitude as $b_{i-1}$.

Depending on which of the following conditions is met, we set the $b_{i-1}$ as follows:

• If $det\left(M_{2i-2}\right)=0$, we get $b_{i-1}=\frac{-({s^{\left(i\right)}}^2-a_i^2)P_{2i-2}\left(s^{\left(i\right)}\right)-s^{\left(i\right)}{c}_{i-1}^{2}det\left(R_{2i-3}\right)}{(-1{)}^{i}2a_{i}det(N_{2i-2})}.$

• If $({s^{\left(i\right)}}^2-a_i^2)P_{2i-2}\left(s^{\left(i\right)}\right)-s^{\left(i\right)}{c}_{i-1}^{2}det\left(R_{2i-3}\right)=0$, we set $b_{i-1}=\frac{(-1{)}^{i}2a_{i}det(N_{2i-2})}{-det\left(M_{2i-2}\right)}.$

From condition 3, Equation (17(17) $\begin{array}{rl}& -b_{i-1}^{2}det\left(M_{2i-2}\right)+(-1{)}^{i}2a_i{b}_{i-1}det(N_{2i-2})\\ & +({s^{\left(i\right)}}^2-a_i^2)P_{2i-2}\left(s^{\left(i\right)}\right)-s^{\left(i\right)}{c}_{i-1}^{2}det\left(R_{2i-3}\right)=0.\end{array}$(17) ) does not have double zero roots, therefore in all of mentioned cases we get nonzero $b_i,i=1,\dots ,n-2$.

Finally, from Equation (11(11) $\begin{array}{rl}& c_{i-1}{x}_1+a_i{x}_i={\lambda }^{\left(n\right)}{x}_i,i=2,\dots ,n,\end{array}$(11) ), we get $b_{{}_{n-1}}=\frac{({\lambda }_1^{\left(n\right)}-a_1)x_1-\sum _{i=1}^{n-2}{b}_i{x}_{i+1}}{x_n},$from condition 4, $b_{n-1}$ is nonzero. So it completes the proof.

Remark 3.1

By selecting another root of $det(s^{\left(i\right)}{I}_{2i}-B_{2i})=0,i=2,\dots ,n-1$ or $a_1=-s^{\left(1\right)}$ this problem will have at most $2^{n-1}$ solutions.

The resulting algorithm takes the form of Algorithm 1.

4. Numerical experiments

In this section, we present the numerical results of ISVPNA. The computational results are provided by MATLAB software.

Example 4.1

In graph theory, the energy of a graph with n vertexes is defined by $E\left(G\right)=\sum _{i=1}^n|{\lambda }_i|$. By obtaining any principal submatrices of $A_6$, we can get energy of graph with adjacency matrix $B_{2k}$. Let $\begin{array}{rl}{s}^{\left(1\right)}& =1,s^{\left(2\right)}=0.4915,s^{\left(3\right)}=1.0910,s^{\left(4\right)}=2.3246,s^{\left(5\right)}=3.8403,\\ {\lambda }_1^{\left(6\right)}& =3.9209,{\lambda }_2^{\left(6\right)}=0.5884,\end{array}$and vectors $\begin{array}{rl}{X}_6& =(-0.6953,-0.0986,-0.2753,-0.1245,-0.6093,-0.2104{)}^T,\\ X_6^{\prime }& =(0.0289,-0.0226,-0.1150,0.9429,-0.3103,-0.0065{)}^T.\end{array}$By applying Algorithm 1, we get $A_6=\left[\begin{array}{cccccc}1.0000& 0.7399& 0.8192& 0.9012& 2.4001& 0.7502\\ 0.4000& 1.1000& 0& 0& 0& 0\\ 1.2001& 0& 0.8900& 0& 0& 0\\ 0.6000& 0& 0& 0.5700& 0& 0\\ 2.7000& 0& 0& 0& 0.8399& 0\\ 0.4300& 0& 0& 0& 0& 2.5000\end{array}\right].$Table 1 weights of graph G with adjacency matrix $B_{2k},k=1,\dots ,6$, eigenvalues ${\lambda }_i^{\left(k\right)},i=1,2,\dots ,2k$, energy of graph $E\left(G\right)$ and $s^{\left(k\right)}\left(A_k\right)$ to compare with data of this problem are presented. The corresponding eigenvectors of ${\lambda }_1^{\left(6\right)}=3.9209$ and ${\lambda }_2^{\left(6\right)}=0.5884$ are as follows: $\begin{array}{rl}{X}_6& =(-0.6953,-0.0986,-0.2753,-0.1245,-0.6093,-0.2104),\\ X_6^{\prime }& =(-0.0289,0.0226,0.1151,-0.9428,0.3107,0.0065{)}^T.\end{array}$

Table 1. Results of graph G by ISVPNA.

k	Weights of graph G	${\lambda }_i^{\left(k\right)}$	$E\left(G\right)$	$s^{\left(k\right)}\left(A_k\right)$
1	$a_1=1.0000$	−1.0000, 1.0000	2.0000	1.0000
2	$\begin{array}{c}{\displaystyle a_1=1.0000,}\\ {\displaystyle b_1=0.7399,}& c_1=0.4000,& a_2=\mathrm{1.100.}\end{array}$	$\begin{array}{c}{\displaystyle -1.6358,-0.4915}\\ {\displaystyle 1.6358,0.4915}\end{array}$	4.2546	$\begin{array}{c}{\displaystyle 1.6358}\\ {\displaystyle 0.4915}\end{array}$
3	$\begin{array}{c}{\displaystyle a_1=1.0000,}\\ {\displaystyle b_1=0.7399,}& c_1=0.4000,& a_2=1.100,\\ {\displaystyle b_2=0.8192,}& c_2=1.2001,& a_3=\mathrm{0.8900.}\end{array}$	$\begin{array}{c}{\displaystyle -2.1462,-1.0910}\\ {\displaystyle -0.1562,2.1462}\\ {\displaystyle 1.0910,0.1562}\end{array}$	6.7868	$\begin{array}{c}{\displaystyle 2.1462}\\ {\displaystyle 1.09100}\\ {\displaystyle 0.1562}\end{array}$
4	$\begin{array}{c}{\displaystyle a_1=1.0000,}\\ {\displaystyle b_1=0.7399,}& c_1=0.4000,& a_2=1.100,\\ {\displaystyle b_2=0.8192,}& c_2=1.2001,& a_3=0.8900,\\ {\displaystyle b_3=0.9012,}& c_3=0.6000,& a_4=\mathrm{0.5700.}\end{array}$	$\begin{array}{c}{\displaystyle -2.3246,-1.1018}\\ {\displaystyle -0.7410,-0.3888}\\ {\displaystyle 2.3246,1.1018}\\ {\displaystyle 0.7410,0.3888}\end{array}$	9.1124	$\begin{array}{c}{\displaystyle 2.3246}\\ {\displaystyle 0.3888}\\ {\displaystyle 1.1018}\\ {\displaystyle 0.7410}\end{array}$
5	$\begin{array}{c}{\displaystyle a_1=1.0000,}\\ {\displaystyle b_1=0.7399,}& c_1=0.4000,& a_2=1.100,\\ {\displaystyle b_2=0.8192,}& c_2=1.2001,& a_3=0.8900,\\ {\displaystyle b_3=0.9012,}& c_3=0.6000,& a_4=0.5700,\\ {\displaystyle b_4=2.4001,}& c_4=2.700,& a_5=\mathrm{0.8399.}\end{array}$	$\begin{array}{c}{\displaystyle -3.8403,-2.0167}\\ {\displaystyle -1.0722,-0.8783}\\ {\displaystyle 0.8783,0.5808}\\ {\displaystyle -0.5808,3.8403}\\ {\displaystyle 2.0167,1.0722}\end{array}$	16.7766	$\begin{array}{c}{\displaystyle 3.8403}\\ {\displaystyle 2.0167}\\ {\displaystyle 0.5808}\\ {\displaystyle 1.0722}\\ {\displaystyle 0.8783}\end{array}$
6	$\begin{array}{c}{\displaystyle a_1=1.0000,}\\ {\displaystyle b_1=0.7399,}& c_1=0.4000,& a_2=1.100,\\ {\displaystyle b_2=0.8192,}& c_2=1.2001,& a_3=0.8900,\\ {\displaystyle b_3=0.9012,}& c_3=0.6000,& a_4=0.5700,\\ {\displaystyle b_4=2.4001,}& c_4=2.700,& a_5=0.8399,\\ {\displaystyle b_5=0.7502,}& c_5=0.4300,& a_6=\mathrm{2.5000.}\end{array}$	$\begin{array}{c}{\displaystyle -3.9627,-2.4626}\\ -2.0111,-1.0725\\ -0.8784,-0.5809\\ {\displaystyle 2.4626,3.9627}\\ 0.5809,0.8784\\ 1.0725,2.0111\end{array}$	21.9364	$\begin{array}{c}{\displaystyle 0.5809}\\ {\displaystyle 2.4626}\\ {\displaystyle 2.0111}\\ {\displaystyle 1.0725}\\ {\displaystyle 0.8784}\\ {\displaystyle 3.9627}\end{array}$

5. Conclusion

In this paper, an ISVP called ISVPNA, for ahead arrow matrices is studied. We constructed the matrix by one singular value from each of the leading principal submatrices and two eigenpairs of the required matrix. For this purpose, we have used Jordan–Willant matrix and the relation between singular values of $A_i$ and eigenvalues of $B_{2i},i=1,\dots ,n$. Given that the dimensions of $B_{2i}$ are always even, the recursive relationships are organized based on the reduction of two indices in each iteration. Also by using different blocking, characteristic polynomial of $B_{2i}$ is obtained as a second-order polynomial in $b_{i-1}$. The conditions under which the ISVPNA will have solution are obtained and we showed that it is possible to have at most $2^{n-1}$ solutions to ISVPNA. To the best of our knowledge, this is the first work that studied recursive construction of matrices by singular values. As a future work, it would be interesting to study the application of ISVPNA to perturbation problems related to the $A_n$ in control theory.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 Inverse Singular Value Problem for Nonsymmetric Ahead arrow matrix.