Algebraic tunings

Abstract

We propose an approach to tuning systems in which octave doubling ratio is replaced by a suitable algebraic unit τ, and note frequencies are proportional to a subset of the ring $\mathbb{Z}\left[\tau \right]$. Then it is possible for many difference tones between notes in the tuning to also appear in the tuning. After outlining more general principles, we consider in detail some natural examples based on the golden ratio $\varphi =(1+\sqrt{5})/2$, limited by norm or by the number of digits in the greedy β-expansion. We discuss additive and multiplicative properties, implementation and composition using these tunings. The Online Supplement contains MIDI and websynths files to implement the tuning $S_{\text{β}}^5\left(\varphi \right)$ (based on β-expansions to ${\varphi }^{-5}$) on websynths.com and a composition Three Places.

Keywords:

• Algebraic unit
• beta expansion
• composition
• harmony
• Pisot number
• tunings

2020 Mathematics Subject Classification:

• 00A65
• 11B75
• 11K16
• 11R04

1. Introduction

Conventional modern Western music is based on a 12 tone equal temperament (12TET) tuning in which consecutive pitches differ by a ratio $2^{1/12}\approx 1.059$, so that 12 of these smallest intervals (semitones) give a ratio of 2 (conventional octave). This choice allows music to be transposed exactly into any key. Rational frequency ratios other than powers of 2 are also available, albeit only approximately, for example 7 semitones gives $2^{7/12}\approx 1.498\approx \frac{3}{2}$. For music using only a few keys, including much composed prior to 1700, tuning in other temperaments may be preferred, in which these intervals are exact or closer to rational approximations; see Lindley (2001). This is particularly an issue for keyboard music; performers of many other instruments (including voice) are able to a greater or lesser extent adjust the pitch during performance.

One motivation for temperaments using exactly rational frequency ratios is that of difference tones (Greated 2001). Due to nonlinearities in the ear, these tones may be perceived when intervals or chords are played. Their frequency is the difference, or another simple linear combination, of the original frequencies, the latter termed “combination tones.” If the frequencies in the scale are exact rational ratios, difference tones will then often correspond to other frequencies in the scale. A recent discussion of difference tones and their use in electronic music composition may be found in Chechile (2020).

There are also many tuning systems quite different from 12-TET, either from many non-Western musical traditions though it should be noted that 12TET originated in China (Cho 2010) or of more recent origin, in theory, instruments and composition. These are often termed “microtonal” though the intervals may not be smaller than in 12TET. Intervals are still typically measured in cents. As standard in music, the interval corresponding to frequency ratio $f_2/f_1$ is defined to be (1) $1200{\log }_2\left(\frac{f_2}{f_1}\right)\mathrm{cents}$(1) so that a 100 cent interval is a 12TET semitone.

Perception of octave equivalence for a frequency ratio of 2 is not universal, for example the Tsimané people of Bolivia do not appear to have this (or any other) octave equivalence (Jacoby et al. 2019). This suggests that the human ear may become accustomed to other interval equivalence.

The ninth century treatises Musica enchiriadis and Scolica enchiriadis (Erickson 2001) use “dasian” notation which has equivalence at a perfect fifth (frequency ratio 3/2), and a 3-limit tuning system, that is, frequency ratios that are multiples of powers of 2 and 3. This fits naturally with monophonic chant, and with parallel organum using an interval of a perfect fifth, but not with parallel organum with a fourth (ratio 4/3) or with one or more parts doubled at an octave (ratio 2), also common in this period as described in these treatises.

A notable recent example of a tuning system with a different octave is the Bohlen-Pierce (BP) scale (Mathews et al. 1988), where consecutive pitches differ by a ratio $3^{1/13}$. This is periodic with a frequency ratio of 3 (“tritave”) and has intervals approximating ratios involving 3, 5 and 7. This makes it well suited for instruments with strong odd harmonics, such as the clarinet, and BP-tuned instruments are available commercially. Interestingly, one motivation for this scale was that of difference tones (Mathews et al. 1988).

The aim of this work is to use the above ideas for generating tuning systems, namely difference tones and non-standard octaves, in the context of algebraic number theory. Namely, we observe that if the octave periodicity is an algebraic unit τ, and frequencies are proportional to elements of the corresponding ring $\mathbb{Z}\left[\tau \right]$, then difference tones also lie in the ring. The simplest case is the golden ratio $\tau =\varphi =(1+\sqrt{5})/2\approx 1.618$. The frequencies involve two integers, being proportional to $\mathrm{a\varphi }+b$ where $a,b\in \mathbb{Z}$, and in this sense have the same complexity as the rational numbers. This will be our main example, but we also motivate and develop this approach in more generality.

First, we discuss some relevant approaches in the existing literature. O'Connell (1993) noted that $2^{25}=33554432$ is close to ${\varphi }^{36}\approx 33385282$, so that dividing each semitone in thirds (that is, 36TET) yields an interval (25/3 semitones, or close to 833 cents) very close to the golden ratio, motivated as below by sum and difference tones. A very similar scale is obtained by splitting a golden octave (frequency ratio of ϕ) into 25 equally spaced intervals. He then described compositions based on pentachords noting the factorization of 25. Frequency ratios of 2, $\sqrt{5}$ and 3 were highlighted. In the present work the main ratio is ϕ, although the above ratios also appear.

Some related history and scales can be found in Smethurst (2016). Of note is the Bohlen 833 scale, which does not appear otherwise published except on websites such as Bohlen (2012). This scale consists of a fundamental and its 2, 3 and 4 harmonics and subharmonics, repeated every golden octave. Unlike the equally tempered approach of O'Connell, this scale now has closest intervals of three different sizes. It also has several difference tones in the scale, though the distinct sums and differences are not much less than the generic value of $n(n+1)/2$ for n notes; see Figure 2 below.

Figure 1. Arithmetic sequences in the golden scales, with notes at $x=\mathrm{a\varphi }+b$ for integers $(a,b)$. The sequences are straight line segments in the $(a,b)$ plane, but curved in these coordinates. See section 5.

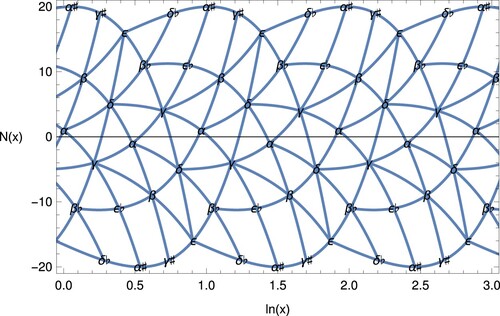
Figure 2. Sum-product phenomenon for the $S_N$ scale (upper), $S_{\text{β}}$ scale (middle) and Bohlen 833 scale (lower). The number of distinct sums, positive differences, and products are shown in blue, orange and green, respectively, plotted against the number of notes used. See section 7.

In this paper we continue further in this direction, constructing scales with many difference tones equal to each other and/or contained in the scale. This has the effect that almost all intervals (ie multiplicative ratios) are different.

In section 2, we begin by generalizing the difference tone rationale, and discuss the algebraic number systems and choice of the octave periodicity ratio τ. Section 3 contains relevant properties of ϕ and similar algebraic numbers. Section 4 defines the scales we propose, based on ϕ. Section 5 considers their additive properties (ie difference tones) and section 6 their multiplicative properties (ie intervals). Section 7 gives a relation to an interesting open mathematical problem, the sum-product conjecture. Section 8 gives considerations in implementing and experimenting with these scales, and section 9 some ideas for composition, and discussion of a first composition, Three Places.

2. Octave equivalence using algebraic units

Define a scale $\hat{S}\subset {\mathbb{R}}_{>0}$ as a nonempty set of positive real numbers representing frequencies, measured in Hz. One element $f\in \hat{S}$ denotes the “fundamental” frequency. We consider $S=\{x:\mathrm{fx}\in \hat{S}\}$ for now; this is equivalent to setting f = 1. In section 4, we will choose another convenient value. We also assume that S is locally finite away from zero.

We require that S be log-periodic, that is, the set of logarithms of elements of S has period $\ln \tau$ for some real number $\tau >1$. In other words, $\mathrm{\forall }x\in S$, $\mathrm{\tau x}\in S$ and ${\tau }^{-1}x\in S$; the pitch class of x is the set ${\tau }^{n}x$ for $n\in \mathbb{Z}$. In most traditional scales, $\tau =2$, corresponding to the octave, but here it will differ. We choose τ to be the smallest such value, since S is also invariant under multiplication and division by integer powers of τ. Though S is locally finite away from zero by assumption, the log-periodicity implies that S accumulates at zero.

We now introduce some standard definitions in algebraic number theory. We denote $\mathbb{Z}[\tau ,{\tau }^{-1}]$ to be the minimal set containing $\{1,\tau ,{\tau }^{-1}\}$ and closed under addition, subtraction and multiplication. This consists of any integer linear combination of arbitrary positive and negative powers of τ, and so is in general not a finitely generated space over $\mathbb{Z}$. However, if τ is an algebraic integer of degree d i.e. has minimal polynomial of degree d with integer coefficients and leading coefficient 1, then all powers $\ge d$ in the sum can be written in terms of powers $0\dots d-1$. If in addition, τ is an algebraic unit, i.e. its minimal polynomial also has constant term $\pm 1$, then all negative powers in the sum can be written in terms of the powers $0\dots d-1$. In this case ${\tau }^{-1}$ is in $\mathbb{Z}\left[\tau \right]$ and we can use the latter notation rather than $\mathbb{Z}[\tau ,{\tau }^{-1}]$. The space now has dimension d over $\mathbb{Z}$ and a good candidate to construct scales with (in some reasonable sense) many difference tones in the scale.

One more standard definition needed here is that of the (field) norm of an element of $\mathbb{Z}\left[\tau \right]$. Multiplication by an element $x\in \mathbb{Z}\left[\tau \right]$ corresponds to a d-dimensional linear operator over $\mathbb{Z}$. The norm $N\left(x\right)$ is the determinant of this operator, and hence is multiplicative, ie $N\left(\mathrm{xy}\right)=N\left(x\right)N\left(y\right)$. Strictly speaking, the norm is defined relative to the original ring $\mathbb{Z}$ and extension $\mathbb{Z}\left[\tau \right]$ but these are clear in the context and omitted from the notation.

Later we will need the norm in $\mathbb{Z}\left[\varphi \right]$, where $\varphi =(1+\sqrt{5})/2$ is the golden ratio. The minimal polynomial $x^2-x-1$ has highest and lowest terms with coefficient $\pm 1$, so ϕ is an algebraic unit. If we write $x\in \mathbb{Z}\left[\varphi \right]$ as $x=\mathrm{a\varphi }+b$, then ${\varphi }^2=\varphi +1$ implies that $\mathrm{x\varphi }=(a+b)\varphi +a$ and the determinant of the multiplication operator is (2) $N(\mathrm{a\varphi }+b)=\left|\begin{array}{cc}a+b& a\\ a& b\end{array}\right|=b^2+\mathrm{ab}-a^2$(2) In conventional just intonation scales, the octave equivalence is $\tau =2$ (not an algebraic unit). Frequencies are of the form $p_1^{k_1}{p}_2^{k_2}\dots /2^q$ where the numerator is typically given as a product of small non-negative powers of primes (for example 2, 3, 5 for 5-limit tuning). Combining the numerator into a single integer p, we can reduce the number of required integer parameters to two, that is, frequencies are dyadic rational numbers of the form $p/2^q\in \mathbb{Z}\left[1/2\right]$. The dasian scale discussed in the introduction has $\tau =3/2$ (not an algebraic integer). Frequencies are of the 3-limit form $2^{k_1}{3}^{k_2}=p/6^q\in \mathbb{Z}\left[1/6\right]$, where now $k_1$ and $k_2$ are integers satisfying $5\le k_1+k_2\le 8$. Representing either in terms of p and q or $k_1$ and $k_2$ there are two integer parameters.

The same number of parameters is required for τ a degree 2 (i.e. quadratic) algebraic unit. These are solutions to $x^2-\mathrm{ax}\pm 1=0$ for integer a, thus those greater than unity are of the form $(a+\sqrt{a^2\mp 4})/2$, and easily enumerated. Those less than 3 are the golden ratio $\varphi \approx 1.618$, the silver ratio $s=1+\sqrt{2}\approx 2.414$, and also ${\varphi }^2\approx 2.618$. The degree 3 (i.e. cubic) units in contrast are dense unless there is an additional condition such as the Pisot property discussed in the next section.

3. The golden ratio, properties and generalizations

In this paper we will focus on the golden ratio ϕ as the ratio for octave equivalence. This section describes some other properties of ϕ, that are relevant in selecting algebraic units on which to base alternative scales, and in selecting elements of $\mathbb{Z}\left[\tau \right]$ to include in the scale.

Algebraic numbers give the asymptotic growth of solutions of linear recurrences with coefficients from their minimal polynomial. For ϕ, this is the Fibonacci sequence defined by $F_1=F_2=1$, $F_n=F_{n-1}+F_{n-2}$. It is easy to show (for example by induction) that (3) $\begin{array}{rl}{\varphi }^n-(-\varphi {)}^{-n}& =F_n\sqrt{5}\end{array}$(3) (4) $\begin{array}{rl}{\varphi }^n+(-\varphi {)}^{-n}& =F_{n+1}+F_{n-1}\end{array}$(4) Equation (3(3) $\begin{array}{rl}{\varphi }^n-(-\varphi {)}^{-n}& =F_n\sqrt{5}\end{array}$(3) ) may be used to calculate $F_n$. Equation (4(4) $\begin{array}{rl}{\varphi }^n+(-\varphi {)}^{-n}& =F_{n+1}+F_{n-1}\end{array}$(4) ) shows that for large n, ${\varphi }^n$ is close to an integer; this is due to the following property.

A Pisot number (Bertin et al. 2012) is a real algebraic integer greater than 1 with all Galois conjugates (i.e. roots of the minimal polynomial) of complex magnitude less than 1. The distance between the nth power of a Pisot number and the nearest integer converges to zero as $n\to \mathrm{\infty }$. A positive power of a Pisot number is Pisot. The golden ratio is Pisot; this can be confirmed from the roots of the minimal polynomial. In general there are criteria using inequalities for the coefficients of the minimal polynomial; see Theorem 2.2 of Akiyama and Gjini (2005). The quadratic and cubic Pisot units less than 3 are tabulated in Table 1. This table also includes information about the β-expansion (see below) and common names for the golden ratio and some of the others.

Table 1. Pisot units of degree 2 and 3, of magnitude less than 3, and not powers of smaller Pisot units.

Value	Minimal polynomial	$d_{\text{β}}\left(1\right)$	Name (Symbol)
1.32472	$x^3-x-1$	0.10001	Plastic(p)
1.46557	$x^3-x^2-1$	0.101	Supergolden
1.61803	$x^2-x-1$	0.11	Golden(ϕ)
1.83929	$x^3-x^2-x-1$	0.111	Tribonacci
2.20557	$x^3-2x^2-1$	0.201
2.24698	$x^3-2x^2-x+1$	$0.2\overline{01}$	Cyclotomic-7
2.41421	$x^2-2x-1$	0.21	Silver(s)
2.54682	$x^3-2x^2-x-1$	0.211
2.76929	$x^3-3x^2+x-1$	0.2201
2.83118	$x^3-2x^2-2x-1$	0.221
2.87939	$x^3-3x^2+1$	$0.22\overline{1}$	Cyclotomic-9

Note: The β-expansion of one (defined below) is $d_{\text{β}}\left(1\right)$ where the over bar denotes a periodic sequence of symbols. “Symbol” gives the notation in this paper; notation varies in the literature. Cyclotomic Pisot numbers (which also include ϕ and s) are discussed in Dettmann and Frankel (1993) and Bell and Hare (2005).

A β-expansion (Charlier, Cisternino, and Dajani 2021) is an expression for a real number in powers of an arbitrary real $\text{β}>1$, (5) $x=\sum _{j=-\mathrm{\infty }}^{j_{max}}{c}_j{\text{β}}^j$(5) where $c_j\in \mathbb{Z}\cap [0,\text{β})$. In general this is non-unique: there are many possible $\left\{c_j\right\}$ that satisfy equation (5(5) $x=\sum _{j=-\mathrm{\infty }}^{j_{max}}{c}_j{\text{β}}^j$(5) ). The greedy β-expansion is obtained by starting from the largest possible $j_{\max }$ and choosing the largest possible $c_j$ for each j decreasing towards $-\mathrm{\infty }$. The β-expansion of 1, denoted $d_{\text{β}}\left(1\right)$ is the greedy β-expansion starting from j = −1. For Pisot β it is known to be finite or repeating; see Table 1. The greedy condition can be written that no consecutive set of $c_j$ is lexicographically greater or equal than $d_{\text{β}}\left(1\right)$. For $\tau =\varphi$ we have $d_{\text{β}}\left(1\right)=0.11$ and leads to the simple condition $c_j{c}_{j+1}=0$, that is, that the finite sequences of $c_j$ in the greedy β-expansion are exactly those without consecutive 1s (also, similar to the infinite trailing sequence of 9s that does not occur in decimal expansions, the β-expansion excludes an infinite trailing sequence of $\overline{01}$). Here, we use β-expansions as an approach to deciding what elements of $\mathbb{Z}\left[\text{β}\right]$ to include in the scale.

Finally, we mention the Diophantine properties of the golden ratio and related algebraic units (see for example Rockett and Szusz 1992), in other words, how close are intervals to rational frequency ratios appearing in conventional (just intonation) music? It turns out that the golden ratio is, in a precise sense, maximally irrational, that is, badly approximable by rationals. Hurwitz's theorem states that for any irrational τ, the equation (6) $|\tau -\frac{p}{q}|<\frac{K}{q^2}$(6) has infinitely many integer solutions for $(p,q)$ if $K\ge \frac{1}{\sqrt{5}}$. If $\tau =\frac{a+\mathrm{b\varphi }}{c+\mathrm{d\varphi }}$ for integers a, b, c, d with $|\mathrm{ad}-\mathrm{bc}|=1$ then this bound is sharp. If $\tau =\frac{a+\mathrm{bs}}{c+\mathrm{ds}}$ with $|\mathrm{ad}-\mathrm{bc}|=1$ with $s=1+\sqrt{2}$ (the silver ratio) then the bound $K\ge \frac{1}{\sqrt{8}}$ is sharp. All other irrationals are better approximated by rationals, in that the bound may be replaced by $K\ge \frac{5}{\sqrt{221}}=\frac{1}{\sqrt{8.84}}$. Each quadratic irrational has its own bound; these are exactly the numbers with eventually periodic continued fraction expansions. There is a quadratic irrational ratio in 12TET, namely six semitones gives a frequency ratio $2^{6/12}=\sqrt{2}$.

However, for algebraic numbers of higher degree, the continued fraction expansions appear to have similar properties to generic real numbers but less is known; it is conjectured that K may be made arbitrarily small in equation (6(6) $|\tau -\frac{p}{q}|<\frac{K}{q^2}$(6) ) and it is known that replacing $q^2$ by $q^{2+ϵ}$ leads to only finitely many solutions (Roth 1955). In summary, cubic units have more irregular approximation properties than quadratic units. For musical purposes, the ear can distinguish only the first few approximations, for example the plastic number p is 11 cents from 4/3. The next approximant has an error of less than 1 cent, but at 49/37 is not a simple ratio. Other cubic units have approximations with larger denominators, for example the supergolden number is 1 cent from 22/15 and the tribonacci number 6 cents from 11/6. For comparison, the cubic irrationals in 12TET are four and eight semitones, with frequency ratios $2^{1/3}$ and $2^{2/3}$; these are about 14 cents from 5/4 and 8/5 respectively, and less than 1 cent from 63/50 and 100/63 respectively.

4. Defining scales

Since scales consist of isolated frequencies, we must keep only a finite number of values per τ-octave. There are at least two natural choices based on the definitions we have considered so far. We can use the norm as a bound, that is, define $S_N^B\left(\tau \right)=\{x>0||N(x)|\le B\}$ where the unit τ appears implicitly in the norm N, and the fact it is a unit implies the log-periodicity of the set. Another approach is to note that the set of x>0 with $N\left(x\right)>0$ forms a cone, and if convex (and it is for ϕ) is closed under both addition and multiplication and hence suitable for defining a scale $S_N^{B+}\left(\tau \right)$, replacing the inequality in the equation above by $0<N\left(x\right)\le B$; we will not consider this further here, except to note that $S_N^{36+}\left(\varphi \right)$ has the same number of notes as $S_{\text{β}}^5\left(\varphi \right)$ and so fits on a MIDI keyboard (see equations (7(7) $S_{\text{β}}^B\left(\tau \right)=\{x>0|\mathrm{\exists }{c}_j\text{greedy, so that}x=\sum _{j_{max}-B}^{j_{max}}{c}_j{\tau }^j\}$(7) ), (8(8) $1200\frac{\log {\varphi }^3}{\log 2}\approx 2499.27$(8) ) below).

Alternatively, we can use the greedy β-expansion and define (7) $S_{\text{β}}^B\left(\tau \right)=\{x>0|\mathrm{\exists }{c}_j\text{greedy, so that}x=\sum _{j_{max}-B}^{j_{max}}{c}_j{\tau }^j\}$(7) which is again log-periodic by definition. It is possible (but perhaps less natural) to remove the greedy condition, and impose only $c_j<\tau$. We will not consider this further here, except to note that $S_{\text{β}}^5(\varphi {)}_{\text{greedy}}=S_{\text{β}}^4(\varphi {)}_{\text{non-greedy}}$.

We now focus on the golden ratio, and consider two scales in $\mathbb{Z}\left[\varphi \right]$ satisfying the previously defined properties. The scale $S_{\text{β}}^5\left(\varphi \right)$ consists of notes with greedy β-expansion of $\le 6$ digits, leading to 8 notes per ϕ-octave, and will be denoted $S_{\text{β}}$ for brevity. The scale $S_N^{20}\left(\varphi \right)$ contains notes with norms of magnitude $\le 20$, leading to 10 notes per golden octave, which turns out to be those of $S_{\text{β}}$ together with two others (of 7 digit beta representation). This will be denoted $S_N$ for brevity.

As noted in the previous section, the greedy β-expansion base ϕ is characterized by sequences with no consecutive 1s. The norm is given in equation (2(2) $N(\mathrm{a\varphi }+b)=\left|\begin{array}{cc}a+b& a\\ a& b\end{array}\right|=b^2+\mathrm{ab}-a^2$(2) ) above. We have $N\left(\varphi \right)=-1$, so that multiplying or dividing by ϕ, corresponding to going up or down by a golden octave, leads to a change of sign in the norm. Using these definitions, the notes of the scales $S_N$ and $S_{\text{β}}$ defined above are those presented in Table 2.

Table 2. Notes of the golden scale $S_N$.

Name	Frequency ratio	β-expansion	Lattice	Exact	Norm
α	1.00000	1	(0,1)	1	1
$\alpha \mathrm{♯}$	1.05573	1.000001	(−8, 14)	$2\sqrt{5}/{\varphi }^3$	20
$\text{β}\mathrm{♭}$	1.09017	1.00001	(5, −7)		−11
β	1.14590	1.0001	(−3, 6)	$3/{\varphi }^2$	9
γ	1.23607	1.001	(2, −2)	$2/\varphi$	−4
$\gamma \mathrm{♯}$	1.29180	1.001001	(−6, 11)		19
$\delta \mathrm{♭}$	1.32624	1.00101	(7, −10)		−19
δ	1.38197	1.01	(−1, 3)	$\sqrt{5}/\varphi$	5
$ϵ\mathrm{♭}$	1.47214	1.01001	(4, −5)		−11
ϵ	1.52786	1.0101	(−4, 8)	$4/{\varphi }^2$	16

Note: The scale $S_{\text{β}}$ consists of these apart from $\alpha \mathrm{♯}$ and $\gamma \mathrm{♯}$. The β-expansion and norm are to base ϕ. The lattice column gives $(a,b)$ for the expression $\mathrm{a\varphi }+b$. Transposing by a golden octave (factor of ϕ) flips the sign of the norms.

The naming of the pitch classes uses $\{\alpha ,\text{β},\gamma ,\delta ,ϵ\}$ for numbers represented by at most 5 digits in the β-expansion. A ♭ or ♯ corresponds to taking or adding ${\varphi }^{-6}$ to these, respectively. For more general $S_{\text{β}}^B\left(\tau \right)$ or $S_N^B\left(\tau \right)$, it is natural to give notes in scales with smaller B separate letters, and accidentals for the rest, but it seems difficult to make from this a precise and workable standard nomenclature.

The $S_{\text{β}}$ scale of eight pitch classes can be deployed by retuning a MIDI keyboard, since three golden octaves (24 notes) are close to the same number of semitones, more precisely (8) $1200\frac{\log {\varphi }^3}{\log 2}\approx 2499.27$(8) cents, that is, just under 25 semitones. The $S_N$ scale has too many pitch classes for a MIDI keyboard but the advantage that it contains more arithmetic progressions, chords of fixed difference tone frequency.

For a suitable choice of fundamental frequency f, there are sequences of the form $f{\varphi }^n$ which for large n are all close to integers following from the Pisot property of ϕ above. We choose f to be $f={\varphi }^{10}/\sqrt{5}\approx 55.0036$ Hz, which due to equation (3(3) $\begin{array}{rl}{\varphi }^n-(-\varphi {)}^{-n}& =F_n\sqrt{5}\end{array}$(3) ) is close to a Fibonacci number. The Fibonacci frequency 55 Hz is A1 on the usual 12TET scale, being three octaves below concert pitch ($440\mathrm{Hz}=55\times 2^3\mathrm{Hz}$). Here we use Greek letters for notes on the golden scale, and denote the fundamental frequency $\alpha 1$. The frequencies for both scales are given in Table 3 and a mapping (of $S_{\text{β}}$) to a MIDI keyboard is given in Table 4; see also the Online Supplement files described at the end of this paper. Note that we have shifted this correspondence by two semitones, so $\alpha 1$ corresponds to B1, in order to reduce the amount of tuning required in higher octaves, and also to balance the most extreme accidentals (C♭ and E♯).

Table 3. Frequencies in the golden scales.

	α	$\alpha \mathrm{♯}$	$\text{β}\mathrm{♭}$	β	γ	$\gamma \mathrm{♯}$	$\delta \mathrm{♭}$	δ	$ϵ\mathrm{♭}$	ϵ
−4								6.854	7.301	7.578
−3	8.025	8.472	8.748	9.196	9.919	10.37	10.64	11.09	11.81	12.26
−2	12.98	13.71	14.16	14.88	16.05	16.78	17.22	17.94	19.12	19.84
−1	21.01	22.18	22.90	24.07	25.97	27.14	27.86	29.03	30.93	32.10
0	33.99	35.89	37.06	38.95	42.02	43.91	45.08	46.98	50.04	51.94
1	55.00	58.07	59.96	63.03	67.99	71.05	72.95	76.01	80.97	84.04
2	89.00	93.96	97.02	102	110	115	118	123	131	136
3	144	152	157	165	178	186	191	199	212	220
4	233	246	254	267	288	301	309	322	343	356
5	377	398	411	432	466	487	500	521	555	576
6	610	644	665	699	754	788	809	843	898	932
7	987	1042	1076	1131	1220	1275	1309	1364	1453	1508
8	1597	1686	1741	1830	1974	2063	2118	2207	2351	2440
9	2584	2728	2817	2961	3194	3338	3427	3571	3804	3948
10	4181	4414	4558	4791	5168	5401	5545	5778	6155	6388
11	6765	7142	7375	7752	8362	8739	8972	9349	9959	10336
12	10946	11556	11933	12543	13530	14140	14517

Note: All frequencies over 100Hz are within 0.05 of integers.

Table 4. Keyboard mapping of $S_{\text{β}}$, over the full MIDI range.

	α	$\text{β}\mathrm{♭}$	β	γ	$\delta \mathrm{♭}$	δ	$ϵ\mathrm{♭}$	ϵ
−4						C-1	D♭-1	D-1
−3	D♯-1	E-1	E♯-1	F♯-1	G-1	G♯-1	A-1	A♯-1
−2	B-1	C0	C♯0	D0	E♭0	E0	F0	F♯0
−1	G0	A♭0	A0	B♭0	C♭1	C1	D♭1	D1
0	D♯1	E1	E♯1	F♯1	G1	G♯1	A1	A♯1
1	B1	C2	C♯2	D2	E♭2	E2	F2	F♯2
2	G2	A♭2	A2	B♭2	C♭3	C3	D♭3	D3
3	D♯3	E3	E♯3	F♯3	G3	G♯3	A3	A♯3
4	B3	C4	C♯4	D4	E♭4	E4	F4	F♯4
5	G4	A♭4	A4	B♭4	C♭5	C5	D♭5	D5
6	D♯5	E5	E♯5	F♯5	G5	G♯5	A5	A♯5
7	B5	C6	C♯6	D6	E♭6	E6	F6	F♯6
8	G6	A♭6	A6	B♭6	C♭7	C7	D♭7	D7
9	D♯7	E7	E♯7	F♯7	G7	G♯7	A7	A♯7
10	B7	C8	C♯8	D8	E♭8	E8	F8	F♯8
11	G8	A♭8	A8	B♭8	C♭9	C9	D♭9	D9
12	D♯9	E9	E♯9	F♯9	G9

Note: The enharmonic equivalents are chosen so that the pitch classes $\{\alpha ,\text{β},\gamma ,\delta ,ϵ\}$ correspond to a minor scale on D♯, B or G.

5. Additive properties – arithmetic sequences

Arithmetic sequences are one of the main motivations for considering scales based on number fields, since they have common difference tones, which may also be in the scale. Looking at the lattice representations of the notes in Table 2 it is clear that there are some arithmetic sequences, for example $\{\alpha ,\gamma ,ϵ\mathrm{♭}\}$. However, it is not obvious how to identify all such sequences, given the repetition of the scale in different octaves. If all can be identified for a given fixed scale, it is still not clear how to choose a finite set of pitch classes to maximise (in some precise sense) the number of such sequences.

Whilst we cannot give a definitive answer to these questions here, we can point to a useful approach for identifying arithmetic sequences. In Figure 1 we plot the notes of the scale with log magnitude $\ln (\mathrm{a\varphi }+b)$ on the x-axis and norm $b^2+\mathrm{ab}-a^2$ on the y-axis. The plot is invariant under transposition by a ϕ-octave, which corresponds to translation by $\ln \varphi \approx 0.4812$ to the right and reflection across the horizontal axis.

Arithmetic sequences are straight lines in $(a,b)$ space, which become suitably curved in these coordinates. We included the most relevant curved segments in Figure 1; clearly they are in fact dense. The additional two notes in $S_N$, $\alpha \mathrm{♯}$ and $\gamma \mathrm{♯}$, are thus helpful in providing the long arithmetic sequence $\{ϵ1,\delta \mathrm{♭}2,\alpha \mathrm{♯}3,\gamma \mathrm{♯}3,ϵ3,\text{β}\mathrm{♭}4,\gamma 4,\delta 4,ϵ4\}$ and in extending two of the others.

6. Multiplicative properties – intervals

Given the emphasis on additive properties, that is, many difference tones are equal, it is not surprising that with regard to multiplicative properties, the reverse is true, that is, almost all ratios (corresponding to musical intervals) are different. The intervals, up to three golden octaves, are given in Table 5.

Table 5. Intervals in the golden scales, in cents.

	α	$\alpha \mathrm{♯}$	$\text{β}\mathrm{♭}$	β	γ	$\gamma \mathrm{♯}$	$\delta \mathrm{♭}$	δ	$ϵ\mathrm{♭}$	ϵ
$\alpha \mathrm{♯}$	94
$\text{β}\mathrm{♭}$	149	56
β	236	142	86
γ	367	273	217	131
$\gamma \mathrm{♯}$	443	349	294	207	76
$\delta \mathrm{♭}$	489	395	339	253	122	46
δ	560	466	411	324	193	117	71
$ϵ\mathrm{♭}$	669	576	520	434	303	226	181	109
ϵ	734	640	584	498	367	291	245	174	64
α	833	739	684	597	466	390	344	273	164	99
$\alpha \mathrm{♯}$	927	833	778	691	560	484	438	367	257	193
$\text{β}\mathrm{♭}$	983	889	833	747	616	539	494	422	313	249
β	1069	975	919	833	702	626	580	509	399	335
γ	1200	1106	1051	964	833	757	711	640	531	466
$\gamma \mathrm{♯}$	1276	1182	1127	1041	909	833	788	716	607	543
$\delta \mathrm{♭}$	1322	1228	1172	1086	955	879	833	762	652	588
δ	1393	1299	1244	1157	1026	950	904	833	724	659
$ϵ\mathrm{♭}$	1503	1409	1353	1267	1136	1059	1014	943	833	769
ϵ	1567	1473	1417	1331	1200	1124	1078	1007	897	833
α	1666	1572	1517	1430	1299	1223	1177	1106	997	932
$\alpha \mathrm{♯}$	1760	1666	1611	1524	1393	1317	1271	1200	1091	1026
$\text{β}\mathrm{♭}$	1816	1722	1666	1580	1449	1372	1327	1256	1146	1082
β	1902	1808	1752	1666	1535	1459	1413	1342	1232	1168
γ	2033	1939	1884	1797	1666	1590	1544	1473	1364	1299
$\gamma \mathrm{♯}$	2109	2016	1960	1874	1743	1666	1621	1549	1440	1376
$\delta \mathrm{♭}$	2155	2061	2006	1919	1788	1712	1666	1595	1485	1421
δ	2226	2132	2077	1990	1859	1783	1737	1666	1557	1492
$ϵ\mathrm{♭}$	2336	2242	2186	2100	1969	1892	1847	1776	1666	1602
ϵ	2400	2306	2251	2164	2033	1957	1911	1840	1731	1666
α	2499	2405	2350	2263	2132	2056	2010	1939	1830	1765
$\alpha \mathrm{♯}$		2499	2444	2357	2226	2150	2104	2033	1924	1859
$\text{β}\mathrm{♭}$			2499	2413	2282	2205	2160	2089	1979	1915
β				2499	2368	2292	2246	2175	2066	2001
γ					2499	2423	2377	2306	2197	2132
$\gamma \mathrm{♯}$						2499	2454	2382	2273	2209
$\delta \mathrm{♭}$							2499	2428	2319	2254
δ								2499	2390	2326
$ϵ\mathrm{♭}$									2499	2435
ϵ										2499

Table 2 illustrates this, in that since the norm is multiplicative, the ratios are seen to differ for almost all combinations. Even where two norms have magnitude 11 or 19, the ratios are not algebraic integers, since the only units in $\mathbb{Z}\left[\varphi \right]$ are powers of ϕ.

Table 2 also illustrates some special intervals using the “exact” column. There are rational intervals with ratios 2 ($\alpha 1$-$\gamma 2$, $\gamma 1$-$ϵ2$, $\delta 1$-$\alpha \mathrm{♯}3$), 3 ($\alpha 1$-$\text{β}3$) and related combinations (4/3, 3/2, 4), as well as maximally irrational intervals ϕ (all notes up a golden octave) and $\sqrt{5}$ ($\alpha 1$-$\delta 2$, $\gamma 1$-$\alpha \mathrm{♯}3$). Combining ϕ with the other intervals also yields combinations that occur more than once, for example a golden third of ratio $2/\varphi =\sqrt{5}-1\approx 1.236$, is found for $\alpha 1$-$\gamma 1$, $\gamma 1$-$ϵ1$ and $\delta 1$-$\alpha \mathrm{♯}2$. This interval lies between that of minor and major thirds, for example the just minor third $6/5=1.2$ and 12TET minor third $2^{1/4}\approx 1.189$ and just major third $5/4=1.25$ and 12TET major third $2^{1/3}\approx 1.260$. Similarly for other intervals such as a golden fourth ${\varphi }^2/2\approx 1.309$ which is a little less than just perfect fourth $4/3\approx 1.333$ and 12TET perfect fourth $2^{5/12}\approx 1.335$ and corresponds to $\gamma 1$-$\alpha 2$, $ϵ1$-$\gamma 2$ and $\alpha \mathrm{♯}1$-$\delta 1$. The only geometric sequences are $\mathrm{\alpha a}$-$\mathrm{\gamma b}$-$\mathrm{ϵc}$ and $\mathrm{\xi a}$-$\mathrm{\xi b}$-$\mathrm{\xi c}$ where $(a,b,c)$ are integers in arithmetic progression (including all equal) and ξ is any pitch class.

Equation (3(3) $\begin{array}{rl}{\varphi }^n-(-\varphi {)}^{-n}& =F_n\sqrt{5}\end{array}$(3) ) gives some large “approximately integer” intervals. For $\delta 1$-$\mathrm{\alpha n}$ we have a frequency ratio ${\varphi }^n/\sqrt{5}$, and for large n the ${\varphi }^{-n}$ can be neglected leading to a Fibonacci interval. For example n = 6: (9) $\frac{{\varphi }^6}{\sqrt{5}}\approx 8.0249$(9) which is about 4 cents above three conventional octaves.

7. The sum-product conjecture

The observation referred to above, that there are few differences suggests that there are many intervals, is close to a well known problem in the mathematical literature. The sum-product phenomenon asserts that for a finite set A in a suitable ambient space (here $\mathbb{R}$), at least one of the sum set A + A and the product set AA should be large. One form of this is the Erd$ó$s-Szemerédi sum-product conjecture which states that for all large $|A|$ we have (10) $max\{|A+A|,|\mathrm{AA}|\}\ge |A{|}^{2-o\left(1\right)}$(10) The best rigorous bound has an exponent of 1.335 (Rudnev and Stevens 2022).

Our scales have relatively few sums but many products, whilst the closest relative, the Bohlen 833 scale (see the introduction), has fewer products. This is depicted in Figure 2. Note that our scales have fewer sums and differences as expected, with a transition to quadratically increasing behaviour at around five golden octaves, the precision of the β-expansion. For seven octaves of $S_N$, we have $|A|=70$, $|A+A|=516$, $|\mathrm{AA}|=678$, so both $|A+A|$ and $|\mathrm{AA}|$ are less than $|A{|}^{1.54}$. This suggests that a growing sequence of sets along these lines (for example, all elements of a ring with bounds on magnitude and norm) may be a possible example to test the sum-product conjecture.

8. Implementing the scales

It is possible to synthesize sounds of arbitrary waveform and frequency electronically, though many software packages assume octave equivalence for powers of 2, even where notes within each octave may be tuned individually. One option for either computer or MIDI keyboard is websynths.org; Tables 3, 4 provide the relevant mappings; see the Online Supplement files.

It may also be possible to retune stringed instruments. Guitars with retuned strings and moved frets are commonly used in microtonal music (Nielsen 2003). Similarly for bowed stringed instruments or the piano (using the above keyboard mapping), though we have not yet tried and cannot vouch for the safety. Similarly, it is possible using instruments allowing arbitrary pitch including trombone and voice.

Musical instruments apart from synthesized sine waves generate harmonics other than the fundamental frequency. For those with uniform strings or columns of air, these are at close to integer multiples of the fundamental, which is one of the main explanations for rational frequency ratios in music. These however do not correspond to notes on the golden ratio scales except where the fundamental is α or δ.

It is possible to design strings to have specified overtones by using variable thickness. Unfortunately it does not seem practical in this way to generate all the powers of ϕ, which would thus lie in the scale for all the notes; see Sethares and Hobby (2018). As a simpler case, we have considered a string of length L and mass $m_S={\mu }_{S}L$ with a small weight at a point xL along it of mass $m_2$ using the formalism in the above paper; see equations (1(1) $1200{\log }_2\left(\frac{f_2}{f_1}\right)\mathrm{cents}$(1) )–(4(4) $\begin{array}{rl}{\varphi }^n+(-\varphi {)}^{-n}& =F_{n+1}+F_{n-1}\end{array}$(4) ) there. More specifically, we have a string of three segments with linear mass densities ${\mu }_j$ and lengths $l_j$ where $l_1=\mathrm{xL}$, $l_3=(1-x)L$, ${\mu }_3={\mu }_1={\mu }_S$ and ${\mu }_2=m_2/l_2$. Taking the limit $l_2\to 0$ with $m_2$ fixed, the mode equation with appropriate boundary conditions (equation (4(4) $\begin{array}{rl}{\varphi }^n+(-\varphi {)}^{-n}& =F_{n+1}+F_{n-1}\end{array}$(4) ) in the above paper) reduces to (11) $\frac{\sin \tilde{\omega }}{\tilde{\omega }}=\frac{m_2}{m_S}\sin \left(\tilde{\omega }x\right)\sin \left(\tilde{\omega }\right(1-x\left)\right)$(11) where $\tilde{\omega }=\omega \sqrt{m_S/T}$ is a dimensionless frequency and T is the string tension. Optimising to find x = 0.116934 and $m_2/m_S=0.519991$, the frequencies of vibration relative to the fundamental become $\{1,1.618,2.618,3.812,5.037,6.271,\dots \}$. In other words, it is possible with only a single additional mass to make the harmonic series of a string start with frequency ratios $1:\varphi :{\varphi }^2$.

Alternatively, geometric sequences of vibration modes may be created in fractal structures; see Strichartz (1999). Note that irrational harmonics lead to aperiodic wave-forms; for harmonics of sufficiently large amplitude, they may have interesting non-differentiable or fractal properties, along the lines of Weierstrass's original construction of a nowhere-differentiable function (Kaplan, Mallet-Paret, and Yorke 1984).

9. Composition

Some ideas and principles can be found in the previous literature on (especially) tunings with a golden ratio octave (refer to the introduction). The main characteristics of the tunings considered here are the arithmetic progressions and many different intervals.

The arithmetic progressions have common difference tones (refer to Figure 1), and can be used for scales and chords. The long progression containing $\text{β}\mathrm{♭}$ and $ϵ\mathrm{♭}$ is relatively close to the harmonic series (the frequencies are in ratios $n-{\varphi }^{-4}$ for integer n).

The large variety of intervals can also be used to great effect. For example, the dissonant interval $ϵ\mathrm{♭}1-\text{β}3$ of just greater than an octave at 1232 cents can resolve to the perfect octave $\alpha 1-\gamma 2$, where the $\gamma 2$ is a perfect fifth below the $\text{β}3$. The golden third and sixth intervals are paradoxical in that thirds and sixths are normally considered consonant, but these are as irrational as possible, in the sense given in section 3.

Ideally, composition using the golden tuning should be on its terms, rather than imitating well known 12TET approaches. The 12TET tuning is homogeneous and cyclic: Each note is equivalent, and keys are arranged in the well known circle of fifths. In contrast, the golden tunings are based on a linear backbone of α notes, decorated by the other notes, each with its own place and character, at increasing distance from the backbone. Distance here can refer to the number of digits needed in the β-expansion, resulting in the ordering α, δ, γ, $\{\text{β},ϵ\}$, $\{\text{β}\mathrm{♭},\delta \mathrm{♭},ϵ\mathrm{♭}\}$, $\{\alpha \mathrm{♯},\text{β}\mathrm{♯},\gamma \mathrm{♯},\delta \mathrm{♯},ϵ\mathrm{♯}\}$, …. Or, it can refer to the norm, which gives the similar ordering α, γ, δ, β, $\{\text{β}\mathrm{♭},ϵ\mathrm{♭}\}$, ϵ, $\{\gamma \mathrm{♯},\delta \mathrm{♭}\}$, $\alpha \mathrm{♯}$, ….

The parallel organum common in ninth century chant mentioned in the introduction also works here, with the perfect fourth or fifth replaced by the golden ratio octave. We could alternatively (or as well) use two golden ratio octaves, which is 34 cents below a 12TET perfect eleventh.

The composition Three Places (in the Supplemental Online material) is written using the keyboard mapping of $S_{\text{β}}$ shown in Table 4. The intention was to approach the tuning system entirely intuitively, allowing the ear to guide the process and pick out interesting chords and pitch combinations. Given the lack of octave periodicity, the piece is formed from three localized musical ideas and their interactions. Each musical idea is described as a ‘place’, and whilst the notes contained in each idea are relatively consonant, the transition from one idea to the next can be abrupt and surprising. With music composed using unfamiliar tuning systems, a ‘settling in’ period of adjustment can be helpful to the listener, provided in Three Places by the oscillating tones at the opening of the piece.

10. Conclusion

Golden ratio scales have led us to wide vistas of mathematics, including many aspects of algebraic number theory, the sum-product conjecture, and non-differentiable curves. There are many open mathematical questions, for example, if we constrain the number of notes per octave, are these scales optimal from the point of view of the number of arithmetic sequences or of sum or difference tones in the scale? From a musical point of view there remains the challenging task of further developing relevant principles of melody and harmony. The same approach, defining scales by bounding the β-expansion or norm, can be applied to other algebraic units, such as those in Table 1.

Acknowledgments

The authors acknowledge helpful discussions with Dan Fretwell, Jake Langham and Misha Rudnev.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplemental data

Supplemental data for this article can be accessed online at http://dx.doi.org/10.1080/17459737.2023.2234126.

Additional information

Funding

The authors are grateful for the support of the University of Bristol School of Mathematics composer-in-residence project, in conjunction with CREATE-REACT.