Polynomial interpolation and residue currents

Abstract

We show that a global holomorphic section of $\mathcal{O}\left(d\right)$ restricted to a closed complex subspace $X\subset {\mathbb{P}}^n$ has an interpolant if and only if it satisfies a set of moment conditions that involves a residue current associated with a locally free resolution of ${\mathcal{O}}_X$. When X is a finite set of points in ${\mathbb{C}}^n\subset {\mathbb{P}}^n$ this can be interpreted as a set of linear conditions that a function on X has to satisfy in order to have a polynomial interpolant of degree at most d.

KEYWORDS:

• Polynomial interpolation
• residue currents
• moment conditions
• Hermite interpolation

AMS SUBJECT CLASSIFICATIONS:

• 32A27
• 32C30

1. Introduction

Let $i:X\hookrightarrow {\mathbb{C}}^n$ be a subvariety or complex subspace whose underlying space, $X_{red}$, is a finite set of points $\{p_0,\dots ,p_r\}\subset {\mathbb{C}}^n$. Let g be a holomorphic function on X, i.e. a global holomorphic section of ${\mathcal{O}}_X$, and let $G\in \mathbb{C}[{\zeta }_1,\dots ,{\zeta }_n]$ be a polynomial. We say that G interpolates g if the pull-back of G to X equals g, i.e. $i^{\ast }G=g$.

If X is reduced, then a holomorphic function g on X is just a function from $X_{red}=\{p_0,\dots ,p_r\}$ to $\mathbb{C}$, and we have that G interpolates g if $G\left(p_j\right)=g\left(p_j\right)$ for each $j=0,\dots ,r$. In the univariate case this is referred to as Lagrange interpolation. If X is not reduced, then at each point $p_j$, G also has to satisfy some conditions on its derivatives. In the univariate case this is referred to as Hermite interpolation, see Example 4.3.

The motivating question for this note is the following. What are the necessary and sufficient conditions on g for the existence of an interpolant of degree at most d?

Let $A_X$ denote the vector space of holomorphic functions on X, i.e. $A_X=H^0({\mathbb{C}}^n,{\mathcal{O}}_X)$. Since the set of holomorphic functions on X that have an interpolant of degree at most d is a linear subspace of $A_X$, we have that a function $g\in A_X$ has an interpolant of degree at most d if and only if it satisfies a finite set of linear conditions. In this note we will show how these linear conditions can be explicitly realized as a set of moment conditions that involves a so-called residue current associated with a locally free resolution of ${\mathcal{O}}_X$.

Recall that since $X_{red}$ is a finite set of points, X can be viewed as a closed complex subspace of ${\mathbb{P}}^n$, and we have that polynomials of degree at most d on ${\mathbb{C}}^n$ naturally correspond to global holomorphic sections of the line bundle $\mathcal{O}\left(d\right)\to {\mathbb{P}}^n$ via d-homogenization. This motivates the following more general notion of interpolation that we shall consider in this note. Let $i:X\hookrightarrow {\mathbb{P}}^n$ be a closed complex subspace of arbitrary dimension. Let Φ and φ be global holomorphic sections of $\mathcal{O}\left(d\right)$ and ${\mathcal{O}}_X\left(d\right)=i^{\ast }\mathcal{O}\left(d\right)$, respectively. We say that Φ interpolates φ if $i^{\ast }\mathrm{\Phi }=\phi$.

From a minimal graded free resolution of the homogeneous coordinate ring of X, $S_X$, we obtain a locally free resolution of ${\mathcal{O}}_X$ of the form (1) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_{{\mathbb{P}}^n}⟶{\mathcal{O}}_X⟶0$(1) where $E_k=\underset{\ell }{⨁}\mathcal{O}(-\ell {)}^{{\text{β}}_{k,\ell }}$, see [1] and [2, Section 6]. The ${\text{β}}_{k,\ell }$ are referred to as the graded Betti numbers of $S_X$. We equip the $E_k$ with the natural Hermitian metrics. In [2], Andersson and Wulcan showed that with (1(1) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_{{\mathbb{P}}^n}⟶{\mathcal{O}}_X⟶0$(1) ), one can associate a residue current R that generalizes the classical Coleff–Herrera product [3], see Section 2. It can be written as $R=\sum _{k,\ell }{R}_{k,\ell }$, where each $R_{k,\ell }$ is an $\mathcal{O}(-\ell {)}^{{\text{β}}_{k,\ell }}$-valued $(0,k)$-current. In [4], the same authors proved a result which as a special case gives a cohomological condition in terms of the current R for when Φ interpolates φ. In Section 3 we will show that in our setting this condition amounts to the following set of moment conditions.

Theorem 1.1

Let $X\subset {\mathbb{P}}^n$ be a closed complex subspace, and let R be the residue current associated with  (1(1) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_{{\mathbb{P}}^n}⟶{\mathcal{O}}_X⟶0$(1) ). Moreover, let ω be a nonvanishing holomorphic $\mathcal{O}(n+1)$-valued n-form. A global holomorphic section φ of ${\mathcal{O}}_X\left(d\right)$ has an interpolant if and only if for each ℓ it holds that (2) ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$(2) for all global holomorphic sections h of $\mathcal{O}(\ell -d-n-1)$.

Recall that the interpolation degree of X is defined as $inf\{d:\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{f}{\mathcal{O}}_{\mathrm{X}}\left(\mathrm{d}\right)\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}\}.$ In particular, if $X_{red}$ is a finite set of points in ${\mathbb{C}}^n$, then the interpolation degree of X is the smallest number d such that any $g\in A_X$ has an interpolant of degree at most d. Define (3) $t_k\left(S_X\right)=sup\{\ell :{\text{β}}_{k,\ell }\ne 0\}.$(3) (We use the convention that the supremum of the empty set is $-\mathrm{\infty }$.) As a consequence of Theorem 1.1 we get the following bound of the interpolation degree.

Corollary 1.2

Let $X\subset {\mathbb{P}}^n$ be a closed complex subspace with homogeneous coordinate ring $S_X$. The interpolation degree of X is less than or equal to $t_n\left(S_X\right)-n$.

It can be shown by purely algebraic means that the interpolation degree of X is in fact equal to $t_n\left(S_X\right)-n$, see e.g. [5, Corollary 1.6]. If $X_{red}$ consists of a finite set of points, then it can be shown that $t_n\left(S_X\right)-n$ is equal to the Castelnuovo–Mumford regularity of $S_X$, see [1, Exercise 4E.5], and the statement in this case is Theorem 4.1 in [1].

In Section 4 we will consider the case when $X_{red}$ is a finite set of points in ${\mathbb{C}}^n$. In this case the corresponding versions of Theorem 1.1 and Corollary 1.2 first appeared in [6]. We will consider some examples where we explicitly write down the conditions for when $g\in A_X$ has an interpolant of degree at most d. In particular, we will obtain the precise conditions for when the Hermite interpolation problem has a solution.

2. Residue currents

Let f be a holomorphic function in an open set in ${\mathbb{C}}^n$. Let ξ be a smooth $(n,n)$-form with compact support. In [7], using Hironaka's desingularization theorem, Herrera and Lieberman proved that the limit (4) $\underset{ϵ\to 0}{lim}{\int }_{|f|>ϵ}\frac{\xi }{f}$(4) exists. Thus (4(4) $\underset{ϵ\to 0}{lim}{\int }_{|f|>ϵ}\frac{\xi }{f}$(4) ) defines a current known as the principal value current, which is denoted by $\left[1/f\right]$. The residue current $R^f$ of f is the $(0,1)$-current $\overline{\mathrm{\partial }}\left[1/f\right]$. It is easy to see that $R^f$ has its support on $V\left(f\right)=f^{-1}\left(0\right)$, and that it satisfies the following duality principle: A holomorphic function Φ belongs to the ideal $\left(f\right)$ if and only if $R^f\mathrm{\Phi }=0$.

Example 2.1

Let ${\zeta }_0\in \mathbb{C}$. We have that the action of $\overline{\mathrm{\partial }}\left[1/\right(\zeta -{\zeta }_0\left)\right]$ on a test form $\xi \left(\zeta \right)\mathrm{d}\zeta$ is given by (5) $〈\overline{\mathrm{\partial }}\left[\frac{1}{\zeta -{\zeta }_0}\right],\xi \left(\zeta \right)\mathrm{d}\zeta 〉=2\pi i\xi \left({\zeta }_0\right).$(5)

2.1. Residue currents associated with generically exact complexes

We will now consider a generalization of the above construction due to Andersson and Wulcan. Consider a generically exact complex of Hermitian holomorphic vector bundles over a complex manifold Y of dimension n, (6) $0⟶E_n\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}{E}_1\stackrel{f_1}{⟶}{E}_0⟶0,$(6) i.e. a complex that is exact outside an analytic variety $Z\subset Y$ of positive codimension. The vector bundle $E=\underset{k}{⨁}{E}_k$ has a natural superbundle structure, i.e. a ${\mathbb{Z}}_2$-grading, $E=E_{+}\oplus E_{-}$, where $E_{+}=\underset{k}{⨁}{E}_{2k}$ and $E_{-}=\underset{k}{⨁}{E}_{2k+1}$, which we shall refer to as the subspaces of even and odd elements, respectively. This induces a ${\mathbb{Z}}_2$-grading on the sheaf of E-valued currents $\mathcal{C}\left(E\right)$; if $\omega \otimes \xi$ is an E-valued current, where ω is a current and ξ is a smooth section of E, then the degree of $\omega \otimes \xi$ is the sum of the degree of ξ and the current degree of ω modulo 2.

We say that an endomorphism on E is even (resp. odd) if it preserves (resp. switches) the degree. If α is a smooth section of $\mathrm{E}\mathrm{n}\mathrm{d}E$, then it defines a map on $\mathcal{C}\left(E\right)$ via $\alpha (\omega \otimes \xi )=(-1{)}^{(\mathrm{deg}\alpha )(\mathrm{deg}\omega )}\omega \otimes \alpha (\xi ),$ where ω is a current and ξ is a smooth section of E. In particular, the map $f=\sum _{k=1}^n{f}_k$ defines an odd map on $\mathcal{C}\left(E\right)$. We define an odd map on $\mathcal{C}\left(E\right)$, $\mathrm{\nabla }=f-\overline{\mathrm{\partial }}$, which, since f and $\overline{\mathrm{\partial }}$ anti-commute, satisfies ${\mathrm{\nabla }}^2=0$. The map ∇ extends to an odd map on $\mathcal{C}\left(\mathrm{E}\mathrm{n}\mathrm{d}E\right)$ via Leibniz's rule, $\mathrm{\nabla }\left(\alpha \xi \right)=\left(\mathrm{\nabla }\alpha \right)\xi +(-1{)}^{\mathrm{deg}\alpha }\alpha \mathrm{\nabla }\xi .$ In [2], Andersson and Wulcan constructed $\mathrm{E}\mathrm{n}\mathrm{d}E$-valued currents $U=\sum _{\ell }{U}^{\ell }=\sum _{\ell }\sum _{k\ge \ell +1}{U}_k^{\ell },$ and $R=\sum _{\ell }{R}^{\ell }=\sum _{\ell }\sum _{k\ge \ell +1}{R}_k^{\ell },$ where $U_k^{\ell }$ and $R_k^{\ell }$ are $\mathrm{H}\mathrm{o}\mathrm{m}(E_{\ell },E_k)$-valued currents of bidegree $(0,k-\ell -1)$ and $(0,k-\ell )$, respectively, which satisfy (7) $\mathrm{\nabla }U={\mathrm{i}\mathrm{d}}_E-R,\mathrm{\nabla }R=0.$(7) The current R is referred to as the residue current associated with (6(6) $0⟶E_n\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}{E}_1\stackrel{f_1}{⟶}{E}_0⟶0,$(6) ) and it has its support on Z.

Suppose that the complex of locally free sheaves corresponding to (6(6) $0⟶E_n\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}{E}_1\stackrel{f_1}{⟶}{E}_0⟶0,$(6) ), (8) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}\mathcal{O}\left(E_0\right),$(8) is exact. When the $E_k$ are equipped with Hermitian metrics, we shall refer to (8(8) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}\mathcal{O}\left(E_0\right),$(8) ) as a Hermitian resolution of the sheaf $\mathcal{O}\left(E_0\right)/\mathrm{i}\mathrm{m}{f}_1$. In this case it holds that $R^{\ell }=0$ if $\ell \ge 1$, and henceforth we shall write $R_k$ for $R_k^0$. Moreover, we have that R satisfies the following properties:

Duality principle: A holomorphic section Φ of $E_0$ belongs to $\mathrm{i}\mathrm{m}{f}_1$ if and only if $R\mathrm{\Phi }=0$.

Dimension principle: If $\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{i}\mathrm{m}Z>k$, then $R_k=0$.

Note that the second equality in (7(7) $\mathrm{\nabla }U={\mathrm{i}\mathrm{d}}_E-R,\mathrm{\nabla }R=0.$(7) ) is equivalent to (9) $\begin{array}{rl}& f_1{R}_1=0,\end{array}$(9) (10) $\begin{array}{rl}& f_{k+1}{R}_{k+1}-\overline{\mathrm{\partial }}{R}_k=0,1\le k\le n-1,\end{array}$(10) (11) $\begin{array}{rl}& \overline{\mathrm{\partial }}{R}_n=0.\end{array}$(11) Let $i:X\hookrightarrow Y$ be a closed complex subspace with ideal sheaf ${\mathcal{I}}_X$, and suppose that ${\mathcal{O}}_X=i^{\ast }{\mathcal{O}}_Y$, which we identify with ${\mathcal{O}}_Y/{\mathcal{I}}_X$, has a Hermitian resolution of the form (12) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_Y⟶{\mathcal{O}}_X⟶0,$(12) cf.(8(8) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}\mathcal{O}\left(E_0\right),$(8) ) where $E_0$ is the trivial line bundle. For the associated residue current $R=R_1+\cdots +R_n$, we can view each $R_k$ as an $E_k$-valued $(0,k)$-current. Since $\mathrm{i}\mathrm{m}{f}_1={\mathcal{I}}_X$, we have that $i^{\ast }\mathrm{\Phi }=0$ if and only if $R\mathrm{\Phi }=0$ by the duality principle. More generally, let $L\to Y$ be a holomorphic line bundle. If we equip L with a Hermitian metric, then we obtain a Hermitian resolution of $i^{\ast }L={\mathcal{O}}_X\otimes L$ by tensoring (12(12) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_Y⟶{\mathcal{O}}_X⟶0,$(12) ) with L, and we have that R is the associated residue current with this resolution as well.

2.2. The Coleff–Herrera product

Let $f=(f_1,\dots ,f_p):{\mathbb{C}}^n\to {\mathbb{C}}^p$ be a holomorphic mapping such that $V\left(f\right)=f^{-1}\left(0\right)$ has codimension p. In [3] Coleff and Herrera gave meaning to the product (13) ${\mu }^f=\overline{\mathrm{\partial }}\left[\frac{1}{f_1}\right]\wedge \cdots \wedge \overline{\mathrm{\partial }}\left[\frac{1}{f_p}\right],$(13) which is known as the Coleff–Herrera product. In particular, if each $f_j$ only depends on ${\zeta }_j$, then (13(13) ${\mu }^f=\overline{\mathrm{\partial }}\left[\frac{1}{f_1}\right]\wedge \cdots \wedge \overline{\mathrm{\partial }}\left[\frac{1}{f_p}\right],$(13) ) is just the tensor product of the one-variable currents $\overline{\mathrm{\partial }}\left[1/f_j\right]$ described above. The current ${\mu }^f$ is $\overline{\mathrm{\partial }}$-closed, has support $V\left(f\right)$, and is anti-commuting in the $f_j$. Moreover, ${\mu }^f$ satisfies the duality principle, i.e. ${\mu }^f\mathrm{\Phi }=0$ if and only if $\mathrm{\Phi }\in \mathcal{I}\left(f\right)$, where $\mathcal{I}\left(f\right)$ is the ideal sheaf generated by f.

Let $H\to Y$ be a holomorphic Hermitian vector bundle of rank p, and let f be a holomorphic section of the dual bundle $H^{\ast }$. Let $E_k=\stackrel{k}{\bigwedge }H$, and define ${\delta }_k:E_k\to E_{k-1}$ as interior multiplication by f. This gives a generically exact complex (6(6) $0⟶E_n\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}{E}_1\stackrel{f_1}{⟶}{E}_0⟶0,$(6) ). Suppose $f=f_1{e}_1^{\ast }+\cdots +f_p{e}_p^{\ast }$ in some local holomorphic frame $e_j^{\ast }$ for $H^{\ast }$. If $\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{i}\mathrm{m}{f}^{-1}\left(0\right)=p$, then the corresponding complex of sheaves is a Hermitian resolution of ${\mathcal{O}}_Y/\mathcal{I}\left(f\right)$ known as the Koszul complex, and it was proven in [8] that the associated residue current is given by $R=R_p={\mu }^f{e}_1\wedge \cdots \wedge e_p$.

2.3. A comparison formula for residue currents

We have the following comparison formula for residue currents, see Theorem 1.3 and Corollary 4.7 in [9]. Let $X\subset X^{\prime }$ be complex subspaces of codimension p of Y. Suppose that there exist Hermitian resolutions of length p of ${\mathcal{O}}_X$ and ${\mathcal{O}}_{X^{\prime }}$, respectively, and let R and $R^{\prime }$ be the associated residue currents. Moreover, suppose that there exists a map of complexes

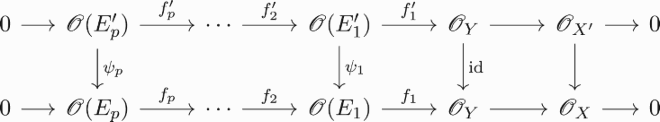
Then $R_p={\psi }_p{R}_p^{\prime }$.

3. Interpolation and residue currents

Let Y be a complex manifold of dimension n, and let $i:X\hookrightarrow Y$ be a closed complex subspace. Let $L\to Y$ be a holomorphic line bundle, and let Φ and φ be global holomorphic sections of L and $i^{\ast }L$, respectively. We say that Φ interpolates φ if $i^{\ast }\mathrm{\Phi }=\phi$.

Suppose that there exists a Hermitian resolution of ${\mathcal{O}}_X$ of the form (12(12) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_Y⟶{\mathcal{O}}_X⟶0,$(12) ), and let R denote the associated residue current. For each point $x\in Y$ there is a neighbourhood $\mathcal{U}$ and a holomorphic section $\tilde{\phi }$ of L such that $i^{\ast }\tilde{\phi }=\phi$ on $\mathcal{U}$. We define the current $R\phi$ on Y locally as $R\tilde{\phi }$. This is well-defined since if ${\tilde{\phi }}^{\prime }$ is another section such that $i^{\ast }{\tilde{\phi }}^{\prime }=\phi$, then $R(\tilde{\phi }-{\tilde{\phi }}^{\prime })=0$ by the duality principle.

We have the following result which follows immediately as a special case of Lemma 4.5 (ii) in [4].

Lemma 3.1

Let Φ and φ be global holomorphic sections of L and $i^{\ast }L$, respectively. Then Φ interpolates φ if and only if there exists a current w such that $\mathrm{\Phi }-R\phi =\mathrm{\nabla }w$.

In other words, φ has an interpolant if and only if there exist currents $w_1,\dots ,w_n$ such that $\overline{\mathrm{\partial }}{w}_n=R_n\phi$, and (14) $\overline{\mathrm{\partial }}{w}_k=f_{k+1}{w}_{k+1}+R_k\phi ,1\le k\le n-1.$(14) Moreover, in this case an interpolant of φ is given by $\mathrm{\Phi }=f_1{w}_1$. Note that Φ is holomorphic since $\overline{\mathrm{\partial }}\mathrm{\Phi }=-f_1\overline{\mathrm{\partial }}{w}_1=-f_1(f_2{w}_2+R_1\phi )=-\left(f_1{R}_1\right)\phi =0$. Here the last equality follows from (9(9) $\begin{array}{rl}& f_1{R}_1=0,\end{array}$(9) ).

Let us now consider interpolation on $Y={\mathbb{P}}^n$ with respect to the line bundle $L=\mathcal{O}\left(d\right)$. Recall that there is a Hermitian resolution of ${\mathcal{O}}_X$ of the form (1(1) $0⟶\mathcal{O}\left(E_n\right)\stackrel{f_n}{⟶}\cdots \stackrel{f_2}{⟶}\mathcal{O}\left(E_1\right)\stackrel{f_1}{⟶}{\mathcal{O}}_{{\mathbb{P}}^n}⟶{\mathcal{O}}_X⟶0$(1) ). We write $R_{k,\ell }$ for the $\mathcal{O}(-\ell {)}^{{\text{β}}_{k,\ell }}$-valued component of $R_k$.

If $R_n\phi =\overline{\mathrm{\partial }}{w}_n$ for some current $w_n$, then one can successively find currents $w_{n-1},\dots ,w_1$ such that (14(14) $\overline{\mathrm{\partial }}{w}_k=f_{k+1}{w}_{k+1}+R_k\phi ,1\le k\le n-1.$(14) ) holds since, in view of (10(10) $\begin{array}{rl}& f_{k+1}{R}_{k+1}-\overline{\mathrm{\partial }}{R}_k=0,1\le k\le n-1,\end{array}$(10) ), $\overline{\mathrm{\partial }}(f_{k+1}{w}_{k+1}+R_k\phi )=-f_{k+1}\overline{\mathrm{\partial }}{w}_{k+1}+\left(\overline{\mathrm{\partial }}{R}_k\right)\phi =-(f_{k+1}{R}_{k+1}-\overline{\mathrm{\partial }}{R}_k)\phi =0,$ and it follows from, e.g. [10, Theorem 10.7] that $H^{0,k}({\mathbb{P}}^n,E_k\otimes \mathcal{O}(d\left)\right)=0,1\le k\le n-1.$ We thus have the following condition for the existence of an interpolant.

Lemma 3.2

A global holomorphic section φ of ${\mathcal{O}}_X$ has an interpolant if and only if $R_n\phi$ is $\overline{\mathrm{\partial }}$-exact, i.e. there exists a current η such that $R_n\phi =\overline{\mathrm{\partial }}\eta$.

Proof

Proof of Theorem 1.1

By Serre duality we have that $R_{n,\ell }\phi$ is $\overline{\mathrm{\partial }}$-exact if and only if ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge \eta =0$ for all global $\overline{\mathrm{\partial }}$-closed $\mathcal{O}(\ell -d)$-valued $(n,0)$-forms η. Note that each such form is of the form $h\omega$ for some global holomorphic section h of $\mathcal{O}(\ell -d-n-1)$. Since $R_n\phi$ is $\overline{\mathrm{\partial }}$-exact if and only if each component $R_{n,\ell }\phi$ is, the statement follows from Lemma 3.2.

Proof

Proof of Corollary 1.2

Let $d\ge t_n\left(S_X\right)-n$, see (3(3) $t_k\left(S_X\right)=sup\{\ell :{\text{β}}_{k,\ell }\ne 0\}.$(3) ), and let φ be a global holomorphic section of ${\mathcal{O}}_X\left(d\right)$. We have for each ℓ that ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$ for all global holomorphic sections h of $\mathcal{O}(\ell -d-n-1)$. Indeed, if $\ell \le d+n$, the only such h is the zero section, and if $\ell >d+n$, then $R_{n,\ell }=0$ since ${\text{β}}_{n,\ell }=0$. Therefore φ has an interpolant by Theorem 1.1.

4. Polynomial interpolation

Let us now return to the topic of polynomial interpolation. Recall that the setting is that X is a complex subspace of ${\mathbb{C}}^n$ such that $X_{red}$ is a finite set of points. The aim of this section is to give some examples where we explicitly compute the residue current R associated with a Hermitian resolution of ${\mathcal{O}}_X$ and write down the moment conditions that Theorem 1.1 imposes on a function $g\in A_X$ for the existence of an interpolant of degree at most d. We do this by identifying g with a global holomorphic section φ of ${\mathcal{O}}_X\left(d\right)$ and use the fact that g has an interpolant of degree at most d if and only if φ has an interpolant. More precisely, we let $\left[z\right]=[z_0:\dots :z_n]$ denote homogeneous coordinates on ${\mathbb{P}}^n$, and we view ${\mathbb{C}}^n$ as an open complex subspace of ${\mathbb{P}}^n$ via the embedding $({\zeta }_1,\dots ,{\zeta }_n)\mapsto [1:{\zeta }_1:\dots :{\zeta }_n]$. Recall that on ${\mathbb{C}}^n$ there is a frame e for $\mathcal{O}\left(1\right)$ such that a global holomorphic section Φ of $\mathcal{O}\left(d\right)$ is given by $\mathrm{\Phi }({\zeta }_1,\dots ,{\zeta }_n)=G({\zeta }_1,\dots ,{\zeta }_n)e({\zeta }_1,\dots ,{\zeta }_n{)}^{\otimes d},$ where G is a polynomial of degree at most d on ${\mathbb{C}}^n$.

Throughout this section we shall let ω in Theorem 1.1 be the nonvanishing holomorphic $\mathcal{O}(n+1)$-valued n-form on ${\mathbb{P}}^n$ such that $\omega =\mathrm{d}{\zeta }_1\wedge \cdots \wedge \mathrm{d}{\zeta }_n\otimes e^{\otimes (n+1)}$ on ${\mathbb{C}}^n\subset {\mathbb{P}}^n$.

Note that the dimension principle gives that $R=R_n$, and throughout this section we write $R_{\ell }$ rather than $R_{n,\ell }$ for the $\mathcal{O}(-\ell {)}^{{\text{β}}_{n,\ell }}$-valued component of $R_n$.

Example 4.1

Let $X=\left\{\right(0,0),(1,0),(0,1),(1,1\left)\right\}\subset {\mathbb{C}}^2\subset {\mathbb{P}}^2$. We have that X is defined by the homogeneous ideal $I_X=(f_1,f_2)$, where $f_1=z_1(z_1-z_0)$ and $f_2=z_2(z_2-z_0)$. A Hermitian resolution of ${\mathcal{O}}_X$ is given by the Koszul complex, see Section 2.2, where we interpret $(f_1,f_2)$ as a global holomorphic section of $\mathcal{O}(2{)}^2$. Thus the associated residue current takes values in $\mathcal{O}(-4)$, and is given by the Coleff–Herrera product, see Section 2.2, $R=R_4=\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1({\zeta }_1-1)}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2({\zeta }_2-1)}\right]e^{\otimes (-4)}.$ By a straightforward computation, cf.(4(4) $\underset{ϵ\to 0}{lim}{\int }_{|f|>ϵ}\frac{\xi }{f}$(4) ), we get $\begin{array}{rl}{R}_4& =\left(\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]-\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1-1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]\right.\\ & -\left.\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2-1}\right]+\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1-1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2-1}\right]\right)e^{\otimes (-4)}.\end{array}$ By Theorem 1.1, we now get the following. Since $R_{\ell }=0$ for $\ell \ge 5$, we have that any $g\in A_X$ has an interpolant of degree at most 2. Moreover, g has an interpolant of degree at most 1 if and only if (2(2) ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$(2) ) holds when $\ell =4$ and h = 1. In view of (5(5) $〈\overline{\mathrm{\partial }}\left[\frac{1}{\zeta -{\zeta }_0}\right],\xi \left(\zeta \right)\mathrm{d}\zeta 〉=2\pi i\xi \left({\zeta }_0\right).$(5) ) this amounts to (15) $g(0,0)-g(1,0)-g(0,1)+g(1,1)=0,$(15) which is expected since the values of g at $(0,0)$, $(1,0)$, and $(0,1)$ uniquely determines a polynomial of degree at most 1 that takes the value $g(1,0)+g(0,1)-g(0,0)$ at $(1,1)$. Note that this gives that the interpolation degree of X is 2.

We have that g has a constant interpolant if and only if (2(2) ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$(2) ) holds for all global holomorphic h of $\mathcal{O}\left(1\right)$. By linearity we only need to check $h=z_0,z_1,z_2$, which amounts to (15(15) $g(0,0)-g(1,0)-g(0,1)+g(1,1)=0,$(15) ), $g(1,1)-g(1,0)=0$, and $g(1,1)-g(0,1)=0$. This amounts to $g(0,0)=g(1,0)=g(0,1)=g(1,1)$ as expected.

Example 4.2

Let $X=\left\{\right(0,0),(1,0),(0,1),(0,2\left)\right\}\subset {\mathbb{C}}^2\subset {\mathbb{P}}^2$. We have that X is defined by the homogeneous ideal $I_X=(z_1{a}_1,z_1{z}_2,z_2{a}_2)$, where $a_1=z_1-z_0$ and $a_2=(z_2-z_0)(z_2-2z_0)$. We have Hermitian resolutions of ${\mathcal{O}}_{{\mathbb{P}}^2}/\mathcal{I}(z_1{a}_1,z_2{a}_2)$ and ${\mathcal{O}}_X$ and a map of complexes:

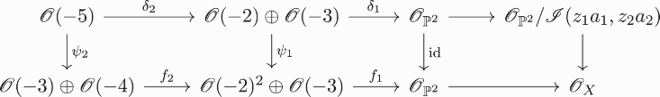
where the upper complex is the Koszul complex, see Section 2.2. Moreover, $f_1=\left[\begin{array}{ccc}{z}_1{a}_1& z_1{z}_2& z_2{a}_2\end{array}\right],f_2=\left[\begin{array}{cc}-z_2& 0\\ a_1& -a_2\\ 0& z_1\end{array}\right],$ and ${\psi }_1=\left[\begin{array}{cc}1& 0\\ 0& 0\\ 0& 1\end{array}\right],{\psi }_2=\left[\begin{array}{c}{a}_2\\ a_1\end{array}\right].$ Let R and $R^{\prime }$ denote the residue currents associated with the resolutions of ${\mathcal{O}}_X$ and $\mathcal{O}/\mathcal{I}(z_1{a}_1,z_2{a}_2)$, respectively. We have that $R^{\prime }=R_5^{\prime }$ takes values in $\mathcal{O}(-5)$ and is given by the Coleff–Herrera product, see Section 2.2, $R_5^{\prime }=\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1({\zeta }_1-1)}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2({\zeta }_2-1)({\zeta }_2-2)}\right]e^{\otimes (-5)}.$ Thus by the comparison formula, see Section 2.3, $R={\psi }_2{R}^{\prime }=R_3\oplus R_4$. A straightforward computation gives that $\begin{array}{rl}{R}_3& =\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1({\zeta }_1-1)}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]e^{\otimes (-3)}\\ & =\left(-\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]+\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1-1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]\right)e^{\otimes (-3)},\end{array}$ and $\begin{array}{rl}{R}_4& =\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2({\zeta }_2-1)({\zeta }_2-2)}\right]e^{\otimes (-4)}\\ & =\left(\frac{1}{2}\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2}\right]-\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2-1}\right]+\frac{1}{2}\overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_1}\right]\wedge \overline{\mathrm{\partial }}\left[\frac{1}{{\zeta }_2-2}\right]\right)e^{\otimes (-4)}.\end{array}$ By Theorem 1.1, we now get the following. Since $R_{\ell }=0$ for $\ell \ge 5$, we have that any $g\in A_X$ has an interpolant of degree at most 2. Moreover, g has an interpolant of degree at most 1 if and only if (2(2) ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$(2) ) holds when $\ell =4$ and h = 1. (Note that there is no condition involving $R_3$ since $\ell -d-n-1<0$ in this case.) In view of (5(5) $〈\overline{\mathrm{\partial }}\left[\frac{1}{\zeta -{\zeta }_0}\right],\xi \left(\zeta \right)\mathrm{d}\zeta 〉=2\pi i\xi \left({\zeta }_0\right).$(5) ) we get the condition (16) $\frac{1}{2}g(0,0)-g(0,1)+\frac{1}{2}g(0,2)=0,$(16) which is expected since g has an interpolant of degree at most 1 if and only if $g(0,1)$ is the average of $g(0,0)$ and $g(0,2)$. Note that this gives that the interpolation degree of X is 2.

We get that g has a constant interpolant if and only if (2(2) ${\int }_{{\mathbb{P}}^n}{R}_{n,\ell }\phi \wedge h\omega =0$(2) ) holds when $\ell =4$ for $h=z_0,z_1,z_2$, and when $\ell =3$ and h = 1. Since $z_1$ vanishes on the support of $R_4$, this amounts to Equation (16(16) $\frac{1}{2}g(0,0)-g(0,1)+\frac{1}{2}g(0,2)=0,$(16) ), $g(0,2)-g(0,1)=0$ and $g(1,0)-g(0,0)=0$. This amounts to $g(0,0)=g(1,0)=g(0,1)=g(0,2)$ as expected.

We end this note by considering Hermite interpolation. We refer to, e.g. [11–13], and references therein for a classical survey of this topic.

Example 4.3

Let $p_0,\dots ,p_r\in \mathbb{C}$, and let g be a holomorphic function on the complex subspace $X\subset \mathbb{C}$ defined by the ideal generated by $\prod _{j=0}^r(\zeta -p_j)$. Here we allow for the possibility that $p_i=p_j$ for some i, j, so that X is nonreduced in general, and we denote the number of times that $p_j$ occurs by $m_j$. We have that a polynomial G interpolates g if and only if, for each $j=0,\dots ,r$, $G^{\left(k\right)}\left(p_j\right)=g^{\left(k\right)}\left(p_j\right),k=0,\dots ,m_j-1.$ We say that a polynomial interpolates g with respect to $p_0,\dots ,p_k$, $k\le r$, if it interpolates the pull-back of g to the complex subspace defined by the ideal generated by $\prod _{j=0}^k(\zeta -p_j)$. We denote the unique polynomial that interpolates g with respect to $p_0,\dots ,p_k$ by $H[g;p_0,\dots ,p_k]$. The coefficient of its ${\zeta }^k$-term is referred to as the kth divided difference of g and we denote it by $g[p_0,\dots ,p_k]$. By induction it is not difficult to see that $H[g;p_0,\dots ,p_r]\left(\zeta \right)=\sum _{k=0}^{r}g[p_0,\dots ,p_k]\prod _{j=0}^{k-1}(\zeta -p_j),$ see [11, Theorem 1.8]. This is referred to as Newton's formula.

We claim that $g\in A_X$ has an interpolant of degree at most d if and only if $\left(gh\right)[p_0,\dots ,p_r]=0$ for all polynomials h of degree at most r−d−1. Let us show how this condition follows from Theorem 1.1. Since the ideal is generated by a single element, we have that the associated residue current is given by $R_{r+1}=\overline{\mathrm{\partial }}\left[\frac{1}{\prod _{j=0}^r(\zeta -p_j)}\right]e^{\otimes (-r-1)}.$ Theorem 1.1 together with Stokes' formula gives that g has an interpolant if and only if ${\int }_{\mathbb{C}}\overline{\mathrm{\partial }}\left[\frac{1}{\prod _{j=0}^r(\zeta -p_j)}\right]gh\wedge \mathrm{d}\zeta ={\int }_{C_R}\frac{H[gh;p_0,\dots ,p_r]\left(\zeta \right)}{\prod _{j=0}^r(\zeta -p_j)}\mathrm{d}\zeta =0$ for all polynomials h of degree at most r−d−1, where $C_R$ is a circle of radius $R\gg 0$. Here we have used the fact that $H[gh;p_0,\dots ,p_r]$ interpolates gh. By letting $R\to \mathrm{\infty }$, a direct calculation gives that the second integral is equal to $2\pi i\cdot \left(gh\right)[p_0,\dots ,p_r]$, and hence the claim follows.

Acknowledgments

I would like to thank Elizabeth Wulcan and Mats Andersson for helpful discussions and comments on preliminary versions of this note.

Disclosure statement

No potential conflict of interest was reported by the author(s).