Derived from the traditional principles of Islamic geometry, a methodology for generating non-periodic long-range sequences in one-dimension for 8-fold, 10-fold, and 12-fold rotational symmetries

Abstract

This paper explores the use of traditional principles of Islamic geometry to generate the long-range order of different non-period sequences in one-dimension. The discovery of quasicrystals with forbidden long-range order has uncovered a range of puzzling non-periodic symmetries, triggering a variety of investigations into understanding their complicated structural logic. The discovery of historical patterns in Islamic architecture with similar quasi-periodic formations is providing new insights into understanding the mathematical properties of these complicated formations. This paper argues that the hierarchical self-similar logic underlying the construction process of the historical patterns can serve as the key ingredient for resolving the long-range order of the one-dimensional non-periodic sequences. A case study approach is employed to test the hypotheses. Three historical patterns with non-period symmetries were tested: 10-fold rotational symmetry, 8-fold rotational symmetry and 12-fold rotational symmetry. The results show that the methodology is successful in generating three different non-periodic sequences in one-dimension.

GRAPHICAL ABSTRACT

KEYWORDS:

• Long-range order
• non-periodic sequence
• one-dimension
• Islamic geometry
• Fibonacci

Introduction

The discovery of quasicrystals (Shechtman et al., 1984) brought to light a new family of structures that exhibit long-range non-periodic order. The atoms in this new state of matter are not arranged in a periodic manner similar to traditional crystals, but exhibit a complicated long-range translational order that is not periodic (Levine & Steinhardt, 1984; Socolar et al., 1985; Levine & Steinhardt, 1986; Ishii & Fujiwara, 2008; Al Ajlouni, 2011). The discovery of these forbidden symmetries have inspired a substantial theoretical research concerning systems that are situated between perfectly periodic and chaotically random. Since its discovery, the interest in describing these systems has been of importance to many theoretical, scientific and applied fields (Macia, 2006, 2022). Specifically for the fields of Art and Architecture, these unusual formations exhibit astonishing visual and physical qualities, which can be ideally suited for investigating new applications, providing a rich source of formative and performative geometries (Ajlouni, 2018, 2021a, 2021b). Of special interest are the non-periodic long-range sequences in one-dimension. The most popular non-periodic long-range system has been defined by the Fibonacci sequence. This is due to its direct relationship to the three-dimensional Penrose tiling (Penrose, 1974). Also of interest are the generalized Fibonacci sequences (Horadam, 1961; Wolfram, 1998) and the Thue-Morse sequence (Thue, 1906, 1912; Morse, 1921). The most common methods for generating these non-periodic sequences are the use of substitution rules and the cut and project method. The goal of this paper is to present a new methodology based on the traditional principles of Islamic geometry that is able to generate different types of non-periodic sequences in one dimension.

Non-periodic geometry in Islamic art

The discovery of historical Islamic patterns exhibiting non-periodic geometry has triggered an interest in understanding the traditional principles that generated these complicated formations (Makovicky, 1992; Lu & Steinhardt, 2007; Al Ajlouni, 2012, 2013; Ajlouni, 2017). To date, three types of rotational symmetries have been documented. These include 10-fold quasi-periodic patterns (Makovicky, 1992; Makovicky et al., 1998; Lu & Steinhardt, 2007; Al Ajlouni, 2012), 8-fold quasi-periodic patterns (Emil Makovicky & Fenoll Hach-Alı, 1996; Al Ajlouni, 2013), and 12-fold non-periodic patterns (Makovicky & Makovicky, 2011). Figure 1 shows the central cartwheel formations of three historical examples; the pattern on Darb-i Imam shrine in Esfahan (1453) (Figure 1a), the pattern on the walls of the Hall of the Ambassadors in Alhambra, Spain (1354) (Figure 1d) and the dodecagonal pattern found in the tympanum of the entrance of the Zaouia Moulay Idriss II in Fez, Morocco (1308) (Figure 1g).

Figure 1. Three different nested networks exhibiting self-similar relational logic that grows based on a fixed ratio: (a–c) analysis of the central cartwheel formation of the pattern on Darb-i Imam shrine in Esfahan (1453), (d–f), analysis of the central cartwheel formation of the pattern on the walls of the Hall of the Ambassadors in Alhambra, Spain (1354), and (g–i) analysis of the central cartwheel formation of the dodecagonal pattern found in the tympanum of the entrance of the Zaouia Moulay Idriss II in Fez, Morocco (1308).

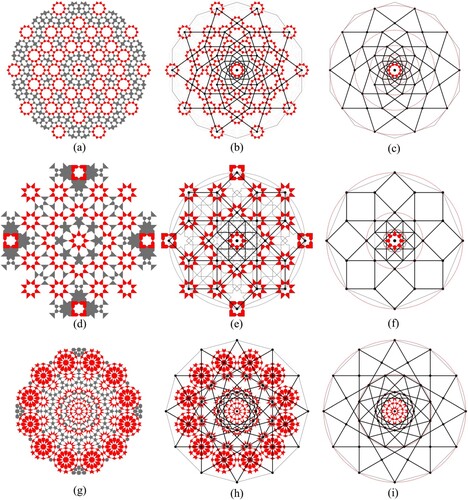
In an effort to understand the generating principals of these complicated formations, few methods have been investigated. This paper utilizes a multi-level hierarchical framework method, which was introduced by Ajlouni in 2012. The process utilizes an underlying framework of nested polygrams to construct the infinite formations of the non-periodic patterns. The process of generating the long-range non-periodic order is based on building a multi-level hierarchical logic, in which every hierarchy is based on the previous level. The hierarchical logic is achieved by building a progression of nested self-similar polygrams based on the different rotational symmetries. Examples of 10-fold, 8-fold and 12-fold networks of nested polygrams are demonstrated in Figure 1. These networks are constructed by drawing rotational lines connecting points or mid-points on the initial polygon, which produces a smaller scale internal polygon. By repeating the same process on the smaller polygon, a new generation of the smaller polygon appears. The different nested polygrams networks exhibit unique self-similar relational logic that grows based on a fixed ratio. By examining the three networks of nested polygrams in Figure 1c, f, i, we find that if we denote the radius of any of the nested polygrams by r and the radius of the next larger polygram by r + 1, then the ratio of (r + 1)/r is equal to the golden ratio (1+√5)/2 for the 10-fold network (Figure 1c), the irrational factor of √2 + 1 for 8-fold network (Figure 1f), and the square irrational factor of √(2+√3) for 12-fold network (Figure 1i).

If we analyse the different historical patterns in Figure 1, we find that the intersection points of the nested polygrams correspond to the central points of the high rotational symmetries (stars) within the different historical patterns (Figure 1b, e, and h). It is worth noting that the size of the central polygon in all three networks, is proportional to the system and is often used as the seed unit (Figure 1c, f, and i). Copies of these central seed units are placed on the intersection points of the hierarchical network to generate the high symmetry points in the pattern. The area between the different seed units can be filled with different artistic formations. The most common one is generated by extending the lines of the star shape within the seed units until they meet. The construction process of these different non-periodic patterns is based on manipulating two main components, the underlying hierarchical grid of nested polygrams, which is responsible for defining the type of symmetry and the internal line formation within the seed units (polygons) which derives the different design variations for every pattern. By manipulating the designs within the seed units, a wide range of design variations can be attained without changing the underlying symmetry. In this tightly controlled system, the underlying hierarchical grid is the key ingredient for organizing the relational logic in the whole system.

Derived from the same process, this paper investigates the use of the hierarchical principle to generating the long-range translational order of non-periodic sequences in one dimension.

Methods

The aim of this research is to explore the use of a simple geometrical method for generating the long-range order of non-periodic sequences in one dimension. The new method is derived from traditional principles of Islamic Geometry. This paper argues that the underlying hierarchical logic used to generate the three historical non-period patterns in Figure 1, can be used to generate the non-periodic long-range sequences in one dimension. Accordingly, the long-range order of this hierarchical logic can be expanded infinitely while keeping a very tightly controlled relational system. This paper hypothesizes that the different frameworks of nested polygrams provide the structural grids for generating and infinitely growing the non-periodic one-dimensional sequences of different rotational symmetries. A case study approach is utilized to test the stated hypotheses. While the general population includes all types of non-periodic symmetries, this research focuses on testing the three most common symmetries. These include 10-fold non-periodic rotational symmetry, 8-fold non-periodic rotational symmetry and 12-fold non-periodic rotational symmetry. The presented methodology utilises the graphical software (AutoCAD) to generate the different non-periodic sequences. In the next few sections, the progression of nested polygrams is utilized as the base structure for generating three types of non-periodic sequences in one-dimension.

The 10-fold non-periodic rotational symmetry

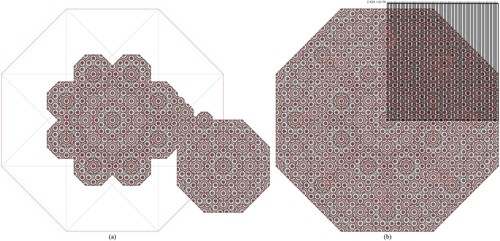
The process of generating the 10-fold-driven non-periodic sequence in one-dimension is based on building a progression of nested decagrams that grows based on the golden ration (Figure 1c). The process starts by constructing the initial decagon (Figure 2a). The first round of nested decagrams is constructed by drawing lines connecting every point on the initial decagon to every fourth point on the same decagon, resulting in an internal smaller decagon. The second round of nested decagrams is constructed by drawing lines connecting every point on the smaller decagon to every fourth point on the same decagon (Figure 2a). In this progression, every nested decagon is proportional to the whole system and can be used as the seed unit for constructing the generating quasi-periodic geometry. For this specific formation, the third internal nested decagon is used as the seed unit for generating the non-periodic sequence. In the next step, copies of the seed decagon are placed on every point of the initial decagon (Figure 2b). As shown in Figure 2b, the seed units on the outer decagon meet perfectly edge to edge without any gaps or overlaps. In this initial formation, the distance between the centre of the seed decagon and the centre of any external decagon generates the first large distance (L) of the non-period sequence.

Figure 2. The process of generating the first four levels of Fibonacci sequences based on 10-fold rotational symmetry.

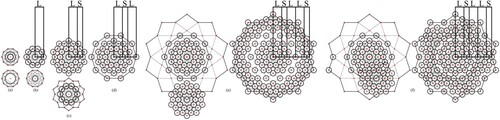
This initial cluster represents the basic unit for building the infinite quasi-periodic sequence in one dimension. By growing the framework of nested decagrams, a structural map is generated for the placement of the seed units as shown in the next steps. In the third step a larger generation of the nested decagrams is created outwards by extending the lines of the smaller decagram (Figure 2c). Copies of the central seed decagon are then placed on all 20 points on the extended decagram, resulting in a larger cluster formation (Figure 2c). In this new formation a new smaller distance is generated, which represent the second smaller distance (S) of the non-period sequence. In this system, the ratio of the large distance to the small distance is the golden ratio (1+√5)/2, which indicates that this sequence is actually the Fibonacci sequence (LS). By extending the lines of the external decagram in Figure 2c, a new larger decagon is used to map the locations the seed decagons (Figure 2d), generating the next level of the Fibonacci sequence (LSL).

Generated the next level cluster follows the same process. A new generation of the nested decagrams is created by extending the lines of the previous level (Figure 2e). In this level, the final formation generated in Figure 2c acts as the seed cluster. Copies of this cluster are placed at every point on the external decagram as shown in Figure 2e. In this step, the portions outside of the decagram are omitted (Figure 2e), defining the limits of the fourth level of the Fibonacci sequence (LSLLS). Figure 2f shows a different placement of the seed clusters, which still preserves the same Fibonacci sequence (LSLLS). The placement of the seed cluster is primarily defined by the intersection points of the underlying structural map of the nested decagrams. However, the different choices between overlapping the seed clusters or keeping them intact are often driven by a process of trial and error with the guidance from the non-periodic sequence itself. In this case, the two formations in Figure 2e and f are both used to grow the long range order of the Fibonacci sequence.

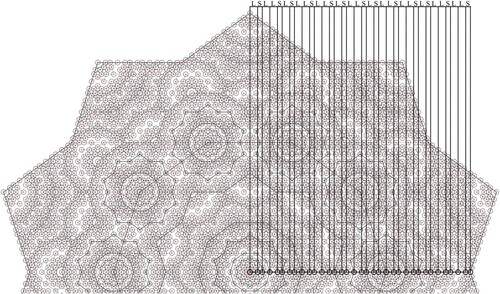
The process of generating the next two orders of the Fibonacci sequence is shown in Figure 3. Building on the same process in Figure 2, a new generation of the nested decagrams is constructed by extending the lines of the previous level. In this new hierarchy, the final formation generated in Figure 2d acts as the seed cluster for this level. Copies of this cluster are placed at every point on the external decagon, generating the next level of the Fibonacci sequence (LSLLSLSL) (Figure 3a and b). Similarly, the next sequence is generated by building a new generation of the nested decagrams as shown in Figure 3c. In this hierarchy, the final generated formation in Figure 2e acts as the seed cluster for this level. Copies of this cluster are located at every intersection point on the external decagram generating the next level Fibonacci sequence (LSLLSLSLLSLLS) (Figure 3c). Building on this process, the final generated formation in Figure 3b acts as the seed cluster for the next hierarchy. By placing copies of this cluster at every intersection point on the external decagram, the next level Fibonacci sequence is generated (LSLLSLSLLSLLSLSLLSLSL) (Figure 4a).

Figure 3. The process of generating the fifth and sixth levels of Fibonacci sequences based on 10-fold rotational symmetry.

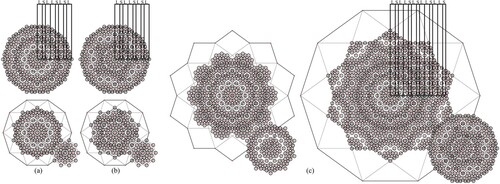
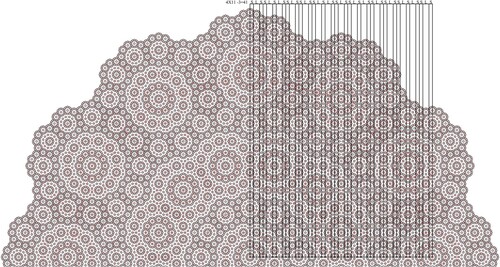
Figure 4. The process of generating the seventh level of Fibonacci sequence based on 10-fold rotational symmetry.

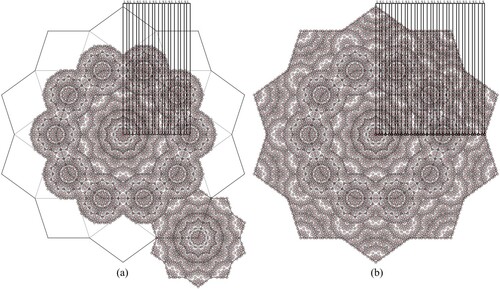
In the next level, the final generated formation in Figure 3c acts as the seed cluster for this hierarchy (Figure 4a). By placing copies of this cluster at every intersection point on the external decagram, the next level Fibonacci sequence is generated (LSLLSLSLLSLLSLSLLSLSLLSLLSLSLLSLLS) (Figure 4b).

This process can be repeated infinitely to generate the infinite long-range order of the Fibonacci sequence based on 10-fold rotational symmetry. Figure 5 shows a close up view of the final generated Fibonacci sequence, highlighting how every line of this sequence corresponds to a centre point of a seed decagon.

Figure 5. A close up view of the final generated Fibonacci sequence.

The 8-fold non-periodic rotational symmetry

The process of generating the 8-fold-driven non-periodic sequence is based on building a progression of nested octagrams that grows based on the root 2 proportion (Figure 1f). The process starts by constructing the initial octagon (Figure 6a). The first round of nested octagrams is constructed by drawing lines connecting mid-points on the initial octagon to every fourth mid-point on the same octagon resulting in an internal smaller octagon. The smaller nested octagon is proportional to the whole system and can be used as the seed unit for generating the quasi-periodic geometry. Copies of the seed octagon are then placed on every mid-point of the initial octagon (Figure 6a). As shown, the seed units on the initial octagon meet perfectly edge to edge without any gaps or overlaps. In this initial formation, the distance between the centre of the main seed octagon and the centre of any external octagon generates the first small distance (S) of the 8-fold non-period sequence.

Figure 6. The process of generating the first four levels of Root 2 non-periodic sequences based on 8-fold rotational symmetry.

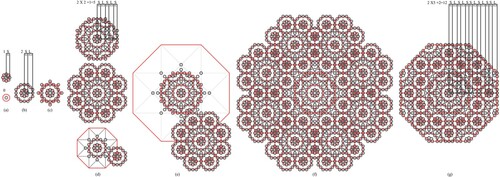
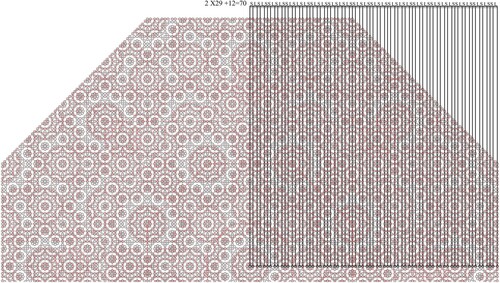
By growing the framework of nested octagrams, a structural map is generated for the placement of the seed units as shown in the nest two steps (Figure 6b and c). In these two steps, the lines of the initial nested octagram are extended outwardly to form a new generation of a larger proportional octagram. This new formation provides a structural map for the placement of the seed octagon as shown in Figure 6b and c. In this new formation, a larger distance is generated, which represent the second larger distance (L) of the 8-fold non-period sequence. In this system, the ratio of the large distance to the small distance is root 2 ratio (1.414 …). In the third step a larger generation of the nested octagrams is created outwards by extending the lines of the previous smaller octagram (Figure 6d). In this hierarchy, the final formation constructed in Figure 6b acts as the seed cluster for this level. Copies of these formations are then placed on all 8 mid-points of the external octagon, resulting in a larger cluster formation (Figure 6d). The formation is then trimmed out to the limit of the extended octagon, generating the next level of the root 2 non-periodic sequence (SLSLS). Generating the next level cluster follows the same process. A new generation of the nested octagrams is created by extending the lines of the previous level (Figure 6e). In this level, the formation generated in previous level (Figure 6d) acts as the seed cluster. Copies of this cluster are placed at every point on the external octagon as shown in Figure 6f. In the next step, the portions outside of the octagon are trimmed out (Figure 2e), defining the limits of the fourth level of the root 2 sequence (SLSLSSLSLSSL).

The process of generating the next level order of root 2 sequence is shown in Figure 7. Building on the same process in Figure 6, a new generation of the nested octagrams is constructed by extending the lines of the previous level. In this new hierarchy, the final formations generated in Figure 6d and g act as the two seed clusters for this level. Copies of the cluster in Figure 6d are placed at every intersection point on the internal formation and copies of the larger cluster in Figure 6g are placed at every intersection point on the external octagon. This new formation generates the next level of root 2 sequence (SLSLSSLSLSSLSLSLSSLSLSSLSLSLS) (Figure 7c).

Figure 7. The process of generating the fifth level of Root 2 non-periodic sequence based on 8-fold rotational symmetry.

Similarly, the next sequence is generated by building a new generation of the nested octagrams as shown in Figure 8. In this hierarchy, the final generated formation in previous level (Figure 7c) acts as the seed cluster for this level. Copies of this cluster are located at every intersection point on the external octagram, generating the next level root 2 sequence (SLSLSSLSLSSLSLSLSSLSLSSLSLSLSSLSLSSLSLSSLSLSLSSLSLSSLSLSLSSLSLSSLSLSSL) (Figure 8c). Building on this process, the root 2 sequence can be expanded infinitely without repeating its formation. Figure 9 shows a close up of the final generated sequence highlighting how every line of this sequence corresponds to a centre point of a seed octagon.

Figure 8. The process of generating the sixth level of Root 2 non-periodic sequence based on 8-fold rotational symmetry.

Figure 9. A close up of the final generated Root 2 non-periodic sequence based on 8-fold rotational symmetry.

The 12-fold non-periodic rotational symmetry

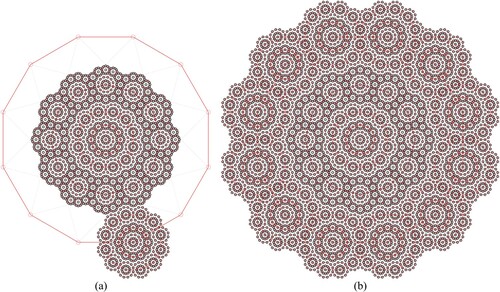
The process of generating the 12-fold-driven non-periodic sequence is based on building a progression of nested dodecagrams that grows based on the root 3 proportion (Figure 1i). The process starts by constructing the initial dodecagon (Figure 10a). The first round of nested dodecagrams is constructed by drawing lines connecting every point on the initial dodecagram to every fifth point on the same dodecagram. This process creates an internal smaller dodecagram that is rotated by 15 degrees in relation to the external one. By repeating the same process on the internal dodecagon, a new smaller generation of the nested decagrams is constructed, serving as the seed unit for growing the system. In this hierarchical system, every nested dodecagram is proportional to the whole system and relates to each other by root 3 ratio. In the next step, copies of the seed dodecagon are placed on every point of the external dodecagon (Figure 10a). The seed units meet perfectly edge to edge without any gaps or overlaps. In this initial formation, the distance between the centre of the main seed dodecagon and the centre of the external dodecagon generates the first small distance (S) of the 12-fold non-period sequence.

Figure 10. The process of generating the first three levels of Root 3 non-periodic sequences based on 12-fold rotational symmetry.

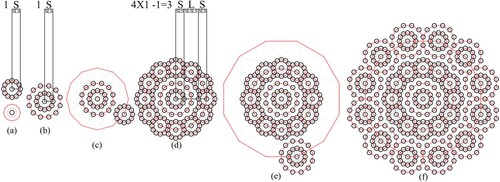
By growing the framework of nested dodecagrams, a structural map is generated for the placement of the seed dodecagons (Figure 10b). In this process, the lines of the external dodecagram are extended outwardly to form a new a larger proportional dodecagram. In the next level, the final generated arrangement in Figure 10a, acts as the seed cluster (Figure 10c). Copies of the this cluster are places on the external points of the larger dodecagon. In this level a new sequence is generated (SLS) for the 12-fold non-period sequence (Figure 10d). In this proportional system, the ratio of the large distance (L) to the small distance (S) is equal to root 3 ratio (1.732 …). Following the same process, a larger generation of the nested dodecagrams is created outwards by extending the lines of the previous dodecagram (Figure 10e). In this level hierarchy, the final formation constructed in Figure 10b acts as the seed cluster. Copies of this formation are placed at every point of the external dodecagon (Figure 10f). It is important to note, that generating the complete sequence of the next root 3 non-period order, requires building two generation of the nested dodecagrams. This is shown in Figure 11, in which the third complete sequence of root 3 (SLSSLSLSSLS) is generated by constructing the second formation of nested dodecagrams.

Figure 11. The process of generating the fourth level of Root 3 non-periodic sequence based on 12-fold rotational symmetry.

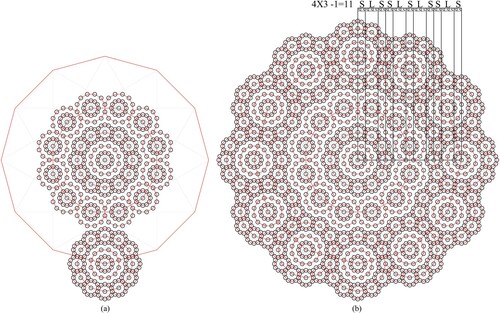
Similarly, generating the next level hierarchy of root 3 non-periodic sequence, requires building two generation of the nested dodecagrams as shown in Figures 12 and 13. For the process in Figure 12, the final constructed formation in Figure 10f acts as the seed cluster for the next level. In the next hierarchy (Figure 13), the formation generated in Figure 11b acts as the seed cluster for this level. Copies of this cluster are placed at every point on the external dodecagon, generating the complete fourth level hierarchy of the root 3 sequence (SLSSLSLSSLSSLSSLSLSSLSSLSLSSLSSLSSLSLSSLS).

Figure 12. The process of growing the non-periodic pattern based on 12-fold rotational symmetry.

Figure 13. The process of generating the fifth level of Root 3 non-periodic sequence based on 12-fold rotational symmetry.

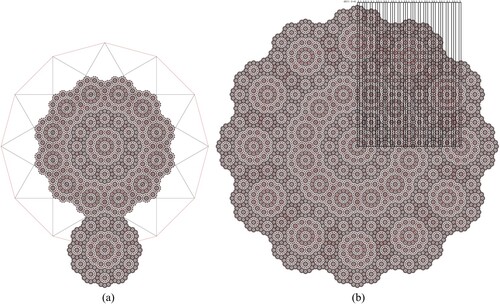
Figure 14 shows a close up view of the final generated root 3 non-periodic sequence, highlighting how every line of this sequence corresponds to a centre point of a seed dodecagon.

Figure 14. A close up of the final generated level of Root 3 non-periodic sequence based on 12-fold rotational symmetry.

Results and discussion

Fibonacci sequence

If we analyse the relationship between the generated Fibonacci sequence in Figures 2–5, we find that they confirm to the well-known substitution rules for Fibonacci, S→ L for the small distance, and L→ LS for the large distance.

L

LS

LSL

LSLLS

LSLLSLSL

LSLLSLSLLSLLS

LSLLSLSLLSLLSLSLLSLSL

LSLLSLSLLSLLSLSLLSLSLLSLLSLSLLSLLS

The number of units in every level can be generated recursively. If F₀=  0, and F₁=  1; for n > 1, then F_n= F_n-1+ F_n-2, which generates the well-known Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. etc.

Root 2 sequence

If we analyse the relationship between the generated root 2 sequences based on the 8-fold rotational symmetry in Figures 6–9, we find that they confirm to the substitution rules, S→ SL for the small distance, and L→ SLS for the large distance.

S

SL

SLSLS

SLSLSSLSLSSL

SLSLSSLSLSSLSLSLSSLSLSSLSLSLS

SLSLSSLSLSSLSLSLSSLSLSSLSLSLSSLSLSSLSLSSLSLSLSSLSLSSLSLSLSSLSLSSLSLSSL

By analysing the number of units in every sequence we find that the numbers begin with 0, 1, and each level equals the previous level times two plus the level before that. The number of units in every level can be generated recursively, if F₀=  0, and F₁=  1; for n > 1, then F_n= (2)F_n-1+ F_n-2, which generates the well-known Pell numbers: 0, 1, 2, 5, 12, 29, 70, 169, 408, etc.

Root 3 sequence

If we analyse the relationship of between the different Root 3 sequences generated based on the 12-fold rotational symmetry, we find that they confirm to the substitution rule S→ SLS for the small distance and L→ SLSLS for the large distance.

S

SLS

SLSSLSLSSLS

SLSSLSLSSLSSLSSLSLSSLSSLSLSSLSSLSSLSLSSLS

By analysing the number of units in every sequence we find that the numbers begin with 1, 1, and each level equals four times the previous level minus the level before that. The number of units in every level can be generated recursively, if F₀ = 1, and F₁ = 1; for n > 1, then F_n = (4)F_{n-1 –} F_n-2, which generates the numbers: 1, 1, 3, 11, 41, 153, etc.

Conclusion

In conclusion, derived from the traditional principles of Islamic geometry, this paper presented a methodology for generating non-periodic sequences in one-dimension. Three different non-periodic sequences were generated, Fibonacci sequence based on 10-fold rotational symmetry, root 2 sequence base on 8-fold rotational symmetry and root 3 sequence based on12-fold rotational symmetry.

By examining the relationship between the three generated non-periodic sequences and their associated rotational symmetries, a unique correlation between the three networks of nested polygrams and the ratio of the non-periodic sequence is evident. For 10-fold rotational symmetry, we find that the recursive ratio of nested decagrams is equal to the golden ratio (1+√5)/2. For the 8-fold rotational symmetry, we find that the recursive ratio of nested octagrams is equal to the irrational factor of √2 + 1. For the 12-fold rotational symmetry, we find that the recursive ratio of nested dodecagrams is equal to the square irrational factor of √(2+√3).

The results in this paper provide a deeper understanding of the non-periodic patterns in Islamic geometry and their traditional methods of construction. The hierarchical self-similar logic underlying the construction process of the historical patterns serves as the key ingredient for resolving the long-range order of the one-dimensional non-periodic sequences. This relational logic is derived from the nature of the design tools themselves (a compass and a straight edge) and not based on isolated procedures or discrete quantities. The generating process highlights the relationships inherent within the whole system, which allows a higher level of organization to happen intuitively. In this process, the networks of nested polygrams provide the relational logic for mapping the locations of the seed units/clusters and are responsible for defining the underlying symmetry and are the key ingredient for organizing the relational logic in the whole system.

Moreover, for the benefit of the wider research community, it is critical that new methods for the description of non-periodicity are proposed without relying on abstract or complicated mathematics. Non-periodic formations are often obtained by the cut and project approach from a higher dimension; a method that is too abstract for the human mind to understand. The need for alternative models that operate within the real physical (Euclidean) space is essential to eliminate a major roadblock for many researchers outside the field of crystallography and material science. The presented method utilizes a simple graphical method to generate the different non-periodic sequences, making it accessible for researchers in the design and applied fields to study and explore the use of these non-periodic systems.

The results suggest that it is possible to generalize the presented methodology to generate other non-periodic sequences in one-dimension. Future research should include testing the methodology on non-periodic symmetries, 7-fold, 14-fold, 9-fold, 11-fold, etc.

Disclosure statement

No potential conflict of interest was reported by the author(s).