Enhanced modelling of the glucose–insulin system and its applications in insulin therapies

Abstract

It is well known that Michaelis–Menten kinetics is suitable for the response function in chemical reaction, when the reaction rate does not increase indefinitely when an excess of resource is available. However, the existing models for insulin therapies assume that the response function of insulin clearance is proportional to the insulin concentration. In this paper, we propose a new model for insulin therapy for both type 1 and type 2 diabetes mellitus, in which the insulin degradation rate assumes Michaelis–Menten kinetics. Our analysis shows that it is possible to mimic pancreatic insulin secretion by exogenous insulin infusions, and our numerical simulations provide clinical strategies for insulin–administration practices.

Keywords:

• diabetes
• glucose–insulin regulator system
• insulin therapy
• time delay
• periodic solution

AMS Subject Classifications :

• 92C50
• 34C60
• 92D25

1. Modelling the glucose–insulin feedback system

Diabetes mellitus is a disorder of the glucose–insulin endocrine metabolic regulatory system. It is caused by the fact that either the pancreas does not produce enough insulin to consume the glucose, or the insulin is not used efficiently by the cells to metabolize the glucose. The diabetic population accounts for approximately 7% of the whole population in US, and the health expense is huge (≈132 billion US dollars annually, ADA, http://www.diabetes.org). Many researchers have been attracted to the study of glucose–insulin regulatory system with an ultimate goal of providing more efficient, effective, and economic insulin therapies for diabetics (e.g., 1,6–9,12 13 15 17 18 21 29 30 37 39 40 43 48 49).

In the last two decades, several mathematical models have been proposed and studied with the aim of understanding the system better, investigating possible pathways to diabetes mellitus, or providing more reasonable insulin administration practices (4 5 10 13 14 25 27 28 33 35 36 41 42 44 48 49 and references therein.) For example, recently, according to the mass conservation law, Li et al. 28 proposed a two-delay model for understanding the self-constrained regulatory mechanism of the system better. With the explicit delays, the model is more accurate for depicting glucose–insulin endocrine metabolic dynamics. The model is given as follows.

where G _in stands for the constant glucose exogenous infusion (enteral nutrition or constant infusion), f ₂(G) stands for the insulin-independent glucose consumptions, stands for the insulin-dependent glucose utilizations, f ₅(I) stands for the hepatic glucose production with the delayed effect (τ₂), f ₁(G) stands for the insulin secretion from the pancreas because of the stimulations of elevated glucose concentration, τ₁ reflects the time lag of the stimulation, and d _i is the insulin degradation rate.

However, the existing insulin therapy models are inadequate 13 14 48 49, either only type 1 diabetes insulin administration is considered 49, or some factor in the system is oversimplified. For example, the insulin degradation rate is assumed to be proportional to insulin concentration 28 45 48. It is well known that in a chemical reaction, the change rate typically increases with the increasing resource, but does not increase indefinitely when an excess of resource is available. In the glucose–insulin metabolic system, the number of insulin receptors of each cell changes vice versa with the circulating insulin concentration level. An increased insulin circulating level reduces the number of insulin receptors per cell, and the decreased circulating level of insulin triggers the number of receptors to increase. The number of receptors is increased during starvation and decreased in obesity and acromegaly. But, the receptor affinity is decreased by excess gluco-corticoids. The affinity of the receptor for the second insulin molecule is significantly lower than for the first bound molecule. This may explain the negative cooperative interactions observed during high insulin concentrations. That is, as the concentration of insulin increases and more receptors become occupied, the affinity of the receptors for insulin decreases. Conversely, at low insulin concentrations, positive cooperation has been recorded. In other words, the binding of insulin to its receptor at low insulin concentrations seems to enhance the binding further 46. Thus, it is more realistic to assume that the insulin degradation rate obeys Michaelis–Menten kinetics given by

where d ₁ is the maximum insulin clearance rate and d ₂ is the half-saturation value. The idea of this paper is to propose an insulin therapy model suitable for both type 1 and type 2 diabetes mellitus, and to incorporate the Michaelis–Menten response function as the insulin degradation rate. The model is given by

with initial conditions I(0)>0, G(0)>0, and for , τ₁>0, where $\alpha>0$ and β∈[0, 1]. For type 1 diabetics, β=0, as no insulin would be secreted from the pancreas. For type 2 diabetics, observing that some, although not enough, amount of insulin can be secreted from pancreas 31. The positive parameter α in Equation (2) describes insulin-dosage adjustment, which could improve the control of glucose concentration of the subjects. Furthermore, it has been revealed that the oscillatory insulin delivery with an ultradian periodicity is more efficient in reducing blood glucose levels than constant insulin administration 42. In model 2, we assume that insulin injection I _in and glucose intake G _in are positive periodic functions with a common period, ω>0. The common period is determined by the timing of meal ingestion and by subcutaneous insulin administration on a period sufficiently large to imagine both the glucose insulin mass administered eventually diffused in the IV compartment at the end of the period. Since Equation (2) models the exogenous insulin administration for both types of diabetes, the oscillations of insulin concentration and glucose concentration are resulted from the forced terms with common period ω; and the delay τ₁ for insulin production is more significant than the delayed effect of hepatic glucose production (τ₂ in model (1)). So, for simplicity, this delayed effect is neglected in Equation (2) for qualitative behaviour.

Throughout the paper, we assume the following conditions:

• (H1) G _in, , (0, ∞)) are positive ω-periodic functions.

• (H2) f ₁(x), f ₂(x), f ₃(x), are positive for x > 0. , $f_2(0) {=} f_3(0)=0$, f ₄(0)>0.

• (H3) f′₁(x), f′₂(x), f′₃(x), f′₄(x) are positive on (0;∞).

• (H4)  is positive on [0,∞), f′₅(x) is negative on [0, ∞).

• (H5) There exist positive numbers b ₂, a ₃, b ₃ such that, for ,

  and

• (H6) .

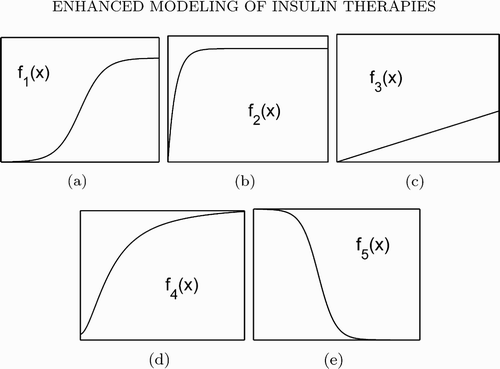
Assumptions (H1)–(H6) are quite natural. Note that if f ₂ takes the form in Equation (5), then . Thus, it is easy to see that conditions (H1)–(H5) cover the model functions in Equations (5)–(8) used in 25 27 41 44 48 for numerical simulations. Assumption (H6) indicates that the maximum insulin clearance rate is larger than the addition of the maximum insulin infusion and production rates. Physiologically, the shapes of the functions are important instead of their forms 22 (Figure 1). The shapes of the functions are detailed in earlier studies 22 25 28 41.

Figure 1. Shapes of functions f ₁ (a), f ₂ (b), f ₃ (c), f ₄ (d) and f ₅(e). Note: These figures are adapted from 28.

2. Mathematical analysis

In this section, the positivity and boundedness of solutions of Equation (2) will be examined. We will also state results for the existence of a positive solution of Equation (2) and its stability. Detailed proofs of the existence and stability will be carried out in Appendices. Throughout this section, we assume conditions (H1–H6) are true.

Lemma 2.1

All solutions of Equation (2) exist for t>0, and they are positive and bounded from above.

Proof

The solution for Equation (2) with the described initial conditions exist and is unique 24. Let (G(t), I(t)) be a solution of Equation (2) with initial conditions I(0)>0, G(0)>0, and for . If G(t) is not positive, then t>0, exists such that G(t)=0. Let . Then, G(t ₀)=0 and . However,

which is a contradiction. Therefore, G(t)>0 for t>0. By the same argument, I(t) is positive for all t>0.

Now we show the boundedness of (G(t), I(t)).

From Equation (2), we have

where m ₄>0 is the lower bound of f ₄(I(t)) on [0,∞]. Therefore,

The boundedness also implies that G(t) exists for all t>0.

Now considering the second equation of (2), we have

where , and d ₁−L>0, according to (H6).

Now if then I′(t)<0. In fact, we can easily prove, by Lemma 2.2,

Thus, I(t) is bounded and also implies that I(t) exists for all t>0.   ▪

Let (I(t), G(t)) be a solution of Equation (2). We define

and

Lemma 2.1 implies that G¯, G, Ī, I are all finite. The well-known fluctuation lemma is stated below without proof. Its proof can be found in, e.g., Hirsch et al. 20.

Lemma 2.2

Let f:R→R be a differentiable function. If , then there are sequences , such that for all k, , and .

Lemma 2.3

Equation (2) is uniformly persistent, i.e. solutions of Equation (2) are eventually uniformly bounded from above and away from zero.

Proof

We only need to show that and . By the fluctuation lemma, there exist a sequence , such that

Thus, the second equation of (2) gives, for all k,

and as f ₄ is increasing and f ₅ is non-negative, we have

where . Letting k→1, we have

If , we have

which is a contradiction. Thus, . It remains to show that . Again by the fluctuation lemma, there exist a sequence such that

Thus, the second equation of (2) gives, for all k,

and as f ₁ is non-negative, we have

Letting k→∞, we have

If , we have

which is a contradiction. This completes the proof of the lemma.   ▪

To have a positive periodic solution, the left side of the second equation of (2) must change sign. If the rates of insulin injection and insulin production, , are too large, then the rate of change of insulin, dI/dt, may be always positive and therefore Equation (2) does not have a periodic solution. In the following existence theorem, we assume that is small enough so that inequality Equation (16) in Appendix 1 holds.

Theorem 2.4

If is sufficiently small, then Equation (2) has a positive periodic solution (G*, I*).

Finally we state the stability result in the following theorem.

Theorem 2.5

The periodic solution (G*, I*) of Equation (2) is locally asymptotically stable if conditions (18) and (19) in Appendix 2 are satisfied.

Precise mathematical expressions of conditions (18) and (19) are given in Appendix 2. Based on the expressions of (18) and (19), and inequality Equation (3), if the maximal insulin clearance rate d ₁ is large, the delay τ₁ is small, then, as a lower bound of , σ₀ can be large so that Ĉ>0. Similarly, if f′₂ and f′₃ f ₄ are large, that is, the insulin utilizations are more effective, then [Dcirc]>0. These observations are in agreement with the study of Li and Kuang 25.

The proof of Theorem 2.4 is based on the Krasnoselskii fixed point theorem (Lemma A.1), and see Appendix 1 for details. The proof of Theorem 2.5 is based on a standard construction of a Lyapunov functional and will be carried out in Appendix 2.

3. Applications in clinical insulin therapies

In this section, we will discuss an application of model (2) in clinical insulin therapies. The simulations demonstrate that the new model (2) is suitable for the study of the effectiveness of clinical insulin therapies. In particular, we will see that model (2) is more realistic. In a normal subject, the liver releases glucose into the blood. This helps the body to maintain cells functioning all 24 h. The pancreas responds by releasing a small but steady amount of insulin (basal) into the bloodstream day and night in a pulsatile manner. After meals, a large amount of insulin (bolus) is released enough to uptake the glucose produced when food is digested. The goal of intensive insulin therapy is to mimic the natural pattern of insulin release from the pancreas so that plasma glucose levels can be kept close to normal.

Currently, various insulin analogues are available for subcutaneous injection, for example, rapid-acting insulin analogues (Lispro and Aspart), short-acting insulin analogues (buffered regular insulin), intermediate-acting insulin analogues (Lente, NHP), and long-acting insulin analogues (Glargine and Ultralente). Table 1 (adapted from 11) lists the time needed for the onset, peak, and duration of several types of insulin.

Table 1. Pharmacokinetics of available insulin products 11.

Insulin	Onset	Peak	Duration
Lispro	5–15 min	30–90 min	3–5 h
Aspart	10–20 min	1–3 h	3–5 h
Regular insulin	30–60 min	1–5 h	6–10 h
Buffered regular insulin	30–60 min	1–3 h	8 h
Lente	1–3 h	6–14 h	16–24 h
NPH	1–2 h	6–14 h	16–24+ h
Glargine	1.1 h	None	24 h
Ultralente	4–6 h	8–20 h	>24 h

Our simulations are carried out with the same functions used in previous researches (5 25 28 41 44). These functions, f _i ; i=1, 2, 3, 4, 5, take the following forms with experimentally determined parameters given in Table 2 41 44. Model (2) utilizes the functions f ₁ to f ₅ in Equations (5)–(8) and the parameter values in Table 2 from 41 44, which are based on experimental data. These experimental data were taken from normal subjects. With proper insulin treatments, patients can maintain plasma glucose within a normal range, although hypoglycaemia and hyperglycaemia can arise. Therefore, these functions and parameters can be used in the insulin therapy model (2) for diabetic patients.

Table 2. Parameters of the functions in Equations (5)–(8).

Parameters	Units	Values
V g	1	10
U b	mg·min^−1	72
C 2	mg·l^−1	144
C 3	mg·min^−1	1000
V p	1	3
V i	1	11
t i	min	100
R m	mU·min^−1	210
C 1	mg·l^−1	2000
a 1	mg·l^−1	300
U 0	mg·min^−1	40
U m	mg·min^−1	940
β		1.77
C 4	mU·l^−1	80
R g	mg·min^−1	180
αˆ	l·mU^−1	0.29
C 5	mU·l^−1	26
E	l·min^−1	0.2
V g	l	10

The units of G and I in the functions (5)–(8) are in milligrams and respectively. They are converted to mg dl⁻¹ and μU ml⁻¹ when plotting the figures.

Now, we consider model (2) with τ₁=5 min, , and d ₂=2300.

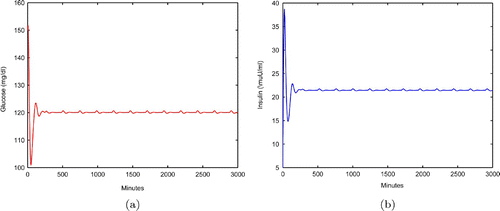
If there is no insulin injection, or , the profiles of glucose and insulin of Equation (9) is shown in Figure 2. We see that the blood glucose level is always above 120, which is considered to be abnormal blood glucose level. Therefore, insulin injections are needed to bring the blood glucose level down to normal.

Figure 2. (a) Glucose profile of (2) without insulin therapy. (b) Insulin profile of (2) without insulin therapy.

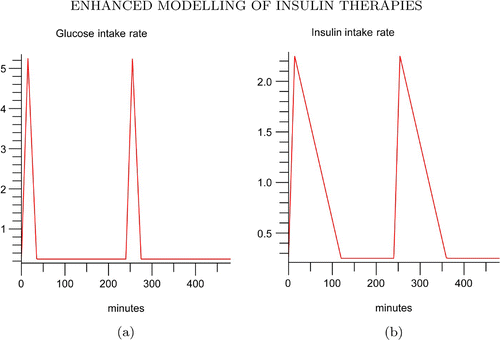
As an example, to demonstrate how model (2) can be used in clinical insulin therapy strategies, we select the combination of Lispro and Glargine to mimic the bolus insulin and basal insulin infusion. For simplicity, we assume that G _in(t) and I _in(t) are periodic piecewise linear functions defined by the following two expressions over a period of ω=240 min. That is, we assume that both the meal digestion and the diffusion of subcutaneous insulin injection are linearly dependent on time. They can be extended to a periodic continuous function on [0, ∞). Namely, a subject consumes meal and is given insulin injection every 4 h. The maximum glucose intake was at 5 mg/min attained at 15 min mark. The whole duration of the glucose intake lasted for 35 min. Equation (10) is the glucose intake rate, G _in (Figure 3).

Figure 3. (a) Glucose intake rate. (b) Insulin Lispro injection rate.

We consider the combination of Glargine and Lispro insulins. The piecewise functions of in Equation (11) and in Equation (12) mimic the insulin infusion rate if a patient takes Lispro or Glargine. The rapid-acting insulin mimics the bolus ultradian insulin secretion stimulated by the elevated glucose concentration level, while the long-acting insulin mimics the basal pulsatile insulin secretion. It is clear that the common period for G _in(t) and I _in(t) is ω=240 min.

and

With τ₁=5 min and the simulation in Figure 4 (a) and (b) demonstrate the glucose and insulin concentration profiles of four injections a day of bolus insulin Lispro and one injection a day of basal insulin Glargine. The insulin injection rate is the combination of and . Therefore, I _in in Equation (9) takes the following expression.

It is easy to see that I _in in Equation (13) <10 and for . Thus, the condition (H6), , is satisfied for model (9).

Figure 4. Glucose and insulin profiles with the combination of Lispro and Glargine for Monod insulin-degradation model (9) (a) Glucose profile of Equation (9). (b) Insulin profile of Equation (9).

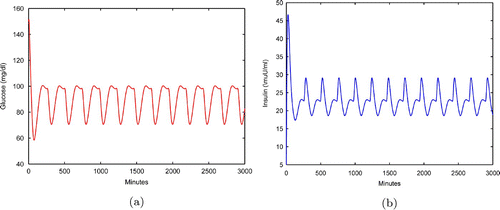
The glucose level shown in Figure 4 (c) for model (9) is between 70 and 100 mg dl⁻¹. It is seen that the profiles are close to the profiles of a normal subject. We should also point out that blood glucose levels could be close to 160 mg dl⁻¹ after meals 32.

4. Discussions

To optimize the strategies of insulin adminstration, we choose the combination of insulin Glargine and Lispro as basal and bolus insulin, respectively, because clinical trials have shown that insulin Glargine plus insulin Lispro can improve glycaemic control of type 1 diabetes 2. In their study, the combination of insulin Glargine with insulin Lispro was compared with NPH insulin plus unmodified human insulin. It is reported that there was as much as 44% reduction of monthly rate of nocturnal hypoglycaemia with Glargine plus Lispro. These improvements in blood glucose control were obtained without any increase in episodes of hypoglycaemia. In fact, in another clinical trial by Murphy et al. 34, it has been documented that combination therapy with insulin Glargine plus insulin Lispro reduced the incidence of nocturnal hypoglycemia and was at least as effective as R/NPH insulin therapy in maintaining glycaemic control.

Currently, an insulin pump is the most advanced method of insulin administration for type 1 diabetes 26. With careful integration of the existing models for glucose absorption from the gut and/or subcutaneous insulin absorption and the regulation of glucose–insulin, an artificial pancreas can be created and put forward in clinical applications. The model proposed in this paper when integrated with the models proposed in earlier studies 25 26, can form a solid foundation for an artificial pancreas.

Model (2) does not take into account individual patient factors, such as age, treatment schedule, and exercise. Patient factors, including individual variations in insulin absorption, levels of exercise, local massage, and especially, local subcutaneous blood flow that can influence the effectiveness of an insulin regimen 16. The time taken to absorb one-half of an injected dose of insulin may vary by 25–50% among individual patients 19. Thus, it is important to implement individualized therapies, which are flexible to fit the needs of the patient. Model (2) can be adjusted to reflect the patient factors by incorporating a time delay in I _in.

In model (2), we neglect the delayed effect of hepatic glucose production in f ₅. In fact, the delayed effect on the dynamics of glucose and insulin for normal subjects under continuous and constant glucose infusion can be significant 25 28. We will further investigate the delayed effect in a future research.

Experimental results by Rassam et al. 38 demonstrated that the injection of Lispro insulin 15–30 min before meal can optimally reduce postprandia hyperglycaemia. In our simulation, we assume that lispro insulin is injected 15 min before meal. Other regular insulins are recommended to be injected 30 or 45 min before meal. In practice, patients often inject insulin closer to mealtime, causing a higher postprandial serum glucose level and an increased potential for hypoglycaemia in the postabsorptive period. Thus, Lispro insulin results in more satisfactory postprandial glucose control.

In summary, we propose a new insulin therapy model using Michaelis–Menten kinetics. We are focusing on studying the dynamics of the model, and will continue the research and validate the model to fit actual data of the subjects.

Acknowledgements

This work is dedicated to Professor Ken Cooke. This work is partially supported by ASU MGIA-2006-08. The third author is also supported by DMS-0436341 and DMS/NIGMS-0342388. We are grateful to the anonymous referees and the editor whose careful reading, valuable comments, and suggestions greatly enhanced the original manuscript.

Appendix 1. Proof of Theorem 2.4

In this section, we will give a proof of Theorem 2.4. A related result can be found in 47. Before we state the Krasnoselskii fixed point theorem, let us recall some concepts and conclusions of an operator in a cone in 23. Let X be a Banach space and K be a closed, non-empty subset of X. K is said to be a cone if (1) for all u, v∈K and all and (2) u,− u ∈ K, imply u=0. Assume Ω is a bounded open subset in X with the boundary , and let be completely continuous, such that Tx ≠ x for .

Lemma .1

Krasnoselskii's Fixed Point Theorem 23. Let X be a Banach space and let K∈X be a cone in X. Assume that Ω₁, Ω₂ are open subsets of X with and let

be a completely continuous operator, such that either

1. and

   or

2. and

is true. Then T has a fixed point in .

First, since f ₄ is bounded below and above, we can assume there exist two positive numbers m ₄ and M ₄, such that

Also, since f ₅(x) is bounded above and G _in(t) is positive periodic on [0, ∞), there exist two positive numbers m ₅ and M ₅, such that

Now, consider the Banach space

with . Define a cone K in X by

where A, B, C, D are defined by the following expressions:

It can be verified that A < B and C < D. Indeed, (H5) implies b ₃≥a ₃. Now from the fact that M ₄≥m ₄, we have , which implies that . Now since , we can obtain A < B. Noting , by the same argument, we have C < D.

We then define two open sets and as

and

Note that and

Define the map by

and

where

and

Note that

Thus

In addition, for

and

In order to use the above fixed point theorem we need the following lemma.

Lemma .2

is compact and continuous.

Proof

We only consider the first component T ₁(u, v). The proof for T ₂(u, v) is the same. In view of the definition of T ₁, for (u, v)∈K, we have

It is easy to see that is a constant because of the periodicity of . One can show that, for and ,

Thus and it is easy to show that T is compact and continuous.   ▪

Lemma .3

If (u, v) is a fixed point of T in , then (u, v) is a positive periodic solution of (2).

Proof

If and T ₁(u, v)=u, then

In the same way, we can show that

Thus, (u, v) is a non-negative ω-periodic solution of (2), which is also positive. We are now in a position to prove the existence of periodic solution of (2). Then for , we have

Thus, for

On the other hand, for , we have

and

Now, since is sufficient small and we can assume that

Thus, we have

Consequently,

It follows from Lemma A.1 that T has a fixed point in , and hence Equation (2) has a positive ω-periodic solution. This completes the proof of Theorem 2.4.   ▪

Appendix 2: Proof of Theorem 2.5

In this section, we shall show that the periodic solution of Equation (2) is locally asymptotically stable. Our proof is based on the construction of Lyapunov functionals. Before we proceed to discuss stability, we state a lemma from 3 without proof, which will be employed to establish stability.

Lemma .4

Let h be a real number and f be a non-negative function defined on [h, ∞) such that f is integrable on [h, ∞) and is uniformly continuous on [h, ∞). Then .

Now assume (G(t), I(t)) is a solution of Equation (2) with initial condition I(0)>0, G(0)>0, and for . For simplicity we use the transformation

Also let

Note that both I and I* are bounded for t≥0. Therefore, there exist a positive number σ₀ such that

Thus

and

where ξ₁ is between G(t−τ₁) and , and ξ₂, ξ₃>0 are between G(t) and G*(t), ξ₄>0 is between I(t) and is between I(t) and I*(t). Note that is negative because of (H4). We can also assume that f ₃(G(t)) and f ₄(I*) are bounded by the following positive values

and

where are constants. In addition, it is easy to find positive constants σ _i and , so that and are bounded by the following positive values

and

Define a function

Then, we calculate the derivative of V ₁(t) along the solution of Equation (2).

We will make use of the inequality

to estimate V˙ ₁(t). In particular, we choose ε=1 for the terms without integrals and for the integral terms and produce the following estimates.

We now define four additional functions in order to handle the four terms with integrals.

and

Note that

and

Now consider a Lyapunov functional

and differentiate V(t) along the solution of Equation (2). After rearranging the terms, we get

Now if

and

then Equation (17) becomes

It is easy to see that V(t) is decreasing. Integrating on both sides of Equation (20) from 0 to t and rearranging the terms, we produce

Hence, . It is also easy to see that v ², u ², and their derivatives are bounded on [0, ∞). Then, it follows that u ² and v ² are uniformly continuous on [0, ∞). By Lemma A.4 we have

and

Therefore, the periodic solution is locally asymptotically stable.