Continuous-time predator–prey models with parasites

Abstract

We study a deterministic continuous-time predator–prey model with parasites, where the prey population is the intermediate host for the parasites. It is assumed that the parasites can affect the behavior of the predator–prey interaction due to infection. The asymptotic dynamics of the system are investigated. A stochastic version of the model is also presented and numerically simulated. We then compare and contrast the two types of models.

Keywords:

• predator-prey-parasite interaction
• global asymptotic stability
• uniform persistence
• continuous–time Markov chain

AMS Subject Classifications :

• 92D40
• 92D30

1. Introduction

Since the pioneering work of Kermack and McKendrick 17 on an SIRS model, epidemic models have received considerable attention in the scientific community. Many of these mathematical models have contributed to the understanding of the evolution of the diseases and provide valuable information for control strategies. We refer the reader to 3 5 8 13 19 and literature cited therein for general epidemic models. On the other hand, the majority of the epidemic models in the literature deal with evolution of the disease within a population. More recently, researchers have investigated predator–prey models with infectious diseases 7 11 12.

It is well documented that parasites can play an important role in shaping population and community dynamics and maintaining bio-diversity 15 16. For trophically transmitted parasites, the populations are transmitted up the food chain from immediate host species to the definite host populations via predation. Consequently, the interactions between prey and predator are affected by the presence of the parasites. For instance, it is often found that infected individuals are less active and hence can be caught more easily 14. However, for the parasites to be successful, it is important to restrict host's predation mortality as well as the disease related mortality.

In this manuscript we study a deterministic predator–prey model with parasites, where the parasites are not explicitly modeled. The modeling assumptions are similar to that given by Fenton and Rands 10. The community under current investigation is composed of two host species, one preys on the other. The predator–prey populations harbor parasites that use the prey species as an intermediate host to transmit the disease to the definitive host, the predator species. The infection rate is modeled by the simple mass action and we use a Holling type I function to model the functional response of the predator. The resulting model consists of four ordinary differential equations. Existence conditions for boundary and interior steady states are derived and some global results are obtained using a simple comparison method. We also perform numerical simulations to study the model. A stochastic model based on the deterministic model is formulated in terms of continuous time Markov chain and simulated numerically. We then compare and contrast the two models.

The deterministic model presented here is different from the predator–prey models studied by Chattophadhyay and Arino 7, by Hadeler and Freedman 11, and by Han et al. 12. In 11, it is assumed that both the infected and uninfected prey can reproduce at the same rate and there is no disease related mortality for both the infected prey and predator. Moreover, the authors use a Holling II functional to model the predation. However, the force of infection is also modeled using simple mass action. Han et al. 12 on the other hand study four predator prey models with infectious diseases, where both simple mass action and standard incidence are investigated. However, their models are based on the decomposition of the logistic differential equation. In 7, it is also assumed that both infected and uninfected prey can reproduce and with the same rate.

Our model derivation is based on a model proposed by Fenton and Rands 10. Although no rigorous mathematical analysis was presented in 10, it was found in 10 that increasing the parasite's manipulation will decrease the uninfected predator population size and so that the population may become extinct in the stochastic reality of the natural world if parasite's manipulation is too high. Our numerical study shows that increasing the parasite's manipulation increases both the infected prey and predator population sizes of the periodic solution. Therefore increasing parasite manipulation is likely to increase its persistence in the deterministic world. Moreover, the persistence result for the parasite derived in this study is expressed in terms of a threshold that involves only the nontrivial boundary steady state with nonzero uninfected populations. The expression is very easy to verify and also shows that the parasite will be more likely to survive if its manipulation is larger. These analytical results no longer hold when we consider a corresponding continuous-time Markov chain model. Both the infected and uninfected prey and predator populations may become extinct in the stochastic model while they can persist in the deterministic model.

In the following section a deterministic model is presented. A stochastic model is given in Section 3 and the final section provides a brief summary and discussion.

2. A deterministic model

We assume that the parasite is a microparasite and so the parasite population is not explicitly modeled in the system. We only consider an individual of each species as infected or uninfected. Let x ₁ and x ₂ denote the uninfected and infected prey populations, respectively, and y ₁ and y ₂ be the uninfected and infected predators, respectively. In the absence of the predator and the parasite, the prey population reproduces at per capita rate r with carrying capacity 1/q. It is assumed that the infected prey does not reproduce.

We adopt a simple Holling type I function as the functional response, and let e denote the predator conversion rate. Since infected prey may increase its probability of being preyed upon, we let θ denote the factor that effects the interaction between prey and predator. The predator preys on both infected and uninfected prey indiscriminately when θ=1. If θ<1, then the infected prey has a less chance of being captured. The infected prey will be more likely to be preyed upon if θ>1. The natural death rates of the infected prey and predator are denoted by d ₁ and d ₂ respectively. The disease related mortality rates of the prey and predator populations are denoted by α₁ and α₂. These parameters are assumed to be constants.

A simple mass action is used to model the force of infection between infected prey and uninfected predator. The parasites in the predator produce infective stages at a constant rate λ, which are passed into the environment where they either die at rate μ or are consumed by the prey at a rate ν. For simplicity, it is assumed that the external parasite stages are short and fast and so we do not model them explicitly in the model. Under these biological assumptions, the model takes the following form:

where all the parameters are positive with 0<e≤1. Model (1) along with other models have been simulated in 10.

We first convert system (1) into a dimensionless form. Let

We have

Letting

and drop off all the primes with , we have the following system:

In the following we study the dimensionless system (2).

Lemma 2.1

Solutions of system (2) remain non-negative and are bounded.

Proof

Since , and , solutions of system (2) remain non-negative. Let . Then . It is clear that there exists M>0 such that x ₁ (t)≤M for all t≥0. Hence , where . As a result, and solutions of system (2) are bounded.   ▪

If initially there is no predator population, then the prey population will stabilize in its carry capacity level K. That is, if , then for t>0 and if x ₁ (0)>0. On the other hand if , then for all t>0 and system (2) reduces to the following two-dimensional system:

This is the classical Lotka–Volterra predator–prey model with density dependence on the prey and its dynamical behavior are well known 2. In particular, if the interior steady state exists, i.e., if K > d ₂, then solutions of Equation (3) with positive initial condition converge to . Therefore, in the absence of the parasites, the predator and prey populations can coexist in a stable equilibrium fashion.

We now begin to study simple solutions of system (2). The system always has two steady states: E ₀=(0, 0, 0, 0), the extinction steady state where both prey and predator populations cannot survive, and E ₁=(K, 0, 0, 0), where only the uninfected prey can survive. The Jacoban matrix of system (2) evaluated at E ₀ has the following form:

It follows that E ₀ is always unstable. Similarly, the Jacoban matrix of Equation (2) evaluated at E ₁ is given by

We conclude that E ₁ is locally asymptotically stable if K < d ₂ and unstable if K > d ₂. It can be easily shown that E ₁ is globally asymptotically stable in whenever it is locally asymptotically stable.

Lemma 2.2

The steady state E ₁=(K, 0, 0, 0) is globally asymptotically stable for system (2) in if K<d ₂.

Proof

Notice . Since , for any given ϵ>0 there exists t ₀>0 such that for t ≥ t ₀. We choose ϵ>0 so that . It follows that for t ≥ t ₀ and hence . Therefore for any given ϵ>0 we can find t ₁>0 such that for t ≥ t ₁. Thus for t ≥ t ₁ implies since ϵ>0 was arbitrary. Consequently, for any ϵ>0, there exists t ₂>0 such that for t ≥ t ₂, and from the x ₂ equation in system (2), we obtain . As a result, if x ₁(0)>0 and the proof is complete.   ▪

We now assume K > d ₂ for the remainder of the discussion. Letting x ₂=y ₂=0, we obtain another steady state , where x¯ ₁=d ₂ and . This is the steady state for which only the uninfected prey and predator can survive and the parasites cannot invade the populations. The corresponding Jacoban matrix has the following form:

which is similar to the following matrix:

Let the upper left 2×2 submatrix and the lower right 2×2 submatrix of the above matrix be denoted by J ₁ and J ₂, respectively. Since , , and , we see that E ₂ is locally asymptotically stable if

Observe that inequality (4) holds if is small. Thus steady state E ₂ is locally asymptotically stable when E ₁ just loses its stability, i.e., when E ₂ just appears. A straightforward computation shows that and thus eigenvalues of the Jacoban matrix of system (2) evaluated at E ₂ are all real numbers. Therefore E ₂ will lose its stability via either a saddle node, a transcritical, or a pitchfork bifurcation when . In the following, we provide a sufficient condition for which E ₂ is globally asymptotically stable in Γ, where .

Lemma 2.3

Let K>d ₂. Then steady state exists, where x¯₁=d ₂ and . If , then E ₂ is globally asymptotically stable in Γ.

Proof

Since d ₂<K, steady state E ₂ exists. We apply a simple comparison method. Observe that . Given any ϵ>0 we can find t ₀>0 such that for t ≥ t ₀. By our assumption, we can choose ϵ>0 so that . Then for t ≥ t ₀ we have

where . This shows that . Therefore system (2) is asymptotically autonomous to the two-dimensional system (3). It follows from 18 that solutions of system (2) with initial condition lying in Γ converge to E ₂. It is also easy to see that E ₂ is locally asymptotically stable since inequality (4) holds. Hence E ₂ is globally asymptotically stable in Γ.   ▪

Since Hopf bifurcation is impossible to occur for system (2) when E ₂ loses its stability by the discussion just before Lemma 2.3, we next investigate the existence of interior steady states. Let (x ₁, x ₂, y ₁, y ₂) denote a positive equilibrium. Its components must satisfy the following equations:

Hence and . It follows that the x ₁-component of the steady state must satisfy

and

where

and

Let . Using the assumption d ₂<K, we see that

Notice

and the left-hand side of inequality (4) can be rewritten as

Consequently, inequality (4) holds if and only if f(d ₂)<0.

Lemma 2.4

Let K>d ₂. Then system (2) has no interior steady state if inequality (4) holds, i.e., if E ₂ is locally asymptotically stable, and system (2) has a unique interior steady state if (4) is reversed, i.e., if E ₂ is unstable. Moreover, system (2) is uniformly persistent if inequality (4) is reversed.

Proof

Suppose (4) holds. Then f(d ₂)<0. We claim that system (2) has no interior steady state. If β≤e, then f is concave up with f(0)=c. If c≤0, then Equation (6) has a positive solution x ₁*>K. Hence system (2) has no feasible interior steady state by Equation (5). Similarly, if c>0, then Equation (6) may have two positive solutions. However, since f(d ₂)<0 and f(K)<0, these two solutions will not lie between d ₂ and K as required in Equation (5), and hence system (2) has no interior steady state. If β>e, then f is concave down. If c≥0, then since f (d ₂)<0 there is no interior steady state by Equation (5). Observe that the solutions of Equation (6) vary continuously with respect to coefficients a, b, and c. Fix any a, b, and c with a<0. If c=0, then Equation (6) has a unique positive solution −(b / a) provided b>0, where −(b / a)<d ₂ since f(d ₂)<0. Suppose c<0. If Equation (6) has a unique positive solution then this positive solution is (−b/2a) with b>0 and b ²−4ac=0, which is clearly less than d ₂ since . If Equation (6) has two positive solutions denoted by x ₁₁* and x ₁₂* with , then it is necessary that b>0. It follows that . We conclude that system (6) has no solutions satisfying system (5) and as a result system (2) has no interior steady state. Suppose inequality (4) is reversed. Then steady state E ₂ is unstable and it is necessary that β>e, i.e., f is concave down. If f(0)≥0, then since f(d ₂)>0 and f(K)<0, system (6) has a unique positive solution x ₁* that lies between d ₂ and K. Hence system (2) has a unique interior steady state. Similar conclusion is reached if f(0)<0. We conclude that system (2) has a unique interior steady state if inequality (4) is reversed. To prove uniform persistence of system (2), first notice system (2) is dissipative by the proof of Lemma 2.1. It is clear from J(E ₀) that the stable manifold of E ₀ lies on the x ₂ y ₁ y ₂-hyperplane and the unstable manifold lies on the x ₁-axis. Since an eigenvector of J(E ₁) with respect to can be chosen to be , the unstable manifold of E ₁ lies outside of the positive cone of ℝ⁴ and the stable manifold of E ₁ lies on the x ₁ x ₂ y ₂-hyperplane. Furthermore, since inequality (4) is reversed, J(E ₂) has a unique positive eigenvalue . An eigenvector of J(E ₂) belonging to λ₊ within scalar multiplications is with [ytilde] ₁<0 and, therefore, the unstable manifold of E ₂ also lies outside of . Let denote the negative eigenvalue of J ₂. Then an eigenvector of J(E ₂) associated to λ₋ has the form with ŷ ₂<0. Therefore, the stable manifold of E ₂ also lies outside of the interior of . We conclude that the boundary flow of system (2) is isolated and acyclic with acyclic covering {E ₀, E ₁, E ₂}, where the stable set of each E _i does not intersect with the interior of for i=0, 1, 2. Consequently, system (2) is uniformly persistent by 6.   ▪

From an earlier discussion, we can conclude that system (2) undergoes a transcritical bifurcation when E ₂ becomes nonhyperbolic. Recall in the boundary equilibrium we have x¯ ₁=d ₂ and . Therefore , and

Consequently, in the coexistence equilibrium the uninfected prey has a larger population size and the uninfected predator has a smaller population size than the corresponding population sizes in the equilibrium for which both populations can survive but not the parasites. Notice is also the coexistence equilibrium for the predator–prey system (3) when parasites are absent. Therefore, the introduction of parasites can promote the prey population by increasing its population size and diminishing its predator's population size at least in the equilibrium level.

Furthermore, using the original model parameters, inequality (4) can be rewritten as

where is the corresponding boundary steady state for the original system (1). The first fraction in Equation (7) can be interpreted as the number of new infections in the prey population for each infectious predator and the second fraction is the number of new infections in the predator population per infected prey when both populations consist of only uninfected individuals. The parasites cannot invade the populations if the product of these two quantities is less than one. Notice the left-hand side of inequality (7) as a function of θ is increasing. Therefore, increasing θ will enable the parasites to invade the populations. In other words, the parasites will be more likely to persist if infected prey can be caught more easily by its predator. Similarly, increasing either ν or λ, or decreasing either , or δ will also enhance the persistence of parasites.

We remark that the left-hand side of inequality (7) is different from R ₀, the basic reproductive ratio, defined in Equation (2) of 10. Indeed, in terms of our notations of system (1), R ₀ defined in 10 is

where x ₁, x ₂, y ₁, y ₂ are the population sizes of uninfected prey, infector prey, uninfected predator, and infected predator, respectively. It is clear that the left-hand side of inequality (7) is different from the right-hand side of Equation (8). The parameter R ₀ presented in 10 is derived from the work by Dobson and Keymer [9, p. 362]. R ₀ is termed as the basic reproductive rate of the parasite life history in 9 which depends on the population sizes of both intermediate and definite hosts. The parasite needs sufficient definite host of both infected and uninfected populations for its survival. On the other hand, inequality (7) is derived from local stability of E ₂. It depends on the population sizes of uninfected prey and predator at the equilibrium. The parasite population can persist if inequality (7) is reversed.

We now use numerical simulations to study system (2). We adopt the following parameter values: K=5, d ₂=0.5000, , , e=0.1000, and . Since K > d ₂, steady state E ₁=(K, 0, 0, 0) is unstable and there is another boundary steady state with x¯ ₁=0.5, and y¯ ₁=10. We calculate θ for which the left-hand side of (7) is one, denoted by θ _c , where for our parameter values. Recall that E ₂ is locally asymptotically stable when inequality (7) holds. In particular, inequality (7) is true if and only if . Although it is not presented here, numerical simulations showed that solutions with positive initial conditions converge to E ₂ for for the initial conditions randomly chosen.

Once θ passes beyond θ _c , steady state E ₂ becomes unstable and the model has a unique interior steady state E* by our earlier mathematical analysis. Simulations do reveal the existence of a unique interior steady state E* and all solutions with positive initial conditions randomly simulated converge to the interior steady state when θ is only little larger than θ _c . Therefore, numerical simulations confirm our earlier observation that Hopf bifurcation cannot occur when E ₂ loses its stability. However, as we increase θ to 0.0571, a positive periodic solution exists. Therefore, a Hopf bifurcation has occurred when θ is larger than and less than 0.0571. 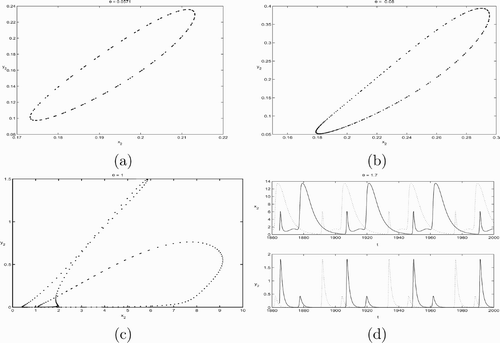The x ₂, y ₂ components of the periodic solution are plotted in Figure 1a and b with different θ values.

Notice the positive periodic solution that appears in Figure 1a corresponds to a positive fixed point of the associated Poincaré map for system (2). The bifurcation of the fixed point for the Poincaré map is itself a bifurcation of the periodic solution for system (2). If it is a saddle node bifurcation of the map, then it would imply the birth and disappearances of two periodic solutions. If it is a period two bifurcation, then the positive periodic solution will double its period.

As we increased θ, we noticed that the positive periodic solution becomes nonoval. It was suspected that the periodic solution either doubled its period or the system has two positive periodic solutions as shown in Figures 1c and d. However, a closer examination reveals that the same periodic solution persists with roughly the same period. See Figure 1d for the x ₂, y ₂ components of the solution with initial condition and when θ=1.7. The solutions took much longer to converge to the positive periodic solution. Therefore, we conjecture that the positive periodic solution is globally asymptotically stable whenever it exists. We also tested the system for sensitive dependence on initial conditions for large values of θ and found that the model is not sensitive to initial conditions.

Figure 1. This figure plots solutions of system (2) with parameter values K=5, d ₂=0.5000, α₂=0.2000, β=0.8000, e=0.1000, and γ=0.2000. When θ=0.0571, the x ₂, y ₂ components of the solution is plotted in (a). (b) provides the x ₂, y ₂ components of the solution with θ=1.0. (c) plots the x ₂, y ₂ components of a solution with initial condition (1.8252, 2.6981, 1.8207, 0.4637) after some transient behavior has been truncated with θ=1. (d) plots x ₂ and y ₂ components of two solutions against time with θ=1.7.

3. A stochastic model

In the previous section we used a deterministic model to study the interaction between prey, predator, and parasites. It was implicitly assumed in the model that only one possible reality can evolve under time by obeying the laws governed by the ordinary differential equations (1). Since the process of population interaction might evolve in an indeterminacy manner, in this section we propose a stochastic model, a counterpart of system (2), to study population interaction. Specifically, we will use a continuous-time Markov chain model to study the population interaction under random effects. We refer the reader to 1 4 for stochastic models with applications to biology.

Let , and y ₂(t) denote the random variables of the uninfected prey, infected prey, uninfected predator, and infected predator, respectively. The time t is continuous, however, the values of the random variables are discrete. Given the deterministic model (2), we assume for Δ t sufficiently small that the transition probabilities are given by

where .

Of course, there are many different stochastic models that correspond to the same deterministic model (2), but we shall use the above formulation. Similar to the Poisson process, the random variable for the interevent time has an exponential distribution. The resulting model is a multivariate process and we will not pursue the study analytically. Instead we will focus on numerical simulations to study the stochastic process.

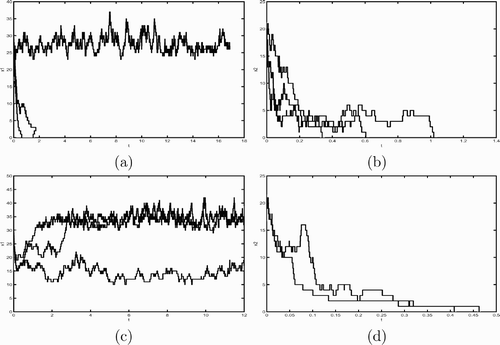
To simulate our model, we use the same parameter values as for the deterministic model (2). Specifically, we choose d ₂=0.5000, , , e=0.1000, , and K=5. When θ=0.02, the deterministic model assures that both the uninfected prey and predator can persist. This is not the case for our stochastic model. From the sample paths given in Figure 2a we see that some uninfected prey populations do go to extinction. However, for the sample paths provided in Figure 2b that the infected prey all become extinct. We then increase θ to 0.55. According to our previous study on the deterministic system, it is known that both the infected and uninfected prey and predator can persist. This is not true again for the continuous-time Markov chain model. Although it is clear that the uninfected prey populations can survive for the sample paths simulated in Figure 2c, it is not the case for the infected prey population as shown in Figure 2d.

Figure 2. This figure plots three sample paths of the continuous-time Markov chain model with parameter values d ₂=0.5000, α₂=0.2000, β=0.8000, e=0.1000, θ=0.2, γ=0.2000, and K=5. (a) and (b) plot three sample path for x ₁ population size and x ₂ population size, respectively, when θ=0.02. (c) and (d) plot x ₁ and x ₂ populations, respectively, when θ=0.55. The initial population size is (50, 1, 20, 1) for all simulations.

4. Discussion

In this manuscript we investigated a deterministic predator–prey model with an infectious disease. Both the uninfected prey and predator can become infected and thus infectious when they interact with infected individuals in the other species. In terms of the original parameters, we see that the predator will become extinct if . This is due to the predator's large natural death rate which cannot be compensated by the predation. Notice that this inequality does not depend on θ.

When the above inequality is reversed and inequality (7) holds, then only the uninfected prey and predator can persist. Observe now that θ plays a role in the persistence of the infected populations. In particular, inequality (7) is true if θ is small when other parameter values are kept at the same values. The left-hand side of inequality (7) increases with increasing θ. When inequality (7) is reversed, it was showed that there is a unique interior steady state and hence the infected populations can survive. Consequently, we conclude that the parasites are more likely to persist if the infected prey is more likely to be preyed upon. On the other hand, since the left-hand side of inequality (7) is a decreasing function of α₁ and α₂, we see that decreasing disease related mortality for both the prey and predator populations can promote persistence of the parasites. Therefore, the parasite cannot be too lethal in order for its survival.

Moreover, as we increase θ, the interior equilibrium becomes unstable and there is a positive periodic solution for the system. As a result, there is a periodic outbreak of the disease in the populations. The infected population levels remain low for sometime before they reach high population sizes. This phenomenon may cause serious problems if the prey and/or predator populations are our natural resources.

We also formulate a stochastic model using a continuous-time Markov chain, where the time is continuous and the random variables are discrete. No mathematical analysis is performed on this stochastic model. However, numerical simulations for this specific formulation conclude that populations can always become extinct due to random effects of demography, predation, and transmission of the disease, as compared with the circumstance when the populations can persist in the deterministic model. The results of the stochastic model make the interaction between these populations more unpredictable. In addition to the life strategies that evolve over time to increase fitness for the populations, the persistence of the populations may however depend largely on chance.

Additional information

Notes on contributors

Sophia R.-J. Jang

Current address: Department of Mathematics Statistics, Texas Tech University, Lubbock, TX, USA