The basic reproduction number in epidemic models with periodic demographics

Abstract

Patterns of contact in social behaviour and seasonality due to environmental influences often affect the spread and persistence of diseases. Models of epidemics with seasonality and patterns in the contact rate include time-periodic coefficients, making the systems nonautonomous. No general method exists for calculating the basic reproduction number, the threshold for disease extinction, in nonautonomous epidemic models. However, for some epidemic models with periodic coefficients and constant population size, the time-averaged basic reproduction number has been shown to be a threshold for disease extinction. We extend these results by showing that the time-averaged basic reproduction number is a threshold for disease extinction when the population demographics are periodic. The results are shown to hold in epidemic models with periodic demographics that include temporary immunity, isolation, and multiple strains.

Keywords:

• basic reproduction number
• differential equations
• epidemic models
• periodic coefficients

AMS Subject Classification :

• 92D25
• 92D30

1. Introduction

Periodicity in epidemics often occurs due to patterns of contact in social behaviour or due to seasonality from environmental factors 13 23. Influenza is a disease that is well-known to have a recurrent seasonal pattern every year, a new viral strain is often introduced each year 23. Meningococcal meningitis in western Africa also varies seasonally, where there is a strong asso- ciation between annual epidemics and atmospheric circulation 29 36. The human immune system follows a cyclic pattern in which the body may either become more susceptible or more resilient to certain diseases seasonally during the year 13 23 28. In addition to the disease parameters exhibiting periodicity, the underlying population demographics may also exhibit periodicity. In animal populations, the birth and death rates and carrying capacity may vary periodically due to environmental factors or to the reproductive cycle 8 17 18 21 31 32 38. Disease models with periodicity in births, deaths, and carrying capacity have been applied to the study of hantavirus in bank voles 31 32 38. Seasonality has been studied in many types of epidemic models, showing that periodic solutions exist, period doubling and chaos occur, or providing conditions for disease extinction 3 6,10–12,14 15 17 22 23,24–27,30,33–35.

In this investigation, we concentrate on providing conditions for disease extinction. The well-known disease extinction threshold in epidemic models is known as the basic reproduction number, the number of secondary infections caused by one infective individual in an entirely susceptible population 19. For autonomous differential equations or difference equations, the basic reproduction number can be calculated from the next generation matrix approach 5 9 37 or by linearization about a disease-free equilibrium (DFE). But for nonautonomous models, there is no standard procedure to calculate the basic reproduction number. We show, in some periodic nonautonomous epidemic models, expressed in terms of differential equations, that the basic reproduction number can be obtained from the corresponding autonomous model by using the time-average of the coefficients. Ma and Ma 24 and Greenhalgh and Moneim 14 27 showed in some nonautonomous SIR-type epidemic models with periodic contact rate β (t) and constant population size that the basic reproduction number for the nonautonomous epidemic model is the same as that for the autonomous SIR epidemic model, where β (t) and other periodic coefficients are replaced by their averages, e.g.,

These results depend very much on the fact that the population size is constant and there is no delay in infection (no latent class). We show that the population size does not have to be constant but may be periodic and the results still apply.

In the next section, we assume that, in the absence of disease, the population size satisfies a nonautonomous logistic equation with periodic birth rate, death rate, and carrying capacity. We show that solutions to this nonautonomous logistic equation are bounded and converge to a periodic solution. Then in Section 3, we study populations with periodic demographics, where disease is introduced, and the contact rate, recovery rate, and other rates may also be periodic. We assume that the disease does not result in additional mortality and that the mode of transmission can be either standard or mass action. In each of the models, it is shown that the basic reproduction number for the time-averaged autonomous epidemic model is also a basic reproduction number for the nonautonomous model. In particular, if , then the population becomes disease-free, but if , then the disease-free state is unstable. In Section 4, the effects of isolation are added to the epidemic model, and in Section 5, an epidemic model with multiple strains is studied. Some numerical examples are presented in Section 6 to illustrate the results. Then the results are summarized in the conclusion.

2. Periodic population dynamics

Let the total population size at time t be denoted as P(t). Let denote the intrinsic growth rate, the per capita birth rate minus the per capita density-independent death rate. Let k(t)P(t) denote the per capita density-dependent death rate. The parameters b(t), d(t), and k(t), defined for , are continuous, nonnegative, bounded, and periodic with the same period p>0. The period p may not be the minimal period for some of the functions because we will allow some of them to be constant or to have different minimal periods. But p is the common period for all of the parameter functions b(t), d(t), and k(t) and the minimal period for at least one of the functions. Thus, , and k(t+p)=k(t) for all t≥0. Let [bcirc], [dcirc], and [kcirc] denote their respective averages, e.g.,

Then the model for the population size has the form of the logistic growth differential equation,

where P(0)>0. In addition, we make the following three assumptions for model (1):

i.	[bcirc]>0;
ii.	;
iii.	.

We will show that solutions P(t) to (1) are bounded above and below by positive constants and are periodic. The proof for boundedness of solutions to (1) follows closely a proof by Ireland et al. [21, Lemma 1, pp. 43–44].

Theorem 2.1

Assume (i)–(iii) for model (1). Then there exists positive constants P _min and P _max such that for all .

Proof

Notice that . Let (assumptions (ii) and (iii)). If P(t)>M, then P˙(t)<0. Hence, for all .

To prove that P(t) is bounded below by a positive constant, choose δ>0 such that and

where . Suppose P(t) is not bounded below, then for each , there exists an interval [t ₁, t ₂] such that , and P(t)<δ for t∈(t ₁, t ₂).

Let and , where and b _max>0. Then for t∈[t ₁, t ₂]. If , for t∈[t ₁, t ₂]. In this case, it follows that , which is a contradiction. Thus, it must be the case that

In this case, for t∈[t ₁, t ₂]. Then for t∈[t ₁, t ₂]. Thus, for or equivalently,

By the continuity and boundedness assumption on the periodic coefficients, it follows that

for all , where [rcirc] is defined in assumption (ii). Since ε can be chosen arbitrarily close to zero, inequality (3) implies T=t ₂−t ₁ can be sufficiently large so that

For ε chosen sufficiently small such that inequality (4) holds on the interval [t ₁, t ₂], . Thus,

But by choice of δ in Equation (2), the preceding inequality leads to the contradiction, . Therefore, the population size P must be bounded below by a positive constant, P _min.   ▪

Making the change of variable in Equation (1), u=1/P, we are led to the following linear differential equation:

Theorem 2.1 implies u(t) is bounded by positive constants, . For continuous periodic coefficients r(t) and k(t) of period p, it follows from the theory of linear differential equations that a solution u(t) of period p exists if and only if u(t) has at least one bounded solution [16, Theorem 1.1, p. 408]. Since all solutions u(t) are bounded, there exists a periodic solution of period p. Denote this periodic solution as u*(t). In the next theorem, we show that u*(t) is unique and stable. The corresponding periodic solution of model (1) is denoted as . We show that the solution P(t) of model (1) approaches the periodic solution P*(t).

Theorem 2.2

The solution P(t) of model (1) converges uniformly to a unique periodic solution P*(t) with period p.

Proof

We prove that u(t) converges uniformly to the periodic solution u*(t) and u*(t) is unique. Hence, P(t) converges uniformly to the periodic solution P*(t). Let . Because u*(t) is periodic of period for . The periodic solution

The solution

Substituting Equation (5) into the preceding expression leads to

In general, for t∈[0, p) implies for t∈[0, p). By induction, it follows that for t∈[0, p). Hence, u(t+np) converges uniformly to the periodic solution u*(t) as n→∞ for t∈[0, p). There cannot be two periodic solutions since the solution u(t) to the initial value problem is unique. Hence, all solutions u(t) converge uniformly to the periodic solution u*(t).   ▪

3. SIRS epidemic model with seasonal births, deaths, and transitions

We consider an SIRS model with temporary immunity. The variable S denotes the number of susceptible individuals, variable I the number of infected and infectious individuals, and variable R the number of individuals that have recovered from the disease with temporary immunity. We assume that there are no disease-related deaths. Parameter γ (t) is the recovery rate and ρ(t) is the rate that recovered individuals lose their immunity. The periodic epidemic model is given by the following system of differential equations:

where , and the total population size satisfies model (1). The coefficient Ω(t, P) may take one of the following two forms:

a.	;
b.	.

Form (a) leads to standard incidence, β SI/P (also known as frequency-dependent incidence), whereas form (b) leads to mass action incidence, β SI (also known as density-dependent incidence). All coefficients are nonnegative, continuous, bounded, and periodic with period p. We assume that their average values satisfy (i)–(iii) and

• (iv) , and .

In the trivial case, where the coefficients are constant functions, model (6) reduces to an autonomous system. It follows from the theory of differential equations and the assumptions on the coefficients that solutions to (6) exist and are unique. In addition, solutions are nonnegative and bounded.

When , then model (6) simplifies to an SIR epidemic model with permanent immunity. When both parameters , then model (6) simplifies to an SI epidemic model.

Applying the substitutions s=S/P, i=I/P, and r=R/P, we arrive at a system of proportions, where , and

where, in the two cases,

a.	;
b.	.

Surprisingly, the density-independent and density-dependent factors d(t) and k(t) appear to play no role in disease extinction. However, these terms have an impact on P(t), which affects disease extinction in the case of mass action incidence. The DFE for the proportions is given by (s, i, r)=(1, 0, 0). System (7) is the proportional SIRS model defined by Ma and Ma 24 when there are no disease-related deaths and incidence is standard (case (a)).

Define the basic reproduction number as

where, in the two cases,

a.	;
b.	.

The threshold (8) is the basic reproduction number for the time-averaged autonomous system, where all the coefficients in Equation (6) are replaced by their averages and P(t) is replaced by the function P*(t). (In the case (b) of mass action incidence, is replaced by ωˆ.) It is important to note if i(t)→0 as t→∞, then I(t)→0 because P(t) is bounded by positive constants (Theorem 2.1).

For case (a) of standard incidence, the next theorem follows directly from Ma and Ma [24, Theorem 7, p. 168] and Theorems 2.1 and 2.2. For case (b) of mass action incidence, these previous theorems can also be applied with a slight modification.

Theorem 3.1

Assume (i)– (iv) and for t∈[0, p) for model (7). Let be defined as in (8). If , then the DFE (1, 0, 0) for model (7) is locally asymptotically stable. If , then the DFE (1, 0, 0) for model (7) is unstable.

Proof

We verify the results for case (b), mass action incidence. Let . We analyse the DFE for the proportions (s, i, r)=(1, 0, 0). Linearization of i(t) in (7) leads to with solution

For ε>0, there exists T sufficiently large such that for t≥T. Hence, for t>0, the integral in the preceding expression satisfies

But ε can be chosen sufficiently small such that the expression in the square brackets is negative. Hence, for the linearization, i(t)→0 as t→∞. The solution r is given by

Taking the limit as t→∞ and applying L'Hôpital's rule,

For the limit to exist, it must be the case that for t∈[0, p). Thus, r(t)→0 implies s(t)→1. This result implies local stability of the DFE (1, 0, 0) in model (7).

Let . Consider the linearization of model (7). For ε>0, there exists T>0 such that for . Since ε can be chosen sufficiently small so that , it follows that as t→∞. But this means the disease-free state (1, 0, 0) for model (7) is unstable.   ▪

It can be proved that global disease extinction occurs in case .

Theorem 3.2

Assume (i)–(iv) and for t∈[0, p) for model (6). Let be defined as in (8). If , then disease extinction occurs in model (6), , and , where P*(t) is the periodic solution of model (1).

Proof

To show the global stability of the disease-free state, consider first the proportional model (7). For ε>0, there exists T sufficiently large such that for . For case (a), standard incidence, . For case (b), mass action incidence, it follows for . In both cases, (see proof of Theorem 3.1), which means , , and in model (6) as t→∞.   ▪

4. SIXS model with seasonal isolation

Our results apply to an epidemic model with isolation, originally developed by Hethcote et al. 20, where we allow the parameters to be periodic functions. This model describes the long-term dynamical behaviour when there is isolation of infectious individuals. Quarantine or isolation (confinement of exposed or infectious individuals, respectively) have been practiced for human diseases such as leprosy, tuberculosis, measles, and scarlet fever and animal diseases such as foot and mouth disease, psittacosis, and rabies 20. The variable X represents the number of infected and infectious individuals I that are isolated. For example, isolation may mean bed rest at home during holidays or during school breaks which often occur seasonally. The periodic function ν(t) is the rate at which infected individuals are isolated; ε(t) is the rate at which infected individuals are removed from isolation because they are no longer infectious; they are put in the susceptible class. The periodic function γ (t) is the rate of recovery of infectious individuals; no immunity is assumed. Other parameters are the same as in the SIRS model in the previous section. The SIXS model has the following form:

where , and satisfy model (1). The parameter Ω(t, P) is defined as in the SIRS model. The coefficients , and ν(t) are continuous, nonnegative, bounded, and periodic of period p. We assume that their average values satisfy (i)–(iii) and

• (v) , and .

Solutions to (9) are nonnegative and bounded.

Rewriting system (9), in terms of proportions, s=S/P, i=I/P, and x=X/P,

where s, i, x≥0 and s+i+x=1. The DFE for the system of proportions is (1, 0, 0). Define the basic reproduction number as

This time-averaged basic reproduction number is the basic reproduction number for the time-averaged autonomous epidemic model, where the coefficients in Equation (9) are replaced by their time averages. If the infected population is not isolated , then the model is essentially an SIS model.

Theorem 4.1

Assume (i)– (iii), (v), and for t∈[0, p) for model (10). Let be defined as in (11). If , then the DFE (1, 0, 0) for model (10) is locally asymptotically stable. If , then the DFE (1, 0, 0) for model (10) is unstable.

Proof

The local stability can be determined by linearizing the system about the DFE,

Note that the linearized differential equation in i is independent of s and x. Thus, solving for i,

If , then i(t)→0 (this follows from Ma and Ma 24 for case (a) and from the proof of Theorem 3.1 for case (b)). The solution for x is given by

Taking the limit as t→∞ and applying L'Hôpital's rule for , it follows as in the case of r(t) in the proof of Theorem 3.1 that

where for t∈[0, p). Thus, s(t)→1.

If , then and as t→∞. The DFE (1, 0, 0) is unstable.   ▪

Using arguments similar to the proof for the linearized system, we are able to prove that the infection dies out in model (9) if .

Theorem 4.2

Assume (i)–(iii), (v), and for t∈[0, p) for model (9). Let be defined as in (11). If , then disease extinction occurs in model (9); , , and , where P*(t) is the periodic solution of model (1).

Proof

Note that in Equation (10), . Applying the methods in the proofs of Theorem 3.2 and 4.1, it follows that as t→∞ for , which imply , and as t→∞.   ▪

5. SIRS model with multiple strains and cross-immunity

We apply our results to SIRS models with multiple strains, models studied by Ackleh and Allen 1 2. But we generalize the models by including periodic parameter functions. Each strain provides immunity from infection by other related strains, referred to as cross-immunity. Cross-immunity between strains can lead to competitive exclusion in which an aggressive strain can drive the other strains to extinction 1 2. We assume that there are periodic contacts and the other coefficients may be periodic as well. Individuals may be infected with one of the n different strains, where the number of individuals infected and infectious with strain j is denoted as . Recovery from infection by strain j occurs at a rate γ _j (t). We make the additional assumption that recovery may be only temporary; loss of immunity occurs at a rate ρ (t). We assume that there are no disease-related deaths, so that the total population size satisfies model (1).

The model with multiple strains takes the following form:

where , and satisfy model (1). The coefficient has one of the following two forms:

a.	;
b.	.

The periodic coefficients , and ρ (t) are continuous, nonnegative, bounded, and periodic of period p, and their average values satisfy

• (vi) .

Solutions to Equation (13) are nonnegative and bounded.

When there is just a single strain, n=1, the differential equations in Equation (13) reduce to model (6). When , then model (13) simplifies to an epidemic model with permanent immunity. When the parameters and , then there is no immunity.

Rewriting system (13) in terms of proportions, , and r=R/P,

where has one of the two forms:

a.	,
b.	.

The set is invariant, where .

Define the strain reproduction number as

where has one of the two forms:

a.	,
b.	.

Then the basic reproduction number is defined as

It is important to note that if the coefficients in model (13) are replaced by their average values, then the basic reproduction number for the resulting autonomous, time-averaged model is given by Equation (15). We verify the local and global stability of the DFE if and instability if .

Theorem 5.1

Assume (i)– (iii), (vi), and for t∈[0, p) for model (14). Let be defined as in (15). If , then the DFE (1, 0, …, 0) for model (14) is locally asymptotically stable. If , then the DFE (1, 0, …, 0) for model (14) is unstable.

Proof

Linearizing system (14) about the DFE (1, 0, …, 0),

Then

Similar to the proof of Theorems 3.1 and 4.1, it follows that if , then i _j (t)→0 as t→∞. Therefore, if , then i _j (t)→0 as t→∞ for j=1, …, n. It follows as in the proof of Theorem 3.1 that r(t)→0 if and also s(t)→1 as t→∞. If some , then in the linear model. Hence, if , the DFE is unstable.   ▪

Theorem 5.2

Assume (i) – (iii), (vi), and for t∈[0, p) for model (13). Let be defined as in (15). If , then disease extinction occurs in model (13), , j=1, …, n, , and , where P*(t) is the periodic solution of model (1).

Proof

Note that i _j in the proportional model (13) satisfies . Hence, it follows as in the proofs of Theorems 3.2 and 4.2 for that there is extinction of I _j . Disease extinction of all I _j , j=1, …, n, requires all strain reproduction numbers to be less than one or .   ▪

6. Numerical examples

Several numerical examples illustrate our results for the SIRS model (Theorems 3.1 and 3.2) discussed in Section 3. Let

and

where the time unit is 1 year. The common period of these three functions is p=3 years. The minimal period for birth and density-independent mortality is 1 year, but the minimal period for the carrying capacity is 3 years. Figure 1 shows the solution to the total population size when P(0)=1030; the solution converges to a periodic solution P*(t) with period p=3.

Figure 1. Solution P(t) to the periodic logistic differential equation (1) with P(0)=1030 converges to a periodic solution P*(t) with period p=3 years and [Pcirc]=1516. Parameter functions b(t), d(t), and k(t) are defined in the text.

For the SIRS epidemic model (6), let the parameters for recovery and transmission be defined as

where different values of βˆ>0 are chosen to illustrate cases of standard or mass action incidence for and . The contact rate varies seasonally. In Figure 2 (i) and (ii), when , solutions I(t) converge to zero and S(t) converges to the periodic solution given in Figure 1. However, in Figure 2 (iii) and (iv), when , the number of infected individuals converges to a periodic solution with period p=3.

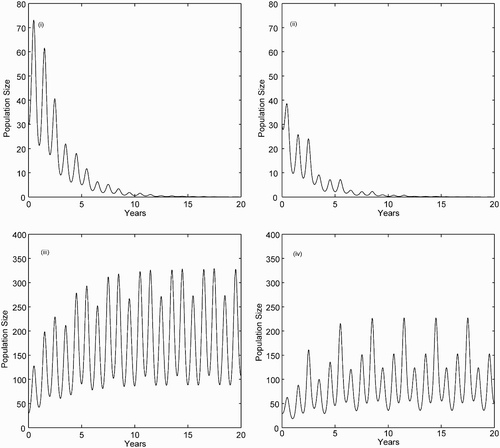
Figure 2. Number of infectious individuals I(t) for the SIRS model (6). For solutions graphed in (i) and (iii), we assume standard incidence, whereas in (ii) and (iv), we assume mass action incidence. The parameters b(t), d(t), k(t), γ (t), ρ(t), and β(t) are defined in the text, S(0)=1000, I(0)=30, and R(0)=0. (i) Standard incidence, βˆ=3.6 and ˆℛ₀=0.90. (ii) Mass action incidence, βˆ=0.0024 and ˆℛ₀=0.91. (iii) Standard incidence, βˆ=4.4 and ˆℛ₀=1.10. (iv) Mass action incidence, βˆ=0.003 and ˆℛ₀=1.14.

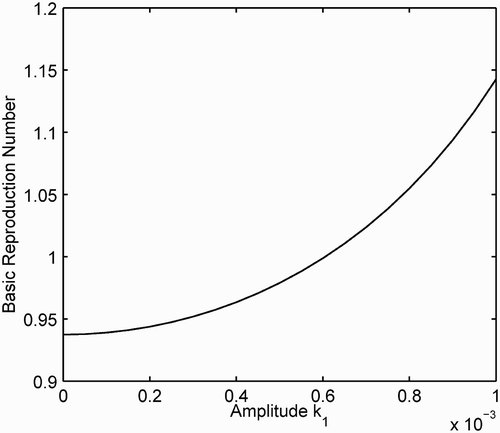
Calculation of for standard incidence is straightforward by applying Equation (8) because , [bcirc]=2, and . To calculate for the mass action case requires the estimation of

In Figure 2 (ii), , so that . In Figure 2 (iv), , so that .

The population size has a direct impact on the basic reproduction number in the case of mass action incidence (as can be seen in formula (17)). Even when the average values of the parameter functions are constant, the amplitude of the density-dependent mortality function k(t) can change the dynamics of P*(t), which in turn affects . Let , where . Let all other parameter functions be as defined previously with . Then and (Figure 3).

Figure 3. The basic reproduction number for the SIRS model with mass action incidence is graphed as a function of the amplitude k ₁ of the density-dependent mortality k(t)=0.001+k ₁ cos(2π t/3). All other parameter functions are defined in the text, where βˆ=0.0025 and P(0)=1500.

7. Conclusion

The effects of seasonality in epidemic models reflect the population and disease dynamics that often occur in nature and provide greater biological realism of the mechanisms that may be behind the emergence of disease outbreaks in human and wildlife systems. For epidemic models with periodic coefficients, it is important to be able to estimate the basic reproduction number. We have shown that the basic reproduction number for periodic nonautonomous epidemic models can be computed from the corresponding time-averaged autonomous epidemic models in some cases. Periodicity can occur in contact rates, birth rates, death rates, carrying capacity, recovery, and isolation. These results extend previous results, where it was assumed that the population size remained constant 14 24 27. We have shown that the population size can also be periodic. The results hold for the standard and mass action incidence and can be applied to periodic nonautonomous epidemic models with temporary immunity, isolation, and multiple strains. An important restriction in our results is that there are no disease-related deaths. Additional mortality due to disease changes the dynamics of the total population size, P(t), and could result in total population extinction. Our results have applications to a zoonotic disease carried by wild rodents, hantavirus. Certain species of rodents serve as reservoirs for hantavirus infection, but no additional mortality results from the infection 4 7. Bank voles, reservoirs for the hantavirus known as Puumala virus, have been shown to exhibit population cycles of either 3–4 years or 1 year in different parts of Europe 31 32 38.

Acknowledgements

Financial support was provided by the National Science Foundation, DMS-0718302 (LJSA) and the Fogarty International Center, no. #R01TW006986-02 under the NIH NSF Ecology of Infectious Diseases initiative (LJSA, CLW). We thank E.J. Allen and M. Langlais for helpful comments and for providing references for this work. In addition, we thank two anonymous reviewers for their helpful suggestions.