Species decline and extinction: synergy of infectious disease and Allee effect?

Abstract

Host–parasite models with density-dependent (mass action) incidence and a critical Allee effect in host growth can explain both species decline and disappearance (extinction). The behaviour of the model is consistent with both the novel pathogen hypothesis and the endemic pathogen hypothesis for chytridiomycosis. Mathematically, the transition from decline to disappearance is mediated by a Hopf bifurcation and is marked by the occurrence of a heteroclinic orbit. The Hopf bifurcation is supercritical if intra-specific host competition increases with host density at a large power and subcritical if the power is small. In the supercritical case, host–parasite coexistence can be at equilibrium or periodic; in the subcritical case it is only at equilibrium.

Keywords:

• amphibian disappearance
• epidemic
• chytridiomycosis
• novel versus endemic pathogen hypothesis
• incidence
• global climate change

Introduction

Emerging infectious diseases (as caused by a virus in the African wild dog, the fungal pathogen Aphanomyces astaci in the noble crayfish, chydrid fungi in frogs and rana-viruses in salamanders) are among the suspected causes of species decline and disappearance (see 14 18 29,37–40 and the literature cited therein). Epidemic models with standard (or frequency-dependent) incidence, in different parameter regions, are known to show both decline of the host from a disease-free to an endemic equilibrium and extinction of the host 8 9 19 20 32 42 45, but empirical evidence of a population or species eliminated by frequency-dependent parasites seems elusive 14. The usual epidemic models with mass action (or density-dependent) incidence only show extinction of the parasite or decline of the host population to an endemic equilibrium 3. In this paper, we make the case that density-dependent incidence can also lead to host extinction when the host population underlies a critical Allee effect. This is already conjectured in 14 29 and is also investigated in 15 23 with somewhat different models. Compared with other possible mechanisms (frequency-dependent incidence, disease reservoirs, spatial dynamics), small population size appears to be the most widely reported driver of disease-induced extinction in natural populations 14. In fact, it is an obvious idea that the synergy of infectious disease and a critical host Allee effect can lead to host (and disease) extinction: by increasing the mortality and/or lowering the reproductivity, the disease drives the host to a low density at which the Allee effect takes over to drive the population into extinction. Still the precise dynamics of this synergy are interesting and have only recently been studied.

Disease incidence is the number of new infections per unit of time. Let C(N) be the number of contacts that an average host makes per unit of time in a host population of density N and p the probability that the contact between a susceptible host and an infective host leads to an infection. If S is the density of susceptible individuals, the rate of contacts made by all susceptible individuals is C(N) S. If I is the density of infective individuals, I/N is the probability that a given contact actually occurs with an infective individual. So the incidence is p C(N) S(I/N). Mass action or density-dependent incidence σ SI results if one assumes that C(N) is proportional to N, while standard or frequency-dependent incidence σ SI/N results from assuming that C(N) is a constant which does not depend on N. Which of the two incidences is more appropriate in a model for host–parasite dynamics depends on how the host population reacts to the impact of the disease. Standard incidence is appropriate if the hosts would move closer together when being decimated, leave part of their habitat unoccupied and keep up the same population density in the part of the habitat they still occupy. Mass action incidence would apply if the hosts would not react to the thinning of their ranks by the disease. For discussions and references concerning the right form of incidence, see 15 22 30 33 43, Sec.19.1 and their bibliography.

While in models with standard incidence the infectious disease can drive the host to extinction in an appropriate parameter range, in models with mass action incidence the disease at worst reduces the host from a disease-free to an endemic equilibrium provided that the host population is subject to non-critical growth in the absence of the disease 3. Non-critical growth is characterized by positive growth rates at low population densities. In the simplest case (the Verhulst scenario), there are two equilibria for the host dynamics, the extinction equilibrium 0 and the carrying capacity (or saturation equilibrium) K: the host population, unless extinct from the beginning, always converges to K as time tends to infinity.

The Allee effect has its name from the pioneering work of Allee 1. A precise definition seems difficult 41. For the purpose of this paper, the Allee effect in population growth is characterized by the per capita growth being the largest at intermediate population densities. The critical Allee effect (also called critical depensation 10) is characterized by negative growth rates at low and high population densities and a positive growth rate at intermediate population density. More precisely, there are three equilibria for the host dynamics in the absence of the disease: the extinction equilibrium 0, the carrying capacity (or saturation) equilibrium K and a watershed (or breakpoint or threshold) equilibrium W, 0<W<K, which is characterized as follows: if the host population starts at a density below W, then it dies out; if it starts at a density above W, then its density converges to K.

The disease can be characterized by a parameter S*, which gives the density of the susceptible, uninfected, part of the population at the endemic equilibrium if this happens to exist. We will show that the host–parasite dynamics strongly depend on S*. If S*>K, the disease will die out if it is introduced in small numbers into a host population close to the saturation equilibrium K, and the host density will converge to K. If S*<W or S* is between W and K but closer to W, then the host population will become extinct if the disease is introduced. If S* is between W and K but closer to K, then a host population of about the density K will converge to the endemic equilibrium if the disease is introduced with a small number of infective individuals. The transition between these two dynamics is mediated by a Hopf bifurcation which, depending on the host growth function, can be subcritical or supercritical. The periodic orbits that are created this way blow up to a heteroclinic orbit and then disappear.

A predator–prey model with a critical Allee effect in the prey, which is similar to our epidemic model, has been used to explain the extinction of the passenger pigeon in North America 11. An earlier mathematical analysis can be found in 4 5; the role of heteroclinic cycles for the understanding of the model dynamics has been further explored in 44. This model cannot be directly used for epidemics because it uses the common Allee-type per capita growth function (W−N)(N−K), which is difficult to separate into a per capita birth and a per capita mortality rate in a natural way such that both rates are positive at all population densities N. This becomes an issue for our epidemic model because susceptibles and infectives belong to the same species, whereas prey and predator typically belong to different species. As a reward for considering new Allee-type per capita growth rates, we find that the Hopf bifurcations mentioned above are supercritical if intra-specific host competition increases with host density at a large power and subcritical if the power is small.

Predator–prey models with an Allee effect in the prey and host–parasitoid models with an Allee effect in the host have been widely investigated 26–28,31, Sec.12.1, 34 35. A typical phenomenon that we will also meet in our epidemic model is an initial-condition-dependent outcome (extinction or survival of both species) even if the host (prey) population density initially is above its watershed equilibrium. Both host and parasite will become extinct if there are sufficiently many infectives at the beginning. Our main interest, however, will be in the specific dynamics that result if initially the host population is close to its carrying capacity and the number of infectives is very small. This appears to us as the typical initial scenario triggering species decline or disappearance. The paper is structured as follows:

1.	Some single species population dynamics
2.	The epidemic model with density-dependent incidence
3.	Verhulst growth and host persistence
4.	Allee effect and host extinction
5.	Discussion

1. Some single species population dynamics

We consider the differential equation N′=N g(N) as a model for the dynamics of a single (unstructured) population. The function , is the per capita growth rate. We make the following assumptions.

Assumption 1.1

The per capita growth rate has the following properties:

• (G)  is continuous and bounded on ℝ₊ and continuously differentiable on (0, ∞).

• (K)  g(N)<0 for all sufficiently large N>0.

Then there exists a smallest number such that g(N)<0 for all N>K.

K is uniquely determined. If g(N)<0 for all N>0, then K=0. If K>0, then g(K)=0. In either case, K is an equilibrium of N′=Ng(N). K is called the carrying capacity for the population or the saturation equilibrium of the population. This name is motivated by the following result, which can easily be proved.

Theorem 1.2

Let be differentiable and satisfy N′≤Ng(N) on ℝ₊. Then or there exists some r≥0 such that N(t)≤K for all t≥r.

The per capita growth function g is said to be non-critical if g(0)>0, of weak Verhulst type if K>0 and g(N)>0 for all N∈[0, K) and of strong Verhulst type (or purely compensating 10) if g(0)>0 and g is strictly decreasing on ℝ₊.

Corollary 1.3

Let g be of weak Verhulst type. Then all solutions of N′=Ng(N) with N(0)>0 converge to K as t→∞.

The per capita growth function g is said to be of critical Allee type (or critically depensating 10) if there exists some

Then g(W)=0 and W is also an equilibrium for N′=Ng(N).

Corollary 1.4

Let g be of critical Allee type. Then the solutions of N′=Ng (N) have the following behaviour as t→∞,

The equilibrium W is called watershed or breakpoint or threshold equilibrium.

Example 1.5

Strong Verhulst: let p>0 and the per capita birth rate be given by , b>0 and β₀>0, and the constant per capita mortality rate μ satisfy . Then is of strong Verhulst type with .

Critical Allee: let p>1 and b>0, κ>0, and the per capita birth rate be given by

Then β(0)=0 and as N→∞. For , we notice that β′(N)>0 if 0≤N<M, and β′(N)<0 if N>M. So β is strictly increasing on [0, M] and strictly decreasing on [M, ∞) and has a local and global maximum at N=M. Let the mortality rate μ be constant and . Then the per capita growth rate is of critical Allee type with . The biological motivation for N in the numerator of Equation (2) is that in a sexually reproducing population, the chance of finding a mate is assumed to be proportional to the population density. The power p in the denominator describes how the intra-specific host competition grows with host density.

In the literature, one often finds the following Allee-type per capita growth function (or a positive multiple of this expression), which is an adaptation of the logistic per capita growth function K−N 6. This growth function is also used in predator–prey models with a critical Allee effect in the prey 5, Sec.3.5.5 4 11 31, Sec.12.1 and in epidemic models 15 23 24. While mathematically convenient, this growth function has the disadvantage that it is not possible to identify the per capita birth and death rates, β(N) and μ(N), g=β−μ, in a way that for all population densities N, the rates β(N) and μ(N) are non-negative and, more seriously, make biological sense. The splitting of the growth rate into a birth and death rate is less of a problem in a predator–prey model because predator and prey typically are different species. In an epidemic model, infectious individuals are subject to the same natural death rate as susceptible individuals, which may be augmented by a disease death rate. So, unless one assumes complete vertical transmission 15, it cannot be avoided that the natural death rate appears as a separate entity in the model.

We will consider growth functions of the form as in Example 1.5. Here the density-dependence (in particular the Allee effect) is concentrated in the per capita birth rate β. This is appropriate for species that, when faced with a lack of resources, first allocate them to survival rather than reproduction. It conforms with an Allee effect that is caused by mating. We choose this form mainly for mathematical reasons: since the birth rate β only affects susceptible individuals (unless there is vertical transmission) whereas the mortality rate μ affects both susceptible and infective individuals, this choice keeps the model as simple as possible. An epidemic model where the density-dependence is concentrated in the per capita death rate μ is considered in 15.

2. The epidemic model with density-depen-dent incidence

We consider a host population the density of which is denoted by N. The disease divides the population into susceptible and infected parts, the densities of which are denoted by S and I, N=S+I. There is no recovery from the disease. We assume that infected individuals can either not reproduce or the offspring of infected individuals soon die and can be disregarded. We also assume that infected individuals are too weak to compete for resources such that only the susceptible individuals take part in the resource sharing. For this reason, the per capita birth rate β(S) depends on S rather than N. We assume a constant per capita mortality rate μ for all individuals and a constant per capita disease mortality rate α for infectious individuals. We model infection by mass action (density-dependent) incidence with a proportionality constant σ,

Remark 2.1

If both susceptibles and infectives were to reproduce and compete with same effectiveness, one would use the equation for the susceptible part of the population. Again, we make our modelling choice mainly for mathematical reasons. This way we avoid complications such as multiple endemic equilibria 23 and can drive home our main point (host extinction by synergy of density-dependent transmission and the critical Allee effect) by a simple and almost complete analytic treatment.

We rewrite system (3)

Here

and

The notation S* is motivated by the fact that it is the susceptible component of the endemic equilibrium if this one exists.

Remark 2.2

A predator–prey model would have the form

with prey S and predator I and yield constant η. Replacing I by I/η brings the predator–prey system to the form (4).

Standard arguments imply this global existence result [43, Thm.A.4].

Theorem 2.3

Let Assumptions 1.1 (G) be satisfied. Then, for all S ₀, I ₀≥0, there exist unique which solve Equation (4) and the initial conditions S(0)=S ₀, I(0)=I ₀.

Assumption 1.1 (K) is satisfied for if as S→∞. Then the host population has a carrying capacity K. Notice that is the replacement ratio (disease reproduction number) at carrying capacity, i.e. the average number of secondary infections produced by one typical infected individual that is introduced into an otherwise completely susceptible population at carrying capacity. From now on, we use the following notation for a function :

For the rest of the paper, we assume Assumptions 1.1.

Theorem 2.4

For any solution of Equation (4) with non-negative initial data, the following hold:

a.	S(t)→K for t→∞ or there exists some r≥0 such that S(t)≤K for all t≥r.
b.	or .
c.	There exists some c>0 such that for each solution there exists some r>0 such that for all t≥r.

Proof

Since S≥0 and S′≤S g(S), the first statement follows from Theorem 1.2.

Suppose that . Then there exist some r≥0 and some ε>0 such that

By the first equation in (4), and S(t)→0 as t→∞. This implies that there is some s≥0 such that for all t≥s. Then, for t≥s, and I(t)→0 as t→∞.

We define . In 43, Sec. A.5, we have just shown that our system is uniformly weakly ρ-persistent. Set . Then the first part of Condition (C) in 43, Thm.A.32 is satisfied.

To check the second part, let and , (S, I)∈B and . Then S≤K+1 and . So .

It follows from 43, Thm.A.32 that our system is uniformly strongly ρ-persistent. This implies that there exists some ε>0 such that . In particular, there exists some r≥0 such that for all t≥r. So for all t≥r and .   ▪

Theorem 2.5

a.	If I(0)>0, .
b.	If S*≥K (i.e. ), then I(t)→0 as t→∞.

Proof

a.	If S*≥K, this follows from Theorem 2.4 (a). Suppose that S*<K and . Then and if I(0)>0, a contradiction to Theorem 2.4 (b).
b.	We first assume that S*>K. By Theorem 2.4, there exists some and some r≥0 such that for all t≥r. Then, for t≥r, . This implies that I(t)→0 as t→∞.

Let us assume that S*=K. By Theorem 2.4, there are two cases:

Case 1 There exists some r≥0 such that S(t)≤S* for all t≥r.

Case 2 S(t)≥S* for all t≥0.

In both cases, I′ eventually has a constant sign. So I is eventually monotone and has a limit I*. To show that I*=0, we assume that I*>0. Then for large times. This implies that and in turn I(t)→0 as t→∞.   ▪

3. Verhulst growth and host persistence

In the non-critical case g(0)>0, the disease can lead to host decline, but not to host extinction. Recall that Assumptions 1.1 hold throughout the remainder of the paper.

Theorem 3.1

If g(0)>0, the host population persists uniformly strongly in the following sense: there exists some ε>0 such that for every solution with S(0)>0, I(0)≥0.

Here S _∞ and later S ^∞ are defined analogously to Equation (7).

Proof

We first prove a weaker statement. The host population persists uniformly weakly in the following sense: there exists some ε>0 such that for every solution with S(0)>0, I(0)≥0. Suppose that the uniform weak persistence statement is false. Then, given an arbitrary ε>0, there exists a solution with S(0)>0, I(0)≥0 and some r>0 such that for all t≥r. Notice that S(t)>0 for all t≥0. We can choose . Then for t≥r and I(t)→0 as t→∞. Choose ε>0 and δ>0 also so small that g(S)>δ for all . There exists some s>r such that for all t≥s. For t≥s, . This implies that as t→∞, a contradiction to Theorem 2.4. We now apply 43, Thm.A.32. Set with c>0 from Theorem 2.4 and ρ(S, I)=S. Then conditions (i) and (ii) are satisfied. It follows from our previous considerations that our system is uniformly weakly ρ-persistent. By 43, Thm.A.32, we have uniform strong ρ-persistence which implies our claim.   ▪

We settle the weak Verhulst scenario in order to put the upcoming Allee scenario into perspective.

Theorem 3.2 (weak Verhulst case)

Assume that K>0 and g(S)>0 for all S∈[0, K).

a.	If S*≥K (i.e. g(S)<0 for all S>S*), then I(t)→0 and S(t)→K as t→∞ for all solutions with S(0)>0. Further (K, 0) is locally asymptotically stable.
b.	If S*<K (or equivalently, g(S*)>0), then both host and disease persist uniformly strongly, i.e. there exists some ε>0 such that and for all solutions with S(0)>0, I(0)>0.
c.	[Strong Verhulst case  Assume that g is strictly decreasing on [0, K) and 0<S*<K. If S(0), I(0)>0, then S(t)→S* and I(t)→I*, where . Further (S*, I*) is locally asymptotically stable.

Proof

(a) Consider . By Equation (4), the orbital derivative of V satisfies

Since g(S)>0 for S<K and g(S)<0 for S>K, (S−K)g(S)<0, unless S=K. This shows that ˙ V≤0. Further V(K, 0)=0 and V(S, I)>0 otherwise. This implies that (K, 0) is locally stable 7, Thm.5.1. Since as or S→0, we conclude that S and I are bounded and S is bounded away from 0. So the ω-limit set of a solution is non-empty, compact, invariant, connected and attracts the solution. By the Lyapunov–LaSalle theorem, it is an invariant subset of {˙ V=0}. If S*>K, it is the set {(K, 0)}. Let S*=K. Then ω, the ω-limit set of a solution, is a connected invariant subset of S=S*=K. Consider a solution in ω with I(0)>0. Then I(t)=I(0) and S(t)=K. So , a contradiction. So also in this case, which implies the statement.

(b) The host persists uniformly strongly by Theorem 3.1, i.e. there exists some such that for all solutions with S(0)>0, I(0)>0. We first show that the disease persists uniformly weakly, i.e. there exists some ε>0 such that for all solutions with S(0)>0. Suppose otherwise. Then, for each ε>0, there exists some solution with S(0)>0, I(0)>0 such that . Choose some . Then

Choose ε>0 such that . By the fluctuation method [25, 43, Prop. A.22], there exists a sequence such that and S′(t _j )→0 as j→∞. From the first equation in (4),

Suppose that . Since , and so a contradiction. We conclude that . So, for large t,

and as t→∞, contradicting the boundedness of I proved in Theorem 2.4. Set . In 43, Thm. A.32, we have proved uniform weak ρ-persistence. Uniform strong ρ-persistence and thus uniform strong disease persistence follows from 43, Thm. A.32, with and c>0 from Theorem 2.4.

(c) Consider . The orbital derivative of V satisfies

So if 0≤S≤K. Further V(S, I)=0 if S=S* and I=I* and V(S, I)>0 otherwise. This implies that (S*, I*) is locally stable 7, Thm.5.1. Every orbit with S(0)>0 and I(0)>0 is eventually contained in the set S≤K. So for large t and S=S* for all . Suppose ω contains an element (S*, I ₀) with I ₀≠I*. The solution through this point satisfies S(t)=S*, I(t)=I ₀ and so , a contradiction.   ▪

4. Allee effect and host extinction

In addition to Assumption 1.1, we assume as a technical assumption that is three times continuously differentiable on (0, ∞). Biologically, we assume that there are numbers

such that the per capita growth rate g satisfies

In particular, the per capita growth rate g is strictly increasing on [0, M] and strictly decreasing on [M, ∞). W is the watershed equilibrium for the disease-free dynamics N′=N g(N) and K the carrying capacity. At M, g has a global and local maximum. In our motivating Example (5), if β(0)=0, −g(0) is the natural per capita mortality rate and g(N)−g(0) the per capita birth rate.

Our system has three disease-free equilibria: the origin (0, 0) and the boundary equilibria (W, 0) and (K, 0).

Endemic equilibria. If there exists an endemic (or interior) equilibrium, its susceptible component is S*. The infective component of the endemic equilibrium is provided I*>0. So there is an (unique) endemic equilibrium if and only if W<S*<K. The Jacobian matrix of the vector field of the system (4) is

Evaluated at the endemic equilibrium,

The trace of J(S*, I*) is S* g′(S*) and the determinant . So the endemic equilibrium is a sink if M<S*<K and a source if W<S*<M. Since g′(M)=0, we have a Hopf bifurcation at S*=M. Also notice that (S*, I*) is an unstable node if S* is close to W and an unstable spiral point if W<S*<M and S* is close to M. If M<S*<K and S* is close to M, then (S*, I*) is a stable spiral point while it is a stable node when S* is close to K. Notice that as S*→W or S*→K. At the origin,

Since g(0)<0, both eigenvalues are strictly negative: the origin is locally asymptotically stable. For the watershed boundary equilibrium (W, 0),

Since g′(W)>0, the equilibrium (W, 0) is a saddle for W<S* and a source for S*<W. For the boundary equilibrium involving the carrying capacity, (K, 0),

Since g′(K)<0, this equilibrium is locally asymptotically stable for S*>K and a saddle for S*<K. We summarize.

Theorem 4.1

a.	The extinction equilibrium (0, 0) is always locally asymptotically stable. Its domain of attraction (the initial values of the solutions that converge to (0, 0)) contains the line segment , the strip and an epigraph Here is strictly increasing and concave, .
b.	The watershed boundary equilibrium (W, 0) is always unstable. It is locally asymptotically stable in backward time if S*≤W, and a saddle if W<S*, with the I=0 axis being the unstable manifold.
c.	The saturation boundary equilibrium (K, 0) is locally asymptotically stable for S*≥K and a saddle for S*<K, with the I=0 axis being the stable manifold.
d.	The endemic (interior) equilibrium exists if and only if . It is a sink if M<S*<K and a source if W<S*<M. It undergoes a Hopf bifurcation at S*=M.

Proof

(a) We still need to prove the statement concerning the domain of attraction of (0, 0). By Equation (4), for S≤W. This implies that the region is forward invariant and that any solution starting in this region has S(t) monotone decreasing in t. By the fluctuation method, S(t) has a limit that satisfies and so is either 0 or W. If S(0)<W, and S ^∞=0. If S(0)≤W and I(0)>0, then S(r)<W for r>0 and again S ^∞=0. By Equation (4), and so , t≥0. Again by Equation (4),

We integrate this inequality

Assume that . Then the right hand side has its minimum at and

The population converges to (0,0) if S(t ₀)≤W, i.e. if

ψ is a strictly increasing convex function on the domain with range [0, ∞) which has an inverse function with range . Choose . Since ψ⁻¹ is strictly increasing and concave, φ is strictly increasing and concave. (b) If S*=W, consider the Lyapunov function 7, Thm.5.1. V also works for S*<W, but then we can use linearization instead. (c) If S*=K, consider the Lyapunov function 7, Thm.5.1. V also works for S*>K, but then we can use linearization instead.   ▪

Remark 4.2

It may be worthwhile to record that

where , .

Theorem 4.3

Let 0<S*≤W. Then the population goes extinct whenever I(0)>0. In other words, the extinction equilibrium is globally asymptotically stable for the region {I>0}.

Proof

Assume that I(0)>0. Then I(t)>0 for all t≥0.

It is sufficient to show that there exists some r>0 such that S(r)<W because the extinction equilibrium attracts all such solutions by Theorem 4.1 (a).

Suppose not. Then for all t≥0. By Equation (4), I′(t)≥0 for all t→0 and I(t)≥I(0) for all t≥0. Thus the ω-limit set of the solution lies in (0, ∞)². By the Poincaré Bendixson theorem, the ω-limit set contains an endemic equilibrium or is a periodic orbit which would need to surround an endemic equilibrium. This is a contradiction because there is no endemic equilibrium if S*≤W.   ▪

There are two extreme global scenarios we understand quite well. If S*≤W, the extinction equilibrium is globally asymptotically stable. If S*≥K, there is a bistable scenario where the extinction equilibrium is locally asymptotically stable and the disease-free equilibrium (K, 0) is locally asymptotically stable with a thin manifold separating their domains of attraction. The transition between the two scenarios is mediated by the emergence of an endemic equilibrium which undergoes a Hopf bifurcation, but we do not understand all the details.

More about the Hopf bifurcation: stability of the bifurcating periodic orbits. A formula for the stability of the periodic orbits generated by the Hopf bifurcation is available for the case that the Jacobian matrix has the form with γ>0. We set with a parameter ξ>0 still to be determined,

We set u=S/M, u*=S*/M and w=I/M,

We choose ξ=σ M and scale time. Then we obtain

Now we set w=γ v with γ>0 to be determined later,

By construction, h′(1)=0. Further, there exist such that h(u _j )=0 and h is strictly increasing on [0, 1] and strictly decreasing on [1, ∞). This system has the endemic equilibrium u=u* and provided that h(u*)>0, i.e. u ₁<u*<u ₂. The Jacobian matrix at the endemic equilibrium is

For u*=1, this matrix equals  

We choose γ such that , i.e. . The Jacobian is always positive, while the trace of the Jacobian matrix has the same sign as h′(u*). From the form of the matrix, we see that there is a Hopf bifurcation at u*=1 because h′(1)=0. The stability of the bifurcating periodic orbit is determined by the sign of the following number, a 21, (3.4.11):

Here the subscripts mean partial derivatives. The partial derivatives need to be evaluated at the bifurcation point, in this case u*=1. If a<0, the bifurcating periodic orbits are asymptotically stable; this case is called supercritical bifurcation: the periodic orbits occur for those bifurcation parameters (close to the bifurcation value) for which the equilibrium is unstable.

If a>0, the bifurcating orbits are unstable; this case is called subcritical bifurcation: the (unstable) periodic orbits occur for those bifurcation parameters (close to the bifurcation value) for which the equilibrium is stable. In our case,

All third-order partial derivatives of F ² are 0, whereas is the only third-order partial derivative of F ¹ which is not 0. So

Evaluated at the Hopf bifurcation point,

We see that the sign of a does not change if h is multiplied by a positive constant.

Theorem 4.4

Let , where h is of critical Allee type and takes its maximum at 1. Then the Hopf bifurcation of (4) at S*=M is supercritical if and subcritical if .

An example. Let

with positive constants and p>1. Then g can be represented in the form

with

and

Then

By the quotient rule,

This shows that ˜ β (and h) are strictly increasing on [0, 1] and strictly decreasing on [1, ∞). So h is of critical Allee type if 0<ν<1. By Equation (22), g is of critical Allee type if

We use the quotient rule one more time,

We notice that h and ˜ β are concave on [0, (p+1)^1/p ] and convex on . For later use, we note

We use the product and quotient rule,

We evaluate at x=1, Then a in Equation (4) has the same sign as

So we have a subcritical Hopf bifurcation with unstable periodic orbits if 1<p<3 and a supercritical Hopf bifurcation with stable periodic orbits if p>3.

Synopsis of the Allee effect. We try to understand how the host–parasite dynamics change as we vary . Different values of S* can reflect different susceptibilities of local host populations or different virulence of the parasite.

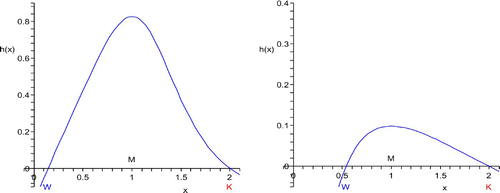
We recall that the origin is always a sink and host populations below the watershed equilibrium density W are bound to become extinct. As illustration we use the birth rate ˜ β from the previous section with p=6 and p=1.5 and g(x)=h(x). Its maximum is taken at M=1. The natural per capita rate μ has been chosen in such a way that the saturation equilibrium is K=2, see Figure 1. Finally we set σ=1.

Figure 1. Critical Allee type per capita growth rates h(x) for p=6 (left) and p=1.5 (right).

Case 1

0<S*≤W. The disease drives the population into extinction.

There is no endemic equilibrium and consequently no periodic orbit. The watershed disease-free equilibrium (W, 0) is locally asymptotically stable in backward time, and the carrying capacity disease-free equilibrium (K, 0) is a saddle with the I=0 axis being the stable manifold. All solutions starting in the endemic of the first quadrant converge to (0,0) by the Poincaré–Bendixson theorem. The unstable manifold of (K, 0) connects to the origin. This means that the host population dies out, whenever the disease is introduced.

Case 2

S*≥K. The disease cannot invade.

The boundary equilibrium (K, 0) is locally asymptotically stable. The stable manifold of the saddle (W, 0) separates its domains of attraction from the domain of attraction of the origin which is also a sink. If the disease is introduced in small amounts into the host population which is at or close to the carrying capacity K, the disease dies out and the host population returns to the carrying capacity.

Case 3

W<S*<K.

Both (W, 0) and (K, 0) are saddles. The axis I=0 is the unstable manifold of (W, 0) and the stable manifold of (K, 0). The fate of a host population which is at or close to the carrying capacity K and is exposed to the introduction of a small amount of disease is approximately described by the unstable manifold of (K, 0). It dies out if and only if the unstable manifold connects to (0,0). If the population does not die out, it may connect to the endemic equilibrium (but only if this is a sink), or to a stable periodic orbit or to a heteroclinic orbit connecting the two saddles. As we will explain below, the occurrence of the heteroclinic orbit is the critical case which separates host survival from extinction.

Case 3.1

W<S*, S* close to W. The disease eradicates the population (Figure 2, left).

Figure 2. W<S*<K. Left: S* close to W, host disappearance. The unstable manifold of (K, 0) connects to (0,0), the stable manifold of (W, 0) connects to (S*, I*), which is an unstable spiral point. Right: S* close to K, host decline to the endemic equilibrium (S*, I*), which is a stable focus. The stable manifold of (W, 0) separates the basins of attraction of (0, 0) and (S*, I*). The unstable manifold of (K, 0) connects to (S*, I*). In the left figure, the unstable manifold of (K, 0) lies above the stable manifold of (W,0), whereas it is the other way around in the right figure. As S* is moved from W to K, one expects that the two manifolds meet for a particular value of S*.

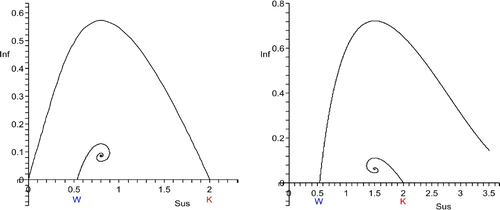
This is a special case of Case 3, but some of the dynamic behaviour is inherited from Case 1. As S* crosses W from below to above, the boundary equilibrium (W, 0) turns from a source to a saddle whose unstable manifold is the I=0 axis. Simultaneously, an endemic equilibrium comes into existence, which is an unstable node. It is suggestive to assume that it is connected to the boundary equilibrium (W, 0) by the stable manifold of (W, 0) and that all solutions starting in the interior of the first quadrant converge to (0,0), except those starting on that stable manifold. The equilibrium (K, 0) is also a saddle, but the I=0 axis is its stable manifold. As in Case 1, one expects the unstable manifold to connect to the origin. If the disease is introduced into a host population that is close to the carrying capacity K, it eradicates the host population.

Case 3.2

S*<K, S* close to K. The host and disease coexist after disease invasion: host decline (Figure 2, right).

This is another special case of Case 3, but some of the dynamic behaviour is inherited from Case 2. As S* crosses K from above to below, the boundary equilibrium (K, 0) turns from a sink into a saddle whose stable manifold is the I=0 axis. Simultaneously, the endemic equilibrium with the first component S* comes into existence, which is a sink. One expects the unstable manifold of the saddle (K, 0) to connect to the endemic equilibrium. The stable manifold of the boundary equilibrium (W, 0) now separates the domain of attractions of (0,0) and the endemic equilibrium. If the disease is introduced in small amounts into a host population that is at or close to the carrying capacity K, the host and parasite populations tend to the endemic equilibrium where they coexist.

Case 3.3

W<S*<K, S* neither close to W and K.

There must be a transition between Case 3.1 and Case 3.2 (Figure 2), where the stable manifold of (W, 0) coincides with the unstable manifold of (K, 0) and there is a heteroclinic orbit connecting the two equilibria (Figures 3 and 4). This marks the transition from survival to extinction of a host population which was at the carrying capacity before the introduction of the disease. This transition is brought about by the Hopf bifurcation at S*=M. If the Hopf bifurcation is supercritical, the unstable manifold of (K, 0) is detached from the endemic equilibrium and now connects to the stable periodic orbits that come into existence (Figure 3). If the Hopf bifurcation is subcritical (Figure 4, left), the stable manifold of (W, 0) is detached from the endemic equilibrium and now connects to the unstable period orbits that come into existence (Figure 4, right).

Figure 3. W<S*<K, transition from host decline to host disappearance for p=6. The unstable manifold of (K, 0) is shown for four values of S*. The values of S* can be identified from where the orbits end or where they take their maximum. The Hopf bifurcation at S*=1 is supercritical. So there is coexistence both at equilibrium and in periodicity. The second orbit from above is heteroclinic.

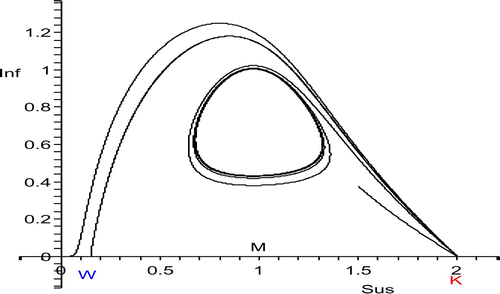
Figure 4. W<S*<K, transition from host decline to host disappearance for p=1.5: on the left, the unstable manifolds of (K, 0) and on the right the stable manifolds of (W, 0), for four values of S*, respectively. The orbits take their maximum at S*. The choices of S* are not the same on the left and the right. The Hopf bifurcation at S*=1 is subcritical: there is no periodic coexistence. The second orbits from above are heteroclinic. One curve is the isocline for the infectives.

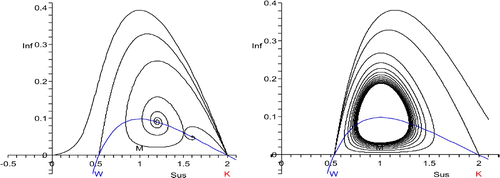
In either case, the periodic orbits expand until they touch the manifold of the other saddle, in which case we have the heteroclinic orbit that connects (W, 0) and (K, 0) and surrounds (S*, I*). If the Hopf bifurcation is supercritical, one expects the heteroclinic orbit to occur for S*<M; if it is subcritical for S*>M (Figures 3 and 4). However, this is not necessarily always so, as the stability information obtained from the Hopf bifurcation is only local.

5. Discussion

In order to demonstrate that infectious diseases can be responsible for both species decline and species disappearance (extinction) as they have been observed in the last decades, we consider an epidemic model with mass action (or density-dependent) incidence for the disease and a critical Allee-type growth function for the host. It is known from mathematical models that standard (or frequency-dependent) incidence can cause both host decline and disappearance, but there seems to be little empirical evidence 14. There seems to be strong empirical evidence, however, that populations that have reached a low density are at high risk to become extinct (at least locally) as one would expect from a population subject to a critical Allee effect. For our purposes, the critical Allee effect is characterized by two equilibrium densities 0<W<K such that the population dies out if the initial density is below W and converges to density K if the initial density is above W. W is called the watershed equilibrium and K the carrying capacity (saturation equilibrium). Further we assume that there is a unique M between W and K where the per capita growth rate takes a (local and global) maximum. We believe and assume that the typical initial configuration for species decline or disappearance caused by an infectious disease is that the host population is at the carrying capacity and a very small number of infectious individuals is introduced. Under such a scenario, the outcome of the disease is determined by the compound parameter . Here μ is the natural per capita mortality rate and α the additional per capita mortality rate that is due to the disease. The parameter σ is the transmission coefficient: 1/σ is the time for an average susceptible individual to become infected if the density of infectives is at the unit level. In our model, S* turns out to be the equilibrium density of susceptibles if an endemic equilibrium exists. We show analytically that the host goes extinct if S*≤W, whereas the disease dies out and the host returns to its carrying capacity if S*≥K. A combination of analytical and computational arguments suggests the existence of a threshold S ^♯ for S*, , such that we have extinction for , and mere host decline if . How S ^♯ compares to M depends on whether the Hopf bifurcation that occurs at S*=M is supercritical or subcritical. In the supercritical case, S ^♯<M and host and disease coexist in period oscillations if , while they coexist at equilibrium for M<S*<K. In the subcritical case, S ^♯>M and host and disease generically coexist at equilibrium if , while there is no stable periodic coexistence. In either case, S ^♯ turns out to be quite close to M; for practical purposes, the disease causes extinction if S*<M and mere decline if S*>M. This also means that the parameter region for periodic coexistence in the supercritical case is small, and it would be daunting to use this model as an explanation for undamped oscillations in host abundance. Mathematically, however, the Hopf bifurcation is indispensable to explain the transition from host decline to host disappearance. The threshold parameter S ^♯ is characterized as that value of S* at which the periodic solutions that bifurcate from the endemic equilibrium at S*=M morph into a heteroclinic orbit and disappear. For undamped oscillations in age-structured models with an Allee effect, see 13.

Our findings show that species decline becomes more severe and that disappearance becomes more likely the larger the coefficient of transmission and the lower the disease mortality rate. The latter depends on our tacit assumption that, cum grano salis, a dead host can no longer transmit the disease, which holds for some diseases but not for all. It also depends on our assumptions that infective individuals do not reproduce and that the disease has no reservoir. Since dead frogs are scavenged or decompose quickly 40, they do not appear to play a large role in fungal frog diseases such as Chytridiomycosis. Amphibian chytrid fungi may have reservoirs, however (see 40 and the literature cited therein).

The behaviours of our model solutions are consistent both with the ‘novel pathogen hypothesis’ 37 (or spreading pathogen hypothesis 40) and with the ‘endemic pathogen hypothesis’ 37 40 for chytridiomycosis. Our model shows massive host decline or even disappearance (the second for ) if the pathogen is freshly introduced even if the initial number of infected individuals is small. It also shows that a decrease of S* from above to below S ^♯ (possibly by environmental change) leads to a transition from an endemic equilibrium to host (and pathogen) extinction.

Our findings shed little light on the hypothesis that global climate change drives amphibian extinction from epidemic diseases 16 36 40 because changing temperatures may simultaneously increase (or decrease) disease transmission and disease death rates, which both would increase with pathogen proliferation rate.

Our model oversimplifies many aspects of the interplay between host demographics and disease transmissions. Frogs can contract chytridiomycosis already as tadpoles, but only die from it after they have metamorphosed. Stage-structured models that can take this into account are considered in 2 17 18 39. It remains to be seen whether our results stay the same when more population structure is introduced into the model.

Further we have assumed that only susceptible individuals reproduce and compete effectively for resources. Although this is a reasonable assumption for some diseases (e.g. rabies), it is not for others. We have made this assumption because it makes the mathematical analysis, in particular of the Hopf bifurcation, easier. The epidemic models with the critical host Allee effect in 15 23 assume that both susceptible and infective individuals reproduce and effectively compete for resources, but show similar decline and extinction results. However, a much more complex behaviour (multiple endemic equilibria, Takens–Bogdanov point) is reported in 23. The model analysis in 15 shows that a critical Allee effect in the host can make it more difficult for the disease to be established. This phenomenon is not present in our model, presumably because, by design of the model, the infective part of the population is not directly affected by the Allee effect.

Acknowledgements

This paper is dedicated to Jim Cushing on the occasion of his 65th birthday in acknowledgement of his numerous outstanding contributions to mathematical population biology, among others to the Allee effect 12 13.

The work by Thanate Dhirasakdanon and Horst Thieme was partially supported by the NSF grants DMS-0314529 and DMS-0715451. We thank Frank Hilker for making the work of Hilker et al. 23 available to us before it was published, through which we became aware of the works by Deredec and Courchamp 15 and Lafferty and Gerber 29.