Kolmogorov-type competition model with finitely supported allocation profiles and its applications to plant competition for sunlight

Abstract

A Kolmogorov-type competition model featuring allocation profiles, gain functions, and cost parameters is examined. For plant species that compete for sunlight according to the canopy partitioning model [R.R. Vance and A.L. Nevai, Plant population growth and competition in a light gradient: a mathematical model of canopy partitioning, J. Theor. Biol. 245 (2007), pp. 210–219] the allocation profiles describe vertical leaf placement, the gain functions represent rates of leaf photosynthesis at different heights, and the cost parameters signify the energetic expense of maintaining tall stems necessary for gaining a competitive advantage in the light gradient. The allocation profiles studied here, being supported on three alternating intervals, determine “interior” and “exterior” species. When the allocation profile of the interior species is a delta function (a big leaf) then either competitive exclusion or coexistence at a single globally attracting equilibrium point occurs. However, if the allocation profile of the interior species is piecewise continuous or a weighted sum of delta functions (multiple big leaves) then multiple coexistence states may also occur.

Keywords:

• Kolmogorov-type competition model
• canopy partitioning model
• plant competition
• light competition
• phytoplankton competition
• vertical leaf profile
• allocation profile
• gain function

1. Introduction

Consider two species (i=1, 2) that obey the Kolmogorov-type competition model 21,32

where x _i (t) denotes the population density of species i at time t≥0; the allocation profile s _i (z) is a fixed probability density function defined for z≥0 with complementary cumulative distribution function ; the gain function φ _i (x) is a positive, continuously differentiable, and strictly decreasing function of x≥0,  which approaches zero as ; and γ _i , σ _i , and C _i are positive constants.

System (1) describes the interactions of two clonal plant species that compete for sunlight by placing their leaves at multiple heights 21,32. For species i, its total leaf area is denoted by x _i , its vertical leaf area density with respect to height z (i.e. its vertical leaf profile) is indicated by s _i (z), the rate of photosynthesis performed by its leaves when shaded from above by cumulative leaf area x is given by the energy gain function φ _i (x), its leaf light extinction coefficient is σ _i , its growth constant is γ _i , and the energetic cost of maintaining its leaves, stems, and roots is represented by C _i . The growth and cost parameters γ _i and C _i in turn depend on close to a dozen primary plant parameters such as tissue mass, mean stem height, and tissue metabolic rate. For a complete description of these parameters and functions and how they relate to Equation (1) see 32.

The application of Equation (1) to light competition is not limited to terrestrial plants only. For example, Weissing and Huisman 34 proposed earlier a related system of equations to model phytoplankton that compete for sunlight in a lake. Both models are members of a more general class of systems

first introduced in 1936 by Kolmogorov 20. Previous researches on Equation (2) have centered primarily on Hardin’s 8 competitive exclusion principle 2,15,26, establishing conditions under which all species can persist 3,7,12,14,16,18,29, and the influence of horizontal spatial heterogeneity 4,5,17. However, it is difficult to apply many of these results directly to Equation (1) because the allocation profiles and gain functions combine in a complicated way to form the per-capita growth rate functions f _i in Equation (2).

Furthermore, it is usually of great interest to establish the manner in which the allocation profiles and gain functions influence the outcome of competition in Equation (1). Toward this end, it is known that

1. if two species have allocation profiles which are supported on non-overlapping intervals then either competitive exclusion or coexistence at a single globally attracting equilibrium point occurs 21;

2. if two species have rectangular (i.e. uniform) allocation profiles supported on overlapping but non-nested intervals, and the species share a common gain function, then either competitive exclusion or coexistence at a single globally attracting equilibrium point occurs 21;

3. there exist pairs of species possessing rectangular allocation profiles and distinct gain functions such that multiple non-trivial equilibrium points occur 19;

4. there exist pairs of species, one with a rectangular allocation profile surrounded by a bi-rectangular allocation profile belonging to the other, such that multiple non-trivial equilibrium points occur, even when the two species share the same gain function 19;

5. if two species possess rectangular allocation profiles, they share a common gain function, and there exists some τ>0 such that s ₂(z)=s ₁(z−τ) and C ₂=C ₁+bτ, then the competitive ability of species 2 diminishes from dominant to compatible to inferior as the allocation difference τ increases 22.

In summary, it has been found that when two plant species possess overlapping rectangular leaf profiles (as it occurs for many grasses, e.g. alkali seaheath (Frankenia grandifolia) and Virginia glasswort (Salicornia virginica)) then the degree to which their leaves overlap can have a marked influence on the outcome of competition. However, other kinds of leaf overlap are also possible; for example, some pairs of species interlace their leaves in an alternating fashion over multiple discrete heights, e.g. corn (Zea mays) and soybean (Glycine max). We can express the associated canopy patterns using a short-hand notation; for example, (2A–2B–A) denotes a five-leaf canopy in which the two lowest leaves belong to species A, the two middle leaves belong to species B, and the highest leaf belongs to species A. We seek the simplest such patterns for which coexistence can arise at multiple locally stable equilibrium points. As mentioned earlier, these discrete-leaf patterns cannot be of the form (kA–ℓB). The three-leaf pattern (A–B–A) is the simplest one that remains, and we remark that it also describes the simplest canopy in which the leaves of two species can interlace nontrivially. Of the simplest canopy patterns which remain are (A–2B–A) and (A–B–A–B), although we consider the former pattern to be less complex than the latter because it has fewer transitions between species.

In this article, we characterize the simplest canopy patterns that can produce coexistence at multiple equilibrium points for two theoretical species that compete for sunlight and obey model (1).

We emphasize that many other factors are known to influence the outcome of plant competition, including seed dispersal and root competition for both soil nutrients and water 32. Here, we focus exclusively on whether competition for sunlight alone can produce multiple equilibrium points and we concentrate on examining the minimal complexity of interleaving patterns sufficient for such outcomes.

2. Asymptotic behaviour

Given any nonnegative initial condition, a nonnegative solution to Equation (1) exists for all time, it is unique, and it always approaches some finite equilibrium within the closure of the first (or quadrant as 13, pp. 144 and 250]). Thus, to determine the asymptotic behaviour of the dynamical system, it suffices to restrict our attention to nullclines and their with each other and with the coordinate axes. In general, the (non-trivial) nullcline for species i is the set of all (x ₁, x ₂) in the closed first quadrant that satisfy the equation

So that exists non-trivially, the inequality φ _i (0)>C _i must be satisfied. When this condition holds, we will say that species i is viable. We define the trivial equilibrium to be the origin (0, 0), a semi-trivial equilibrium to be a point which lies on or a point which lies on , and a non-trivial equilibrium to be a point inside the open positive quadrant which lies on both and . It is not difficult to see from Equations (1) and (3) that the trivial equilibrium always exists, and that two semi-trivial equilibrium points also exist whenever both species are viable. Thus, our main results focus on the number (and stability) of non-trivial equilibrium points, and we will often drop the qualifier non-trivial.

So that we may state our results precisely, we must first make some preliminary definitions.

Recall from 32 that φ _i (x) can be interpreted as the rate at which a unit area of leaves belonging to species i performs photosynthesis at a fixed height when shaded from above by cumulative leaf area x. This rate depends continuously on the overlying leaf area, it is always positive, it decreases as the overlying leaf area increases, and very large overlying leaf areas produce correspondingly very small rates of photosynthesis. Following 32, we define φ _i (x) to be a gain function if it satisfies the following properties:

• (P₁) φ _i is a continuously differentiable function of x≥0.

• (P₂) φ _i (x)>0 for x≥0.

• (P₃) φ _i ′(x)<0 for x≥0.

• (P₄) φ _i (x)→0 as .

To denote that φ _i is a gain function, we will write φ _i ∈Π. A special case arises when φ₁ and φ₂ both have the particular form

for some positive constants ϕ _i , I _in (independent of i), J _i , and π _i 32. When this occurs, we say that φ₁ and φ₂ are in parametric form and we write . For situations in which parameters such as I _in, J ₁, and J ₂ are fixed a priori we will write .

It will also be useful to introduce new mathematical notation so that we may later distinguish important leaf locations (such as the understory and overstory) within a canopy. Let denote the set of all allocation profiles, that is, if and only if s(z) is nonnegative for z≥0 and . Let Ω _s denote the support of a given . For , we define the following parameterized subsets of :

1. ,

2. C(a, c)={s(z)∈M(a, c):s(z) is piecewise continuous and everywhere finite},

3. ,

4. ,

5. , , and ,

6. , , and .

Some comments are in order. First, these definitions are not mutually exclusive. For example, . Second, if s(z)∈C(a, c) and then

whenever ψ(x) is a continuous function of x≥0. Third, B(a) consists of a single Dirac-delta function, s(z)=δ(z−a), and we will refer to allocation profiles of this form as singular. Observe that in this case

is independent of a. Fourth, if s(z)∈B(a ₁, a ₂, …, a _m ) then for some positive parameters ℓ₁, ℓ₂, …, ℓ _m satisfying ℓ₁+ℓ₂+⋯+ℓ _m =1. These multi-singular profiles satisfy, upon suitable relabeling of a ₁, a ₂, …, a _m ,

where L _i =ℓ₁+ℓ₂+⋯+ℓ _i . Finally, if s(z)∈U(a) ⊕ O(c) or s(z)∈B(a) ⊕ O(c) then the allocation profile of the species has two arbitrary but non-trivial portions, one supported in (0, a) or on {a} and one in . In the former case, we can write

A similar equation applies for the latter case, but with the first integral on the right-hand side replaced by ψ(1).

In applications of the model to plant competition for sunlight, allocation profiles in B(a) and B(a ₁, a ₂, …, a _m ) represent, respectively, the situation in which a plant species places its leaves exclusively at a single height or at m different heights. For allocation profiles in U(a) ⊕ O(c), the intervals (0, a) and represent the understory (U) and overstory (O), respectively.

3. Statement of the main results

Below we assume that:

1. the supports of the two species’ allocation profiles do not overlap, and

2. the support of the allocation profile belonging to species 2 surrounds the support of the allocation profile belonging to species 1 on both sides.

This happens, for example, when s ₁(z)=B(a) and s ₂(z)=U(a) ⊕ O(a). In naming the theorems, we will also use notation such as “U–B–O” to denote the form of the corresponding pair of allocation profiles.

Our first main result concerns a situation in which s ₁(z) is singular and s ₂(z) is arbitrary but subject to conditions (i) and (ii).

Theorem 1 (U–B–O)

Suppose that s ₁(z)∈B(a) and s ₂(z)∈U(a) ⊕ O(a) with a>0,  and let φ₁, φ₂∈Π and σ₁, σ₂, C ₁, C ₂>0 be given. Then at most one non-trivial equilibrium point exists,  and when one does exist,  it is always globally asymptotically stable with respect to the (open) positive quadrant. The same result also holds for s ₂(z)∈M(0, a) or .

Our second main result concerns the case in which s ₁(z) is piecewise continuous and finite and s ₂(z) is bi-singular.

Theorem 2 (B–C–B)

Let s ₁(z)∈C(a, c) and s ₂(z)∈B(a, c) with and let σ₁, σ₂, C ₁, C ₂>0 be given. Then there exist φ₁, φ₂∈Π such that infinitely many non-trivial equilibrium points exist. Examples exist where the two nullclines coincide on an interval with the nonempty interior; there also exist examples with infinitely many locally asymptotically stable,  and infinitely many unstable isolated equilibrium points. If S ₂(c)C ₁<C ₂<C ₁ then all this can even be arranged so that φ₁ ≡ φ₂.

The hypothesis of Theorem 2 excludes some pairs of profiles that are of type “B–M–B”. The next result partially fills in this gap by addressing situations in which s ₁(z) is multi-singular.

Theorem 3 (B–mB–B)

Let s ₁(z)∈B(z ₁, z ₂, …, z _m ) and s ₂(z)∈B(a, c) with and let σ₁, σ₂, C ₁, C ₂>0 be given.

1. If S ₁(z ₁)<S ₂(c) then there exist φ₁, φ₂∈Π such that infinitely many non-trivial equilibrium points exist. Examples exist where the two nullclines coincide on an interval with the nonempty interior; there also exist examples with infinitely many locally asymptotically stable,  and infinitely many unstable isolated equilibrium points. If S ₂(c)C ₁<C ₂<C ₁ then all this can even be arranged so that φ₁ ≡ φ₂.

2. If S ₁(z ₁)≥S ₂(c),  then given any φ₁, φ₂∈Π at most one non-trivial equilibrium point exists,  and when one does exist,  it is always globally asymptotically stable with respect to the open first quadrant. This final result also holds for s ₂(z)∈B(a) ⊕ O(c).

We remark that when m=1, then the assumption in part (b) of Theorem 3 is always satisfied. In this case, Theorem 3 is simply a special case of Theorem 1.

The final result concerns a special case of the situation occurring in Theorem 3 in that it restricts attention to cases in which s ₁(z) and s ₂(z) are both bi-singular. However, its conclusion is different because of its restriction to gain functions in parametric form.

Theorem 4 (B–2B–B)

Let and σ₁, σ₂, C ₁>0 be given. Then there exist s ₁(z)∈B(z ₁, z ₂),  s ₂(z)∈B(a, c),  and C ₂>0,  such that at least two non-trivial equilibrium points exist. In addition, 

1. φ₁ and φ₂ may be chosen so that for any given I _in, J ₁, J ₂>0,  even when C ₂>0 is also given, 

2. φ₁ and φ₂ may be chosen so that φ₁≡φ₂.

Note that neither part (a) nor part (b) of Theorem 4 implies the other. If , then these functions may still differ in the parameters ϕ _i and π _i appearing in Equation (4). Similarly, although the gain functions may be chosen to have the same parametric form, it may not be possible to specify values a priori for the parameters I _in, J ₁, J ₂, and C ₂.

The biological implications of these results, as they pertain to plants that compete for sunlight are outlined in the Discussion.

4. Proof of Theorem 1 (U–B–O)

In this section, we prove Theorem 1. Suppose first that s ₁(z)∈B(a) and s ₂(z)∈U(a) ⊕ O(a) with a>0, and let φ₁, φ₂∈Π and σ₁, σ₂, C ₁, C ₂>0 be given. Then the species 1 nullcline satisfies

and the species 2 nullcline satisfies

Observe from Equation (5) that is a line with constant slope θ=−σ₁/[σ₂ S ₂(a)]. We can show that at most one equilibrium point exists, and that when it does exist it is always globally asymptotically stable with respect to the open first quadrant, by demonstrating that the slope of always exceeds θ. Implicit differentiation of Equation (6) with respect to x ₁ implies that

Since φ₂′<0, it follows that

The last inequality holds because S ₂(0)=1, S ₂(z) is a decreasing function, and S ₂(a)∈(0, 1). Therefore, the slope of everywhere exceeds the slope of , and thus the two nullclines can coincide at most once. We conclude that at most one equilibrium point exists, and that when such a point does exist, it is always globally asymptotically stable with respect to the open first quadrant. (The stability of the equilibrium point is determined by the relative positions of the nullclines in the state space, see 13, Figure 11.13]). For cases in which s ₂(z)∈M(0, a) or , then either is vertical and is strictly decreasing, or is horizontal and is strictly decreasing. In either case, the result is immediate. This completes the proof of Theorem 1.

5. Proof of Theorem 2 (B–C–B)

In this section, we prove Theorem 2. Suppose that s ₁(z)∈C(a, c) and s ₂(z)∈B(a, c) with , and let σ₁, σ₂, C ₁, C ₂>0 be given. We will construct φ₁, φ₂∈Π such that Equation (1) has infinitely many equilibrium points.

Step 1: Getting started.

Define k=S ₂(c)∈(0, 1).

• (1a) Select Y ₁>X ₁>X ₀>0 and Y ₀>Y ₁+(1/k−1)(X ₁−X ₀).

• (1b) Define ω_ℓ=Y _ℓ−X _ℓ and Z _ℓ=ω_ℓ+(1/k)X _ℓ for ℓ∈{0, 1}.

Observe from the earlier-mentioned construction that (i) ω₀>ω₁, (ii) X _ℓ<Y _ℓ<Z _ℓ for ℓ∈{0, 1}, and (iii) Z ₀>Z ₁. For γ∈[0, 1], define

• (1c) X(γ)=X ₀+γ(X ₁−X ₀) and Y(γ)=Y ₀+γ(Y ₁−Y ₀).

• (1d) ω(γ)=Y(γ)−X(γ) and Z(γ)=ω(γ)+(1/k)X(γ).

Observe that X(γ), Y(γ), ω(γ), and Z(γ) are all linear and they satisfy X(γ)∈[X ₀, X ₁], Y(γ)∈[Y ₁, Y ₀], ω(γ)∈[ω₁, ω₀], and Z(γ)∈[Z ₁, Z ₀] for γ∈[0, 1].

Step 2: Select φ₁.

We construct φ₁ as follows.

• (2a) Define and select so that

  • (i) φ₁(x)>0 and φ₁′(x)<0 for ,

  • (ii)  for γ∈[0, 1].

  (2b) Extend φ₁(x) elsewhere so that φ₁∈Π.

We remark that the operation in Equation (2a) is well-defined. To see this, first select a function ψ(x)∈C ¹([X ₀, X ₁]) which satisfies (a) ((X ₁−X ₀)/(Y ₁−Y ₀))ψ(X ₀)+C ₁>0 and (b) ψ(x)>0 and ψ′(x)<0 for x∈[X ₀, X ₁]. Next, extend ψ to [Y ₁, Y ₀] by setting ψ(Y (γ))=((X ₁−X ₀)/(Y ₁−Y ₀))ψ(X(γ)) for γ∈[0, 1]. Extend ψ further to be a function in which satisfies and ψ′(x)<0 for . Finally, define φ₁(x)=ψ(x)+C ₁ for . Observe from (1c) that and therefore that for γ∈[0, 1]. Since φ₁(Y ₀)>0, and the integral in part (ii) represents the average value of φ₁ on [X(γ), Y(γ)], it is straightforward to see that φ₁ satisfies the conditions in (2a).

Step 3: Select φ₂.

We construct φ₂ as follows. First, select λ₀>λ₁>μ₁>μ₀>0 so that kλ_ℓ+(1−k)μ_ℓ=C ₂ for ℓ∈{0, 1} and define φ₂(X(γ))=(1−γ)λ₀+γλ₁ and φ₂(Z(γ))=(1−γ)μ₀+γμ₁ for γ∈[0, 1]. Next,

• (3a) extend φ₂(x) elsewhere so that φ₂∈Π.

It is straightforward to show that

• (3b) kφ₂(X(γ))+(1−k)φ₂(Z(γ))=C ₂ for γ∈[0, 1].

5.1. An interval of equilibrium points

Observe from steps 1 and 2 with γ=0 that

and from steps 1 and 3 with γ=0 that

Consequently, the species 1 nullcline and the species 2 nullcline both exist. Equations for these nullclines are obtained from Equation (3) with s ₁(z)∈C(a, c) and s ₂(z)∈B(a, c). That is, satisfies

and satisfies

In view of (2a), (3b), Equations (7) and (8), and (1d), let

Then (u(γ), v(γ)) is an equilibrium point within the interior of the first quadrant for every γ∈[0, 1]. We conclude that the two nullclines coincide on an interval with a nonempty interior.

5.2. Isolated equilibrium points

We now modify the earlier-mentioned construction to get infinitely many locally asymptotically stable, and infinitely many unstable isolated equilibrium points. First, select an infinite sequence γ₁, γ₂, … satisfying 0<γ₁<γ₂<⋯<1. Then

and

Next, let u _j =u(γ _j ) and v _j =v(γ _j ) for j≥1. Again, each of the infinitely many pairs (u _j , v _j ) is an equilibrium point. Finally, we redefine φ₂ on the set so that

and we do so without violating condition (3a). We have sufficient freedom here to choose φ₂ on so that will cross at (u _j , v _j ) from below to above when j is even and from above to below when j is odd. To see that this can be done, note that the slope of is given as

If φ₂ satisfies (3b), then Equation (11) also gives the slope of at (u(γ), v(γ)), since the two nullclines coincide on an interval. Now redefine φ₂ so that Equations (9) and (10) are both satisfied and so that φ₂ is very close to horizontal or vertical in small neighbourhoods around Z(γ _j ) when j is even or odd, respectively. Since this modification alters neither the slope of nor the value of the first term in the denominator of Equation (11), it follows that when j is even then the point (u _j , v _j ) will be locally asymptotically stable ( crosses from below to above here and so by examining direction fields it is clear that sufficiently small neighbourhoods are positively invariant, see Figure 11.13 in 13) and when j is odd the point will be unstable. Hence, we will obtain infinitely many locally asymptotically stable, and infinitely many unstable isolated equilibrium points.

5.3. The same gain function

To complete the proof, it remains only to show that if C ₂∈(k C ₁, C ₁) then we can modify the earlier-mentioned construction above so that φ₁ ≡ φ₂. Recall that φ₁ was subject to a certain integral condition on [X ₀, Y ₀] in step 2 and that φ₂ was subject to a linear condition on [X ₀, X ₁] and [Z ₁, Z ₀] in step 3. Below, we arrange for the intervals [X ₀, Y ₀] and [Z ₁, Z ₀] to be disjoint so that we will have sufficient freedom to make φ₁ ≡ φ₂. First, we repeat step 1 but replace (1a) with

• (1a’) Select Y ₁>X ₁>X ₀>0 so that X ₁−X ₀<((1−k)/2)X ₁.

• (1a”) Select θ∈(1/k, 2/k) and define Y ₀=Y ₁+θ(X ₁−X ₀).

These modifications allow us to directly compare Y ₀ and Z ₁:

We now obtain the following string of inequalities

In particular, the intervals [X ₀, Y ₀] and [Z ₁, Z ₀] are disjoint. Now we repeat (2a), but we do so in such a way that the following two additional conditions are also satisfied: (iii) kφ₁(X ₀)<C ₂ and (iv) kφ₁(X ₁)+(1−k)φ₁(Y ₀)>C ₂. Since it is assumed that C ₂∈(k C ₁, C ₁), all of this can be achieved if φ₁ is chosen to be sufficiently close to C ₁ throughout the interval [X ₀, Y ₀]. Next, we define φ₁ on [Z ₁, Z ₀] so that (3b) is satisfied, but with φ₁ in place of φ₂. Finally, we perform (2b). This modified construction again produces an interval of equilibrium points as argued earlier but with φ₁ in place of φ₂. Since Z(γ _j ) exceeds Y ₀ for all j≥1, again the function φ₁ can be further modified on to alter but not , and thus create infinitely many isolated equilibrium points as described earlier. The proof of Theorem 2 is complete.

6. Proof of Theorem 3 (B–mB–B)

In this section, we prove Theorem 3 using an approach that resembles the one used in the proof of Theorem 2. However, since both allocation profiles considered here are discrete, we will need notation and arguments that are very different.

Suppose that s ₁(z)∈B(z ₁, z ₂, …, z _m ) and s ₂(z)∈B(a, c) with , and let σ₁, σ₂, C ₁, C ₂>0 be given.

6.1. Proof of Theorem 3 part (a)

To prove part (a), we will again construct φ₁, φ₂∈Π such that Equation (1) has infinitely many equilibrium points. Let [m]={1, 2, …, m}. Recall that s ₁(z) has the form

for some positive parameters h ₁, h ₂, …, h _m satisfying h ₁+h ₂+⋯+h _m =1. Define H _i =h ₁+h ₂+⋯+h _i for i∈[m] and k=S ₂(c)∈(0, 1), and let us suppose that h ₁<k as the hypothesis of part (a) requires.

The construction begins as follows. First, select , ω₁>0, and

Next, define h* so that and let , for ℓ∈{0, 1} and i∈[m], and for ℓ∈{0, 1}. Finally, define ω(γ)=(1−γ)ω₀+γω₁ for γ∈[0, 1], for γ∈[0, 1] and , and for γ∈[0, 1]. It is straightforward to verify that (see Figure 1) (i) , (ii) for ℓ∈{0, 1}, (iii) for i∈{0, 1}, (iv) for i∈{2, 3, …, m}, (v) , (vi) for γ∈[0, 1], (vii) X ⁱ (γ)=H _i ω(γ)+X ⁰(γ) for γ∈[0, 1] and i∈[m], (viii) for γ∈[0, 1], and (ix) X*=h*ω(γ)+X ⁰(γ) for γ∈[0, 1]. We remark that (ix) is obtained in the following manner:

We also require a technical lemma whose proof appears in Appendix A.

Lemma 1

There exist φ₁, φ₂∈Π such that

for γ∈[0, 1].

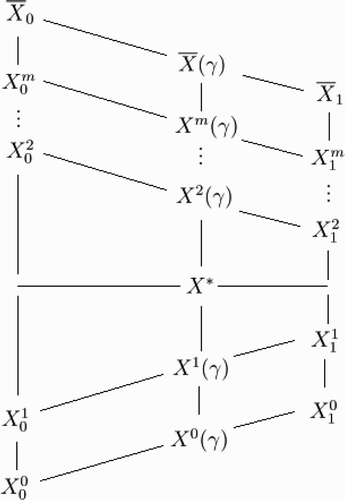
Figure 1. The relative magnitudes of certain quantities appearing in the proof of Theorem 3. Some but not all quantities can be directly compared. Quantities appearing higher are provably larger than quantities that appear lower when they are path-connected by upward lines or ellipses. For example, is greater than X* and any quantity on the bottom two diagonals but less than any other quantity on the upper m diagonals. However, the relative position of X ²(γ) with respect to the quantities in the column above is unknown.

6.1.1. An interval of equilibrium points

Observe from Lemma 1 with γ=0 that

and

Consequently, the species 1 nullcline and the species 2 nullcline both exist. Equations for these nullclines are obtained from (3) with s ₁(z)∈B(z ₁, z ₂, …, z _m ) and s ₂(z)∈B(a, c). That is, satisfies

and satisfies

In view of (vii), (viii), and Lemma 1, let

Then (u(γ), v(γ)) is an equilibrium point within the interior of the first quadrant for every γ∈[0, 1]. We conclude that the two nullclines coincide on an interval with a nonempty interior.

6.1.2. Isolated equilibrium points

The procedure to obtain infinitely many locally asymptotically stable, and infinitely many unstable isolated equilibrium points is completely analogous to the construction given in the proof of Theorem 2. First, select an infinite sequence γ₁, γ₂, … satisfying 0<γ₁<γ₂<⋯<1. Then modify φ₂ on the interval so that will cross at (u(γ _j ), v(γ _j )) from below to above when j is even and from above to below when j is odd. We omit the details.

6.1.3. The same gain function

To complete the proof of part (a), it remains only to show that if C ₂∈(k C ₁, C ₁) then we can modify the earlier-mentioned construction so that φ₁ ≡ φ₂. The proof of the next lemma appears in Appendix A.

Lemma 2

If the following conditions are satisfied

then we can choose φ₁ and φ₂ in Lemma 1 so that φ₁ ≡ φ₂.

Observe that we can always choose , , and ω₁ from the outset so that conditions (b) and (c) of Lemma 2 are satisfied. As in the construction presented in the proof of Theorem 2, conditions (A) and (B) in the proof of Lemma 2 give us sufficient freedom to choose φ on the intervals and in such a way that the two nullclines coincide along an interval with a nonempty interior, or meet at infinitely many locally asymptotically stable, and infinitely many unstable isolated equilibrium points. This completes the proof of part (a).

6.2. Proof of Theorem 3 part (b)

To prove part (b), let us assume that φ₁, φ₂∈Π are given. Using the same notation as in the proof of part (a), we need only to show that if h ₁≥k then at most one equilibrium point exists, and that when one does exist it is always globally asymptotically stable with respect to the open first quadrant. First, we argue by contradiction to show that the slope of cannot exceed −(σ₁ h ₁/σ₂ k). For suppose otherwise, i.e. that . It follows from implicit differentiation of Equation (13) with respect to x ₁ that

Observe that φ₁′<0 and for all i∈[m]. Thus, the left-hand side of Equation (15) is negative, a contradiction. We conclude that the slope of nowhere exceeds −(σ₁ h ₁/σ₂ k). Next, we show that the slope of everywhere exceeds −(σ₁/σ₂). Implicit differentiation of Equation (14) with respect to x ₁ implies that

As φ₂′<0, we obtain . Since , the two nullclines can coincide at most once. We conclude that at most one equilibrium point exists, and that when such a point does exist, it is always globally asymptotically stable with respect to the open first quadrant, as can be seen in Figure 4(g) in [14]. For the case s ₂(z)∈B(a) ⊕ O(c), a similar argument applies but with the first term in the denominator of replaced by . This completes the proof of Theorem 3.

7. Proof of Theorem 4 (B–2B–B)

In this section, we prove Theorem 4. Let and σ₁, σ₂, C ₁>0 be given.

7.1. Proof of Theorem 4 part (a)

To prove part (a), we fix C ₂, I _in, J ₁, J ₂>0 and seek s ₁(z)∈B(z ₁, z ₂), s ₂(z)∈B(a, c), and such that Equation (1) has at least two equilibrium points. For ε>0, let

We require a technical lemma whose proof appears in Appendix A.

Lemma 3

There exist 0<ε≪1 and such that

Let s ₁(z)=ε²δ(z−z ₁)+(1−ε²)δ(z−z ₂) and s ₂(z)=2εδ(z−c)+(1−2ε)δ(z−a). Then s ₁(z)∈B(z ₁, z ₂) and s ₂(z)∈B(a, c), and equations for the species nullclines and can be obtained from Equation (3). That is, satisfies and satisfies . In view of Lemma 3 and Equation (16), let u ₁=(σ₁)⁻¹, u ₂=(εσ₁)⁻¹, v ₁=(2εσ₂)⁻¹, and v ₂=(2σ₂)⁻¹. Then the two species coexist at the two equilibrium points (u ₁, v ₁) and (u ₂, v ₂) within the interior of the first quadrant. Other equilibrium points may also exist. This completes the proof of part (a).

7.2. Proof of Theorem 4 part (b)

To prove part (b), we will select s ₁(z)∈B(z ₁, z ₂), s ₂(z)∈B(a, c), , and C ₂>0 such that φ₁ ≡ φ₂ and at least two equilibrium points exist. For ζ and ε, define

We will require the following lemma whose proof appears in Appendix A.

Lemma 4

There exist 0<ε≪1,  C ₂>0,  and such that

Let and s ₂(z)=(1−ε)δ(z−c)+εδ(z−a). Then s ₁(z)∈B(z ₁, z ₂) and s ₂(z)∈B(a, c), and equations for the species nullclines and can be obtained from Equation (3). That is, satisfies

and satisfies

In view of Lemma 4 with φ₁, φ₂ ≡ φ and Equation (17), let

Then the two species coexist at the two equilibrium points (u ₁, v ₁) and (u ₂, v ₂) within the interior of the first quadrant. Other equilibrium points may also exist. This completes the proof of Theorem 4.

8. Discussion

In analytical studies of terrestrial plant competition, it is usually assumed that model species place their leaves at a single height 23,25,27,35,36 or, if a coarse distinction between sun leaves and shade leaves is to be made, then at two heights (see 6,30). Such simplified approaches involving big-leaf species are appropriate when studying multiple factors in combination that together influence plant competition (e.g. light-limitation, nutrient-limitation, and dispersal) because they can make otherwise intractable problems more amenable to mathematical methods. Yet, situations remain in which sunlight appears to be the limiting resource for plants in competition 10,11,28,33,34. In such cases, we consider it appropriate to include a fuller account of the competitors’ vertical leaf profiles (or VLPs) because higher leaves everywhere receive more sunlight energy than lower leaves and therefore can perform photosynthesis at higher rates 1,9,11. Furthermore, higher leaves must be supported by taller stems, which are energetically more expensive to construct and to maintain than shorter stems 24.

The mechanistic Canopy Partitioning Model 21,32 can be used to predict the outcome of competition between two plant species with fixed VLPs that occupy a relatively constant environment. The defining feature of the model is that it accommodates arbitrary shapes for the competitors’ VLPs. It can therefore capture in real time subtle (and usually nonlinear) changes in leaf photosynthesis rates at different heights, which result when plant populations change in leaf area over time. Although initial applications of the model focused on species possessing VLPs that are constant functions over a height interval (rectangular profiles) or a pair of disjoint height intervals (bi-rectangular profiles) 19,21,22, it can equally well accommodate species with big-leaves positioned at multiple discrete heights in a canopy. The purpose of this study is to examine this latter situation.

In general, a central problem is to determine how many non-trivial equilibrium points the Kolmogorov-type competition model (1) can have and to establish their stability or instability. Earlier work by Nevai and Vance 21,22 delineated conditions under which at most one such equilibrium can exist and demonstrated that if this unique equilibrium exists for rectangular VLPs, it must globally attract the interior of the first quadrant when the species share the same photosynthesis gain function. In 19 it was shown that there exist pairs of species with rectangular VLPs and distinct gain functions for which any finite number of stable and unstable equilibrium points are possible. It was also shown that at least two equilibrium points are possible even if the species share the same gain function, provided that one of their VLPs is bi-rectangular and surrounds the other. However, no non-trivial examples of plant species pairs that obey (1) and admit infinitely many equilibrium points were previously known; neither were there known examples of such systems with multiple equilibrium points in which both gain functions are in parametric form (4) (see Figure 2).

Figure 2. Allocation profiles that are arbitrary on nontrivial intervals (rounded), piecewise constant on nontrivial intervals (rectangular), or with finite support (thick horizontal lines). In the first row, the allocation profiles are assumed to be the same. If ∀ appears in the upper left corner of a cell then the number of nontrivial stable (m) and unstable (n) equilibrium points satisfies the given conditions for all pairs of model species. However, if ∃ appears in the corner of a cell then there exist pairs of model species such that m and n both satisfy the given conditions. Degenerate situations under which two species nullclines coincide everywhere are excluded. A [p] or (q) in the lower right corner indicates that the result appears in citation [p] or as Theorem q in this article, respectively.

All of our theorems here concern cases in which at least one species has a VLP composed of one or more big-leaves (i.e. with finite support) and the canopy is partitioned into three height zones: an upperstory consisting only of leaves belonging to species 2, a middlestory consisting only of leaves belonging to species 1, and an understory consisting only of leaves belonging to species 2. Thus, we may refer to species 1 as the interior species and to species 2 as the exterior species. We would like to point out that this framework applies equally well to phytoplankton that compete for sunlight in lakes according to the well-known model of Weissing and Huisman 34.

We show in Theorem 1 that when the interior species has a single big-leaf and it is surrounded from below and above by an arbitrary VLP belonging to the exterior species, then there are only two long-term possibilities: either competitive exclusion results with the identity of the surviving species depending only on parameter values but not on initial plant population abundances, or else competitive coexistence occurs at a single globally attracting equilibrium point. Below, we will refer to either of these competitive outcomes as being of “type I.” We remark that type I outcomes do not admit the possibility of competitive exclusion owing to founder control. These same comments also apply when one species has a single big-leaf lying entirely above or below an arbitrary VLP belonging to the other, which complements a similar result obtained in 21 for two species with uniform but non-overlapping VLPs.

The situation changes markedly when the VLP of the interior species consists of multiple big-leaves situated at different heights.

Theorem 2 shows that there exist many pairs of model species that can experience both type I competitive outcomes and also coexistence at any one of infinitely many equilibrium points (“type II”). In particular, one may specify a priori a VLP for the interior species which is not concentrated at any single point, a VLP for the exterior species which consists of two big-leaves (one lying in the overstory and one in the understory), and arbitrary cost parameters. Then corresponding species can be found whose nullclines coincide at infinitely many points. This remarkable conclusion continues to hold even when it is required that both species share the same photosynthesis gain function. The actual construction of this gain function is performed in the proof of Theorem 2. The numerous basins of attraction that are possible in Theorem 2 constitute a form of founder control in which different initial species abundances lead to different equilibrium abundances without necessarily resulting in competitive exclusion for either species.

Theorem 3 concerns canopies in which the interior species has an arbitrary but finite number of big-leaves and the exterior species still has a single big-leaf in both the overstory and understory. Again, there exist pairs of species for which type II competitive outcomes occur. However, in these cases, the uppermost leaf belonging to the interior species must bear a smaller fraction of the plant’s total leaf area than the highest leaf of the exterior species does relative to its own total leaf area. If not, then we can deduce from Theorem 3 (b) that no combination of parameters and functions exist for which two species can coexist at multiple equilibrium points and the competitive outcome will always be of type I. The distinction that arises between the results in parts (a) and (b) warrants corroboration by empirical results.

Finally, Theorem 4 implies that if the interior species has exactly two big-leaves and they are surrounded on either side by a single big-leaf belonging to the exterior species, then parametric photosynthesis gain functions which produce coexistence at multiple equilibrium points can be chosen. The shared parameter I _in represents the constant irradiance striking the upper surface of the canopy, and J ₁ and J ₂ are half-saturation constants 31 of the species. The proof of Theorem 4 uses the Intermediate Value Theorem in both parts. In the proof of part (a), we carefully choose constants and functions so that the two gain functions are in parametric form for specified values of I _in, J ₁, and J ₂. Our construction involves two species that allocate small fractions (ε² and 2ε) of their total leaf area to their upper leaves. When ε is very small, these two upper leaves each carry very low leaf areas. Thus, the lower leaf of the interior species experiences nearly full sunlight and is capable of casting substantial shade on the understory leaf belonging to the exterior species. In the proof of part (b), we have more freedom to obtain the parameters and functions in our construction, but we need to ensure that the two gain functions coincide. We accomplish this by letting the interior species be fairly balanced in its allocation of leaf area to its two leaves and then letting the proportion of leaf area in the overstory (which belongs to the exterior species) tend to 1.

Our results open up several new avenues for future research. In particular, it is an open question to determine which of our results have analogs for competitive systems in which both VLPs are continuous on their supports. For example, if the VLP for the interior species is rectangular and the VLP for the exterior species is bi-rectangular and surrounds the first, then can there be infinitely many equilibrium points? Can one obtain multiple equilibrium points for any non-trivial pair of VLPs, continuous on their supports, when both photosynthesis gain functions are required to be in parametric form?

Acknowledgements

The authors thank the reviewers for valuable comments and the Mathematical Biosciences Institute at The Ohio State University for support of this project. This study is based upon work supported by the National Science Foundation under Agreement No. 0112050.

Additional information

Notes on contributors

Andrew L. Nevai

Present address: Department of Mathematics, University of Central Florida, Orlando, FL 32816, USA.

Appendix

Proof of Lemma 1

We first construct φ₁ as follows.

• (2a) Define α=h ₁(h ₁−h*)<0 and .

• (2b) Select ε>0 so that .

• (2c) For δ>0 define

• (2d) Select 0<δ*≪1 so that .

Since φ₁(X*−ε;δ*)>C ₁>φ₁(X*+ε;δ*), we can

• (2e) Extend φ₁(x;δ*) to a function φ₁∈Π defined for x≥0.

This construction implies then (with δ* now omitted) that for γ∈[0, 1]. To see that this equation holds, apply (vii) and (ix) and then (2c) and (2a) to get

We now construct φ₂ as follows.

• (3a) Select so that for ℓ∈{0, 1}.

• (3b) Define φ₂(X ⁰(γ))=(1−γ)λ₀+γλ₁ and for γ∈[0, 1].

• (3c) Extend φ₂(x) elsewhere so that φ₂∈Π.

It is straightforward to show that for γ∈[0, 1].

Proof of Lemma 2

It follows from condition (b) that

and therefore that . In addition, it can be seen from condition (c) and the definition of ω₀ that . Thus, we are assured that the interval where φ₁ was initially defined in (2c) of Lemma 1 is disjoint from the intervals and on which φ₂ was initially defined in (3b). Next, let φ be the restriction of φ₁ to the interval . We now extend φ so that it belongs to Π and satisfies the following three conditions:

1. .

2. .

3. for γ∈[0, 1].

Since C ₂∈(k C ₁, C ₁), these conditions can easily be satisfied if δ* in (2d) is chosen to be sufficiently small.

Proof of Lemma 3

Step 1: Select φ₁.

To begin, let 0<ε≪1 and define X ₁=1+ε², Y ₁=2ε, X ₂=2, and Y ₂=1/ε+ε as in the main proof. For ν>1 and γ>0, also define

Here, θ is taken to be the positive constant I _in/J ₁. Then

because for sufficiently small ε we will have F(ε, ν, 1) ≈ (θ+ν²)⁻¹. In contrast,

For the last inequality, observe that ε²[θ+ν ^z/ε]⁻¹→0 and (1−ε²)[θ+ν ^z/ε]⁻¹→0 as ε→0 for fixed z>0. Since Y ₁≪X ₁ and X ₂≪Y ₂, we may disregard X ₁ and Y ₂, and since as ε→0, the expression

becomes negative for sufficiently small ε. Thus, there exists γ*=γ*(ε, ν) ∈ (1, 1/ε) such that

This equation can be rewritten as

where . Letting Q(ε, ν) denote the common value on both sides, define ϕ₁ so that ϕ₁×Q(ε, ν)×θ=C ₁, and let

Then by construction, φ₁∈Π and (X ₁, Y ₁, X ₂, Y ₂) satisfies

Step 2: Select φ₂.

The argument to select φ₂ is similar to the one used to select φ₁, but it requires the use of different constants. With ε as mentioned earlier, let X ₀=1, Y ₀=ε, X ₃=1/2ε+1, and as in the main proof. Also, for ν>1 and γ>0 (not necessarily the same as before) define

This time θ is taken to be the positive constant I _in/J ₂. Observe that

due to the estimate K(ε, ν, ε) ≈ (θ+ν^1/2)⁻¹−(θ+ν)⁻¹. On the other hand,

For the last inequality, observe that 2ε[θ+ν ^z/ε]⁻¹→0 and (1−2ε)[θ+ν ^z/ε]⁻¹→0 as ε→0 for fixed z>0. Since Y ₀≪X ₀ and X ₃≪Y ₃, we may disregard X ₀ and Y ₃, and since as ε→0, the expression

becomes negative for sufficiently small ε. Thus, there exists γ^**=γ^**(ε, ν)∈(ε, 1/ε) such that

We can rewrite this equation as

where . Letting Q(ε, ν) denote the common value on both sides, define ϕ₂ so that ϕ₂×Q(ε, ν)×θ=C ₂, and let

Then by construction, φ₂∈Π and (X ₀, Y ₀, X ₃, Y ₃) satisfies

Furthermore, it is clear from Equations (A1), (A2), and (4) that .

Proof of Lemma 4

Although the following argument uses similar notation as in the proof of Lemma 3, it relies on a different set of techniques. For and 0<ε≪1, consider the quantities defined in Equation (17). Since 0<ε≪1, we have (i) X ₃ ≈ 4, Y ₀ ≈ 0, Y ₁ ≈ 2−4ζ, Y ₂ ≈ 4, and Y ₃=Y ₂+ε³/(1−ε) ≈ 4, (ii) Y ₀<X ₀<X ₃<Y ₃, (iii) Y ₁<X ₁<X ₂<Y ₂, (iv) X ₀−Y ₀=1−ε², (v) , (vi) Y ₂−X ₂=2ε/1−ε+ε² ≈ 2ε, and (vii) Y ₃−X ₃=ε+ε²/(1−ε) ≈ ε. For γ>0 and θ>0, let

and

In view of the estimate

let us define

We remark that if ε, γ, and ζ are fixed so that M(ε, γ, ζ) is nonzero, then the pair of functions M(ε, γ, ζ) and F(ε, γ, ζ, θ) have the same sign when θ is sufficiently large, and that a similar relationship holds between N(ε, γ) and K(ε, γ, θ).

We now show that there exists some such that . For the moment, fix 0<δ≪1, let , and let ε tend to zero. Then , and

Here we used the approximations 1−e ^x ≈ x for x small and Y ₃−X ₃ ≈ ε. The last estimate in turn implies that , since , δ>0 is fixed, and ε tends to zero. By repeating the procedure mentioned earlier with , we obtain . It follows that for sufficiently large θ we also have and . Since K(ε, γ, θ) is a continuous function of γ, there exists some such that . In addition, .

We now turn to the pair of functions M(ε, γ, ζ) and F(ε, γ, ζ, θ). Recall that

and that . First, when we have the estimate

and when we have

Next, we note that and . Also, recall that Y ₃=Y ₂+ε³/(1−ε). Thus, we can estimate

Also, . Therefore,

It follows from Equations (A5) to (A8) that for sufficiently small ε we have both and . Hence, for sufficiently large θ we also have and . Since depends continuously on ζ, there exists some such that . Thus, we have shown that there exist ε, , and such that

Finally, with , we observe from Equations (A3) and (A9) that

Now let Q denote the common value on both sides, define ϕ such that ϕ×Q×θ=C ₁, and let

Here, we require that I _in/J=θ and . Then Equation (A10) implies that

A similar argument involving Equations (A4) and (A9) shows that, for the same function φ and some positive constant C ₂,