Effect of a sharp change of the incidence function on the dynamics of a simple disease

Abstract

We investigate two cases of a sharp change of incidencec functions on the dynamics of a susceptible-infective-susceptible epidemic model. In the first case, low population levels have mass action incidence, while high population levels have proportional incidence, the switch occurring when the total population reaches a certain threshold. Using a modified Dulac theorem, we prove that this system has a single equilibrium which attracts all solutions for which the disease is present and the population remains bounded. In the second case, an increase of the number of infectives leads to a mass action term being added to a standard incidence term. We show that this allows a Hopf bifurcation to occur, with periodic orbits being generated when a locally asymptotically stable equilibrium loses stability.

Keywords:

• epidemiology
• incidence function

1. Introduction

One of the most critical aspects in modelling disease propagation is the choice of the incidence function, which describes the rate at which new infectives are produced. If there are S susceptible individuals and I infective individuals in a population, then the rate of creation of new infectives typically involves a product of terms involving S and I. The most common incidence functions are mass action SI, proportional incidence SI/N, where N is the total population, and general incidence S ^p I ^q , but there are many other functions that have been used. There has been a debate for quite some time about the nature of the functions to use; see, for example, McCallum et al. 9 and the references therein. Most studies conducted to this day assume that the form of the incidence function is fixed for a given model. In models where there are several groups, parameters of the incidence function can vary from group to group, but the general nature of the function is unique. In Fromont et al. 3, a model is introduced where different geographical locations have different types of incidence functions; in this case, this is justified by the fact that some of the locations are farms, others are villages, leading to different contact structures. In single populations 15, a number of SI and SIS models are formulated with various types of demographic components, with a smooth, density-dependent incidence function. Further mathematical results on some of those models are provided in Zhou 14. In Brauer 1, the incidence takes the form β(N)SI, with β(N) differentiable. In Zegeling and Kooij 13, an SI model is studied for micro- and macro-parasitic diseases, with strong dependence of the incidence on the population size. In Liu et al. 8, an incidence function that takes into account the number of hospitalized infectives is used; in both Liu et al. 8 and Zegeling and Kooij 13, it is shown that such dependence leads to oscillations. See also, for instance, 4 10 11.

In the present paper, we consider an SIS model for the spread of an infectious disease in a single population. These models, with the population split between susceptible and infective individuals, constitute the most elementary description of the spread of a disease in a population, and have been extensively studied in the literature. However, we suppose that there is a population level across which the contact structure is fundamentally modified. Hence, contrary to models with varying contact levels 1, there is a sharp threshold where the nature of the incidence function itself changes. A similar situation was considered in Kribs-Zaleta 7, with logistic dynamics.

We consider here an SIS model in an exponential population dynamics framework, with no self-regulation effects due to intra-specific competition (crowding). Thus, if the birth rate is too low or too high, the population can go extinct or become unbounded. In Section 2, we consider this general model with unspecified incidence and establish some elementary properties.

We then specialize this framework to two different incidence functions with switching.

The first case we consider, in Section 3, has the same incidence form as in Kribs-Zaleta 7. The switching occurs when the total population reaches a certain threshold, with mass action incidence for small populations and standard incidence for large populations. This can model a global (and abrupt) modification of the contact structure for high population levels. To study the stability of the endemic equilibrium, we use an extension of Dulac's theorem that is developed in Appendix A.

The second switching scenario addresses the situation where treatment facilities are overcome. At low incidence levels, standard incidence is used; when a certain threshold number of infectives is reached, a mass action type term is added to the incidence function. This describes the situation where, for example, a community has a limited number of hospital beds. When this capacity is overcome, infectives are treated at home rather than in hospital, where their contact pattern is more prone to the propagation of the disease. This change in the incidence is manifested in the incidence function; if the number of infectives is below a threshold value then the incidence is given by proportional mixing, whereas the additional incidence due to any amount of infectives above the threshold is of mass action form. We formulate and analyse this model in Section 4, studying in particular the occurrence of periodic solutions.

We now call attention to an important difference in the dynamics exhibited by the two models. For the second model, it is possible to have a Hopf bifurcation, whereas this cannot happen for the first model.

2. The general framework

We make the following assumptions. There is no vertical transmission of the disease, so all newborns are susceptibles; birth occurs with rate constant b>0, proportional to the total population. The mortality coefficient for non-disease-related reasons is d>0. Infective individuals are subject to disease-induced death, which occurs with rate constant δ≥0. Infective individuals may recover after an average duration of infection of 1/γ time units. Finally, contacts between susceptible and infective individuals result in new infection with rate F(S, I). We thus consider the following SIS epidemic model,

The precise nature of the incidence function F will be made explicit later. For now, we only assume that it is a continuous piecewise differentiable non-negative function such that . It follows that the non-negative quadrant is positively invariant under Equation (1). Let N=S+I. Then,

Clearly, if N tends to zero, then so must S and I.

2.1. Equilibria

Disease-free equilibria are obtained by setting I=0 in Equation (1). This yields the extinction equilibrium (S, I)=(0, 0), which is present for all parameter values; whereas, if b=d, then (S, I)=(S, 0) is an equilibrium for any S>0. In this paper, we assume that b≠d and so we ignore this latter case.

From Equation (2), endemic equilibria (EEP), that is, equilibria (S*, I*) such that I*>0, can only exist if , and must satisfy

where N*=S*+I* is determined by the exact form of the incidence function F that is used in Equation (1). Additionally, if b=d+δ, then Equation (2) implies that an endemic equilibrium would satisfy N*=I*, and so S* would be zero. Substituting this into Equation (1b) yields I*=0. Thus, endemic equilibria are only possible if .

Proposition 1

A necessary condition for the SIS model (1) to have endemic equilibria is that

2.2. The system in proportions

In order to simplify the problem, we consider from now on the system in proportions. We let

and, noting that s+i=1, we transform Equation (1) into a system in terms of (i, N). Differentiating i with respect to t gives

Substituting Equation (1b) into this expression and using the notation

we obtain

This definition of f is only valid for N>0, so we define

and require that this limit exist for i∈[0, 1]. This precludes, for example, the possibility that is sublinear in α near 0.

The system under consideration is then

Under the dynamics of Equation (4), i(t) remains in [0, 1] for all positive times since f is zero if i is 0 or 1. If a solution starts with i(0) less than or equal to one, then i(t) is strictly less than one for all positive time. Also, if N(0)≥0, then N(t) remains non-negative for all time, and satisfies , giving the following result.

Proposition 2

Solutions to system (4) beginning in the positively invariant rectangular half-strip of the (i, N)-plane defined by

exist for all positive times.

Equation (4b) is separable, yielding

Considering this in the cases b<d and d+δ<b gives a monotone function for N.

• If b<d, then for some .

• Since i(t)≤1 for all t, , and it follows that if b>d+δ, then for some .

The following result has been proved.

Proposition 3

If b<d, then solutions of Equation (4) satisfy . If b>d+δ and N(0)>0, then solutions of Equation (4) satisfy .

The Jacobian matrix associated with system (4) will often be used. At an arbitrary point (i, N) for which f is differentiable, the Jacobian is given by

3. The model with switching on population density

The novelty of the model discussed here lies in the incidence function F. In this section, we assume that the incidence is a continuous function of the form

The situation described by Equation (6) is one where the type of contact structure varies sharply as the total population density crosses a threshold value. Here, the population has been scaled to this threshold so that the transition occurs at N=1. When the population is small enough, it is assumed that every infective individual can potentially meet every susceptible in the population, so that the incidence is of mass action type. As the population becomes larger, this hypothesis must be relaxed, and every infective is able to make contact with only a certain fraction of the susceptible population, leading to the use of proportional incidence. Note that , as assumed in Section 2.

3.1. The system in proportions

The incidence function f for the system in proportions is as follows:

This incidence function is substituted into Equation (4) to obtain the main equations for this section. For N≤1, the dynamics are described by

whereas if N>1, we have

We call Equation (8) the lower system and Equation (9) the higher system. We distinguish between the low strip 𝒟 _L , where N≤1, and the high strip 𝒟 _H , where N≥1.

3.2. Exact solution in 𝒟 _H

Let us first remark that the nature of those parts of a solution of Equation (4) that lie in 𝒟 _H are known. Indeed, we have the following theorem.

Proposition 4

Suppose that, at some instant τ≥0, we have . Then there exists a potentially infinite interval ℐ with left endpoint τ such that, for all , we have with

where and .

Proof

Assume that for some τ≥0. Then consider the initial value problem consisting of Equation (9) together with the initial condition and . Integration of Equation (9b) gives, for t≥τ,

We denote by ℐ the interval on which it remains true that . Now note that, denoting , Equation (9a) can be written as follows:

a Bernoulli equation (it is also separable). It follows that we have, for ,

where

Therefore, for ,

Substituting Equation (12) into Equation (11), we obtain the result for .   ▪

There are two ways for a solution curve to intersect 𝒟 _H . It can start in 𝒟 _H , that is, correspond to an initial condition in 𝒟 _H , or it may correspond to a switching of incidence functions because N=1 is crossed as N increases. To take this information into account, we introduce the sequence {t _k } of switching times, which we define as follows. For k=1, 2, …, the are the times at which there is a change in Equation (6), that is, when N crosses the value 1, with if there is no such crossing for t>t _k . We take t ₀=0 to be the initial time; so N(t ₀) is the initial condition. For subsequent t _k , N(t _k )=1. So if the solution enters 𝒟 _H at t _k , then the integral (11) can be written as follows:

for .

3.3. Local stability analysis

Theorem 1

For all values of the parameters, the disease-free equilibrium is given by

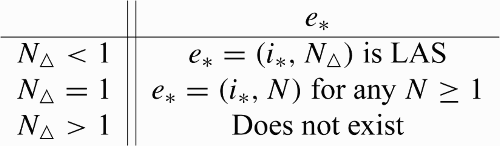If b<d, then there are no other equilibria and e ₀ is globally asymptotically stable. If d<b, then e ₀ is unstable. If , then the presence of endemic equilibria , where , is related to the quantity . If , then there are no endemic equilibria.

Proof

For all parameter values, e ₀ is an equilibrium of the lower system. The point e _* is an equilibrium of the lower system if , guaranteeing that i _*∈(0, 1), and N _*<1. A third solution to the equilibrium equations for the lower strip exists, but it is not biologically relevant since it occurs at , which lies outside of 𝒟. The higher system (9) only yields equilibria for which N _*>1 if . In this case, there is a continuum of equilibria of the form for N>1. However, the condition is satisfied with probability zero, and so these equilibria are not considered to be biologically significant.

Evaluating the Jacobian matrix (5) at e ₀, we have

It follows that the local stability of e ₀ is ruled by the sign of b−d, with e ₀ locally asymptotically stable if b<d and unstable if b>d.

In the case b<d, Theorem 3 implies that N(t)→0 as t→∞. Now rewrite Equation (8a) as follows:

since i≤1. As N(t)→0, there exists τ≥0 such that β N(t)<b for t≥τ. As a consequence, for sufficiently large t, i′<−γ i and it follows that i(t)→0 as t→∞. Thus e ₀ is globally asymptotically stable for b<d.

For , the sign pattern of J(e _*) is

which is a sign stable pattern 6, and so e _* is locally asymptotically stable when it lies in the low strip 𝒟 _L .   ▪

3.4. Ruling out periodic solutions

Note that under the flow (4), the set {i=0} is positively invariant, as is the set {N=0}. Also, when i=1. This implies that any periodic solution of Equation (4) is bounded away from {i=0}, {N=0} and {i=1}, that is, any periodic solution lies entirely in the interior of 𝒟.

We apply Theorem 6 (Appendix 1), taking , with , and . Then hypotheses (H1) and (H2) in Appendix 1 are satisfied.

We use the Dulac function getting

(which is strictly negative) on both D ₁ and D ₂. Thus, by Theorem 6 (Appendix 1), there are no simple closed curves that are invariant under the flow (4). This rules out periodic solutions, homoclinic orbits and heteroclinic cycles. Since e ₀ repels solutions from the interior of 𝒟, we have the following theorem.

Theorem 2

Suppose . If , then each bounded solution in the interior of 𝒟 limits to the endemic equilibrium e _*. If , then there are no bounded solutions in the interior of 𝒟.

We note that if i=0 is attracting for N>1, then for d<b there are solutions for which i tends to zero and N tends to infinity. Thus, the presence of e _* does not guarantee that it is globally stable.

This is distinct from the behaviour of the system studied in Kribs-Zaleta 7, where the endemic equilibrium can be shown (using the extended Dulac theorem in Appendix 1) to be globally stable whenever it is present. The difference in dynamics stems from the fact that the model in Kribs-Zaleta 7 includes logistic demographics which prevents solutions from being unbounded.

4. A model where infection overcomes treatment facilities

In this section, we consider the case where instead of switching for a given value of N, the switching occurs for a given value of I.

We want to model a situation, such as would occur in the event of overflow of treatment capacities. Suppose that a given population, say a city, has a certain number of hospital beds available, and that the disease under consideration requires hospitalization. While the number of infectives remains lower than the number of beds, infectives are cared for in the hospital, in what can be considered ideal conditions: their contacts with susceptibles from the general population are much less frequent. Then, as the epidemic progresses, there is a point where not enough beds are available, and some patients are sent home. In this situation, the contact pattern is much less favourable, with some infectives mixing more freely in the population (or, at least, in a less controlled setting). We suppose that the incidence function takes the form

where ˆ I>0 is given. The term describes the additional infections caused by an elevated mixing rate for the non-hospitalized infectives.

Note that this is a toy model. It is generally assumed (as is done, for example, in Section 3) that proportional incidence is more appropriate to describe high population densities. Here, however, we want to focus on the effect of a sudden change in the contact pattern that results in the contacts becoming much more frequent. Hence the form chosen for Equation (15).

The basic analysis is very similar to the case of Section 3, and many results can be adapted.

4.1. The system in proportions

We consider the system in proportions, and so the incidence function is given by

Substituting into Equation (4), we obtain the main equations for Section 4. For iN≤ˆ I, the lower system is given by

whereas if iN>ˆ I, we consider the higher system

One difference with the case of switching on the population density lies in the nature of the low and high strips, 𝒟 _L and 𝒟 _H . Here, the boundary Γ is given, for i∈(0, 1], by the hyperbola N=ˆ I/i. Once the strips are thus defined, some of the analysis of Section 3 carries through to the present model with little adaptation.

Note that Theorem 4 holds in 𝒟 _L , so that an explicit expression of the solution can be found in the lower strip.

In the lower strip 𝒟 _L , there are two nullclines. The i nullcline, resulting from Equation (17a), is given by

for all . The second nullcline is the N nullcline, resulting from Equation (17b). It is given by

for all (it exists both in the lower and upper strips). In the upper strip, apart from Equation (20), there is a nullcline resulting from Equation (18a) given by

Note that the nullclines i _LS and N _HS coincide with the hyperbola Γ, providing a strong connection between the lower and the upper strips.

Evidently, if i _LS=i _N , then there is a continuum of equilibria in the lower strip. However, the set of parameters for which this happens has measure zero in parameter space, and we choose to ignore this situation. So the equilibria are e ₀=(0, 0), , ), when .

Theorem 3

System (4) with incidence function (16) potentially has three equilibria, whose existences and stabilities are summarized in the following table where

Proof

The equilibrium e _* does not exist if i _N does not belong to (0, 1), hence the cases for e _*. (e _* might not exist even when i _N ∈(0, 1), which is treated in Theorem 4). The extinction equilibrium e ₀=(0, 0) always exists. At e ₀, the Jacobian matrix (5) takes the form

Thus, e ₀ is locally asymptotically stable if, and only if, b<d and ℰ<1. Furthermore, if b<d then N tends to 0. In this case, the asymptotic dynamics of i are governed by Equation (17a). If ℰ<1, then i tends to 0, and if ℰ>1, then i tends to i _LS. Thus, for b<d, if ℰ<1 then e ₀ is globally asymptotically stable, and if ℰ>1 then ē is globally asymptotically stable. (Note that ℰ>1 requires , making i _LS<1.) For , it follows from the Jacobian matrix that e ₀ is unstable. (The other equilibria are treated in Theorem 4.) Now suppose b>d+δ. Then, e _* does not exist and both e ₀ and ē are unstable (since in this case, i _N >1, implying that both Jacobians are evaluated on the left of i _N ). Also, note that from Theorem 3, N(t) becomes unbounded.   ▪

Note that ℰ resembles the classical basic reproduction number ℛ₀ in its interpretation. Indeed, is the mean time spent in the infective class, if natural death is replaced with birth as is the case when working in proportions. Multiplied by the rate β₁ at which individuals enter the infective class, this gives an estimation of the average number of new infections produced by an infective individual. However, for b<d, as ℰ passes through 1, the stability merely passes rom one equilibrium with N _*=0 to another. Since this role is very different from the classical role of ℛ₀, we use a different notation.

From now on, we choose to consider only the cases when all three nullclines exist in the interior of 𝒟, that is, . There are three cases to consider, which are shown in Figure 1. The following theorem summarizes these cases.

Theorem 4

Suppose that . Then, for system (4) with incidence function (16), e ₀ is unstable, and the stability of ē and the existence and stability of e _* are summarized in the table where

is the slope of N _HS at e _*, when e _* exists.

Figure 1. Phase plane situations when the incidence function takes the form (16), with the equilibria represented (circles are unstable, squares are stable). In each panel, the switching curve is the monotone decreasing curve, the nullcline for N′ is given by i=i _N , and the nullcline for i′ is the curve which has i=1 as an asymptote (given by N=N _HS(i)).

Proof

That e ₀ is unstable is established in Theorem 3. When evaluated at and to the left of i _N (i.e. when i _LS<i _N ), the sign pattern of the Jacobian (5) is

(where * corresponds to a quantity that may be positive or negative), and thus ē is unstable when i _LS<i _N because there is at least one positive eigenvalue. At ē and to the right of i _N (i.e. when i _N <i _LS), the sign pattern is

and since ℰ>1 when ē exists, ē is locally asymptotically stable. That it is also globally asymptotically stable follows from a phase plane argument. First, because i _LS>i _N (see Figure 1(c)), it is clear that the strip is positively invariant under the flow of Equation (4) with incidence function (16). Second, all points such that i<i _N satisfy . It follows that all solutions with i<i _N enter in finite time. When a solution is in , N decreases so that eventually, the system is governed by the lower system. When this happens, Theorem 4 applies with , and since ℰ>1, and Equation (10) implies that as t→∞. If i _N <i _LS, then lies below the switching curve. Thus, if i _N <i _LS, then e _* is not present. For i _N >i _LS, the equilibrium e _* is present. We now determine the stability of e _* for i _LS<i _N . Evaluating the derivative of N _HS(i) at i _N gives the slope 𝒮 _N of the tangent to N _HS(i) at e _*, when e _* exists. Then, at e _*, the Jacobian matrix (5) takes the form

and thus has the sign pattern

(The sign of J ₂₁ results from the fact that ). If , this is a stable sign pattern 6, and so e _* is locally asymptotically stable. If , then this is an unstable pattern and so e _* is unstable.   ▪

Interestingly, when it exists the stability of e _* is thus determined by the sign of the slope of the tangent to the nullcline N _HS at e _*. In fact, we show in the next section that when the sign of this slope changes, a Hopf bifurcation occurs at e _*.

4.2. Existence of periodic solutions

Theorem 4 states that the loss of stability of e _* occurs when 𝒮 _N changes sign. The following result relates this change in stability to a Hopf bifurcation. We treat 𝒮 _N as a bifurcation parameter, noting that by using β₂, we may consider 𝒮 _N to be independent of b, d, δ, i _LS and i _N . In the theorem statement and proof, denotes the open ball centred at e _* with radius ε.

Theorem 5

Suppose that and i _LS<i _N . Then for any ε>0 and any , there exists such that system (4) with incidence function (16) has a non-trivial periodic orbit in for .

Proof

Using Lemma 1 in Appendix 2 with , we see that the eigenvalues of the Jacobian matrix at e _* are purely imaginary conjugates when , and the real part of these eigenvalues decreases with 𝒮 _N in a neighbourhood of . By using 𝒮 _N as a bifurcation parameter (or β₂ as a proxy for 𝒮 _N ), the transversality as it passes through 0 is immediate. It follows that a Hopf bifurcation occurs at 5. In particular, e _* is attracting for and is repelling for . The Hopf bifurcation is occurring at e _* as 𝒮 _N passes through 0, but always with the underlying assumption that i _LS<i _N . Since 𝒮 _N is the derivative of N _HS(i) at i=i _N (as is the case at e _*), it follows that the bifurcation is happening in the interior of the high strip where the vector field is C ³. Any points of non-differentiability on the periodic orbit are the result of further (minor) bifurcations as the expanding periodic orbit crosses the switching curve. It remains to be shown that periodic orbits exist for negative 𝒮 _N . 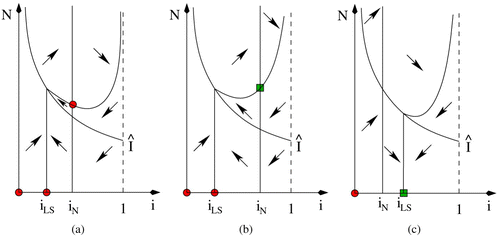As seen in Figure 2, any solution for which N(0) is sufficiently large begins in one of the Regions I, II, III or IV (where the divisions between the regions are the isoclines and the switching curve). In any case, the solution will eventually advance to Region IV. In Region IV, however, N is bounded below by N ₁. Then, after leaving Region IV, the N coordinate of the positive semi-trajectory is bounded above by N ₂. Thus, solutions are bounded and do not approach e ₀ or ē. However, for 𝒮 _N negative, e _* is repelling. Thus, by the Poincaré–Bendixson Theorem, the omega limit set of a solution starting near e _*, or in Regions I, II, III or IV, must be a periodic orbit. In fact, aside from e _*, any solution for which i(0) and N(0) are non-zero must limit to a periodic orbit.   ▪

Figure 2. Phase plane diagram showing the nullclines, directions (empty headed arrows) as well as two solutions (filled head arrows), for the system with incidence function (16), in parameter regions where a periodic solution exists.

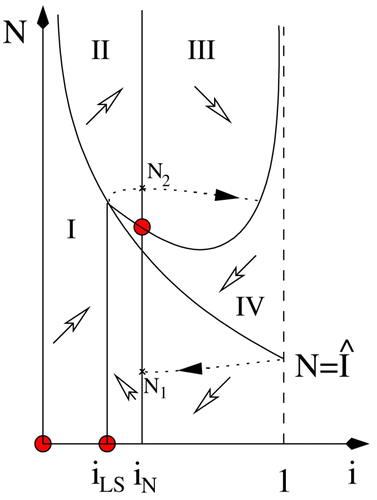
In Figure 3, the parameters are 1/b=20 years, 1/d=80 years, , γ=1/3, β₁=0.4 and . The initial population is N(0)=1000, with one infective individual, and the switching occurs at ˆ I=150.

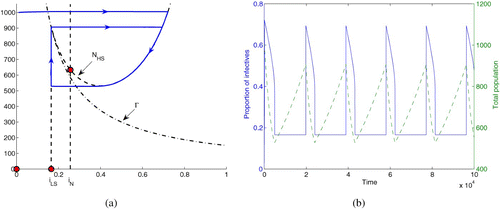
Figure 3. (a) Phase plane diagram showing the nullclines (dashed curves), switching boundary Γ (dash-dotted curve), as well as one solution along the hysteresis loop, for the system with incidence function (16). Parameters are indicated in the text. (b) A solution along the hysteresis loop in the case of Figure 3(a). The left vertical axis shows the proportion of infectives in the population, corresponding to the solid curve, while the right vertical axis shows the total population, corresponding to the dashed curve.

Note (Figure 3(a)) that the periodic orbit intersects both the lower and the upper strips. This is the situation after a so-called grazing bifurcation 2, where the periodic orbit whose existence is established in Theorem 5 hits a smooth switching boundary.

5. Discussion

The model we introduce here is, in essence, quite different from other models that were published on the subject. It does share some common properties with other models with exponential demography and disease induced death, in which two extreme cases occur when the birth rate is either too low or too high. For b<d, the population size limits to zero and extinction is inevitable, independent of the disease dynamics. For b>d+δ, the population size grows without bounds. In this case, it is impossible for the disease to limit the population growth. In between these two extreme cases is a region where the disease persists.

For the model with switching on the population density of Section 3, if the population does not become extinct because of excessive disease-induced death, then the disease remains endemic. This result could be foreseen: we assume that the system switches between two well-studied vector fields, with the upper vector field having no equilibrium per se. To show that the endemic equilibrium attracts all bounded solutions, we use an extension of Dulac's theorem for switching vector fields developed in Appendix 1.

A different situation arises in the model of Section 4, with switching on the number of infectives. An analysis of the phase plane, for the case when , shows that there are three major configurations. In each of them, there are two equilibria where the population becomes extinct, one that is always unstable, and one whose local stability depends on the sign of an ℛ₀-type quantity. In two of the configurations, there also exists an endemic equilibrium. We show that either this endemic equilibrium is locally asymptotically stable, or it is unstable and there is a periodic orbit. In Zhou and Hethcote 15, periodic orbits are not present. There are several major differences between the model presented here and that of Zhou and Hethcote 15, so pinpointing one single cause for these oscillations is hard. However, it is likely that the single most important difference between the models lies in the fact that in 15, the incidence function is a non-decreasing function of the total population, whereas here it is a function of the infective population. Note that the expression of 𝒮 _N suggests that oscillations occur when β₂ and ˆ I are rather large. This means that in order to observe oscillations, the prevalence of the disease in the population and the ‘cost’ of being treated outside the hospital must both be quite high. If, as in Zhou and Hethcote 15, incidence depended on the total population, then prevalence cannot reach such high levels as it does here.

It is clear that the period of the oscillations obtained in Section 4 are unrealistic (e.g. 120 years in the case of Figure 3). However, a more thorough exploration of the parameter space may reveal areas where such behaviours occur with more realistic frequencies. The models we develop here are toy models; SIS models are seldom used in real case studies, because of their simplicity. More realistic SEIRS models would most likely exhibit the same type of behaviour as our models here, if the same incidence functions were used, with perhaps more realistic oscillation periods. Furthermore, the oscillations we observe seem quite robust to the type of incidence functions used, provided the switching occurs as I passes through some threshold. For example, another way to model the saturation of treatment resources of Section 4 would be to use an incidence of the form

with ˆ I>0 given. Such an incidence function produces the same type of oscillations as Equation (15).

Acknowledgements

The authors thank two anonymous referees for helpful suggestions. The work of both the authors was supported in part by NSERC. The work of J.A. is supported in part by MITACS.

Appendix 1. A Dulac-type theorem

We give here an extension of Dulac's Theorem that can be used to rule out periodic solutions when the vector field is C ¹ everywhere except on a curve Γ on which it is non-differentiable. It was brought to our attention that this result is quite similar to a result of Wang 12. However, the result here covers the more general case of the non-differentiability occurring along a curve rather than along a straight line.

Let D be a simply connected open subset of ℝ². Let be a simple curve such that consists of two components D ₁ and D ₂. We require the following:

• (H1) For each ε>0, there exist simple C ¹ curves in D _j , j=1, 2, such that the C ¹ distance is less than ε.

A sufficient (but not necessary) condition for (H1) to be satisfied is that Γ be C ².

Consider the differential equation

where x∈D, g is a C ⁰ vector field given by

and g _j is C ¹ on D _j , j=1, 2. (Note that we are assuming g to be C ¹ everywhere except at Γ, where it is not differentiable.) We also assume the following:

• (H2) Solutions to Equation (A1) are unique, and are transverse to Γ except possibly at a finite number of points.

Figure A1. Example of a situation covered by Theorem 6.

Theorem 6

(A Dulac-type Theorem)Let α be a scalar function on D, bounded on compact subsets of D. If has constant sign on D ₁∪D ₂, then there are no piecewise smooth, simple closed curves in D which are invariant under (A1)}.

Proof

Suppose is a piecewise smooth, simple closed curve which is invariant under Equation (A1). The possibility of γ being contained entirely in D ₁ or D ₂ is precluded by Dulac's Theorem. Thus we may assume that γ intersects Γ. Let (see Figure A1). By the Jordan Curve Theorem, there is a connected region U which is bounded by γ. Let . (We note that U ₁ and U ₂ may not be connected.) Take ε>0 small enough so that intersects each component of U _j . Let U _jε be the maximal subset of U _j which is bounded by γ _j and and let C _jε be its boundary. Finally, let and be the parts of C _jε which coincide with γ _j and , respectively. Then denoting g=(u, v) and , and using Green's Theorem, we have

Note that d x/d t=u and d y/d t=v on γ, it is clear that the integral over has an integrand which is zero leaving

Note that the integrations along and are well-defined as ε tends to zero, and are taken in opposite directions in the sense that for ε=0, they would involve integrating along the same segment of Γ but in opposite directions. Since the C ¹ distance and α, u and v are bounded on the closure of U, it follows that as ε tends to zero, the right-hand side of Equation (A3) tends to zero. On the other hand, the left-hand side of Equation (A3) is bounded away from zero. To see this, we note that there is an open set Ũ which is contained in for sufficiently small ε. Combining this with the fact that has constant sign on implies that the left-hand side of Equation (A3) is bounded away from zero for sufficiently small ε. This gives a contradiction and so we see that a piecewise smooth, simple closed curve in D cannot be invariant under Equation (A1).   ▪

Appendix 2. A small lemma on eigenvalues

Lemma 1

Let

where α, a, b are C ¹ functions of a parameter . Suppose and . Then at , the matrix M has a pair of purely imaginary eigenvalues λ_{1, 2} that satisfy

Proof

The characteristic equation is

It follows that eigenvalues of M are given by , where . When , we obtain which implies λ_{1, 2} form a pair of purely imaginary eigenvalues, since ab>0. Since Δ is negative at ¯τ, it is negative on a neighbourhood of ¯τ, and so in this neighbourhood. On differentiating, we obtain Equation (A5).   ▪