Darwinian dynamics and evolutionary game theory

Abstract

Evolutionary games, here modelled by systems of ordinary differential equations, encapsulate Darwin's theory of evolution by natural selection. An evolutionary game can reach a local minimum, allowing invasion by mutants to drive the system out of its minimum and engender speciation. Games based on optimality considerations do not resist invasion. Nash equilibrium does not resolve to evolutionary stable strategies – mutants can invade existing communities of species.

Keywords:

• evolutionary games
• population dynamics
• tutorial

1. Classical vs. evolutionary games

Evolutionary games mimic evolution by natural selection, as presented by Darwin 4. It can be distilled to three axioms 3:

• (1) Variation in trait values which in turn cause

• (2) fitness differences that are

• (3) inherited.

Like classical games, an evolutionary game consists of players, rules, strategies, payoffs and a solution concept. In evolutionary games, players are phenotypes (usually individual organisms). They are defined by a unique set of values of phenotypic traits. The rules are dictated by evolution by natural selection. Strategies consist of a unique set of values of the adaptive traits. Payoffs consist of fitness. And the solution concept results in indefinite persistence of a unique set of strategy values and the density of organisms that exhibit these values.

Unlike classical games, strategy values are passed on by organisms via inheritance. These values are inherited with small variation. Players are not required to be rational. They are not required to know the rules. They are not required to know the solution concept. And they are not even aware that they are playing a game. The rules are dictated by evolution by natural selection. They consist of the sum effect of population densities of growth and decline rates1 and of strategy values. These are influenced by the environment and interactions with contemporary individuals of species populations (players). The dynamics of the game are followed by the species mean value of the set of phenotypic traits. The mean is unique for a species. The phenotypic traits are subject to natural selection.

Throughout, we use strategy and strategy-values interchangeably. The meaning should be clear from its context. Except here and there, we discuss scalar strategies only. Expansion to vector strategies is (almost) trivial 2.

1.1 Some variations of classical games

In a static game, n players choose their strategies to maximize

where . Here u _i and H _i encapsulate player i’s strategy and payoff, respectively.

A dynamic game consists of a set of ODE

where is the instantaneous payoff function for player i. The solution for player i is x _i . It depends on the set of strategies and solutions of all players. The vectors and (of dimension n) are called state and control vectors. The set of strategies, , where m≤n, may be functions of time. The optimal strategy is determined when the system arrives at a predetermined target set. The target must be feasible in the sense that there exist initial conditions whose orbits reach the target set. The definition of payoff is arbitrary. Often, payoffs are obtained from the integral of some function of the control vector and the value of the state vector as the system approaches the target.

We require that is a subset from a strategy set 𝒰.2 The set 𝒰 is a subset of the n-dimensional Euclidean space ℝ ⁿ . If 𝒰 is finite, then is said to be a set of pure strategies. If 𝒰 is continuous, then is a set of continuous strategies.

1.2. Game theory milestones

The game theory generalizes the optimization theory. It was first introduced by the engineer/economist Pareto 10 with the so-called non-commensurable multi-criteria payoff functions. With it, the optimization problem becomes one of maximizing an m vector of payoff functions subject to the same conditions on as above. One may think of this problem in two ways. As a single player with m payoff criteria such as cost, weight, and reliability. Or as m players, each controlling a single component of that maximizes a single component of . Thus, Pareto introduced the first static game.

The publication of ‘Theory of Games and Economic Behavior’ by Von Neumann and Morgenstern 15 marked a significant progress in game theory. They began with the two-player matrix game. There is a large and growing body of literature on the theory and applications of matrix games, particularly in economics, where the evolutionary perspective is frequently adopted 13 23.

Currently, classical games are identified with one of three categories: matrix games, continuous static games, and differential games. Matrix games are static with a finite number of pure strategies. After each choice of strategy, the payoff to each player is determined as an element of a matrix. One player's strategy corresponds to the selection of a row. The other player's strategy corresponds to the selection of a column. All possible payoffs are given by the elements of the matrix. The particular payoff a player receives is determined by this combination of strategies. In continuous static games, the strategies are drawn from a continuous set. The strategies and payoffs are related in a continuous manner 19. The game is static in the sense that an individual's strategy is a constant parameter. Differential games 6 are characterized by continuously time-varying strategies and payoffs. They are determined from a dynamic system of ODE equations. Differential games generalize the optimal control theory 11. The latter may be perceived as a dynamic game with a single player.

Maynard Smith and Price 8 and Maynard Smith 7 introduced the concept of an evolutionarily stable strategy (ESS). Thus began the evolutionary game theory. Evolutionary games are dynamic with a solution concept (ESS) and unspecified target set. Strategies evolve by means of natural selection. They represent adaptive phenotypic traits – those traits that are subject to natural selection. A player's strategy set is the set of all evolutionarily feasible strategies. Payoffs correspond to fitness.

Fitness refers to the relative density of a species population (compared with other species populations that participate in the game) at a particular time. When the population is at the stable-point equilibrium, fitness is constant. Otherwise, we have the so-called instantaneous fitness. The fitness of an individual is defined as fitness divided by the total population. It influences changes in the strategy's frequency within the population.

Evolutionary games differ from classical games in some fundamental features. Classical games focus on strategies that optimize players payoffs. Evolutionary games focus on strategies that persist through time. Through births and deaths, players come and go. But their strategies pass on from generation to generation. In classical games, players choose strategies from a well-defined strategy set. This set is part of the game's definition. In evolutionary games, players inherit their strategies with small mutations. The strategy set, determined by physical and environmental constraints, may change with time. In classical games, each player may have a separate strategy set. Separate payoffs may be associated with separate strategies. In evolutionary games, there are groups of evolutionarily identical individuals. Players are evolutionarily identical if they share the same strategy set and the same payoffs from using the same strategy 16 17. In classical games, the optimizing rule is based on rational or self-interest choice of strategy. Consequently, players select predictable strategies. In evolutionary games, the optimizing rule is based on natural selection. Consequently, players do not select strategies. In classical games, the concepts of inner and outer games do not exist. In evolutionary games they do 16. In evolutionary games, the inner game involves short-term ecological dynamics. It corresponds to classical game dynamics. Within the inner game, players interact with others in a dynamic setting. They receive payoffs based on their own and others’ strategies. The outer game refers to dynamic evolutionary processes. Its time scale is usually long. Natural selection engenders the outer game.

2. Nash equilibrium, optimization and ESS

2.1. The inner game

The ecological dynamics associated with the evolutionary game are somewhat similar to Equation (2). Here, however, the dynamics are written in terms of a so-called fitness function H _i , i=1, …, n. The function encapsulates the instantaneous per capita growth rate of a group of individuals (species) whose density is x _i .

Throughout, we address the single phenotypic trait only; but see 2. Consider n species and let . Individuals in a population are identified by their value of a heritable phenotypic trait that is subject to natural selection. Individuals with approximately equal trait-values belong to a single species. A species is identified by the mean of these trait values. Strategy dynamics refers to changes in this mean. Let u _i be the strategy of individuals of species i. In general, population dynamics of species i depends on the density of all other species and on the strategies of all species. Consequently, the ecological dynamics are given by

where . All of the variables have essentially the same meaning as in the classical dynamic game.

Denote by the processes that encapsulate the rate of growth of species i’s population. Similarly, denote by the processes that lead to the rate of decline. Then Equation (3) becomes

Both and are assumed continuous bounded positive definite functions of their arguments.

Equation (4) includes various special cases. For example, in

the rate of change of the population of species i is decoupled from all other species. If environmental influences (input and output) are included in either Y _i or N _i , then each species evolves independently.

2.2. The G-function

Vincent and Brown 18 developed the concept of a G-function as a means to describe the fitness of many species by means of a single mathematical expression. A function is said to be a fitness generating function (G-function) of the population dynamics (3) if

where and in G are the same vectors as in H _i , and v is a virtual variable. Replacing v in the G-function with u _i yields the fitness of an individual in a population of individuals defined by the same G-function. This definition follows from the observation that players in the evolutionary game may be grouped according to those who are evolutionarily identical. Recall that evolutionarily identical individuals share the same strategy set and the same payoffs from using the same strategy. Thus we can separate one species from another. It does not follow that the fitness functions for all species can be determined from a single G-function. A single G-function refers only to those individuals who are closely related – with respect to strategy values – evolutionarily and ecologically. For example, a single G-function can be used to determine the fitness of many different species of shore birds. In a prey–predator system (say shore birds and raptors) two G-functions would be required.

Consequently, we can write the population dynamics (4) as

For example, consider the Lotka–Volterra competition model with n species. Assume that the carrying capacity for all species is identical. Further, assume that the carrying capacity is a function of u _i , such that

where K _m is a positive constant. Denote the competition function between species i and species j by . Then

Replacing u _i by v, we obtain the G-function for all evolutionary identical species thus

A reasonable choice of α is

The parameter σ _k in Equation (7) is interpreted as the phenotypic plasticity of u _i with respect to the carrying capacity. Similarly, in Equation (10), σ _a is the phenotypic plasticity with respect to competition. In this game, each player gains or loses according to its strategy value with respect to the environment and according to the distance of his value from those of all other players.

2.3. The outer game of the dynamics of evolution by natural selection

Consider solving Equation (6) for fixed . Then in general, one obtains solutions that are neither evolutionarily stable nor at maximum fitness 14. The outer game determines how components of the strategy vector evolve through time. The outer game is played by simultaneously solving the population dynamics equation with a strategy dynamics equation (here called Darwinian dynamics 18). (One must keep in mind that each u _i represents the average of phenotypes’ distribution around this average. The distribution is assumed symmetric with small variance 22, where strategy dynamics were first introduced.) The solutions may not result in ESS or maximum fitness. They encapsulate the rules of evolution by natural selection.

To obtain an expression for the strategy dynamics, recall the definition of the G-function in Equation (5) and the population dynamics given by Equation (6). Strategies evolve according to the dynamics

18, where the positive parameter σ² is the variance of the distribution of strategy-values among phenotypes of a single species. It scales the rate of evolutionary change. Equations (6) and (11) constitute the Darwinian dynamics. Solved together, they often possess an equilibrium solution for and . Adopting the game theory vernacular, the non-zero solutions for x _i and their associated u _i form a ‘coalition’ of strategies. If these strategies resist invasion by other, mutant strategies, they are called ESS.3 A necessary condition for an ESS is that the G-function takes on a maximum at zero with respect to v 18. ESS values refer to specific population densities, number of species that form the coalition and strategy values. Thus, we see how the G-function can be used to find coalitions that cannot be invaded.

2.4. Evolutionary game landscapes

The fitness of individuals of a species is a function of its strategy. A plot of fitness vs. strategy provides insight into why some strategies ‘win’ and others ‘lose’. This plot defines a landscape. We distinguish between two types of landscapes. The first, the ‘fitness landscape’, is derived from optimality principles 14. The second, the ‘adaptive landscape’, is derived from the $G$-function 18. The fitness landscape is a plot of fitness (vertical axis) in Equation (1) vs. strategy. The adaptive landscape is a plot of the G-function (vertical axis), in Equation (5) vs. the strategy. The fitness function and the G-function may arrive at the same solution. However, plotting both illustrates the difference between optimally derived and evolutionary derived landscapes.

2.4.1. The fitness landscape

If one chooses a strategy vector , and initial conditions for the densities , Equation (3) may be integrated to produce a solution for as a function of time. Typically, there exists an equilibrium solution with and at least one . It follows from the population dynamics that the fitness for those species with must be negative. The fitness for those with must be zero. Given that the strategy vector and its corresponding equilibrium solution , we define the fitness landscape by varying a component u _i of while holding all other components and the equilibrium constant.

Definition 1

(Fitness landscape) A fitness landscape for a surviving species i is a plot of H _i (w) vs. w. This function is obtained by replacing u _i in by w holding all other strategies fixed.

For example, consider Equation (8): n denotes the number of species; r the intrinsic growth rate common to all species; K(u _i ) the carrying capacity of species i; and the interference (competition) coefficients. Definition 1 implies that only when w=u _i . When w=u _i , equilibrium requires that . As explained below, a strategy leading to a higher population density will not be evolutionarily stable if it is not at a maximum point on the adaptive landscape.

2.4.2. Adaptive landscape

The adaptive landscape comes about using the methods of evolutionary games as developed in 18. There are as many fitness landscapes as there are species (n). There is only one adaptive landscape for all species. It is given by the G-function (9).

Definition 2

(Adaptive landscape) For a given strategy vector , assume that there exists an equilibrium solution with at least one . The adaptive landscape corresponds to a plot of vs. v where and are held fixed.

One way to think about this landscape is that it is a plot of the fitness of individuals using the strategy v at a density near zero when played against all other strategies at their respective equilibrium population densities. It can be shown that a necessary condition for a given strategy to be evolutionarily stable is that it must correspond to a maximum point on the adaptive landscape 18. As we shall see below, optimization-based solutions do not always satisfy this condition. Hence, such solutions are not evolutionarily stable. Any individual that can benefit by not using the group optimal strategy will increase their own fitness at the expense of others. The principal property of an ESS is that if all individuals in a population are using it, then other individuals using a ‘mutant’ strategy cannot invade. The adaptive landscape provides a useful tool for determining the evolutionary stability of a given strategy.

2.4.3. Optimization-based and evolutionary-based solutions

Assume that the optimization-based solution is obtained by playing a dynamic Nash game. Then we must modify the Nash 9 definition for a static game to:

Definition 3

(Nash equilibrium solution) A Nash equilibrium solution for the payoff functions H _i (·) is such that if any player makes a unilateral change in his strategy (to some other point in 𝒰), then his payoff can be no higher.

From the definition we immediately obtain

Lemma 1

(Nash equilibrium solution) Let with u _i in replaced by . It follows from Definition 3 that a point is a Nash equilibrium solution for the functions H _i (·) if and only if for each i=1, … n

Thus, Nash equilibrium solution applies to the dynamic game given by Equation (3). Consequently, we extend Definition 3 to

Definition 4

(Dynamic Nash equilibrium solution) A strategy vector is said to be a global dynamic Nash solution for the evolutionary game if and only if system (3) at equilibrium satisfies Definition 3; i.e. given an initial condition and a strategy , the solution of Equation (3) results in an equilibrium solution for such that

If lies in the neighbourhood of then the strategy vector is said to be a local dynamic Nash solution for the evolutionary game.

In Definition 4, we assume that exists. Both solutions (based on Definitions 3 and 4) reduce to a simple maximum definition when n=1.

Rearrange such that x ₁>0, and x _c+1=0, . Set and similarly for . Now n=c+m with 1≤c≤n. Let be the catenation of two vectors, and , associated with and with the corresponding elements of so that

For a given strategy vector , let the equilibrium solution to Equation (3) be

Definition 5

(ESS) A strategy vector is said to be an ESS if and only if system (3) is resistant to invasion. This means that for every initial condition and , the solution of Equation (3) tends to the equilibrium where . If lies in the neighbourhood of then is said to be a local ESS.

Maynard Smith's 7 original definition is a local ESS with both and scalars. Definition 5 represents a generalization of his idea in the context of evolutionary games governed by a system of ordinary differential equations.

Lemma 2

(ESS) It follows from Definition 5 that if is an ESS then

It follows from the Lemma 2 that for any i=1, …, c and any ,

In terms of the G-function, we have

These two inequalities constitute the ESS maximum principle 18

which is a constructive necessary condition for determining an ESS for , and the size of the ESS coalition, c. The maximum principle in 18 was proved for vector strategies; i.e. v becomes and u _i becomes . The latter represents the set of strategies for species i. For further details, see 18.

3. Evolutionary games and Darwinian dynamics

Recall that a fitness landscape is based on optimality design, which in turn corresponds to Nash dynamics (see Definition 4). An adaptive landscape is based on Darwinian dynamics that satisfy the ESS maximum principle. The difference between these dynamics (even if the solutions are the same!) is highlighted by their generated landscapes. In both cases, analytical solutions cannot be expected. Consequently, one must rely on numerical solutions, using algorithms such as ‘hill climbing’.

The dynamics of strategy for Darwinian dynamics is given by Equation (11). For optimality design, the gradient algorithm 20 of the form

resembles Equation (11). Because contains u _i , solutions based on Equation (12) frequently result in different dynamics for u _i with different equilibrium solutions (compared with Darwinian dynamics). Equations (3) and (12) solved together (optimal dynamics) result in a solution for and . This solution maximizes the H _i functions.

3.1. Landscape layouts

Figures that provide landscape layout plots are instructive. They emphasize the difference between adaptive and fitness landscapes. In the following examples, when results do not depend on initial conditions, they are not specified.

Example 1 (Frequency dependence)

The term frequency dependence implies that fitness of any individual depends on the strategies used by all individuals in the population.4 Let us use the standard probability density function Beta to mimic Y in Equation (4) (see also Example 1). The Beta density with shape parameters p and q is

for p>0, q>0 and . Here, Γ is the gamma function. The boundary values at u _i =0 or u _i =1 are defined by continuity (as limits). Equation (13) has no biological underpinning. It is useful because Y depends on v only; because its domain is bounded; and because its asymmetry is controlled by the values of p and q. Note that Y(v) depends only on the strategy choice made by individuals of species i. In the following simulation, we use p=2 and q=3. Consequently, Equation (13) is asymmetric. For frequency dependence, we use

corresponding to Equation (4). Figure 1 illustrates the landscape layout obtained when both the population and strategy dynamics are Darwinian (G-function) and optimality-based (H). The initial conditions are u ₁(0)=0.8 and x ₁(0)=10. Here, optimal dynamics and Darwinian dynamics produce different landscapes. Under Darwinian dynamics, the ESS is obtained with equilibrium values of u ₁=0.3334 and . The optimal strategy, corresponding to the maximum value of H, cannot coexist with the ESS strategy. In fact, no other strategy can coexist with the ESS strategy.

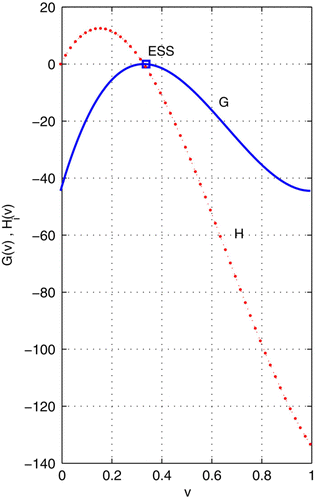
Example 1 illustrates the difference between fitness (H-based) and adaptive (G-based) landscapes. The maximum principle is a necessary condition. Therefore, the numerical solution of G-based landscapes may settle on a minimum. This minimum is not an ESS. It happens to be identical to the maximum of the fitness landscape. Here is an example.

Figure 1. With frequency dependence given in Equation (14), the ESS and maximum fitness solutions are different.

Example 2

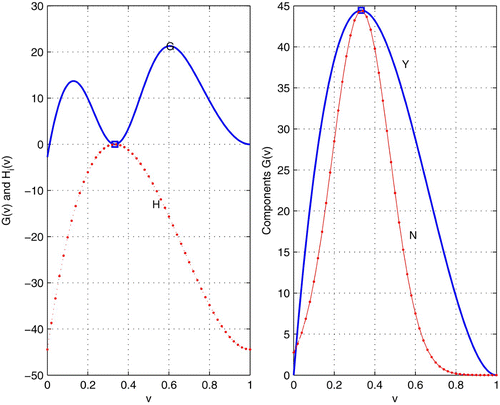
Let

where is given in Equation (10). For , we obtain Figure 2.

Figure 2. Left: local minimum on the adaptive landscape and maximum on the fitness landscape coincide. Right: Y as in Equation (13) and N as in Equation (15).

3.2. Future research

The G-function approach lends itself to interesting future research. Among others: (i) Replace Y in Equation (13) with a biologically motivated growth function. (ii) Are there interpretable relations between the maximum of G in the adaptive landscape, , and ? (iii) Similarly for and ? (iv) Are there relations between maximum G and maximum H based on (i) and (ii)? These derivatives may shed light on the requirements for minimum or maximum for G and H.

Casting the theory in stochastic framework will represent a significant progress.

4. Discussion

The ESS maximum principle is constructive with respect to the global maximum (G=0) and with respect to the size of the ESS coalition (number of species, n). Consequently, the maximum principle dictates species diversity at ESS in the evolutionary game. The crucial parameter in the models we use is the phenotypic plasticity with respect to carrying capacity; i.e., σ _k in Equation (7). The larger σ _k is, the larger the coalition. Local minima (as in Figure 2) shed light on speciation in the evolutionary game. An invading mutant, close to the minimum, breaks the local strategy that minimizes the value of the G-function in two and thereby causes two uphill climbing species.

Coexistence, adaptation and speciation remain fundamental research topics in biology. All three shed light on the complex nature of life. Some of this complexity (speciation, invasion, stability) can be illustrated with the G-function method. Fitness landscapes cannot reveal whether or not species can invade the system. Adaptive landscapes can.

There are situations where Darwinian dynamics ends at a minimum and optimal dynamics at a maximum where both coincide (Figure 2). This situation, where frequency dependence is not a factor, could serve as a model for the numerous cell types coexisting in complex organisms.

In some cases, where an ESS does not exist at equilibrium because the G-function is flat, an infinite number of species can be added to the system (via invasion or mutation). Such a case is not realistic. Here, the mean strategies carrying heritable variation may exhibit random walk (so much so, because there is no advantage among strategies) which represents genetic drift. In a game theoretic context, if the G-function has portions that are flat and portions that are not, drift combined with Darwinian dynamics can drive the system to maximal points in the G-function 14.

The journey from optimization, to game theory, to evolutionary game theory provides insights into the differences between optimal design and Darwinian evolution. In optimal design, individuals are not constrained by others. As soon as individuals become constrained by others (as is the case with frequency dependence), the evolutionary game takes over. Evolutionary dynamics can drive species to a stable maximum or minimum. However, if the maximum is not an ESS, novel strategies may evolve until the size of the ESS coalition is achieved. Such is the case at the minimum of the G-function.

The strength of the G-function approach to evolutionary game theory lies in its flexibility. The G-function provides potential explanations of phenomena such as unoccupied niches, limiting similarity, invasion, relative abundance 21, and the emergence of cancer 5. The $G$-function approach allows for modelling different biological communities with scalar strategies, vector strategies 2, multiple G-functions 1, multistage G-functions 12, and even intelligent design 14.

Finally, in the modelling of cell growth using evolutionary game methods, Gatenby and Vincent 5 discovered an underlying reason why the strategies used by cells are ‘cooperative’. This may be a situation where Darwinian evolution (under competition) and optimization (under cooperation) yield the same strategy. Unless carefully controlled (e.g. via DNA), a cooperative optimal strategy is subject to ‘cheating’. The onset of cancer appears to be associated with a breakdown in the optimal control structure which, consequently, allows for the coexistence of mutant cells. Also, mutant cells change their own local environment. Thus, Darwinian evolution of the mutant cells breaks the cooperative nature of the game. The mutant cells evolve to a destructive state that defines cancer that can lead to the destruction of the individual.

Additional information

Notes on contributors

Thomas L. Vincent

Unfinished manuscripts by the late T.L. Vincent, compiled and interpreted by T.L.S. Vincent.

Notes

Professor Vincent was fond of calling growth and decline rates Yin and Yang, respectively, reflecting the ancient Chinese philosophy of two primal opposing but complementary forces in all things in nature.

Strictly speaking, 𝒰 is dense.

The formal definition as given in 18 requires, in addition, that an ESS be convergent stable.

The frequency at which a given strategy is present in a population is proportional to the fraction of individuals using that strategy.