On the role of the degradation rates for the dominance of the fittest in Eigen's quasispecies model

Abstract

The existence of an error threshold of the mutation rate in Eigen's quasispecies model has been computationally demonstrated exclusively in the case when the degradation rates of all model genotypes are equal. Here we explore the case with different degradation rates and demonstrate examples for which the type that has highest fitness in the absence of mutation can preserve its dominance independently of the value of the mutation rate. The examples are formulated based on analysis of the equilibria at the two extreme mutation rate values and suggest absence of an error threshold in a number of cases, most prominently when the degradation rate of the wild type is much smaller that the degradation rates of the mutants.

Keywords:

• quasispecies
• viral evolution
• error threshold
• genotype dominance
• spectral abscissa
• quasi-positive matrix
• asymptotic stability

1. Introduction

RNA viruses exist as heterogeneous populations of diverse genotypes in cell culture experiments 40 41, within individual hosts 1 18 22 26 29 and in populations of hosts 21 32. The origin of this diversity is in the high frequency of mutation occurring during virus replication within the host cell. Indeed, it has been estimated that the mutation rate of RNA viruses, defined as the number of misincorporations per nucleotide copied, can be as high as 10⁻³ 8. Because RNA viral genomes vary in length between 10³ and 3.10⁴, the estimates of RNA viral mutation rate lead to the conclusion that during RNA genome replication very few progeny genomes escape mutation 11. A fraction of the mutant progeny is capable of repeating the replication and diversification rounds in millions of host cells, which leads to the formation of a heterogeneous population of viral genotypes, called quasispecies.

The concept of a viral quasispecies, defined as ‘a dynamic distribution of non-identical but closely related mutant and recombinant viral genomes subjected to genetic variation, competition and selection and which acts as a unit of selection’ 8 is currently relatively widely adopted within the virology community (7 9 23 25 30 33 34 40, among many others) to qualify the variability of genetic sequences corresponding to the same virus species.

It is remarkable that viral quasispecies theory originated from a mathematical model of self-replicating macromolecules with non-perfect fidelity of replication by Eigen and collaborators 12 14, which was not originally meant to model virus evolution. As such, the model is quite general and does not incorporate assumptions reflecting the specifics of RNA viral replication. Such specifics include the dependence of viral replication on the presence and quantity of viral polymerase and other virus encoded non-structural and structural proteins and the possible role of complementation and phenotypic mixing for maintaining the existence of mutants that would be otherwise unable to replicate.

One of the predictions of Eigen's model, the existence of the error threshold of the mutation rate, and specifically its application to virus evolution, has been an object of controversy. In the model, if the mutation rate is increased, initially the equilibrium frequency of the wild type – the one with the highest fitness value – decreases and the frequencies of the mutants increase. Above a certain value of the mutation rate – the error threshold – the original master sequence (the wild type) loses its dominance, becoming a very small fraction of the population and the quasispecies consists of a large number of genotypes in low concentrations. This was interpreted as information loss 13, and the conjecture that virus quasispecies exist near the error threshold was put forward. Assuming that there is no back mutation of the mutants to the original master sequence, Eigen and Schuster 14 calculated the approximate value of the error threshold as inversely proportional to the sequence length. The error threshold was demonstrated in computational experiments with Eigen's model by Swetina and Schuster 37 and later repeated by other authors 15 35 44.

Several authors express skepticism regarding the value and even the existence of the error threshold for viral quasispecies. Iranzo and Manrubia 20 point out that the quasispecies model does not take into account the large number of genotypes expressing the same phenotype; thus viral quasispecies would be expected to withstand significantly higher error thresholds 20. Cases-Gonzales et al. 6 suggest that with real viruses, a large expansion through sequence space cannot occur, and that the increase in error rate results in a decrease of specific infectivity, which can lead to the extinction of the population with modest expansion in sequence space. Based on a simpler model approximating Eigen's, Summers and Litwin 36 argue that the error threshold in Eigen's model exists only because of the unrealistic assumption that all mutant genotypes, different from the master sequence from which they originated, are able to replicate, no matter how many errors they contain compared to the master. Similarly, Belshaw et al. 2 consider a simple model approximating the behaviour of Eigen's system and demonstrate that (according to their model) the wild type sequence would lose dominance if the mutants can replicate but would not mutate back to the wild type. One can see easily (in this model) that if back mutation is allowed, this model 2 does not exhibit an error threshold.

It is important to note that all simulations exhibiting the error threshold (37 and later repeated by other authors 15 35 37 44) were done for single-peak fitness landscapes (where the wild type has the highest fitness and the rest of the genotypes have equal or lower fitness). However, since the dynamical properties of a model may differ for different model parameters, it is plausible to expect that if certain relations between the replication and degradation rates hold, the model wild type may not lose its dominance no matter how high the mutation rate becomes. Indeed, Wiehe 43 considered a simplification of Eigen's model and demonstrated that while the error threshold exists in a single-peak landscape, this is no longer true for other fitness landscapes.

However, simulations of the Eigen model demonstrating the error threshold 15 37 44 were done not only just for single-peaked landscapes but also exclusively for degradation rates that were equal among all genotypes, including the wild type. Similarly, most of the theoretical studies make the same assumption. It is reasonable to assume that well adapted virus genotypes would be more effective in disabling cellular mechanisms of antiviral defense, including RNA interference mechanisms for degrading genomic and mRNA [p.195; 42]17 27. Indeed, several authors reviewed in 38 provide evidence of fast virus adaptation to viral mRNA degradation by short interfering RNA exhibited by HIV 4 and by polio virus 18. Knipe et al. 24 find that temperature-sensitive VSV mutant proteins were degraded at a significantly higher rate than the wild type virus; Runkler et al. 31 show that single residue substitutions at a specific position of the M protein of measles virus that exist only in lab conditions have a higher degradation rate than the wild type and a similar mutant existing in nature. While it is also possible that some mutants may have lower degradation rates than the wild type, in general there is no reason to expect that all genotypes would have equal degradation rates.

Therefore, it would be instructive to explore how differing degradation rates and multi-peak fitness landscapes would affect the dominance of the wild type, and therefore, the existence of an error threshold, in Eigen's model. This paper provides analysis of the dependence of the equilibrium of Eigen's quasispecies model on the magnitude of the mutation rate with this goal in mind. We ask the question whether the wild type can remain dominant for all values of the mutation rate. To answer this question we analyse which is the highest sequence frequency when the mutation rate changes from 0 to 1. Mathematical analysis was possible only for small (approximately 0) and large (approximately 1) values of the mutation rate. One could argue that considering values of the mutation rate close to 1 lacks realism. The goal of the analysis for values of the mutation rate close to 1 is to gain insight about the movement of the quasispecies equilibrium in quasispecies space when the mutation rate increases. The equilibrium is a point in quasispecies space that lies on a curve, parameterized by the mutation rate parameter q and connecting, as we show, the unique stable equilibrium at q=0 and the unique stable equilibrium at q=1. It is conceivable that if we find the conditions on the Eigen model parameters for which the wild type is dominant for both low and high mutation rates, it might remain dominant for all values of the mutation rate and, therefore, preclude the existence of an error threshold. We do establish such conditions and further show, by computational experiments with Eigen's model, that this indeed is possible. Interestingly, our mathematical analysis shows that if the model parameters satisfied the conditions of the computational experiments published in 37 and others, i.e. if the degradation rates were equal and the fitness landscape had a single peak, the wild type cannot remain dominant for all values of the mutation rate. Furthermore, our analysis not only explains the computational observations in 37 but also derives the conditions under which, according to Eigen's model, a mutant genotype may emerge as dominant.

2. Methods, notations and definitions

The following represent a comprehensive list of notations and definitions used throughout the text.

q is the mutation rate, equal to the probability of one point mutation per one sequence replication; S _j is the binary (made of 0 and 1) ‘genotype’ sequence indexed j; n is the number of positions in a sequence; N is the number of all possible sequences of length n (N=2 ⁿ ); d(i, j) is the Hamming distance between S _j and S _i , i.e. the number of positions at which S _j and S _i differ.

Sequences S _i and S _j are called complementary if they differ in all positions (this means that if S _i has a 0 at some position, the complementary sequence has 1 at the same position); i.e. their Hamming distance is equal to n.

Q _ij is the probability of mutation of S _j into S _i during one sequence replication; Q _ii the fidelity of replication of S _i ; . We assume uniform per nucleotide mutation rate and independent events of point mutations. Then

Q=(Q _ij ) is the mutation probability matrix; A _i >0 is the replication rate of S _i ; , (diagonal matrix with elements A _i ) is the replication rate matrix; D _i is the degradation rate of S _i ; is the degradation rate matrix; A _i Q _ii −D _i is the fitness of S _i for a given fidelity of replication Q _ii <1; is the excess productivity of type i, also here called ‘nascent fitness’ (to distinguish from the fitness when replication is not perfect); is the nascent fitness matrix. By I _m we denote the identity m×m matrix.

In the proofs of the results below we use the well known concepts of local and global stability of an equilibrium of a dynamical system. We use the sufficient conditions that guarantee that an equilibrium is (i) locally asymptotically stable (l.a.s.) or (ii) unstable i.e. that the eigenvalues of the Jacobian of the system have, respectively (i) only negative, or (ii) at least one positive real part. To prove the existence of a continuous curve of equilibria we use the Implicit Function Theorem. In various parts of the proofs we use the following properties of quasi-positive matrices.

Definition. A square matrix M is called quasi-positive, if its off-diagonal elements are non-negative.

In particular, if a quasi-positive matrix has only positive off-diagonal entries, it is irreducible and has the properties described below.

Spectral property of irreducible quasi-positive matrices. If M is an irreducible quasi-positive matrix, it has a simple real eigenvalue s(M) such that for all other eigenvalues λ _i of M, and a positive eigenvector corresponding to s(M) such that any positive eigenvector of M is a multiple of . s(M) is called the spectral abscissa of M.

Majorization property of quasi-positive matrices. If M and L are quasi-positive matrices and M<L, then s(M)<s(L). Here the inequality M<L implies that each element of M is less or equal to the respective element of L and M ¬=L.

(ℳ) In particular, if L has positive off-diagonal entries, then M+L is irreducible. Thus, if M and L

are quasi-positive and L has positive off-diagonal entries and M<L, then s(M)<s(L).

These properties are easy corollaries of similar ones for non-negative matrices derived in 3.

2.1. The model

Eigen's quasispecies model has the form

where ˙ x denotes time derivative, is the average excess productivity, also equal to the average fitness in the absence of mutation (average nascent fitness) and the mutation probabilities are symmetric: Q _ij =Q _ji and satisfy the relation .

We note that if the initial conditions satisfy , then

(Indeed, this is easily seen by summing up all equations of the model: . Obviously and the same zero sum is valid for all higher derivatives of which implies , i.e. .)

Because of the relation (3), x _i (t) has the meaning of concentration or frequency of the genotype sequence S _i .

Further, if all sequences are capable of replication, i.e. A _i >0, for all i, and if the probabilities of mutation Q _ij are positive, Eigen's model (2) has a unique positive equilibrium (where is the frequency of S _j at equilibrium), that satisfies

This follows from the spectral property of the irreducible quasi-positive matrix ; is the positive vector belonging to satisfying the relation .

It is easy to see that all solutions of system (2) with initial conditions in R ⁿ ₊ remain in R ⁿ ₊, i.e. the model is well posed. In all considerations further we assume that .

Since the excess productivities F _i ≥0, then . This implies that the equilibrium is globally asymptotically stable (g.a.s.) in the positive cone R ^N ₊, i.e. all solutions of the model, with initial conditions in R ^N ₊, converge to . Indeed, if , i.e. f≡ 0, the system (2) is linear and can be solved directly for to see that . If , then the substitution transforms (2) into a linear system . It is then easy to show (as done in 15) that x _i (t) has the form

where and and B _i are constants and that , i.e. is g.a.s. in R ⁿ ₊.

Since we consider mutation probabilities Q _ij of the form (1), then the mutation probability matrix and the equilibrium are functions of the mutation rate . For 0<q<1, the mutation probability matrix Q(q) is a positive matrix. Therefore, exists, is unique and globally stable in R ₊ ^N for all q in the open interval (0, 1) and is the solution of

The Jacobian J of Equation (2) at has the form

where Φ is a matrix with elements .

In what follows, we assume without loss of generality that the nascent fitness of genotype S ₁ is the highest:

3. Results

3.1. A simple model with N=2

We first consider a case of Equation (2) with only two genotypes representing two sub-populations of the quasispecies: one with higher nascent fitness than the other. Apart from bringing new insight, this example will be helpful in analysing a more complex model with N>2. We assume again that S ₁ has higher nascent fitness than S ₂:

The quasispecies model then takes the form:

where and .

We shall prove the following result.

Theorem 3.1

Suppose that Equation (8) holds. Then the wild type remains dominant for all q∈(0, 1); i.e. for all q∈[0, 1] if and only if one of the following two conditions holds:

Comment. Before proceeding to the proof we note that while condition (8) guarantees that when the fidelity of replication is perfect (i.e. the mutation rate q=0) the sequence with the higher excess production rate (i.e. the wild type) will be dominant (this is proved for the general case in the next section), conditions (a) and (b), together with Equation (8), guarantee that the wild type is dominant for very high mutation rates (q≈ 1).

When conditions (8) and (a) are valid together, they imply that D ₂>D ₁, i.e. the mutant is degraded at a higher rate. When the mutation rate is very high, the replication of the mutant would contribute mostly to production of wild type and the wild type would contribute mostly to production of mutant; however the mutant would produce wild type at a higher rate (A ₂>A ₁) than the wild type would produce the mutant. However, this is not sufficient to ensure the dominance of wild type at high mutation rates; it is also necessary that the mutant is degraded faster than the wild type.

Conditions (8) and (b) imply again that D ₂>D ₁, i.e. the mutant is degraded at a higher rate. However, since the replication rate of the wild type is higher than the replication rate of the mutant, and thus, at high mutation rates the wild type would produce the mutant at a higher rate (A ₁>A ₂) than the mutant would produce wild type. To guarantee that the wild type will be dominant for high mutation rates, it now not sufficient that D ₂>D ₁, but it is necessary that the superiority of the mutant's degradation rate over the wild type's is higher than the superiority of the wild type's replication rate over the mutant's: .

In conclusion, as the theorem shows, the combination of condition (8) with either (a) or (b) guarantees that the wild type remains dominant independently of how large the mutation rate becomes, i.e. the fulfillment of these conditions precludes the existence of an error threshold.

Proof

We can write the equilibrium equation as

where

As and because L is quasi-positive, it follows from the spectral property (above) that is the unique eigenvector corresponding to s(L) and .

where . Therefore, and from which we obtain

Let us now find conditions (if any) for which , i.e. , for all q∈(0, 1). Using Equations (13) and (14) after simple but tedious algebraic calculations we obtain

Because of Equation (8), the latter inequality is possible for all q∈(0, 1) only if .

• (a) If , the latter is always true.

• [ (b) If A ₁−A ₂>0, the inequality is possible only if for all q∈(0, 1), which is valid if and only if which is equivalent to A ₁−A ₂>0 and .

Therefore, the wild type would remain dominant for all values of q∈(0, 1) if and only if or A ₁−A ₂>0 and .   ▪

3.2. General case

3.2.1. Analysis for q≈ 0

(a) In the absence of mutation (q=0) the wild type is the only one that persists.

If q=0, and the system can be written as

Theorem 3.2

If the equilibrium of Equation (16) is g.a.s. in R ⁿ ₊.

Proof

Obviously is an eigenvector of the eigenvalue F ₁ and an equilibrium of Equation (2). All other equilibria are unstable because the Jacobian at each such equilibrium always has the eigenvalue . Further, system (16) is equivalent to . Using this equality, and the following one:

we solve for f:

and take the limit at t→∞ to obtain

Therefore, it follows from Equation (16) that x _i (t)→0 for all i¬=1 and because of Equation (3), it follows that .   ▪

(b) For q>0 but close to 0, the equilibrium lies on a smooth curve starting at q=0

from . For small values of q the wild type frequency decreases but remains larger than the frequencies of the remaining types which increase.

Theorem 3.3

For q in some interval there exists a smooth (of class C ^∞) R ^N curve C ₀ parameterized by q, such that for q∈I ₀, the unique positive equilibrium of the system (16) lies on C ₀ and such that . In this interval the wild type frequency decreases and the frequencies of the remaining types decrease.

Proof

The existence of a smooth (of class C ^∞) R ^N function of q in an interval around 0 is easily established by the Implicit Function Theorem, keeping in mind that the Jacobian is non-singular at (1, 0, …, 0) and that Q _ij (q) are polynomials of q, i.e. infinitely differentiable. However, we need to verify that . This is easy to see by finding the derivatives of at q=0. Specifically, we find that

If d(1, j)=1, i.e. the sequence with index j is only one mutation away from the wild type:

For the sequences that are two mutations away from the wild type, i.e. d(1, j)=2:

while , and in general, if

while all lower derivatives are equal to 0. From the above inequalities we see that for small values of decreases when q increases () and for j>1, are increasing functions of q: , where k=d(1, j). Therefore, for small q>0 the continuation of and thus coincides with the unique positive equilibrium of Equation (16).

Obviously, as are continuous, it follows that in some interval , x ₁>x _i , i=2, …, N.   ▪

3.3. Analysis for q≈ 1

(a) For q=1 model (2) has a l.a.s. non-negative equilibrium which is an eigenvector to the spectral abscissa. When q=1, Q _ik =1 if d(i, k)=n (i.e. S _i and S _k are complementary) and Q _ik =0 otherwise. We rearrange the sequences S _i in the following way: the index of the wild type (with the largest nascent fitness) is 1 and the index of its complement is 2; next, we pick any sequence different from these two and give it an index 3 and give its complement sequence index 4, and continue in the same way, pairing complementary sequences. Then Q (1) A−D has the block diagonal form

where

and is a two-dimensional square zero matrix.

Note that since for each i, L _i are quasi-positive, they have two real eigenvalues, one of which is s(L _i ). Let k ₀ be the index for which has the largest spectral abscissa: . Obviously .

Theorem 3.4

Let q=1. Then has a non-negative eigenvector belonging to s(QA−D) which is an l.a.s. equilibrium of Equation (2).

Proof

We first consider the case when has multiplicity 1, i.e. we assume that

In this case has a unique eigenvector such that ζ _i =0, for or 2k ₀ and solve the system

Here is the positive eigenvector of , corresponding to such that ζ_2k0−1+ζ_2k0 =1. We also recall that . The Jacobian (6) at is a block diagonal matrix where

and

Since , then and . Therefore, is a quasi-positive matrix and . Therefore .

Further, for i¬=k ₀, . This proves the local asymptotic stability of ζ.

In the case when has multiplicity m>1, let be those for which and let be their positive 2×2 eigenvectors. Then the vector with coordinates and zeros otherwise is an eigenvector of . Using a method similar to the above, we can see that the Jacobian at Equation (6) satisfies , i.e. is l.a.s.   ▪

(b) For q<1 but close to 1, the positive equilibrium of Equation (2) lies on a smooth curve starting at q=1 from the unique l.a.s. equilibrium .

Theorem 3.5

For q in some interval there exists a smooth (of class C ^∞) R ^N curve C ₁ parameterized by q, such that for q∈I ₁, the unique positive equilibrium of the system (16) lies on C ₁ and .

Proof

The existence of C ₁ is guaranteed by the Implicit Function Theorem because the eigenvalues of the Jacobian of Equation (2) at lie in the left half of the complex plane, i.e. the Jacobian is non-singular. The C ^∞ smoothness follows from the fact that Q _ij are polynomials of q, i.e. infinitely differentiable. Let us assume that the curve is defined by the R ^N function ξ(q). We need only show that for q sufficiently close to 1. Because the non-zero coordinates of are between 0 and 1, we need only show that if ζ _i =0, then for q≈ 1. We show this by finding the derivatives of ξ _i with respect to q.

Without loss of generality, let ξ _i =0, for i=2l−1 for some l. Then ξ_2l =0 as well since this is the frequency of the complementary sequence with index 2l−1. Differentiating the right-hand side of Equation (2) with respect to q, we obtain for p=2l−1 and p=2l:

We next note that for q=1: Q _{p, j} =1, if d(p, j)=n and 0 otherwise, and

Using these, we get the following equations for

The sum at the right is either 0 or less than 0, when keeping in mind Equation (28) and the form og . If it is less than zero, we note that the matrix is an M-matrix and thus, its inverse is positive. \noindent It follows that is a negative vector. If the sum at the right in Equation (29) is zero, we consider the second and further derivatives, as was done for the case q=0 in the previous sub-section. We find that eventually the higher order derivatives are negative.   ▪

3.4. For q ∈[0, 1] the positive equilibria lie on a smooth curve connecting (1, …, 0)^T and the l.a.s. equilibrium ζ

Theorem 3.6

defines a smooth curve (of class C ^∞) C in R ^N .

Proof

is the eigenvector of Q(q)A−D belonging to the spectral abscissa . Note that for q∈(0, 1), Q(q) is a positive matrix, i.e. is irreducible and quasi-positive.

• (a) We first note that since s*(q) is a simple root of the characteristic polynomial , it is a smooth (of class C ^∞) function of q. (This follows easily from the Implicit Function Theorem and is a well known result.)

• [ (b) Further, let us represent as

  where and as
  where B is an quasi-positive matrix.

Therefore, if was invertible, would be a smooth (C ^∞) function of q determined from

To complete the proof we will show that is invertible. Let

Obviously Z(q) is a quasi-positive matrix, and is an irreducible quasi-positive matrix. From the Majorization property (Section 2) it follows that . Therefore

Therefore, is invertible.   ▪

We have also proved that for q≈ 0 and for q≈ 1 there exist curves C ₀ and C ₁ starting, respectively, from the l.a.s. equilibria , for q=0 and ζ, for q=1 and containing the positive equilibria. As we know, for each q∈(0, 1), is unique. Therefore, for q∈(0, 1) C ₀ and C ₁ coincide with C. Thus, C has endpoints at , for q=0 and ζ, for q=1.

3.5. Explicit relations between replication and degradation rates to infer the dominant sequence at high mutation rates

If we assume that is a simple eigenvalue, then for q=1, the larger of the two positive coordinates or is the dominant frequency. If k ₀=1, then either the wild type or its complement is dominant at q=1. Using Theorem 3.1 we can discriminate between these two possibilities. This implies the following result.

Theorem 3.7

Let the sequences comprising the quasispecies be indexed as described in the beginning of Section 3.3 and the conditions, used throughout the paper

be satisfied.

• (i) If the following condition holds,

  then the wild type is dominant for high mutation rates if and only if

• (ii) If (c) is true, but instead of (d), its negation is true: A ₁−A ₂>0 and the complement sequence of the wild type is dominant for high mutation rates.

• (iii) If (c) is not fulfilled, neither the wild type nor its complement will be dominant for high mutation rates (q ≈ 1). Then for the index k ₀>1 satisfying (23), one of the sequences or will be dominant for high mutation rates. Namely, if, for example, and either or and then is dominant for q≈ 1.

Comment. When the mutation rate is very high, each sequence mutates with high probability into its complementary sequence and with very low probability into any other sequence. As seen from the analysis in Theorem 3.4, at very high mutation rates the couple sequence S _2l−1 – complement S _2l , which has the highest average fitness wins the competition and dominates the quasispecies. Thus, condition (c) guarantees that at very high mutation rates the couple of the wild type and its complement dominates the quasispecies population if it has the highest average fitness. In addition, at high mutation rates, the wild type will dominate its complement if and only if (see comments after Theorem 3.1) the degradation rate of the complement is sufficiently higher than the wild type's one.

Note. If D _i =D (uniform degradation rates) and A ₁>A _i , i>1 (single-peak fitness landscape), as assumed in 15 37 44, the model satisfies the conditions (ii) of Theorem 3.7.

3.6. Necessary conditions for the dominance of the wild type

Obviously, the validity of (a), (b), (c) and (d) implies that the curve of equilibria ends at a point with . If we consider separately the curves , the fulfillment of (a)–(d) is a necessary (but not sufficient) condition for the curve x ₁(q) to be located entirely above any of the other curves x _i (q), i.e. for the frequency of the wild type to be higher than any other frequencies, for all q, i.e. the wild type to retain its dominance independently of the value of the mutation rate. If (c) or (d) do not hold, the wild type will lose dominance for some value of the mutation rate when it increases from 0. Conditions (a)–(d) could also be sufficient for dominance of the wild type throughout the mutation rate range in some cases. Indeed, in Examples 1 and 2 below, we demonstrate that the fulfillment of (a)–(d) can guarantee dominance of the wild type for all mutation rate values. Further, Example 3 demonstrates the emergence of a new dominant type because of the violation of condition (c).

3.7. Examples

We constructed examples to demonstrate the preservation of the wild type dominance over the full range of variation of the mutation rate from 0 to 1, as well as cases when the wild type loses dominance, as predicted by the theory developed in the previous section. The quasispecies model with mutation probability matrix Q as defined in Section 2 and parameter values given below was solved using Matlab on a sufficiently long time interval so that at the end of the interval the solution was in the vicinity of the equilibrium point and did not change up to the 16th digit. The value of the mutation rate q was varied from 0.01 to 0.99 and the equilibrium concentrations for each q were plotted. The parameters of the three examples are presented in Table 1.

Table 1. Parameters used in the numerical examples.

Example	n	N	Values of	Values of
1	2	4	2, 1.4, 1.5, 1.8	0.1, 1.3, 1.3, 1.5
2	4	16	2, 0.5, 1.9, 1.8, 1.8, 1.7, 1.9, 1.7, 1.7, 1.65, 1.95, 1.9, 1.65, 1.8, 1.8, 1.9	1, 0.4, 1.8, 1.75, 1.7, 1.6, 1.85, 1.6, 1.6, 1.6, 1.85, 1.85, 1.6, 1.75, 1, 1
3	4	16	2, 0.05, 1.9, 1.8, 1.8, 1.7, 1.9, 1.7, 1.7, 1.65, 1.95, 1.9, 1.65, 1.8, 1.8, 1.9	1, 0.01, 1.8, 1.75, 1.7, 1.6, 1.85, 1.6, 1.6, 1.6, 1.85, 1.85, 1.6, 1.75, 1, 1

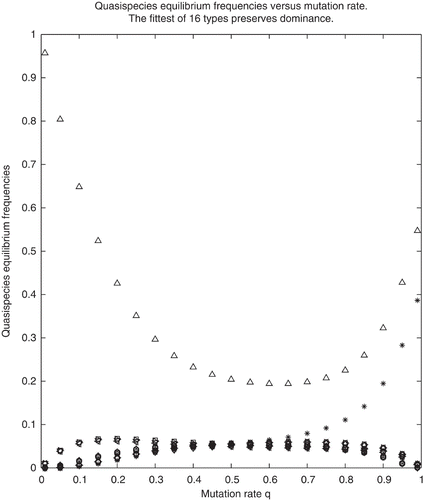
In Examples 1 and 2 the parameters were chosen so that the conditions (a)–(d) of Theorem 3.7 are fulfilled. Indeed, in Example 1, conditions (a), (b) and (d) are obviously fulfilled and and . Based on Theorem 3.7, it is expected that for Example 1, and for q≈ 1, i.e. . As seen on Figure 1, not only is this true, but the wild type remains dominant for all values of the mutation rate q. Similarly, in Example 2, (a), (b) and (d) hold and s(L ₁) is the largest spectral abscissa and not only it is true that for q ≈ 1 but this relation holds for all values of q∈(0, 1) as is seen on Figure 2.

Figure 1. Equilibrium concentrations calculated for Example 1. ‘ Δ′→x ₁, ‘ *′→x ₂, ‘+′→x ₃, ‘·′→x ₄.

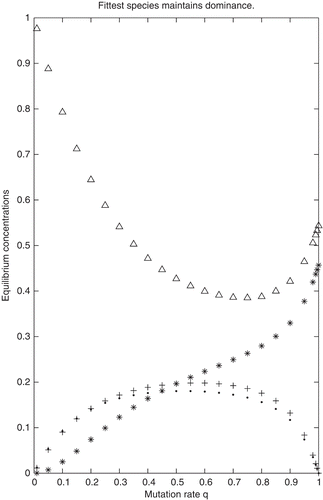
Figure 2. Equilibrium concentrations calculated for Example 2. ‘ Δ′→x ₁, ‘ *′→x ₂, the complement of the wild type. The wild type remains dominant for all values of q. All other 14 frequencies are represented with various symbols that overlap on the plot.

In Example 3 we chose the parameters so that condition (c) of Theorem 3.7 is not fulfilled. Specifically, while s(L ₈) is the largest of all s(L _i ) and equal to 0.8493. As expected from Theorem 3.7, S ₁₅ and S ₁₆ are the dominant sequences for q≈ 1. (Figure 3). The wild type (depicted by triangle symbols) loses dominance for and never regains it.

Figure 3. Equilibrium concentrations calculated for Example 3. ‘ Δ′→x ₁, ‘ *′→x ₂, the complement of the wild type, ‘ °′→x ₁₅, ‘ ⋄′→x ₁₆. The wild type loses dominance for all values of q. All other 14 frequencies are represented with various symbols that overlap on the plot.

4. Discussion

The role of the degradation rates in the quasispecies model has been neglected in the literature. As mentioned in Section 1, the usual assumption has been that the degradation rates of all model genotypes are equal. However, this assumption implies that the relation between the fitnesses of any two sequences remains the same when the mutation rate changes. Indeed, if the nascent fitness (or, excess production rate) F ₁ of sequence S ₁ (the wild type) is higher than the nascent fitness F ₂ of another sequence S ₂ (the mutant), but their degradation rates are equal: (A ₁−D>A ₂−D), this same relation is preserved for any value of the mutation rate: (since according to the model, the fidelity of replication has the same dependency on the mutation rate for all sequences: ). In addition, such an assumption also implies that genotypes with higher fitness also have higher replication rate: . However, if the rates of degradation of the wild type and the mutant differ, these implications may no longer be valid. First, the fact that the wild type has higher nascent fitness no longer implies that it has a higher replication rate. Second, since an increase in the mutation rate leads to a decrease in the fidelity of replication but has no effect on the rate of degradation, the fitness of the wild type may become lower than the fitness of the mutant when the fidelity of replication goes down. Thus, the concept of fitness is dependent on the value of the mutation rate. To differentiate between the case with no mutation and the one with mutation, we introduced the term nascent fitness.

Our study demonstrates that, according to the quasispecies model, when all genotype degradation rates are assumed equal, the wild type always loses dominance, since this assumption leads to the violation of condition (d) of Theorem 3.7. Specifically, for a single-peak fitness landscape (), conditions (a)–(c) of Theorem 3.7 are valid but condition (d) is violated and the wild types loses its dominance to its complement for some value of the mutation rate q. Further, for equal degradation rates and a multiple-peak fitness landscape, any model genotype S _k , k=2i or 2i−1 satisfying the relation will eventually become dominant above some value of the mutation rate. Finally, if the degradation rate of the wild S ₁ type is sufficiently higher than the degradation rate of another sequence S _i , so that condition (c) is violated, S _i will eventually become the dominant sequence. However, if the degradation rate of the wild type is sufficiently lower that the degradation rates of all other sequences so that (c) and (d) hold, the wild type might remain dominant for all values of the mutation rate, as exemplified in Examples 1 and 2.

We note that the use of the terms model genotype or sequence emphasizes the fact that the results and conclusions refer to the outcomes of Eigen's model. Indeed, the existence and even dominance of the complementary sequence of a given sequence is improbable in the case of a viral quasispecies.

Our computational examples based on the theoretical analysis for the extreme values of the mutation rate demonstrate the possibility that the error threshold may not exist when the degradation rates are not uniformly equal. Notably, if the degradation rate of the wild type is much smaller than the degradation rates of the mutants, it is easy to formulate examples where the wild type retains its dominance. This is yet another piece of evidence that, apart from the references mentioned in the Introduction, that the error threshold may not necessarily exist.

Viral quasispecies possess enormous plasticity that may enable them to avoid phenomena like the error catastrophe. Experiments with ribavirin that were meant to demonstrate the existence of the error threshold in poliovirus 7 showed that the increase in mutation rate caused by the drug was accompanied by a steep decrease in infectivity. This was interpreted as the virus having passed the error threshold. However it was later shown that poliovirus developed resistance to ribavirin enabled by the emergence of a genotype coding for a polymerase with increased fidelity, which narrowed down the quasispecies diversity 28 39. The propensity for poliovirus to adapt and avoid error catastrophe cannot be predicted by the quasispecies model because it does take into account the complexity of the virus replication mechanism.

We note that the error threshold as a concept is not well understood and is frequently mistaken for the extinction threshold, both in theory 20 35 36 42 and experiment 10 39. The conceptual difference between error threshold and extinction threshold was made clear in 5 and recently reiterated by Holmes 19. Extinction threshold is a term used to explain an abrupt change in density or number of a population brought on by changes in important parameters, such as habitat loss or increased death rate due to various factors (e.g. human factors, disease). Whereas Eigen's model can demonstrate the existence of an error threshold, it does not support the existence of an extinction threshold. The mathematical structure of Eigen's model is such that for each set of parameters there is only one equilibrium, which is strictly positive and globally stable. This means that independently of the initial genotype frequencies, the quasispecies population converges with time to an equilibrium in which each of the genotypes is present. Therefore, in Eigen's model the quasispecies does not have an extinction threshold.

In conclusion, we believe that while indeed, RNA viruses exist as a quasispecies (as defined in Section 1), viral quasispecies theory is in need of further development. Viral quasispecies models should include more realism, both in the representation of the genome sequences (note that in the current paper we have restricted the analysis to binary sequences) and in reflecting the intricate mechanisms of viral replication and adaptation.

Acknowledgements

This work was performed partially under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. The work was supported by an LLNL–LLNS internally funded grant to T.K. and C.Z. through the Laboratory Directed Research and Development program. T.K.’s research was also funded by NSF. Any opinion, finding, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation. The authors express gratitude to Professor Raul Andino (UCSF) for many insightful discussions of the quasispecies phenomenon, which helped in understanding the limitations of the quasispecies model. Last but not least, the authors are deeply thankful for the thoughtful criticisms of an anonymous reviewer which significantly improved the paper.