Effect of resource subsidies on predator–prey population dynamics: a mathematical model

Abstract

The influence of a resource subsidy on predator–prey interactions is examined using a mathematical model. The model arises from the study of a biological system involving arctic foxes (predator), lemmings (prey), and seal carcasses (subsidy). In one version of the model, the predator, prey and subsidy all occur in the same location; in a second version, the predator moves between two patches, one containing only the prey and the other containing only the subsidy. Criteria for feasibility and stability of the different equilibrium states are studied both analytically and numerically. At small subsidy input rates, there is a minimum prey carrying capacity needed to support both predator and prey. At intermediate subsidy input rates, the predator and prey can always coexist. At high subsidy input rates, the prey cannot persist even at high carrying capacities. As predator movement increases, the dynamic stability of the predator–prey-subsidy interactions also increases.

Keywords:

• predator–prey
• resource subsidy
• population dynamics
• patch model
• stable equilibrium
• arctic fox

1. Introduction

Sustained temporal fluctuations in natural population densities are common 59, and predator–prey systems in particular are often noted for their oscillations 34 39 61. Murdoch 41 suggested that such interactions can be stabilized when predators are able to switch from a preferred prey that is rare to alternatives that are more common 10. Early mathematical modelling of communities involving one predator feeding on multiple prey species produced theoretical evidence validating this conjecture 11 42, and the resulting predator-mediated interaction was soon identified as apparent competition between the prey because their common predator can potentially increase numerically when feeding on either species 24. Whether this interaction must always be negative to both prey species has been a source of intense research for three decades 2 60. Indeed, when one predator consumes two nutritionally substitutable and self-reproducing (i.e. logistic-type) prey species, then in some cases, the prey may benefit from the interaction (apparent mutualism) 4. The properties and shapes of predator functional and numerical responses may be predictors for the kind of apparent interaction observed 7.

For predator–prey systems that are dynamically unstable, the indirect effects of a second resource are often different from those predicted by equilibrium dynamics 6 7 46. Adaption of predator behaviours, such as consumption rate constants and relative time spent in searching in distinct patches, can hinder predators from achieving an ideal free distribution and may instead promote oscillation or even chaos 3. An alternative prey available at constant density can have both stabilizing and destabilizing effects on predator–prey dynamics 9 32 56. In unstable systems, a predator's ability to adapt its attack rate can be either beneficial or harmful to a prey species when it is at low density 5. For a predator having fixed fractional population abundances in two different patches, switching food sources can destabilize dynamics and, in some cases, cause chaotic dynamics to occur at sufficiently high prey carrying capacities 33. Oscillation can also occur due to a Hopf bifurcation when predators switch because of group defense in prey 31 40.

Many empirical studies suggest that the introduction of allochthonous resources (or resource subsidies) may disrupt otherwise stable food web linkages 12 20 22. Such knowledge is particularly important for resource management purposes; for example, reintroduced wolves in Yellowstone Park will switch to bison when their preferred ungulate prey, namely elk, are rare 16. In a theoretical study, seasonal subsidies can stabilize a consumer–resource relationship when external subsidy inputs complement the availability of in situ resources through time 57. The persistence of a predator whose dynamics are slow relative to a preferred prey species having fast dynamics and a constant resource subsidy (i.e. one having infinitely fast dynamics) can be threatened, for a short time only, by rare subsidies but never by more common ones 48. The timing of subsidy availability in part of a habitat can result in mixed (i.e. positive and negative) indirect effects on an in situ resource that occurs throughout the habitat 58. Allochthonous inputs can also have striking effects on larger food webs 13 28 29.

Holt, in studying a model involving a predator that can move between a patch containing prey and a second prey-free patch, notes that ‘passive dispersal can stabilize an otherwise unstable predator–prey interaction’ 26. The results remains true when logistic-type prey occur in both patches 27, although if the movement rate is very small, then the effect may be destabilizing 36. Still, non-diffusive movement (caused, e.g. by prey-handling time effects) can by itself generate oscillation 1 27. The rapid evolution of migration probabilities can also produce non-equilibrium dynamics 62.

In this paper, we examine a series of predator–prey models in which the predator can also consume a non-living resource subsidy. Our motivating example shall be that of the predation of arctic foxes (Alopex lagopus) on lemmings (Cricetidae family). In coastal habitats, arctic foxes are believed to partially subsist in the winter on both the local lemming population and a resource subsidy, namely seal (Phocidae family) carcasses, which are provided by polar bear (Ursus maritimus) predation on the sea ice 52. Our primary interest is to determine situations in which dynamical stability and instability occur so as to understand more fully how resource subsidies may impact predators and their prey.

We begin in Section 2 by examining two differential equation models for the interactions between a predator species (e.g. arctic foxes) and either a prey species (e.g. lemmings) or a donor-controlled resource subsidy (e.g. seal carcasses). In Section 3, we study a model that includes all three components (predator, prey, and subsidy) in a single spatial location. We then study in Section 4 a spatial model in which the predator must move between two separate locations, one containing the prey species and the other containing the resource subsidy. The different predictions made by these models, as well as their biological implications, are considered in Section 5. In Section 6, we extend the model to include seasonal and long-term variations in subsidy amount, as well as spatial separation between prey and subsidy. We also relate our results to the original arctic system and make some additional conclusions.

2. A pair of elementary models

Before introducing either three-species model in full, we mention first some properties possessed by two relevant sub-models.

2.1. Predator and prey system

Let x(t) and y(t) be the population size of a prey and predator species, respectively, at time t≥0, and suppose that these functions obey the Gause-type model 17

where r is the intrinsic growth rate of the prey, k is its carrying capacity, θ is the maximum rate at which predators can consume prey, a is a half-saturation constant, ε is a conversion factor, and δ is the mortality rate for the predator. It is assumed that all constants are positive, that ε is no greater than unity, and that x(0)>0 and y(0)>0. In addition, we assume that so that the predator's per-capita growth rate is positive for sufficiently large values of x.

We can predict the kind of ecological outcome that will occur by defining two critical values of k. Toward this end, let

and observe that (in fact, ). It is well-known that if then the prey always approaches its carrying capacity (x→k) and the predator becomes extinct (y→0) (Exercise 4.4.1 in 23). However, if , then both prey and predator population sizes approach unique positive equilibrium values (x→x* and y→y*) (Theorem 4.4.3 in 23), and if k>[ktilde] then the predator and prey population sizes oscillate towards a single stable limit cycle 35. These results are summarized in Table 1 and Figure 1(a). In view of the remarks above, represents the prey population abundance that results in zero predator growth. The destabilization of the positive equilibrium due to an increase in the carrying capacity k beyond [ktilde] is commonly referred to as the paradox of enrichment 18 19 39 51 54.

Figure 1. Outcome of (a) the predator–prey model (I) for different carrying capacities k and (b) the predator-subsidy model (II) for different subsidy input rates i.

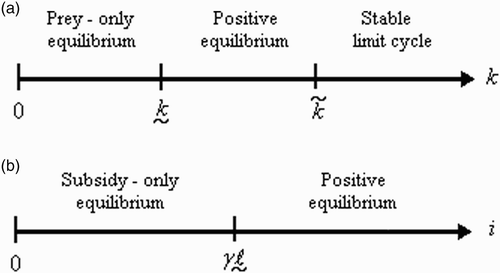
Table 1. Equilibrium properties of the predator–prey model (I).

Equilibrium	x*	y*	Feasible	Stable (when feasible)
Trivial	0	0	Always	Never
Prey-only	k	0	Always
Positive
^aA stable limit cycle occurs when k>[ktilde].

2.2. Predator and subsidy system

Let s(t) be the amount of a donor-controlled resource subsidy, and y(t) be the population size of a species that consumes the subsidy (henceforth known simply as predator), at time t≥0. Suppose that these functions obey

where i is the rate at which the subsidy appears, γ is the rate at which it disappears or otherwise becomes inedible, ψ is the maximum rate at which predators can exploit the subsidy, c is a half-saturation constant, η is a conversion factor, and δ is the mortality rate for the predator. It is assumed that all constants are positive, that η is no greater than unity, and that s(0)>0 and y(0)>0. As before, we assume that so that the predator's per-capita growth rate is positive for sufficiently large values of s.

We can distinguish cases in which the predator persists from those in which it does not by defining

The quantity has a role here similar to the one played by before (it is the subsidy amount needed for zero predator growth). If then the subsidy amount always approaches its natural value and the predator becomes extinct (y→0). However, if , then both subsidy amount and predator population size approach unique positive equilibrium values (s→s* and y→y*). A proof of this latter result appears in the appendix.

The equilibrium properties of model (II) are summarized in Table 2 and Figure 1(b) portrays the behaviour of the model for different values of the subsidy input rate i.

Table 2. Equilibrium properties of the predator-subsidy model (II).

Equilibrium	s*	y*	Feasible	Stable (when feasible)
Subsidy-only	i/γ	0	Always
Positive				Always

3. Predator and prey system with a non-spatial subsidy

Suppose that the prey and subsidy described above occur in the same habitat, and that they are both exploited by a single generalist predator according to the following equations

All assumptions on the parameters remain the same, the half-saturation constant e is assumed to be positive, and x(0)>0, s(0)>0, and y(0)>0.

Since the form of the predator's functional response allows it to become satiated on a combination of prey and subsidy, we assume that either or (otherwise, the predator's per-capita growth rate is always negative). From a biological standpoint, it is sensible to restrict attention further to nutrient-rich prey and subsidy, so that the predator can subsist on either resource when it is in unlimited supply. Our interest then is to understand predator strategy for situations in which prey and subsidy abundances are both limited. In view of the preceding remarks, we now assume that both and .

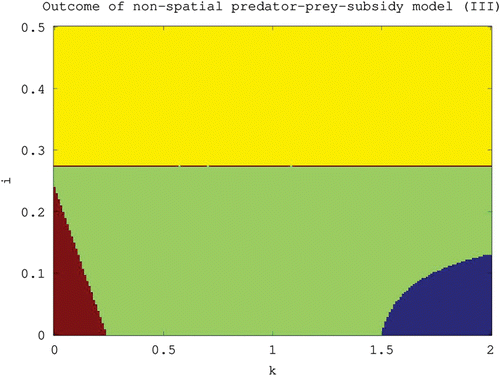
It can be seen in Figure 2 that several different outcomes are possible, including (i) a predator-free equilibrium, (ii) a prey-free equilibrium, (iii) an equilibrium in which the predator, prey, and subsidy coexist, and (iv) coexistence under stable limit cycles. Our goal is to distinguish situations in which these different outcomes occur, and to understand the influence of parameter values on these outcomes.

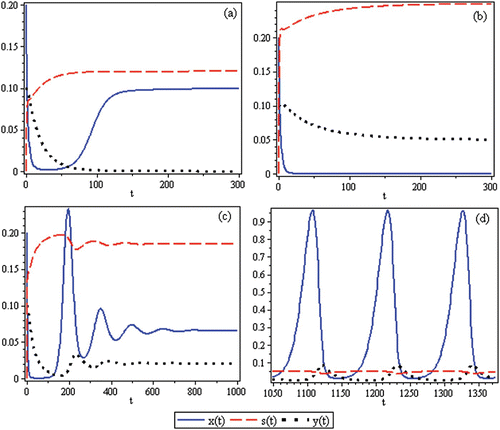
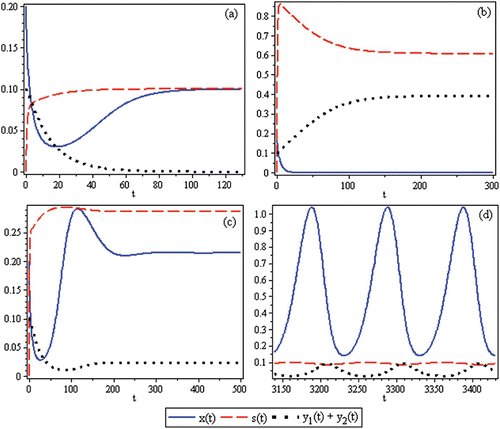
Figure 2. Time-series for the non-spatial predator–prey-subsidy model (III) with the following parameter values: r=0.1, θ=5, e=1, γ=1, ψ=5, ε=0.1, η=0.1, and δ=0.1. In (a) the prey population size approaches a positive equilibrium value, the subsidy amount approaches its natural value, and the predator becomes extinct (k=0.1 and i=0.12). In (b) the prey becomes extinct, the subsidy amount approaches its natural value, and the predator population size approaches a positive equilibrium value (k=0.1 and i=0.3). In (c) the predator and prey population sizes approach positive equilibrium values and the subsidy amount approaches its natural value (k=0.4 and i=0.2). In (d) the predator, prey, and subsidy all persist in a stable limit cycle (k=2 and i=0.05). In all figures, x(0)=0.2, y(0)=0.1, s(0)=0, k =0.25, and ℓ=0.25.

The complete system possesses several equilibrium states (Table 3). Their local stability is determined by the eigenvalues of the Jacobian matrix

Here, we define . Observe that although the parameter i does not appear explicitly in the expression for J, it may appear implicitly via the equilibrium states.

Table 3. Equilibrium properties of the predator–prey-subsidy model (III).

Equilibrium	x*	s*	y*	Feasible	Stable (when feasible)
Subsidy-only	0	i/γ	0	Always	Never
Predator-free	k	i/γ	0	Always	and i<i *(k)
Prey-free	0				i>i*
Positive	x*	s*	y*	and	Always^a
				and i<i*	Always^a
				k>[ktilde] and i<i*
Note: The quantities k , , i *(k), and i* are defined in Equations (2), (4), and (6).
^aConjecture.
^bLimit cycles (or other non-equilibrium dynamics) are conjectured to occur when i<i **(k).

3.1. Subsidy-only equilibrium

At the subsidy-only equilibrium , the Jacobian matrix

is block diagonal. Since J has at least one eigenvalue with positive real part (r>0), the equilibrium is never stable.

3.2. Predator-free equilibrium

At the predator-free equilibrium , the associated Jacobian matrix

is triangular. Its eigenvalues (which lie on the diagonal) are all negative provided that

In a manner similar to before, let us define

It follows then that the equilibrium is stable if and only if

Defining a new parametric function

the results above can be stated as follows.

Theorem 1 (Predator-free equilibrium)

The predator-free equilibrium is stable if and only if and i<i _*(k).

The case in which a predator-free equilibrium is stable is represented in Figure 2(a).

3.3. Prey-free equilibrium

A prey-free equilibrium exists and is unique when , and so we now assume this to be the case. The corresponding Jacobian matrix

is block triangular and has the same eigenvalues as its diagonal blocks. The fact that J ₃₃=0 is obtained from setting dy/dt=0 with x*=0 and y*>0. Observe that J ₁₁<0 when , and this occurs when

Here, we used the fact that J ₃₃=0. Hence the eigenvalues of the lower block (say, λ and μ) satisfy

It is clear that the sum is always negative and the product is always positive. Therefore, the equilibrium is stable if and only if condition (5) is satisfied. Equivalently, if we let

then we have the following result.

Theorem 2 (Prey-free equilibrium)

A prey-free equilibrium exists if and only if and is stable if and only if i>i*. When the equilibrium exists, it is unique.

The situation in which a prey-free equilibrium is stable is illustrated in Figure 2(b).

3.4. Positive equilibrium

We now turn to equilibrium states , which are positive in each component. These states satisfy

Theorem 3 (Existence and uniqueness of positive equilibrium)

A positive equilibrium (𝒫) for system (III) exists under the following conditions:

	(a) If then 𝒫 exists .
	(b) If then 𝒫 exists ⇔ i<i*.

Furthermore, when 𝒫 exists then it is unique.

Proof

First, we examine conditions under which one or more positive equilibrium states are feasible. It is clear from Equation (7a) that y* can be expressed in terms of x* and s*,

The relation above and Equation (7b) together imply that

from which it follows that x* can itself be expressed in terms of s*,

Based on Equations (8) and (9), a necessary and sufficient condition for to be positive is that

Unfortunately, there is no easy way to determine whether the inequality in Equation (10) is satisfied without computing s* explicitly. To this end, Equation (7c) implies that

With k and defined as in Equation (2), we obtain

Substituting x* in Equation (9) into this equation and then multiplying both sides by s* yields

Hence, s* satisfies a quadratic equation of the form

where

Applying the quadratic formula, the feasibility condition (10) can now be expressed in terms of model parameters alone.

We now obtain a complete description of when 𝒫 exists and whether it is unique. Let

denote the upper and lower solutions of Equation (13), respectively. As and , we have A>0>C and where

There are several cases depending on the relative magnitudes of k, k*, and k .

	(i) Suppose first that , so that B>0. Treating and as functions of i, we have , and at i=0. Among the coefficients appearing in Equation (13), only C depends on i and it does so proportionally. Since B 2−4 A C is a continuous and increasing function of i, it follows that is also a continuous and increasing function of i and that remains negative (and is therefore extraneous). At i=0 it can be shown that Since is increasing and concave downwards, it follows that satisfies Equation (10) along an open interval of i-values whose left endpoint is i=0 and whose right endpoint occurs when . Noticing from Equations (12) and (6) that at i=i* and , we obtain that Equation (10) is satisfied only for 0<i<i*.
	(ii) Suppose next that , in which case we still have B>0. Then the same argument holds except that at i=0. This time, satisfies Equation (10) along an open interval of i-values whose left endpoint occurs when (the right endpoint is the same as before). It can be seen from Equations (12) and (4) that at i=i *(k) and . Therefore, Equation (10) is satisfied only when .
	(iii) Finally, suppose that k<k* (i.e. B<0). Similar arguments establish that is continuous, increasing, and concave downward except that now at i=0. Again, is non-positive and therefore extraneous. As with the previous case, satisfies Equation (10) only for .

  ▪

In deriving conditions for the existence and uniqueness of 𝒫, it was necessary to discern the behaviour of s* as a function of i. Specifically, we found that

•	s* is increasing and concave downward
•	s*(i=0)>0 when k<k* and s*(i=0)=0 when k>k*
•	when
•	.

We now consider the behaviour of x* and y* as functions of i. First, it is clear from Equations (9) and (11) that

•	x* is decreasing and concave upward
•	when k<k* and when k>k*
•	when
•	.

Next, we see from Equation (8) that

•	y*>0 when s*>0 and 0<x*<k
•	y* (i=0)<0 when and y* (i=0)>0 when
•	when
•	.

We now have a complete description of how the components of 𝒫 depend on the parameter i. It remains to study the stability of 𝒫, for which our analytical results are only partial. We begin by considering different elements of the Jacobian in Equation (1). Observe from Equation (8) that

In view of this calculation and Equation (11), define

It follows then that J ₁₁<0 when and J ₁₁>0 when . Next, we obtain from Equation (7c) that

and that . A similar argument shows that and . Finally

again by Equation (7c). Consequently, the Jacobian in Equation (1) has a sign pattern

A necessary condition for J to be stable is if its characteristic polynomial has positive coefficients. These coefficients are

When then

To prove that J is stable, it remains to show that the Routh–Hurwitz condition is also satisfied 15 (notice that if the Routh–Hurwitz condition is satisfied then we also obtain ω₂>0). Unfortunately, determining analytically whether holds based strictly on a knowledge of parameter values alone appears to be a difficult problem. The situation when is even more complicated because in that case the signs of ω₁ and ω₃ cannot be obtained by inspection alone.

Thus, our results in this direction are based partly on numerical evidence. We conjecture the following statement.

Conjecture 1 (Stability of positive equilibrium) There exists a bifurcation function i _**(k) defined for k>[ktilde] (with e in place of a) such that

	(a) i **(k) is continuous, increasing, and concave downward
	(b)  and
	(c) if k<[ktilde] then 𝒫 is stable whenever it exists
	(d) if k>[ktilde] then 𝒫 is stable only for
	(e) if k>[ktilde] then a globally attractive limit cycle occurs for 0<i<i **(k)
	(f) the bifurcation curve i=i **(k) coincides with the set on which in the ki-plane.

Again, all of our numerical investigations support this conjecture (Figure 3). The parameter region in which 𝒫 is conjectured to be stable is represented in Figure 2(c), and the region in which it is conjectured to be unstable is represented in Figure 2(d).

Figure 3. Outcome of the non-spatial predator–prey-subsidy model (III) for different values of the carrying capacity (k) and subsidy input rate (i) based on local stability analysis. The system moves to a predator-free equilibrium in the lower-left region (red), to a prey-free equilibrium in the upper region (yellow), to a positive equilibrium in the central region (green), and to a stable limit cycle involving predator, prey, and subsidy in the lower-right region (blue). The lower-left boundary is given by i=i _*(k), the upper boundary is given by i=i*, and the lower-right boundary is given by i=i _**(k). All results are theoretical except for the stability of the positive equilibrium in the central and lower-right regions which is based instead on numerical evidence. The parameter values used are the same as in Figure 2.

4. Predator and prey system with a spatial subsidy

Here we recast the non-spatial model (III) into a spatial one involving movement of the predator between two patches, one of which contains only the prey and the other containing only the subsidy. Whether a predator consumes prey or the subsidy depends entirely on its location. A related model for predator movement in a continuous habitat 45 is described in Section 6.

Let x(t) be the population size of a prey species (in patch 1), s(t) be the amount of a donor-controlled resource subsidy (in patch 2), and y ₁(t) and y ₂(t) be the population sizes of a predator species (in patches 1 and 2) at time t≥0. Suppose that these functions obey

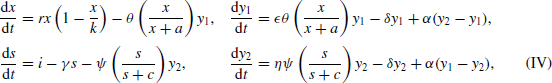
where all parameters have the same interpretation as before, and the diffusion coefficient α denotes the rate at which predators randomly move between the two patches. It is assumed that all constants are positive, that ε and η are no greater than unity, and that x(0)>0, y ₁(0)>0, y ₂(0)>0, and s(0)>0. In addition, and for reasons similar to those offered earlier, we will restrict attention to nutrient-rich prey and subsidies, i.e. to parameter combinations in which both and .

As illustrated in Figure 4, several different outcomes are possible, including (i) a predator-free equilibrium, (ii) a prey-free equilibrium, (iii) an equilibrium in which the predator, prey, and subsidy all persist, and (iv) the persistence of predator, prey, and subsidy in a stable limit cycle. As with the non-spatial model described earlier, we wish to distinguish situations in which these different outcomes occur, and to understand the influence of parameter values on these outcomes.

Figure 4. Time-series for the spatial predator–prey-subsidy model (IV) with the following parameter values: r=0.1, θ=5, a=1, γ=1, ψ=5, c=1, ε=0.1, η=0.1, δ=0.1, and α=0.8. In (a) the prey population size approaches a positive equilibrium value, the subsidy amount approaches its natural value, and the predator becomes extinct (k=0.1 and i=0.1). In (b) the prey becomes extinct, the subsidy amount approaches its natural value, and the predator population sizes approach positive equilibrium values (k=0.1 and i=1.0). In (c) the predator and prey population sizes approach positive equilibrium values and the subsidy amount approaches its natural value (k=0.4 and i=0.3). In (d) the predator, prey, and subsidy all persist in a stable limit cycle (k=2.4 and i=0.1). In all figures, x(0)=0.2, y ₁(0)=0.1, y ₂(0)=0, s(0)=0, k (α)=0.25, and ℓ(α)=0.65.

At equilibrium, the equations above become

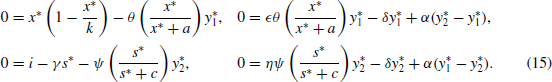
It is clear from the two equations on the right that if the predator is absent from one patch (say, ) then necessarily it will also be absent from the other . As we will consider both the feasibility and stability of the different equilibrium states (Table 4), we will make frequent use of the Jacobian. With the state variables ordered as (x, y ₁, y ₂, s), the Jacobian can be written as

Notice that if the predator does not move between patches (α=0), then the remaining blocks of J are simply the Jacobians of the two sub-systems (I) and (II).

Table 4. Equilibrium properties of the spatial predator–prey-subsidy model (IV).

Equilibrium	x*	s*			Feasible	Stable (when feasible)
Subsidy-only	0	i/γ	0	0	Always	Never
Predator-free	k	i/γ	0	0	Always	and
Prey-free	0
Positive	x*	s*			and	Always ^a
					and	Always ^a
					and	^a, b
Notes: The quantities , , , and i*(α) are defined in Equations (19)–(22). All statements involving the positive equilibrium assume that and are finite and that is infinite.
^aConjecture.
^bLimit cycles (or other non-equilibrium dynamics) are conjectured to occur when .

4.1. Subsidy-only equilibrium

At the subsidy-only equilibrium , the Jacobian matrix

is block diagonal and has at least one eigenvalue with positive real part (r>0). Therefore, the equilibrium is never stable.

4.2. Predator-free equilibrium

At the predator-free equilibrium , the Jacobian matrix has the form

The equilibrium is stable provided that the two eigenvalues of the central block have negative real part. This occurs when

and

The inequality on the left implies that at least one bracketed quantity must be negative, and the inequality on the right implies that they both must be. Using these facts, the stability condition becomes

where

and

Notice that (i) , (ii) , and (iii) is positive. We can write the stability conditions (16) in terms of k, α, and i directly, but doing so requires considering multiple cases. First, it is helpful to define the following composite quantities

Since is finite (), it follows that is finite for sufficiently small α. Also, is an increasing function of α along the interval where it is finite. Similar comments hold for . Observe also that , with equality occurring only when α=0 or neither is finite. Next, notice that (i) when then , (ii) when then and X(k,α) is negative, and (iii) when then and X(k,α) is a positive and decreasing function of k. Now, define

and notice that if and only if . The remarks above imply the following.

Theorem 4 (Predator-free equilibrium)

The predator-free equilibrium is stable if and only if and .

Notice that the equilibrium is stable whenever ; indeed, since , it is stable whenever α is sufficiently small. The case in which a predator-free equilibrium is stable is represented in Figure 4 (a).

4.3. Prey-free equilibrium

A prey-free equilibrium has the form . We will first determine its form and then its stability. Let us define

Since is finite (), it follows that is finite for sufficiently small α. Also, is an increasing function of α along the interval where it is finite. Similar comments hold for . Observe also that , with equality occurring only when α=0 or neither is finite. Next, notice that (i) when then , (ii) when then , and (iii) when then . For parameter combinations satisfying , then a unique prey-free equilibrium exists and has components

For situations in which , and this includes when is infinite, then no such equilibrium exists. We assume now that . To study the equilibrium's stability, we consider the associated Jacobian

whose form is block triangular. The upper left block is negative when , and this occurs when where we define

We remark that , and therefore i*(α), depends on neither k nor i. Next, the lower block and its sign matrix can be written as

It remains to determine conditions under which K is stable. Let be its characteristic polynomial. We first show that has positive coefficients. Expanding along its minors, we find that , , and . Hence, has positive coefficients. According to the Routh–Hurwitz criterion 15, the characteristic polynomial is stable if and only if . Based on the sign matrix for K, we compute

We conclude that K is always stable. In view of the previous remarks, we have the following result.

Theorem 5 (Prey-free equilibrium)

A prey-free equilibrium exists if and only if and is stable if and only if . When the equilibrium exists, it is unique.

The case in which a prey-free equilibrium is stable is portrayed in Figure 4(b).

4.4. Positive equilibrium

In view of Equation (15), a positive equilibrium satisfies the following equations

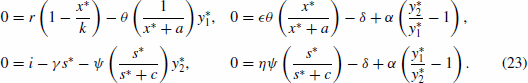
As can be seen from Equation (23), necessary conditions for an equilibrium to be positive are and 0<x*<k. However, it is not clear whether these conditions are sufficient (yet), and so we will explore this here.

Proposition 1

	(a) If then 𝒫 exists .
	(b) If then 𝒫 exists .

Proof

Observe from Equation (23) that

where

For a positive equilibrium to exist, it is necessary and sufficient that , W(α)>0 and . Let us assume then that and try to express the two remaining conditions in terms of s*. The reader will find it useful to recall the definitions of X(k,α), , , , , , and i*(α) in Equations (17), (19)–(22) and their properties as they will be used liberally below. It follows from Equations (24) and (21) that

Assume that these inequalities do hold. Next, it can be seen by inspection and Equation (21) that

Assuming that these inequalities also hold, it remains to establish when . As noted above, a positive equilibrium cannot occur with x*>k. Hence, given that , W(α)>0, and Z(α)>0, the inequalities and x*<k are equivalent, and based on Equation (24), the latter occurs when . Several cases arise.

	(i) If then
	(ii) If then
	(iii) If then .

This completes the proof.   ▪

As a reminder, whether k lies above or below depends in a straightforward manner on the quantities , a, and . The next results provides a similarly simple description for predicting the relative magnitudes of s*, , and .

Proposition 2

Suppose that and are finite and that is infinite.

	(a) If then s* is an increasing function of i on with at and at . Moreover, if then .
	(b) If then s* is an increasing function of i on with s*=0 at i=0 and at . Moreover, if then .

Proof

Suppose that and are finite and that is infinite. Substituting the expressions for x*, , and in Equation (24) into the upper left equation of (23) yields

Letting , we obtain after rearrangement

Applying the relation produces

Multiplying both sides by s*+c and using the relation yields

At last we arrive at a cubic equation for s*

where we define

Notice that (i) because is finite and is infinite, (ii) , (iii) , (iv) because is finite, (v) and denote the limits of m and n as a→0 or k→∞, and (vi) the parameter i appears once in Equation (26).

To prove part (a) of the proposition, we assume that and observe that i in Equation (26) can be solved for as a continuous and differentiable function of s*>0,

The denominator does not vanish because both and are positive. Recall from the properties of X(k,α) in Equation (17) and the finiteness of that . Therefore, in Equation (20) is positive.

To compute the value of i at , we observe from Equation (20) that

Multiplying both sides of the equation above by (a positive quantity) produces

We will show that the right-hand side vanishes. After rearrangement, it becomes

Equation (17) implies that the bracketed expression is equivalent to

After further rearrangement, we obtain

Thus, . It follows from Equation (27) and the positivity of that when .

Now, we compute the value of i at . We begin by noticing that

Since is independent of a, a similar calculation implies that . Hence,

It remains to show that i is an increasing function on . Towards this end, we calculate

Several cases arise. If then . Suppose now that , and, without loss of generality, that . To distinguish this particular value of s*, we denote it by . Recall that i=0 at s*=0, i is a continuous and differentiable function of s*>0, and at . Hence, it must be that for some . Consequently,

In view of Equation (28), we obtain . In both cases, on , and, on that interval, the function i(s*) has a continuous and differentiable inverse s*(i) satisfying the properties in (a).

The proof of (b) is similar. Assume first that . It is clear that i=0 at s*=0. The argument showing at is the same as above. To establish that i is increasing on the interval , we recall Equation (28)

Notice that this time and . Hence for . Again, we conclude that the function i(s*) has a continuous and differentiable inverse s*(i) on satisfying the properties in (b).   ▪

Although statements similar to Proposition 2 can be made for situations in which or is infinite or is finite, we will make no attempt to exhaust all possibilities. Propositions 1 and 2 above together imply the following.

Theorem 6 (Existence and uniqueness of positive equilibrium)

Suppose that and are finite and that is infinite. Then the positive equilibrium (𝒫) for system (IV) exists under the following conditions:

	(a) If then 𝒫 exists .
	(b) If then 𝒫 exists .

Furthermore, when 𝒫 exists then it is unique.

In proving Proposition 2, we found that the behaviour of s* as a function of i was as follows.

•	s* is increasing along any interval where 𝒫 exists
•	at when
•	at

The behaviours of x*, , and as functions of i can be obtained from Equations (23)– (25)

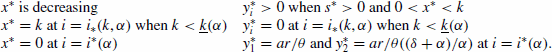
We now have a complete description of how the components of 𝒫 depend on the parameter i. It remains to study the stability of 𝒫, for which our analytical results are again only partial. Towards this end, it is useful to define functions based on the right-hand side quantities appearing in (IV),

The Jacobian matrix then becomes

Here, we have also denoted when possible the signs of the various matrix elements. These are

The signs of , G _x *, H _s *, and I _s * are clear by inspection. To obtain the sign of , we observe that

A similar argument shows that . The sign of F _x * remains ambiguous.

Recall that the stability of the equilibrium is determined entirely by the eigenvalues of J, which in turn are the zeros of its characteristic polynomial. This polynomial has the form

where we define

Although a ₁ has ambiguous sign, it is clear that . It is convenient to express the characteristic polynomial as

where, noting that , we have

A necessary and sufficient condition for 𝒫 to be stable is that the coefficients ω _k (k=1, 2, 3, 4) satisfy the Routh–Hurwitz criteria 15

Unfortunately, determining exactly when these inequalities hold based strictly on a knowledge of parameter values seems like a hard problem. Notice, however, that at minimum all coefficients must be positive, and this occurs when

Since

we find that a ₁<0 (and hence all coefficients are positive) if and only if 2 x*+a>k.

As with the non-spatial model, our stability results are again based partly on numerical evidence.

Conjecture 2 (Stability of positive equilibrium) There exists a bifurcation function defined for such that

	(a)  is continuous, increasing, and concave downward
	(b)  and
	(c) if then 𝒫 is stable whenever it exists
	(d) if then 𝒫 is stable only for
	(e) if then a globally attractive limit cycle occurs for
	(f) the curve i=i **(k) coincides with the set on which in the ki-plane.

Again, all of our numerical investigations support this conjecture (Figure 5). The parameter regions in which 𝒫 is conjectured to be stable and unstable are represented in Figure 4(c) and (d), respectively.

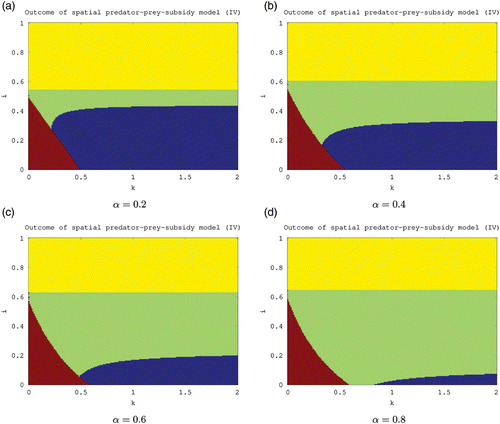
Figure 5. Outcome of the spatial predator–prey-subsidy model (IV) for different values of the carrying capacity (k), subsidy input rate (i), and predator-movement rate (α) based on local stability analysis. The system moves to a predator-free equilibrium in the lower-left region (red), to a prey-free equilibrium in the upper region (yellow), to a positive equilibrium in the central region (green), and to a stable limit cycle involving predator, prey, and subsidy in the lower-right region (blue). The lower-left boundary is given by i=i _*(k,α), the upper boundary is given by i=i*(α), and the lower-right boundary is given by i=i _**(k,α). The lower-left and upper boundaries both increase as α increases. All results are theoretical except for the stability of the positive equilibrium in the central and lower-right regions which is based instead on numerical evidence. The parameter values used are the same as in Figure 4 unless noted otherwise.

5. Biological implications

Here we compare the features of, and the predictions made by, the predator–prey model (I), the predator-subsidy model (II), the non-spatial predator–prey-subsidy model (III), and the spatial predator–prey-subsidy model (IV).

In keeping with our previous analysis, and the bifurcations diagrams in Figures 3 and 5, we will usually treat prey carrying capacity (k), subsidy input rate (i), and predator movement rate (α) as variables and all other model parameters as arbitrary but fixed. Also, we remind the reader that the predator is entirely food limited; it can persist only with sufficient food availability as measured by a combination of prey abundance and subsidy amount. In addition, the predator is an efficient consumer of both prey () and subsidy () in the sense that it can persist on either food type alone provided that it occurs at sufficiently high density. Finally, so that comparisons between models can be made, we will assume that the half-saturation constants a and c (in I, II, and IV) are interchangeable with e (in III) when appropriate.

For reference, the equilibrium properties of all models are stated in Tables 1–4.

5.1. Subsidy-only equilibrium

In (II), the subsidy-only equilibrium is always feasible, and it is stable when the subsidy input rate (i) is too low to support the persistence of a predator which relies on it exclusively. In contrast, the corresponding equilibrium in (III) and (IV) is always feasible but never stable. The instability of this equilibrium in the latter models occurs because the prey can always invade a habitat in which the predator is absent.

5.2. Predator-free equilibrium

The predator-free (or prey-only) equilibrium in Equation (I) is always feasible, but it is stable only when prey carrying capacity (k) does not meet the minimum prey abundance needed to support a predator population (). The corresponding equilibrium in (II) coincides with the subsidy-only equilibrium and is treated above.

In (III), the predator-free equilibrium is always feasible but stable only in habitats where overall food productivity is low (i.e. for combinations of k and i in which both are small). The corresponding region in parameter space where the equilibrium is stable is illustrated in Figure 3. Notice that the stability condition (3) can be rewritten as

The quantity k is the minimum prey density required by an unsubsidized (i=0) predator to persist (it equals when a=e). As expected, when the predator is unsubsidized then we recover the stability condition for the corresponding equilibrium in the original predator–prey system . In general, the right-hand side of Equation (29) is the minimum prey density required by a subsidized predator to persist. As the predator becomes increasingly subsidized (i.e. i increases), then the right-hand side decreases, and because prey carrying capacity is assumed to be relatively small , there is a critical subsidy input rate (i) at which the two sides become equal and this forms the stability boundary i _*(k) seen in Figure 3. As expected, the presence of the subsidy reduces the predator's reliance on prey to persist. The close relationship between the stability conditions is also clear biologically – if the predator's maximum energy gain (capture rate times conversion efficiency) from the subsidy (η ψ) exceeds the predator's mortality rate (δ) by only a very small amount, then only prey abundance should matter.

Many of the same remarks apply to (IV), at least in a qualitative way (Figure 5). Namely, prey carrying capacity must lie below a threshold amount for a mobile but unsubsidized predator to be excluded. If the predator is a relatively inefficient consumer of the subsidy then, when the subsidy is introduced, the predator will still be excluded because its movement pattern cancels out (although in a complicated manner) any benefit earned from obtaining the subsidy. However, if the subsidized predator is highly efficient then it can only be excluded when the subsidy input rate is small . For predators that move slowly the latter situation will always prevail because . As the movement rate (α) increases, then the minimum prey carrying capacity for an unsubsidized predator to persist also increases because of wasted movement effort. In addition, the relation and Equation (20) together imply that the stability boundary increases as α increases. Thus, given a fixed combination of parameters near this boundary, a slow predator (α small) may persist whereas a swift predator (α large) will become extinct.

5.3. Prey-free equilibrium

A prey-free equilibrium is never feasible in Equation (I) because a predator must consume something to persist. In (III), such an equilibrium can occur, but only when the rate of subsidy input is sufficiently high . This condition corresponds perfectly with the condition for predator persistence in (II). In both models, and represent the minimum amount of subsidy (i/γ) needed to support a predator (when c=e they are equal). In (II), the equilibrium is stable whenever it exists. However, the equilibrium in (III) is stable only when i lies above a still higher critical value, namely, (see Figure 3). If prey have no ability to invade (r=0) then the prey-free equilibrium is, naturally enough, stable when feasible . However, as the ability of prey to invade (r) increases, only highly subsidized predators can continue to exclude them (i>i*). Interestingly, the subsidy amount in a prey-free equilibrium is always , regardless of the subsidy input rate (i) but provided that it is large enough. Thus, to maintain equilibrium, the predator must skim all subsidy above a fixed amount . Notice that a similar thing occurs for the predator–prey equilibrium in Equation (I).

As can be seen in Figure 5, similar remarks apply again to (IV). However, a prey-free equilibrium exists only in situations where the predator is a highly efficient consumer of the subsidy . When this occurs, then the equilibrium is feasible for and stable for . Here, and i*(α) have the same interpretations as and i* above, although they are somewhat more complicated quantities to define. It can be seen from Equations (21) and (22) that the feasibility and stability boundaries and i*(α) both increase as the predator movement rate (α) increases. Consequently, the parameter region in which the prey cannot invade (i.e. where the prey-free equilibrium is stable) is largest when the predator moves slowly (α small) and it diminishes in area as the predator becomes faster. Also, since and i*(α) both become infinite at sufficiently high α, it follows that the prey can always invade when the predator is swift (α large). Recalling that the subsidy can never be excluded at equilibrium, our results contradict those of a similar model in which apparent competition is found to be strongest when the predator is swift 25. However, the latter model differs significantly from (IV); namely, it assumes that the prey species both increase exponentially and that the predator functional response is linear. We believe that the precise source of conflict between the models’ predictions regarding the strength of apparent competition versus predator mobility warrants further investigation.

5.4. Positive equilibrium

The positive equilibrium of (I) exists when but is stable only for k<[ktilde]. When k>[ktilde] the equilibrium is unstable and is famously surrounded by a unique and globally attractive limit cycle, a phenomenon known as the paradox of enrichment 18 19 39 51 54.

A positive equilibrium in (III) can occur as follows. Consider first a predator which cannot rely on prey alone to support it . In this case, a small subsidy input rate (i<i _*(k)) will cause the predator to remain excluded and a large subsidy input rate (i>i*) will cause the prey to be excluded (see above). In these situations, a positive equilibrium cannot occur. However, the equilibrium can occur at intermediate subsidy input rates . We conjecture that when the positive equilibrium does occur, then it is always stable. Suppose now that an unsubsidized predator can persist with the prey at either a stable equilibrium or in a stable limit cycle (k>[ktilde]). In this case, small and intermediate sized subsidies (i<i*) will always permit a positive equilibrium to continue to occur, whereas large subsidies (i>i*) will again cause the prey to be excluded. Here, we conjecture that when an unsubsidized predator can persist at equilibrium with the prey then any amount of subsidy input which allows for a positive equilibrium to occur will enable that equilibrium to be stable; however, when an unsubsidized predator coexists with its prey only in a stable limit cycle (k>[ktilde]), then small subsidy input rates (i<i _**(k)) do not destroy the structural stability of the limit cycle, and only intermediate sized subsidies (i>i _**(k)) enable a positive equilibrium to be stable. Thus, small subsidy inputs cannot eliminate oscillation altogether, whereas larger subsidy inputs can. Furthermore, we conjecture that i _**(k) is an increasing function, i.e. larger carrying capacities require higher subsidy input rates to eliminate oscillation.

Again, similar comments apply for the feasibility and stability of the positive equilibrium in (IV) (Figure 5). The corresponding stability boundaries and i*(k) are described in detail above. For this model, numerical evidence suggests that an increase in the predator movement rate (α) will enlarge the stability region of the positive equilibrium, with a concomitant decrease in the stability region for the limit cycle (Figure 5). Thus, it is likely that a slow predator (α small) will persist in oscillation, and a swift predator (α large) will persist at equilibrium.

6. Discussion

The use of secondary resources by species from adjacent habitats or ecosystems is widespread 46 50 52. These allochthonous resources, or resource subsidies, can strongly affect the abundance and space use of consumers in recipient ecosystems, with cascading effects on in situ resources 28 30 38 50 53. However, the impact of resource subsidies on recipient communities can be affected by several factors, including the productivity of the donor and recipient habitats, amount of input, trophic level receiving the input, and temporal variability in subsidy input rates 29 37 55 58. Not only the magnitude, but the direction of the indirect effect on in situ resources can vary. If consumers respond numerically to increased food availability through resource subsidies, local prey could decline because of increased predation, an effect known as apparent competition 24. However if predators aggregate toward areas of high subsidy availability, consumption of local prey in other areas may be reduced (apparent mutualism 4). Furthermore, local stability of food webs can be affected by the addition of resource subsidies, with a potential loss of species 28 29.

6.1. Future directions

We have considered the influence of a donor-controlled resource subsidy on predator–prey interactions by use of a mathematical model. Both a non-spatial model, in which the subsidy occurs in the same location as the predator and prey, and a spatial model, in which the predator must move between two patches (one containing only the prey and the other containing only the subsidy) were considered. Conditions for the feasibility and stability of various equilibrium states were developed for each. In all cases, we find that moderate resource subsidy inputs can promote the stable coexistence of predator and prey, whereas large subsidy inputs can push the prey to extinction.

In our theoretical analysis, we found that the complicated forms of the Routh–Hurwitz conditions precluded a successful local stability analysis for positive equilibria in terms of prey carrying capacity (k), subsidy input rate (i), and predator movement (α). In particular, we were unable to prove that a positive equilibrium is stable in the region of conjectured dynamical stability (the central regions in Figures 3 and 5) and unstable in the region of conjectured dynamical instability (the lower-right regions in Figures 3 and 5). Yet, we strongly suspect that a positive equilibrium is in fact globally attractive in the former region and that a unique globally attractive limit cycle exists in the latter region.

Our numerical explorations of the non-spatial model (III) indicate that the time required for relaxation to a limit cycle can vary greatly with parameter values. We have even found cases in which a trajectory repeatedly moves from one cycle of finite amplitude to another before finally settling down to the asymptotically attracting cycle. In general, it is unknown how k, i, and α influence the time to relaxation, as well as the amplitude and average predator and prey densities in a limit cycle.

The spatial model (IV) assumes that predator movement occurs via the density-independent process of diffusion. Natural predators probably make use of density-dependent cues as well, involving predator and prey density and subsidy abundance. Whether such rules by themselves can produce dynamical instability remains unknown. Seasonal and migrational effects that produce temporal variation in the predator movement rate (α) may be introduced 44. Another extension to the spatial model would be to incorporate allochthonous subsidies transported into several patches differing in prey productivity; it may be that a locally inferior prey species can coexist regionally with a locally superior competitor 43.

Below we consider several important modifications to the models that make them more applicable to the arctic system in which arctic foxes (predators) consume both lemmings (prey) and seal carcasses (subsidy).

6.1.1. Seasonal and long-term variability in subsidy amount

In the arctic, seal carcass availability varies in time due to seasonal and long-term changes in temperature, sea ice cover, and polar bear activity. For illustrative purposes, suppose that the mean temperature on day n is given by

where τ₀ represents the mean yearly temperature in the absence of long-term temperature change, m prescribes the influence of long-term temperature change (see below), and A ₀ is the amplitude of yearly temperature fluctuations. For simplicity, we consider neither diurnal temperature patterns nor long-term fluctuations in amplitude (A ₀). If m>0 then mean daily temperatures increase on a yearly basis, if m<0 then they decrease, and if m=0 then every year is the same (i.e. there are no long-term changes in temperature patterns). Suppose further that the subsidy input and decay rates depend on temperature in the following manner:

Thus, as temperatures increase, the amount of subsidy available to the predator decreases due to a combination of a slower input rate and a faster decay rate. Replacing i and γ in the predator–prey-subsidy model (III) or (IV) with i(τ(t)) and would produce dynamics that more closely mirror those of the original arctic fox-lemming-seal system. Although the system becomes more difficult to analyse mathematically, we believe that some interesting results could still be obtained (see 49 for a similar approach).

6.1.2. Spatial separation of prey and subsidy

Another important feature of the arctic system is that lemmings and seal carcasses are spatially separated, with the former occurring inland and the latter occurring on ice floes surrounding the coastline. In our patch model (IV), the distinct spatial locations are implicit. A more realistic way to include spatial separation of prey and subsidy is to assume that the habitat Ω is a closed and bounded subset of ℝ² consisting of an inner domain Ω₁ on which only the prey occurs and an outer annular domain Ω₂ on which only the subsidy occurs. In this case, a system of partial differential equations such as

may apply. Here, the predator, prey, and subsidy both move randomly inside their respective domains, but at different rates (a subsidy such as seal carcasses is carried by slowly moving ice floes). Along the respective boundaries, no-flux boundary conditions are assumed. The behaviour of this model is the subject of current investigation by the first author 45.

6.2. Conclusions

Holt 25 developed models for two species of immobile prey segregated into two patches coupled by predator movement and suggested that habitat partitioning could be a mechanism allowing alternative prey species to coexist. In these models, one of the prey species may become extirpated by the subsidized predator consuming abundant prey in another patch. In the models considered in the present paper, a highly subsidized predator should indeed drive a prey species to extinction, regardless of whether the prey and subsidy occur in the same location. Though apparent competition 24 is still evident in both the spatial and non-spatial models (an increase in subsidy input rate (i) results in lower equilibrium prey density), in the spatial model a predator must travel between patches, which is less efficient than simply consuming both prey and subsidy in the same patch. As such, prey extinction appears more likely in the non-spatial model, in a qualitative sense.

We also find that an increase in predator movement rate (α) can also stabilize the system – a predator having greater access to a subsidy would be more likely to persist when prey are difficult to find. In general, predator movement has a ‘smoothing’ effect, with local differences in patch quality being of less consequence as the movement rate increases. Qualitatively, the two patches behave increasingly as though they were a single patch. Such knowledge can be useful in mitigating local disturbances. For example, in areas of melting coastal ice, foraging arctic foxes must rely increasingly on lemmings inland to survive because of reduced access to seal carcass subsidies along the coast.

Returning to our motivating example, our results suggest that seal carcass availability may have a stabilizing influence on arctic fox and lemming population dynamics – provided that the input rate is relatively moderate. Since arctic foxes must move off the tundra onto the sea ice to exploit the subsidy, our spatial model (IV), in which two distinct habitat patches each contained a different resource for the predator, may better represent this particular biological system. The warming climate and decline in sea ice are already having a negative impact on ringed seals and polar bears 14 47, and our results suggest the loss of this subsidy could destabilize the dynamics of coastal fox and lemming populations, in the sense that arctic fox populations relying on the seal subsidy may be greatly reduced in number, or perhaps even pushed to extinction, due to a decline in the subsidy.

Many of our results are qualitatively similar to a previous study using a very different model that found small subsidy inputs stabilized food web dynamics, whereas large subsidy inputs were destabilizing 28. However, our model consists of just two trophic levels, with only the top predator receiving additional resources from the subsidy. Previous studies of a non-spatial tritrophic food chain model found the trophic level into which the subsidy entered the community affected species Â' persistence and population-level variance 29. A tritrophic model with a spatial component added would likely be analytically intractable, but numerical simulations could be explored to investigate how space and trophic level interact to affect the impact of subsidies on food web stability.

Acknowledgements

We thank J.D. Roth for helping to initiate this project and for comments on early versions of the manuscript. We thank D.J. Kaup and J. Shi for insightful discussions. We thank two anonymous reviewers for their helpful suggestions. R.A. Van Gorder was supported in part by NSF grant DMS-0505566.

Notes

This is a paper based on an invited talk given at the 3rd International Conference on Math Modeling & Analysis, San Antonio, USA, October 2011.

Appendix. Global asymptotic stability of positive equilibrium for predator-subsidy system (II)

Here, we prove that the positive equilibrium of the predator-subsidy system (II) is globally asymptotically stable when . Adapting an argument from Ardito and Ricciardi 8 (they consider a logistic-type resource rather than a donor-controlled one), let

Then there exists a unique positive equilibrium (s*, y*) and it satisfies , , and q(s*)=0. For s>0, we have p(s)>0, , and

with equalities being achieved only at s=s*. Let I ₁=(0, s*), , , and

Observe that G is defined for s∈I. Define and . For s∈I, we have g(s)>0 and . It follows that for s∈I and therefore that . Next, it can be seen that . For s>0 and y>0, define

Since for s>0, we obtain that

The first inequality is strict unless s=s* and the second inequality is strict unless y=y*. We conclude that V(s, y)≥0 with equality being achieved only at (s*, y*). Furthermore, according to Leibniz's rule for differentiation of integrals,

When s∈I ₁ then because q(s)<0 and . When s=s* then because q(s)=0 and the parenthetical quantity also vanishes. When s∈I ₂ then because q(s)>0 and . Finally, when then because q(s)>0, g(s)<0, p(s)>0, and Φ(s)>0. We conclude that with equality being achieved only when s=s*. Next, we show that V(s, y) is radially unbounded. Observe from Equation (A1) that as s→0 or s→∞. In addition, it can be seen by inspection that . Hence, if (s, y) approaches one of the coordinate axes (s→0 or y→0) or (s→∞ or y→∞) then either Equation (A2) or Equation (A3) implies that . Thus, V(s, y) is radially unbounded. Hence, for every K≥0 the set is compact and positively invariant. Since is the largest invariant set in , we conclude from Theorem 9.25 in 21 that (s*, y*) is globally asymptotically stable with respect to positive initial conditions.