Study on dynamic characteristics’ change of hippocampal neuron reduced models caused by the Alzheimer’s disease

ABSTRACT

In the paper, based on the electrophysiological experimental data, the Hippocampal neuron reduced model under the pathology condition of Alzheimer’s disease (AD) has been built by modifying parameters’ values. The reduced neuron model’s dynamic characteristics under effect of AD are comparatively studied. Under direct current stimulation, compared with the normal neuron model, the AD neuron model’s dynamic characteristics have obviously been changed. The neuron model under the AD condition undergoes supercritical Andronov–Hopf bifurcation from the rest state to the continuous discharge state. It is different from the neuron model under the normal condition, which undergoes saddle-node bifurcation. So, the neuron model changes into a resonator with monostable state from an integrator with bistable state under AD’s action. The research reveals the neuron model’s dynamic characteristics’ changing under effect of AD, and provides some theoretic basis for AD research by neurodynamics theory.

KEYWORDS:

• Neurodynamics
• Alzheimer’s disease
• neuron

1. Introduction

The Alzheimer’s disease (AD) is a progeria dementia neural disease which progresses gradually. In recent years, research about AD’s pathogenesis is gaining increasing attention. Some research results of the pathologists have shown that features such as deposition of amyloid β-amyloid (Aβ) protein, entanglement of senile plaques and nerve fibers have appeared in the AD patients’ brains. Intracephalic Aβ’s mass deposition and nerve fiber’s entanglement caused by the aneurotransmitter’s lack, the amyloid precursor protein gene’s mutation, and the metabolic pathway’s abnormality of the precursor protein β-APP are considered the important mechanisms of AD’s attack. So far, the amyloid protein cascading hypothesis is the most notable in lots of hypothesizes of AD’s attack mechanism. In the amyloid protein cascading hypothesis, Aβ has the core function in the process of AD’s attack, and can cause a series of neurotoxicity [7]. Aβ can cause dysfunction or death of neurons, and leads to dementia. More and more evidence shows that Aβ is the common path of many factors causing AD’s attack and the indispensable key factor of AD’s formation and development. Therefore, research of AD often simulates different levels of morbid states of AD by action of different concentrations of Aβ.

Hippocampus plays a major role in learning and memory in the nervous system. Its cognition and memory function is closely related to many neural diseases such as AD [2]. The existing findings have proved that AD can cause electrophysiological characteristics’ change of the hippocampal neuron, and especially can cause change of the potassium ion channel characteristics [1,18,21]. Dependent on electrophysiological experiments and new technologies, such as optics imaging, some models of hippocampal pyramidal neurons based on ionic conductance have been successfully constructed [3,4,5,6,9,11–14,19,23–27].

The hippocampal CA1 pyramid neuron has plenty of discharge behaviors. Yue et al. found that bursting behavior persists in adult CA1 pyramidal cells after almost complete truncation of the apical dendrites. The bursting mechanism is different from the ‘ping-pong’ mechanism, which depends on integrity of apical dendrites [25–27]. Based on the CA1 pyramidal neuron’s membrane ionic channel theory and its electrophysiological experimental data, according to the basic frames of the Hodgkin–Huxley(H–H) class of neuron models, Golomb et al. developed the one-compartment model of CA1 pyramidal neuron [5], which is different from the former multi-compartment cable model of the hippocampal pyramid neuron. This model omits effects of apical dendrites and its complexity is reduced, which not only can simulate many electrophysiological features and experimental results of the hippocampal CA1 pyramid neuron, but also can spontaneously generate regular firing, tonic firing, and rhythmic bursting. But this model is still a nine-dimension complex ordinary differential equation set, which is very inconvenient to analyze and discuss deeply specified dynamic characteristics or given parameters’ effect of the neuron model. In recent years, reduction work of the nine-dimension one-compartment complex model of CA1 pyramid neuron is done by He and Peng [8] and Peng et al. [16,17]. They have reduced the nine-dimension complex neuron model to minimal models and the two-dimension reduced model, and analyzed comparatively dynamic characteristics of the original model and reduced models [17].

In this paper, we take the reduced models of CA1 pyramid neuron [17] as the object. Based on the electrophysiological experimental data under the AD pathology condition, we build the reduced neuron models under the AD pathology condition by modifying suitably parameters’ values, and discuss comparatively neuron models’ dynamic characteristics’ change before and after effect of AD.

2. The minimal neuron model’s dynamic characteristics’ change under the AD pathology condition

Based on the electrophysiological experimental data under the pathology condition of AD [15], we can only modify suitably parameters’ values of the normal $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model [17], and get the $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model under the AD pathology condition.

2.1. The hippocampal neuron’s electrophysiological characteristics under the AD’S pathology condition

In recent years, people have simulated different morbid states of AD by injecting different concentrations of Aβ. They have studied electrophysiological characteristics of the neuron under the morbid state of AD, and have acquired many research findings and conclusions [15,18,20,22].

Xiaoliang Wang [15] simulated the morbid state of AD by injecting the aggregated Aβ_25–35 into the lateral ventricle. They recorded and studied the electrophysiological characteristics’ change of the hippocampal pyramid neuron’s voltage-gated currents (the A-type instantaneous K⁺ current (I_A) and the delay rectification K⁺ current (I_Kdr)) under the morbid state of AD. Experimental results are as follows:

1. The aggregated Aβ_25–35’s injecting into the lateral ventricle in one shot has some effect on the amplitude and the density of A-type instantaneous K⁺ current (I_A). But from the neurodynamics angle, A-type instantaneous K⁺ current’s stable activation dynamic characteristics and stable inactivation dynamic characteristics have no significant difference [15].

2. The aggregated Aβ_25–35’s injecting into the lateral ventricle in one shot has great effect on the amplitude and the density of the delay rectification K⁺ current (I_Kdr). After the aggregated Aβ_25–35 is injected into the lateral ventricle, the delay rectification K⁺ current is notably increased and has voltage-gated characteristics. When the neuron is depolarized to +40 mV, the amplitude of the delay rectification K⁺ current under the Aβ_25–35 condition is notably larger than that under the normal condition, and increase 68.9% (p < .01). The half activation maximal voltage(V_1/2) of the delay rectification K⁺ current shifts left from −6.2 ± 1.5 mV (n = 12) (the normal condition) to −14.3 ± 1.3 mV (n = 14, p < .01) (the Aβ_25–35 condition); The slope factor k decreases from −21.1 ± 0.9 mV (n = 12) (the normal condition) to −18.4 ± 0.6 mV (n = 15, p < .05) (the Aβ_25–35 condition); The stable state activation curve shifts −8 mV toward the hyperpolarizing direction [15].

Therefore, after the aggregated Aβ_25–35 is injected into the lateral ventricle, A-type instantaneous K⁺ current’s dynamic characteristics have no significant difference. But the delay rectification K⁺ current’s dynamic characteristics have significant difference. In the following, on building the neuron model under the AD pathology condition, we only consider the delay rectification K⁺ current’s electrophysiological characteristics and dynamic characteristics under the Aβ_25–35 condition.

2.2. The AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model

The AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model has the same form as the normal $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model described by formula (1), which has been discussed in reference [17].

The neuron model described by formula (1) has three time variables: the membrane potential V, the transient Na⁺ current inactivation variable h, and the delayed rectified K⁺ current activation variable n. On calculation of the AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model, except for parameters related to the delay rectification K⁺ current (I_Kdr), other parameters’ values are the same as the normal minimal neuron model (1) $\begin{array}{rl}C\frac{\mathrm{d}V}{\mathrm{d}t}& =-g_{\mathrm{L}}(V-V_{\mathrm{L}})-g_{\mathrm{Na}}{m}_{\mathrm{\infty }}^3\left(V\right)h(V-V_{\mathrm{Na}})-g_{\mathrm{Kdr}}{n}^4(V-V_{\mathrm{K}})+I_{\mathrm{APP}},\\ \frac{\mathrm{d}h}{\mathrm{d}t}& =\frac{h_{\mathrm{\infty }}\left(V\right)-h}{{\tau }_h\left(V\right)},\\ \frac{\mathrm{d}n}{\mathrm{d}t}& =\frac{n_{\mathrm{\infty }}\left(V\right)-n,}{{\tau }_n\left(V\right)}\end{array}$(1)

where C is the membrane capacitance, V is the membrane potential, I_APP is the stimulation current. Other parameters’ physical meanings of formula (1) are given in reference [17].

The delay rectification K⁺ current’s dynamic characteristics have the significant change under the AD condition, which are shown in Section 2.1. Based on the electrophysiological experiment data of Section 2.1, we can modify the delay rectification K⁺ current’s parameters’ values, and get parameters’ values related to the delay rectification K⁺ current in formula (1).

Allowing for differences of neurons and decreasing errors, we only consider changes caused by AD. From the electrophysiological experimental data of Section 2.1, changes caused by AD are as follows: Under the action of AD, compared with the normal neuron model, the current conductance (g_Kdr) is increased about 0.689 times; the half-activation maximal voltage (V_1/2) shifts left about 8.1 mV. The slope factor (k) decreases about 2.7 mV; other parameters have no changes. So parameters’ values related to the AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model and the normal $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model are shown in Table 1.

Table 1. Neuron models’ parameter values.

Parameters	The normal model	The AD model
	$g_{\mathrm{Kdr}}=6\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2$;	$g_{\mathrm{Kdr}}=10\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2$;
The different values	$n_{\mathrm{\infty }}\left(V\right)={\displaystyle \frac{1}{1+\exp \left({\displaystyle \frac{-35-V}{10}}\right)}}$	$n_{\mathrm{\infty }}\left(V\right)={\displaystyle \frac{1}{1+\exp \left({\displaystyle \frac{-43.1-V}{7.3}}\right)}}$
	$C=1\mu F/\mathrm{c}{\mathrm{m}}^2$; $g_{\mathrm{Na}}=35\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2$; $V_{\mathrm{Na}}=55\mathrm{mV}$; $g_{\mathrm{L}}=0.05\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2$;
	$V_{\mathrm{L}}=-70\mathrm{mV}$; $V_{\mathrm{K}}=-90\mathrm{mV}$; ${\tau }_{\mathrm{n}}\left(V\right)=0.1+0.5\times {\displaystyle \frac{1}{1+\exp \left({\displaystyle \frac{-27-V}{-15}}\right)}}$;
The same values	$m_{\mathrm{\infty }}\left(V\right)={\displaystyle \frac{1}{1+\exp \left({\displaystyle \frac{-30-V}{9.5}}\right)}}$; $h_{\mathrm{\infty }}\left(V\right)=\frac{1}{1+\exp \left({\displaystyle \frac{-45-V}{-7}}\right)}$;
	${\tau }_h\left(V\right)=0.1+0.75\times {\displaystyle \frac{1}{1+\exp \left({\displaystyle \frac{-40.5-V}{-6}}\right)}}$

The AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model has the similar dynamic characteristics with the normal $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$ minimal neuron model, and can also perform spontaneously the period discharge pattern, the bursting discharge pattern, and the chaos discharge pattern. Figure 1 shows the ISIs (interspike intervals) figure of the minimal neuron model before and after effect of AD, where the stimulation current’s changing step is 0.05 nA, and the simulation time is 0–2000 ms.

Figure 1. The ISIs bifurcation figure of the neuron model before and after effect of AD under the direct current’s stimulation. (a) The normal condition and (b) the AD condition.

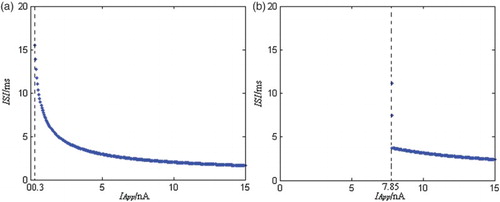
From Figure 1, when the stimulation current amplitude is increased according to 0.05 nA, the neuron models’ ISIs both decrease gradually under the normal condition and under the AD condition, and their discharge patterns are both period 1. Compared with the normal minimal neuron model, the ISIs distribution range of the AD neuron model is smaller. That is to say, the discharge frequency range of the AD neuron model is less than the normal neuron model’s. For the normal neuron model, when the stimulation current amplitude is about 0.3 nA, the neuron model begins to discharge, so the discharge’s current strength threshold is about 0.3 nA. For the AD minimal neuron model, when the stimulation current amplitude is about 7.85 nA, the neuron model begins to discharge, so the discharge’s current strength threshold is about 7.85 nA. Compared with the normal neuron model, the AD neuron model’s discharge current strength threshold is surprisingly increased. So the AD neuron model’s excitability under the external stimulation is greatly lowered. In addition, for the AD neuron model, because its discharge frequency is also in a certain frequency band, and it has also the specific discharge current strength threshold, the model has also class II neural excitability as the normal neuron model (Class 2 neural excitability [10] is that action potentials of neurons are generated in a certain frequency band, which is relatively insensitive to changes in the strength of the applied current).

3. The two-dimension reduced neuron model’s dynamic characteristics’ change under the AD pathology condition

The AD minimal neuron model described by formula (1) is a set of three-dimension equations. The three-dimension model can be reduced, and become the two-dimension reduced neuron model. The two-dimension reduced model is convenient to express in the plane, and is also simple and advantageous to numerical calculation and analysis. In the following, we reduce the AD minimal neuron model described by formula (1) into the two-dimension reduced neuron model by the model reduction theory and the polynomial regression algorithm [17]. Then, we analyze and discuss comparatively the two-dimension reduced neuron model’s dynamic changing characteristics before and after effect of AD.

3.1. The two-dimension reduced neuron model under the AD pathology condition

In the AD minimal neuron model described by formula (1), the variable h and the variable n are indispensable in the minimal model, but their effects are the same. We can firstly decide the certain functional relation between h and n, then remove one variable of these two variables to reduce the dimension of the neuron model by the functional relation between h and n, and get the two-dimension reduced neuron model.

In the AD $I_{\mathrm{Na}}+I_{\mathrm{Kdr}}$-minimal model, variable h and variable n are functions about the membrane potential variable V. They have the proximal line relation, which is proved in the Hodgkin–Huxley neuron model and is consistent with results of the numerical simulation calculation [10]. The functional relation between h and n is decided by the polynomial regression algorithm [17]. The variable h and the variable n are fit by the first-order polynomial, and suppose that the relation of h and n is (2) $h=a_0+a_{1}n,$(2) where a₀, a₁ are coefficients of the polynomial, which are decided according to the simulation data of h and n.

The regression fit data of h and n are from the AD minimal neuron model described by formula (1). Based on the simulation data, h and n are fit by the polynomial regression function in MATLAB, and values of parameter a₀ and a₁ are obtained. The simulation time of the neuron model is 0–2000 ms. Table 2 shows corresponding regression fit values of a₁ and a₂, where the stimulation current I_App changes from 8 to 27 nA according to the 1 nA step.

Table 2. The corresponding fitting values of the polynomial parameters under the stimulation current change.

Group i	Stimulation current IApp (nA)	Parameter a0	Parameter a1
1	8	0.9305	−1.0725
2	9	0.9233	−1.0607
3	10	0.9166	−1.0499
4	11	0.9101	−1.0401
5	12	0.9042	−1.0315
6	13	0.8985	−1.0234
7	14	0.8933	−1.0162
8	15	0.8883	−1.0094
9	16	0.8837	−1.0033
10	17	0.8794	−0.9977
11	18	0.8754	−0.9925
12	19	0.8717	−0.9877
13	20	0.8682	−0.9834
14	21	0.8650	−0.9794
15	22	0.8619	−0.9756
16	23	0.8591	−0.9723
17	24	0.8564	−0.9691
18	25	0.8539	−0.9662
19	26	0.8517	−0.9636
20	27	0.8496	−0.9612

In order to widen the stimulation current’s dynamic range and decrease error of fitting, the final fitting polynomial parameters’ values are obtained by averaging values of 20 groups in Table 2. The results are as follows: (3) $\begin{array}{rl}{a}_0& =\frac{1}{20}\sum _{i=1}^{20}{a}_{0i}=\frac{1}{20}(0.9305+0.9233+\cdots +0.8496)=0.8820,\\ a_1& =\frac{1}{20}\sum _{i=1}^{20}{a}_{1i}=\frac{1}{20}\left[\right(-1.0725)+(-1.0607)+\cdots +(-0.9612\left)\right]=-\mathrm{1.0028.}\end{array}$(3)

In formula (2), a₀ and a₁ are substituted by the above corresponding values, and the function relation of h and n is shown by the following formula: (4) $h=0.8820-1.0028n.$(4)

The AD minimal neuron model described by formula (1) is reduced by formula (4). The variable h is eliminated, and the AD two-dimension reduced neuron model is obtained, which has only two state variables: V and n. The variable h is eliminated, but its effect exists and is represented by formula (4).

The AD two-dimension reduced neuron model is: (5) $\begin{array}{rl}C\frac{\mathrm{d}V}{\mathrm{d}t}& =-g_{\mathrm{L}}(V-V_{\mathrm{L}})-g_{\mathrm{Na}}{m}_{\mathrm{\infty }}^3\left(V\right)(0.8820-1.0028n)(V-V_{\mathrm{Na}})\\ & -g_{\mathrm{Kdr}}{n}^4(V-V_{\mathrm{K},})+I_{\mathrm{APP}}\\ \frac{\mathrm{d}n}{\mathrm{d}t}& =\frac{n_{\mathrm{\infty }}\left(V\right)-n}{{\tau }_n\left(V\right)},\end{array}$(5) where physical meanings of parameters related to the model equation are shown in reference [17].

The two-dimension reduced neuron model described by formula (5) has only two time variables: the membrane potential V and the delayed rectified K⁺ current activation variables n. At numerical calculation, values of model parameters are as follows: $\begin{array}{rl}C& =1\mu \mathrm{F}/\mathrm{c}{\mathrm{m}}^2;g_L=0.05\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2;V_{\mathrm{L}}=-70\mathrm{mV};g_{\mathrm{Na}}=35\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2;\\ g_{\mathrm{Kdr}}& =10\mathrm{mS}/\mathrm{c}{\mathrm{m}}^2;V_{\mathrm{Na}}=55\mathrm{mV};V_{\mathrm{K}}=-90\mathrm{mV};\\ m_{\mathrm{\infty }}\left(V\right)& =\frac{1}{1+\exp \left(\frac{-30-V}{9.5}\right)};n_{\mathrm{\infty }}\left(V\right)=\frac{1}{1+\exp \left(\frac{-43.1-V}{7.3}\right)};\\ {\tau }_n\left(V\right)& =0.1+0.5\times \frac{1}{1+\exp \left(\frac{-27-V}{-15}\right)}.\end{array}$

In addition, the state variables of the neuron model are also (V, n). In order to eliminate effects of neuron models’ initial states, the initial state of the AD neuron model is the same as the normal neuron models, and it is (−65, 0.8).

3.2. The two-dimension reduced neuron model’s equilibrium points’ characteristics under the AD pathology condition

The equilibrium point is the intersection point of nullclines in the phase plane. The equilibrium points can be divided into two kinds: the stable and the unstable. The stable equilibrium points are often expressed by the black circles, and the unstable equilibrium points are expressed by the white circles.

The normal two-dimension reduced neuron model’s dynamic characteristics have been discussed in detail in reference [17]. In the following, we discuss the AD two-dimension reduced neuron model’s dynamic characteristics.

The nullcline equations of the AD two-dimension reduced neuron model described by formula (5) are as follows:

V-nullcline: $I_{\mathrm{APP}}-g_{\mathrm{Na}}{m}_{\mathrm{\infty }}^3\left(V\right)\left(\right(0.8820-1.0028n\left)\right)(V-V_{\mathrm{Na}})-g_{\mathrm{Kdr}}{n}^4\left(V-V_{\mathrm{K}}\right)-g_{\mathrm{L}}\left(V-V_{\mathrm{L}}\right)=0.$

n-nullcline: $n-n_{\mathrm{\infty }}\left(V\right)=0.$

Values of above parameters are shown in Section 3.1. The equilibrium points of the AD two-dimension reduced neuron model described by formula (5) are intersection points of its V-nullcline and n-nullcline.

Figure 2 shows the intersection points of V-nullcline and n-nullcline in the V–n phase plane of the two-dimension reduced neuron model where I_App is zero. From Figure 2, the normal two-dimension reduced neuron model has three equilibrium points, whose dynamic characteristics have been discussed in reference [17]. For the normal two-dimension neuron model, when the stimulation current is zero, only the eigenvalues’ real parts of the equilibrium point A are all less than zero, so only the equilibrium point A is stable, and it is corresponding to the resting state of the neuron model. However, for the equilibrium points B and C, there are both one eigenvalue’s real part more than zero, so the equilibrium points B and C are both unstable [17]. But the AD two-dimension reduced neuron model has only one equilibrium point.

Figure 2. Intersection points of V-nullcline and n-nullcline in the V–n phase plane where I_App is zero. (a) The normal neuron model (from reference [17]) and (b) the AD neuron model.

In the following, we discuss the stability of the equilibrium point of the AD two-dimension reduced neuron model. The equilibrium point’s coordinate in the V–n phase plane can be obtained by the nonlinear value solution method of MATLAB. The equilibrium point’s coordinate is (−69.7488, 0.0253).

For the equilibrium point $A^{\mathrm{\prime }}$, the Jacobian matrix is $J_{A^{\mathrm{\prime }}}=\left[\begin{array}{cc}-0.0462& -0.0279\\ 0.0043& -1.7462\end{array}\right].$

The eigenvalues of Jacobian matrix $J_{A^{\mathrm{\prime }}}$ are ${\lambda }_{A^{\mathrm{\prime }}1}=-0.0462;{\lambda }_{A^{\mathrm{\prime }}2}=-\mathrm{1.7462.}$

According to eigenvalues of the equilibrium point $A^{\mathrm{\prime }}$, when the stimulation current is zero, the eigenvalues of the equilibrium point are both less than zero, so the equilibrium point $A^{\mathrm{\prime }}$ is stable, and it is corresponded to the resting state of the neuron model.

From Figure 2, when the stimulation current is zero, the dynamic characteristics of the two-dimension reduced neuron model are substantially changed under the pathology condition of AD. Under AD’s action, the equilibrium point’s number of the neuron model changes from three to one. The two unstable equilibrium points disappear, and only one equilibrium point corresponded to the resting state of the neuron model is preserved.

3.3. The two-dimension reduced neuron model’s dynamic bifurcation characteristics under the AD pathology condition

The dynamic bifurcation characteristics of the normal two-dimension neuron model under the stimulation of the direct current have been discussed in detail in reference [17]. The main results in reference [17] are as follows: When the stimulation current gradually increases from zero, the normal two-dimension neuron model undergoes the saddle-node bifurcation. The neuron model is equivalent to a bistable integrator, and has the common dynamic properties of the integrator such as definite threshold value and class 2 neural excitability. In addition, the stimulation current’s discharge threshold of the neuron model is near 0.326 nA. Because the normal neuron model is the bistable integrator, the stable limit cycle (the continuous discharge state) and the stable equilibrium point (the resting state) can coexist in the subthreshold voltage range.

When the stimulation current gradually increases from zero, the discharge pattern of the AD two-dimension neuron model described by formula (5) can also change from the resting state to the continuous discharge state. During the changing process, the AD two-dimension neuron model undergoes the complex dynamic bifurcation which is different from the normal two-dimension neuron model. Figure 3 shows the dynamic bifurcation process of the AD two-dimension neuron model in the V–n phase plane under the stimulation of current I_App, where the simulation time is 0–1000 ms.

Figure 3. The dynamic bifurcation process of the AD neuron model under the stimulation current’s changing, where the stable equilibrium points are expressed by the black circles, and the unstable equilibrium points are expressed by the white circles. (a) I_App = 0 nA, (b) I_App = 0.2 nA, (c) I_App = 0.25 nA, (d) I_App = 0.3 nA, (e) I_App = 0.31 nA, (f) I_App = 0.35 nA, (g) I_App = 4 nA, (h) I_App = 8 nA, (i) I_App = 8.69 nA, (j) I_App = 8.7 nA, (k) I_App = 9 nA and (l) I_App = 12 nA.

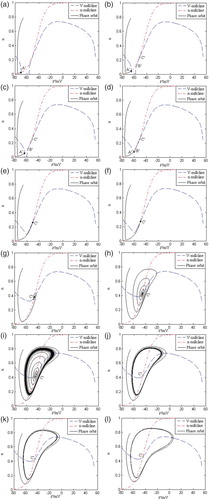
From Figure 3, when the stimulation current gradually increases from zero, the stable equilibrium point $A^{\mathrm{\prime }}$ in the V–n phase plane moves to the right along the V axis, and at the same time the V-nullcline shifts upward. The V-nullcline intersects with the n-nullcline, and gives birth to the two unstable equilibrium points ($B^{\mathrm{\prime }}$ and $C^{\mathrm{\prime }}$). With the stimulation current’s increasing, the stable equilibrium point $A^{\mathrm{\prime }}$ and the unstable equilibrium point $B^{\mathrm{\prime }}$ approach and coalesce with each other. At last, they annihilate, and at the same time, the unstable equilibrium point $C^{\mathrm{\prime }}$ becomes stable. With the stimulation current’s increasing, the stable equilibrium point $C^{\mathrm{\prime }}$ gradually loses stability and gives birth to a small-amplitude subliminal oscillating phase trajectory around the equilibrium point $C^{\mathrm{\prime }}$. The oscillating amplitude is damped according to the exponential form. Moreover, these subliminal oscillating phase trajectories finally return to the stable equilibrium point $C^{\mathrm{\prime }}$ (the resting state of the neuron model). When the stimulation current I_App reaches some value(near 8.7 nA), the subliminal oscillating phase trajectories do not return to the stable equilibrium point, and give birth to a small-amplitude limit cycle attractor. At the same time, the stable equilibrium point $C^{\mathrm{\prime }}$ loses stability. As I_App keeps on increasing, the amplitude of the limit cycle also increases and it becomes the full-size spiking limit cycle. The AD neuron model undergoes the supercritical Andronov–Hopf bifurcation process, which is different from the normal neuron model’s saddle-node bifurcation process.

Under the pathology condition of AD, the AD two-dimension reduced neuron model has different dynamic characteristics. From the property of the supercritical Andronov–Hopf bifurcation, the AD neuron model is equivalent to a monostable resonator, which is different from the normal two-dimension neuron model’s bistable integrator. So, it has the common dynamic properties of the resonator such as the subliminal discharge behaviour, and class 2 neural excitability. When I_App is near 8.7 nA (shown in Figure 3(j)), the stable limit cycle attractor begins to arise, and the AD neuron model goes into the stable ‘all or none’ discharge state. So, the AD neuron model undergoes the supercritical Andronov–Hopf bifurcation near 8.7 nA. In addition, because the AD neuron model is the monostable resonator, the stable limit cycle (the continuous discharge state) and the stable equilibrium point (the resting state) cannot coexist, which is different from the normal two-dimension neuron model. Compared with the normal neuron model, the AD neuron model has lower excitability in the subthreshold voltage range, which shows that the neuron model’s activity is greatly lower under the pathology condition of AD.

4. Conclusion

In the paper, the reduced model of CA1 pyramid neuron is taken as the object. Based on the electrophysiological experimental data under the AD pathology condition, the two-dimension reduced neuron model under the AD pathology condition is built by modifying suitably parameters’ values. The reduced neuron model’s dynamic characteristics under AD’s effect are comparatively analyzed and discussed.

Compared with the normal neuron model, the dynamic characteristics of the AD neuron model are obviously changed, such as the increase of discharge current threshold, the lowness of excitability, and the decrease of equilibrium point’s number. Under stimulation of the direct current, the neuron model under the AD condition undergoes the supercritical Andronov–Hopf bifurcation from the rest state to the continuous discharge state, which is different from the normal neuron model which undergoes the saddle-node bifurcation. So, under AD’s action, the neuron model changes into a resonator with monostable state from an integrator with bistable state, and its dynamics characters are substantially changed.

The research reveals the neuron model’s dynamic characteristics’ changing under effect of AD, and provides some theoretic basis for AD research by neurodynamics theory.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by China Postdoctoral Science Foundation funded project. The project name is ‘Study on the Alzheimer Disease’s Attack Dynamic Mechanism and Its Relevance to the Cortex EEGs (No. 2013M542355)’.