Stability analysis of an artificial biomolecular oscillator with non-cooperative regulatory interactions

ABSTRACT

Oscillators are essential to fuel autonomous behaviours in molecular systems. Artificial oscillators built with programmable biological molecules such as DNA and RNA are generally easy to build and tune, and can serve as timers for biological computation and regulation. We describe a new artificial nucleic acid biochemical reaction network, and we demonstrate its capacity to exhibit oscillatory solutions. This network can be built in vitro using nucleic acids and three bacteriophage enzymes, and has the potential to be implemented in cells. Numerical simulations suggest that oscillations occur in a realistic range of reaction rates and concentrations.

KEYWORDS:

• Nonlinear systems
• nonlinear oscillations
• biological applications
• biochemistry
• molecular biology

AMS SUBJECT CLASSIFICATION:

• 34A34
• 34C15
• 78A70
• 92C40

1. Introduction

All organisms require timing circuits to orchestrate processes related to their life cycle, such as cell growth, metabolism, and division [36]. By building molecular timers from the bottom up, we have an opportunity to understand the design requirements to programme periodic biochemical behaviours. In addition, synthetic oscillators are useful components to direct autonomous molecular operations in vivo and in vitro [11,13,30,33,35].

In vitro nucleic acid oscillators can be built with a small number of parts, and their behaviour is quantitatively predictable [15,16,19,22,35]. Nucleic acids have become molecular building blocks for a variety of logic and dynamic circuits, because their thermodynamic and kinetic interactions can be programmed by choosing their sequence content with rational optimization algorithms. Existing nucleic acid oscillators however cannot be ported to the cellular environment, because they rely on the presence of multiple single-stranded or partially single-stranded DNA species, which are incompatible with the cellular machinery [15,16,19,22]. Here we describe a new nucleic acid oscillator architecture that has the potential to overcome this limitation, as it does not require single-stranded DNA molecules. A particularly interesting aspect of our circuit is that all regulatory interactions are non-cooperative. Therefore, the corresponding model does not include Hill-type nonlinearities, present in the majority of models for molecular non-equilibrium circuits.

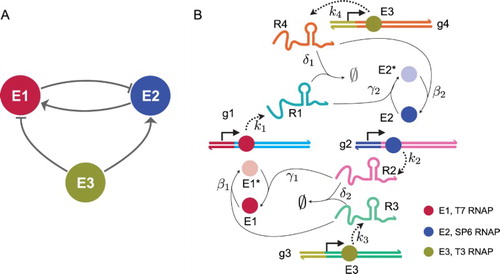
Our oscillator comprises three polymerases, two of which mutually regulate each other (Figure 1(a )). The interactions among enzymes are defined by four synthetic genes and four RNA species (Figure 1(b )). The activity of two of the enzymes is modulated by RNA species that serve as inhibitors or activators. The third enzyme species controls the baseline production of two of the RNA species, and has a net effect of counteracting the mutual regulation of the other two enzymes. For instance, let us consider the pathway by which enzyme $E_2$ is inhibited by enzyme $E_1$ and activated by enzyme $E_3$. $E_1$ produces RNA species $R_1$ by transcribing gene $g_1$; $R_1$ binds to and inhibits enzyme $E_2$, converting it to inactive enzyme $E_2^{\ast }$ (a reaction experimentally demonstrated, for instance, in [23, 24]). RNA species $R_4$ (transcribed by $E_3$) counteracts this pathway and causes reactivation of $E_2$ (conversion of $E_2^{\ast }$ to $E_2$), because it is designed to displace $R_1$ bound to $E_2$, and to titrate free $R_1$ as well. Similar reactions generate inhibition and activation pathways for $E_1$ (due to $E_3$ and to $E_2$, respectively). Overall, these interactions contribute to creating a negative feedback loop. This system can be experimentally implemented using T7, T3, and SP6 bacteriophage RNA polymerases [20,21,31], which can be purchased off-the-shelf from many vendors. RNA sequences (known as aptamers [12]) that bind to bacteriophage RNA polymerases and work as inhibitors have been experimentally characterized  [23,24]. RNA activators can be designed as strands whose sequences are complementary to the sequences of the inhibitors via the mechanism of strand displacement and strand titration [18,37].

Figure 1. (a) Architecture of the three-node oscillator: enzymes $E_1$ and $E_2$ mutually regulate their concentration (arrows indicate activation, flat arrows indicate repression) generating a negative feedback loop; enzyme $E_3$ counteracts the loop regulation.(b) Schematic of the chemical reactions underlying the oscillator architecture. Different enzyme species are indicated as circles of different colour ; bright colour indicates active enzyme, and dim colour indicates inactive enzyme. RNA species are transcribed (dashed arrows) from synthetic genes present at constant concentration; enzymes are activated or inhibited by a given RNA species according to the illustrated reactions and corresponding rates. The full set of reactions is listed in Section 2, and result in ODE systems (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ).

We describe this system by means of ordinary differential equations (ODEs) built using the law of mass action, starting from a list of chemical reactions reported in Section 2. We demonstrate that the system is a candidate oscillator due to the sign pattern of its Jacobian matrix [4, 5]; in particular we show that the system admits transitions to instability that are exclusively oscillatory.

Our analysis relies on monotone systems theory (background is provided in Section 3) and the theory of invariant sets. In Section 4 we study the capacity of this dynamical system to structurally exhibit sustained oscillations whenever it becomes unstable, in view of its particular Jacobian structure; this approach can be applied to a variety of chemical reaction networks, as we have shown, for instance, in the context of other titration-based regulatory networks [9]. Structural (namely, parameter-free) results can greatly help unravel the functioning of biological systems, which are affected by intrinsic uncertainties and variabilities in their parameters, but can nonetheless exhibit an extraordinary robustness and resilience [3]. We conclude with a numerical bifurcation analysis and study of period and amplitude as a function of variations in individual parameters, showing that for realistic reaction rates the system exhibits oscillatory behaviours (Section 5). We previously described a two-enzyme oscillator relying on RNA aptamers [2,10]; we claim that a three-enzyme system is more tunable, and simulation results indicate that in a certain region of parameter space its amplitude can be modulated independently of the period.

2. A three-enzyme oscillator regulated by first- and second-order reactions

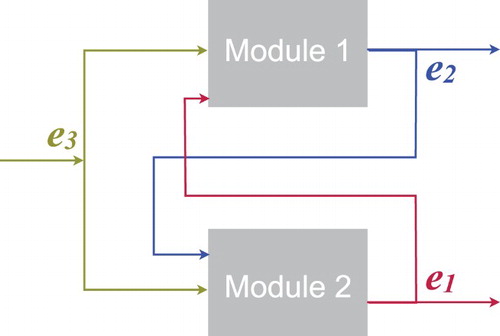
In the following, capital letters represent chemical species and the corresponding lowercase letters represent species concentrations (e.g. species A has concentration a). Our three-node oscillator is described by the biochemical reactions below. Reactions are grouped in two sets corresponding to functional modules (Figure 2), whose common external input is $E_3$. For simplicity we assume a common degradation rate for all products $R_i,i=1,\dots ,4$.

Figure 2. Schematic of the interconnections between reaction Modules 1 and 2, with enzyme concentrations as inputs and outputs.

The differential equations describing Module 1 are: (1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1)

The differential equations describing Module 2 are: (2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2)

The total concentration of $E_1$ and $E_2$ is assumed to be constant, and equal to $e_1^{\mathrm{tot}}$ and $e_2^{\mathrm{tot}}$, respectively; hence, mass conservation laws yield $e_1^{\ast }=e_1^{\mathrm{tot}}-e_1$ and $e_2^{\ast }=e_2^{\mathrm{tot}}-e_2$. The two modules are interconnected and form a feedback loop: Module 1 (associated with variables $r_1$, $r_3$ and $e_2$) receives input $e_1$ from Module 2; in turn, Module 2 (associated with variables $r_2$, $r_4$ and $e_1$) receives input $e_2$ from Module 1. Both modules receive input $e_3$, which we assume is constant (Figure 2); we assume that the timescale at which $e_3$ binds to a gene and transcribes RNA is fast relative to the other timescales in the system, so that its dynamics can be neglected; this assumption is sensible for short transcripts (30–60 bases). In the next sections we demonstrate that transitions to instability in this system can occur exclusively due to a pair of complex conjugate eigenvalues crossing the imaginary axis, hence sustained oscillations necessarily arise whenever the system is driven to instability. From numerical simulations it is apparent that the system can actually be destabilized, for suitable parameter choices, and is therefore a good candidate oscillator.

3. Background

We summarize several background notions that are required to introduce our main results in Section 4. Additional information can be found in references [4,5]. Consider a system: (3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) where μ is a real-valued parameter and $f(\cdot ,\cdot )$ is a sufficiently smooth function, continuous in μ, satisfying the following Assumptions for every admissible value of μ.

Assumption 1.

All the solutions of (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) are globally uniformly asymptotically bounded in the compact set $\mathcal{S}\subset {\mathbb{R}}^n$.

Hence, system (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) admits an equilibrium $\overline{x}$ in $\mathcal{S}$ [25,26,29].

Assumption 2.

$\mathrm{\partial }{f}_i/\mathrm{\partial }{x}_j$ is either always positive, always negative, or always null in the considered domain.

Assumption 3.

For all i, $\mathrm{\partial }{f}_i/\mathrm{\partial }{x}_i<0,$ that is, the system is non-autocatalytic.

Due to the monotonicity of $f_i(\cdot )$ with respect to each argument $x_j$, the Jacobian matrix $\mathbf{\text{J}}$ of system (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) is sign definite.

Definition 3.1.

Given a system with a sign-definite Jacobian $\mathbf{\text{J}}$, its structure is the sign pattern matrix $\mathrm{\Sigma }=\mathrm{sign}\left[\mathbf{\text{J}}\right]$.

The structure Σ of system (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) is assumed to be invariant with respect to μ. Assumption 1 ensures that an equilibrium exists; all the following definitions refer to this equilibrium, which is, in general, a function of μ: $f({\overline{x}}_{\mu },\mu )=0$. We assume that ${\overline{x}}_{\mu }$ depends continuously on μ. Note that a suitable change of coordinates always allows us to shift the equilibrium to the origin, without affecting our analysis.

Definition 3.2.

System (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) undergoes a transition to instability $($TI$)$ at $\mu ={\mu }^{\ast }$ iff its Jacobian matrix $\mathbf{\text{J}}\left({\overline{x}}_{\mu }\right)$ is asymptotically stable in a left neighbourhood of ${\mu }^{\ast }$, and unstable in a right neighbourhood.¹ A TI is simple if at most a single real eigenvalue or a single pair of complex conjugate eigenvalues crosses the imaginary axis.

Definition 3.3.

System (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ) undergoes an oscillatory transition to instability $($OTI$)$ at $\mu ={\mu }^{\ast }$ iff its Jacobian matrix $\mathbf{\text{J}}\left({\overline{x}}_{{\mu }^{\ast }}\right)$ has a single pair of pure imaginary eigenvalues, while all the other eigenvalues have negative real part: $\sigma \left(\mathbf{\text{J}}\right({\overline{x}}_{{\mu }^{\ast }}\left)\right)=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\},\mathrm{where}{\lambda }_{1,2}=\pm j\omega ,$ with $Re\left({\lambda }_k\right)<0$ for k>2 and $Re\left({\lambda }_k\right)>0$ for k=1,2 in a right neighbourhood of ${\mu }^{\ast }$.

We now provide general definitions for candidate oscillatory and multistationary systems. We consider system (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ), with its given structure Σ (invariant with respect to μ), under Assumptions 1, 2 and 3.

Definition 3.4.

A system of the form (3(3) $\dot{x}\left(t\right)=f\left(x\right(t),\mu ),x\in {\mathbb{R}}^n,$(3) ), with structure Σ, is structurally a candidate

1. oscillator in the weak sense iff it admits an OTI for some $\mu ={\mu }^{\ast }$;

2. oscillator in the strong sense iff every simple TI (if any) is an OTI;

Necessary and sufficient conditions characterizing strong and weak oscillators/ multistationary systems are provided in [4] in terms of cycles in the structure graph. We associate matrix Σ with a directed n-node graph, whose arcs are positive ($+1$), negative ($-1$), or zero depending on the sign of the corresponding matrix entries.

Definition 3.5.

Given a graph, a cycle is an oriented, closed sequence of distinct nodes connected by distinct directed arcs. A cycle is negative (positive) if the number of negative arcs is odd (even). The order of a cycle is the number of arcs involved in the cycle. We say a system is critical when all negative cycles (if any) are of order two.

Proposition 3.6.

A non-critical system is a candidate oscillator in the weak sense if and only if its structure has at least one negative cycle $($necessarily of order greater than two$)$.

Proposition 3.7.

A non-critical system is a candidate oscillator in the strong sense if and only if its structure has only negative cycles.

Proofs for Propositions 3.6 and 3.7 can be found in [4].

Remark 1.

The results above are verified as well if we drop Assumption 1 and we restrict our analysis to solutions that belong to a compact positively invariant set $\mathcal{S}$, with a non-empty interior and with no equilibrium points on the boundary.

The graph-based results in [4] have been generalized in [5] to the case of systems that are the sign definite interconnection of subsystems that are either monotone or anti-monotone (as in the case of our system). We provide below the definitions of monotone and anti-monotone system.

Definition 3.8.

A system (4) $\dot{x}\left(t\right)=f\left(x\right(t),u(t\left)\right),$(4) where $u(\cdot )\in \mathbb{R}$ is a scalar, time varying input, is input-to-state monotone if, denoting as $x_1\left(t\right)$ and $x_2\left(t\right)$ the solutions of the system corresponding to inputs $u_1\left(t\right)$ and $u_2\left(t\right)$, the fact that $x_2\left(0\right)\ge x_1\left(0\right)$ and $u_2\left(t\right)\ge u_1\left(t\right)$ for t>0 implies that $x_2\left(t\right)\ge x_1\left(t\right)$ for t>0, where inequalities are intended to hold componentwise. The system is input-to-state anti-monotone if the input has the opposite effect on the state, that is, if $x_2\left(0\right)\ge x_1\left(0\right)$ and $u_2\left(t\right)\le u_1\left(t\right)$ for t>0, then $x_2\left(t\right)\ge x_1\left(t\right)$ for t>0. If the system includes an output $y=g\left(x\right)$, the system is input–output monotone (anti-monotone) if it is input-to-state monotone (anti-monotone) and if $x_2\ge x_1$ implies $g\left(x_2\right)\ge g\left(x_1\right).$

A simple characterization of input-to-state monotonicity and anti-monotonicity [1, 28] can be provided by exploiting the concept of Metzler matrix: a matrix is Metzler if its elements satisfy $a_{ij}\ge 0$, $\mathrm{\forall }(i,j)$ such that $i\ne j$.

Theorem 3.9.

System (4(4) $\dot{x}\left(t\right)=f\left(x\right(t),u(t\left)\right),$(4) ) is input-to-state monotone if its Jacobian matrix $\mathbf{\text{J}}=\mathrm{\partial }f/\mathrm{\partial }x$ is a Metzler matrix and $\mathrm{\partial }f/\mathrm{\partial }u\ge 0$ componentwise. Conversely, system $\left(4\right)$ is input-to-state anti-monotone if its Jacobian matrix $\mathbf{\text{J}}=\mathrm{\partial }f/\mathrm{\partial }x$ is a Metzler matrix and $\mathrm{\partial }f/\mathrm{\partial }u\le 0$ componentwise.

A more general concept, which we will use in the following, is given by monotonicity (or anti-monotonicity) with respect to a given signature tuple $(s_1,\dots ,s_n)$, where $s_i=1$ or $-1$ for all i [14]: this amounts to requiring that, after changing the sign of the state variables as ${\hat{x}}_i=s_i{x}_i$ for all i, the system becomes monotone (or anti-monotone). Hence, Theorem 3.9 applies to the system in the new coordinates.

4. Analytical results

4.1. Existence of equilibria

First, we show that this system always admits a steady state (equilibrium).

Proposition 4.1.

Consider the interconnection of systems (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ). For any constant $e_3>0,$ there exists a suitably large $\rho \in {\mathbb{R}}^{+}$ such that the compact set ${\mathcal{S}}_{\rho }=\{r_1,r_2,r_3,r_4,e_1,e_2\ge 0:r_1+r_3\le \rho ,r_2+r_4\le \rho ,e_1\le e_1^{\mathrm{tot}},e_2\le e_2^{\mathrm{tot}}\}$ is positively invariant. Moreover, all of the solutions of the system are globally uniformly asymptotically bounded in ${\mathcal{S}}_{\rho },$ hence the interconnection of systems $\left(1\right)$ and $\left(2\right)$ satisfies Assumption 1.

Proof.

The inequalities $e_1\left(t\right)\le e_1^{\mathrm{tot}}$ and $e_2\left(t\right)\le e_2^{\mathrm{tot}}$ are always satisfied by construction. Consider the constraint $r_1+r_3\le \rho$ and assume that at some point $r_1+r_3=\rho$. Then $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}(r_1+r_3)& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1+{\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3\\ & \le {\alpha }_1{e}_1^{\mathrm{tot}}+{\alpha }_3{e}_3-\phi r_1-\phi r_3={\alpha }_1{e}_1^{\mathrm{tot}}+{\alpha }_3{e}_3-\phi \rho <0\end{array}$ for ρ large enough: $\rho >({\alpha }_1{e}_1^{\mathrm{tot}}+{\alpha }_3{e}_3)/\phi$. Hence, the constraint $r_1+r_3\le \rho$ cannot be violated. Analogously, the constraint $r_2+r_4\le \rho$ cannot be violated because, if at some point $r_2+r_4=\rho$, then $\frac{\mathrm{d}}{\mathrm{d}t}(r_2+r_4)\le {\alpha }_2{e}_2^{\mathrm{tot}}+{\alpha }_4{e}_3-\phi r_2-\phi r_4={\alpha }_2{e}_2^{\mathrm{tot}}+{\alpha }_4{e}_3-\phi \rho <0$ for $\rho >({\alpha }_2{e}_2^{\mathrm{tot}}+{\alpha }_4{e}_3)/\phi$. Then, any value $\rho >max\{({\alpha }_1{e}_1^{\mathrm{tot}}+{\alpha }_3{e}_3)/\phi ,({\alpha }_2{e}_2^{\mathrm{tot}}+{\alpha }_4{e}_3)/\phi \}$ ensures that ${\mathcal{S}}_{\rho }$ is positively invariant. Also, since $\left(\mathrm{d}/\mathrm{d}t\right)(r_1+r_3)$ is negative whenever $r_1+r_3\ge \rho$ and $\left(\mathrm{d}/\mathrm{d}t\right)(r_2+r_4)$ is negative whenever $r_2+r_4\ge \rho$, any trajectory of the system is uniformly asymptotically bounded in ${\mathcal{S}}_{\rho }$ (indeed, $V_1=r_1+r_3$ and $V_2=r_2+r_4$ can be taken as Lyapunov-like functions for modules 1 and 2, respectively, to show that all the trajectories of the system are uniformly ultimately bounded in the compact set ${\mathcal{S}}_{\rho }$ [6]).

Proposition 4.2.

The dynamical system defined by the interconnection of systems (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ) always admits the existence of a steady-state.

Proof.

The existence of the compact invariant set ${\mathcal{S}}_{\rho }$ where the solutions of the system are globally uniformly asymptotically bounded (Proposition 4.1) implies the existence of a steady-state  [25,26,29].

We later demonstrate that this steady state is unique.

Remark 2.

The presence of degradation reactions (at rate $\phi >0$) is essential to have structural boundedness. In fact, if we set $\phi =0$ and we consider the function $\psi =-r_1+r_3+e_2$, we have $\dot{\psi }=-\dot{r_1}+\dot{r_3}+\dot{e_2}=-{\alpha }_1{e}_1+{\alpha }_3{e}_3\ge -{\alpha }_1{e}_1^{\mathrm{tot}}+{\alpha }_3{e}_3,$ which may grow unbounded for a large value of $e_3$.

4.2. Monotonicity properties and uniqueness of equilibrium point

Now we show that the overall system is the feedback interconnection of two subsystem, corresponding to the modules defined earlier, that are, respectively, anti-monotone and monotone. This property further implies that the system admits a unique equilibrium.

We individually linearize subsystems (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ) around an equilibrium point (which is guaranteed to exist), and we begin by studying each subsystem in isolation. (6) $\mathrm{Module}1:\dot{z}={\mathbf{\text{A}}}_{\mathbf{\text{1}}}z+{\mathbf{\text{B}}}_{\mathbf{\text{1}}}\delta e_1,$(6) (6) $\mathrm{Module}2:\dot{w}={\mathbf{\text{A}}}_{\mathbf{\text{2}}}w+{\mathbf{\text{B}}}_{\mathbf{\text{2}}}\delta e_2,$(6) where the linearized state variables of each subsystems are $z=[\delta r_1\delta r_3\delta e_2{]}^{\mathrm{\top }}$ and $w=[\delta r_2\delta r_4\delta e_1{]}^{\mathrm{\top }}$. We denote equilibrium values of each variable with a $\overline{}$ symbol (e.g. ${\overline{e}}_1$ is the equilibrium of $e_1$). The linearized dynamics are defined by matrices: ${\mathbf{\text{A}}}_{\mathbf{\text{1}}}=\left[\begin{array}{cccc}-{\beta }_1{\overline{e}}_2-{\delta }_1{\overline{r}}_3-\phi & -{\delta }_1{\overline{r}}_1& -{\beta }_1{\overline{r}}_1& \\ -{\delta }_1{\overline{r}}_3& -{\gamma }_1{\overline{e}}_2^{\ast }-{\delta }_1{\overline{r}}_1-\phi & {\gamma }_1{\overline{r}}_3\\ -{\beta }_1{\overline{e}}_2& {\gamma }_1{\overline{e}}_2^{\ast }& -{\beta }_1{\overline{r}}_1-{\gamma }_1{\overline{r}}_3\end{array}\right],{\mathbf{\text{B}}}_{\mathbf{\text{1}}}=\left[\begin{array}{c}{\alpha }_1\\ 0\\ 0\end{array}\right]$ and ${\mathbf{\text{A}}}_{\mathbf{\text{2}}}=\left[\begin{array}{ccc}-{\gamma }_2{\overline{e}}_1^{\ast }-{\delta }_2{\overline{r}}_4-\phi & -{\delta }_2{\overline{r}}_2& {\gamma }_2{\overline{r}}_2\\ -{\delta }_2{\overline{r}}_4& -{\beta }_2{\overline{e}}_1-{\delta }_2{\overline{r}}_2-\phi & -{\beta }_2{\overline{r}}_4\\ {\gamma }_2{\overline{e}}_1^{\ast }& -{\beta }_2{\overline{e}}_1& -{\gamma }_2{\overline{r}}_2-{\beta }_2{\overline{r}}_4\end{array}\right],{\mathbf{\text{B}}}_{\mathbf{\text{2}}}=\left[\begin{array}{c}{\alpha }_2\\ 0\\ 0\end{array}\right].$ The two linearized subsystems are stable, and the matrices defining their dynamics (Jacobian matrices of the nonlinear systems) are Metzler up to changes in the sign of some variables. This can be easily shown by changing sign to the first component of z and to the second component of w: $z_1:=-z_1$ and $w_2:=-w_2$. This is equivalent to changing sign to $\delta r_1$ and $\delta r_4$, where $r_1$ and $r_4$ are variables of the original system, and provides matrices: (7) ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}=\left[\begin{array}{cccc}-{\beta }_1{\overline{e}}_2-{\delta }_1{\overline{r}}_3-\phi & +{\delta }_1{\overline{r}}_1& +{\beta }_1{\overline{r}}_1& \\ +{\delta }_1{\overline{r}}_3& -{\gamma }_1{\overline{e}}_2^{\ast }-{\delta }_1{\overline{r}}_1-\phi & {\gamma }_1{\overline{r}}_3\\ +{\beta }_1{\overline{e}}_2& {\gamma }_1{\overline{e}}_2^{\ast }& -{\beta }_1{\overline{r}}_1-{\gamma }_1{\overline{r}}_3\end{array}\right],{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{1}}}=\left[\begin{array}{c}-{\alpha }_1\\ 0\\ 0\end{array}\right],$(7) and (8) ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{ccc}-{\gamma }_2{\overline{e}}_1^{\ast }-{\delta }_2{\overline{r}}_4-\phi & +{\delta }_2{\overline{r}}_2& {\gamma }_2{\overline{r}}_2\\ +{\delta }_2{\overline{r}}_4& -{\beta }_2{\overline{e}}_1-{\delta }_2{\overline{r}}_2-\phi & +{\beta }_2{\overline{r}}_4\\ {\gamma }_2{\overline{e}}_1^{\ast }& +{\beta }_2{\overline{e}}_1& -{\gamma }_2{\overline{r}}_2-{\beta }_2{\overline{r}}_4\end{array}\right],{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{c}{\alpha }_2\\ 0\\ 0\end{array}\right].$(8)

Remark 3.

We have applied a local change of variables, since $z_1=\delta r_1$ and $w_2=\delta r_4$ are variables of the linearized system. This is equivalent to applying the linear transformations $z=T_1\hat{z}$ and $w=T_2\hat{w}$, with $T_1=\mathrm{diag}\{-1,1,1\}$ and $T_2=\mathrm{diag}\{1,-1,1\}$. This leads to the transformed state matrices ${\hat{A}}_1=T_1^{-1}{A}_1{T}_1$ and ${\hat{A}}_2=T_2^{-1}{A}_2{T}_2$, and to the transformed input matrices ${\hat{B}}_1=T_1^{-1}{B}_1$ and ${\hat{B}}_2=T_2^{-1}{B}_2$.

Proposition 4.3.

Matrices ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}$ in Equation $\left(7\right)$ and ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}$ in Equation $\left(8\right)$ are Metzler and are Hurwitz stable. Moreover, their inverse matrices are $($element-wise$)$ negative.

Proof.

Consider systems (5(6) $\mathrm{Module}1:\dot{z}={\mathbf{\text{A}}}_{\mathbf{\text{1}}}z+{\mathbf{\text{B}}}_{\mathbf{\text{1}}}\delta e_1,$(6) ) and (6(6) $\mathrm{Module}2:\dot{w}={\mathbf{\text{A}}}_{\mathbf{\text{2}}}w+{\mathbf{\text{B}}}_{\mathbf{\text{2}}}\delta e_2,$(6) ), which after the sign change have matrices (7(6) $\mathrm{Module}2:\dot{w}={\mathbf{\text{A}}}_{\mathbf{\text{2}}}w+{\mathbf{\text{B}}}_{\mathbf{\text{2}}}\delta e_2,$(6) ) and (8(7) ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}=\left[\begin{array}{cccc}-{\beta }_1{\overline{e}}_2-{\delta }_1{\overline{r}}_3-\phi & +{\delta }_1{\overline{r}}_1& +{\beta }_1{\overline{r}}_1& \\ +{\delta }_1{\overline{r}}_3& -{\gamma }_1{\overline{e}}_2^{\ast }-{\delta }_1{\overline{r}}_1-\phi & {\gamma }_1{\overline{r}}_3\\ +{\beta }_1{\overline{e}}_2& {\gamma }_1{\overline{e}}_2^{\ast }& -{\beta }_1{\overline{r}}_1-{\gamma }_1{\overline{r}}_3\end{array}\right],{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{1}}}=\left[\begin{array}{c}-{\alpha }_1\\ 0\\ 0\end{array}\right],$(7) ). Since all of their off-diagonal entries are non-negative, ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}$ and ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}$ are Metzler matrices. They are also irreducible.² Hurwitz stability (all the eigenvalues of the Jacobian $\mathbf{\text{J}}=\mathrm{\partial }f/\mathrm{\partial }x\left(\overline{x}\right)$ have a negative real part) immediately follows from the fact that ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}$ and ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}$ are Metzler and diagonally dominant, with negative diagonal entries (this is a consequence of Gershgorin's circle theorem). Finally, any stable and irreducible Metzler matrix has an element-wise negative inverse (see [6] for details).

We are now ready to demonstrate the monotonicity properties of the two nonlinear modules.

Proposition 4.4.

Systems $\left(1\right)$ and $\left(2\right)$ are, respectively, input-to-state anti-monotone and monotone after the sign change in the relative variables: (9) $\widehat{\delta r_1}=-\delta r_1\mathrm{and}\widehat{\delta r_4}=-\delta r_4.$(9)

Proof.

This follows from Theorem 3.9, since the state matrices ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}$ and ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}$ are Metzler, while the input matrices ${\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{1}}}$ and ${\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{2}}}$ are, respectively, non-positive and non-negative.

Monotonicity and stability have important consequences on the static input-state and input–output characteristics (input–output equilibrium conditions) and on uniqueness of the equilibrium point. Indeed, the feedback of two systems that are either monotone or anti-monotone always admits a single equilibrium point (if any).

We have shown in Proposition 4.2 that an equilibrium always exists; we prove below, for completeness, that the static input–output characteristics of the two modules are monotonic, hence such an equilibrium point is unique.

Proposition 4.5.

We assume that inputs $e_1$ and $e_2$ in systems $\left(1\right)$ and $\left(2\right)$ are constant. Then, the steady-state values of the modules, ${\overline{r}}_1\left(e_1\right),$ ${\overline{r}}_3\left(e_1\right),$ ${\overline{e}}_2\left(e_1\right)$ and ${\overline{r}}_2\left(e_2\right),$ ${\overline{r}}_4\left(e_2\right),$ ${\overline{e}}_1\left(e_2\right),$ depend monotonically on the inputs. Precisely, ${\overline{r}}_2\left(e_2\right),$ ${\overline{r}}_4\left(e_2\right)$ and ${\overline{e}}_1\left(e_2\right)$ monotonically increase as a function of $e_2,$ while ${\overline{r}}_1\left(e_1\right),$ ${\overline{r}}_3\left(e_1\right)$ and ${\overline{e}}_2\left(e_1\right)$ monotonically decrease as a function of $e_1$.

Proof.

We recall that, for a generic system $\dot{x}=f(x,u)$, the steady-state characteristic $\overline{x}\left(u\right)$ is implicitly defined by $0=f(\overline{x},u).$ We can apply the implicit function theorem to find its derivative: $\frac{\mathrm{d}}{\mathrm{d}u}\overline{x}\left(u\right)={\left(-\frac{\mathrm{\partial }f}{\mathrm{\partial }\overline{x}}\right)}^{-1}\frac{\mathrm{\partial }f}{\mathrm{\partial }u}.$ Consider Module 1, after the sign change in the variables in Equation (9(8) ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{ccc}-{\gamma }_2{\overline{e}}_1^{\ast }-{\delta }_2{\overline{r}}_4-\phi & +{\delta }_2{\overline{r}}_2& {\gamma }_2{\overline{r}}_2\\ +{\delta }_2{\overline{r}}_4& -{\beta }_2{\overline{e}}_1-{\delta }_2{\overline{r}}_2-\phi & +{\beta }_2{\overline{r}}_4\\ {\gamma }_2{\overline{e}}_1^{\ast }& +{\beta }_2{\overline{e}}_1& -{\gamma }_2{\overline{r}}_2-{\beta }_2{\overline{r}}_4\end{array}\right],{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{c}{\alpha }_2\\ 0\\ 0\end{array}\right].$(8) ): $\frac{\mathrm{d}}{\mathrm{d}{e}_1}\overline{z}\left(e_1\right)=-({\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{1}}}{)}^{-1}{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{1}}}<0.$ The inequality holds componentwise (Proposition 4.3), hence after the sign change equilibria ${\overline{r}}_1\left(e_1\right)$, ${\overline{r}}_3\left(e_1\right)$ and ${\overline{e}}_2\left(e_1\right)$ are monotonically decreasing functions of $e_1$.

As for Module 2, after the sign change in Equation (9(8) ${\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{ccc}-{\gamma }_2{\overline{e}}_1^{\ast }-{\delta }_2{\overline{r}}_4-\phi & +{\delta }_2{\overline{r}}_2& {\gamma }_2{\overline{r}}_2\\ +{\delta }_2{\overline{r}}_4& -{\beta }_2{\overline{e}}_1-{\delta }_2{\overline{r}}_2-\phi & +{\beta }_2{\overline{r}}_4\\ {\gamma }_2{\overline{e}}_1^{\ast }& +{\beta }_2{\overline{e}}_1& -{\gamma }_2{\overline{r}}_2-{\beta }_2{\overline{r}}_4\end{array}\right],{\widehat{\mathbf{\text{B}}}}_{\mathbf{\text{2}}}=\left[\begin{array}{c}{\alpha }_2\\ 0\\ 0\end{array}\right].$(8) ): $\frac{\mathrm{d}}{\mathrm{d}{e}_2}\overline{w}\left(e_2\right)=-({\widehat{\mathbf{\text{A}}}}_{\mathbf{\text{2}}}{)}^{-1}{\widehat{\mathbf{\text{B}}}}_2>0$ componentwise, hence after the sign change ${\overline{r}}_2\left(e_2\right)$, ${\overline{r}}_4\left(e_2\right)$ and ${\overline{e}}_1\left(e_2\right)$ are monotonically increasing functions of input $e_2$.

Proposition 4.6.

The interconnection of systems (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ) admits a unique equilibrium.

Proof.

The system always admits a steady state, as shown in Proposition  4.2. Due to Proposition 4.5, ${\overline{e}}_2\left(e_1\right)$ is a decreasing function and ${\overline{e}}_1\left(e_2\right)$ is an increasing function. Thus, the system of equations: $\begin{array}{r}{e}_2={\overline{e}}_2\left(e_1\right),\\ e_1={\overline{e}}_1\left(e_2\right),\end{array}$ has a unique solution.

It is possible to demonstrate that this unique equilibrium is strictly positive, and there cannot be equilibria with zero components. This claim can be proved by showing that the two equilibrium equations intersect for positive values of $e_1$ and $e_2$. Then, we can show that all other variables have a positive steady-state from their equilibrium conditions, which are all derived analytically in the appendix.

4.3. The interconnected system admits exclusively oscillatory transitions to instability

Based on the properties demonstrated in the previous sections, we establish that our three-enzyme network has the appropriate structure to exhibit sustained oscillations, whenever it is driven to instability. More precisely, the network admits exclusively oscillatory transitions to instability.

Proposition 4.7.

The interconnection of systems $\left(1\right)$ and $\left(2\right)$ is a strong candidate oscillator.

Proof.

The Jacobian of the overall system, with variables ordered as ($\delta r_1$, $\delta r_3$, $\delta e_2$, $\delta r_2$, $\delta r_4$, $\delta e_1$) and with the variable sign change $\widehat{\delta r_1}=-\delta r_1$ and $\widehat{\delta r_4}=-\delta r_4$, highlights that the system is the negative feedback interconnection of two monotone subsystems: 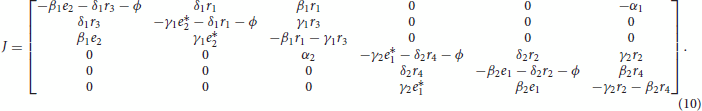Due to Proposition 4.1, the system satisfies Assumption 1. By inspecting the Jacobian matrix, it is apparent that Assumptions 2 and 3 are also satisfied. Therefore, the system is a strong candidate oscillator [4,5]. This means that the system can transition to instability exclusively due to a pair of complex conjugate eigenvalues crossing the imaginary axis (OTI) and yielding oscillatory dynamics.

5. Numerical analysis

Model (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) )–(2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ) was integrated using the MATLAB routine ode23. Bifurcation analysis, period and amplitude computation was also done writing MATLAB scripts ad hoc.

In the numerical analysis that follows, we choose nominal parameters (Table 1) that are compatible with reaction rates measured in nucleic acid strand displacement reactions and in vitro transcription. An example solution trajectory for Model (1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) )–(2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) ), integrated with the nominal parameters, is shown in Figure 3.

Figure 3. Left: Time evolution of $e_1$ and $e_2$ when parameters are chosen as in Table 1. Right: Trajectories in the plane $e_1$– $e_2$ (black) and equilibrium conditions (red and blue).

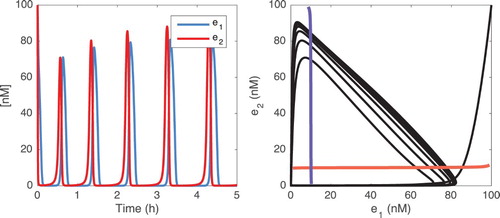
Table 1. Nominal simulation parameters.

Rate	Description	Value	Other studies
${\alpha }_1={\alpha }_2={\alpha }_3={\alpha }_4$ (/s)	Production of RNA	0.1	${10}^{-3}-1$ Refs. [8, 34]
${\beta }_1={\beta }_2$ (/M/s)	Inhibition	$5\cdot {10}^5$	${10}^4-{10}^6$ Refs. [18, 38]
${\gamma }_1={\gamma }_2$ (/M/s)	Activation	${10}^5$	${10}^4-{10}^6$ Refs. [18, 38]
${\delta }_1={\delta }_2$ (/M/s)	Titration	$4\cdot {10}^4$	${10}^4-{10}^6$ Refs. [18, 38]
φ (/s)	Degradation of RNA	$5\cdot {10}^{-5}$	${10}^{-5}-{10}^{-3}$ Refs. [7, 17]
$e_1\left(nM\right)$	Concentration	100
$e_2\left(nM\right)$	Concentration	100
$e_3\left(nM\right)$	Concentration	10

5.1. Randomized parameter sampling

First, we selected random values for the parameters sampling from a uniform distribution in the interval ${10}^{-2}$ to ${10}^2$ times the nominal parameter value (Table 1). We locate peaks and wells of the oscillations and compute period and amplitude as averaged over all the measured peaks and wells. A trajectory is classified as oscillatory if at least three oscillations are measured, if the period of the trajectory is between 0.5 and 40 h, and its amplitude is larger than 1 nM. This plot highlights that high degradation rates and low concentrations of $e_1$ and $e_2$ are associated with loss of oscillations (Figure 4).

Figure 4. We randomly choose parameters in the interval ${10}^{-2}$ to ${10}^2$ times their nominal value (listed in Table 1). Each black dot in this plot indicates that the (randomly) chosen parameter vector results in oscillations. Axes are in log scale. Orange diamonds represent the nominal value of each parameter (Table 1).

5.2. Bifurcation analysis

Using analytical equilibrium conditions (expressions (A.1(A.1) ${\overline{e}}_2({\overline{e}}_1,{\overline{e}}_3)=\frac{{\alpha }_4{\overline{e}}_3+\phi {\overline{r}}_2({\overline{e}}_1,{\overline{e}}_3)-\phi {\overline{r}}_4({\overline{e}}_1,{\overline{e}}_3)}{{\alpha }_2}.$(A.1) ) and (A.2(A.2) ${\overline{e}}_1({\overline{e}}_2,{\overline{e}}_3)=\frac{{\alpha }_3{\overline{e}}_3+\phi {\overline{r}}_1({\overline{e}}_2,{\overline{e}}_3)-\phi {\overline{r}}_3({\overline{e}}_2,{\overline{e}}_3)}{{\alpha }_1}.$(A.2) ) reported in the appendix), we find equilibria numerically and compute the eigenvalues of Jacobian (10(A.1) ${\overline{e}}_2({\overline{e}}_1,{\overline{e}}_3)=\frac{{\alpha }_4{\overline{e}}_3+\phi {\overline{r}}_2({\overline{e}}_1,{\overline{e}}_3)-\phi {\overline{r}}_4({\overline{e}}_1,{\overline{e}}_3)}{{\alpha }_2}.$(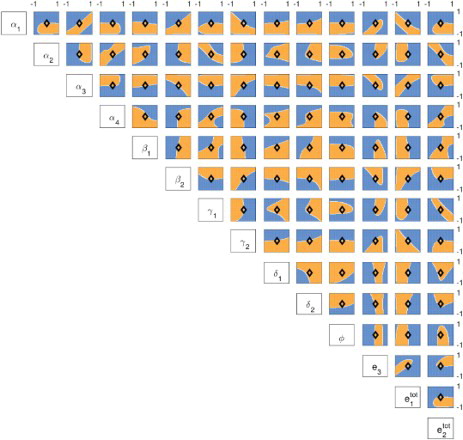A.1) ) at the equilibria. If at least one pair of complex conjugate eigenvalues with non-negative real part is found, the equilibrium is classified as oscillatory. We vary two parameters simultaneously, while all others are kept constant as in Table 1. Oscillatory regions are shown in orange in Figure 5, while stable regions are shown in blue.

Figure 5. Log plots showing how varying pairs of parameters influences the stability of the equilibrium. Each parameter was varied between one tenth to 10 times its nominal value (black diamond; nominal values listed in Table 1). Orange regions indicate oscillatory behaviour; blue regions indicate a single stable equilibrium.

5.3. Period and amplitude

We focus on the influence of reaction rates and total concentrations of $e_i$ on the period and amplitude. Parameters ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$, $e_3$, $e_1^{\mathrm{tot}}$ and $e_2^{\mathrm{tot}}$ are particularly relevant because they are experimentally easy to change (Figure1(b)): ${\alpha }_i$, $i=1,\dots ,4$, are transcription rates, which can be tuned by mutating the promoter region; $e_1^{\mathrm{tot}}$, $e_2^{\mathrm{tot}}$ and $e_3$ can be chosen by the experimenter.

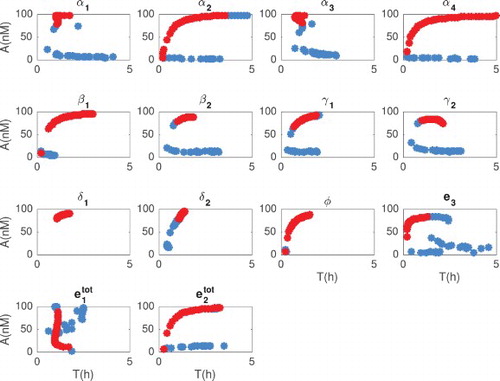
We compute the period and amplitude from integrated solutions to the ODEs. As explained in Section 5.1, we locate peaks and wells of the oscillations and compute period and amplitude as averaged over all the measured peaks and wells. A trajectory is classified as oscillatory if its period is between 0.5 and 40 h, and its amplitude is larger than 1  nM. The results are shown in Figures 6 and 7, where each individual parameter is varied in the range of one tenth to 10 times its nominal value, while other parameters are held fixed at their nominal value (Table 1). Correlation between period and amplitude is shown in Figure 8. To discriminate between damped and sustained oscillations, we check the sign of the real part of complex conjugate eigenvalues of the Jacobian matrix (evaluated at the considered combination of parameters). In Figures 6–8, damped oscillations are marked by blue circles, and sustained oscillations are marked by red circles.

Figure 6. Period (h) as a function of each parameter (x axis in log scale). The period was computed numerically for damped and sustained oscillations. We classify a solution as oscillatory (damped or sustained) as long as the period is between 0.5 and 40  h, and the amplitude is larger than 1   nM. Blue circles indicate when the Jacobian has at least one pair of complex eigenvalues with negative real part (damped oscillations). Red circles indicate when the Jacobian has at least one pair of complex eigenvalues with positive real part (sustained oscillations). The parameters were changed in the range of one tenth to 10 times their nominal values.

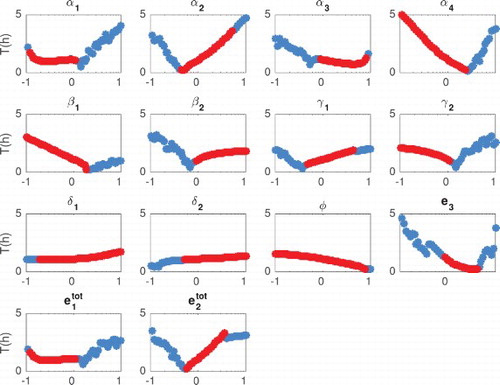
Figure 7. Amplitude (nM) as a function of each parameter (x axis in log scale). We computed numerically the amplitude of the solutions, as long as they classify as damped or sustained oscillations (period between 0.5 and 40 h and amplitude larger than 1   nM). Blue circles indicate when the Jacobian has at least one pair of complex eigenvalues with negative real part (damped oscillations). Red circles indicate when the Jacobian has at least one pair of complex eigenvalue with positive real part (sustained oscillations). The parameters were changed in the range of one tenth to 10 times their nominal values.

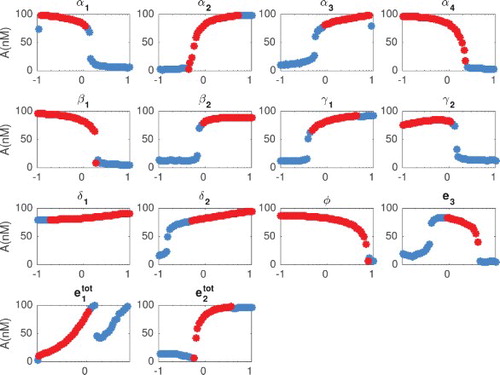
Figure 8. Period (h) and amplitude (nM) correlation. This figure combines the results plotted in Figures 6 and 7. Amplitude and period of the solutions were computed numerically for both damped and sustained oscillations (period between 0.5 and 40 h and amplitude larger than 1   nM). Blue circles indicate when the Jacobian has at least one pair of complex eigenvalues with negative real part (damped oscillations). Red circles indicate when the Jacobian has at least one pair of complex eigenvalues with positive real part (sustained oscillations). Parameters were changed in the range of 0.1–10 times their nominal values.

From Figures 6 and 7 we observe that the period can be tuned from 0 to 5 hours. Also, the parameters related to the kinetics rate can change the period up to 3 hours in the range of one tenth to 10 times their nominal value.

These plots show that when varying $e_3$ in a range between 0.1 and 10 times its nominal value, the period remains flat. In that same range, amplitude varies significantly. We also observe that varying ${\delta }_1$ between 0.1 and 10 times its nominal value, amplitudes stays flat while the period varies between 0 and 3  h. It is worth noting that the titration rates ${\delta }_1$ and ${\delta }_2$ do not affect drastically neither amplitude nor period, which indicates that the system performance is robust relative to variations in the titration rates.

We observe that there is a range in which parameters ${\alpha }_2$ and ${\alpha }_4$ could be varied to tune exclusively the period, while the amplitude remains nearly constant. Alternatively, there is a range in which parameters $e_1^{\mathrm{tot}}$ and $e_3$ could be varied to modulate exclusively the amplitude, keeping the period nearly unchanged (and slow).

6. Conclusion

We have described an artificial three-enzyme biochemical network that has the capacity to oscillate. The network is designed for in vitro implementation with nucleic acid components and bacteriophage RNA polymerases, but has the potential to be implemented in vivo as well. The polymerases transcribe synthetic genes whose RNA transcripts in turn regulate enzyme activity, generating a negative feedback loop that is necessary for oscillations (the famous Thomas' conjecture [27,32]). We analytically demonstrate that this architecture can exclusively undergo oscillatory transitions to instability, due to the structure of its Jacobian matrix. Numerical analysis shows that in a range of realistic parameters the system oscillates; simulations are useful to direct the experimental implementation of this circuit, which is currently being pursued.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the US National Science Foundation under grant [CMMI 1266402].

Notes

1 The definition holds as well for systems transitioning to instability from the right to the left neighbourhood of ${\mu }^{\ast }$: just take $\hat{\mu }={\mu }^{\ast }-\mu$ as the bifurcation parameter.

2 A matrix is irreducible if there does not exist a permutation of its rows or columns that transforms it into a block triangular matrix.

Appendix 1. Equilibrium conditions

Here we derive equilibrium conditions for Modules 1(1) $\begin{array}{rl}\dot{r_1}& ={\alpha }_1{e}_1-{\beta }_1{r}_1{e}_2-{\delta }_1{r}_1{r}_3-\phi r_1,\\ \dot{r_3}& ={\alpha }_3{e}_3-{\gamma }_1{r}_3{e}_2^{\ast }-{\delta }_1{r}_1{r}_3-\phi r_3,\\ \dot{e_2}& ={\gamma }_1{r}_3{e}_2^{\ast }-{\beta }_1{r}_1{e}_2.\end{array}$(1) and 2(2) $\begin{array}{rl}\dot{r_2}& ={\alpha }_2{e}_2-{\gamma }_2{r}_2{e}_1^{\ast }-{\delta }_2{r}_2{r}_4-\phi r_2,\\ \dot{r_4}& ={\alpha }_4{e}_3-{\beta }_2{r}_4{e}_1-{\delta }_2{r}_2{r}_4-\phi r_4,\\ \dot{e_1}& ={\gamma }_2{r}_2{e}_1^{\ast }-{\beta }_2{r}_4{e}_1.\end{array}$(2) . From ${\dot{r}}_2-{\dot{r}}_4=0$ and ${\dot{e}}_1=0$ $(e_1\equiv {\overline{e}}_1)$, we obtain: ${\alpha }_2{\overline{e}}_2={\alpha }_4{\overline{e}}_3+\phi {\overline{r}}_2-\phi {\overline{r}}_4.$ From ${\dot{r}}_1-{\dot{r}}_3=0$ and ${\dot{e}}_2=0$ ($e_2\equiv {\overline{e}}_2$), we obtain: ${\alpha }_1{\overline{e}}_1={\alpha }_3{\overline{e}}_3+\phi {\overline{r}}_1-\phi {\overline{r}}_3.$ From ${\dot{r}}_4=0$ and ${\dot{e}}_1=0$, ${\overline{r}}_4=\frac{{\alpha }_4{\overline{e}}_3}{{\beta }_2{\overline{e}}_1+{\delta }_2{\overline{r}}_2+\phi }=\frac{{\gamma }_2{\overline{r}}_2{\overline{e}}_1^{\ast }}{{\beta }_2{\overline{e}}_1}.$ We obtain the quadratic equation $a_1{\overline{r}}_2^2+b_1{\overline{r}}_2+c_1=0$, where $\begin{array}{rl}{a}_1& ={\delta }_2{\gamma }_2{\overline{e}}_1^{\ast }\\ b_1& ={\gamma }_2{\overline{e}}_1^{\ast }({\beta }_2{\overline{e}}_1+\phi )\\ c_1& =-{\beta }_2{\overline{e}}_1{\alpha }_4{\overline{e}}_3\\ {\overline{r}}_2({\overline{e}}_1,{\overline{e}}_3)& =\frac{-b_1+\sqrt{b_1^2-4a_1{c}_1}}{2a_1}\\ {\overline{r}}_4({\overline{e}}_1,{\overline{e}}_3)& =\frac{{\gamma }_2{\overline{e}}_1^{\ast }{\overline{r}}_2({\overline{e}}_1,{\overline{e}}_3)}{{\beta }_2{\overline{e}}_1}.\end{array}$ Then we find ${\overline{e}}_2$ (the equilibrium value of $e_2$) as a function of ${\overline{e}}_1$ and ${\overline{e}}_3$: (A.1) ${\overline{e}}_2({\overline{e}}_1,{\overline{e}}_3)=\frac{{\alpha }_4{\overline{e}}_3+\phi {\overline{r}}_2({\overline{e}}_1,{\overline{e}}_3)-\phi {\overline{r}}_4({\overline{e}}_1,{\overline{e}}_3)}{{\alpha }_2}.$(A.1) Moreover, from ${\dot{r}}_3=0$ and ${\dot{e}}_2=0$, ${\overline{r}}_3=\frac{{\alpha }_3{\overline{e}}_3}{{\gamma }_1{\overline{e}}_2^{\ast }+{\delta }_1{\overline{r}}_1+\phi }=\frac{{\beta }_1{\overline{r}}_1{\overline{e}}_2}{{\gamma }_1{\overline{e}}_2^{\ast }}.$ We obtain the quadratic equation $a_2{\overline{r}}_1^2+b_2{\overline{r}}_1+c_2=0$, where $\begin{array}{rl}{a}_2& ={\delta }_1{\beta }_1{\overline{e}}_2\\ b_2& ={\beta }_1{\overline{e}}_2({\gamma }_1{\overline{e}}_2^{\ast }+\phi )\\ c_2& =-{\gamma }_1{\overline{e}}_2^{\ast }{\alpha }_3{\overline{e}}_3\\ {\overline{r}}_1({\overline{e}}_2,{\overline{e}}_3)& =\frac{-b_2+\sqrt{b_2^2-4a_2{c}_2}}{2a_2}\\ {\overline{r}}_3({\overline{e}}_2,{\overline{e}}_3)& =\frac{{\beta }_1{\overline{e}}_2{\overline{r}}_1({\overline{e}}_2,{\overline{e}}_3)}{{\gamma }_1{\overline{e}}_2^{\ast }}.\end{array}$ Finally, we find ${\overline{e}}_1$ (the equilibrium value of $e_1$) as a function of ${\overline{e}}_2$, and ${\overline{e}}_3$. (A.2) ${\overline{e}}_1({\overline{e}}_2,{\overline{e}}_3)=\frac{{\alpha }_3{\overline{e}}_3+\phi {\overline{r}}_1({\overline{e}}_2,{\overline{e}}_3)-\phi {\overline{r}}_3({\overline{e}}_2,{\overline{e}}_3)}{{\alpha }_1}.$(A.2)