Selfish altruism, fierce cooperation and the predator^*

* Draft of May 10, 2018. Earlier versions of this paper were presented at the IZA brown bag seminar on two occasions (February 2012 and January 2013). Subsequent versions were presented at the 2014 Conference on ‘Norms, Actions, Games’, the 16th Conference on the Foundations of Utility and Risk and the 25th International Conference on Game Theory at Stony Brook University.

ABSTRACT

This paper suggests a new way to think about a famous question: what explains cooperation in nature and in particular in humans? I argue that, for an evolutionary biologist as well as a quantitative social scientist, the triangle of two ‘teammates’ in the presence of a predator (passing and shooting in two-on-one situations) is one of the fundamental conceptual building-blocks for understanding these phenomena because in such a situation the fact that life is packaged in many distinct enclosures (and not in one big monolithic blob) can unfold its comparative advantage. I show how, in the presence of a predator, cooperative equilibria emerge among entirely selfish teammates if we infinitesimally bias the lead player in the selfish direction or assign a computational burden on the predator due to the presence of a teammate. I argue that ‘predators’ are common in the biological jungle but also in everyday human settings. Intuitively, this paper builds on the simple idea – a familiar one to a biologist observing the natural world but perhaps less so to social scientists – that everybody has enemies.

KEYWORDS:

• Evolutionary game theory
• fitness
• altruism
• cooperation
• decoy
• Nash equilibrium
• repeated matching-pennies game
• predator
• emergence

JEL CLASSIFICATIONS:

• C71
• C73
• C57
• D87

1. Introduction

Cooperation and altruism play a fundamental role in the formation of complex life forms out of simpler ones. This statement is true in a ‘scale invariant manner’ from the protozoan ooze of the depths of time to the formation of firms, economies and nations¹. The abundance of instances of cooperation and altruism, on the other hand, contradicts selfish competition, the central axiom of evolution. This antinomy makes the understanding of these phenomena important research subjects in both economics and evolutionary theoretical biology and reminds us of the proximity of the two disciplines much of whose overlap occurs within game theory².

Very much in the tradition of Hamilton [13] and inspired by passing and shooting in two-on-one situations in soccer/basketball and its similarity to predator inspection in certain types of fish (Dugatkin [4] and Milinski [17]) I show that, in the presence of a predator, cooperative equilibria are emergent phenomena not despite selfishness but because of it. I do so by studying the dynamics of three evolutionary agents playing a matching-pennies game which involves a goalie/predator Z with a defensive allocation dilemma and a striker pair X,Y with shoot-pass and decoy-spite dilemmas respectively. For the sports fans among the readers the situation appears again and again in team sports in the form of two-on-one fast breaks, ‘pick and roll’, or two strikers in the finishing stages of a play where the striker with the ball must decide whether to shoot or to pass. I model this situation in the form of a stage game and studying it in repetition results in an autonomous system of ODEs describing the Lotka-Volterra replicator dynamics of three distinct populations. I show that if we bias player X (the ball possessor) in the selfish direction by infinitesimally perturbing his ODE then, surprisingly, the trajectories of this new system of ODEs flow towards a cooperative equilibrium where X passes half the time, Y decoys all the time and Z defends by basically flipping a coin.

While this setting is somewhat of a departure from the ‘orthodox paradigm’ used to study cooperation and altruism in economics it is certainly more prevalent in evolutionary biology as can be witnessed by the rich literature developed in the historical shadow of Hamilton [13] such as Dugatkin and Godin [5], Garay [10] or Fryxell et al. [9] to mention but a few or by consulting a more recent overview of the state of the art in J. Theor. Biol. [16]. My paper adds a novel mechanism to this literature which contributes to explaining why and how ‘cooperation, altruism, and self-sacrifice’ rise and fall with ‘the great heartbeat of nature’ [19].

In a game of two-on-one, i.e., two strikers against one defender/goalie, the player with ball possession may choose to shoot (defect) or pass (cooperate or be altruistic) while his teammate may choose to decoy (i.e. make himself available for a pass i.e. cooperate) or defect (this may range from just resigning or holding back to sabotaging). The defender's predicament is the optimal allocation of defensive energy (the allocation ranges from defending the ball possession exclusively to defending the pass exclusively) while the two players are completely selfish and in fact want to outscore each other as the loser will perish. Complexity ensues in the repeated setting.

The ball possessor, utilizing the distraction of the defender by the decoy, will rack up goals and establish himself as the primary source of danger for the defender, by being completely selfish (never passes). He thus triggers two processes. The defender may increase his vigilance against him since he does not have to worry about the decoy (no passes occur) and at the same time the decoy may moderate his devotion and cease to decoy. Both of these new developments will make scoring increasingly hard for the ball possessor who eventually will be better off passing than shooting. As the ball possessor starts passing, the defender has his entire defensive energy focused on ball possession and he is hence exposed to scoring from the decoy. The latter then reaps the benefits of the circumstance. It will not take long for the defender to revise his defence allocation and pay more attention to the decoy who meanwhile has become the prime source of danger. This will eventually make it worthwhile again for the ball possessor to shoot the ball to his own benefit. The decoy will tolerate the increased shooting for a while before he revises his devotion again. Eventually, the defender will refocus back on ball possession and the cycle will repeat. These are the fundamental forces at play in a two-on-one setting. Both players are purely selfish but in a way indirectly kind to each other as they adopt their behaviour to the payoff volatility caused by the defender who, in his own turn, adjusts his defensive allocation according to the behaviour of the offensive players. It is this example which will inspire the rest of the discussion in this paper.

The evolutionary origin of the two-on-one situation is life in the presence of a predator. Anyone who ever observed a lion zig-zag-chasing two or more antelopes knows the value of not being alone in the visual field of a predator, i.e., the value of having a decoy or a spotter. While the predator zig-zags to ‘compute’ the slowest prey, all the antelopes need to do is outrun their slowest companion. The same principle is at work in the various flavours of the school yard game of tagging: if you are ‘it’ (i.e. the predator) you zig-zag-chase to tag the slowest child and if you are on the run you try to hide in numbers. The same principle is at work in experimental settings, in the case of predator inspection by certain fish, who dare a closer inspection of a predator when in company than otherwise. An example of a more economic setting for the game of tagging is when company downsizings occur: the key to keeping your job is to simply outperform your colleagues and competitors but you need to have them around and be able to do so in the first place so you support them when you can. The presence of a predator provides us with the unique setting where the fact that life is packaged in many distinct, small and spatially distributed enclosures (and not in one big monolithic blob) unfolds its comparative advantage. In economic terms, the predator may also be a regulator of some kind.

Cooperation is typically studied by means of two-player games with two-pure strategies for each player and certain conditions imposed on their payoff matrix. On the one hand, these conditions make, cooperating with a cooperator more profitable than defecting against a defector (this has an obvious evolutionary significance: populations where intra-cooperator encounters are common are doing better than those where defector encounters are more common) and, on the other hand, they give defection a conditional premium over cooperation (temptation vs. sucker). In the economists' parlance these conditions create an opportunity cost of cooperating (the competing option being to defect) for any fixed strategy of the opponent. Formally if T is the pay-off of a defector against a cooperator (the Temptation), R is the payoff of cooperators playing against each other (the Reward), P is the (Punishment payoff) of two defectors playing each other and S is the (Sucker) payoff of a cooperator playing a defector then a game is called a cooperation game if T>R>P>S.In the repeated setting one imposes that 2R>T+S to prevent players from averaging Temptation and Sucker rewards. A special case of such a game is prisoner's dilemma whose non-repeating version reaches its Nash equilibrium when both players defect because, due to the aforementioned conditions, this is how they maximize payoffs regardless of whether the opponent is a cooperator or a defector. The iterated prisoner's dilemma is the ‘orthodox paradigm for the evolution of cooperation among selfish individuals’ [20]. An altruist in the literature is, like its vernacular counterpart, a player who foregoes some portion of his payoff or fitness in order to benefit others and all attempts to explain altruism in evolutionary terms use ‘models designed to take the altruism out of altruism’ [24] in other words to convert it to ‘as-if altruism’ [8]. A typical result is that altruism is non-altruistic, i.e., it is (ultimately) beneficial to the self and hence evolutionarily preferred whenever the ratio of the cost of the benefactor to the benefit of the recipient of his altruism exceeds some threshold involving quantities such as the degree of relatedness between them.

A surprisingly common simplifying assumption across the two-player literature is that the payoffs of the stage game remain constant across encounters. Life on the other hand is often more complex than that and the payoffs of a pure strategy may depend on additional factors, other than the opponent's pure strategy, such as ambient environmental conditions (replicator dynamics often account for that - Pagen and Nowak [21]) or the players' various biological ‘homeostatics’. Homeostasis is called ‘diminishing returns’ in economics: recent winnings devaluate a future winning increment causing an agent to put less vehemence into winning an additional unit. Similarly, a totally selfish player who always shoots rather than passes suffers a deterioration of his scoring ability because the goalie figures him out. A beautiful neurological proof of the workings of these homeostatics in this context is the paper of Takahashi et al. [23]. Unfavourable comparisons (envy) in ‘domains of self-relevance’ are shown to activate the anterior cingulate cortex, where pain is also known to take place while favourable ones activate the ventral striatum where rewards are processed. This nicely demonstrates my idea. Envy is, like pain, a self-preservation alarm prompting us to compete while schadenfreude is the reward we feel when we outcompete our competitor which causes us to diminish our vigilance. The long term effect of these homeostatics is what my paper attempts to highlight and perhaps explain: while outcompeting our adversaries/teammates is of evolutionary significance we are well advised to not completely eliminate them (hence to perhaps be altruistic or at least ‘not kick a man when he is down’) because in the presence of a predator it is nice to have them around, an idea whose heritage goes back to Hamilton [13]. While such things as fatigue or saturation are prime examples of such systemic homeostatics I propose the predator as an explanation of their origin. A predator is a primordial generator of payoff variation in a repeated two-player stage-game and in fact provides an explanation for why homeostatics driven by envy and schadenfreude might have evolved in the first place. The reader will also indulge my suggestion, based simply on intuition, that a predator might have played a significant role in the formation of groups, group identity but also on human ‘gregariousness’ [14] and ‘fashion’ [2].

The mechanisms currently known to partially explain how evolution favours cooperation (and to which I aspire to add my predator driven approach) are Haldane and Hamilton's ‘kin selection’ [12], direct reciprocity in the repeated setting [12], a mechanism important in human behaviour [6] and with many subtleties [7, 25], indirect reciprocity (players do not repeat-encounter directly but indirectly, i.e., they play new players but carry along the aggregation of past encounters in the form of a reputation), group selection (in which groups of cooperators are shown to do better than groups of defectors), punishment, signalling (‘green beard’ models) etc. These mechanisms are important because they explain how evolution which works with mutation and natural selection nonetheless possesses the ‘remarkable ability to generate cooperation in a competitive world’ [18].

The rest of the paper is organized as follows. I define the stage game in Section 2 motivated by the two-one-game above, compute its Nash equilibria and finish by writing down an autonomous system of ODEs for its replicator dynamics. In Section 3 I solve the system of ODEs analytically while in Section 4 I define a new system of ODEs by perturbing the original one. The perturbation amounts to biassing the ball possessor in the selfish direction or alternatively imposing a computational cost on the predator due to the burden of figuring out which direction to attack. I show how the perturbation leads to a sustainable cooperative equilibrium and in Section 5 I run a simulation for a discrete time, an evolutionary game which verifies my analytical proof. The paper closes with a discussion of the consequences of the main result.

2. The stage game: matching pennies

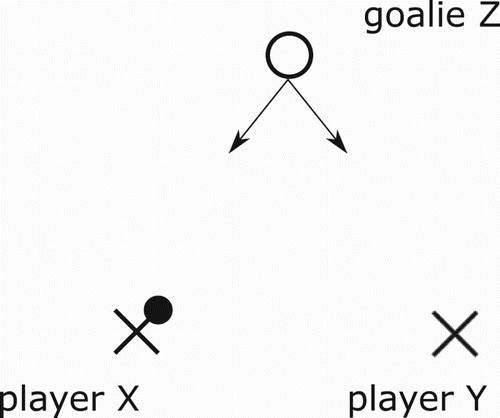
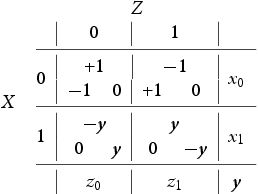
I now define the three-player stage game³. A goalie Z is faced with the predicament of defending a striker duo X (ball possessor) and Y (a decoy or spotter). Striker X's predicament is to either shoot the ball (this is his selfish behaviour and I say that X plays 0) or pass it to Y (this is X's cooperative or altruistic behaviour and I say that X plays 1). The options of Y are to spot X in the attack (i.e. to decoy/cooperate and I say that Y plays 0 in this case) or to hold back (i.e. to spite/defect and I say that Y plays 1). The goalkeeper's predicament is how to divide his defensive energies. Figure 1 depicts in ‘X's and O's notation’ our passing stage game. I assume that once Z guesses correctly he is fully successful at defending his goalpost and hence our game is in the ‘matching pennies’ family. When Z defends X I say that Z plays 0 and when he defends Y I say that he plays 1. Let $x_i,z_i$ be the probabilities of X,Z to play i and let y be the probability of Y to decoy (i.e. to play 0). I summarize all this in the payoff matrix (1) below⁴. The payoffs are arranged in a triangle (inherited from Figure 1) in each of the four cells containing the options so that at the top is the payoff of Z and the bottom left is the payoff of X and bottom right is the payoff of Y . It is interesting to point out that the asymmetry between players X and Y , i.e., between ball possessor and decoy is reminiscent of the Stackelberg Model of Duopoly (see for example Gibbons [11]). It is important here to point out that this is a three species model where each species has two pure strategies, i.e., we are studying three population types which encounter each other in this three player game: Z is a population of ‘goalies’, X is a population of ‘ball-possessing strikers’ and Y is a population of ‘decoying strikers’.

Figure 1. Two strikers against one goalie in ‘Xs and Os notation’.

By setting $x_1=1-x_0$ and $z_1=1-z_0$ and simplifying notation so that $x=x_0$ and $z=z_0$ (so that x,y,z are the mixed strategies of X,Y,Z, i.e., their respective probabilities for playing their own 0 pure strategy) I can now write the expected payoffs $E{U}_w$ of each player $w\in \{X,Y,Z\}$ as a function of their mixed strategies as in 2(2a) $\begin{array}{rl}E{U}_X& =-z_0{x}_0+z_1{x}_0\\ & =x(1-2z),\end{array}$(2a) below. I reiterate the description of the probabilities for the convenience of the reader: x is the probability that X plays 0, i.e., that X is selfish, i.e., shoots, y is the probability that Y plays 0, i.e., that Y decoys (is cooperative) and z is the probability that Z plays 0, i.e., that Z defends against X: (2a) $\begin{array}{rl}E{U}_X& =-z_0{x}_0+z_1{x}_0\\ & =x(1-2z),\end{array}$(2a) (2b) $\begin{array}{rl}E{U}_Y& =z_0{x}_{1}y-z_1{x}_{1}y\\ & =y(1-x)(2z-1),\end{array}$(2b) (2c) $\begin{array}{rl}E{U}_Z& =z_0{x}_0-z_1{x}_0-y{z}_0{x}_1+y{z}_1{x}_1\\ & =(2z-1)\left[x\right(y+1)-y].\end{array}$(2c) If $w\in [0,1]$ denotes the share of the population W playing its corresponding 0 strategy for $(w,W)\in \left\{\right(x,X),(y,Y),(z,Z\left)\right\}$, then we can write the replicator equation for each of the three species as follows: (3) $\dot{w}=w(E{U}_W^0-{\overline{EU}}_W),\mathrm{for}(w,W)\in \left\{\right(x,X),(y,Y),(z,Z\left)\right\},$(3) where $E{U}_W^i$ is the expected pay-off from playing i=0,1 and ${\overline{EU}}_W$ is the expected utility across the population for W=X,Y,Z (see Pagen and Nowak [21] for a unifying treatment of evolutionary dynamics). From the pay-off matrix 1 we can easily see (4a) $E{U}_X^0=1-2z,E{U}_X^1=0,{\overline{EU}}_X=x(1-2z),$(4a) (4b) $E{U}_Y^0=(1-x)(2z-1),E{U}_Y^1=0,{\overline{EU}}_Y=yE{U}_Y^0,$(4b) (4c) $E{U}_Z^0=x(y+1)-y,E{U}_Z^1=-E{U}_Z^0,{\overline{EU}}_Z=E{U}_Z^0(2z-1).$(4c) By substituting Equation (4(4a) $E{U}_X^0=1-2z,E{U}_X^1=0,{\overline{EU}}_X=x(1-2z),$(4a) ) in Equation (3(3) $\dot{w}=w(E{U}_W^0-{\overline{EU}}_W),\mathrm{for}(w,W)\in \left\{\right(x,X),(y,Y),(z,Z\left)\right\},$(3) ) we obtain the Lotka-Volterra replicator equation for the continuous population dynamics of each of the three species: (5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) (5b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(5b) (5c) $\dot{z}=2\left[x\right(y+1)-y]\lambda \left(z\right),$(5c) where $\lambda \left(w\right)=w(1-w)$ and $x=x\left(t\right),y=y\left(t\right),z=z\left(t\right)$ are functions of time t. I use the dot notation for the derivatives $\dot{x},\dot{y},\dot{z}$ of x,y,z with respect to time t. One can alternatively think of these equations as describing three evolutionary agents X,Y and Z playing mixed strategies $x=x\left(t\right),y=y\left(t\right)$ and $z=z\left(t\right)$ at time t and which follow gradients of increasing returns⁵. In other words, one can think of the system of autonomous ODEs (5(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) ) as describing the dynamics of such a repeated game. The dynamics take place in the unit cube $B=[0,1]\times [0,1]\times [0,1]$. Notice that the set of interior Nash equilibria of the stage game is the curve (6) $\left\{\right(x,y,z):x=y/(y+1)\wedge z=1/2\}$(6) in the unit cube B of mixed strategies. Notice that the hyperplane $z=1/2$ is the indifference locus of X and Y and the hyper-surface $x=y/(y+1)$ is the indifference set of Z.

3. Solving the dynamics of shooting and passing

I now describe the dynamics of Equation (5(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) ). By solving 5a(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) and 5b(5b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(5b) for 1−2z and setting their right hand sides equal to each other I obtain a single differential equation, valid in the interior of B, which can be solved by separation of variables. The solution relates x and y explicitly as follows: (7) $y=\frac{a}{x+a},a>0.$(7) So one obtains a one parameter (i.e. a) family of invariant surfaces in other words, depending one initial conditions, the first two equations, (5a(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) ) and (5b(5b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(5b) ), trap x and y on the surface $y=\left(a/\right(x+a\left)\right),z$ for some constant a. 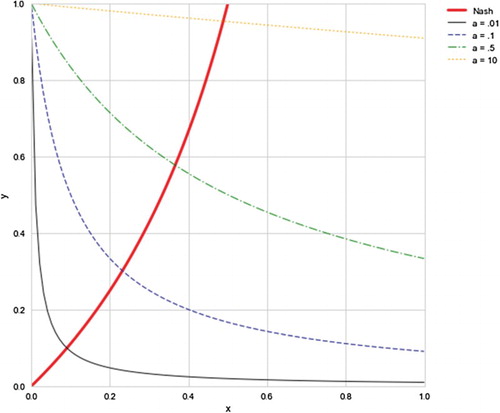Notice that (8) $\underset{a\to \mathrm{\infty }}{lim}y=1.$(8) Figure 2 summarizes these considerations visually projected on the xy-plane.

Figure 2. Projected on the xy-plane the set of interior Nash equilibrium points together with four instances selected from the one parameter family of invariant surfaces for selected values of a. Notice how y tends to 1 as a increases.

I leave it as an easy exercise to the reader to check that the solution space of the autonomous system of ODEs given by Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ), in the interior of the unit cube B, consists of closed curves on these surfaces centred around the Nash fixed point at the intersection of the curve given by Equation (6(6) $\left\{\right(x,y,z):x=y/(y+1)\wedge z=1/2\}$(6) ) and these invariant surfaces given by Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ). To verify this claim substitute y in 5c(5c) $\dot{z}=2\left[x\right(y+1)-y]\lambda \left(z\right),$(5c) using 7(7) $y=\frac{a}{x+a},a>0.$(7) and obtain a system of two ODEs in x and z (i.e. 5a(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) and 5c(5c) $\dot{z}=2\left[x\right(y+1)-y]\lambda \left(z\right),$(5c) ) which describe the dynamics on the invariant surfaces given by Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ). Now compute the Jacobian of the two by two system evaluated at its fixed point $z=1/2$ and $x=-a+\sqrt{a^2+a}$. The trace of the Jacobian is easily seen to vanish and the determinant to be positive (equal to $+2$, i.e. the Jacobian has two imaginary conjugate eigenvalues at the fixed point) so that the fixed point in question is a centre (compare Hofbauer and Sigmund [15]).

In other words, in the presence of a predator selfish agents will go through bouts of defection followed by eras of, what I call, selfish altruism and fierce cooperation, trapped in closed orbits, given be Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ) and depicted in Figure 2, which depend of initial conditions. This concludes the analysis of the replicator equations.

In the next section, I will discus a modified system of ODEs which introduces an intuitively motivated perturbation which biases the lead player in the selfish direction.

4. Solving the perturbed dynamics

I now wish to study a new dynamical system which is a modification of the one given by Equation (5(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) ). The new system, given by Equation (9(9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) ) below is obtained by simply perturbing Equation (5a(5a) $\dot{x}=(1-2z)\lambda \left(x\right),$(5a) ) by a non-negative, infinitesimally valued function $c=c(x,y,z)$. (9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) (9b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(9b) (9c) $\dot{z}=2\left[x\right(y+1)-y]\lambda \left(z\right).$(9c) I interpret this by saying that X displays an infinitesimal bias towards shooting, i.e., towards its selfish pure strategy. This is so because the sign of $\dot{x}$ changes from positive to negative at $z=\frac{1}{2}$ in the unperturbed case and at $z=\left(1+c\right)/2$ in the perturbed case. This means I introduced an ‘imperfection’ in X which causes him to continue shooting between $z\in [\frac{1}{2},(1+c\left)/2\right]$, in other words, X displays an infinitesimal preference for shooting past the point it would be deterministically prudent to stop doing so and revert to passing. This bias is consistent with the behaviour of strikers in soccer and other team sports who repeatedly and consistently choose to overshoot even when a pass is a better option. To put it in a different way, c is the amount by which the lead player X continues to ‘push his luck’ before it becomes apparent to him that shooting is counterproductive. From this discussion, it also becomes apparent that imposing the condition $\mathrm{\partial }c/\mathrm{\partial }x<0$ is reasonable since it simply says that the more shooting X does the smaller his bias towards shooting becomes, a statement consistent with both physiological homeostatics and the principle of diminishing marginal returns. Similar considerations make it reasonable to assume $\mathrm{\partial }c/\mathrm{\partial }z<0$ since it would simply mean that the more Z attacks X the less prone X is to overshoot.

Notice that one way such a c can intrude into our dynamics is by means of a slightly modified stage game given by Table 10 below which is a modification of the original stage game given in Table 1:

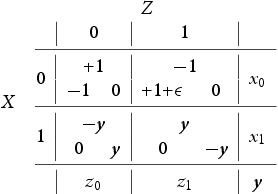
Here $ϵ=ϵ(x,y,z)$ is once again an infinitesimally valued, non-negative function. The meaning of this quantity is that X has an infinitesimally better pay-off when scoring in the presence of a decoy rather than in his absence. This could, for example, be due to the additional computational cost of Z in figuring out the direction the danger is coming from thus hence improving the chances of a realized payoff for X. Computing the replicator dynamics of this stage game results in 9(9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) for $c=(1-z)ϵ$. In this case the condition $\mathrm{\partial }c/\mathrm{\partial }z<0$ is met even if ε is independent of z. Imposing $\mathrm{\partial }ϵ/\mathrm{\partial }x<0$ is reasonable because the more X is shooting the more certain Z becomes the danger comes from X and hence the smaller his computational burden. A typical example for $ϵ=ϵ(x,y,z)$ is to set $ϵ=\delta (1-x)$ for some infinitesimal constant δ.

I now set out to analyse the system of Equation (9(9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) ) assuming $c\ge 0$ is infinitesimal with non-zero values as time grows and $\mathrm{\partial }c/\mathrm{\partial }z<0$, $\mathrm{\partial }c/\mathrm{\partial }x<0$. In a manner similar to how Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ) was derived, it is easy to see that the perturbed Equation (9a(9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) ) and (9b(9b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(9b) ) have the same solution as in Equation (7(7) $y=\frac{a}{x+a},a>0.$(7) ) for: (11) $a=b{\int }^{t}c(1-x(s\left)\right)\mathrm{d}s,$(11) for some constant b. Since c is non-negative, as t goes to infinity so does a hence y converges to 1 by means of Equation (8(8) $\underset{a\to \mathrm{\infty }}{lim}y=1.$(8) ). This means under these dynamics Y becomes a completely devoted spotter, i.e., cooperator. To put it in different words when X displays a bias towards his selfish behaviour he breeds Y into a completely devoted helper!

Lastly, I want to see what happens when y=1. In that case, I get a reduced system of ODEs in x and z given by: (12a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(12a) (12b) $\dot{z}=2(2x-1)\lambda \left(z\right).$(12b) The isoclines of this system in the interior of the wall of the unit cube B at y=1 are give by x=.5 and the solutions to the equation $z=\left(1+c\left(z\right)\right)/2$, where $c\left(z\right)=c(.5,1,z)$ (the reader might check that such solutions exist when considering the example $c=\delta (1-x)(1-z)$ for some constant δ and that hence a fixed point exists). I wish to compute the Jacobian at the fixed points to figure out whether the fixed points are sources, sinks or centres. I leave it as an exercise to the reader to verify that the Jacobian of 12(12a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(12a) , evaluated at the fixed points given by x=.5 and the solutions to $z=\left(1+c\left(z\right)\right)/2$, is give by: (13a) $\frac{\mathrm{\partial }\dot{x}}{\mathrm{\partial }x}=\frac{\mathrm{\partial }c}{\mathrm{\partial }x},\frac{\mathrm{\partial }\dot{x}}{\mathrm{\partial }z}=\frac{1}{4}\left(\frac{\mathrm{\partial }c}{\mathrm{\partial }z}-2\right),$(13a) (13b) $\frac{\mathrm{\partial }\dot{z}}{\mathrm{\partial }x}=4\lambda \left(z\right),\frac{\mathrm{\partial }\dot{z}}{\mathrm{\partial }z}=0.$(13b) Hence the trace of the Jacobian is $\frac{1}{4}\left(\mathrm{\partial }c/\mathrm{\partial }x\right)<0$ and the determinant is $(2-(\mathrm{\partial }c/\mathrm{\partial }z\left)\right)\lambda \left(z\right)>0$, which means that the fixed points are either sink nodes or spiral sink nodes.

I have shown, in other words, that when the lead player depicts an infinitesimal selfish bias c or when X has ε more from scoring in the presence of Y than in his absence (due to Z's increased computational burden in the presence of Y) then in the long run Y evolves into a dedicated helper. Assuming furthermore that c (resp. ε) decreases with x and z (an assumption with a well motivated interpretation) implies that in the long run, X shares the ball fairly with Y, imposing a similar randomization on Z, who depicts a slight preference for attacking the lead player (the fixed points can be seen to be slightly off x=z=.5).

The careful reader might have noticed that in imputing a computational cost on Z in Y's presence I broke the zero sum principle between X and Z in the modified stage game 10. Even in the case however where the zero sum is preserved, the conclusions hold. Indeed even if I modified the payment of Z to be as in 14 below:

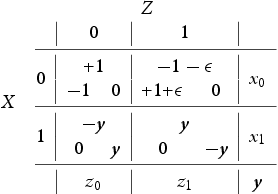
and hence I obtained the system in 15(15a) $\dot{x}=\left[(1+c)-(2+c)z\right]\lambda \left(x\right),$(15a) below: (15a) $\dot{x}=\left[(1+c)-(2+c)z\right]\lambda \left(x\right),$(15a) (15b) $\dot{y}=(2z-1)(1-x)\lambda \left(y\right),$(15b) (15c) $\dot{z}=2\left[x\right(y+1+c/2)-y]\lambda \left(z\right),$(15c) for $c=ϵ=\delta (1-x)(1-z)$ for example for some constant δ then y can still be easily seen to approach 1 and the resulting reduced system in x and z given by 16(16a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(16a) below (16a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(16a) (16b) $\dot{z}=2(2x-1)\lambda \left(z\right),$(16b) can still be shown to firstly have a fixed point near $x=z=1/2$ and secondly have a Jacobian with negative trace and positive determinant at the fixed point. The main conclusion would still hold therefore that assigning extra utility on X in the presence of Y and corresponding disutility to Z by imputing extra computational costs for Z then an evolutionary Y would end up totally devoted to X while X would practically share with Y and Z would practically flip a coin (the fixed point for $c=\delta (1-x)(1-z)$ can be readily seen to be $x=-4+2(\delta +4{)}^{1/2}$ and $z=(\delta +6-3(\delta +4{)}^{1/2}\left)/\right(\delta +4-2(\delta +4{)}^{1/2})$, i.e., for small δ, z is slightly above $.5$ and x slightly below. The trace of the Jacobian is $\left(\mathrm{\partial }ϵ/\mathrm{\partial }x\right)\left(2/(4+ϵ{)}^2\right)+\left(\mathrm{\partial }ϵ/\mathrm{\partial }z\right)\left(\right(2(1+ϵ)\left)/\left(\right(4+ϵ\left)\right(2+ϵ{)}^2)\right)<0$ while the determinant is $\delta \left[\right(\left(1-x\right)/(4+ϵ{)}^2)-(2(1-z)/(2+ϵ{)}^2\left)\right]+1$ which is positive provided δ is small enough. Trace and determinant need to of course be evaluated at the fixed point but their sign is seen by inspection without evaluating).

It is interesting to remark here that indeed the effect of our ε-perturbations is reminiscent of what happens when we violate the relationship T>R between temptation and reward pay-offs in the prisoners dilemma game (see page 4) which amounts to adding a ‘synergistic’ premium of sorts to cooperation thus turning the prisoners dilemma to the stag hunt game which is known to support a cooperative equilibrium. In that case, cooperation is an ESS⁶. The twist in our ε-perturbation is that firstly it is infinitesimal and secondly it has an interpretation as a selfish bias.

5. A simulation with a discrete model

Derived from the system of ODEs 9(9a) $\dot{x}=(1-2z+c)\lambda \left(x\right),$(9a) I run some simulations which examine the behaviour of three myopic evolutionary agents playing the game in discrete time i with revision protocols given by: (17a) $x_{i+1}=max\left[0,min\{1,(1-2z_i+c\left)h\right\}\right],$(17a) (17b) $y_{i+1}=max\left[0,min\{1,(2z_i-1\left)\right(1-x_i\left)h\right\}\right],$(17b) (17c) $z_{i+1}=max\left[0,min\{1,2[x_i(y_i+1)-y_i\left]h\right\}\right],$(17c) for some infinitesimal constant h. Notice that this discrete revision protocol describes three players which are evolutionary in the sense of Press and Dyson [22]. The players follow the gradient of increasing returns by making incremental changes (i.e. h) in the direction of their increasing expected utility, essentially applying Euler's method.

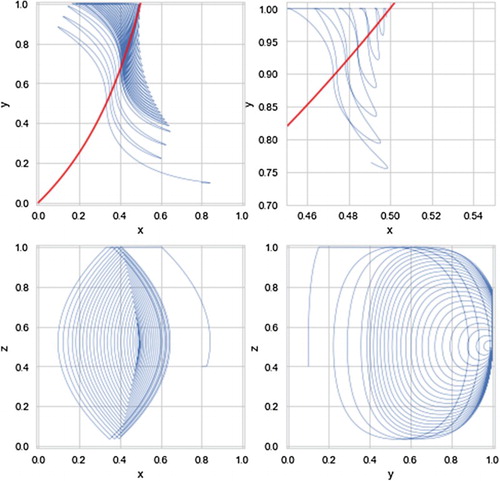
Figure 3 shows the evolution of the players towards a cooperative equilibrium in the depth of time while Figure 4 shows the pairwise dynamics as follows: the top left shows (projection on the x,y-plane) how X and Y rotate around the Nash equilibrium climbing the invariant surfaces of the state space along the Nash curve, the top right shows just the last 30,000 iterations of this projection so as to be able to clearly see what is going on: x and y write ‘figure eights’ of ever decreasing size, finally the bottom left and bottom right show the converging dynamics of x,z and y,z, respectively.

Figure 3. I run 110,000 rounds of the discrete model given by Equation (17(17a) $x_{i+1}=max\left[0,min\{1,(1-2z_i+c\left)h\right\}\right],$(17a) ) with initial conditions x=.8 (near complete selfishness), y=.1 (near complete defector), and z=.4 with e=1 and c=.1. As in the continuous case, y tends to 1 and x,z to $.5$.

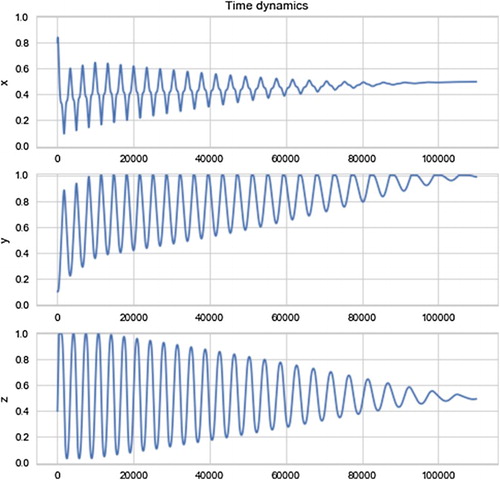
Figure 4. Pairwise dynamics of 110,000 rounds of the discrete model given by Equation (17(17a) $x_{i+1}=max\left[0,min\{1,(1-2z_i+c\left)h\right\}\right],$(17a) ) with initial conditions x=.8, y=.1, and z=.4 with e=1 and c=.1.

6. Concluding remarks

Inspired by predator inspection in fish and its intuitively obvious relation to two-on-one fast breaks in team sports I devised a matching-pennies, three-player game and it used to argue that the triangle of two players in the presence of a predator⁷ is one of the fundamental blocks for furthering our understanding of ‘cooperation, altruism and self-sacrifice’. Two-on-one fast breaks in soccer give us a toy example to understand these issues in a new if somewhat unorthodox way but definitely one with a long tradition.

The soccer application is that if you are a coach you want your strikers to be intelligent enough to eventually pass but selfish enough to shoot rather than pass. In fact, your want them to have a selfish tendency. The defender/predator will take care of the rest and, before you know it, they will ‘tiqui-taca’ their way to super-cooperative dominance. I have shown that whenever the lead player is biased ‘in the selfish direction’ (i.e. displays an even infinitesimal preference towards shooting rather than passing i.e. c>0), or when he benefits more from scoring in the presence of his teammate than in his absence (as a result of, say, extra computational burden on Z) then the long term equilibrium is a cooperative and sustainable one where the lead player shares the ball fairly having ‘nurtured’ a completely devoted decoy (teammate) leaving the predator/goalie with flipping a coin, slightly biased towards X, to allocate his defensive energies. The oppositely signed bias (c<0 ) leads to the other end of the stage game equilibrium line, where the lead player totally surrenders the ball to the decoy but the decoy is never there to receive it (ball possessor disappoints the decoy, decoy abandons ball possessor and ball possessor begs the decoy to come back in vain) and the predator does whatever. That equilibrium is unsustainable and such triangles will perish as there is no chance of scoring.

Purely statistically it is a lot more likely that the bias will be non-zero (a statement a mathematician would summarize by saying that ‘being biased is a generic or transversal condition’). So, to recap, starting from randomly chosen initial states in the unit cube of mixed strategies, a non-biased system will orbit around the Nash equilibrium locus of the stage game in closed trajectories for ever, its aggregate phenotype oscillating between shooting and passing (X), decoying and defecting (Y ) and guarding the ball or the pass (X) while a negative bias will lead to unsustainable and hence perishable ends leaving us with only the positive bias (‘in the selfish direction’) which leads to cooperative and sustainable equilibria.

I call the positive bias a selfish one because that is what the semantics would suggest, i.e., because this is the direction where a shooter actively draws utility by shooting to score. It could be argued that such a bias is in the altruistic direction since the agent is not adapting fast enough when he ought to be doing so. Even so, though one thing remains constant: it is still the only bias which leads to sustainable, and cooperative at that, equilibria. If I chose to call the positive bias an altruistic one then the negative bias would be a selfish one and lead to unsustainable triangles that perish. So our phenotypical conclusion is either that ‘selfish behaviours lead to cooperative equilibria’ or that ‘altruism is evolutionarily fitter than selfishness’). In a world of perpetual oscillations between cooperation and defection semantics are bound to be blurry so in the presence of a predator (and we know that every life form has enemies) ‘selfish altruism’ and ‘fierce cooperation’ are far from contradictory pairs.

Acknowledgements

I was inspired by talks on biology and economics by Andrew Oswald whom I would like to also thank for discussions, comments and readings of earlier versions along with Kostas Tatsiramos and Lorens Imhof. This paper was presented to ‘Norms, Actions, Games 2014’, the 16th Conference on the Foundations of Utility and Risk and the 25th International Conference on Game Theory at Stony Brook University from where I received and incorporated helpful comments. The final draft owes to referee criticisms and suggestions which strongly improved exposition.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

Nikolaos Askitas  http://orcid.org/0000-0002-3134-6616

Notes

* Draft of May 10, 2018. Earlier versions of this paper were presented at the IZA brown bag seminar on two occasions (February 2012 and January 2013). Subsequent versions were presented at the 2014 Conference on ‘Norms, Actions, Games’, the 16th Conference on the Foundations of Utility and Risk and the 25th International Conference on Game Theory at Stony Brook University.

1. See Bowles and Gintis [1] for a wonderful account of a good deal of this story and an excellent starting point into a good portion of the existing literature.

2. It is an extremely interesting experience, for example, to read Fontaine [8] and trace how biological ideas on altruism mutate and reincarnate themselves in the economic literature.

3. Economics and Biology literature seem to have conspicuously kept a certain distance to three or more player games in the study of cooperation perhaps because they are known to be PPAD and hence hard [3].

4. For the convenience of the reader, the mnemonic rule for assigning values is as follows. I fix the convention of thinking of X as player 0 and Y as player 1 and everything else follows from that. That means when X plays 0 (resp. 1) he plays in favour of player 0 (resp. 1), i.e., he shoots (resp. passes). Similarly for Y to play 0 (resp. 1) is to favour X (resp. Y ), i.e., to decoy (resp. spite). Finally, Z plays 0 when choosing to defend against the shot, i.e., player 0.

5. One might argue of course that an evolutionary agent might not necessarily slow down at the boundary as imposed by the factor λ. In Section 5 a simulation of a model is studied without λ, in discrete time and with discrete increments along the gradient of increasing returns.

6. I would like to thank the referee for pointing this out.

7. Note that even prisoner's dilemma, the ‘orthodox paradigm’ for the study of cooperation, involves a (silent) third player: the interrogator. Its role is negligible of course because of the symmetry in the game. My game is one in which the interrogator may discriminate…