Bifurcation analysis of an age-structured alcoholism model

ABSTRACT

In this paper, we investigate a new alcoholism model in which alcoholics have age structure. We rewrite the model as an abstract non-densely defined Cauchy problem and obtain the condition which guarantees the existence of the unique positive steady state. By linearizing the model at steady state and analyzing the associated characteristic transcendental equations, we study the local asymptotic stability of the steady state. Furthermore, by using Hopf bifurcation theorem in Liu et al. (Z. Angew. Math. Phys. 62 (2011) 191–222), we show that Hopf bifurcation occurs at the positive steady state when bifurcating parameter crosses some critical values. Finally, we perform some numerical simulations to illustrate our theoretical results and give a brief conclusion.

KEYWORDS:

• Age structure
• alcoholism model
• stability
• Hopf bifurcation

1. Introduction

Globally, alcohol consumption results in approximately 3.3 million deaths each year(or $5.9\mathrm{\%}$ of all deaths), this is greater than, for example, the proportion of deaths from HIV/AIDS ($2.8\mathrm{\%}$), violence ($0.9\mathrm{\%}$) or tuberculosis (1.7%) [28]. Alcohol consumption has been identified as a component cause for more than 200 diseases, injuries and other health conditions as described in the International Statistical Classification of Diseases and Related Health Problems (ICD) 10th Revision (WHO, 1992), more than 30 include alcohol in their name or definition. This indicates that these disease conditions do not exist at all in the absence of alcohol consumption. A strong association exists between alcohol consumption and HIV infection, sexually transmitted diseases [27]. Alcohol consumption can result in harm to other individuals, such as assault, homicide (intentional) or traffic crash, workplace accident (unintentional). Moreover, alcohol consumption results in a significant economic burden on society at large. $5.1\mathrm{\%}$ of the global burden of disease and injury is attributable to alcohol [28]. As discussed above, alcohol consumption has a severe effect on the health and wellbeing of individuals and populations.

Recently, it has been realized that mathematical models are important to understand the process of drinking. Mulone et al. [24] studied a two-stage model for youths with serious drinking problems and their treatment. The youths with alcohol problems were divided into two component, namely those who admitted to having the problem and those who did not admit. The stability of two steady states was analysed. Xiang et al. [32] developed a drinking model with public health educational campaigns. Mathematical analyses established that the global asymptotically stability of the equilibria were determined by the basic reproduction number $R_0$. If $R_0\le 1$, the alcohol-free equilibrium was globally asymptotically stable, and if $R_0>1$, the alcohol present equilibrium was globally asymptotically stable, and they concluded that the public health educational campaigns of drinking individuals could slow down the drinking dynamics. Huo et al. [11] introduced a novel alcoholism model which involved the impact of Twitter. Stability of all the equilibria were obtained in terms of the basic reproductive number $R_0$. Backward and forward bifurcation, Hopf bifurcation were also analysed. For other alcoholism or epidemoc models, we referred to [2, 12–15, 30, 33, 34].

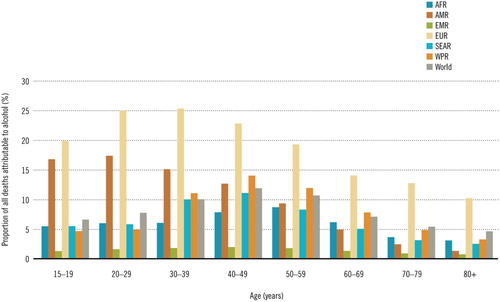
The age-structured models have been studied by many authors, such as Webb [31], Iannelli [16] and Cushing [7]. Age-structured epidemic models were known to be effective tools for studying epidemic dynamics [3–5, 17, 19, 35] and many authors regarded alcoholism as a social epidemic disease [11, 30]. According to the WHO report, alcohol-related deaths were related to age (see Figure 1[1]). Therefore, establishment of alcoholism model should consider age factor and the model becomes more reasonable. However, so far, works on alcoholism models with age structure are very scarce.

Figure 1. Proportion of alcohol-attributable deaths $\left(\mathrm{\%}\right)$ of total deaths by age group, 2012.

In 1990, Thieme [26] observed that age-structured models could be regarded as non-densely defined Cauchy problems, subsequently, Magal and Ruan [22], Liu et al. [18] developed center manifold theory and Hopf bifurcation theorem for non-densely defined Cauchy problems, respectively. By using the above theory and theorem, Liu et al. [20] showed that age-structured model of consumer-resource mutualism exhibited Hopf bifurcation at the positive equilibrium under some conditions. Wang and Liu [29] considered an age-structured compartmental pest-pathogen model. Their results showed that Hopf bifurcation occurred at a positive steady state as bifurcating parameter passed values. Tang and Liu [25] studied a new predator-prey model with age structure and exhibited Hopf bifurcation at a positive steady state.

Motivated by above works, the aim of this paper is to investigate the existence of Hopf bifurcation for an alcoholism model with age-structure. Our model consists of three variables : susceptible drinkers at time t are denoted by $S\left(t\right)$, who do not drink or drink only moderately; alcoholics at time t with alcoholism age a are denoted by $A(t,a)$, who strongly desire to consume alcohol, having difficulties in controlling of its use, persisting in its use despite harmful consequences; and the people who recover from alcoholism after treatment are denoted by $R\left(t\right)$. Alcoholism as a long-standing social epidemic disease, it is difficult to eliminate for a short time. So we put the alcoholism problem into the population growth model to study. So we suppose new recruits enter the population at a rate $r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)$. The population flow among those classes is shown in the following diagram (Figure 2).

Figure 2. The flow diagram of our model, where $\left[A\right],\left[\beta A\right]$ represent ${\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a,$ ${\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a,$ respectively.

The flow diagram leads to the following alcoholism model: (1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) where alcoholics are assumed to be age-structured, whereas susceptible drinkers and recuperator are not age-structured. r is the birth rate, μ is the natural death rate, $a_1,a_2$ are the death rates of excessive drinking, respectively. δ is the transfer rate from alcoholics to recovered individuals, ρ is the relapse rate from recovered individuals to alcoholics. The coefficient α is the fraction of susceptible drinkers $S\left(t\right)$ develop into alcoholics because of some of their own reasons, such as losses of earnings, unemployment or family problems, etc. The incidence rate at time t and alcoholism age a is $S\left(t\right)\beta \left(a\right)A(t,a)$, where $\beta \left(a\right)$ is the transmission rate due to pressure from alcoholics with alcoholism age a, $\beta \left(a\right)$ is defined by (2) $\beta \left(a\right)=\left\{\begin{array}{ll}{\beta }^{\ast },& a\ge \tau ,\\ 0,& \mathrm{otherwise},\end{array}\right.$(2) and $K_0:={\int }_0^{+\mathrm{\infty }}\beta \left(a\right){\mathrm{e}}^{-(\mu +a_1+\delta )a}\mathrm{d}a$, i.e. ${\beta }^{\ast }=(\mu +a_1+\delta )K_0{\mathrm{e}}^{(\mu +a_1+\delta )\tau },$ where τ represents the time span that a person from the initial alcoholism to a potential inviter, who invites susceptible drinkers to increase alcohol consumption. The $K_0$ represents the total number of secondary alcoholics produced by a primary alcoholic. For the convenience of computation, we assume that $K_0$ is a constant. The ${\beta }^{\ast }$ is the rate that a alcoholic with alcoholism age a $(a\ge \tau )$ will successfully infect a susceptible drinker.

The remainder of this paper is organized as follows. Section 2, we summarize the main results on Hopf bifurcation theorem, which obtained in [18]. In Section 3, the stability of the steady state and the existence of Hopf bifurcation are investigated. In Section 4, we perform numerical simulations to verify our analytical results. Finally, a brief conclusion is given.

2. Preliminaries

We recall the Hopf bifurcation theorem in Liu et al. [18] for the following non-densely defined abstract Cauchy problem: (3) $\frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=Au\left(t\right)+F(\mu ,u(t\left)\right),t\ge 0,u\left(0\right)\in \overline{D\left(A\right)},$(3) where $\mu \in \mathbb{R}$ is the bifurcation parameter, $A:D\left(A\right)\subset X\to X$ is a linear operator on a Banach space X with $D\left(A\right)$ not dense in X and A not necessary to be a Hille-Yosida operator, $F:\mathbb{R}\times \overline{D\left(A\right)}\to X$ is a $C^k$ map with $k\ge 4$. Set $X_0:=\overline{D\left(A\right)},$ and $A_0$ is the part of A in $X_0$, which is defined by $A_{0}x=Ax,\mathrm{\forall }x\in D\left(A_0\right)=\{x\in D(A):Ax\in X_0\}.$ We denote by $\left\{T_A\right(t){\}}_{t\ge 0}$ the $C_0-$semigroup of bounded linear operators on X $($respectively $\left\{S_A\right(t){\}}_{t\ge 0}$ the integrated semigroup$)$ generated by A.

Definition 2.1

Let $L:D\left(L\right)\subset X\to X$ be the infinitesimal generator of a linear $C_0-$semigroup $\left\{T_L\right(t){\}}_{t\ge 0}$ on a Banach space X. Define the growth bound ${\omega }_0\left(L\right)\in (-\mathrm{\infty },+\mathrm{\infty })$ of L by ${\omega }_0\left(L\right):=\frac{\ln (\parallel T_L(t\left){\parallel }_{\mathcal{L}\left(X\right)}\right)}{t}.$ The essential growth bound ${\omega }_{0,\mathrm{ess}}\left(L\right)\in (-\mathrm{\infty },+\mathrm{\infty })$ of L by ${\omega }_{0,\mathrm{ess}}\left(L\right):=\frac{\ln (\parallel T_L(t\left){\parallel }_{\mathrm{ess}}\right)}{t},$ where $\mathcal{L}\left(X\right)$ is the space of bounded linear operators from X into X, $\parallel T_L\left(t\right){\parallel }_{\mathrm{ess}}$ is the essential norm of $T_L\left(t\right)$ defined by $\parallel T_L\left(t\right){\parallel }_{\mathrm{ess}}=\kappa \left(T_L\right(t\left)B_X\right(0,1\left)\right)$, where $B_X(0,1)=\{x\in X:\parallel x{\parallel }_X\le 1\}$, and each bounded set $B\subset X$, $\kappa \left(B\right)=\inf \{\epsilon >0:B$ can be covered by a finite number of balls of radius $\le \epsilon \}$ is the Kuratovsky measure of non-compactness.

We make the following assumptions on the linear operator A and the nonlinear map F.

Assumption 2.1

Assume that $A:D\left(A\right)\subset X\to X$ is a linear operator on a Banach space $(X,\parallel \cdot \parallel ),$ there exist two constants ${\omega }_A\in \mathbb{R}$ and $M_A\ge 1,$ such that $({\omega }_A,+\mathrm{\infty })\subset \rho \left(A\right)$ and the following properties are satisfied

1. $\underset{\lambda \to +\mathrm{\infty }}{lim}(\lambda I-A{)}^{-1}x=0,\mathrm{\forall }x\in X;$

2. $\parallel (\lambda I-A{)}^{-k}{\parallel }_{\mathcal{L}\left(X_0\right)}\le M_A/(\lambda -{\omega }_A{)}^k,\mathrm{\forall }\lambda >{\omega }_A,k\ge 1$.

Assumption 2.1 implies that $A_0$ is the infinitesimal generator of a $C_0$-semigroup $\left\{T_{A_0}\right(t){\}}_{t\ge 0}$ on $X_0$ and $\parallel T_{A_0}\left(t\right){\parallel }_{\mathcal{L}\left(X_0\right)}\le M_A{\mathrm{e}}^{{\omega }_{A}t},t\ge 0.$ By Proposition 2.6 in Magal and Ruan [22], we know if Assumption 2.1 is satisfied, then A generates a unique integrated semigroup $\left\{S_A\right(t){\}}_{t\ge 0}$. If we assume in addition that A is a Hille-Yosida operator, then we have $\parallel S_A\left(t\right)-S_A\left(s\right){\parallel }_{\mathcal{L}\left(X\right)}\le M_A{\int }_s^t{\mathrm{e}}^{w_{A}l}\mathrm{d}l,\mathrm{\forall }t,s\in [0,+\mathrm{\infty })\mathrm{with}t\ge s\ge 0.$ Next, we consider the non-homogeneous Cauchy problem (4) $\frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=Au\left(t\right)+f\left(t\right),t\ge 0,u\left(0\right)\in \overline{D\left(A\right)},$(4) where $f\in L^1\left(\right(0,\tau ),X)$.

Assumption 2.2

There exists a map $\delta \left(t\right):[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ with $\underset{t\to 0^{+}}{lim}\delta \left(t\right)=0,$ such that for each $\tau >0$ and $f\in C\left(\right[0,\tau ],X),t\to {\int }_0^t{S}_A(t-s)f\left(s\right)\mathrm{d}s$ is continuously differentiable and $∥\frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^t{S}_A(t-s)f\left(s\right)\mathrm{d}s∥\le \delta \left(t\right)\underset{s\in [0,t]}{sup}\parallel f\left(s\right)\parallel ,\mathrm{\forall }t\in [0,\tau ].$

By Corollary 2.11 in Magal and Ruan [22], we know if Assumption 2.1 and 2.2 hold, then for each $\tau >0$, $f\in C\left(\right[0,\tau ],X_0)$, and $x\in X_0$, (4(4) $\frac{\mathrm{d}u\left(t\right)}{\mathrm{d}t}=Au\left(t\right)+f\left(t\right),t\ge 0,u\left(0\right)\in \overline{D\left(A\right)},$(4) ) has a unique integrated solution $u\left(t\right)\in C\left(\right[0,\tau ],X_0)$. Meanwhile, if A is a Hille-Yosida operator, then Assumption 2.8 in [23] holds. By Theorem 2.9 in [23], we know Assumption 2.2 holds.

Assumption 2.3

Let $\epsilon >0$ and $F\in C^k\left(\right(-\epsilon ,\epsilon )\times B_{X_0}(0,\epsilon );X)$ for some $k\ge 4$. Assume that the following conditions are satisfied:

1. $F(\mu ,0)=0,\mathrm{\forall }\mu \in (-\epsilon ,\epsilon )$ and ${\mathrm{\partial }}_{x}F(0,0)=0;$

2. $($Transversality condition$)$ For each $\mu \in (-\epsilon ,\epsilon ),$ there exists a pair of conjugated simple eigenvalues of $(A+{\mathrm{\partial }}_{x}F(\mu ,0){)}_0,$ denoted by $\lambda \left(\mu \right)$ and $\overline{\lambda \left(\mu \right)},$ such that $\lambda \left(\mu \right)=\alpha \left(\mu \right)+i\omega \left(\mu \right),$ the map $\mu \to \lambda \left(\mu \right)$ is continuously differentiable, $\omega \left(0\right)>0,\alpha \left(0\right)=0,\frac{\mathrm{d}\alpha \left(0\right)}{\mathrm{d}\mu }\ne 0,$ and $\sigma \left(A_0\right)\cap i\mathbb{R}=\left\{\lambda \right(0),\overline{\lambda \left(0\right)}\}.$

3. The essential growth rate of $\left\{T_{A_0}\right(t){\}}_{t\ge 0}$ is strictly negative, that is, ${\omega }_{0,\mathrm{ess}}\left(A_0\right)<0.$

Base on the above discussion and assumptions, now we can state the following Hopf bifurcation theorem [18].

Theorem 2.1

Let Assumptions 2.1–2.3 be satisfied. Then there exist ${\epsilon }^{\ast }>0,$ three $C^{k-1}$ maps, $\epsilon \to \mu \left(\epsilon \right)$ from $(0,{\epsilon }^{\ast })$ into $\mathbb{R},$ $\epsilon \to x_{\epsilon }$ from $(0,{\epsilon }^{\ast })$ into $\overline{D\left(A\right)},$ and $\epsilon \to \gamma \left(\epsilon \right)$ from $(0,{\epsilon }^{\ast })$ into $\mathbb{R},$ such that for each $\epsilon \in (0,{\epsilon }^{\ast })$ there exists a $\gamma \left(\epsilon \right)$-periodic function $u_{\epsilon }\in C^k(\mathbb{R},X_0),$ which is an integrated solution of (2.3) with the parameter value equals $\mu \left(\epsilon \right)$ and the initial value equals $x_{\epsilon }$. So for each $t\ge 0,$ $u_{\epsilon }$ satisfies $u_{\epsilon }\left(t\right)=x_{\epsilon }+A{\int }_0^t{u}_{\epsilon }\left(l\right)\mathrm{d}l+{\int }_0^{t}F\left(\mu \right(\epsilon ),u_{\epsilon }(l\left)\right)\mathrm{d}l.$ Moreover, we have the following properties

(a) There exist a neighborhood N of 0 in $X_0$ and an open interval I in $\mathbb{R}$ containing 0, such that for $\hat{\mu }\in I$ and any periodic solution $\hat{\mu }$ in N with minimal period $\hat{\gamma }$ close to $2\pi /\omega \left(0\right)$ of (2.3) for the parameter value $\hat{\mu },$ there exists $\epsilon \in (0,{\epsilon }^{\ast })$ such that $\hat{u}\left(t\right)=u_{\epsilon }(t+\theta )$ (for some $\theta \in [0,\gamma (\epsilon \left)\right),\mu \left(\epsilon \right)=\hat{\mu }$ and$\gamma \left(\epsilon \right)=\hat{\gamma };$

(b) The map $\epsilon \to \mu \left(\epsilon \right)$ is a $C^{k-1}$ function and we have the Taylor expansion $\mu \left(\epsilon \right)=\sum _{n=1}^{\left[(k-2)/2\right]}{\mu }_{2n}{\epsilon }^{2n}+O\left({\epsilon }^{k-1}\right),\mathrm{\forall }\epsilon \in (0,{\epsilon }^{\ast }),$ where $\left[(k-2)/2\right]$ is the integer part of $(k-2)/2$.

(c) The period $\gamma \left(\epsilon \right)$ of $t\to u_{\epsilon }\left(t\right)$ is a $C^{k-1}$ function and $\gamma \left(\epsilon \right)=\frac{2\pi }{\omega \left(0\right)}\left[1+\sum _{n=1}^{\left[(k-2)/2\right]}{\gamma }_{2n}{\epsilon }^{2n}\right]+O\left({\epsilon }^{k-1}\right),\mathrm{\forall }\epsilon \in (0,{\epsilon }^{\ast }),$ where $\omega \left(0\right)$ is the imaginary part of $\lambda \left(0\right)$ defined in Assumption 2.3.

3. Stability of equilibria and existence of Hopf bifurcation

In this section, we will study stability of equilibria and existence of Hopf bifurcation for (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ).

3.1. The transformation of the Cauchy problem

In system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ), let $S\left(t\right)={\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a,R\left(t\right)={\int }_0^{+\mathrm{\infty }}v(t,a)\mathrm{d}a,$ we can rewrite system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) as the following age-structured model (5) $\begin{array}{rl}& \frac{\mathrm{\partial }x(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }x(t,a)}{\mathrm{\partial }a}=-Dx(t,a),\\ & x(t,0)=B\left(x\right(t,\cdot \left)\right),\\ & x(0,a)=x_0\in L_{+}^1\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3),\end{array}$(5) where $x(t,a)=\left(s\right(t,a),A(t,a),v(t,a){)}^{\mathrm{T}}$, $D=\mathrm{diag}(m_1,m_2,m_3),$ $m_1=\mu +\alpha ,$ $m_2=\mu +a_1+\delta ,$ $m_3=\mu +a_2+\rho .$ $\begin{array}{rl}B\left(x\right(t,\cdot \left)\right)& =\left(\begin{array}{c}s(t,0)\\ A(t,0)\\ v(t,0)\end{array}\right)\\ & =\left(\begin{array}{c}r\left({\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+{\int }_0^{+\mathrm{\infty }}v(t,a)\mathrm{d}a\right)-\\ {\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a\\ \begin{array}{c}{\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a\\ +\rho {\int }_0^{+\mathrm{\infty }}v(t,a)\mathrm{d}a+\alpha {\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a\end{array}\\ \delta {\int }_0^{+\mathrm{\infty }}s(t,a)\mathrm{d}a\end{array}\right).\end{array}$ Consider the Banach space $(X,\parallel \cdot \parallel )$ $X={\mathbb{R}}^3\times L^1\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3)$ with $\left(\begin{array}{c}\alpha \\ \varphi \end{array}\right)=\parallel \alpha {\parallel }_{{\mathbb{R}}^3}+\parallel \varphi {\parallel }_{L^1\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3)}.$ Define the linear operator $L:D\left(L\right)\to X$ by $L\left(\begin{array}{c}0\\ \varphi \end{array}\right)=\left(\begin{array}{c}-\varphi \left(0\right)\\ -{\varphi }^{\prime }-D\varphi \end{array}\right)$ with $D\left(L\right)=\left\{0_{{\mathbb{R}}^3}\right\}\times W^{1,1}\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3),$ we notice L is non-densely defined since $X_0:=\overline{D\left(L\right)}=\left\{0_{{\mathbb{R}}^3}\right\}\times L^1\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3)\ne X.$ Define the nonlinear operator $F:\overline{D\left(L\right)}\to X$ by $F\left(\begin{array}{c}\left(\begin{array}{c}0\\ \varphi \end{array}\right)\end{array}\right)=\left(\begin{array}{c}B\left(\varphi \right)\\ 0\end{array}\right).$ Set $w\left(t\right)=\left(\begin{array}{c}0\\ x(t,\cdot )\end{array}\right).$ Now we can rewrite PDEs system (5(5) $\begin{array}{rl}& \frac{\mathrm{\partial }x(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }x(t,a)}{\mathrm{\partial }a}=-Dx(t,a),\\ & x(t,0)=B\left(x\right(t,\cdot \left)\right),\\ & x(0,a)=x_0\in L_{+}^1\left(\right(0,+\mathrm{\infty }),{\mathbb{R}}^3),\end{array}$(5) ) as the following non-densely defined abstract Cauchy problem (6) $\begin{array}{rl}& \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}=Lw\left(t\right)+F\left(w\right(t\left)\right),\\ & \omega \left(0\right)=\left(\begin{array}{c}0\\ x_0\end{array}\right)\in \overline{D\left(L\right)}.\end{array}$(6) The global existence and uniqueness of solutions of system (6(6) $\begin{array}{rl}& \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}=Lw\left(t\right)+F\left(w\right(t\left)\right),\\ & \omega \left(0\right)=\left(\begin{array}{c}0\\ x_0\end{array}\right)\in \overline{D\left(L\right)}.\end{array}$(6) ) follow from the results of Magal [21] and Magal and Ruan [23].

3.2. Existence of equilibria

If $\overline{w}\left(a\right)=\left(\begin{array}{c}0\\ \overline{x}\left(a\right)\end{array}\right)\in X_0$ is an equilibrium of (6(6) $\begin{array}{rl}& \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}=Lw\left(t\right)+F\left(w\right(t\left)\right),\\ & \omega \left(0\right)=\left(\begin{array}{c}0\\ x_0\end{array}\right)\in \overline{D\left(L\right)}.\end{array}$(6) ), we have $\left(\begin{array}{c}0\\ \overline{x}\left(a\right)\end{array}\right)\in D\left(L\right)\mathrm{and}L\left(\begin{array}{c}0\\ \overline{x}\left(a\right)\end{array}\right)+F\left(\begin{array}{c}\left(\begin{array}{c}0\\ \overline{x}\left(a\right)\end{array}\right)\end{array}\right)=0,$ which is equivalent to (7) $\begin{array}{rl}& -{\overline{x}}^{\prime }\left(a\right)-D\overline{x}\left(a\right)=0,\\ & -\overline{x}\left(0\right)+B\left(\overline{x}\right(\cdot \left)\right)=0.\end{array}$(7) Hence we obtain (8) $\overline{x}\left(a\right)=\left(\begin{array}{c}\overline{s}\left(a\right)\\ \overline{A}\left(a\right)\\ \overline{v}\left(a\right)\end{array}\right)={\mathrm{e}}^{-Da}\overline{x}\left(0\right)\mathrm{and}\overline{x}\left(0\right)=\left(\begin{array}{c}r(\overline{S}+\overline{A}+\overline{V})-\overline{S}{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)\overline{A}\left(a\right)\mathrm{d}a\\ \overline{S}{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)\overline{A}\left(a\right)\mathrm{d}a+\rho \overline{V}+\alpha \overline{S}\\ \delta \overline{A}\end{array}\right),$(8) where $\overline{S}={\int }_0^{+\mathrm{\infty }}\overline{s}\left(a\right)\mathrm{d}a,\overline{A}={\int }_0^{+\mathrm{\infty }}\overline{A}\left(a\right)\mathrm{d}a,\overline{V}={\int }_0^{+\mathrm{\infty }}\overline{v}\left(a\right)\mathrm{d}a$. From (8(8) $\overline{x}\left(a\right)=\left(\begin{array}{c}\overline{s}\left(a\right)\\ \overline{A}\left(a\right)\\ \overline{v}\left(a\right)\end{array}\right)={\mathrm{e}}^{-Da}\overline{x}\left(0\right)\mathrm{and}\overline{x}\left(0\right)=\left(\begin{array}{c}r(\overline{S}+\overline{A}+\overline{V})-\overline{S}{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)\overline{A}\left(a\right)\mathrm{d}a\\ \overline{S}{\int }_0^{+\mathrm{\infty }}\beta \left(a\right)\overline{A}\left(a\right)\mathrm{d}a+\rho \overline{V}+\alpha \overline{S}\\ \delta \overline{A}\end{array}\right),$(8) ) we can get $\begin{array}{rl}{m}_1\overline{S}& =r(\overline{S}+\overline{A}+\overline{V})-K_0{m}_2\overline{S}\overline{A},\\ m_2\overline{A}& =K_0{m}_2\overline{S}\overline{A}+\rho \overline{V}+\alpha \overline{S},\\ m_3\overline{V}& =\delta \overline{A}.\end{array}$ It is easy to see the system (7(7) $\begin{array}{rl}& -{\overline{x}}^{\prime }\left(a\right)-D\overline{x}\left(a\right)=0,\\ & -\overline{x}\left(0\right)+B\left(\overline{x}\right(\cdot \left)\right)=0.\end{array}$(7) ) has always trivial equilibrium ${\overline{x}}_1\left(a\right)={\mathrm{e}}^{-Da}(0,0,0{)}^{\mathrm{T}},$ Furthermore, if $\left(H1\right)r>m_1\mathrm{and}{m}_2-\rho \frac{\delta }{m_3}>r\left(1+\frac{\delta }{m_3}\right)$ holds, system (7(7) $\begin{array}{rl}& -{\overline{x}}^{\prime }\left(a\right)-D\overline{x}\left(a\right)=0,\\ & -\overline{x}\left(0\right)+B\left(\overline{x}\right(\cdot \left)\right)=0.\end{array}$(7) ) has a unique positive equilibrium ${\overline{x}}_2\left(a\right)=\left(\begin{array}{c}{\overline{s}}^{\ast }\left(a\right)\\ {\overline{A}}^{\ast }\left(a\right)\\ {\overline{v}}^{\ast }\left(a\right)\end{array}\right)={\mathrm{e}}^{-Da}\left(\begin{array}{c}{m}_1{\overline{S}}^{\ast }\\ m_2{\overline{A}}^{\ast }\\ m_3{\overline{V}}^{\ast }\end{array}\right),$ where $\begin{array}{rl}{\overline{S}}^{\ast }& =\frac{(r-m_1)(m_2-\rho \frac{\delta }{m_3})+\alpha r(1+\frac{\delta }{m_3})}{(r-\mu )K_0{m}_2},\\ {\overline{A}}^{\ast }& =\frac{(r-\mu ){\overline{S}}^{\ast }}{(m_2-\rho \frac{\delta }{m_3})-r(1+\frac{\delta }{m_3})},{\overline{V}}^{\ast }=\frac{\delta }{m_3}{\overline{A}}^{\ast }.\end{array}$

Lemma 3.1

The system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) has always trivial equilibrium $E_1\left(a\right)=(0,0_{L^1\left(\right(0,+\mathrm{\infty }),\mathbb{R})},0{)}^{\mathrm{T}}$. If $r>m_1\mathrm{and}{m}_2-\rho \frac{\delta }{m_3}>r\left(1+\frac{\delta }{m_3}\right)$ hold, there exists a unique positive equilibrium of system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) $E^{\ast }\left(a\right)=\left(\begin{array}{c}{\overline{S}}^{\ast }\\ {\overline{A}}^{\ast }\left(a\right)\\ {\overline{V}}^{\ast }\end{array}\right).$

3.3. Linearized equation

Let $y\left(t\right):=w\left(t\right)-\overline{w}\left(a\right)$, then system (6(6) $\begin{array}{rl}& \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}=Lw\left(t\right)+F\left(w\right(t\left)\right),\\ & \omega \left(0\right)=\left(\begin{array}{c}0\\ x_0\end{array}\right)\in \overline{D\left(L\right)}.\end{array}$(6) ) is equivalent to the following system (9) $\begin{array}{rl}\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =Ly\left(t\right)+F\left(y\right(t)+\overline{w}(a\left)\right)-F\left(\overline{w}\right(a\left)\right),\\ y\left(0\right)& =\left(\begin{array}{c}0\\ x_0-\overline{x}\left(a\right)\end{array}\right)\triangleq y_0\in X_0,\end{array}$(9) and the equilibrium $\overline{w}\left(a\right)$ of system (7(7) $\begin{array}{rl}& -{\overline{x}}^{\prime }\left(a\right)-D\overline{x}\left(a\right)=0,\\ & -\overline{x}\left(0\right)+B\left(\overline{x}\right(\cdot \left)\right)=0.\end{array}$(7) ) is transformed into the zero equilibrium of system (9(9) $\begin{array}{rl}\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =Ly\left(t\right)+F\left(y\right(t)+\overline{w}(a\left)\right)-F\left(\overline{w}\right(a\left)\right),\\ y\left(0\right)& =\left(\begin{array}{c}0\\ x_0-\overline{x}\left(a\right)\end{array}\right)\triangleq y_0\in X_0,\end{array}$(9) ).

The linearized system of system (9(9) $\begin{array}{rl}\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =Ly\left(t\right)+F\left(y\right(t)+\overline{w}(a\left)\right)-F\left(\overline{w}\right(a\left)\right),\\ y\left(0\right)& =\left(\begin{array}{c}0\\ x_0-\overline{x}\left(a\right)\end{array}\right)\triangleq y_0\in X_0,\end{array}$(9) ) at the equilibrium 0 is as follows $\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}=Ay\left(t\right),y_0\in X_{0}t\ge 0,$ where $A=L+DF\left(\overline{w}\right)$. Then system (9(9) $\begin{array}{rl}\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =Ly\left(t\right)+F\left(y\right(t)+\overline{w}(a\left)\right)-F\left(\overline{w}\right(a\left)\right),\\ y\left(0\right)& =\left(\begin{array}{c}0\\ x_0-\overline{x}\left(a\right)\end{array}\right)\triangleq y_0\in X_0,\end{array}$(9) ) can be written as $\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}=Ay\left(t\right)+H\left(y\right(t\left)\right),y_0\in X_{0}t\ge 0,$ where $H\left(y\right(t\left)\right)=F\left(y\right(t)+\overline{w}(a\left)\right)-F\left(\overline{w}\right(a\left)\right)-DF\left(\overline{w}\right)y\left(t\right)$ satisfying $H\left(0\right)=0,$ and $DH\left(0\right)=0$.

Denote $\xi :=min\{m_1,m_2,m_3\},\mathrm{and}\mathrm{\Omega }:=\{\lambda \in \mathbb{C}:\mathrm{Re}(\lambda )>-\xi \}.$ By applying the results of Liu, Magal and Ruan [18], we obtain the following result.

Lemma 3.2

For $\lambda \in \mathrm{\Omega },\lambda \in \rho \left(L\right),$ we have the following formula $(\lambda I-L{)}^{-1}\left(\begin{array}{c}\alpha \\ \psi \end{array}\right)=\left(\begin{array}{c}0\\ \varphi \end{array}\right)$ where $\left(\begin{array}{c}\alpha \\ \psi \end{array}\right)\in X,$ $\left(\begin{array}{c}0\\ \varphi \end{array}\right)\in D\left(L\right)$ and $\varphi \left(a\right)={\mathrm{e}}^{-(\lambda I+D)a}\alpha +{\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\psi \left(s\right)\mathrm{d}s$.

It is readily checked that $\parallel (\lambda I-L{)}^{-1}\parallel \le \frac{1}{\left(\mathrm{Re}\right(\lambda )+\xi )},\mathrm{\forall }\mathrm{Re}(\lambda )>-\xi ,$ so L is a Hille-Yosida operator and (10) $\parallel (\lambda I-L{)}^{-n}\parallel \le \frac{1}{\left(\mathrm{Re}\right(\lambda )+\xi {)}^n},\mathrm{\forall }\mathrm{Re}(\lambda )>-\xi ,n\ge 1.$(10) Define the part of L in $\overline{D\left(L\right)}$ by $L_0,$ $L_0:D\left(L_0\right)\subset X\to X$ with $L_{0}x=Lx\mathrm{for}x\in D\left(L_0\right)=\{x\in D(L):Lx\in \overline{D\left(L\right)}\},$ and we know $D\left(L_0\right)=\left\{\left(\begin{array}{c}0\\ \varphi \end{array}\right)\in \left\{0_{{\mathbb{R}}^3}\right\}\times W^{1,1}\left(\right(0,+\mathrm{\infty })\times ,{\mathbb{R}}^3):\varphi \left(0\right)=0\right\}.$ Then, we can claim that $L_0$ is the infinitesimal generator of a $C_0$-semigroup $\left\{T_{L_0}\right(t){\}}_{t\ge 0}$ on $\overline{D\left(L\right)}$. and for each $t\ge 0$ the liear operator $T_{L_0}\left(t\right)$ is defined by $T_{L_0}\left(t\right)\left(\begin{array}{c}0\\ \varphi \end{array}\right)=\left(\begin{array}{c}0\\ {\hat{T}}_{L_0}\left(t\right)\varphi ,\end{array}\right)$ where (11) ${\hat{T}}_{L_0}\left(t\right)\left(\varphi \right)\left(a\right)=\left\{\begin{array}{ll}{\mathrm{e}}^{-Dt}\varphi (a-t),& \mathrm{if}a\ge t,\\ 0,& \mathrm{otherwise}.\end{array}\right.$(11) Now we estimate the essential growth bound of the $C_0-$semigroup generated by $A_0$ which is the part of A in $\overline{D\left(A\right)}$. We observe that for any $\left(\begin{array}{c}0\\ \varphi \end{array}\right)\in D\left(L\right)$, $DF\left(\overline{w}\right)\left(\begin{array}{c}0\\ \varphi \end{array}\right)=\left(\begin{array}{c}DB\left(\overline{x}\right)\left(\varphi \right)\\ 0\end{array}\right)$ where $DB\left(\overline{x}\right)\left(\varphi \right)=\left(\begin{array}{ccc}r-K_0{m}_2\overline{A}& r& r\\ K_0{m}_2\overline{A}+\alpha & 0& \rho \\ 0& \delta & 0\end{array}\right){\int }_0^{+\mathrm{\infty }}\varphi \left(a\right)\mathrm{d}a+\left(\begin{array}{ccc}0& -\overline{S}& 0\\ 0& \overline{S}& 0\\ 0& 0& 0\end{array}\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)\varphi \left(a\right)\mathrm{d}a.$ Then $DF\left(\overline{w}\right):\overline{D\left(L\right)}\subset X\to X$ is a compact bounded linear operator. From (10(10) $\parallel (\lambda I-L{)}^{-n}\parallel \le \frac{1}{\left(\mathrm{Re}\right(\lambda )+\xi {)}^n},\mathrm{\forall }\mathrm{Re}(\lambda )>-\xi ,n\ge 1.$(10) ) we obtain $\parallel T_{L_0}\left(t\right)\parallel \le {\mathrm{e}}^{-\xi t}.$ Then we have ${\omega }_{0,\mathrm{ess}}\left(L_0\right)\le {\omega }_0\left(L_0\right)\le -\xi <0.$ By applying the perturbation results in Ducrot, Liu and Magal [6], we obtain ${\omega }_{0,\mathrm{ess}}\left(A_0\right)\le -\xi <0.$ Thus, by the above discussion and Theorem 3.5.5 in [1], we obtain the following proposition.

Proposition 3.1

The linear operator A is a Hille-Yoside operator, and the essential growth rate of the strongly continuous semigroup generated by $A_0$ is strictly negative, that is, ${\omega }_{0,\mathrm{ess}}\left(A_0\right)<0.$

In order to apply Theorem 2.1, we remain to precise the spectral properties of $A_0$. Setting $C:=DF\left(\overline{w}\right),$ and let $\lambda \in \mathrm{\Omega }$. Since $(\lambda I-L)$ is invertible, it follows that $\lambda I-(L+C)$ is invertible if and only if $I-C(\lambda I-L{)}^{-1}$ is invertible. If $I-C(\lambda I-L{)}^{-1}$ is invertible, we obtain $(\lambda I-(L+C){)}^{-1}=(\lambda I-L{)}^{-1}(I-C(\lambda I-L{)}^{-1}{)}^{-1}.$ Consider the equation $(I-C(\lambda I-L{)}^{-1})\left(\begin{array}{c}\alpha \\ \varphi \end{array}\right)=\left(\begin{array}{c}\hat{\alpha }\\ \hat{\varphi }\end{array}\right),$ that is $\left(\begin{array}{c}\alpha \\ \varphi \end{array}\right)-C\left(\begin{array}{c}0\\ {\mathrm{e}}^{-(\lambda I+D)a}\alpha +{\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\varphi \left(s\right)\mathrm{d}s\end{array}\right)=\left(\begin{array}{c}\hat{\alpha }\\ \hat{\varphi }\end{array}\right).$ Then, we obtain the system $\begin{array}{rl}& \alpha -DB\left(\overline{x}\right)\left({\mathrm{e}}^{-(\lambda I+D)a}\alpha +{\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\varphi \left(s\right)\mathrm{d}s\right)=\hat{\alpha },\\ & \varphi \left(a\right)=\hat{\varphi }\left(a\right),\end{array}$ this system can be written as $\begin{array}{rl}& \alpha -DB\left(\overline{x}\right)\left({\mathrm{e}}^{-(\lambda I+D)a}\alpha \right)=\hat{\alpha }+DB\left(\overline{x}\right)\left({\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\varphi \left(s\right)\mathrm{d}s\right),\\ & \varphi =\hat{\varphi }.\end{array}$ From the formula of $DB\left(\overline{x}\right)$, we know $\alpha -DB\left(\overline{x}\right)\left({\mathrm{e}}^{-(\lambda I+D)a}\alpha \right)=M\left(\lambda \right)\alpha ,$ where $\begin{array}{rl}M\left(\lambda \right)& =I-\left(\begin{array}{ccc}r-K_0{m}_2\overline{A}& r& r\\ K_0{m}_2\overline{A}+\alpha & 0& \rho \\ 0& \delta & 0\end{array}\right){\int }_0^{+\mathrm{\infty }}{\mathrm{e}}^{-(\lambda I+D)a}\mathrm{d}a\\ & -\left(\begin{array}{ccc}0& -\overline{S}& 0\\ 0& \overline{S}& 0\\ 0& 0& 0\end{array}\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right){\mathrm{e}}^{-(\lambda I+D)a}\mathrm{d}a.\end{array}$ Denote $S(\lambda ,\hat{\varphi })=DB\left(\overline{x}\right)\left({\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\hat{\varphi }\left(s\right)\mathrm{d}s\right).$ Then $M\left(\lambda \right)\alpha =\hat{\alpha }+S(\lambda ,\hat{\varphi }).$ When $M\left(\lambda \right)$ is invertible, we have $\alpha =M\left(\lambda {)}^{-1}\right(\hat{\alpha }+S(\lambda ,\hat{\varphi })).$ From the above discussion and by using the proof of Lemma 3.5 in [29], we obtain the following lemma.

Lemma 3.3

The following results hold:

1. $\sigma (L+C)\cap \mathrm{\Omega }={\sigma }_P(L+C)\cap \mathrm{\Omega }=\{\lambda \in \mathrm{\Omega }:\det (M\left(\lambda \right))=0\};$

2. If $\lambda \in \rho (L+C)\cap \mathrm{\Omega },$ we have the following formula for the resolvent $(\lambda I-(L+C){)}^{-1}\left(\begin{array}{c}\alpha \\ \varphi \end{array}\right)=\left(\begin{array}{c}0\\ \hat{\varphi }\end{array}\right),$ where $\hat{\varphi }\left(a\right)={\mathrm{e}}^{-(\lambda I+D)a}M\left(\lambda {)}^{-1}\right(\alpha +S(\lambda ,\varphi ))+{\int }_0^a{\mathrm{e}}^{-(\lambda I+D)(a-s)}\varphi (s)\mathrm{d}s,$ and $M\left(\lambda \right),S(\lambda ,\varphi )$ defined as above.

From the above discussion, we know that the linear operator A satisfies Assumptions 2.1–2.3(c) holds.

3.4. Stability of the trivial equilibrium

Now, we consider the stability of the trivial equilibrium $E_1\left(a\right)=(0,0_{L^1\left(\right(0,+\mathrm{\infty }),\mathbb{R})},0{)}^{\mathrm{T}},$ we obtain $M\left(\lambda \right)=I-\left(\begin{array}{ccc}r& r& r\\ \alpha & 0& \rho \\ 0& \delta & 0\end{array}\right){\int }_0^{+\mathrm{\infty }}{\mathrm{e}}^{-(\lambda I+D)a}\mathrm{d}a-\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right){\mathrm{e}}^{-(\lambda I+D)a}\mathrm{d}a.$ Thus, we obtain the characteristic equation $\det \left(M\right(\lambda \left)\right)=\frac{f_0\left(\lambda \right)}{(\lambda +m_1)(\lambda +m_2)(\lambda +m_3)}=0$ where $f_0\left(\lambda \right)={\lambda }^3+a_0{\lambda }^2+b_0\lambda +c_0$, and $a_0=(m_1+m_2+m_3-r),b_0=(m_1-r)(m_2+m_3)+(m_2{m}_3-\rho \delta )-r\alpha$, $c_0=(m_1-r)(m_2{m}_3-\rho \delta )-(m_3+\delta )r\alpha$.

It is easy to see that $\{\lambda \in \mathrm{\Omega }:\det M(\lambda )=0\}=\{\lambda \in \mathrm{\Omega }:f_0(\lambda )=0\}.$ If $c_0<0$ holds, then $f_0\left(\lambda \right)=0$ has at least one root with a real part. Hence, the equilibrium $E_1\left(a\right)$ is unstable.

If $c_0>0$ holds, then $\begin{array}{rl}{a}_0& =m_1+m_2+m_3-r>0,\\ b_0& >(m_1-r)(m_2+m_3)-r\alpha >r\alpha \left(\frac{(m_3+\delta )(m_2+m_3)}{m_2{m}_3-\rho \delta }-1\right)>0,\\ a_0{b}_0-c_0& =(m_1+m_2+m_3-r)\left(\right(m_1-r\left)\right(m_2+m_3)+(m_2{m}_3-\rho \delta )-r\alpha )\\ & -(m_1-r)(m_2{m}_3-\rho \delta )+(m_3+\delta )r\alpha \\ & >(m_1+m_2+m_3-r)(m_2{m}_3-\rho \delta )-(m_1-r)(m_2{m}_3-\rho \delta )+(m_3+\delta )r\alpha \\ & =(m_2+m_3)(m_2{m}_3-\rho \delta )+(m_3+\delta )r\alpha >0,\end{array}$ by the Routh-Hurwitz criterion, all the roots of $f_0\left(\lambda \right)=0$ have negative real parts. Hence, the equilibrium $E_1\left(a\right)$ is stable.

Theorem 3.4

If $c_0>0,$ then $E_1\left(a\right)$ is locally asymptotically stable for all $\tau \ge 0$. If $c_0<0,$ then $E_1\left(a\right)$ is unstable for all $\tau \ge 0$.

Remark 3.1

$c_0>0$ means $r<\mu +\alpha -(m_3+\delta )r\alpha /(m_2{m}_3-\rho \delta )$. α is small, then the birth rate r may be less than the mortality rate μ, the whole population is easily extinct. So in reality, the $E_1\left(a\right)$ is more likely to be unstable.

3.5. Stability of the positive equilibrium and Hopf bifurcation

When $\left(H1\right)$ holds, the characteristic equation of system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) about the positive equilibrium $E^{\ast }\left(a\right)$ can be rewritten as $\det \left(M\right(\lambda \left)\right)=\frac{{\lambda }^3+a{\lambda }^2+b\lambda +c+(e+f\lambda +g{\lambda }^2){\mathrm{e}}^{-\lambda \tau }}{(\lambda +m_1)(\lambda +m_2)(\lambda +m_3)}=:\frac{f\left(\lambda \right)}{s\left(\lambda \right)}=0,$ where $\begin{array}{rl}a& =m_1+m_2+m_3-r+K_0{m}_2{\overline{A}}^{\ast },\\ b& =-\rho \delta +m_1{m}_2+m_1{m}_3+m_2{m}_3-K_0{m}_2{\overline{A}}^{\ast }r-r(m_2+m_3)\\ & +K_0{m}_2{\overline{A}}^{\ast }(m_2+m_3)-r\alpha ,\\ c& =-\rho \delta m_1+(r-K_0{m}_2{\overline{A}}^{\ast })\rho \delta -K_0{m}_2{\overline{A}}^{\ast }r\delta +m_1{m}_2{m}_3-K_0{m}_2{\overline{A}}^{\ast }r{m}_3-r{m}_2{m}_3\\ & +K_0{m}_2{\overline{A}}^{\ast }{m}_2{m}_3-r\delta \alpha -r\alpha m_3\\ & =-(r-m_1)(m_2{m}_3-\rho \delta )+K_0{m}_2{\overline{A}}^{\ast }\left(\right(m_2{m}_3-\rho \delta )-r(\delta +m_3\left)\right)-r\alpha (\delta +m_3)\\ & =-(r-m_1)(m_2{m}_3-\rho \delta )+K_0{m}_2{\overline{S}}^{\ast }{m}_3(r-\mu )-r\alpha (\delta +m_3)=0,\\ e& =-K_0{m}_2{\overline{S}}^{\ast }(m_1-r-\alpha )m_3=K_0{m}_2{\overline{S}}^{\ast }(r-\mu )m_3>0,\\ f& =-K_0{m}_2{\overline{S}}^{\ast }(m_1+m_3-r-\alpha ),\\ g& =-K_0{m}_2{\overline{S}}^{\ast }.\end{array}$ Since $K_0{m}_2{\overline{S}}^{\ast }=\frac{(r-m_1)(m_2-\rho \frac{\delta }{m_3})+\alpha r(1+\frac{\delta }{m_3})}{(r-\mu )},K_0{m}_2{\overline{A}}^{\ast }=\frac{(r-\mu )K_0{m}_2{\overline{S}}^{\ast }}{(m_2-\rho \frac{\delta }{m_3})-r(1+\frac{\delta }{m_3})},$ we know the coefficients $a,b,c,e,f,g$ have nothing to do with τ.

It is easy to see that $\{\lambda \in \mathrm{\Omega }:\det M(\lambda )=0\}=\{\lambda \in \mathrm{\Omega }:f(\lambda )=0\}.$ If $\tau =0$, then $f\left(\lambda \right)={\lambda }^3+(a+g){\lambda }^2+(b+f)\lambda +e=0.$ Since $\begin{array}{rl}a+g& =m_1+m_2+m_3-r+K_0{m}_2{\overline{A}}^{\ast }-K_0{m}_2{\overline{S}}^{\ast }\\ & >(m_1+m_2+m_3)-r+\left(r+\frac{r({\overline{A}}^{\ast }+{\overline{V}}^{\ast })}{{\overline{S}}^{\ast }}-m_1\right)-\left(m_2-\rho \frac{\delta }{m_3}\right)\\ & =m_3+\frac{r({\overline{A}}^{\ast }+{\overline{V}}^{\ast })}{{\overline{S}}^{\ast }}+\rho \frac{\delta }{m_3}>0,\\ b+f& =-\rho \delta +m_1{m}_2+m_1{m}_3+m_2{m}_3-K_0{m}_2{\overline{A}}^{\ast }r-r(m_2+m_3)\\ & +K_0{m}_2{\overline{A}}^{\ast }(m_2+m_3)-r\alpha -K_0{m}_2{\overline{S}}^{\ast }(m_1+m_3-r-\alpha )\\ & =(m_2{m}_3-\rho \delta )+m_1(m_2+m_3)-K_0{m}_2{\overline{A}}^{\ast }r-r(m_2+m_3)\\ & +\left(r+\frac{r({\overline{A}}^{\ast }+{\overline{V}}^{\ast })}{{\overline{S}}^{\ast }}-m_1\right)(m_2+m_3)\\ & -r\alpha +K_0{m}_2{\overline{S}}^{\ast }(r-\mu -m_3)\\ & >-K_0{m}_2{\overline{A}}^{\ast }r+(m_2{m}_3-\rho \delta )+\frac{r({\overline{A}}^{\ast }+{\overline{V}}^{\ast })}{{\overline{S}}^{\ast }}(m_2+m_3)\\ & -r\alpha +(r-m_1)\left(m_2-\rho \frac{\delta }{m_3}\right)\\ & +r\alpha \left(1+\frac{\delta }{m_3}\right)-m_3\left(m_2-\rho \frac{\delta }{m_3}\right)\\ & =-K_0{m}_2{\overline{A}}^{\ast }r+\frac{r({\overline{A}}^{\ast }+{\overline{V}}^{\ast })}{{\overline{S}}^{\ast }}(m_2+m_3)+(r-m_1)(m_2-\rho \frac{\delta }{m_3})+r\alpha \frac{\delta }{m_3}\\ & =\frac{1}{{\overline{S}}^{\ast }}\left(r\right(\rho {\overline{V}}^{\ast }+\alpha {\overline{S}}^{\ast }-m_2{\overline{A}}^{\ast })+r({\overline{A}}^{\ast }+{\overline{V}}^{\ast }\left)\right(m_2+m_3\left)\right)\\ & +(r-m_1)\left(m_2-\rho \frac{\delta }{m_3}\right)+r\alpha \frac{\delta }{m_3}>0,\\ e& >0.\end{array}$ By the Routh-Hurwitz criterion, when $\tau =0$ all the roots of $f\left(\lambda \right)=0$ have negative real parts if and only if $\left(H2\right)(a+g)(b+f)>e$ holds.

If $\tau \ne 0$, let $\lambda =i\omega (\omega >0)$ be a purely imaginary roots of $f\left(\lambda \right)=0$. Then, we have $-i{\omega }^3-a{\omega }^2+ib\omega +e{\mathrm{e}}^{-i\omega \tau }+if\omega {\mathrm{e}}^{-i\omega \tau }-g{\omega }^2{\mathrm{e}}^{-i\omega \tau }=0.$ Separating the real part and the imaginary part in the above equation, we can obtain (12) $\begin{array}{rl}& -{\omega }^3+b\omega =(e-g{\omega }^2)\sin \left(\omega \tau \right)-f\omega \cos \left(\omega \tau \right),\\ & -a{\omega }^2=(g{\omega }^2-e)\cos \left(\omega \tau \right)-f\omega \sin \left(\omega \tau \right).\end{array}$(12) Thus, we have (13) $(-{\omega }^3+b\omega {)}^2+(-a{\omega }^2{)}^2=(e-g{\omega }^2{)}^2+(f\omega {)}^2,$(13) i.e. (14) ${\omega }^6+(a^2-2b-g^2){\omega }^4+(b^2-f^2+2ge){\omega }^2-{\mathrm{e}}^2=0.$(14) Denote $z={\omega }^2,$ (14(14) ${\omega }^6+(a^2-2b-g^2){\omega }^4+(b^2-f^2+2ge){\omega }^2-{\mathrm{e}}^2=0.$(14) ) becomes (15) $z^3+(a^2-2b-g^2)z^2+(b^2-f^2+2ge)z-{\mathrm{e}}^2=0.$(15) Let $z_1,z_2$ and $z_3$ be three roots of Equation (15(15) $z^3+(a^2-2b-g^2)z^2+(b^2-f^2+2ge)z-{\mathrm{e}}^2=0.$(15) ). Since $\begin{array}{rl}{a}^2-2b-g^2& =(m_1+m_2+m_3-r+K_0{m}_2{\overline{A}}^{\ast }{)}^2\\ & -2(-\rho \delta +m_1{m}_2+m_1{m}_3+m_2{m}_3-K_0{m}_2{\overline{A}}^{\ast }r\\ & -r(m_2+m_3)+K_0{m}_2{\overline{A}}^{\ast }(m_2+m_3)-r\alpha )-(-K_0{m}_2{\overline{S}}^{\ast }{)}^2\\ & =(r-m_1{)}^2+m_2^2+m_3^2+2\rho \delta +(K_0{m}_2{\overline{A}}^{\ast }{)}^2+2K_0{m}_2{\overline{A}}^{\ast }{m}_1\\ & +2r\alpha -(K_0{m}_2{\overline{S}}^{\ast }{)}^2\\ & >(r-m_1{)}^2+m_2^2+m_3^2+2\rho \delta +(K_0{m}_2{\overline{A}}^{\ast }{)}^2+2K_0{m}_2{\overline{A}}^{\ast }{m}_1\\ & +2r\alpha -{\left(m_2-\rho \frac{\delta }{m_3}\right)}^2\\ & >(r-m_1{)}^2+m_2^2+m_3^2+2\rho \delta +(K_0{m}_2{\overline{A}}^{\ast }{)}^2+2K_0{m}_2{\overline{A}}^{\ast }{m}_1\\ & +2r\alpha -m_2^2>0,\end{array}$ we know $a^2-2b-g^2>0,-{\mathrm{e}}^2<0,$ then $z_1+z_2+z_3=-(a^2-2b-g^2)<0\mathrm{and}{z}_1{z}_2{z}_3={\mathrm{e}}^2>0,$ it is easy to know that (15(15) $z^3+(a^2-2b-g^2)z^2+(b^2-f^2+2ge)z-{\mathrm{e}}^2=0.$(15) ) has only one positive real root. We denote this positive real root by $z^{\ast }$. Then (14(14) ${\omega }^6+(a^2-2b-g^2){\omega }^4+(b^2-f^2+2ge){\omega }^2-{\mathrm{e}}^2=0.$(14) ) has only one positive real root ${\omega }_0=\sqrt{z^{\ast }}$.

Let $g\left(z\right)=z^3+(a^2-2b-g^2)z^2+(b^2-f^2+2ge)z-{\mathrm{e}}^2,$ it is easy to know that $g^{\prime }\left(z\right){|}_{z=z^{\ast }}>0,$ then we have $3z^2+(2a^2-4b-2g^2)z+(b^2-f^2+2eg){|}_{z=z^{\ast }}>0,$ i.e. (16) $3{\omega }^4+(2a^2-4b-2g^2){\omega }^2+(b^2-f^2+2eg){|}_{\omega ={\omega }_0}>0.$(16) From (12(12) $\begin{array}{rl}& -{\omega }^3+b\omega =(e-g{\omega }^2)\sin \left(\omega \tau \right)-f\omega \cos \left(\omega \tau \right),\\ & -a{\omega }^2=(g{\omega }^2-e)\cos \left(\omega \tau \right)-f\omega \sin \left(\omega \tau \right).\end{array}$(12) ), we know that $f\left(\lambda \right)=0$ with $\tau ={\tau }_k,$ has a pair of purely imaginary roots $\pm i{\omega }_0,$ where (17) ${\tau }_k=\left\{\begin{array}{cc}& \frac{1}{{\omega }_0}(\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2k\pi )=0,\eta \ge 0\\ & \frac{1}{{\omega }_0}(-\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2(k+1\left)\pi \right),\mathrm{otherwish},\end{array}\right.$(17) for $k=0,1,2,\dots$ and with $\eta =(g{\omega }_0^2-e)({\omega }_0^3-b{\omega }_0)+af{\omega }_0^3$.

Lemma 3.5

Assume that (H1) be satisfied, then $\frac{\mathrm{d}f\left(\lambda \right)}{\mathrm{d}\lambda }{\mid }_{\lambda =i{\omega }_0}\ne 0.$ Therefore $\lambda =i{\omega }_0$ is a simple root of $f\left(\lambda \right)=0$.

Proof.

Differentiating the equation $f\left(\lambda \right)=0$ with respect to λ, we have ${\left.\frac{\mathrm{d}f\left(\lambda \right)}{\mathrm{d}\lambda }\right|}_{\lambda =i{\omega }_0}=(3{\lambda }^2+2a\lambda +b+(2g\lambda +f){\mathrm{e}}^{-\tau \lambda }-\tau (g{\lambda }^2+f\lambda +e\left){\mathrm{e}}^{-\tau \lambda }\right){|}_{\lambda =i{\omega }_0}$ Thus if ${\left.\frac{\mathrm{d}f\left(\lambda \right)}{\mathrm{d}\lambda }\right|}_{\lambda =i{\omega }_0}=0.$ Separating the real part and the imaginary part in the above equation, we can obtain (18) $\begin{array}{rl}& -3{\omega }_0^2+b=-2g{\omega }_0\sin \left({\omega }_0{\tau }_k\right)-f\cos \left({\omega }_0{\tau }_k\right)+{\tau }_k(e-g{\omega }_0^2)\cos \left({\omega }_0{\tau }_k\right)\\ & +{\tau }_{k}f{\omega }_0\sin \left({\omega }_0{\tau }_k\right),\\ & 2a{\omega }_0=-2g{\omega }_0\cos \left({\omega }_0{\tau }_k\right)+f\sin \left({\omega }_0{\tau }_k\right)-{\tau }_k(e-g{\omega }_0^2)\sin \left({\omega }_0{\tau }_k\right)+{\tau }_{k}f{\omega }_0\cos \left({\omega }_0{\tau }_k\right).\end{array}$(18) Now defining $G\left(\omega \right)=g\left({\omega }^2\right)=({\omega }^3-b\omega {)}^2-(e-g{\omega }^2{)}^2+a^2{\omega }^4-f^2{\omega }^2,$ then $G\left({\omega }_0\right)=0$. $G^{\prime }\left(\omega \right)=2({\omega }^3-b\omega )(3{\omega }^2-b)+2(e-g{\omega }^2)\left(2g\omega \right)+4a^2{\omega }^3-2f^2\omega .$ According to Equations (12(12) $\begin{array}{rl}& -{\omega }^3+b\omega =(e-g{\omega }^2)\sin \left(\omega \tau \right)-f\omega \cos \left(\omega \tau \right),\\ & -a{\omega }^2=(g{\omega }^2-e)\cos \left(\omega \tau \right)-f\omega \sin \left(\omega \tau \right).\end{array}$(12) ), we know (19) $\begin{array}{rl}& -{\omega }_0^3+b{\omega }_0=(e-g{\omega }_0^2)\sin \left({\omega }_0{\tau }_k\right)-f{\omega }_0\cos \left({\omega }_0{\tau }_k\right),\\ & -a{\omega }_0^2=(g{\omega }_0^2-e)\cos \left({\omega }_0{\tau }_k\right)-f{\omega }_0\sin \left({\omega }_0{\tau }_k\right).\end{array}$(19) With the help of Equations (18(18) $\begin{array}{rl}& -3{\omega }_0^2+b=-2g{\omega }_0\sin \left({\omega }_0{\tau }_k\right)-f\cos \left({\omega }_0{\tau }_k\right)+{\tau }_k(e-g{\omega }_0^2)\cos \left({\omega }_0{\tau }_k\right)\\ & +{\tau }_{k}f{\omega }_0\sin \left({\omega }_0{\tau }_k\right),\\ & 2a{\omega }_0=-2g{\omega }_0\cos \left({\omega }_0{\tau }_k\right)+f\sin \left({\omega }_0{\tau }_k\right)-{\tau }_k(e-g{\omega }_0^2)\sin \left({\omega }_0{\tau }_k\right)+{\tau }_{k}f{\omega }_0\cos \left({\omega }_0{\tau }_k\right).\end{array}$(18) ) and (19(19) $\begin{array}{rl}& -{\omega }_0^3+b{\omega }_0=(e-g{\omega }_0^2)\sin \left({\omega }_0{\tau }_k\right)-f{\omega }_0\cos \left({\omega }_0{\tau }_k\right),\\ & -a{\omega }_0^2=(g{\omega }_0^2-e)\cos \left({\omega }_0{\tau }_k\right)-f{\omega }_0\sin \left({\omega }_0{\tau }_k\right).\end{array}$(19) ) we deduce that $G^{\prime }\left({\omega }_0\right)=0$.

However, $G^{\prime }\left({\omega }_0\right)=2{\omega }_0{g}^{\prime }\left({\omega }_0^2\right)=2{\omega }_0{g}^{\prime }\left(z^{\ast }\right)>0,$ thus ${\left.\frac{\mathrm{d}f\left(\lambda \right)}{\mathrm{d}\lambda }\right|}_{\lambda =i{\omega }_0}\ne 0.$ This completes the proof.

Lemma 3.6

Assume that (H1) be satisfied, denote the root $\lambda \left(\tau \right)=\alpha \left(\tau \right)+i\omega \left(\tau \right)$ of $f\left(\lambda \right)=0,$ satisfying $\alpha \left({\tau }_k\right)=0,\omega \left({\tau }_k\right)={\omega }_0,$ where ${\tau }_k$ is defined in (17(17) ${\tau }_k=\left\{\begin{array}{cc}& \frac{1}{{\omega }_0}(\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2k\pi )=0,\eta \ge 0\\ & \frac{1}{{\omega }_0}(-\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2(k+1\left)\pi \right),\mathrm{otherwish},\end{array}\right.$(17) ). Then ${\alpha }^{\prime }\left({\tau }_k\right)=\mathrm{Re}\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right){\mid }_{\tau ={\tau }_k}>0.$

Proof.

Taking the derivative of λ with respect to τ in $f\left(\lambda \right)=0$, it is easy to have $\begin{array}{rl}& (3{\lambda }^2+2a\lambda +b)\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }+(2g\lambda +f){\mathrm{e}}^{-\lambda \tau }\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }-(g{\lambda }^2+f\lambda +e){\mathrm{e}}^{-\lambda \tau }\left(\tau \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }+\lambda \right)=0,\\ & {\left.{\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right)}^{-1}\right|}_{\tau ={\tau }_k}={\left.\left(-\frac{(3{\lambda }^2+2a\lambda +b)}{\lambda ({\lambda }^3+a{\lambda }^2+b\lambda )}+\frac{(2g\lambda +f)}{(g{\lambda }^2+f\lambda +e)\lambda }-\frac{\tau }{\lambda }\right)\right|}_{\tau ={\tau }_k}.\end{array}$ By using (13(13) $(-{\omega }^3+b\omega {)}^2+(-a{\omega }^2{)}^2=(e-g{\omega }^2{)}^2+(f\omega {)}^2,$(13) ), we obtain ${\left.\mathrm{Re}{\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right)}^{-1}\right|}_{\tau ={\tau }_k}=\frac{3{\omega }_0^4+(2a^2-4b-2g^2){\omega }_0^2+(b^2-f^2+2eg)}{(f\omega {)}_0^2+(e-g{\omega }_0^2{)}^2}.$ By using (16(16) $3{\omega }^4+(2a^2-4b-2g^2){\omega }^2+(b^2-f^2+2eg){|}_{\omega ={\omega }_0}>0.$(16) ), it is easy to know that ${\left.\mathrm{Re}{\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\lambda }\right)}^{-1}\right|}_{\tau ={\tau }_k}>0.$ Noting that $\mathrm{sign}\left(\mathrm{Re}{\left.\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right)\right|}_{\tau ={\tau }_k}\right)=\mathrm{sign}\left(\mathrm{Re}{\left.{\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right)}^{-1}\right|}_{\tau ={\tau }_k}\right),$ thus $\mathrm{Re}{\left.\left(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right)\right|}_{\tau ={\tau }_k}>0.$ This completes the proof.

Theorem 3.7

Suppose that (H1), (H2) hold, then the following results hold:

1. If $\tau \in [0,{\tau }_0)$ then the positive equilibrium $E^{\ast }\left(a\right)$ of system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) is asymptotically stable.

2. If $\tau >{\tau }_0,$ the positive equilibrium $E^{\ast }\left(a\right)$ of system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) is unstable.

By Theorem 2.1, the above results can be summarized as the following Hopf bifurcation theorem for system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) )

Theorem 3.8

If (H1) hold. Then there exist ${\tau }_k>0,k=0,1,2,\dots ,$ where ${\tau }_k$ is defined in (17(17) ${\tau }_k=\left\{\begin{array}{cc}& \frac{1}{{\omega }_0}(\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2k\pi )=0,\eta \ge 0\\ & \frac{1}{{\omega }_0}(-\arccos \frac{(f-ag){\omega }_0^4+(ae-bf){\omega }_0^2}{f^2{\omega }_0^2+(g{\omega }_0^2-e{)}^2}+2(k+1\left)\pi \right),\mathrm{otherwish},\end{array}\right.$(17) ), such that age-structured acoholism model (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) undergos a Hopf bifurcation at the positive equilibrium $E^{\ast }\left(a\right)$. In particular, when $\tau ={\tau }_k,$ a non-trivial periodic solution bifurcates from the equilibrium $E^{\ast }\left(a\right)$.

4. Numerical simulations

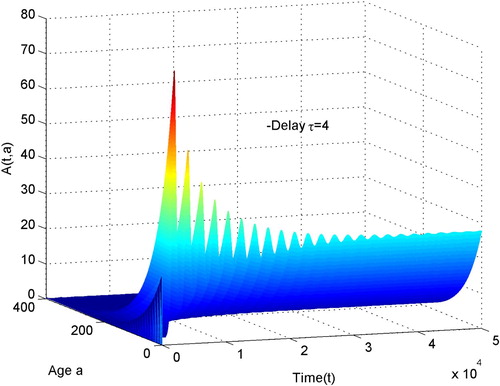
In this section, we present some numerical simulation to verify the main results by using MATLAB programming. Some of the parameters are taken from [24] $\mu =0.25,\delta =0.05,\rho =0.8$. Other parameters are estimated. First, we estimate other parameters as follows $r=0.4,\alpha =0.05,a_1=0.5,a_2=0.35,K_0=0.01,\tau =2$, we can calculate $c_0=-0.137<0$, by Theorems 3.4 we can expect that the trivial equilibrium $E_1\left(a\right)=(0,0_{L^1\left(\right(0,+\mathrm{\infty }),\mathbb{R})},0{)}^{\mathrm{T}}$ is unstable. see Figure 3. On the other hand, we estimate other parameters $r=0.25,\alpha =0.05,a_1=0.5,a_2=0.35,K_0=0.01,\tau =2,$ we can calculate $c_0=0.0359>0,$ by Theorems 3.4 we can expect that the trivial equilibrium $E_1\left(a\right)=(0,0_{L^1\left(\right(0,+\mathrm{\infty }),\mathbb{R})},0{)}^{\mathrm{T}}$ is local asymptotically stable. see Figure 4.

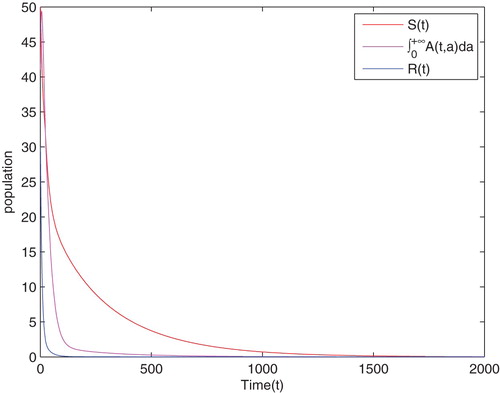
Figure 3. The trajectory of susceptible drinkers $S\left(t\right)$, alcoholics ${\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a$, recuperator $R\left(t\right)$ versus time with the initial condition $(50,20{\mathrm{e}}^{-0.5a},30)$. When $c_0<0$ the equilibrium point $E_1\left(a\right)$ is unstable.

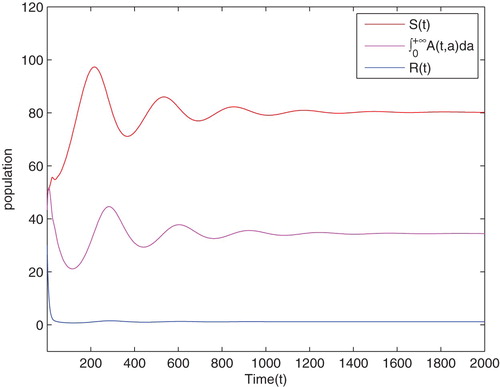
Figure 4. The trajectory of susceptible drinkers $S\left(t\right)$, alcoholics ${\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a$, recuperator $R\left(t\right)$ versus time with the initial condition $(50,20{\mathrm{e}}^{-0.5a},30)$. When $c_0>0$ the equilibrium point $E_1\left(a\right)$ is local asymptotically stable.

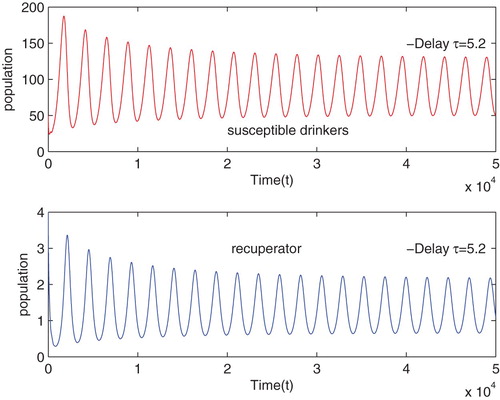
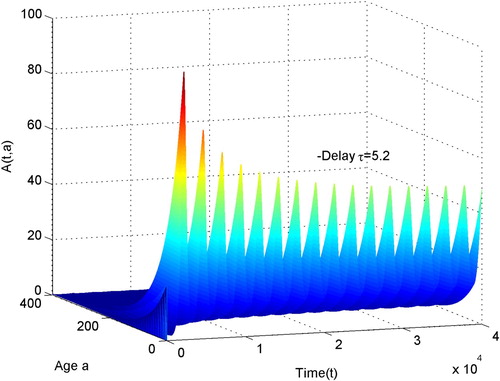
Moreover, we estimate other parameters $r=0.4,\alpha =0.05,a_1=0.5,a_2=0.35,K_0=0.01,$ we can calculate $\left(H1\right)$ holds, then (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) has only one positive equilibrium $E^{\ast }\left(a\right)=(81.5476,27.4{\mathrm{e}}^{-0.8a},1.2232{)}^{\mathrm{T}}.$ By algorithms in the previous sections, we obtain ${\omega }_0=0.1382,{\tau }_0=4.9203,$ and readily checked that the hypothesis of $\left(H2\right)$ holds. Thus, $E^{\ast }\left(a\right)$ is stable when $\tau \in [0,{\tau }_0)$, as depicted in Figure 5–7. From the numerical simulations we can see the solution of system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ) with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$ and parameter $\tau =4$ asymptotically tends to the positive equilibrium $E^{\ast }\left(a\right).$ When τ pass through the critical value ${\tau }_0$, $E^{\ast }\left(a\right)$ loss its stability and Hopf bifurcation occurs at $\tau ={\tau }_0=4.9203$, as depicted in Figure 8–10.

Figure 5. The trajectory of susceptible drinkers and recuperator versus time with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$, when $\tau =4<{\tau }_0$.

Figure 6. The surface of alcoholics $A(t,a)$ versus time t and age a with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$, when $\tau =4<{\tau }_0$.

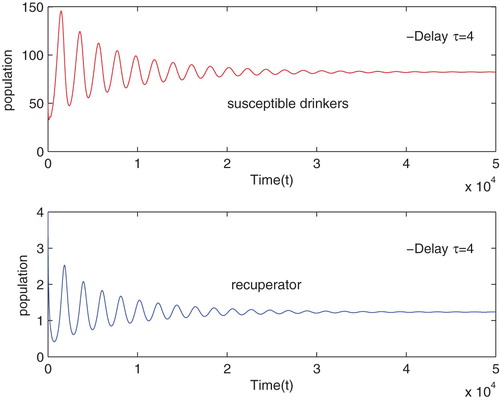
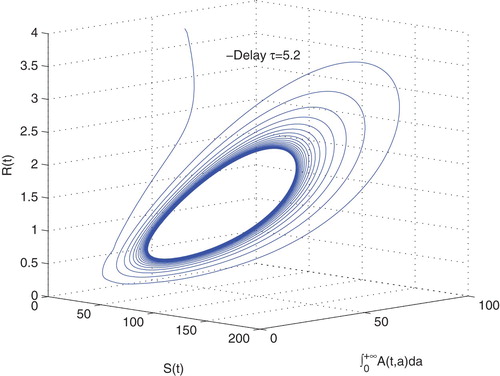
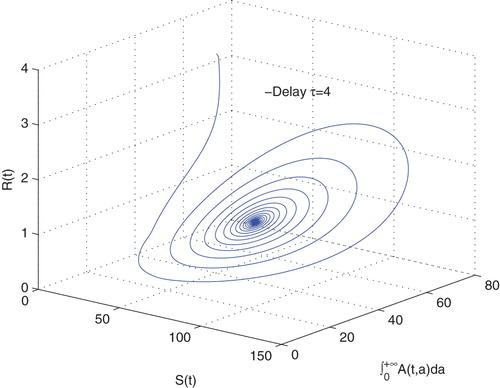
Figure 7. The phase portrait of susceptible drinkers $S\left(t\right)$, alcoholics ${\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a$, recuperator $R\left(t\right)$ with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$, when $\tau =4<{\tau }_0$.

Figure 8. The trajectory of susceptible drinkers and recuperator versus time with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$, when $\tau =5.2>{\tau }_0$.

Figure 9. The surface of alcoholics $A(t,a)$ versus time t and age a with the initial condition $(50,20{\mathrm{e}}^{-0.5a},5)$, when $\tau =5.2>{\tau }_0$.

Figure 10. The phase portrait of susceptible drinkers $S\left(t\right)$, alcoholics ${\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a$, recuperator $R\left(t\right)$ with the initial condition $(50,20{\mathrm{e}}^{-0.5a},4)$, when $\tau =5.2>{\tau }_0$.

5. Conclusion

In this paper, Hopf bifurcation of an age-structured alcoholism model is investigated. Real epidemic data indicate regular periodic fluctuations in disease incidence [8–10] but most models for epidemic diseases predict convergence to a unique stable endemic equilibrium, so it is important to examine under what conditions periodic fluctuations in disease incidence can occur. Because there are people who alcoholism for their own reasons, alcoholism, as a social epidemic disease, is somewhat different from common epidemic diseases. However, in our analysis, we found that regular periodic fluctuations can still arise.

By choosing τ as the bifurcation parameter and analyzing the corresponding characteristic equation, we can conclude that the local asymptotically stability of the trivial equilibrium $E_1\left(a\right)$ is determined by $c_0$. If $c_0<0$, then the trivial equilibrium $E_1\left(a\right)$ is unstable for all $\tau \ge 0$. If $c_0>0$ the trivial equilibrium $E_1\left(a\right)$ is local asymptotically stable for all $\tau \ge 0$. For the positive equilibrium, if $\left(H1\right)$ holds, we establish conditions to ensure the local stability. The parameter τ does not affect the stability of the trivial equilibrium, but can change the stability of the positive equilibrium. By using the center manifold theory [22] and Hopf bifurcation theorem [18], which developed for non-densely defined Cauchy problems, the existence of Hopf bifurcation at the positive equilibrium is obtained. In particular, a non-trivial periodic solution bifurcates from the positive equilibrium when bifurcation parameter τ passes through the critical values ${\tau }_k(k=0,1,2,\dots )$. Our analytical results indicate that introduction of parameter τ can affect the dynamic behavior of the system (1(1) $\begin{array}{rl}& \frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=r\left(S\right(t)+{\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a+R(t\left)\right)-S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a-(\mu +\alpha )S\left(t\right),\\ & \frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }A(t,a)}{\mathrm{\partial }a}=-(\mu +a_1+\delta )A(t,a),\\ & \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\delta {\int }_0^{+\mathrm{\infty }}A(t,a)\mathrm{d}a-(\mu +a_2+\rho )R\left(t\right),\\ & A(t,0)=S\left(t\right){\int }_0^{+\mathrm{\infty }}\beta \left(a\right)A(t,a)\mathrm{d}a+\rho R\left(t\right)+\alpha S\left(t\right),\\ & A(0,a)=A_0\left(a\right)\in L_{+}^1\left(\right(0,+\mathrm{\infty }),\mathbb{R}),S\left(0\right)=s_0>0,R\left(0\right)=r_0>0.\end{array}$(1) ).

Moreover, due to alcoholism is often associated with some of the alcoholics' own reasons, such as losses of earnings, unemployment or family problems, etc. In this sense, as long as the population is not extinct (according to the analysis of Remark 3.1, the $E_1\left(a\right)$ is more likely to be unstable), alcoholics will always exist. Therefore, we hope that alcohol-attributable socioeconomic burden is minimal. This optimal control problem, we will study in future work.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by the NNSF of China (11861044 and 11661050), the NSF of Gansu Province (148RJZA024), and the HongLiu first-class disciplines Development Program of Lanzhou University of Technology.