Dynamical analysis on a predator–prey model with stage structure and mutual interference

Abstract

In this paper, we formulate a stage-structured predator–prey model with mutual interference, in which includes two discrete delays. By theoretical analysis, we establish the stability of the unique positive equilibrium and the existence of Hopf bifurcation when the maturation delay for predators is used as the bifurcation parameter. Our results exhibit that the maturation delay for preys does not affect the stability of the positive equilibrium. However, the maturation delay for predator is able to destabilize the positive equilibrium and causes periodic solutions. Numerical simulations are carried out to illustrate the theoretical results and display the differential impacts of two type delays and mutual interference.

Keywords:

• Stage-structure
• mutual interference
• global stability
• Hopf bifurcation

2010 Mathematics Subject Classifications:

• 92D25
• 34D20

1. Introduction

Since the classical Lotka–Volterra system was proposed, it has been studied by many scholars [1–3,25]. In order to make the model more realistic, some scholars introduce a few concepts to the model, such as mutual interference, stage structure, prey refuge, diffusion and so on [6,10,13,20–22,24,26,27].

The concept of mutual interference was first introduced by Hassell [12] to capture behaviour between a host (a kind of bee) and parasite (a kind of butterfly). It is a measure of the degree of interference between parasites. Furthermore, mutual interference was considered by Freedman [8,9] to describe a phenomenon that predators have the tendency to leave each other when they met. In [8] Freedman proposed a general Volterra model with mutual interference $m(0<m\le 1)$ as follows, (1) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =xg(x)-y^{m}p(x),\\ y^{\mathrm{\prime }}(t)& =y(-s+c{y}^{m-1}p(x)-q(y)),\end{array}$(1) where $g(0)>0$, $g^{\mathrm{\prime }}(0)\le 0$, $g(K)=0$ (for some K), $p(0)=0$, $p^{\mathrm{\prime }}>0$, $q(0)=0$, $q^{\mathrm{\prime }}\ge 0$. In the special case of m = 1, the above system reduces to the traditional predator–prey model.

In nature, the predatory behaviour and reproduction behaviour are mainly completed by adult individuals and these abilities for juvenile can be ignored, and the birth rate and death rate in species' whole life history are obviously different. Based on this facts mentioned above, the population exhibit two distinct stages: immature and mature. It leads to the stage-structured model with delay representing the time from birth to maturity. Aiello and Freedman [4] proposed the following stage-structured single species model (2) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r{x}_2(t)-d{x}_1(t)-r{e}^{-d\tau }{x}_2(t-\tau ),\\ x_2^{\mathrm{\prime }}(t)& =r{e}^{-d\tau }{x}_2(t-\tau )-b{x}_2(t),\end{array}$(2) where $x_i(i=1,2)$ is the immature population densities and mature population densities, respectively. r>0 represents the birth rate, d>0 is the immature death rate, b>0 is the mature death and overcrowding rate, τ is the time from birth to maturity. The term $r{e}^{-d\tau }{x}_2(t-\tau )$ represents those immatures who were born at time $t-\tau$ and survive at time t (with the immature death rate d), and exit from the immature population and enter the mature population.

Many scholars used the idea of Aiello and Freedman to establish stage-structured predator–prey models [6,19,27]. Recently, Li et al. [19] proposed and investigated an autonomous predator–prey system with stage structure and mutual interference. The model is given as follows (3) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d{x}_1-r_1{e}^{-d\tau }{x}_2(t-\tau ),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d\tau }{x}_2(t-\tau )-b_1{x}_2^2(t)-c_1{x}_2(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =y(t)(-r_2-b_{2}y(t)+c_2{x}_2(t)y^{m-1}(t)),\end{array}$(3) where $x_1(t)$, $x_2(t)$ and $y(t)$ represent the densities of immature prey, mature prey and predator, respectively. m with 0<m<1 is the mutual interference constant. $r_1$ is the birth rate of mature prey, d is the death rate of the immature prey, $e^{-d\tau }$ is the surviving rate of each immature prey to reach maturity, τ is the maturation delay for prey, $b_1$ is the self regulation constant of the prey, $c_1$ represents the capturing rate of predator; $r_2$ is the intrinsic death rate of predator, $b_2$ denote the intra-specific competition among the predator, $c_2$ denotes the conversion rate for the predator. Model (3(3) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d{x}_1-r_1{e}^{-d\tau }{x}_2(t-\tau ),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d\tau }{x}_2(t-\tau )-b_1{x}_2^2(t)-c_1{x}_2(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =y(t)(-r_2-b_{2}y(t)+c_2{x}_2(t)y^{m-1}(t)),\end{array}$(3) ) only consider the stage structure in prey. The dynamical behaviour of (3(3) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d{x}_1-r_1{e}^{-d\tau }{x}_2(t-\tau ),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d\tau }{x}_2(t-\tau )-b_1{x}_2^2(t)-c_1{x}_2(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =y(t)(-r_2-b_{2}y(t)+c_2{x}_2(t)y^{m-1}(t)),\end{array}$(3) ) are established in [19]. Furthermore, Huang and Dong [17] improve the related results that the interior equilibrium of (3(3) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d{x}_1-r_1{e}^{-d\tau }{x}_2(t-\tau ),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d\tau }{x}_2(t-\tau )-b_1{x}_2^2(t)-c_1{x}_2(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =y(t)(-r_2-b_{2}y(t)+c_2{x}_2(t)y^{m-1}(t)),\end{array}$(3) ) is always globally asymptotically stable without any additional conditions.

Another problem that attracts us and can not be ignored is the influence of the maturation delay for predator. Actually, there is a big difference between mature predator and immature predator in their survival habits, for example, birth rate, death rate, the ability to feed on and reproduce [27]. In the present paper, in order to study the combined effects of stage structures for prey along with predator and mutual interference, we consider the following delayed predator–prey model, (4) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d_1{x}_1(t)-r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-b_1{x}_2^2(t)-c_1{x}_2(t)y_2^m(t),\\ y_1^{\mathrm{\prime }}(t)& =c_2{x}_2(t)y_2^m(t)-d_2{y}_1(t)-c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2),\\ y_2^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)-r_2{y}_2(t)-b_2{y}_2^2(t),\end{array}$(4) where $x_1(t)$ and $x_2(t)$ represent the densities of immature and mature prey, and $y_1(t)$ and $y_2(t)$ denote the densities of the immature and mature predator, respectively. m, $r_1$, $r_2$, $d_1$, $d_2$, $b_1$, $b_2$, $c_1$, $c_2$ are positive constants, the parameters $r_1$, $d_1$, $b_1$, ${\tau }_1$ are defined in model (1.3). $c_1$ is the capturing rate of mature predators, $c_2/c_1$ describes the rate of conversion of nutrients into the reproduction rate of the mature predators, $d_2$ is the death rate of immature predators, ${\tau }_2$ denotes the maturation delay for predator [14], the term $e^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)$ stands for the number of immature predator that were born at time $t-{\tau }_2$ which still survive at time t and are transferred from the immature stage to the mature stage at time t, $r_2$ is the death rate of mature predator, $b_2$ denotes the intra-specific competition among the mature predator. It is assumed that the mature individual predator only feeds on the mature preys and the immature individual predator have no competence to feed on mature prey and reproduce.

For biological meaning, the initial conditions for system (4(4) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d_1{x}_1(t)-r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-b_1{x}_2^2(t)-c_1{x}_2(t)y_2^m(t),\\ y_1^{\mathrm{\prime }}(t)& =c_2{x}_2(t)y_2^m(t)-d_2{y}_1(t)-c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2),\\ y_2^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)-r_2{y}_2(t)-b_2{y}_2^2(t),\end{array}$(4) ) take the form (5) $\begin{array}{rl}{x}_1(0)>0,x_2(\theta )& =\phi (\theta )>0,\\ y_1(0)>0,y_2(\theta )& =\varphi (\theta )>0,-\tau \le \theta \le 0,\end{array}$(5) where $\tau =max\{{\tau }_1,{\tau }_2\}$. For the continuity of the solution of system (4(4) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d_1{x}_1(t)-r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-b_1{x}_2^2(t)-c_1{x}_2(t)y_2^m(t),\\ y_1^{\mathrm{\prime }}(t)& =c_2{x}_2(t)y_2^m(t)-d_2{y}_1(t)-c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2),\\ y_2^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)-r_2{y}_2(t)-b_2{y}_2^2(t),\end{array}$(4) ), intergrating both sides of the first equation and the third equation of (4(4) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d_1{x}_1(t)-r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-b_1{x}_2^2(t)-c_1{x}_2(t)y_2^m(t),\\ y_1^{\mathrm{\prime }}(t)& =c_2{x}_2(t)y_2^m(t)-d_2{y}_1(t)-c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2),\\ y_2^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)-r_2{y}_2(t)-b_2{y}_2^2(t),\end{array}$(4) ) on $(0,t)$, we have (6) $\begin{array}{rl}{x}_1(t)& ={\int }_{t-{\tau }_1}^t{r}_1{e}^{-d_1(t-s)}{x}_2(s)\mathrm{d}s,t\ge 0,\\ y_1(t)& ={\int }_{t-{\tau }_2}^t{c}_2{e}^{-d_2(t-s)}{x}_2(s)y_2^m(s)\mathrm{d}s,t\ge 0.\end{array}$(6) and $\begin{array}{rl}{x}_1(0)& ={\int }_{-{\tau }_1}^0{r}_1{e}^{d_{1}s}\phi (s)\mathrm{d}s,\\ y_1(0)& ={\int }_{-{\tau }_2}^0{c}_2{e}^{d_{2}s}\phi (s){\varphi }^m(s)\mathrm{d}s.\end{array}$

The equations above mean that $x_1(t)$ and $y_1(t)$ could be decided by $x_2(t)$ and $y_2(t)$, respectively. For simplicity, here we rewrite $x_2(t)$ and $y_2(t)$ as $x(t)$ and $y(t)$. We investigate the asymptotical behaviour for the subsystem of system (4(4) $\begin{array}{rl}{x}_1^{\mathrm{\prime }}(t)& =r_1{x}_2(t)-d_1{x}_1(t)-r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1),\\ x_2^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}{x}_2(t-{\tau }_1)-b_1{x}_2^2(t)-c_1{x}_2(t)y_2^m(t),\\ y_1^{\mathrm{\prime }}(t)& =c_2{x}_2(t)y_2^m(t)-d_2{y}_1(t)-c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2),\\ y_2^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}{x}_2(t-{\tau }_2)y_2^m(t-{\tau }_2)-r_2{y}_2(t)-b_2{y}_2^2(t),\end{array}$(4) ) as follows, (7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) with the initial conditions as follows, (8) $x(\theta )=\phi (\theta )>0,y(\theta )=\varphi (\theta )>0,-\tau \le \theta \le 0.$(8)

Denote $\mathrm{\Phi }=(\phi (\theta ),\varphi (\theta ))\in \mathcal{C}\{[-\tau ,0],R_{+0}^2\}$, the Banach space of continuous functions mapping the interval $[-\tau ,0]$ into $R_{+0}^2$, where we define $R_{+0}^2=\{(x_1,x_2):x_i\ge 0,i=1,2\}.$

Although the dynamical behaviours of the stage-structured species has been well studied by DDE models (see [19,22–27]), most of them considered only the effect of maturation delay in prey or predator, separately. Model (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) includes two types of delay simultaneously. The aim of the present paper is to carry out mathematical analysis of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) and to find out the different influences of maturation delay for prey, maturation delay for predator, and mutual interference. We are interested in whether the prey and predator are always persistent, and whether the ecological system approaches an equilibrium or it varies periodically.

The organization of this paper is as follows. In Section 2, we introduce some useful lemmas and propositions. In Section 3, we analyse the stability of the boundary equilibria of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ). In Section 4, we study the dynamics properties of the positive equilibrium of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ). In Section 5, we give detailed numerical simulations to verify our theoretical analysis above. In the last section, we give a brief discussion.

2. Preliminaries

In the following we will give some propositions and some useful lemmas.

Proposition 2.1

The solutions $(x(t),y(t))$ of the system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) are positive under the initial conditions (8(8) $x(\theta )=\phi (\theta )>0,y(\theta )=\varphi (\theta )>0,-\tau \le \theta \le 0.$(8) ).

Proof.

Assume, by way of contradiction, $x(t)>0$ does not hold. There must exist $T_1\in (-{\tau }_1,+\mathrm{\infty })$ such that $x(T_1)\le 0$. Set $T_1^{+}=inf\{t:t\in (0,T_1),x(t)=0\}.$ We know $x(T_1^{+})=0$, and $x^{\mathrm{\prime }}(T_1^{+})\le 0$. From (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we have (9) $x^{\mathrm{\prime }}(T_1^{+})=r_1{e}^{-d_1{\tau }_1}x(T_1^{+}-{\tau }_1)>0,$(9) which is a contradiction to the fact that $x^{\mathrm{\prime }}(T_1^{+})\le 0$. Hence $x(t)>0$ holds. In a similar way we can proof $y(t)>0$.

The proof is completed.

Lemma 2.1

[21]

Consider the following equation: $\begin{array}{rl}& x^{\mathrm{\prime }}(t)=bx(t-\delta )-a_{1}x(t)-a_2{x}^2(t),\\ & x(\theta )=\varphi (\theta )>0,-\delta \le \theta \le 0,\end{array}$ and assume that $b>0,a_1\ge 0,a_2>0$ and $\delta >0$. Then $\begin{array}{rl}& (1)ifb\ge a_1,then\underset{t\to +\mathrm{\infty }}{lim}x(t)=\frac{b-a_1}{a_2};\\ & (2)ifb\le a_1,then\underset{t\to +\mathrm{\infty }}{lim}x(t)=0.\end{array}$

Lemma 2.2

[7]

Assume that a>0, b>0, $0<\alpha <1$, $t\ge 0$ and $x(0)>0$. Then $\begin{array}{rl}& (1)If{x}^{\mathrm{\prime }}(t)\ge x(t)(-b+a{x}^{\alpha -1}(t)),then\underset{t\to \mathrm{\infty }}{lim inf}x(t)\ge {\left(\frac{a}{b}\right)}^{1/(1-\alpha )};\\ & (2)If{x}^{\mathrm{\prime }}(t)\le x(t)(-b+a{x}^{\alpha -1}(t)),then\underset{t\to \mathrm{\infty }}{lim sup}x(t)\le {\left(\frac{a}{b}\right)}^{1/(1-\alpha )}.\end{array}$

Next, we prove the boundedness of the solutions of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ).

Proposition 2.2

The solutions of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) are bounded for all large t.

Proof.

From the first equation of (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we have (10) $x^{\mathrm{\prime }}(t)\le r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t).$(10) According to Lemma 2.1, we have (11) $\underset{t\to +\mathrm{\infty }}{lim sup}x(t)\le \frac{r_1{e}^{-d_1{\tau }_1}}{b_1}=K_1.$(11) There is $T_1>0$ and ${ϵ}_1>0$ such that (12) $x(t)\le K_1+{ϵ}_1,\text{for }t>T_1.$(12) Now, we show that $y(t)$ is bounded. By a contradiction, we assume that $y(t)$ is boundless. Because of the continuity of the system, there is $T_2>0$ such that (13) $y(t)>1\text{for all }t>T_2+{\tau }_2.$(13) By the second equation of (5(5) $\begin{array}{rl}{x}_1(0)>0,x_2(\theta )& =\phi (\theta )>0,\\ y_1(0)>0,y_2(\theta )& =\varphi (\theta )>0,-\tau \le \theta \le 0,\end{array}$(5) ) and (13(13) $y(t)>1\text{for all }t>T_2+{\tau }_2.$(13) ), we get (14) $\begin{array}{rl}{y}^{\mathrm{\prime }}& \le c_2{e}^{-d_2{\tau }_2}{K}_1{y}^m(t-{\tau }_2)-b_2{y}^2(t),\\ & \le c_2{e}^{-d_2{\tau }_2}{K}_{1}y(t-{\tau }_2)-b_2{y}^2(t)\text{for all }t>T_2+{\tau }_2.\end{array}$(14) According to Lemma 2.1, we have (15) $\underset{t\to +\mathrm{\infty }}{lim sup}y(t)\le \frac{c_2{e}^{-d_2{\tau }_2}{K}_1}{b_2},$(15) which is a contradiction to the assumption. Hence $y(t)$ is bounded. Therefore, $x(t)$ and $y(t)$ are both bounded.

The proof is completed.

System (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) always has two boundary equilibria, which are $E_0(0,0)$ and $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$. Besides, we will prove the existence of the positive equilibrium of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) as follows.

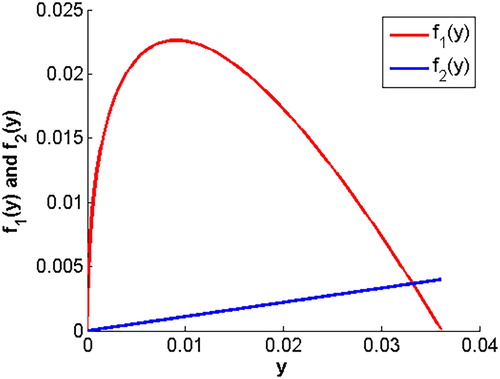
Proposition 2.3

System (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) always has a unique positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$.

Proof.

$(x^{\ast },y^{\ast })$ satisfies the following equations, (16) $\begin{array}{rl}{r}_1{e}^{-d_1{\tau }_1}-c_1{y}^m-b_{1}x& =0,\\ c_2{e}^{-d_2{\tau }_2}x{y}^{m-1}-r_2-b_2& y=0.\end{array}$(16) Noting that $y^{\ast }=0$ is not the solution of (16(16) $\begin{array}{rl}{r}_1{e}^{-d_1{\tau }_1}-c_1{y}^m-b_{1}x& =0,\\ c_2{e}^{-d_2{\tau }_2}x{y}^{m-1}-r_2-b_2& y=0.\end{array}$(16) ). We can rewrite (16(16) $\begin{array}{rl}{r}_1{e}^{-d_1{\tau }_1}-c_1{y}^m-b_{1}x& =0,\\ c_2{e}^{-d_2{\tau }_2}x{y}^{m-1}-r_2-b_2& y=0.\end{array}$(16) ) as another form, (17) $\begin{array}{rl}{b}_{1}x& =r_1{e}^{-d_1{\tau }_1}-c_1{y}^m,\\ (\frac{r_1}{b_1}{e}^{-d_1{\tau }_1}-\frac{c_1}{b_1}{y}^m)y^m& =(\frac{r_2}{c_2}+\frac{b_2}{c_2}y)e^{d_2{\tau }_2}y.\end{array}$(17) Define $f_1(y)$ and $f_2(y)$ as following forms: (18) $\begin{array}{rl}{f}_1(y)& =(\frac{r_1}{b_1}{e}^{-d_1{\tau }_1}-\frac{c_1}{b_1}{y}^m)y^m,y\ge 0,\\ f_2(y)& =(\frac{r_2}{c_2}+\frac{b_2}{c_2}y)e^{d_2{\tau }_2}y,y\ge 0.\end{array}$(18) By simple computations, we have $f_1(0)=f_2(0)$, $\mathrm{d}{f}_1(y)/\mathrm{d}y{|}_{y\to 0^{+}}=+\mathrm{\infty }$, $\mathrm{d}{f}_2(y)/\mathrm{d}y{|}_{y\to 0^{+}}=(r_2/c_2)e^{d_2{\tau }_2}$, $f_1^{\mathrm{\prime }}(y)=m{y}^{m-1}((r_1/b_1)e^{-d_1{\tau }_1}-(2c_1/b_1)y^m)$, which is easy to know that $f_1^{\mathrm{\prime }}(y)$ is a monotony decrease function, namely $f_1^{\mathrm{\prime }\mathrm{\prime }}(y)<0$; $f_2^{\mathrm{\prime }}(y)=(r_2/c_2+2(b_2/c_2)y)e^{d_2{\tau }_2}>0$ and $f_2^{\mathrm{\prime }\mathrm{\prime }}=(2b_2/c_2)e^{d_2{\tau }_2}>0$. Therefore, $f_1(y)$ is a convex function and $f_2(y)$ is an increase function for y>0.

From above analysis, it follows that both curves of (18(18) $\begin{array}{rl}{f}_1(y)& =(\frac{r_1}{b_1}{e}^{-d_1{\tau }_1}-\frac{c_1}{b_1}{y}^m)y^m,y\ge 0,\\ f_2(y)& =(\frac{r_2}{c_2}+\frac{b_2}{c_2}y)e^{d_2{\tau }_2}y,y\ge 0.\end{array}$(18) ) have unique intersection for y>0 (see Figure 1).

Figure 1. The curves of $f_1(y)$ and $f_2(y)$.

In the following we discuss the the uniform permanence of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ).

Proposition 2.4

If $r_1{e}^{-d_1{\tau }_1}-c_1{K}^{m/(1-m)}>0$, where $K=c_2{r}_1{e}^{-(d_1{\tau }_1+d_2{\tau }_2)}/r_2{b}_1$, the system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) with initial conditions (8(8) $x(\theta )=\phi (\theta )>0,y(\theta )=\varphi (\theta )>0,-\tau \le \theta \le 0.$(8) ) is permanent. That is, for any positive solution $(x(t),y(t))$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), one has $\begin{array}{rl}& k_1\le \underset{t\to +\mathrm{\infty }}{lim inf}x(t)\le \underset{t\to +\mathrm{\infty }}{lim sup}x(t)\le K_1,\\ & k_2\le \underset{t\to +\mathrm{\infty }}{lim inf}x(t)\le \underset{t\to +\mathrm{\infty }}{lim sup}x(t)\le K_2.\end{array}$

Proof.

According to Proposition 2.2, we have $\underset{t\to +\mathrm{\infty }}{lim sup}x(t)\le M_1$. Then from the second equation of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we have (19) $y^{\mathrm{\prime }}(t)\le c_2{e}^{-d_2{\tau }_2}{K}_1{y}^m(t-{\tau }_2)-r_{2}y(t).$(19) According to Lemma 2.2, we have (20) $\underset{t\to +\mathrm{\infty }}{lim sup}y(t)\le {\left(\frac{c_2{e}^{-d_2{\tau }_2}{K}_1}{r_2}\right)}^{1/(1-m)}=K_2.$(20) Then combine the above inequation and the first equation of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we have (21) $x^{\mathrm{\prime }}(t)\ge r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-c_{1}x(t)K_2^m-b_1{x}^2(t).$(21) By the Lemma 2.1, we have (22) $\underset{t\to +\mathrm{\infty }}{lim inf}x(t)\ge \frac{r_1{e}^{-d_1{\tau }_1}-c_1{K}_2^m}{b_1}=k_1>0.$(22) Then combine the above inequation and the second equation of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we have (23) $y^{\mathrm{\prime }}(t)\ge c_2{e}^{-d_2{\tau }_2}{k}_1{y}^m(t-{\tau }_2)-(r_2+b_2{K}_2)y(t).$(23) Thus, by the Lemma 2.2, we have (24) $\underset{t\to +\mathrm{\infty }}{lim inf}y(t)\ge {\left(\frac{c_2{e}^{-d_2{\tau }_2}{k}_1}{r_2+b_2{K}_2}\right)}^{1/(1-m)}=k_2.$(24) The proof is completed.

3. Stability analysis for two boundary equilibria

In order to investigate the stability of the equilibria of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), we linearize the system and obtain the characteristic equation evaluated at an equilibrium $E(\tilde{x},\tilde{y})$, given by the following formula, (25) $D(\lambda ,{\tau }_1,{\tau }_2)=P_0(\lambda )+P_1(\lambda )e^{-\lambda {\tau }_1}+P_2(\lambda )e^{-\lambda {\tau }_2}+P_3(\lambda )e^{-\lambda ({\tau }_1+{\tau }_2)}=0,$(25) where λ is an eigenvalue and $\begin{array}{rl}& P_0(\lambda )={\lambda }^2+(r_2+2b_2\tilde{y}+2b_1\tilde{x}+c_1{\tilde{y}}^m)\lambda +(r_2+2b_2\tilde{y})(2b_1\tilde{x}+c_1{\tilde{y}}^m),\\ & P_1(\lambda )=-r_1{e}^{-d_1{\tau }_1}(\lambda +r_2+2b_2\tilde{y}),\\ & P_2(\lambda )=-m{c}_2{e}^{-d_2{\tau }_2}\tilde{x}{\tilde{y}}^{(m-1)}(\lambda +2b_1\tilde{x}),\\ & P_3(\lambda )=r_{1}m{c}_2{e}^{-(d_1{\tau }_1+d_2{\tau }_2)}\tilde{x}{\tilde{y}}^{(m-1)}.\end{array}$ We first discuss the stability of two boundary equilibria.

Theorem 3.1

The equilibrium $E_0(0,0)$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is unstable for any ${\tau }_1,{\tau }_2\ge 0$.

Proof.

From (25(25) $D(\lambda ,{\tau }_1,{\tau }_2)=P_0(\lambda )+P_1(\lambda )e^{-\lambda {\tau }_1}+P_2(\lambda )e^{-\lambda {\tau }_2}+P_3(\lambda )e^{-\lambda ({\tau }_1+{\tau }_2)}=0,$(25) ), we know that y = 0 is meaningless, so $E_0(0,0)$ cannot be substituted into (25(25) $D(\lambda ,{\tau }_1,{\tau }_2)=P_0(\lambda )+P_1(\lambda )e^{-\lambda {\tau }_1}+P_2(\lambda )e^{-\lambda {\tau }_2}+P_3(\lambda )e^{-\lambda ({\tau }_1+{\tau }_2)}=0,$(25) ).

By using the method in [23], we set $\begin{array}{rl}{P}_1(x,y)& =-b_1{x}^2(t)-c_{1}x(t)y^m(t),P_2(x,y)=r_1{e}^{-d_1{\tau }_1}x(t),\\ Q_1(x,y)& =-r_{2}y(t)-b_2{y}^2(t),Q_2(x,y)=c_2{e}^{-d_2{\tau }_2}x(t)y^m(t).\end{array}$ For $E_0(0,0)$, the characteristic equation is given by (26) $(\lambda +r_2)(\lambda -r_1{e}^{-d_1{\tau }_1}{e}^{-\lambda {\tau }_1})=0.$(26) The characteristic equation have a eigenvalue ${\lambda }_1=-r_2$ and another derived by $K(\lambda )=\lambda -r_1{e}^{-d_1{\tau }_1}{e}^{-\lambda {\tau }_1}=0$. It is easy to know that it exist ${\lambda }_0>0$ and $K({\lambda }_0)=0$ from the fact that $K(0)=-r_1{e}^{-d_1{\tau }_1}<0$ and $\underset{\lambda \to +\mathrm{\infty }}{lim}K(\lambda )=+\mathrm{\infty }$, so the equilibrium $E_0(0,0)$ is unstable.

The proof is completed.

Theorem 3.2

The equilibrium $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is unstable for any ${\tau }_1,{\tau }_2\ge 0$.

Proof.

For $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$, noting that $(\mathrm{\partial }{P}_1(r_1{e}^{-d_1{\tau }_1}/b_1,0))/\mathrm{\partial }y$ makes no sense, hence the local stability of $E_1$ cannot be investigated by computing the Jacobian matrix directly. We will study it by investigating the exceptional direction and normal sector of the equilibrium.

Firstly, $E_0(0,0)$ is unstable and $x=0,y=0$ are orbits. y = 0 is along the x-axis into the orbit of $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$ from Lemma 2.1. For 0<m<1, we denote $n=1/m$, then n>1. By using the following change of variables $x=\overline{x},y=\overline{y},\mathrm{d}t={\overline{y}}^n\mathrm{d}s,$ and rewriting $\overline{x},\overline{y},s$ as x, y, t, we obtain another form of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), (27) $\begin{array}{rl}& \frac{\mathrm{d}x}{\mathrm{d}t}=y^n[r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y(t)],\\ & \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{n}[c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y(t-{\tau }_2)y(t)-r_2{y}^{n+1}(t)-b_2{y}^{2n+1}(t)].\end{array}$(27) Then the equilibrium $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$ is high order singular point. Thus we translate the point $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$ to the original $O(0,0)$. By letting $\overline{x}=x-r_1{e}^{-d_1{\tau }_1}/b_1$, $\overline{y}=y$ and rewriting $\overline{x},\overline{y}$ as x, y, we obtain another form of system (27(27) $\begin{array}{rl}& \frac{\mathrm{d}x}{\mathrm{d}t}=y^n[r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y(t)],\\ & \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{n}[c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y(t-{\tau }_2)y(t)-r_2{y}^{n+1}(t)-b_2{y}^{2n+1}(t)].\end{array}$(27) ), (28) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =y^n(r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2-2r_1{e}^{-d_1{\tau }_1}x-c_{1}xy-c_1\frac{r_1{e}^{-d_1{\tau }_1}}{b_1}y)\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =\frac{1}{n}(-r_2{y}^{n+1}-b_2{y}^{2n+1}+c_2{e}^{-d_2{\tau }_2}yy(t-{\tau }_2)x(t-{\tau }_2))\\ & +\frac{c_2{r}_1{e}^{-d_1{\tau }_1-d_2{\tau }_2}}{n{b}_1}yy(t-{\tau }_2)\end{array}$(28) Let $x=r\cos \theta$, $y=r\sin \theta$, system (28(28) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =y^n(r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2-2r_1{e}^{-d_1{\tau }_1}x-c_{1}xy-c_1\frac{r_1{e}^{-d_1{\tau }_1}}{b_1}y)\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =\frac{1}{n}(-r_2{y}^{n+1}-b_2{y}^{2n+1}+c_2{e}^{-d_2{\tau }_2}yy(t-{\tau }_2)x(t-{\tau }_2))\\ & +\frac{c_2{r}_1{e}^{-d_1{\tau }_1-d_2{\tau }_2}}{n{b}_1}yy(t-{\tau }_2)\end{array}$(28) ) can be rewritten as the following equation of polar coordinates: (29) $\frac{1}{r}\frac{\mathrm{d}r}{\mathrm{d}\theta }=\frac{F(\theta )+o(1)}{G(\theta )+o(1)},$(29) where (30) $F(\theta )=\frac{br}{an}{\sin }^3\theta ,G(\theta )=\frac{br}{an}\cos \theta {\sin }^2\theta .$(30) Obviously, ${\theta }_1=\pi /2$ and ${\theta }_2=3\pi /2$ are exceptional directions. Noting that $F(\pi /2)>0$, $G^{\mathrm{\prime }}(\pi /2)<0$ and $F(3\pi /2)<0$, $G^{\mathrm{\prime }}(3\pi /2)>0$, hence the normal sectors of ${\theta }_1$ and ${\theta }_2$ are of second type and there is a unique orbit which is along the exceptional direction ${\theta }_1=\pi /2$ and ${\theta }_2=3\pi /2$ into the equilibrium $(0,0)$ of (28(28) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =y^n(r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2-2r_1{e}^{-d_1{\tau }_1}x-c_{1}xy-c_1\frac{r_1{e}^{-d_1{\tau }_1}}{b_1}y)\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =\frac{1}{n}(-r_2{y}^{n+1}-b_2{y}^{2n+1}+c_2{e}^{-d_2{\tau }_2}yy(t-{\tau }_2)x(t-{\tau }_2))\\ & +\frac{c_2{r}_1{e}^{-d_1{\tau }_1-d_2{\tau }_2}}{n{b}_1}yy(t-{\tau }_2)\end{array}$(28) ). That is, there is a unique orbit of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) in $R_{+}^2$ along the line $x=r/a$ into $E_1$. On the other hand, since (31) ${\frac{\mathrm{d}x}{\mathrm{d}t}|}_{x=r_1{e}^{-d_1{\tau }_1}/b_1}=-c_{1}x{y}^m<0,$(31) it implies that the orbit of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) intersecting with the line $x=r_1{e}^{-d_1{\tau }_1}/b_1$ passes through the right into the left. Hence the equilibrium $E_1(r_1{e}^{-d_1{\tau }_1}/b_1,0)$ is unstable.

The proof is completed.

The two bounded equilibria are all unstable and system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is bounded and positive with the initial conditions (8(8) $x(\theta )=\phi (\theta )>0,y(\theta )=\varphi (\theta )>0,-\tau \le \theta \le 0.$(8) ), which mean that system is persistent. In fact, in an ecological model consisting of predators and preys, if the predator's predation ability is very strong, the population of predator and prey maybe tend to die out. While if there are mutual interference in the predator, the population of predator and prey will be persistence. In the next section, we mainly study the dynamical properties of the positive equilibrium. In other word, on the basic of the fact that predator and prey will be persistence, how do the two maturation time delays for predator and prey affect the population of predator and prey, whether the population of two species tends to a stable steady state or presents a periodic obit.

4. Dynamical analysis for the positive equilibrium

System (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) always has a unique positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$. Now we study the dynamical properties of the positive equilibrium of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) in three cases: (I) ${\tau }_1={\tau }_2=0$; (II) ${\tau }_1>0$, ${\tau }_2=0$; (III) ${\tau }_1=0$, ${\tau }_2>0$.

Case (I) where ${\tau }_1={\tau }_2=0$.

In the case where there is no maturation delay for both prey and predator, (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is reduced to the following ordinary differential equations model, (32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) System (32(32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) ) has the same equilibria as system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) and the boundary equilibria are also unstable. The characteristic equation of system (32(32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) ) at $E^{\ast }(x^{\ast },y^{\ast })$ is as follows, (33) ${\lambda }^2+A\lambda +B=0,$(33) where $\begin{array}{rl}& A=b_1{x}^{\ast }+r_2+b_2{y}^{\ast }+(1-m)(r_2+b_2{y}^{\ast })>0,\\ & B=b_1{b}_2{x}^{\ast }{y}^{\ast }+[b_1(1-m)x^{\ast }+m{c}_1{y}^{\ast m}](r_2+b_2{y}^{\ast })>0.\end{array}$ It follows from the Routh-Hurwitz criteria that all roots of (33(33) ${\lambda }^2+A\lambda +B=0,$(33) ) only have negative real roots. It means that the positive equilibrium $E^{\ast }$ is locally asymptotically stable.

Next, by using the similar Lyapunov function in [15,16], we could establish the global stability of $E^{\ast }(x^{\ast },y^{\ast })$ of system (32(32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) ).

Define a function, $V(t)=x(t)-x^{\ast }-x^{\ast }\ln \frac{x(t)}{x^{\ast }}+\frac{c_1}{c_2}(y(t)-{\int }_{y^{\ast }}^{y(t)}\frac{y^{\ast m}}{{\sigma }^m}\mathrm{d}\sigma ).$ Since $r_1=b_1{x}^{\ast }+c_1(y^{\ast }{)}^m$, we have $\begin{array}{rl}\frac{\mathrm{d}V(t)}{\mathrm{d}t}& =x^{\mathrm{\prime }}(t)(1-\frac{x^{\ast }}{x(t)})+\frac{c_1}{c_2}(1-\frac{(y^{\ast }{)}^m}{y^m(t)})y^{\mathrm{\prime }}(t)\\ & =(r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t))(1-\frac{x^{\ast }}{x(t)})\\ & +\frac{c_1}{c_2}(1-\frac{(y^{\ast }{)}^m}{y^m(t)})(c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t))\\ & =(b_1{x}^{\ast }+c_1(y^{\ast }{)}^m-b_{1}x(t)-c_1{y}^m(t))(x(t)-x^{\ast })\\ & +\frac{c_1}{c_2}(c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t))(1-\frac{(y^{\ast }{)}^m}{y^m(t)})\\ & =-b_1(x(t)-x^{\ast }{)}^2-c_1((y^{\ast }{)}^m-y^m(t))x^{\ast }\\ & -\frac{c_1}{c_2}(r_{2}y(t)+b_2{y}^2(t))(1-\frac{(y^{\ast }{)}^m}{y^m(t)}).\end{array}$ Here we use $c_2{x}^{\ast }(y^{\ast }{)}^m=r_2{y}^{\ast }+b_2(y^{\ast }{)}^2$, then we have $\begin{array}{rl}\frac{\mathrm{d}V(t)}{\mathrm{d}t}& =-b_1(x(t)-x^{\ast }{)}^2-\frac{c_1{b}_2}{c_2}{y}^2(t)[1-{\left(\frac{y^{\ast }}{y(t)}\right)}^{2-m}][1-{\left(\frac{y^{\ast }}{y(t)}\right)}^m]\\ & -\frac{c_1{r}_2}{c_2}y(t)[1-{\left(\frac{y^{\ast }}{y(t)}\right)}^{1-m}][1-{\left(\frac{y^{\ast }}{y(t)}\right)}^m].\end{array}$ For 0<m<1, since (34) $\begin{array}{rl}[1-{\left(\frac{y^{\ast }}{y(t)}\right)}^{2-m}][1-{\left(\frac{y^{\ast }}{y(t)}\right)}^m]& \ge 0,\\ [1-{\left(\frac{y^{\ast }}{y(t)}\right)}^{1-m}][1-{\left(\frac{y^{\ast }}{y(t)}\right)}^m]& \ge 0,\end{array}$(34) it follows that the positive-define function $V(t)$ has non-positive derivative $(\mathrm{d}/\mathrm{d}t)V(t)$. Let $\mathcal{M}$ be the largest invariant subset of $\{(x(t),y(t))|(\mathrm{d}V/\mathrm{d}t)=0\}$. Now we define $\mathcal{M}$. Since $\mathrm{d}V/\mathrm{d}t$ equals to zero if and only if $x(t)=x^{\ast }$, $y(t)=y^{\ast }$, we see that $\mathcal{M}$ is the singleton $\{E^{\ast }\}$. By the LaSalle invariance principle [11], every solution of (32(32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) ) tends to the positive equilibrium $E^{\ast }$, which is globally asymptotically stable.

According to above theoretical analysis, we have the following theorem.

Theorem 4.1

For ${\tau }_1={\tau }_2=0$, the positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is globally asymptotically stable.

Case (II) where ${\tau }_1>0$, ${\tau }_2=0$.

In the case where there is no maturation delay for predator, system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is reduced to a delay differential equations model which includes one maturation delay for prey as follows, (35) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(35)

As a special case of (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ), the complete global stability of (35(35) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(35) ) was established by Huang and Dong in [17].

Theorem 4.2

[17]

For ${\tau }_1>0$, ${\tau }_2=0$, the positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) is globally asymptotically stable for any delay ${\tau }_1>0$.

Case (III) where ${\tau }_1=0$, ${\tau }_2>0$.

In the case where there is no maturation delay for prey, system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) includes one maturation delay for predator as follows, (36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) System (36(36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) ) has the same equilibria as system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) and the boundary equilibria are also unstable. The characteristic equation of system (36(36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) ) at the positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$ is as follows, (37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) whose coefficients are $\begin{array}{rl}A({\tau }_2)& =b_1{x}^{\ast }+r_2+2b_2{y}^{\ast },\\ B({\tau }_2)& =b_1{x}^{\ast }(r_2+2b_2{y}^{\ast }),\\ C({\tau }_2)& =-m(r_2+b_2{y}^{\ast }),\\ D({\tau }_2)& =(r_1-2b_1{x}^{\ast })m(r_2+b_2{y}^{\ast }).\end{array}$ We note that, if $d_2>0$, these coefficients are dependant on the delay ${\tau }_2$, since $x^{\ast }$ and $y^{\ast }$ all include ${\tau }_2$. From case (I), we know that the positive equilibrium $E^{\ast }(x^{\ast },y^{\ast })$ is locally asymptotically stable when ${\tau }_2=0$. Then, we let ${\tau }_2$ vary and investigate the possible bifurcations. For $E^{\ast }(x^{\ast },y^{\ast })$ to become unstable, characteristic roots have to cross the imaginary axis to the right when ${\tau }_2$ increases and $\lambda =0$ can not be a root of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ) since that $D(0,{\tau }_2)=b_1{x}^{\ast }(r_2+2b_2{y}^{\ast })(1-m)+b_1{x}^{\ast }{b}_2{y}^{\ast }>0.$ Let $\lambda =i\omega (\omega >0)$ be a purely imaginary root of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ). Substituting it into (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ) and separating the real and imaginary parts, we obtain (38) $\begin{array}{rl}-{\omega }^2+B({\tau }_2)& =-C({\tau }_2)\omega \sin (\omega {\tau }_2)-D({\tau }_2)\cos (\omega {\tau }_2),\\ A({\tau }_2)\omega & =-C({\tau }_2)\omega \cos (\omega {\tau }_2)+D({\tau }_2)\sin (\omega {\tau }_2).\end{array}$(38) Squaring and adding both equations of (38(38) $\begin{array}{rl}-{\omega }^2+B({\tau }_2)& =-C({\tau }_2)\omega \sin (\omega {\tau }_2)-D({\tau }_2)\cos (\omega {\tau }_2),\\ A({\tau }_2)\omega & =-C({\tau }_2)\omega \cos (\omega {\tau }_2)+D({\tau }_2)\sin (\omega {\tau }_2).\end{array}$(38) ) lead to (39) $F(\omega ,{\tau }_2)={\omega }^4+P({\tau }_2){\omega }^2+Q({\tau }_2)=0,$(39) where $\begin{array}{rl}P({\tau }_2)& =A^2(\tau )-C^2(\tau )-2B({\tau }_2)\\ & =(b_1{x}^{\ast }{)}^2+(b_2{y}^{\ast }{)}^2+(1-m^2)(r_2+b_2{y}^{\ast }{)}^2+2(r_2+b_2{y}^{\ast })b_2{y}^{\ast }>0,\\ Q({\tau }_2)& =B^2({\tau }_2)-D^2({\tau }_2)\\ & =(b_1{x}^{\ast }(r_2+2b_2{y}^{\ast }){)}^2-(r_1-2b_1{x}^{\ast }{)}^2{m}^2(r_2+b_2{y}^{\ast }{)}^2.\end{array}$ A root $i\omega (\omega >0)$ of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ) satisfying $F(\omega ,{\tau }_2)=0$ if and only if $Q({\tau }_2)<0$. Because of $B({\tau }_2)+D({\tau }_2)=b_1{x}^{\ast }(r_2+2b_2{y}^{\ast })+r_1+m(r_1-2b_1{x}^{\ast })(r_2+b_2{y}^{\ast })>0$, $Q({\tau }_2)<0$ is equivalent to $(\mathbf{H}\mathbf{1})B({\tau }_2)-D({\tau }_2)=b_1{x}^{\ast }(r_2+2b_2{y}^{\ast })-m(r_1-2b_1{x}^{\ast })(r_2+b_2{y}^{\ast })<0.$

According to above theoretical analysis, we have the following theorem.

Theorem 4.3

If $(\mathbf{H}\mathbf{1})$ holds, then $F(\omega ,{\tau }_2)=0$ has the positive roots $\omega =\omega ({\tau }_2)$ for ${\tau }_2>0$.

Let $\omega =\omega ({\tau }_2)>0$ be a positive root of $F(\omega ,{\tau }_2)=0$. For $\omega ({\tau }_2)i$ to be a solution of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ), $\omega ({\tau }_2)$ needs to satisfy the system (40) $\begin{array}{rl}& \sin (\omega ({\tau }_2){\tau }_2)=\frac{-C({\tau }_2)\omega (B({\tau }_2)-{\omega }^2)+A({\tau }_2)D({\tau }_2)\omega }{C({\tau }_2{)}^2{\omega }^2+D({\tau }_2{)}^2}=f_1({\tau }_2),\\ & \cos (\omega ({\tau }_2){\tau }_2)=\frac{-C({\tau }_2)A({\tau }_2){\omega }^2-(-{\omega }^2+B({\tau }_2))D({\tau }_2)}{C({\tau }_2{)}^2{\omega }^2+D({\tau }_2{)}^2}=f_2({\tau }_2).\end{array}$(40) Define (41) $\sin \theta ({\tau }_2)=f_1({\tau }_2),\cos \theta ({\tau }_2)=f_2({\tau }_2),$(41) and let $I=\{\tau :0<\tau \le 2\pi \}$ and $\theta ({\tau }_2)\in I$ be the solution of (41(41) $\sin \theta ({\tau }_2)=f_1({\tau }_2),\cos \theta ({\tau }_2)=f_2({\tau }_2),$(41) ).

Following the methods proposed by Beretta and Kuang [5], we set (42) $S_n({\tau }_2)={\tau }_2-\frac{\theta ({\tau }_2)+2n\pi }{\omega ({\tau }_2)}\text{with }n\in \mathbf{N}.$(42) Then $\pm i\omega ({\tau }_2^{\ast })$ are purely imaginary roots of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ) if and only if ${\tau }_2^{\ast }$ is a zero of function $S_n$ for some $n\in \mathbf{N}$.

Following from the following equality $\mathrm{sign}\left({\frac{\mathrm{d}\mathrm{Re}\lambda }{\mathrm{d}\tau }|}_{\lambda =\omega ({\tau }_2^{\ast })i}\right)=\mathrm{sign}(\frac{\mathrm{\partial }F}{\mathrm{\partial }\omega }(\omega ({\tau }_2^{\ast }),{\tau }_2^{\ast }))\times \mathrm{sign}\left({\frac{\mathrm{d}{S}_n(\tau )}{\mathrm{d}\tau }|}_{\tau ={\tau }_2^{\ast }}\right)$ and the fact that $\frac{\mathrm{\partial }F}{\mathrm{\partial }\omega }=4{\omega }^3+2P({\tau }_2)\omega >0,$ we have the following theorem.

Theorem 4.4

Assume that the function $S_n$ has a positive root ${\tau }_2>0$ for some $n\in \mathbf{N}$, then a pair of simple purely imaginary roots $\pm i\omega ({\tau }_2^{\ast })$ of (37(37) $D(\lambda ,{\tau }_2)={\lambda }^2+A({\tau }_2)\lambda +B({\tau }_2)+(C({\tau }_2)\lambda +D({\tau }_2))e^{-\lambda {\tau }_2},$(37) ) exist at ${\tau }_2={\tau }_2^{\ast }$ and $\mathrm{sign}\left({\frac{\mathrm{d}\mathrm{Re}\lambda }{\mathrm{d}{\tau }_2}|}_{\lambda =\pm i\omega }\right)=\mathrm{sign}\left({\frac{\mathrm{d}{S}_n({\tau }_2)}{\mathrm{d}{\tau }_2}|}_{{\tau }_2={\tau }_2^{\ast }}\right).$ Furthermore, the pair of simple purely imaginary roots $\pm i\omega$ cross the imaginary axis to the right at ${\tau }_2={\tau }_2^{\ast }$ if $S_n^{\mathrm{\prime }}>0$.

Be similar to [18], the following properties of $S_n({\tau }_2)$ can be verified using (42(42) $S_n({\tau }_2)={\tau }_2-\frac{\theta ({\tau }_2)+2n\pi }{\omega ({\tau }_2)}\text{with }n\in \mathbf{N}.$(42) ).

1. $S_n({\tau }_2)>S_{n+1}({\tau }_2)$, $n\in \mathbf{N}$. Therefore, if $S_0(\omega ,{\tau }_2)$ has no zeros in $(0,+\mathrm{\infty })$, nor does $S_n(\omega ,{\tau }_2)$, n>0.

2. Let $\tilde{\tau }=sup\{{\tau }_2\in (0,\mathrm{\infty })|\mathbf{(}\mathbf{H}\mathbf{1}\mathbf{)}\mathrm{holds}\}.$ Then $q(\tilde{\tau })=0$, and thus $\omega ({\tau }_2)\to 0$ while $\sin \theta ({\tau }_2)\to 0$ and $\cos \theta ({\tau }_2)\to -1$, as ${\tau }_2\to {\tilde{\tau }}^{-}$. As a consequence, $\theta ({\tau }_2)\to \pi$ and $S_n({\tau }_2)\to -\mathrm{\infty }$, as ${\tau }_2\to {\tilde{\tau }}^{-}$.

3. When ${\tau }_2=0$, because $E^{\ast }$ is asymptotically stable and the first pair of eigenvalues can only cross the imaginary axis at ${\tau }_2>0$.

From the properties (ii) and (iii) we know that $S_0(0)<0$ and if $S_0({\tau }_2)$ has a positive zero, then $S_0({\tau }_2)$ necessarily has at least two positive zeros in $(0,\tilde{\tau })$. Assume that $S_0({\tau }_2)$ has two positive zeros $0<{\tau }_{21}<{\tau }_{22}<\tilde{\tau }$, with $S_0^{\mathrm{\prime }}({\tau }_{21})>0$ and $S_0^{\mathrm{\prime }}({\tau }_{22})<0$. A pair of complex conjugate eigenvalues cross the imaginary axis to the right at ${\tau }_2={\tau }_{21}$, remain to the right for ${\tau }_{21}<{\tau }_2<{\tau }_{22}$ and cross back to the right at ${\tau }_2={\tau }_{22}$. Accordingly, $E^{\ast }$ remains stable for ${\tau }_2\in (0,{\tau }_{21})$, loses its stability for ${\tau }_2\in ({\tau }_{21},{\tau }_{22})$ and regains its stability for ${\tau }_2>{\tau }_{22}$. This is the stability switch phenomenon. In Figure 6, we show that solutions converge to the stable $E^{\ast }$ for ${\tau }_2<{\tau }_{21}$, and that solutions converge to a stable periodic solutions for ${\tau }_2\in ({\tau }_{21},{\tau }_{22})$. According to above theoretical analysis, we have the theorems as follows.

Theorem 4.5

If $(\mathbf{H}\mathbf{1})$ does not hold or $(\mathbf{H}\mathbf{1})$ holds but that $S_0({\tau }_2)$ has no positive zeros, no Hopf bifurcation occurs and the interior equilibrium $E^{\ast }(x^{\ast },y^{\ast })$ remains locally asymptotically stable for all ${\tau }_2\ge 0$.

Theorem 4.6

If $(\mathbf{H}\mathbf{1})$ holds and that $S_n({\tau }_2)$, $n\ge 0$, have positive simple zeros, ${\tau }_{21}<{\tau }_{22}<\cdots <{\tau }_{2k}$, system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) undergoes a Hopf bifurcation at the equilibrium $E^{\ast }$ when ${\tau }_2={\tau }_{2i}$, i = 1, m. The Hopf bifurcation is supercritical at ${\tau }_2={\tau }_{21}$ and subcritical at ${\tau }_2={\tau }_{2m}$. Furthermore, $E^{\ast }$ goes through stability switches: $E^{\ast }$ is asymptotically stable for ${\tau }_2\in [0,{\tau }_{21})\cup ({\tau }_{2m},+\mathrm{\infty })$, and unstable when ${\tau }_2\in ({\tau }_{21},{\tau }_{2m})$.

5. Numerical simulations

Here we perform numerical simulations to verify the above theoretical analysis results. Moreover, we would verify the stability switches as shown in Section 4 and find dynamical behaviour of (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) when two delays are present simultaneously.

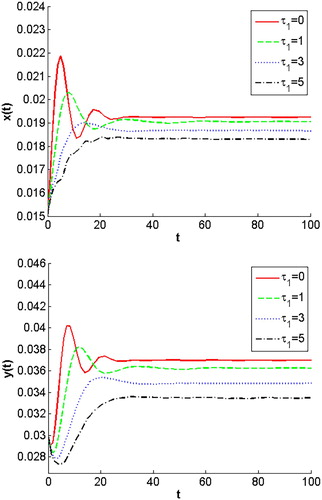
Firstly, we choose a set of parameter values except for $m,{\tau }_1$ and ${\tau }_2$ as follows (43) $\begin{array}{rl}& r_1=1,b_1=2,c_1=5,c_2=5,\\ & d_2=0.02,r_2=0.5,b_2=0.01,d_1=\mathrm{0.01.}\end{array}$(43) From Theorems 4.1 and 4.2, when we only consider the stage structure in prey and ignore the stage structure in predator, the positive (coexistence) equilibrium is always globally asymptotically stable. Actually, the maturation delay for prey does not affect the stability of the system. However, since the curve of $f_1(y)$ will move down with the increase of ${\tau }_1$, the value of x-axis of the intersection of $f_1(y)$ and $f_2(y)$ will decrease. It means that the values of $x^{\ast }$ and $y^{\ast }$ all decrease as the increase of ${\tau }_1$. For biological meaning, this means that longer juvenile maturation for prey leads to both populations decrease of predator and prey when they are in the stable steady state. We give simulations to present the impact of the maturation delay for prey in model (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ). We fix m = 0.5, ${\tau }_2=0$ and vary ${\tau }_1=0,1,3,5$, which correspond to four values of $E^{\ast }=(0.0192,0.0369),(0.0190,0.0362),(0.0187,0.0348),(0.0183,0.0334)$. Figure 2 show that all solutions converge to the equilibrium $E^{\ast }$ with small oscillation and the values of $x^{\ast }$ and $y^{\ast }$ decrease as the increase of ${\tau }_1$.

Figure 2. All solutions converge to the positive equilibrium $E^{\ast }$ for different ${\tau }_1$. Here we fix m = 0.5, ${\tau }_2=0$ and choose the other parameters from (43(43) $\begin{array}{rl}& r_1=1,b_1=2,c_1=5,c_2=5,\\ & d_2=0.02,r_2=0.5,b_2=0.01,d_1=\mathrm{0.01.}\end{array}$(43) ) and the initial value is $(0.015,0.030)$.

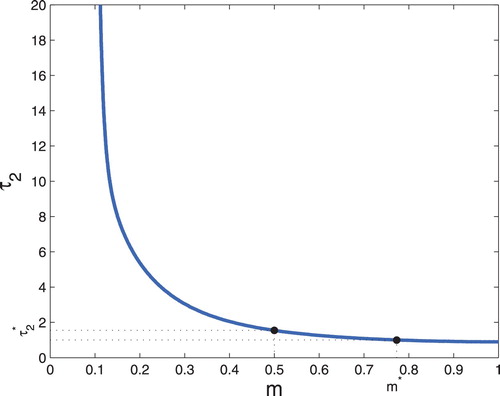
Second, we fix ${\tau }_1=0$ and vary the values of m and ${\tau }_2$, respectively. The stability region of the unique positive equilibrium $E^{\ast }$ and Hopf bifurcation curve in the $m-{\tau }_2$ parameter plane are given in Figure 3. The area below the curve represents the regions of stability of $E^{\ast }$ and the area above the curve represents the regions of instability of $E^{\ast }$. In Figure 3, we could observe that the value of ${\tau }_2$ decreases as the increase of m, which means the critical value of ${\tau }_2^{\ast }$ that change the stability of $E^{\ast }$ of system (36(36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) ) decreasing as the value of m increases. Similarly, we can see that the value of m decrease as the increase of ${\tau }_2$, which means the critical value of $m^{\ast }$ that change the stability of $E^{\ast }$ of system (36(36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) ) decreasing as the value of ${\tau }_2$ increases. For biological meanings, the maturation delay for predator and mutual interference also determine the final state of the ecosystem consisting of predators and preys. The next, we choose two special values to observe the Hopf bifurcation branches and the time evolution curves of system (36(36) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(36) ). When we choose m = 0.5, the value ${\tau }_2$ of bifurcation curve is about 1.545 (see Figure 4). This means that the positive equilibrium $E^{\ast }$ of system (32(32) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_{1}x(t)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(32) ) can become unstable by choose some appropriate values ${\tau }_2$. For example, if we choose ${\tau }_2=1$, the positive equilibrium $E^{\ast }$ is stable (see Figure 6(a)); if we choose ${\tau }_2=5$, the positive equilibrium $E^{\ast }$ becomes unstable and a stable periodic solution with a simple shape appears (see Figure 6(b)); if we choose ${\tau }_2=90$, the positive equilibrium $E^{\ast }$ is still unstable but a stable periodic solution with a complex shape appears (see Figure 6(c)). Corresponding solution curves can be seen in Figure 6(e,f). In fact, the positive equilibrium $E^{\ast }$ will eventually become stable (see Figure 6(d), we choose ${\tau }_2=120$). 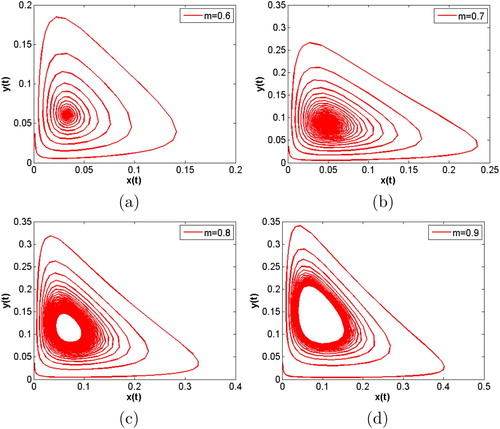When we choose ${\tau }_2=1$, the value m of bifurcation curve is about 0.777 (see Figure 5). This means that the stability of $E^{\ast }$ will change at the value m = 0.777. For example, if we choose m = 0.6, 0.7, $E^{\ast }$ is stable (see Figure 7(a,b)); if we choose m = 0.8, 0.9, $E^{\ast }$ becomes unstable and a stable periodic solution with a simple shape appears (see Figure 7(c,d)).

Figure 3. Hopf bifurcation curves in the $m-{\tau }_2$ parameter plane.

Figure 4. Hopf bifurcation branches are computed when we vary ${\tau }_2$ and keep m = 0.5. The positive equilibrium $E^{\ast }$ goes through stability switches at ${\tau }_2^{\ast }=1.545$.

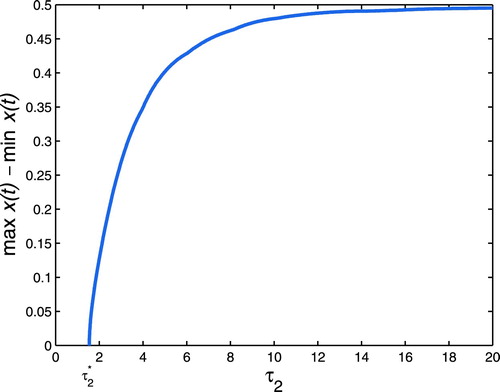
Figure 5. Hopf bifurcation branches are computed when we vary m and keep ${\tau }_2=1$. The positive equilibrium $E^{\ast }$ goes through stability switches at $m^{\ast }=0.777$.

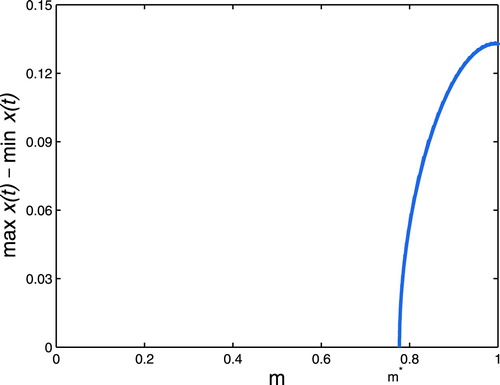
Figure 6. m = 0.5 is fixed. The time evolution curves of system (35(35) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(35) ) corresponding to four values ${\tau }_2=1,5,90,110$. (a) It shows that when ${\tau }_2=1<{\tau }_2^{\ast }=1.55$, the solutions of system tend to the equilibrium $E^{\ast }$; (b) it shows that when ${\tau }_2=5>{\tau }_2^{\ast }=1.55$, a stable periodic solution with a simple shape appears; (c) it shows that when ${\tau }_2=90>{\tau }_2^{\ast }=1.55$, a stable periodic solution with a complex shape appears; (d) it shows that when ${\tau }_2=120$, the solutions of system tend to the equilibrium $E^{\ast }$ again. (e) and (f) show the time evolution curves of $x(t)$ and $y(t)$ when ${\tau }_2=90$, respectively.

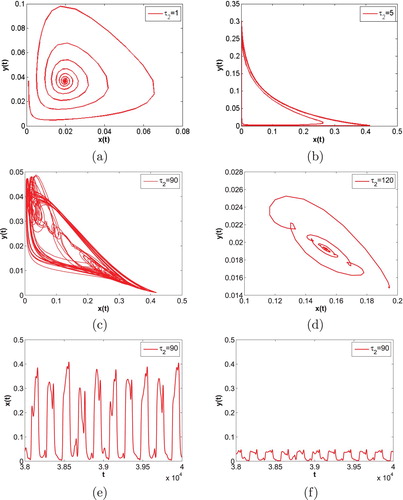
Figure 7. ${\tau }_2=1$ is fixed. The time evolution curves of system (35(35) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_{2}x(t)y^m(t)-r_{2}y(t)-b_2{y}^2(t).\end{array}$(35) ) corresponding to four values m = 0.6, 0.7, 0.8, 0.9. (a) and (b) show that when $m=0.6,0.7<m^{\ast }=0.78$, the solutions of system tend to the equilibrium $E^{\ast }$; (c) and (d) show that when $m=0.8,0.9>m^{\ast }=0.78$, a stable periodic solutions with a simple shape appears.

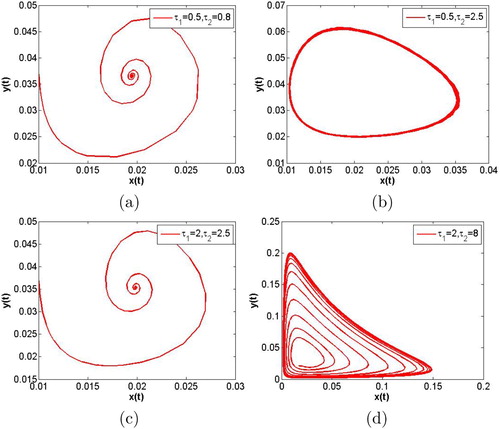
Finally, we fix m = 0.5 and vary the values of ${\tau }_1$ and ${\tau }_2$ to observe the joint effect of ${\tau }_1$ and ${\tau }_2$ on a stable system (see Figure 8(a)). When we choose ${\tau }_1=0.5,{\tau }_2=0.8$, the solution of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) tend to the equilibrium $E^{\ast }$ (see Figure 8(a)); when we choose ${\tau }_1=0.5$, ${\tau }_2=2.5$, a stable periodic solutions appear (see Figure 8(b)); When we choose ${\tau }_1=2$, ${\tau }_1=2.5$, the solution of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) tend to the equilibrium $E^{\ast }$ again (see Figure 8(c)); when we choose ${\tau }_1=2$, ${\tau }_1=8$, a stable periodic solutions appears again (see Figure 8(d)). Comparing Figure 8(a,b), we can easily find out the fact that the system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) will be unstable as the increase of ${\tau }_2$ when ${\tau }_1$ is fixed, which is similar to Figure 6(a,b). While we increase the value of ${\tau }_1$ and fix the value of ${\tau }_2$, the system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) becomes locally stability again (see Figure 8(c)). Comparing Figure 8(c,d), we can easily find out that the stability of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ) switches again as the augment of ${\tau }_2$. The above numerical simulation shows that the augment of ${\tau }_1$ will increase the critical value ${\tau }_2^{\ast }$ changing the stability of $E^{\ast }$ of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ). In other words, when the population of predator is changing periodically, we can let the population of predator in a stable steady state by increasing the maturation delay for prey.

Figure 8. m = 0.5 is fixed. The time evolution curves of system (7(7) $\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =r_1{e}^{-d_1{\tau }_1}x(t-{\tau }_1)-b_1{x}^2(t)-c_{1}x(t)y^m(t),\\ y^{\mathrm{\prime }}(t)& =c_2{e}^{-d_2{\tau }_2}x(t-{\tau }_2)y^m(t-{\tau }_2)-r_{2}y(t)-b_2{y}^2(t),\end{array}$(7) ). (a) When ${\tau }_1=0.5,{\tau }_2=0.8$, the solutions of system tend to the equilibrium $E^{\ast }$. (b) Compared with (a), when we vary ${\tau }_2=2.5$ and fix ${\tau }_1=0.5$, a stable periodic solution with a simple shape appears. (c) Compared with (b), when we vary ${\tau }_1=2$ and fix ${\tau }_2=2.5$, the solutions of system tend to the equilibrium $E^{\ast }$ again, which shows that the augment of ${\tau }_1$ increases the switch value ${\tau }_2^{\ast }$ (d) When ${\tau }_1=2,{\tau }_2=8$, a stable periodic solution with a simple shape appears again.

6. Discussion

In this paper, a class of more general and realistic stage-structured predator–prey model is developed and analysed. The model includes mutual interference and two maturation delays. The maturation time for prey does not effect the globally asymptotically stable, but the maturation time for predator may lead to the model undergo Hopf bifurcation. When maturation time for predator ${\tau }_2$ is small, the positive equilibrium is locally asymptotically stable; when ${\tau }_2$ increases, the positive equilibrium is unstable and it brings the periodic solutions; when ${\tau }_2$ is large enough, the positive equilibrium recovers locally asymptotically stable. The analysis in this paper helps us to understand how delays affect the Lotka–Volterra predator–prey system. Biologically, the theoretical and numeric analysis are also useful to explain that the population of animals raised (or hatched) longer or smaller will be in a stable state. At the same time, the length of incubation has little effect on the dynamics of predator.

Another problem interested us is that the system always has a unique positive equilibrium and the bounded equilibria are always unstable owe to the existence of mutual interference $m(0<m<1)$, in other words, the system is always persistent without any additional conditions. In most Lotka–Volterra predator–prey models, only under some addition conditions will the bounded equilibria be unstable. As the special case where m = 1 (that is, no mutual interference), the positive equilibrium of the system is stable if and only if the condition $r_2{b}_2<r_1(c_2{e}^{-d_2{\tau }_2})$ holds. From the biological viewpoint, it means that the mutual interference $(0<m<1)$ helps the endangered predators survive. The possible reason is that the strength of predation of predators declines sharply causing that the population of prey remain in a relatively high level.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was partially supported by the National Natural Science Foundation of China [grant numbers 11571326, 11901225], the Natural Science Foundation of Hubei Province [grant number 2019CFB189], the Fundamental Research Funds for the Central Universities [grant number CCNU18XJ041].