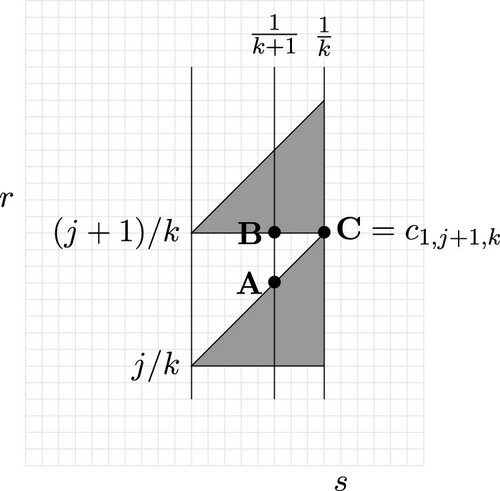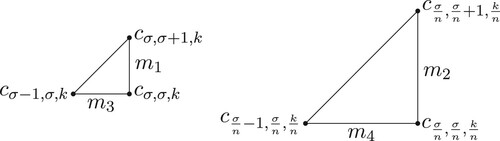Universality of stable multi-cluster periodic solutions in a population model of the cell cycle with negative feedback

Abstract

We study a population model where cells in one part of the cell cycle may affect the progress of cells in another part. If the influence, or feedback, from one part to another is negative, simulations of the model almost always result in multiple temporal clusters formed by groups of cells. We study regions in parameter space where periodic ‘k-cyclic’ solutions are stable. The regions of stability coincide with sub-triangles on which certain events occur in a fixed order. For boundary sub-triangles with order ‘$\mathbf{r}\mathbf{s}\mathbf{1}$’, we prove that the k-cyclic periodic solution is asymptotically stable if the index of the sub-triangle is relatively prime with respect to the number of clusters k and neutrally stable otherwise. For negative linear feedback, we prove that the interior of the parameter set is covered by stable sub-triangles, i.e. a stable k-cyclic solution always exists for some k. We observe numerically that the result also holds for many forms of nonlinear feedback, but may break down in extreme cases.

Keywords:

• Temporal clustering
• phase synchronization
• yeast metabolic oscillations

1. Introduction

1.1. Background

In biology, there are phenomena that may emerge when cells or other dynamical units are coupled and influence each other. One example is synchronization, a state in which units are progressing with identical or nearly identical coordinates. In this manuscript, we consider a related phenomenon, phase synchronization or temporal clustering, in which multiple groups (or clusters) of cells are synchronized. They have the same phase as the other cells in their group, but the phase differs from one group to another. Throughout this manuscript, ‘clustering’ will mean temporal clustering (not spatial clustering).

There is a huge literature about synchronization, but temporal clustering has been studied much less often. It was observed in models of connected neurons [1,14,15,20,38] and models of coupled engineered biological oscillators [11,40]. Temporal clustering has been observed in some experiments, including coupled chemical oscillators based on the Belousov–Zhabotinski reaction [34,35] and engineered electrochemical arrays [16,17,37].

Temporal clustering also has been observed in Yeast Metabolic Oscillations (YMO) experiments that exhibit stable periodic oscillations of budding yeast (Saccharomyces cerevisiae) between aerobic metabolism and anaerobic metabolism. These have been observed in experiments and studied for many years [8,12,19,21,27,31].

The Cell Division Cycle (CDC) of budding yeast is the cyclic process of cell growth and division. A correlation between YMO and bud index, fraction of cells budded, was presented very early [19,21], but the link between YMO and the CDC was unclear due to the fact that the periods of YMO were always shorter than the CDC times in the same experiments. The relationship between YMO and the CDC was mostly ignored until it was noted in genetic expression data [18,31] and investigators began calling such oscillations ‘cell cycle related’. Boczko et al. [3] proposed that temporal clustering is the mechanism linking the metabolism and the CDC in these experiments. Temporal clustering with two clusters was observed in YMO experiments reported in Stowers et al. [33] and Young et al. [39] and it was postulated that cells are segregated into CDC synchronized clusters due to feedback effects on the CDC progression. They proposed that cells in some phase of the cell cycle might produce signalling agents or metabolic products and the levels of these chemicals may affect the growth rate of cells in some other parts of the cycle.

Population level models of the cell cycle that include the effect of such feedback between different parts of the cell cycle were proposed in Boczko et al. [3] and Young et al. [39]. It was observed in [5] that clustering in these models is heavily related to a number theoretic relationship between the number of clusters k and other indices that characterize possible clustered solutions. The main goal of this manuscript is to prove a conjecture made in [5] that for negative feedback, temporal clustering is universal, meaning that it happens for any parameters in the model.

1.2. A cell cycle population model, notations and previous results

We will represent the progress of a cell by a variable (phase) $z_i\in [0,1]$; 0 is the beginning of the cell division cycle and 1 is the end of the cycle. We will identify 0 with 1 and consider $z_i$ as a normalized coordinate on the circle. We will let $S=[0,s)$ and $R=[r,1)$ where 0<s<r<1; see Figure 1. The model of progress of the ith cell in the cell cycle conceptualized in [3] is as follows: (1) $\begin{array}{r}\frac{\text{ d}{z}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{z}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{z}_i\in R,\end{array}\right.\end{array}$(1) where $i=1,\dots ,n$, (2) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:z_i\in S\}}{n}\text{ (fraction of cells in the signalling region).}\end{array}$(2) We will assume that f is a monotone function satisfying $f\left(0\right)=0$ and $f\left(I\right)>-1$. It is perhaps nonlinear.

Figure 1. Schematic with 11 cells where 3 cells are in the S region and 7 cells are in $[0,r)$ (outside the R region). According to the model, $z_1\left(t\right)$ to $z_7\left(t\right)$ are progressing with rate 1 while $z_8\left(t\right)$ to $z_{11}\left(t\right)$ are progressing with rate $1+f\left(\frac{3}{11}\right)$.

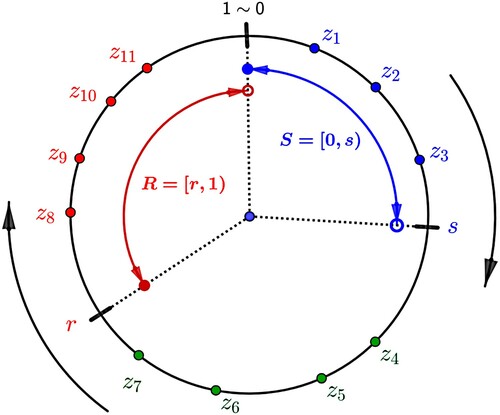
The key feature of the model is that cells in one part of the cycle (denoted by $S=[0,s)$ for signalling) influence the cells in another part ($R=[r,1)$ for responsive). We postulate that the feedback is not direct from cell to cell, but is exerted through the influence of chemicals in the medium that are produced or perhaps consumed by cells in different regions of the cycle. The numbers 0<s<r<1 are fixed for a given application. We will treat them as parameters of the dynamical system. Previous work [39] shows that the number of clusters in asymptotically stable solutions is strongly dependent on s and r.

We do not know how the coordinates of our model correspond to particular phases of the actual cell cycle and so it does not reflect specific biology. However, it is well established that different parts of the cell cycle produce, consume and react differently to different metabolites and other chemicals (see, e.g. [7,9,13,24–26,36,41]). A checkpoint, a phase of the cell cycle where progress may be arrested until sufficient conditions are satisfied [13], is a natural candidate for a responsive phase (R in our model) with negative feedback. This particular mechanism was modelled and studied in [22].

We note that the right-hand side of the differential equation (1(1) $\begin{array}{r}\frac{\text{ d}{z}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{z}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{z}_i\in R,\end{array}\right.\end{array}$(1) ) is piecewise constant. Solutions fail to be differentiable at discrete points in time, and the definition of solution must be generalized to continuous, piece-wise smooth solutions. This was addressed in [39].

Figure 1 provides a visualization of the system in model (1(1) $\begin{array}{r}\frac{\text{ d}{z}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{z}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{z}_i\in R,\end{array}\right.\end{array}$(1) ) for the case of n = 11 where 11 different locations of cells represent the state of each cell in the cycle.

Note that cells are identical in (1(1) $\begin{array}{r}\frac{\text{ d}{z}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{z}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{z}_i\in R,\end{array}\right.\end{array}$(1) ) and so if two cells have the same coordinates at some time $t^{\prime }$, then they will coincide for all $t>t^{\prime }$. A cluster will mean a group of cells whose coordinates are equal and the integer k will be the number of clusters.

When the cells are grouped in k clusters it is sufficient to consider only the k coordinates, $\{X_i{\}}_{i=1}^k$ of the clusters rather than the coordinates of all individual cells. It follows trivially that the progress of clusters is given by (3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) for $i=1,\dots ,k$, and I is again given by (2(2) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:z_i\in S\}}{n}\text{ (fraction of cells in the signalling region).}\end{array}$(2) ). If the k clusters all have the same number of cells, then the progress of evenly clustered solutions can be described by (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) ), with (4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) the fraction of clusters in the signalling region.

Next, we define a special class of periodic, evenly clustered solutions of the system (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )–(4(4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) ) that will be the main object of our study.

Definition 1.1

Let n be the total number of cells in the cycle and $k\ge 2$ be a divisor of n, with n/k cells in each cluster. Suppose that there exists a smallest positive number d such that $X_j\left(d\right)=X_{j+1}\left(0\right)$ for all $j=1,\dots ,k-1$ and $X_k\left(d\right)=X_1\left(0\right)$. Then $\left\{\right(X_1\left(t\right),\dots ,X_k\left(t\right))|t\in {\mathbb{R}}^{+}\}$ is called a k-cyclic solution.

The existence of k-cyclic solutions was proved in [6,39]: For any $f\left(I\right)>-1$ and any pair $(s,r)$, if k is a divisor of n, then a k-cyclic solution exists consisting of n/k cells in each cluster. For negative f and a given pair $(s,r)$, the k-cyclic solution is unique, up to a translation in time.

The main result of this manuscript is that for negative linear feedback, given any pair of parameters $(s,r)$, 0<s<r<1, there is a $k\ge 2$ such that the unique k-cyclic solution corresponding to $(s,r)$ is (locally) asymptotically stable. In order to prove this result, we will first establish new results about stability of k-cyclic solutions for $(s,r)$ in certain subsets. This will require the introduction of quite a bit of terminology.

Let $x_i$ denote the initial condition of $X_i\left(t\right)$ and let ${\mathrm{\Sigma }}_1:=\left\{\right(x_1,\dots ,x_k)|x_1=0\}$. For a solution with an initial condition in ${\mathrm{\Sigma }}_1$, let $t^{\ast }$ be the shortest positive time required for $X_1\left(t\right)$ to return back to its starting position, 0; i.e. when the solution returns to ${\mathrm{\Sigma }}_1$. The Poincaré map $\mathrm{\Pi }:{\mathrm{\Sigma }}_1\to {\mathrm{\Sigma }}_1$ for the flow (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )-(4(4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) ) is defined as follows: (5) $\begin{array}{r}\mathrm{\Pi }(0,x_2,\dots ,x_k)=(0,X_1(t^{\ast }),\dots ,X_{k-1}(t^{\ast }\left)\right).\end{array}$(5) Because we have assumed that $f\left(I\right)>-1$, this Poincaré map is well defined.

Definition 1.2

We define a map F by (6) $\begin{array}{r}F(x_2,\dots ,x_k)=\left(X_1\right(t_k),\dots ,X_{k-1}(t_k\left)\right),\end{array}$(6) where $t_k$ is the shortest time required for $X_k\left(t\right)$ to reach 1.

It was noted that the map $F^k$ is conjugate to the Poincaré map Π [39]. Further, if $(x_2^{\ast },\dots ,x_k^{\ast })$ is a fixed point of F, then $(0,x_2^{\ast },\dots ,x_k^{\ast })\in {\mathrm{\Sigma }}_1$ is the initial condition of a k-cyclic solution of (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )–(4(4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) ) and vice versa. Moses [23] showed that for k even clusters, asymptotic stability in the k clustered phase space implies asymptotic stability in the full phase space of n cells, i.e. system (1(1) $\begin{array}{r}\frac{\text{ d}{z}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{z}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{z}_i\in R,\end{array}\right.\end{array}$(1) )–(2(2) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:z_i\in S\}}{n}\text{ (fraction of cells in the signalling region).}\end{array}$(2) ). Thus, to study the stability of any k-cyclic solution, it is sufficient to study the stability of the fixed points of F.

Note that $0=x_1\le x_2\le \cdots \le x_k\le 1$ can be considered as a (closed) simplex. The map F is defined on the interior of the simplex, i.e. on $0<x_2<x_3<\cdots <x_k<1$. It was shown in [39] that the map F can be extended continuously to the boundary of the simplex and that this continuously extended F permutes components of the boundary of the simplex.

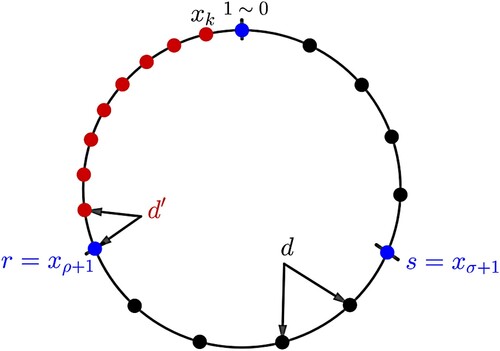
Define σ to be the number of clusters in $S=[0,s)$ at the initial time and define ρ to be the number of clusters in $[0,r)$ (outside of R) at the initial time. That is, (7) $\begin{array}{r}0=x_1<x_2<\cdots <x_{\sigma }<s\le x_{\sigma +1}<\cdots <x_{\rho }<r\le x_{\rho +1}<\cdots <x_k<1.\end{array}$(7) According to Equations (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )–(4(4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) ), clusters may change their rate only when one of them reaches $s,r,$ or 1 which we call events s, r and 1, respectively.

Definition 1.3

Let $\left\{\right(X_1\left(t\right),\dots ,X_k\left(t\right)|t\in {\mathbb{R}}^{+}\}$ be a solution whose initial condition satisfies (7(7) $\begin{array}{r}0=x_1<x_2<\cdots <x_{\sigma }<s\le x_{\sigma +1}<\cdots <x_{\rho }<r\le x_{\rho +1}<\cdots <x_k<1.\end{array}$(7) ). Then, $X_{\sigma }\left(t\right)$ reaching s is called the event $\mathbf{s}$, $X_{\rho }\left(t\right)$ reaching r is called the event $\mathbf{r}$, $X_k\left(t\right)$ reaching 1 is called the event$\mathbf{1}$. A sequence $\mathbf{s}\mathbf{r}\mathbf{1}\dots$ means that the clusters progress with an order of events $\mathbf{s}$, $\mathbf{r}$ and $\mathbf{1}$, respectively. If two or three events happen at the same time, we say that the solution has simultaneous events.

The sequence of events followed by a cyclic solution is periodic and either $\mathbf{s}\mathbf{r}\mathbf{1}\mathbf{s}\mathbf{r}\mathbf{1}\dots$ or $\mathbf{r}\mathbf{s}\mathbf{1}\mathbf{r}\mathbf{s}\mathbf{1}\dots$ or has simultaneous events [5]. Thus, if we wish to study the stability of cyclic solutions, we need only to consider two periodic sequences of events, $\mathbf{s}\mathbf{r}\mathbf{1}$ or $\mathbf{r}\mathbf{s}\mathbf{1}$.

We will call the set of points $\left\{\right(s,r):0<s<r<1\}$ the parameter triangle $\mathrm{△}$.

Definition 1.4

A subset $\tau \subset \mathrm{△}$ is called isosequential for k if the k-cyclic solution corresponding to each parameter pair in the interior of τ has the same σ and ρ and the same order of events:

• ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\rho ,k)=\left\{\right(s,r\left)|X_{\sigma }\right(t\left)\text{ reaches }s\text{ before }{X}_{\rho }\right(t\left)\text{ reaches }r\right\}$,

• ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)=\left\{\right(s,r\left)|X_{\rho }\right(t\left)\text{ reaches }r\text{ before }{X}_{\sigma }\right(t\left)\text{ reaches }s\right\}$.

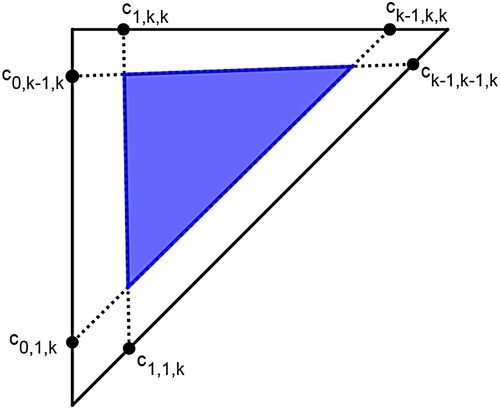
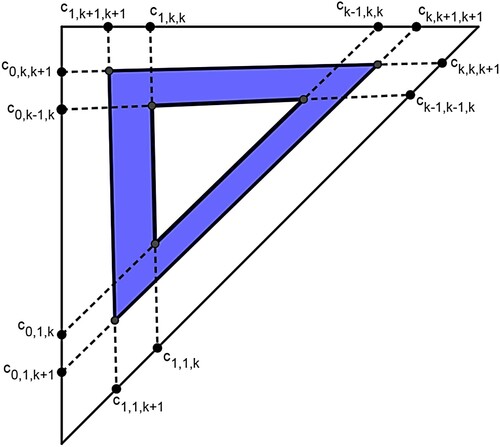
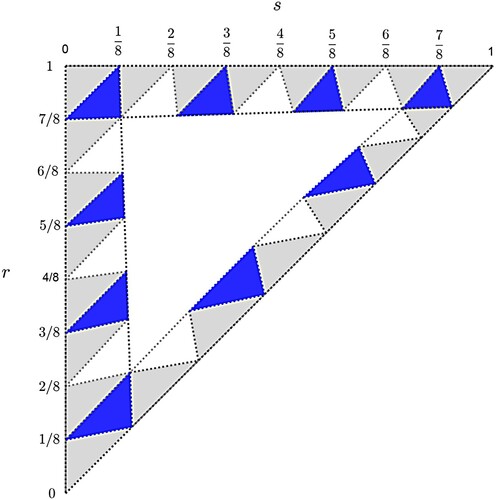
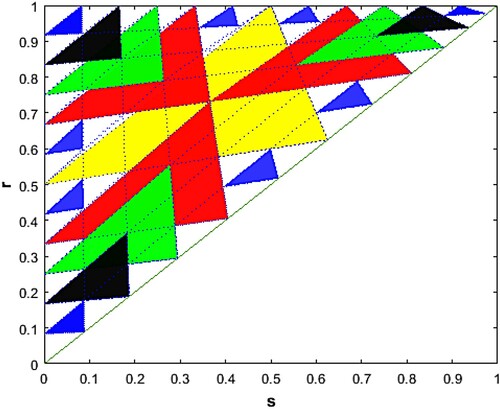
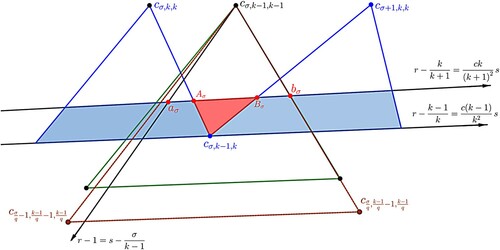
That is, ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\rho ,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$ are regions on which the k-cyclic solutions have the order of events sr1 or rs1, respectively. Figure 2 shows indices of isosequential regions for the case of k = 3. Isosequential regions are in fact sub-triangles [5]. Figure 3 illustrates that the relative positions of the parameters and the clusters of the cyclic solution determine the order of events.

Figure 2. Illustration of how sub-triangles are indexed for the case of k = 3 (and feedback function $f\equiv 0$). Each square corresponds to a pair $(\sigma ,\rho )$. Within squares, upper-left triangles ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\rho ,k)$ have cyclic solutions with the order of events $\mathbf{s}\mathbf{r}\mathbf{1}$, while lower-right triangles ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$ have the order of events $\mathbf{r}\mathbf{s}\mathbf{1}$.

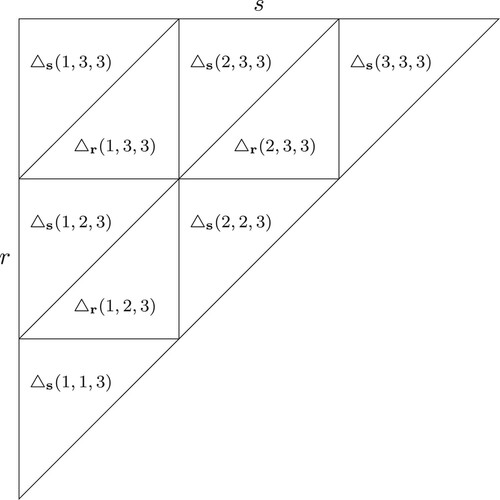
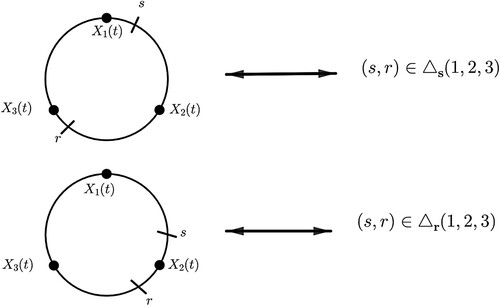
Figure 3. Top: $X_1\left(t\right)$ will reach s before $X_2\left(t\right)$ reaches r, so the pair $(s,r)\in {\mathrm{△}}_{\mathbf{s}}(1,2,3)$. Bottom: $X_2\left(t\right)$ will reach r before $X_1\left(t\right)$ reaches s, so $(s,r)\in {\mathrm{△}}_{\mathbf{r}}(1,2,3)$.

Isosequential regions are important because it was shown in [5] that all the k-cyclic solutions for $(s,r)$ in one of these sub-triangles have the same stability type. We will call a sub-triangle stable if all the k-cyclic solutions corresponding to points in the region are asymptotically stable. An isosequential region will be called unstable if all the k-cyclic solutions corresponding to points in the region are unstable. An isosequential region is called neutral if all the k-cyclic solutions corresponding to points in the region are neutrally stable (stable, but not asymptotically stable). In the context of k-cyclic solutions, stable means that initial conditions near the orbit of the periodic solution will remain near the orbit for all forward time. Asymptotic stability means that nearby solutions not only remain in a neighbourhood of the periodic orbit but also converge to the periodic orbit in forward time.

A point $(s,r)\in \mathrm{△}$ is called a simultaneous point if the k-cyclic solution has events $\mathbf{s}$, $\mathbf{r}$ and $\mathbf{1}$ occurring simultaneously. Note that if $(s,r)$ is a simultaneous point, then the initial condition (assumed to be in ${\mathrm{\Sigma }}_1$) of the k-cyclic solution has one cluster located at s and another one at r. For any f and integer $k\ge 2$ isosequential regions are sub-triangles with simultaneous points at their corners [5]. In the interior of each sub-triangle, all k-cyclic solutions have the same order of events and same stability.

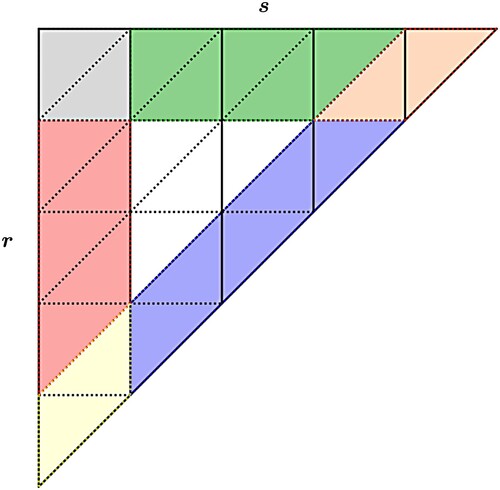
We define the following:

• ${\mathrm{△}}_{\mathbf{s}}(1,\rho ,k)$ and ${\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)$ are called vertical sub-triangles

• ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ are called horizontal sub-triangles

• ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\sigma ,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are called oblique sub-triangles

• all the rest are called interior sub-triangles.

By the boundary sub-triangles, we mean the vertical, horizontal and oblique sub-triangles. Figure 4 shows sub-triangles according to this definition for the case of k = 5.

Figure 4. Boundary sub-triangles for the case of k = 5 and $f\equiv 0$. The red sub-triangles are called vertical sub-triangles. The green sub-triangles are the horizontal sub-triangles. The purple sub-triangles are the oblique sub-triangles. The grey, yellow and orange sub-triangles are on two of the boundaries. The white sub-triangles are called interior sub-triangles.

Next we review previous results about the stability of cyclic solutions.

The vertical and horizontal boundary sub-triangles with order of events sr1, i.e. ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ and ${\mathrm{△}}_{\mathbf{s}}(1,\rho ,k)$, were shown to be neutral for any $f\left(I\right)>-1$ in [5].

For horizontal and vertical sub-triangles with order $\mathbf{r}\mathbf{s}\mathbf{1}$, if $gcd(k,\sigma )=1$ or $gcd(\rho -1,k)=1$, respectively, the sub-triangle is stable for negative feedback. If $gcd(k,\sigma )\ne 1$ or $gcd(\rho -1,k)\ne 1$, then the sub-triangle is neutral.

For positive feedback, all interior sub-triangles are unstable and for negative feedback all interior sub-triangles with the order sr1 are unstable [2,23].

In conclusion, stability under negative and positive feedbacks of the vertical and horizontal sub-triangles was fully investigated in earlier works. However, stability of the oblique sub-triangles has not been previously analysed. The oblique sub-triangles are indexed by ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ and ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\sigma ,k)$ where $1\le \sigma \le k-1$. 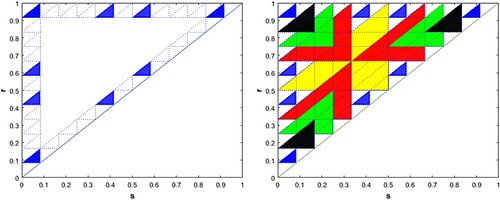All results that had been established previously are shown in Figure 5 for the case of k = 8 where stability of the white sub-triangles has not been investigated before. In this manuscript, we prove that the stability of the oblique triangles follows a similar pattern as the vertical and horizontal sub-triangles.

Figure 5. An illustration of known results for k = 8. The grey regions are neutrally stable by results in [5]. The left panel corresponds to a positive feedback: the red sub-triangles were shown to be unstable in [2,23], the green regions are unstable for large feedback [23]. We will show that they are neutral for small feedback. The right panel corresponds to a negative feedback: the blue regions were shown to be asymptotically stable and the yellow areas neutrally stable in [23], the red regions are unstable [2].

1.3. Main results

As discussed above, the stability of the vertical and horizontal sub-triangles was completely investigated, but the stability of the oblique sub-triangles was open. The ideas presented in Section 3 complete the study of stability of boundary sub-triangles. The stable sub-triangles are those with order of events rs1 and whose index is relatively prime with respect to the number of clusters k. Results in Section 3 can be combined into the following which was conjectured in [5].

Theorem A

Consider the system (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )–(2(2) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:z_i\in S\}}{n}\text{ (fraction of cells in the signalling region).}\end{array}$(2) ) with any negative, non-increasing, feedback function $f\left(I\right)>-1$. For $k\ge 2$, all triangles with edges on the boundary (order $\mathbf{s}\mathbf{r}\mathbf{1}$) of $\mathrm{△}$ are neutral. Boundary triangles with order of events $\mathbf{r}\mathbf{s}\mathbf{1}$ are either neutral or stable. If we number them by an index i, $i:=\left\{\begin{array}{ll}\sigma ,& \text{ for horizontal and oblique sub-triangles,}\\ k-\rho +1,& \text{ for vertical sub-triangles,}\end{array}\right.$then a sub-triangle is stable if k and i are relatively prime and neutral otherwise.

This result is illustrated in Figure 6 for k = 8. The grey (sr1) and white (rs1) areas in Figure 6 are neutral. The blue shaded areas (rs1) in Figure 6 are stable.

Figure 6. The boundary sub-triangles for the case of k = 8 under a negative feedback function. The blue sub-triangles rs1 are stable. The white rs1 and gray sr1 sub-triangles are neutral.

Our method not only clarifies the stability of oblique sub-triangles but also provides an alternative proof for the vertical and horizontal sub-triangles. We establish these results by analysing all eigenvalues of the Jacobian matrix of the map F corresponding to points in each isosequential region.

In Section 5, we prove our main result, which is the following.

Theorem B

For any negative linear feedback $f\left(I\right)=-cI$, c<1, and any pair $(s,r)$ in the interior of the triangle 0<s<r<1, there is a positive integer k, $k\ge 2$, such that the k-cyclic solution corresponding to $(s,r)$ is stable.

This result is important because it means that negative linear feedback systems of this type will always possess an asymptotically stable clustered periodic solution, irrespective of the values of parameters.

This was conjectured more generally in [5]. Numerically, this result appears to hold also for non-linear negative feedback, except possibly for some extreme cases. (See the last section for discussion.)

In Section 4. we prove a version of Theorem thmB in the case of the zero feedback limit where the main ideas are more clear.

These results appeared in expanded form in the dissertation of the first author [28].

2. Some preliminaries

We introduce the following notations that will be used for the rest of this manuscript. ${\text{β}}_{\sigma }:=f\left(\frac{\sigma }{k}\right),{\text{β}}_{\sigma -1}:=f\left(\frac{\sigma -1}{k}\right),\omega :=\frac{{\text{β}}_{\sigma }-{\text{β}}_{\sigma -1}}{1+{\text{β}}_{\sigma -1}},\text{ and}\mu :=\frac{1}{1+{\text{β}}_{\sigma -1}}.$Note that for negative feedback, $-1<\omega <0$.

2.1. Order of events rs1

Suppose that $\sigma <\rho$ and let $\left\{\right(X_1\left(t\right),\dots ,X_k\left(t\right))|t\in {\mathbb{R}}^{+}\}$ be a solution of (3(3) $\begin{array}{r}\frac{\text{ d}{X}_i}{\text{ d}t}=\left\{\begin{array}{ll}1& \text{ if }{X}_i\notin R,\\ 1+f\left(I\right)& \text{ if }{X}_i\in R,\end{array}\right.\end{array}$(3) )–(4(4) $\begin{array}{r}I\equiv \frac{\mathrm{\#}\{i:X_i\in S\}}{k},\end{array}$(4) ) such that its initial condition (where $X_i\left(0\right)=x_i$) satisfies (7(7) $\begin{array}{r}0=x_1<x_2<\cdots <x_{\sigma }<s\le x_{\sigma +1}<\cdots <x_{\rho }<r\le x_{\rho +1}<\cdots <x_k<1.\end{array}$(7) ) and (8) $\begin{array}{r}r-x_{\rho }<s-x_{\sigma }.\end{array}$(8) This condition implies that the solution has order of events rs1.

Recall that $F(x_2,\dots ,x_k)=\left(X_1\right(t_k),\dots ,X_{k-1}(t_k\left)\right)$ as defined in (6(6) $\begin{array}{r}F(x_2,\dots ,x_k)=\left(X_1\right(t_k),\dots ,X_{k-1}(t_k\left)\right),\end{array}$(6) ). Formulas for F and its derivative DF were calculated in [2]. Specifically, $F_{\mathbf{r}\mathbf{s}\mathbf{1}}$ is defined by the following. $X_i\left(t_k\right)=\left\{\begin{array}{ll}{x}_i+\omega x_{\sigma }-\mu x_k-\omega s+\mu & \text{ for }1\le i\le \rho -1,\\ r+(x_{\rho }-r)(1+{\text{β}}_{\sigma })-x_k+1& \text{ for }i=\rho ,\\ x_i-x_k+1& \text{ for }\rho +1\le i\le k-1,\\ 1& \text{ for }i=k.\end{array}\right.$The determinant of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ was calculated to be $det\left(D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}\right)=(-1{)}^k\left(\frac{-1}{1+{\text{β}}_{\sigma }}\right)(1+\omega \left)\right(1+{\text{β}}_{\sigma })=(-1{)}^{k+1}(1+\omega ),$which is less than one in absolute value since $-1<\omega <0$. For $1\le \sigma <\rho \le k$, eigenvalues of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ for sub-triangles ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$ satisfy the equation (9) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega \left[{\lambda }^{\rho -\sigma }\left(\frac{{\lambda }^{k-\rho +1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\left(\frac{{\lambda }^{\rho -1}-1}{\lambda -1}\right)\right],\end{array}$(9) and 1 is not an eigenvalue [2].

2.2. Order of events sr1

Consider a k-clustered solution with order of events sr1. Then, its initial condition satisfies (10) $\begin{array}{r}s-x_{\sigma }<r-x_{\rho }.\end{array}$(10) At the time $t_k$, [2] obtained the solution $X_i\left(t_k\right)=\left\{\begin{array}{ll}{x}_i+\omega x_{\sigma }-\mu x_k-\omega s+\mu & \text{ if }1\le i\le \rho -1,\\ (x_{\sigma }-s)({\text{β}}_{\sigma }-{\text{β}}_{\sigma -1})+(x_i-r){\mu }^{-1}-x_k+r+1& \text{ if }i=\rho ,\\ x_i-x_k+1& \text{ if }\rho +1\le i\le k-1,\\ 1& \text{ if }i=k.\end{array}\right.$This defines the map $F_{\mathbf{s}\mathbf{r}\mathbf{1}}$. The Jacobian matrix of the map DF for the order of events sr1 was shown in [2] to be the following: $det\left(D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}\right)=(-1{)}^k\left(\frac{-1}{1+{\text{β}}_{\sigma }}\right)(1+\omega )\frac{1}{\mu }=(-1{)}^{k+1}.$We note that this implies that k cyclic solutions with order $\mathbf{s}\mathbf{r}\mathbf{1}$ cannot be asymptotically stable. For $1\le \sigma \le \rho \le k$, eigenvalues of $D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}$ for sub-triangles ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\rho ,k)$ satisfy the equation (11) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega {\lambda }^{\rho -\sigma +1}\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\rho }-1}{\lambda -1}\right),\end{array}$(11) and 1 is not an eigenvalue [2].

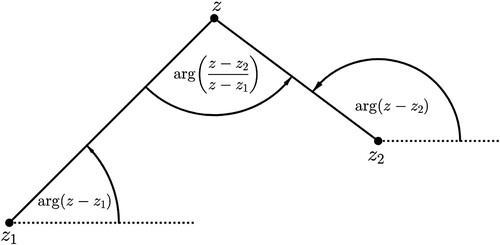
Recall that for a complex number, z = x + iy, an argument of z, $\arg \left(z\right)$, is a number $\varphi \in \mathbb{R}$ such that $x=r\cos \left(\varphi \right)$ and $y=r\sin \left(\varphi \right)$, where $r=|z|$. Figure 7 shows the general picture of $\arg (z-z_1)$, $\arg (z-z_2)$, and $\arg \left(\frac{z-z_2}{z-z_1}\right)$ for given $z,z_1,z_2\in \mathbb{C}$. The argument of $z-z_1$ is the angle between the line from z to $z_1$ and the horizontal line passing $z_1$.

Figure 7. The arguments of $z-z_1$, $z-z_2$, and $\frac{z-z_2}{z-z_1}$, where $z,z_1,z_2\in \mathbb{C}$.

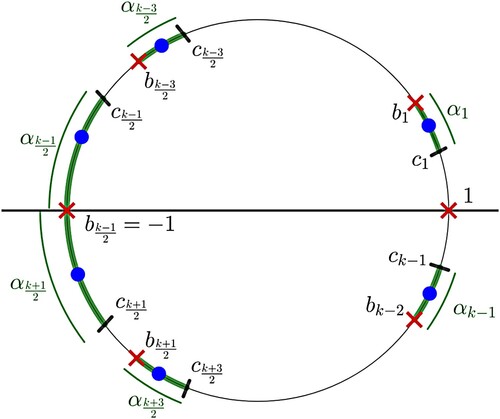
Figure 8. The blue dots are the zeros of $D_1(\lambda ,f_{\theta })$ and the red cross masks are the zeros of $D_2(\lambda ,f_{\theta })$. By the symmetry of zeros on the unit disc, each element of$A_i$ has a complex conjugate in $A_{k-i}$ for $i=1,\dots ,k-1$. Note that $c_i={\overline{c}}_{k-i}$ ($i=1,\dots ,k-1$) and $b_i={\overline{b}}_{k-i-1}$ ($i=1,\dots ,k-2$).

The following lemma might be a known fact, but since we cannot find it in the literature, we state it here.

Lemma 2.1

Let A be the smaller open arc of $S^1=\{z\in \mathbb{C}:|z|=1\}$ bounded by $a\in S^1$ and $b\in S^1$ and θ be the angle of the arc A. Let $\overline{a},\overline{b}$ be the complex conjugates of a and b, respectively. If $\lambda \in A$, $\arg \left(\frac{\lambda -a}{\lambda -b}\right)=\pm \left(\pi -\frac{\theta }{2}\right)\text{ and}\arg \left(\frac{\lambda -\overline{a}}{\lambda -\overline{b}}\right)=\pm \frac{\theta }{2}$(depending on the location of the arc A). If $\lambda \notin A$, $\arg \left(\frac{\lambda -a}{\lambda -b}\right)=\pm \frac{\theta }{2}\text{ and}\arg \left(\frac{\lambda -\overline{a}}{\lambda -\overline{b}}\right)=\mp \frac{\theta }{2}$(depending on the location of the arc A).

We will use the following theorem found in [4] repeatedly.

Theorem 2.2

[4]

All roots of the polynomial $p\left(s\right)=a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0$, $a_n\ne 0$ and $a_i\in \mathbb{R}$ for $i\in \{1,\dots ,n\}$, are in the interior of the unit ball if and only if

• $|\frac{a_0}{a_n}|<1$,

• the zeros of $D_1(s,p):=\frac{1}{2}\left[p\right(s)+s^{n}p(\frac{1}{s}\left)\right]$ and $D_2(s,p):=\frac{1}{2}\left[p\right(s)-s^{n}p(\frac{1}{s}\left)\right]$ are simple, lie on $|s|=1$ and the zeros of $D_1(s,p)$ alternate with the zeros of $D_2(s,p)$.

The following lemma will help us when we use Theorem 2.2.

Lemma 2.3

Let $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ be real monic polynomials of even degree n with their zeros contained in $S^1$. Let $a_1,\dots ,a_n$ be zeros of $p_1\left(\lambda \right)$ and $b_1,\dots ,b_n$ be zeros of $p_2\left(\lambda \right)$, where $a_i\ne b_j$ ($1\le i,j\le n$) and $\begin{array}{rl}0<\arg \left(a_i\right)& \le \arg \left(a_{i+1}\right)<2\pi ,\\ 0<\arg \left(b_i\right)& \le \arg \left(b_{i+1}\right)<2\pi (1\le i\le n-1).\end{array}$Let $A_i$ be the smaller open arc of $S^1$ bounded by $a_i$ and $b_i$ for $i=1,\dots ,n$. Let θ be a real number such that $\theta \in (-1,0)\cup (0,1)$. If the arcs $A_i$ are pairwise disjoint and each element of $A_i$ has a complex conjugate in $A_{n-i+1}$ ($i=1,\dots ,n$), then there is exactly one zero of (12) $\begin{array}{r}\theta \frac{p_1\left(\lambda \right)}{k_0}+(1-\theta )p_2\left(\lambda \right)\end{array}$(12) in each $A_i$ for any positive real number $k_0$.

Proof.

The key idea of this proof is found in [10].

First, let $\theta \in (0,1)$ and $k_0\in {\mathbb{R}}^{+}$. Assume that the arcs $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{n-i+1}$ ($i=1,\dots ,n$). Define a function (13) $\begin{array}{rl}A\left(\lambda \right)& =\frac{p_2\left(\lambda \right)}{p_2\left(\lambda \right)-{\displaystyle \frac{p_1\left(\lambda \right)}{k_0}}}=\frac{1}{1-{\displaystyle \frac{p_1\left(\lambda \right)}{k_0{p}_2\left(\lambda \right)}}}\\ & =\frac{1}{1-{\displaystyle \frac{(\lambda -a_1)\cdots (\lambda -a_{\frac{n}{2}})(\lambda -a_{\frac{n+2}{2}})\cdots (\lambda -a_n)}{k_0(\lambda -b_1)\cdots (\lambda -b_{\frac{n}{2}})(\lambda -b_{\frac{n+2}{2}})\cdots (\lambda -b_n)}}}.\end{array}$(13) For fixed $i\in \{1,\dots ,n\}$, we claim that $A\left(\lambda \right)$ is a continuous real-valued function on each arc $A_i$. Let $\lambda \in A_i$. Consider $q_i=\frac{\lambda -a_i}{\lambda -b_i}\text{ and}{q}_{n-i+1}=\frac{\lambda -a_{n-i+1}}{\lambda -b_{n-i+1}}=\frac{\lambda -\overline{a_i}}{\lambda -\overline{b_i}}.$Let ${\theta }_i$ be the angle of the arc $A_i$. By Lemma 2.1, $\arg \left(q_i\right)=\pm \left(\pi -\frac{{\theta }_i}{2}\right)\text{ and}\arg \left(q_{n-i+1}\right)=\pm \frac{{\theta }_i}{2}.$Thus $\arg \left(q_i{q}_{n-i+1}\right)=\pi$. This implies $q_i{q}_{n-i+1}$ is a negative real number. For $j\in \{1,\dots ,n\}$ and $j\ne i$, Lemma 2.1 implies $\arg \left(q_j\right)=\pm \frac{{\theta }_j}{2}\text{ and}\arg \left(q_{n-j+1}\right)=\mp \frac{{\theta }_j}{2}.$Thus $\arg \left(q_j{q}_{n-j+1}\right)=0$. This implies $q_j{q}_{n-j+1}$ is a positive real number. Hence, $\frac{(\lambda -a_1)\cdots (\lambda -a_{\frac{n}{2}})(\lambda -a_{\frac{n+2}{2}})\cdots (\lambda -a_n)}{k_0(\lambda -b_1)\cdots (\lambda -b_{\frac{n}{2}})(\lambda -b_{\frac{n+2}{2}})\cdots (\lambda -c_n)}=:B\left(\lambda \right)$is a negative real number, so $0<A\left(\lambda \right)=\frac{1}{1-B\left(\lambda \right)}<1$for any $\lambda \in A_i$. Then, $A\left(\lambda \right)$ is a continuous real-valued function of λ on the arc $A_i$. Since $A\left(\lambda \right)$ has the values 0 and 1 at the endpoints of the arc $A_i$, $A\left(\lambda \right)$ must take all values between 0 and 1 on the arc $A_i$. By the Intermediate Value Theorem, there exists $z\in A_i$ such that $A\left(z\right)=\theta$. Then, $\theta =A\left(z\right)=\frac{p_2\left(z\right)}{p_2\left(z\right)-{\displaystyle \frac{p_1\left(z\right)}{k_0}}}.$This implies that $\theta \frac{p_1\left(z\right)}{k_0}+(1-\theta )p_2\left(z\right)=0,$so z is a zero of (12(12) $\begin{array}{r}\theta \frac{p_1\left(\lambda \right)}{k_0}+(1-\theta )p_2\left(\lambda \right)\end{array}$(12) ). This means that there exists a zero of (12(12) $\begin{array}{r}\theta \frac{p_1\left(\lambda \right)}{k_0}+(1-\theta )p_2\left(\lambda \right)\end{array}$(12) ) in each $A_i$ for $i=1,\dots ,n$. Since there are n different zeros of (12(12) $\begin{array}{r}\theta \frac{p_1\left(\lambda \right)}{k_0}+(1-\theta )p_2\left(\lambda \right)\end{array}$(12) ), there is exactly one zero of (12(12) $\begin{array}{r}\theta \frac{p_1\left(\lambda \right)}{k_0}+(1-\theta )p_2\left(\lambda \right)\end{array}$(12) ) in each $A_i(i=1,\dots ,n)$.

In the case that $\theta \in (-1,0)$, we consider $-A\left(\lambda \right)$ instead of $A\left(\lambda \right)$ in (13(13) $\begin{array}{rl}A\left(\lambda \right)& =\frac{p_2\left(\lambda \right)}{p_2\left(\lambda \right)-{\displaystyle \frac{p_1\left(\lambda \right)}{k_0}}}=\frac{1}{1-{\displaystyle \frac{p_1\left(\lambda \right)}{k_0{p}_2\left(\lambda \right)}}}\\ & =\frac{1}{1-{\displaystyle \frac{(\lambda -a_1)\cdots (\lambda -a_{\frac{n}{2}})(\lambda -a_{\frac{n+2}{2}})\cdots (\lambda -a_n)}{k_0(\lambda -b_1)\cdots (\lambda -b_{\frac{n}{2}})(\lambda -b_{\frac{n+2}{2}})\cdots (\lambda -b_n)}}}.\end{array}$(13) ) and proceed with the same method.

3. Classification of sub-triangles for negative feedback

Note that $\frac{{\lambda }^k-1}{\lambda -1}={\lambda }^{k-1}+{\lambda }^{k-2}+\dots +\lambda +1$ for a positive integer k except at $\lambda =1$. Recall also that we define $\omega =\frac{{\text{β}}_{\sigma }-{\text{β}}_{\sigma -1}}{1+{\text{β}}_{\sigma -1}}$, where ${\text{β}}_{\sigma }=f\left(\frac{\sigma }{k}\right)$ and ${\text{β}}_{\sigma -1}=f\left(\frac{\sigma -1}{k}\right)$. For a negative feedback system, we have $-1<\omega <0$. For the reader's convenience, we provide a table of symbols in Appendix.

We now consider the stability of oblique sub-triangles.

Theorem 3.1

For negative feedback and $k\ge 2$, If $gcd(k,\sigma )=1$, then the sub-triangles ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are asymptotically stable, where $1\le \sigma \le k$.

Proof.

By substituting $\rho =\sigma +1$ in Equation (9(9) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega \left[{\lambda }^{\rho -\sigma }\left(\frac{{\lambda }^{k-\rho +1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\left(\frac{{\lambda }^{\rho -1}-1}{\lambda -1}\right)\right],\end{array}$(9) ), eigenvalues of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ for sub-triangle ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ satisfy $\frac{{\lambda }^k-1}{\lambda -1}=\omega \left[\lambda \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right)\right],$and 1 is not an eigenvalue. Let $\theta =-\omega$. In a negative feedback system, we get $0<\theta <1$. Let (14) $\begin{array}{r}{f}_{\theta }\left(\lambda \right):=\frac{{\lambda }^k-1}{\lambda -1}+\theta \left[\lambda \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right].\end{array}$(14) Our claim is that all roots of $f_{\theta }\left(\lambda \right)$ satisfy $|\lambda |<1$. We will use Theorem 2.2 to obtain the claim. First, multiply both sides of (14(14) $\begin{array}{r}{f}_{\theta }\left(\lambda \right):=\frac{{\lambda }^k-1}{\lambda -1}+\theta \left[\lambda \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right].\end{array}$(14) ) by $(\lambda -1{)}^2$, $\begin{array}{rl}(\lambda -1{)}^2{f}_{\theta }(\lambda )& =(\lambda -1)({\lambda }^k-1)+\theta \left[\lambda \right({\lambda }^{k-\sigma }-1\left)\right({\lambda }^{\sigma -1}-1)-({\lambda }^{\sigma }-1\left)\right(\lambda -1\left)\right]\\ & =(\lambda -1)({\lambda }^k-1)+\theta [-{\lambda }^{k+1}+{\lambda }^k\\ & +\lambda -1+{\lambda }^{k+1}-{\lambda }^{k-\sigma +1}-{\lambda }^{\sigma +1}+\lambda ]\\ & =(\lambda -1)({\lambda }^k-1)-\theta [{\lambda }^{k+1}-{\lambda }^k-\lambda +1]+\theta \lambda [{\lambda }^k-{\lambda }^{k-\sigma }-{\lambda }^{\sigma }+1]\\ & =\theta \lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)+(1-\theta )(\lambda -1)({\lambda }^k-1).\end{array}$Thus (15) $\begin{array}{r}{f}_{\theta }\left(\lambda \right)=\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(15) Note that $f_{\theta }\left(\lambda \right)$ is equal to a polynomial of degree k−1, $f_{\theta }^{\prime }\left(\lambda \right)=\theta \lambda ({\lambda }^{\sigma -1}+\cdots +\lambda +1)({\lambda }^{k-\sigma -1}+\dots +\lambda +1)+(1-\theta )({\lambda }^{k-1}+\cdots +\lambda +1)$except at $\lambda =1$. Since we consider $\lambda \ne 1$ in (15(15) $\begin{array}{r}{f}_{\theta }\left(\lambda \right)=\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(15) ), we have $f_{\theta }\left(\lambda \right)=f_{\theta }^{\prime }\left(\lambda \right)$, so we can refer to both as $f_{\theta }\left(\lambda \right)$. The constant term of $f_{\theta }\left(\lambda \right)$ is 1 and the leading coefficient of $f_{\theta }\left(\lambda \right)$ is $1-\theta$. Since $|\frac{1-\theta }{1}|<1$, we achieve the first condition of Theorem 2.2.

Let (16) $\begin{array}{r}{f}_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}\text{ and}{f}_2\left(\lambda \right)=\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(16) Then (17) $\begin{array}{r}{f}_{\theta }\left(\lambda \right)=\theta \lambda f_1\left(\lambda \right)+(1-\theta )f_2\left(\lambda \right).\end{array}$(17) Next, we compute $D_1(\lambda ,f_{\theta })$ and $D_2(\lambda ,f_{\theta })$. Since $\begin{array}{rl}{\lambda }^{k-1}{f}_{\theta }\left(\frac{1}{\lambda }\right)& =\frac{{\lambda }^{k+1}}{{\lambda }^2}\theta \left[\frac{\frac{1}{\lambda }(\frac{1}{{\lambda }^{\sigma }}-1)(\frac{1}{{\lambda }^{k-\sigma }}-1)}{(\frac{1}{\lambda }-1{)}^2}\right]+\frac{{\lambda }^{k+1}}{{\lambda }^2}(1-\theta )\left[\frac{(\frac{1}{\lambda }-1)(\frac{1}{{\lambda }^k}-1)}{(\frac{1}{\lambda }-1{)}^2}\right]\\ & =\theta \frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}\\ & =\theta f_1\left(\lambda \right)+(1-\theta )f_2\left(\lambda \right),\end{array}$we get $\begin{array}{rl}{D}_1(\lambda ,f_{\theta })& =\frac{1}{2}\left(f_{\theta }\left(\lambda \right)+{\lambda }^{k-1}{f}_{\theta }\left(\frac{1}{\lambda }\right)\right)\\ & =\frac{1}{2}\left[\theta \lambda f_1\right(\lambda )+(1-\theta \left)f_2\right(\lambda )+\theta f_1(\lambda )+(1-\theta \left)f_2\right(\lambda \left)\right]\\ & =\theta \frac{(\lambda +1)f_1\left(\lambda \right)}{2}+(1-\theta )f_2\left(\lambda \right).\end{array}$Hence, (18) $\begin{array}{r}{D}_1(\lambda ,f_{\theta })=\theta \frac{(\lambda +1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(18) Similarly, (19) $\begin{array}{r}{D}_2(\lambda ,f_{\theta })=\theta \frac{(\lambda -1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1{)}^2}.\end{array}$(19) To check the second condition of the theorem, we consider two cases of the integer k: it is an odd number and it is an even number.

Case I: k is an odd number.

In this case, $k-\sigma$ can be either an odd or even number. Note that regardless of whether $k-\sigma$ is an odd number or an even number, $-1$ is a zero of $f_1\left(\lambda \right)$. If $k-\sigma$ is an odd number, then $-1$ is a zero of $f_1\left(\lambda \right)$ since σ is must be an even number, see (16(16) $\begin{array}{r}{f}_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}\text{ and}{f}_2\left(\lambda \right)=\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(16) ). If $k-\sigma$ is an even number, $-1$ is a zero of $f_1\left(\lambda \right)$, see (16(16) $\begin{array}{r}{f}_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}\text{ and}{f}_2\left(\lambda \right)=\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(16) ). Since $gcd(\sigma ,k-\sigma )=1$ and k is an odd number, we can write $\begin{array}{rl}{f}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k-2}),\\ \text{ and}{f}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k-1}),\end{array}$where $b_{\frac{k-1}{2}}=-1$, $b_i$ and $c_j$ are in $S^1$, $b_i\ne c_j$, and $\begin{array}{rl}0& <\arg \left(b_i\right)<\arg \left(b_I\right)<2\pi ,\\ 0& <\arg \left(c_j\right)<\arg \left(c_J\right)<2\pi ,\end{array}$for $1\le i<I\le k-2$ and $1\le j<J\le k-1$. Let $C_i$ be the smaller arc of $S^1$ bounded by $c_i$ and $c_{i+1}$ for $i\in \{1,\dots ,k-2\}$. We use the following lemma which we will prove later.

Lemma 3.2

For every $1\le i\le k-2$, the arc $C_i$ contains at most one zero of $f_1\left(\lambda \right)$.

Since there are k−2 zeros of $f_1\left(\lambda \right)$, by Lemma 3.2 each arc $C_i(i=1,\dots ,k-2)$ contains exactly one zero of $f_1\left(\lambda \right)$. We obtain that $b_i\in C_i$ for each i. We may write (20) $\begin{array}{r}(\lambda +1)f_1\left(\lambda \right)=(\lambda -b_1)\cdots (\lambda -b_{\frac{k-3}{2}})(\lambda +1)(\lambda +1)(\lambda -b_{\frac{k+1}{2}})\cdots (\lambda -b_{k-2}).\end{array}$(20) Let $A_i$ be the smaller open arc of $S^1$ bounded by

• $c_i$ and $b_i$, for $i=1,\dots ,\frac{k-1}{2}$,

• $-1$ and $c_{\frac{k+1}{2}}$ for $i=\frac{k+1}{2}$,

• $b_{i-1}$ and $c_i$ for $i=\frac{k+3}{2},\dots ,k-1$.

Note that $b_{\frac{k-1}{2}}=-1$. By our construction, $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{k-i}$ for $i=1,\dots ,k-1$ (see Figure 8). Lemma 2.3 implies $D_1(\lambda ,f_{\theta })=\theta \frac{(\lambda +1)f_1\left(\lambda \right)}{2}+(1-\theta )f_2\left(\lambda \right)$has exactly one zero in each $A_i(i=1,\dots ,k-1)$. Hence, all zeros of $D_1(\lambda ,f_{\theta })$ lie on $S^1$. By the construction of $A_i$ (see Figure 8), the zeros of $D_1(\lambda ,f_{\theta })$ alternate with the zeros of $D_2(\lambda ,f_{\theta })$ for all $\theta \in (0,1)$. Therefore, by Theorem 2.2, all zeros of $f_{\theta }\left(\lambda \right)$ are in the interior of the unit disc, $|\lambda |<1$, for all $\theta \in (0,1)$.

Case II: k is an even number.

In this case, σ and $k-\sigma$ are odd numbers and $\begin{array}{rl}{D}_1(\lambda ,f_{\theta })& =(\lambda +1)\left(\theta \frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2(\lambda +1)}\right),\\ D_2(\lambda ,f_{\theta })& =\theta \frac{(\lambda -1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1{)}^2}.\end{array}$Let $p_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}\text{ and}{p}_2\left(\lambda \right)=\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2(\lambda +1)}.$Note that $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have no common zeros and they both have the same degree k−2, which is an even number. We write $\begin{array}{rl}{p}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k-2}),\\ \text{ and}{p}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k-2}),\end{array}$where $|b_i|=1=|c_j|$, $b_i\ne c_j$ $(1\le i,j\le k-2)$, and $\begin{array}{rl}0& <\arg \left(b_i\right)<\arg \left(b_I\right)<2\pi ,\\ 0& <\arg \left(c_i\right)<\arg \left(c_I\right)<2\pi ,\end{array}$for $1\le i<I\le k-2$. Note that $b_i\ne -1,1$ and $c_j\ne -1,1$. Let $C_i$ be the smaller arc of $S^1$ as follows:

• $C_i$ is bounded by $c_i$ and $c_{i+1}$ for $i\in \{1,\dots ,\frac{k-4}{2}\}$

• $C_{\frac{k-2}{2}}$ is bounded by $c_{\frac{k-2}{2}}$ and $-1$

• $C_{\frac{k}{2}}$ is bounded by $-1$ and ${\overline{c}}_{\frac{k-2}{2}}$

• $C_i$ is bounded by ${\overline{c}}_{k-i}$ and ${\overline{c}}_{k-i-1}$ for $i\in \{\frac{k+2}{2},\dots ,k-2\}$.

Note that $p_1\left(\lambda \right)$ has $\frac{k-2}{2}$ roots whose arguments are between 0 and π. By Lemma 3.2, the arcs $C_i$ each contain one root of $p_1\left(\lambda \right)$ for $i=1,\dots ,\frac{k-4}{2}$. Thus $C_{\frac{k-2}{2}}$ also contains one root of $p_1\left(\lambda \right)$. Hence, $b_i\in C_i$ for $i=1,\dots ,\frac{k-2}{2}$. By the symmetry of complex roots, it follows that $b_i\in C_i$ for $i=1,\dots ,k-2$. Now, let $A_i$ be the smaller arc of $S^1$ bounded by $c_i$ and $b_i$ for $i\in \{1,\dots ,k-2\}$. By our construction, $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{k-i-1}$ ($i=1,\dots ,k-1$). Lemma 2.3 implies that $\frac{D_1(\lambda ,f_{\theta })}{\lambda +1}=\theta \frac{p_1\left(\lambda \right)}{2}+(1-\theta )p_2\left(\lambda \right)$has exactly one root in each $A_i(i=1,\dots ,k-1)$. Hence, all zeros of $D_1(\lambda ,f_{\theta })$ lie on $S^1$. By the construction of $A_i$ in this case, the zeros of $D_1(\lambda ,f_{\theta })$ alternate with the zeros of $D_2(\lambda ,f_{\theta })$ for all $\theta \in (0,1)$. Therefore, by Theorem 2.2, all zeros of $f_{\theta }\left(\lambda \right)$ satisfy $|\lambda |<1$, for all $\theta \in (0,1)$.

Proof

Proof of Lemma 3.2

Let $l\in \{1,\dots ,k-2\}$. Suppose that the arc $C_l$ contains more than one zero of $f_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}$, say $f_1\left(\lambda \right)$ has two zeros inside the arc $C_l$. Note that the angle of the arc $C_l$ is greater than the angle of the arc bounded by the two zeros. Then, one of the two zeros is a zero of $\frac{{\lambda }^{\sigma }-1}{\lambda -1}$ and another zero is a zero of $\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}$. Let $b_1$ and $b_2$ be the two zeros, say $b_1$ is a zero of $\frac{{\lambda }^{\sigma }-1}{\lambda -1}$ and $b_2$ is a zero of $\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}$. Then, there are $q\in \{1,\dots ,\sigma -1\}$ and $r\in \{1,\dots ,k-\sigma -1\}$ such that $\arg \left(b_1\right)=\frac{2\pi q}{\sigma }\text{ and}\arg \left(b_2\right)=\frac{2\pi r}{k-\sigma }.$Since $b_1$ and $b_2$ are contained in arc $C_l$, $\arg \left(c_l\right)<\arg \left(b_1\right)<\arg \left(c_{l+1}\right)\text{ and}\arg \left(c_l\right)<\arg \left(b_2\right)<\arg \left(c_{l+1}\right).$This implies the following: (21) $\begin{array}{r}\frac{l}{k}<\frac{q}{\sigma }<\frac{l+1}{k}\text{ and}\frac{l}{k}<\frac{r}{k-\sigma }<\frac{l+1}{k}.\end{array}$(21) These inequalities are equivalent to (22) $\begin{array}{r}\frac{l}{k(k-\sigma )}<\frac{q}{\sigma (k-\sigma )}<\frac{l+1}{k(k-\sigma )}\text{ and}\frac{l}{k\sigma }<\frac{r}{(k-\sigma )\sigma }<\frac{l+1}{k\sigma }.\end{array}$(22) Adding the inequalities in (22(22) $\begin{array}{r}\frac{l}{k(k-\sigma )}<\frac{q}{\sigma (k-\sigma )}<\frac{l+1}{k(k-\sigma )}\text{ and}\frac{l}{k\sigma }<\frac{r}{(k-\sigma )\sigma }<\frac{l+1}{k\sigma }.\end{array}$(22) ), we get (23) $\begin{array}{r}\frac{l}{(k-\sigma )\sigma }<\frac{q+r}{(k-\sigma )\sigma }<\frac{l+1}{(k-\sigma )\sigma }.\end{array}$(23) Then, l<q + r<l + 1 is a contradiction since q and r are integers.

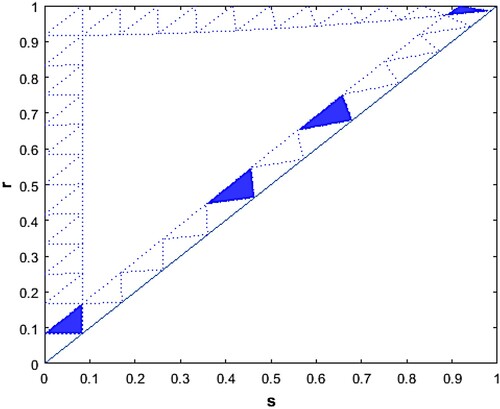
Figure 9 shows stable sub-triangles (blue shaded sub-triangles) for k = 12 with respect to feedback function $f\left(I\right)=-I^2$. Since $gcd(12-1,1)=gcd(12-5,5)=gcd(12-7,7)=gcd(12-11,11)=1,$the sub-triangles ${\mathrm{△}}_{\mathbf{r}}(1,2,12)$ ${\mathrm{△}}_{\mathbf{r}}(5,6,12)$, ${\mathrm{△}}_{\mathbf{r}}(7,8,12)$, and ${\mathrm{△}}_{\mathbf{r}}(11,12,12)$ are asymptotically stable by Theorem 3.1, see Figure 9.

Figure 9. The boundary sub-triangles for the case of k = 12 and feedback function $f\left(I\right)=-I^2$. The blue sub-triangles are stable.

The following theorem was proved in [23] with a different method.

Theorem 3.3

For negative feedback and $k\ge 2$, If $gcd(k,\sigma )=1$, then sub-triangles ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ are asymptotically stable, where $1\le \sigma \le k$.

Proof.

By substituting $\sigma =1$ and $\rho =\sigma +1$ in (9(9) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega \left[{\lambda }^{\rho -\sigma }\left(\frac{{\lambda }^{k-\rho +1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\left(\frac{{\lambda }^{\rho -1}-1}{\lambda -1}\right)\right],\end{array}$(9) ), the eigenvalues of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ for the region ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ satisfy (24) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right),\end{array}$(24) where $\lambda \ne 1$. This is equivalent to (25) $\begin{array}{r}{\lambda }^{\sigma }=\frac{1+\omega }{{\lambda }^{k-\sigma }+\omega }.\end{array}$(25) Since $gcd(k,\sigma )=1$, no zero of Equation (24(24) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right),\end{array}$(24) ) lies on the unit circle; i.e.$|\lambda |\ne 1$. If $|\lambda |>1$, then by (25(25) $\begin{array}{r}{\lambda }^{\sigma }=\frac{1+\omega }{{\lambda }^{k-\sigma }+\omega }.\end{array}$(25) ) (26) $\begin{array}{rl}|{\lambda }^{\sigma }|& =\frac{|1+\omega |}{|{\lambda }^{k-\sigma }+\omega |}\\ & \le \frac{1+\omega }{|{\lambda }^{k-\sigma }|+\omega }\\ & <1,\end{array}$(26) a contradiction. Hence, $|\lambda |<1$ and then the region ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ are stable.

Next, the eigenvalues of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ for the sub-triangle ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ satisfy $\frac{{\lambda }^k-1}{\lambda -1}=\omega \left[{\lambda }^{k-\sigma }\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)-\left(\frac{{\lambda }^{k-1}-1}{\lambda -1}\right)\right].$By simplifying, we have (27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) This is equivalent to (28) $\begin{array}{r}{\lambda }^{k-\sigma }=\frac{1+\omega }{{\lambda }^{\sigma }+\omega }.\end{array}$(28) Note that since $gcd(k,k-\sigma )=1$, no solution of quation (27(27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) ) lies on the unit circle; i.e. $|\lambda |\ne 1$. If $|\lambda |>1$, then by (28(28) $\begin{array}{r}{\lambda }^{k-\sigma }=\frac{1+\omega }{{\lambda }^{\sigma }+\omega }.\end{array}$(28) ) (29) $\begin{array}{rl}|{\lambda }^{k-\sigma }|& =\frac{|1+\omega |}{|{\lambda }^{\sigma }+\omega |}\\ & \le \frac{1+\omega }{|{\lambda }^{\sigma }|+\omega }\\ & <1,\end{array}$(29) a contradiction. Hence, the sub-triangle ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ is stable.

The next corollary is proved by similar ideas as in the proofs of Theorem 3.1. In this corollary, there are some eigenvalues of $D{F}_{\mathbf{r}\mathbf{s}\mathbf{1}}$ lying on the unit disc, $|\lambda |=1$.

Corollary 3.4

For negative feedback with the order of events $\mathbf{r}\mathbf{s}\mathbf{1}$ and $k\ge 2$, the following statements hold.

• If $gcd(k,\sigma )\ne 1$, then triangle regions ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ are neutrally stable.

• If $gcd(k-\sigma ,\sigma )\ne 1$, then triangle regions ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are neutrally stable,

where $1\le \sigma \le k$.

Proof.

Note that (24(24) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right),\end{array}$(24) ) and (27(27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) ) are characteristic polynomials for ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$, respectively.

Since $gcd(k,\sigma )\ne 1$, there is a solution of (24(24) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right),\end{array}$(24) ) that lies on the unit circle. If $|\lambda |>1$, we get a contradiction as shown in (26(26) $\begin{array}{rl}|{\lambda }^{\sigma }|& =\frac{|1+\omega |}{|{\lambda }^{k-\sigma }+\omega |}\\ & \le \frac{1+\omega }{|{\lambda }^{k-\sigma }|+\omega }\\ & <1,\end{array}$(26) ). Hence, all solutions of (24(24) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{\sigma }-1}{\lambda -1}\right),\end{array}$(24) ) satisfy $|\lambda |\le 1$. Thus the regions ${\mathrm{△}}_{\mathbf{r}}(1,\sigma +1,k)$ are neutrally stable.

Equation (27(27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) ) and the condition that $gcd(k,\sigma )\ne 1$ imply that there is a solution of (27(27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) ) on the unit circle. If $|\lambda |>1$, we get a contradiction as shown in (29(29) $\begin{array}{rl}|{\lambda }^{k-\sigma }|& =\frac{|1+\omega |}{|{\lambda }^{\sigma }+\omega |}\\ & \le \frac{1+\omega }{|{\lambda }^{\sigma }|+\omega }\\ & <1,\end{array}$(29) ). Hence, all solution of (27(27) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=-\omega \left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right).\end{array}$(27) ) satisfy $|\lambda |\le 1$. We then obtain that ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ are neutrally stable.

Suppose that $gcd(k-\sigma ,\sigma )=n\ne 1$. We consider (15(15) $\begin{array}{r}{f}_{\theta }\left(\lambda \right)=\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.\end{array}$(15) ) in the proof of Theorem 3.1, $f_{\theta }\left(\lambda \right)=\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1{)}^2}+(1-\theta )\frac{(\lambda -1)({\lambda }^k-1)}{(\lambda -1{)}^2}.$Since $gcd(k-\sigma ,\sigma )=n$, we have $gcd(k,\sigma ,k-\sigma )=n$ and $f_{\theta }\left(\lambda \right)=\frac{{\lambda }^n-1}{\lambda -1}\left(\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{{\lambda }^k-1}{{\lambda }^n-1}\right).$Let $g_{\theta }\left(\lambda \right):=\theta \frac{\lambda ({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{{\lambda }^k-1}{{\lambda }^n-1}.$Then, $f_{\theta }\left(\lambda \right)=\frac{{\lambda }^n-1}{\lambda -1}{g}_{\theta }\left(\lambda \right)$. We claim that all zeros of $g_{\theta }\left(\lambda \right)$ lie in the unit disc. When the claim holds, it follows that no zero of $f_{\theta }\left(\lambda \right)$ is outside the units disc, i.e. $|\lambda |\le 1$. Therefore, ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are neutrally stable. Since $gcd(k,\sigma ,k-\sigma )=n$, the function $g_{\theta }\left(\lambda \right)$ is a polynomial function of degree k−n and $g_{\theta }\left(\lambda \right)$ satisfies the first condition of Theorem 2.2. Let $g_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}\text{ and}{g}_2\left(\lambda \right)=\frac{{\lambda }^k-1}{{\lambda }^n-1}.$Then, (30) $\begin{array}{r}{g}_{\theta }\left(\lambda \right)=\theta \lambda g_1\left(\lambda \right)+(1-\theta )g_2\left(\lambda \right).\end{array}$(30) Next, we compute $D_1(\lambda ,g_{\theta })$ and $D_2(\lambda ,g_{\theta })$ defined in Theorem 2.2. Since $\begin{array}{rl}{\lambda }^{k-n}{g}_{\theta }\left(\frac{1}{\lambda }\right)& =\frac{{\lambda }^{k+1}}{{\lambda }^{n+1}}\theta \left[\frac{\frac{1}{\lambda }(\frac{1}{{\lambda }^{\sigma }}-1)(\frac{1}{{\lambda }^{k-\sigma }}-1)}{(\frac{1}{\lambda }-1)(\frac{1}{{\lambda }^n}-1)}\right]+\frac{{\lambda }^k}{{\lambda }^n}(1-\theta )\left[\frac{\frac{1}{{\lambda }^k}-1}{\frac{1}{{\lambda }^n}-1}\right]\\ & =\theta \frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{{\lambda }^k-1}{{\lambda }^n-1}\\ & =\theta g_1\left(\lambda \right)+(1-\theta )g_2\left(\lambda \right),\end{array}$we get $\begin{array}{rl}{D}_1(\lambda ,g_{\theta })& =\frac{1}{2}\left(g_{\theta }\left(\lambda \right)+{\lambda }^{k-n}{g}_{\theta }\left(\frac{1}{\lambda }\right)\right)\\ & =\frac{1}{2}\left[\theta \lambda g_1\right(\lambda )+(1-\theta \left)g_2\right(\lambda )+\theta g_1(\lambda )+(1-\theta \left)g_2\right(\lambda \left)\right]\\ & =\theta \frac{(\lambda +1)g_1\left(\lambda \right)}{2}+(1-\theta )g_2\left(\lambda \right).\end{array}$Hence, (31) $\begin{array}{r}{D}_1(\lambda ,g_{\theta })=\theta \frac{(\lambda +1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{{\lambda }^k-1}{{\lambda }^n-1}.\end{array}$(31) Similarly, (32) $\begin{array}{r}{D}_2(\lambda ,g_{\theta })=\theta \frac{(\lambda -1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}.\end{array}$(32) To check the second condition of Theorem 2.2, we consider three cases: k is an odd number, k is an even number and n is an odd number, and, k and n are both even.

Case I: k is an odd number.

This case implies that n is an odd number. Then k−n is an even number. Since σ and $k-\sigma$ cannot be both odd numbers in this case, $-1$ is a zero of $g_1\left(\lambda \right)$. By our construction, $g_1\left(\lambda \right)$ and $g_2\left(\lambda \right)$ have no common zero. We can write $\begin{array}{rl}{g}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k-n-1}),\\ \text{ and}{g}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k-n}),\end{array}$where $b_{\frac{k-n}{2}}=-1$, $b_i$ and $c_j$ are in $S^1$, $b_i\ne c_j$, and $\begin{array}{r}0<\arg \left(b_i\right)<\arg \left(b_I\right)<2\pi ,\\ 0<\arg \left(c_j\right)<\arg \left(c_J\right)<2\pi ,\end{array}$for $1\le i<I\le k-n-1$ and $1\le j<J\le k-n$. Now, we write $(\lambda +1)g_1\left(\lambda \right)=(\lambda -b_1)\cdots (\lambda -b_{\frac{k-n-2}{2}})(\lambda +1)(\lambda +1)(\lambda -b_{\frac{k-n+2}{2}})\cdots (\lambda -b_{k-n-1}).$Let $A_i$ be the smaller open arc of $S^1$ bounded by

• $c_i$ and $b_i$, for $i=1,\dots ,\frac{k-n}{2}$,

• $-1$ and $c_{\frac{k+1}{2}}$ for $i=\frac{k-n+2}{2}$,

• $b_{i-1}$ and $c_i$ for $i=\frac{k-n+4}{2},\dots ,k-n$.

Note that $b_{\frac{k-n}{2}}=-1$. By our construction, $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{k-n-i+1}$ ($i=1,\dots ,k-n$). Lemma 2.3 implies that $D_1(\lambda ,g_{\theta })=\theta \frac{(\lambda +1)g_1\left(\lambda \right)}{2}+(1-\theta )g_2\left(\lambda \right)$has exactly one zero in each $A_i(i=1,\dots ,k-1)$. Hence, all zeros of $D_1(\lambda ,g_{\theta })$ lie on $S^1$ and the zeros of $D_1(\lambda ,g_{\theta })$ alternate with the zeros of $D_2(\lambda ,g_{\theta })$ for all $\theta \in (0,1)$. Therefore, all zeros of $g_{\theta }\left(\lambda \right)$ are in the interior of the unit disc, $|\lambda |<1$, for all $\theta \in (0,1)$.

Case II: k is an even number and n is an odd number.

In this case, σ and $k-\sigma$ are odd numbers, k−n is an even number, and we have $\begin{array}{rl}{D}_1(\lambda ,g_{\theta })& =(\lambda +1)\left(\theta \frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{({\lambda }^k-1)}{({\lambda }^n-1)(\lambda +1)}\right),\\ D_2(\lambda ,g_{\theta })& =\theta \frac{(\lambda -1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}.\end{array}$Let $p_1\left(\lambda \right)=\frac{({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}\text{ and}{p}_2\left(\lambda \right)=\frac{({\lambda }^k-1)}{({\lambda }^n-1)(\lambda +1)}.$Note that $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have no common zeros and they both have the same degree k−n−1, which is an even number. We write $\begin{array}{rl}{p}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k-n-1}),\\ \text{ and}{p}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k-n-1}),\end{array}$where $|b_i|=1=|c_j|$, $b_i\ne c_j$ $(1\le i,j\le k-n-1)$, and $\begin{array}{rl}0& <\arg \left(b_i\right)<\arg \left(b_I\right)<2\pi ,\\ 0& <\arg \left(c_i\right)<\arg \left(c_I\right)<2\pi ,\end{array}$for $1\le i<I\le k-n-1$. Note that $b_i\ne -1,1$ and $c_j\ne -1,1$. Let $A_i$ be the smaller arc of $S^1$ bounded by $c_i$ and $b_i$ for $i\in \{1,\dots ,k-n-1\}$. Lemma 2.3 implies $\theta \frac{p_1\left(\lambda \right)}{2}+(1-\theta )p_2\left(\lambda \right)$has exactly one zero in each $A_i$. Hence, all zeros of $D_1(\lambda ,g_{\theta })$ lie on $S^1$ and the zeros of $D_1(\lambda ,g_{\theta })$ alternate with the zeros of $D_2(\lambda ,g_{\theta })$ for all $\theta \in (0,1)$. By Theorem 2.2, all zeros of $g_{\theta }\left(\lambda \right)$ are in the interior of the unit disc for all $\theta \in (0,1)$.

Case III: k and n are even numbers.

In this case, σ, $k-\sigma$, and k−n are even numbers, and we have $\begin{array}{rl}{D}_1(\lambda ,g_{\theta })& =\theta \frac{(\lambda +1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}+(1-\theta )\frac{{\lambda }^k-1}{{\lambda }^n-1}\\ D_2(\lambda ,g_{\theta })& =\theta \frac{(\lambda -1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{2(\lambda -1)({\lambda }^n-1)}.\end{array}$Let $p_1\left(\lambda \right)=\frac{(\lambda +1)({\lambda }^{\sigma }-1)({\lambda }^{k-\sigma }-1)}{(\lambda -1)({\lambda }^n-1)}\text{ and}{p}_2\left(\lambda \right)=\frac{{\lambda }^k-1}{{\lambda }^n-1}.$Note that $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have all zeros on $S^1$ and they have no common zeros. Both $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have the same degree k−n, which is an even number. We write $\begin{array}{rl}{p}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k-n}),\\ \text{ and}{p}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k-n}),\end{array}$where $b_{\frac{k-n}{2}}=-1=b_{\frac{k-n+2}{2}}$, $c_j\notin \{-1,1\}$, $b_i\ne c_j$ $(1\le i,j\le k-n)$, and $\begin{array}{rl}& 0<\arg \left(b_i\right)\le \arg \left(b_I\right)<2\pi ,\\ & 0<\arg \left(c_i\right)\le \arg \left(c_I\right)<2\pi ,\end{array}$for $1\le i<I\le k-n$. Now, let $A_i$ be the smaller arc of $S^1$ bounded by $c_i$ and $b_i$ for $i\in \{1,\dots ,k-n\}$. Then, $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{k-n-i+1}$ ($i=1,\dots ,k-n$). Lemma 2.3 implies that $D_1(\lambda ,g_{\theta })=\theta \frac{p_1\left(\lambda \right)}{2}+(1-\theta )p_2\left(\lambda \right)$has exactly one zero in each $A_i(i=1,\dots ,k-n)$. Hence, all zeros of $D_1(\lambda ,f_{\theta })$ lie on $S^1$ and the zeros of $D_1(\lambda ,g_{\theta })$ alternate with the zeros of $D_2(\lambda ,g_{\theta })$ for all $\theta \in (0,1)$. Therefore, all zeros of $g_{\theta }\left(\lambda \right)$ are in the interior of the unit disc for all $\theta \in (0,1)$.

We prove the following lemma to investigate stability of the boundary sub-triangles corresponding to order of events $\mathbf{s}\mathbf{r}\mathbf{1}$.

Lemma 3.5

Let k and σ be positive integer satisfying $1\le \sigma \le k$ and let $n=gcd(k,k-\sigma +1)$ and $m=gcd(k,\sigma )$, where k + 1−n−m is an even number. Let $p_1\left(\lambda \right)=\frac{({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{({\lambda }^n-1)({\lambda }^m-1)}\text{ and}{p}_2\left(\lambda \right)=\frac{({\lambda }^k-1)(\lambda -1)}{({\lambda }^n-1)({\lambda }^m-1)}.$If $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have no common zeros and $-1,1$ are not their zeros, then the function $h_{\theta }\left(\lambda \right):=\theta p_1\left(\lambda \right)+(1-\theta )p_2\left(\lambda \right)$has all zeros on the unit disc for all $\theta \in (0,1)\cup (-1,0)$.

Proof.

We write $\begin{array}{rl}{p}_1\left(\lambda \right)& =(\lambda -b_1)(\lambda -b_2)\cdots (\lambda -b_{k+1-n-m}),\\ \text{ and}{p}_2\left(\lambda \right)& =(\lambda -c_1)(\lambda -c_2)\cdots (\lambda -c_{k+1-n-m}),\end{array}$where $b_i,c_j\notin \{-1,1\}$, $b_i\ne c_j$ $(1\le i,j\le k-n)$, and $\begin{array}{rl}0& <\arg \left(b_i\right)\le \arg \left(b_I\right)<2\pi ,\\ 0& <\arg \left(c_i\right)\le \arg \left(c_I\right)<2\pi ,\end{array}$for $1\le i<I\le k+1-n-m$. Now, let $A_i$ be the smaller arc of $S^1$ bounded by $c_i$ and $b_i$ for $i\in \{1,\dots ,k+1-n-m\}$. Then, $A_i$ are disjoint and each element of $A_i$ has a complex conjugate in $A_{k-n-m-i+2}$ for $i=1,\dots ,k+1-n-m$. If $\theta \in (0,1)\cup (-1,0)$, Lemma 2.3 implies that $h_{\theta }\left(\lambda \right)$ has exactly one zero in each $A_i$ for $i=1,\dots ,k+1-n-m$. Hence, all zeros of $h_{\theta }\left(\lambda \right)$ lie on $S^1$.

Theorem 3.6

For negative feedback with order of events $\mathbf{s}\mathbf{r}\mathbf{1}$ and $k\ge 2$, all boundary sub-triangles ${\mathrm{△}}_{\mathbf{s}}(1,\sigma ,k)$, ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ and ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\sigma ,k)$, $1\le \sigma \le k$ are neutrally stable. In particular, all eigenvalues of $D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}$ for these triangles lie on the unit circle, $|\lambda |=1$.

Proof.

If we substitute $\sigma =1$ or $\rho =k$ in (11(11) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega {\lambda }^{\rho -\sigma +1}\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\rho }-1}{\lambda -1}\right),\end{array}$(11) ), the left-hand side of (11(11) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega {\lambda }^{\rho -\sigma +1}\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\rho }-1}{\lambda -1}\right),\end{array}$(11) ) becomes zero. Thus the eigenvalues of $D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}$ for the regions ${\mathrm{△}}_{\mathbf{s}}(1,\sigma ,k)$ and ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ satisfy $\frac{{\lambda }^k-1}{\lambda -1}=0.$Thus all eigenvalues of $D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}$ for ${\mathrm{△}}_{\mathbf{s}}(1,\sigma ,k)$ and ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ lie on the unit circle. Hence, ${\mathrm{△}}_{\mathbf{s}}(1,\sigma ,k)$ and ${\mathrm{△}}_{\mathbf{s}}(\sigma ,k,k)$ are neutrally stable.

Next, let $\theta =-\omega$. By substituting $\rho =\sigma$ in (11(11) $\begin{array}{r}\frac{{\lambda }^k-1}{\lambda -1}=\omega {\lambda }^{\rho -\sigma +1}\left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\rho }-1}{\lambda -1}\right),\end{array}$(11) ), we obtain that the eigenvalues of $D{F}_{\mathbf{s}\mathbf{r}\mathbf{1}}$ for sub-triangle ${\mathrm{△}}_{\mathbf{s}}(\sigma ,\sigma ,k)$ satisfy (33) $\begin{array}{r}P\left(\lambda \right):=\frac{{\lambda }^k-1}{\lambda -1}+\theta \lambda \left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right)=0.\end{array}$(33) Then, $\begin{array}{rl}P\left(\lambda \right)& =\frac{{\lambda }^k-1}{\lambda -1}+\theta \frac{{\lambda }^k-{\lambda }^{\sigma }-{\lambda }^{k-\sigma +1}+\lambda +{\lambda }^{k+1}-{\lambda }^{k+1}+1-1}{(\lambda -1{)}^2}\\ & =\frac{{\lambda }^k-1}{\lambda -1}+\theta \frac{-({\lambda }^k-1)(\lambda -1)+({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{(\lambda -1{)}^2}\\ & =(1-\theta )\left(\frac{{\lambda }^k-1}{\lambda -1}\right)+\theta \frac{({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{(\lambda -1{)}^2}.\end{array}$Let $n=gcd(k,k-\sigma +1)$ and $m=gcd(k,\sigma )$. Then, $P\left(\lambda \right)=\left(\frac{{\lambda }^n-1}{\lambda -1}\right)\left(\frac{{\lambda }^m-1}{\lambda -1}\right)\left(\theta \frac{({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{({\lambda }^n-1)({\lambda }^m-1)}+(1-\theta )\frac{({\lambda }^k-1)(\lambda -1)}{({\lambda }^n-1)({\lambda }^m-1)}\right).$If $gcd(k,k-\sigma +1,\sigma )=q$, then there are $i_1,i_2,i_3\in \mathbb{N}$ such that $k=i_{1}q$, $k-\sigma +1=i_{2}q$, and $\sigma =i_{3}q$. Then, $k+1=(i_2+i_3)q$, so $1=(i_2+i_3-i_1)q$. Thus q = 1. Hence, $gcd(n,m)=1$. We claim that $P_{\theta }\left(\lambda \right)=\theta \frac{({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{({\lambda }^n-1)({\lambda }^m-1)}+(1-\theta )\frac{({\lambda }^k-1)(\lambda -1)}{({\lambda }^n-1)({\lambda }^m-1)}$has all zeros on the unit disc. There are three possible cases for the variables $k,\sigma ,k-\sigma +1,n$ and m as follows:

• k is odd. This case n, m, σ and $k-\sigma +1$ are odd numbers.

• k is even and n is odd. Since $n=gcd(k,k-\sigma +1)$ and n is odd, we have that $k-\sigma +1$ is odd. Then, σ is even. Since $m=gcd(k,\sigma )$, it follows that m is even. In this case, $k,\sigma ,m$ are even numbers and $n,k-\sigma +1$ are odd numbers.

• k and n are even. Since $gcd(n,m)=1$ and n is even, it follows that m is odd. Then, σ is odd due to $m=gcd(k,\sigma )$ and k is even. We then get that $k-\sigma +1$ is odd. In this case, k and n are even numbers and $m,\sigma ,k-\sigma +1$ are odd numbers.

Let $p_1\left(\lambda \right)=\frac{({\lambda }^{k-\sigma +1}-1)({\lambda }^{\sigma }-1)}{({\lambda }^n-1)({\lambda }^m-1)}\text{ and}{p}_2\left(\lambda \right)=\frac{({\lambda }^k-1)(\lambda -1)}{({\lambda }^n-1)({\lambda }^m-1)}.$Case I: k, n, m, σ and $k-\sigma +1$ are odd numbers.

In this case, we obtain that k + 1−n−m is an even number. Moreover, $p_1\left(\lambda \right)$ and $p_2\left(\lambda \right)$ have no common zeros and $-1,1$ are not their zeros. By Lemma 3.5, all zeros of $P_{\theta }\left(\lambda \right)$ lie on $S^1$.

Case II: $k,\sigma ,m$ are even numbers and $n,k-\sigma +1$ are odd numbers.

By Lemma 3.5, all zeros of $P_{\theta }\left(\lambda \right)$ lie on $S^1$.

Case III: k and n are even numbers and $m,\sigma ,k-\sigma +1$ are odd numbers.

By Lemma 3.5, all zeros of $P_{\theta }\left(\lambda \right)$ lie on $S^1$.

From this proof, we also get the following corollary:

Corollary 3.7

Let k and σ be positive integers satisfying $1\le \sigma \le k$ and let $\theta \in (0,1)\cup (-1,0)$. The equation $\frac{{\lambda }^k-1}{\lambda -1}+\theta \lambda \left(\frac{{\lambda }^{\sigma -1}-1}{\lambda -1}\right)\left(\frac{{\lambda }^{k-\sigma }-1}{\lambda -1}\right)=0$has all solutions on the unit disc.

Thus we have neutrality of $\mathbf{s}\mathbf{r}\mathbf{1}$ boundary triangles, not only for negative feedback but also for positive feedback, provided $\omega =({\text{β}}_{\sigma }-{\text{β}}_{\sigma -1})/(1+{\text{β}}_{\sigma -1})<1$.

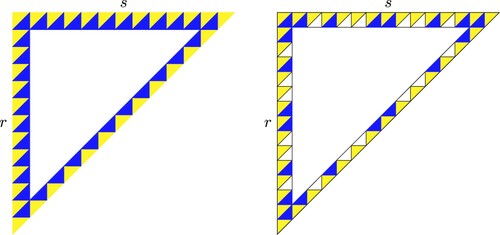
The results in this section identify the location of all asymptotically stable and neutrally stable regions for the boundary sub-triangles. See Figure 10 for an illustration.

Figure 10. Isosequential regions for k = 13 (left) and k = 15 (right) in the limit as ${\text{β}}_{\sigma }\to 0^{-}$. The yellow sub-triangles are neutrally stable by Theorem 3.6. The white sub-triangles are neutrally stable by Corollary 3.4. The blue sub-triangles are asymptotically stable by Theorems 3.1 and 3.3.

We illustrate stability regions of the boundary sub-triangles under negative feedback in Figures 11 and 12. For a given feedback function $f\left(I\right)$ and a given k, a program computes vertices of each boundary sub-triangle and uses the results in the previous section to check stability of each sub-triangle. The vertices of each sub-triangle can be computed by a formula presented in the next section.

Figure 11. Illustrations of stability of the boundary sub-triangles for the case of k = 10 with different feedback functions. The first row: feedback functions are $f\left(I\right)=-0.29I$ and $f\left(I\right)=-I$ respectively from the left. The second row: $f\left(I\right)=-0.4\sqrt{I}$ and $f\left(I\right)=-\sqrt{I}$. The blue shaded sub-triangles are stable and the white sub-triangles are neutral.

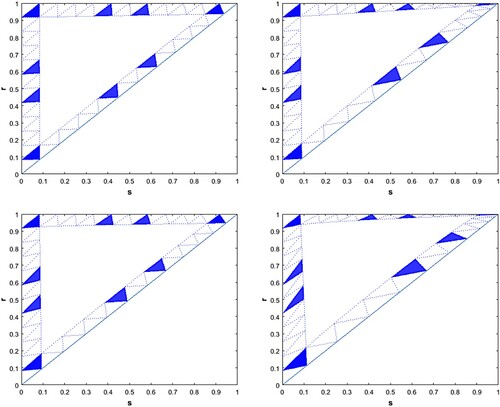
Figure 12. The left column: k = 23 (a prime number). The right column: k = 24 (a composite number). The feedback functions of the figures for each row are the same. The top row: $f\left(I\right)=-0.7I$. The middle row: $f\left(I\right)=-0.9I^2$. The last row: $f\left(I\right)=-\sqrt{I}$. The blue shaded sub-triangles are stable and the white sub-triangles are neutral.

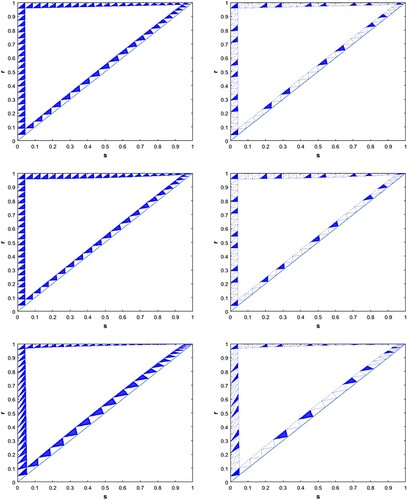
Figure 11 shows the stability of boundary sub-triangles of $\mathrm{△}$ for the case of k = 10 with different negative feedback functions.

In Figure 12, we show stability regions for the cases of k = 23 (prime) and k = 24 (composite) under the different negative feedback functions.

We see in these figures that for different feedback functions, the pattern of stability persists, while the sub-triangles become skewed.

4. The universality of cyclic solutions

In the previous section, we identified which boundary sub-triangles are (asymptotically) stable and which are neutral. In this section, we study how the sub-triangles fit together. For a given linear negative feedback, we prove that the interior of the $\mathrm{△}$ is covered by the asymptotically stable sub-triangles.

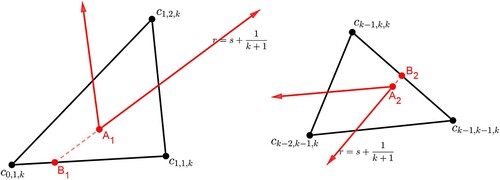
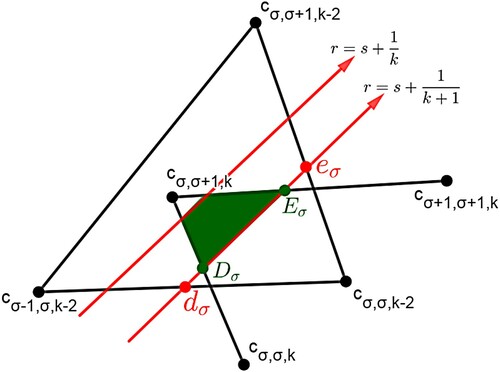
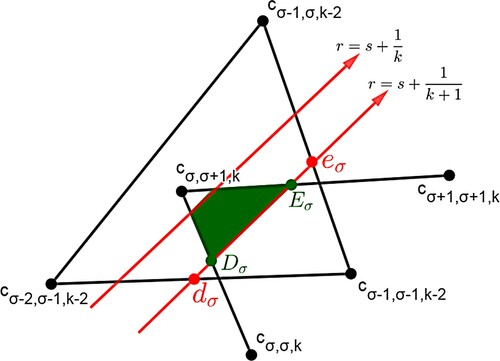
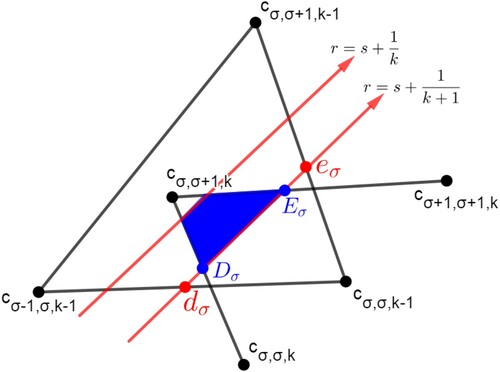
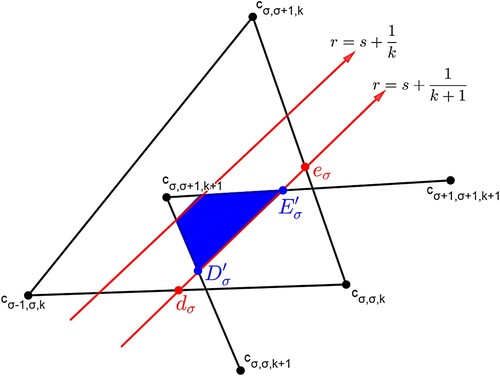
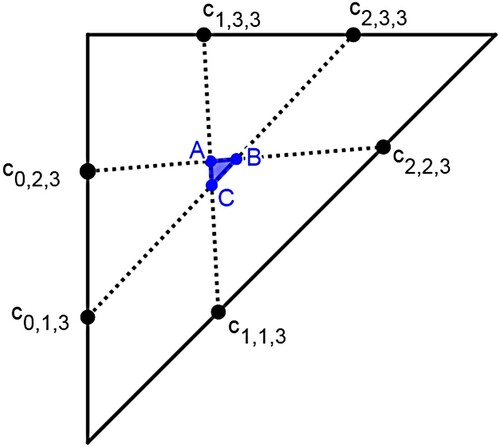
Previously, we saw that an isosequential region has a triangular shape inside $\mathrm{△}$ and its vertices are simultaneous points [5].

We first find the formula of each simultaneous point. A simultaneous point $c_{\sigma ,\rho ,k}$ is a point $(s,r)$ in $\mathrm{△}$ such that the k-cyclic solution corresponding to the point satisfies the following:

• it has events s, r, and 1 occurring simultaneously,

• the solution at the initial time has σ clusters in the S region and it has ρ clusters outside the R region.

Figure 13 illustrates the location of clusters at corner points of ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$.

Figure 13. Numbering of the corners of a sub-triangle ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$.

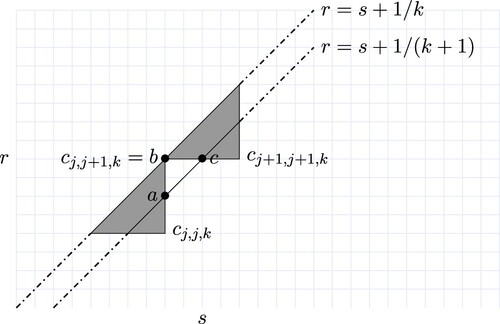
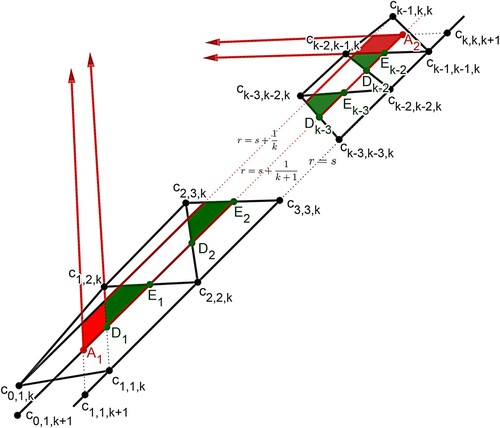
Let $\left\{\right(X_1\left(t\right),\dots ,X_k\left(t\right))|t\in {\mathbb{R}}^{+}\}$ be the k-cyclic solution that corresponds to $c_{\sigma ,\rho ,k}$. We will continue to use $x_i=X_i\left(0\right)$. Then, the k-cyclic solution at the initial time satisfies that $r=x_{\rho +1}$ and $s=x_{\sigma +1}$. The clusters outside the R region are equally distributed by a distance d (as in Definition 1.1 of k-cyclic solution) and the clusters inside the R region are equally distributed by a distance called $d^{\prime }$, see Figure 14. It follows that $\rho d+(k-p)d^{\prime }=1$. Note that distances outside of R correspond directly to time. Let $t_{\rho }$ be the time required for $X_{\rho }\left(t\right)$ to reach $r=x_{\rho +1}$ and $t_k$ be the time for $X_k\left(t\right)$ to reach 1. We will seek conditions for $t_{\rho }=t_k$. Recall that ${\text{β}}_{\sigma ,k}=f\left(\sigma /k\right)$. Thus $t_{\rho }=d\text{ and}{t}_k=\frac{1-x_k}{1+{\text{β}}_{\sigma ,k}}=\frac{d^{\prime }}{1+{\text{β}}_{\sigma ,k}}.$If we require $t_{\rho }=t_k$ and since $\rho d+(k-p)d^{\prime }=1$, we have $d=\frac{1}{k+{\text{β}}_{\sigma ,k}(k-\rho )}\text{ and}{d}^{\prime }=\frac{1+{\text{β}}_{\sigma ,k}}{k+{\text{β}}_{\sigma ,k}(k-\rho )}.$Thus (34) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=(x_{\sigma +1},x_{\rho +1})=(\sigma d,\rho d)=\left(\frac{\sigma }{k+{\text{β}}_{\sigma ,k}(k-\rho )},\frac{\rho }{k+{\text{β}}_{\sigma ,k}(k-\rho )}\right).\end{array}$(34) We now consider the case of no feedback, i.e. $f\left(I\right)=0$ for all I. We include this section in order to illustrate some of the main ideas of the proof of Theorem B in a context that is more clear.

Figure 14. The initial location of the k-cyclic solution corresponding to $c_{\sigma ,\rho ,k}$. Here, $r=x_{\rho +1}$ and $s=x_{\sigma +1}$. The distance between any two adjacent clusters outside the R region is d from Definition 1.1. The distance between any two adjacent clusters inside the R region is $d^{\prime }$. Note that $d^{\prime }<d$ because of negative feedback.

With zero feedback, events and isosequential regions are still defined. The formula of each simultaneous point, (34(34) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=(x_{\sigma +1},x_{\rho +1})=(\sigma d,\rho d)=\left(\frac{\sigma }{k+{\text{β}}_{\sigma ,k}(k-\rho )},\frac{\rho }{k+{\text{β}}_{\sigma ,k}(k-\rho )}\right).\end{array}$(34) ), for $f\equiv 0$ becomes simply (35) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k},\frac{\rho }{k}\right).\end{array}$(35)

Definition 4.1

Let k, σ and ρ be positive integers such that $1\le \sigma <k$ and $2\le \rho \le k$. A sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)$ is a relatively prime sub-triangle if $gcd(\rho -1,k)=1$. If $gcd(\sigma ,k)=1$, sub-triangles ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are also called relatively prime sub-triangles.

For nonzero negative feedback, relatively prime sub-triangles are the ones that are stable as shown in Theorems 3.1 and 3.3.

The next lemma is the main idea of the proof. It states that if a boundary triangle is not relatively stable, then it is included entirely inside a larger boundary triangle that is relatively prime. This idea is illustrated in Figure 16.

Figure 15. Left: ${\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)$, right: ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k}{l})$, and $m_i$ is the slope of each line.

Figure 16. An illustration of Lemma 4.2 for the case k = 12. Left: The boundary sub-triangles for the case of k = 12, where the blue sub-triangles are relatively prime and the white rs1 sub-triangles are not relatively prime. Right: The overlay of relatively prime sub-triangles for k = 2 (yellow), 3 (red), 4 (green) and 6 (black) over k = 12 (blue). The key feature is that these relatively prime sub-triangles perfectly cover the white rs1 boundary sub-triangles on the left.

Lemma 4.2

Let $f\equiv 0$ and $k\ge 3$. Let $2\le \sigma \le k-2$, $3\le \rho \le k-1$, $l=gcd(\rho -1,k)$, and $n=gcd(\sigma ,k)$. Then (36) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho -1}{l}+1,\frac{k}{l}\right),\end{array}$(36) (37) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n}\right),\end{array}$(37) (38) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n}\right).\end{array}$(38)

Proof.

First, we will prove (36(36) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho -1}{l}+1,\frac{k}{l}\right),\end{array}$(36) ). By (35(35) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k},\frac{\rho }{k}\right).\end{array}$(35) ), it follows that $c_{0,\rho -1,k}=(0,\frac{\rho -1}{k})=c_{0,\frac{\rho -1}{l},\frac{k}{l}}$.

In Figure 15, since the slope $m_1=1=m_3$ and $m_2=0=m_4$, it follows that ${\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)\subseteq {\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k}{l})$. Similarly, we can show that ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n}\right)$and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)\subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n}\right).$

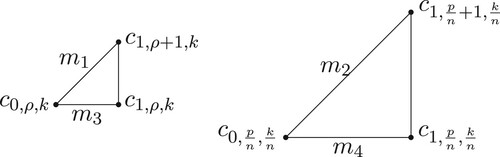
For the rest of this section, we assume zero feedback, $f\equiv 0$.

Note that ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k}{l})$, ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$ and ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n})$ are relatively prime sub-triangles. Figure 16 illustrates that all boundary sub-triangles corresponding to order of events rs1 for the case of k = 12 are covered by the relatively prime sub-triangles for $k\le 12$. In the figure,

• ${\mathrm{△}}_{\mathbf{r}}(6,12,12)\subseteq {\mathrm{△}}_{\mathbf{r}}(\frac{6}{6},\frac{12}{6},\frac{12}{6})={\mathrm{△}}_{\mathbf{r}}(1,2,2)$ (the yellow sub-triangle),

• ${\mathrm{△}}_{\mathbf{r}}(1,3,12)\subseteq {\mathrm{△}}_{\mathbf{r}}(1,\frac{3-1}{2}+1,\frac{12}{2})={\mathrm{△}}_{\mathbf{r}}(1,2,6)$ (a black sub-triangle),

• ${\mathrm{△}}_{\mathbf{r}}(3,3+1,12)\subseteq {\mathrm{△}}_{\mathbf{r}}(\frac{3}{3},\frac{3}{3}+1,\frac{12}{3})={\mathrm{△}}_{\mathbf{r}}(1,2,4)$ (a green sub-triangle).

Let $k\ge 3$ and let ${\mathrm{△}}_k$ be the triangle which has vertices $c_{1,2,k}$, $c_{1,k-1,k}$, $c_{k-2,k-1,k}$ (see Figure 17). Then, the following lemma is obvious.

Figure 17. The shaded triangle area is ${\mathrm{△}}_k$ for $k\ge 3$.

Lemma 4.3

Consider a zero feedback system. Let $(s,r)$ be a point in the parameter triangle $\mathrm{△}$. Then there exist a positive integer $k\ge 3$ and ${\mathrm{△}}_k$ such that the point $(s,r)$ is in the triangle ${\mathrm{△}}_k$.

Note here that the following statements hold for $2\le i\le k-1$:

• $c_{1,i,k}$ are on the line $r=\frac{1}{k}$,

• $c_{i-1,k-1,k}$ are on the line $s=\frac{k-1}{k}$,

• $c_{i-1,i,k}$ are on the line $r=s+\frac{1}{k}$,

The next lemma is the second important idea of the proof. We use induction on k to show that for each k, the ‘gap’ ${\mathrm{△}}_{k+1}\setminus {\mathrm{△}}_k$ is covered by relatively prime sub-triangles. Specifically, the gap is covered by boundary triangles of the form ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k-1)$. While not all of these triangles are relatively prime, they are all included perfectly in a larger relatively prime sub-triangle by Lemma 4.2.

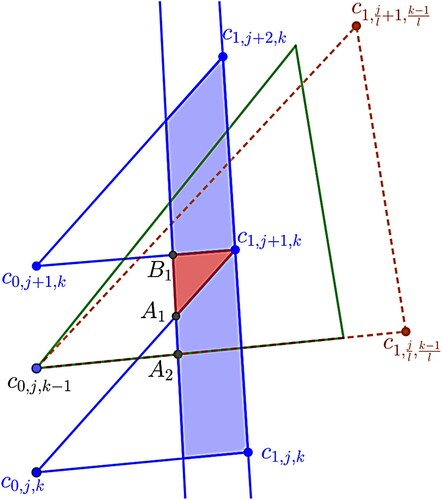
Lemma 4.4

Consider a zero feedback system. For a positive integer $k\ge 3$, ${\mathrm{△}}_k$ is covered by relatively prime sub-triangles.

Proof.

We prove this lemma by induction on k. For k = 3, ${\mathrm{△}}_3=\left\{c_{1,2,3}\right\}\subseteq \mathrm{△}(1,2,2)$ which is a relatively prime sub-triangle. Suppose that ${\mathrm{△}}_k$ is covered by relatively prime sub-triangles. It suffices to find a relatively prime covering of the gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$, that is the region ${\mathrm{△}}_{k+1}\setminus {\mathrm{△}}_k$. The gap can be considered as composed of the vertical, horizontal and diagonal gaps. First, we consider the vertical gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$. Let j be a positive integer such that $1\le j\le k-2$. Let A be the point on the lines $s=\frac{1}{k+1}$ and $r=s+\frac{j}{k}$ and B be the point on the lines $s=\frac{1}{k+1}$ and $r=\frac{j+1}{k}$, and C be the point on the lines $s=\frac{1}{k}$ and $r=\frac{j+1}{k}$. We will show below that $\mathrm{△}ABC$ is covered by the triangle ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k-1)$. See Figure 18 for a visualization of $\mathrm{△}ABC$.

Figure 18. The vertical gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$.

Note that, (39) $\begin{array}{r}\frac{j}{k}<\frac{j}{k-1}<\frac{j+1}{k}.\end{array}$(39) By the definition of points A, B and C, we get $A=\left(\frac{1}{k+1},\frac{kj+j+k}{k(k+1)}\right),B=\left(\frac{1}{k+1},\frac{j+1}{k}\right)\text{ and}C=\left(\frac{1}{k},\frac{j+1}{k}\right).$Moreover, the following inequalities hold: (40) $\begin{array}{r}\frac{j}{k-1}\le \frac{kj+j+k}{k(k+1)}.\end{array}$(40) This inequality implies that the r-coordinate of A is greater than or equal $j/(k-1)$. Since (41) $\begin{array}{r}1\ge \frac{(k-j-1)(k+1)}{k(k-1)},\end{array}$(41) it follows that the slope of line passing $j/(k-1)$ and B is less than or equal to 1. 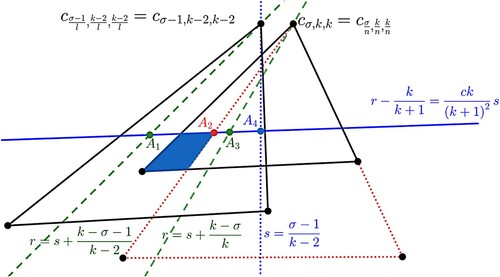Hence, (39(39) $\begin{array}{r}\frac{j}{k}<\frac{j}{k-1}<\frac{j+1}{k}.\end{array}$(39) ), (40(40) $\begin{array}{r}\frac{j}{k-1}\le \frac{kj+j+k}{k(k+1)}.\end{array}$(40) ), and (41(41) $\begin{array}{r}1\ge \frac{(k-j-1)(k+1)}{k(k-1)},\end{array}$(41) ) imply that $\mathrm{△}ABC$ is covered by the sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k-1)$, see Figure 19. 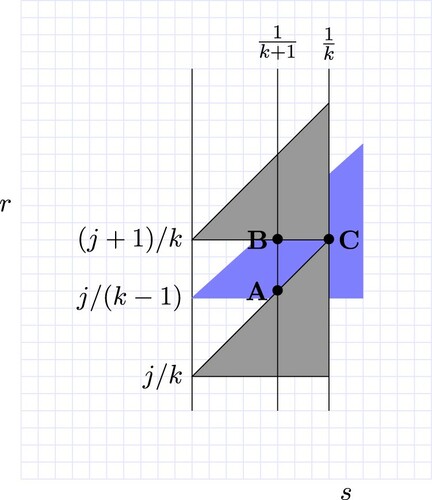Since ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k-1)$ is covered by relatively prime sub-triangle (see (36(36) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho -1}{l}+1,\frac{k}{l}\right),\end{array}$(36) ) in Lemma 4.2), the entire vertical gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$ is covered by relatively prime sub-triangles. A similar idea can be used for the horizontal gap.

Figure 19. $\mathrm{△}ABC$ is covered by the blue triangle ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k-1)$.

Next, we consider the oblique gap, the area inside $\mathrm{△}$ bounded above by $r=s+1/k$ and bounded below by $r=s+1/(k+1)$, see Figure 20. Let j be a positive integer such that $1\le j\le k-1$. Let a be the point on the lines $s=\frac{j}{k}$ and $r=s+\frac{1}{k}$ and b be the point on the lines $s=\frac{j}{k}$ and $r=\frac{j+1}{k}$, and c be the point on the lines $r=s+\frac{1}{k+1}$ and $r=\frac{j+1}{k}$. 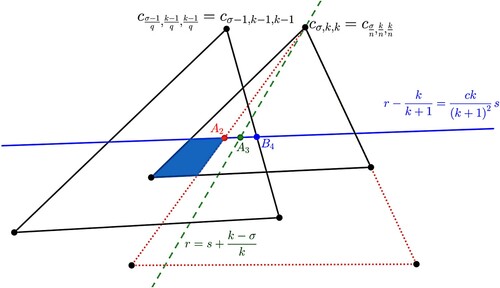We claim that $\mathrm{△}abc$ is covered by triangle ${\mathrm{△}}_{\mathbf{r}}(j,j+1,k-1)$. See Figure 20 as a visualization of $\mathrm{△}abc$. Note that (42) $\begin{array}{r}\frac{j}{k-1}\ge \frac{kj+j+1}{k(k+1)}.\end{array}$(42) We get the formulas for the point a, b, c as follows: $a=\left(\frac{j}{k},\frac{jk+j+k}{k(k+1)}\right),b=\left(\frac{j}{k},\frac{j+1}{k}\right),\text{ and}c=\left(\frac{jk+j+1}{k(k+1)},\frac{j+1}{k}\right).$Inequality (42(42) $\begin{array}{r}\frac{j}{k-1}\ge \frac{kj+j+1}{k(k+1)}.\end{array}$(42) ) implies that the s-coordinate of c is less than or equal to $j/(k-1)$. By inequality (40(40) $\begin{array}{r}\frac{j}{k-1}\le \frac{kj+j+k}{k(k+1)}.\end{array}$(40) ), we have that the r-coordinate of a is greater than or equal to $j/(k-1)$. Hence, $\mathrm{△}abc$ in Figure 20 is covered by triangle ${\mathrm{△}}_{\mathbf{r}}(j,j+1,k-1)$.

Figure 20. The oblique gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$.

Combining Lemmas 4.3 and 4.4, we get the following main theorem.

Theorem 4.5

Consider a zero feedback system. Let $(s,r)$ be a point in the parameter triangle $\mathrm{△}$. Then there exist a positive integer $k\ge 2$ such that the point $(s,r)$ is in the interior of a relatively prime sub-triangle with respect to the positive integer k.

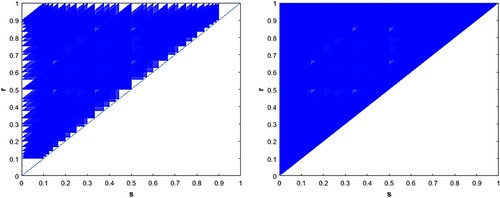
Figure 21 shows that the union of all relatively prime boundary sub-triangles for $2\le k\le 10$ (left panel) covers a large portion of the interior of $\mathrm{△}$ and for $2\le k\le 100$ nearly all of $\mathrm{△}$ is covered.

Figure 21. An overlay of all relatively prime sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\equiv 0$.

5. Covering under negative linear feedback

In this section, treat negative linear feedback function, $f\left(x\right)=-cx$ for $0<c\le 1$.

In the previous section, we have proved under the zero feedback that the parameter triangle $\mathrm{△}$ is covered by relatively prime sub-triangles. The main idea was that boundary sub-triangles that are not relatively prime are included perfectly in larger relatively prime sub-triangles. This fact was used to show that the gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$ is covered by a union of relatively prime sub-triangles.

The calculation here is more complicated since the right angle triangles in Section 4 become a scalene triangles under negative linear feedback and Equations (36(36) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho -1}{l}+1,\frac{k}{l}\right),\end{array}$(36) ) and (37(37) $\begin{array}{rl}{\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)& \subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n}\right),\end{array}$(37) ) in Lemma 4.2 no longer hold. Only the oblique boundary sub-triangles still have this property (Theorem 5.5). For vertical and horizontal sub-triangles, there are thin slices that are not covered by the same larger triangles as in the zero feedback case. The first technical difficulty is showing that these slices are in fact covered by other relatively prime sub-triangles (Lemma 5.9). The second difficulty is showing that these skewed sub-triangles fit together nicely to cover the gap, which is bounded by skewed lines (Lemma 5.10).

Using Equation (34(34) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=(x_{\sigma +1},x_{\rho +1})=(\sigma d,\rho d)=\left(\frac{\sigma }{k+{\text{β}}_{\sigma ,k}(k-\rho )},\frac{\rho }{k+{\text{β}}_{\sigma ,k}(k-\rho )}\right).\end{array}$(34) ), the formula for a simultaneous point $c_{\sigma ,\rho ,k}$ is as follows: (43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) From this formula, we obtain the following four propositions.

Proposition 5.1

Consider a negative linear feedback system. Let σ and k be positive integers such that $1\le \sigma \le k-1$. A simultaneous point $c_{\sigma ,i,k}=(s,r)$ for $i=\sigma ,\dots ,k$ is a point on the line $r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}\left(s-\frac{\sigma }{k}\right).$

This proposition provides the fact that all simultaneous points $c_{\sigma ,i,k}$ lie on the same line for fixed σ and $i=\sigma ,\dots ,k$, see Figure 22 (the black line).

Figure 22. Black line: simultaneous points $c_{\sigma ,i,k}$ ($i=\sigma ,\dots ,k$) lie on the same line. Blue line: simultaneous points $c_{i,\rho ,k}$ ($i=0,\dots ,\rho$) lie on the same line.

Proposition 5.2

Consider a negative linear feedback system. Let ρ and k be positive integers such that $1\le \rho \le k$. A simultaneous point $c_{i,\rho ,k}=(s,r)$ for $i=0,\dots ,\rho$ is a point on the line $r-\frac{\rho }{k}=\frac{c\rho (k-\rho )}{k^2}s.$

This proposition provides the fact that all simultaneous points $c_{i,\rho ,k}$ lie on the same line for fixed ρ and $i=0,\dots ,\rho$, see Figure 22 (the blue line).

Proposition 5.3

Consider a negative linear feedback system. Let ρ and k be positive integers such that $1\le \rho \le k-2$. The slope of the line passing through $c_{0,\rho ,k}$ and $c_{1,\rho +1,k}$ is greater than 1.

Proposition 5.4

Consider a negative linear feedback system. Let σ and k be positive integers such that $2\le \sigma \le k-1$. The slope of the line passing through $c_{\sigma -1,k-1,k}$ and $c_{\sigma ,k,k}$ is less than 1.

The next result clarifies that any oblique sub-triangle corresponding to the order of events rs1 is covered by stable sub-triangles.

Theorem 5.5

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. For any integer $k\ge 3$ and $2\le \sigma \le k-2$, ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)\subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n}\right)$where n is a divisor of σ and k.

Proof.

Let n be a positive divisor of σ and k. By (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), we get $c_{\sigma ,\sigma ,k}=c_{\frac{\sigma }{n},\frac{\sigma }{n},\frac{k}{n}}$. Let $m_1$ be the slope of the line connecting $c_{\sigma ,\sigma +1,k}$ and $c_{\sigma ,\sigma ,k}$, $m_2$ be the slope of the line connecting $c_{\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n}}$ and $c_{\frac{\sigma }{n},\frac{\sigma }{n},\frac{k}{n}}$, $m_3$ be the slope of the line connecting $c_{\sigma -1,\sigma ,k}$ and $c_{\sigma ,\sigma ,k}$, and $m_4$ be the slope of the line connecting $c_{\frac{\sigma }{n}-1,\frac{\sigma }{n},\frac{k}{n}}$ and $c_{\frac{\sigma }{n},\frac{\sigma }{n},\frac{k}{n}}$, see Figure 23. Using (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), the slopes $m_1$, $m_2$, $m_3$ and $m_4$ are as follows: $m_1=\frac{k^2-ck\sigma }{-c{\sigma }^2}=m_2$and $m_3=\frac{c\sigma (k-\sigma )}{k^2}=m_4.$Therefore, ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)\subseteq {\mathrm{△}}_{\mathbf{r}}\left(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n}\right).$

Figure 23. Left: ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$, right: ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{\sigma }{n}+1,\frac{k}{n})$.

Figure 24 is a visualization of Theorem 5.5 for the case of k = 12 and $f\left(I\right)=-0.8I$. The figure indicates that each oblique sub-triangle corresponding to the order of events rs1 for the case of k = 12 and $f\left(I\right)=-0.8I$ is exactly covered by a stable sub-triangle for some $k\le 12$.

Figure 24. An overlay of stable sub-triangles for k = 2 (yellow), 3 (red), 4 (green), 6 (black), 12 (blue) where the negative feedback $f\left(I\right)=-0.8I$. The oblique sub-triangles for the case of k = 12 are covered perfectly by stable sub-triangles of k = 2, 3, 4, 6. However, the vertical and horizontal sub-triangles for the case of k = 12 are only partially covered. Fully covering these missed slices is a main difficulty of the proof for non-zero feedback.

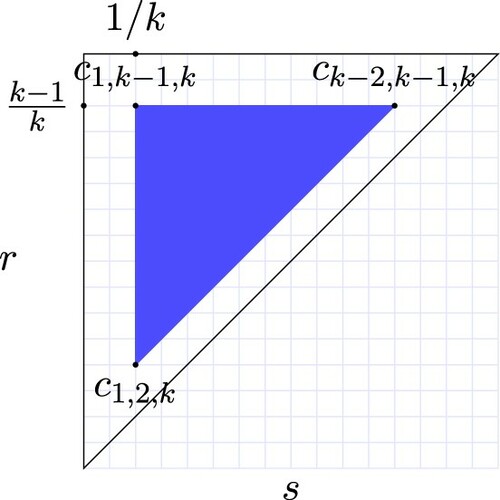
Definition 5.6

Let k be a positive integer such that $k\ge 2$. Define ${\mathrm{△}}_k$ to be the triangle bounded by three line segments defined as follows:

• the line passing through $c_{0,k-1,k}$ and $c_{k-1,k-1,k}$ (vertical boundary of ${\mathrm{△}}_k$),

• the line passing through $c_{1,k,k}$ and $c_{1,1,k}$ (horizontal boundary of ${\mathrm{△}}_k$),

• the line passing through $c_{0,1,k}$ to $c_{k-1,k,k}$ (oblique boundary of ${\mathrm{△}}_k$).

Figure 25 is a visualization of ${\mathrm{△}}_k$. For a negative linear feedback function $f\left(x\right)=-cx$ with $0<c\le 1$, the bounding lines in the sr-plane of the triangle ${\mathrm{△}}_k$ satisfy:

• $r-1=-k\left(\frac{k-c}{c}\right)(s-\frac{1}{k})$, vertical boundary,

• $r-\frac{k-1}{k}=\frac{c(k-1)}{k^2}s$, horizontal boundary,

• $r=s+\frac{1}{k}$, oblique boundary.

Figure 25. The blue shaded area is ${\mathrm{△}}_k$.

The next lemma deals with the gap along the vertical boundary.

Lemma 5.7

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. For $k\ge 4$ and $2\le \rho \le k-1$, the region ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}$ is covered by stable sub-triangles.

Proof.

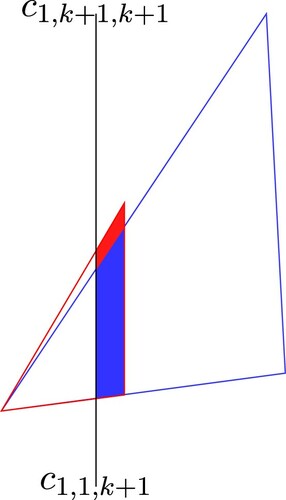
If $gcd(\rho ,k)=1$, then sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)$ is a stable sub-triangle by Theorem 3.3. Thus the theorem holds. Assume that $gcd(\rho ,k)=n>1$. Let $l_1,l_2,l_3,l_4$, and $l_5$ be the lines as follows:

• $l_1$ is the line passing through $c_{0,\rho ,k}$ and $c_{1,\rho +1,k}$,

• $l_2$ is the line passing through $c_{0,\frac{\rho }{n},\frac{k}{n}}$ and $c_{0,\frac{\rho }{n}+1,\frac{k}{n}}$,

• $l_3$ is the line passing through $c_{0,\rho ,k}$ and $c_{1,\rho ,k}$,

• $l_4$ is the line passing through $c_{0,\frac{\rho }{k},\frac{k}{n}}$ and $c_{0,\frac{\rho }{k},\frac{k}{n}}$,

• $l_5$ is the line passing through $c_{1,k+1,k+1}$ and $c_{1,1,k+1}$.

Let $m_1,\dots ,m_4$ be the slopes of $l_1,\dots ,l_4$, respectively, see Figure 26.

Figure 26. Left: ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)$, right: ${\mathrm{△}}_{\mathbf{r}}(1,\frac{p}{n}+1,\frac{k}{n})$.

Note that $c_{0,\rho ,k}=c_{0,\frac{\rho }{n},\frac{k}{n}}$. By (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), $m_1=1+\frac{\rho c(k-\rho -1)}{k^2}$, $m_2=1+\frac{\rho c(k-\rho -n)}{k^2}$ and $m_3=\frac{\rho c(k-\rho )}{k^2}=m_4$. Then $m_1\ge m_2$. Hence, ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}$ is partially covered by stable sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\frac{p}{n}+1,\frac{k}{n})$. Specifically, ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}$ can be considered as having two distinct parts; the part that intersects ${\mathrm{△}}_{\mathbf{r}}(1,\frac{p}{n}+1,\frac{k}{n})$ (the blue shaded area in Figure 27) and the part that intersects ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\mathrm{\setminus }{\mathrm{△}}_{\mathbf{r}}(1,\frac{p}{n}+1,\frac{k}{n})$ (the red shaded region in Figure 27). The blue shaded area is covered by the stable triangle ${\mathrm{△}}_{\mathbf{r}}(1,\frac{p}{n}+1,\frac{k}{n})$. We claim that the red shaded area is covered by another stable sub-triangle. There are two cases depending on ρ to show that the red shaded area in Figure 27 is covered by a stable sub-triangle.

Figure 27. Red triangle: ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)$, blue: ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho }{n}+1,\frac{k}{n})$, black vertical line: the vertical boundary of ${\mathrm{△}}_{k+1}$. The union of the blue- and red shaded regions is ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}$.

Case I: $2\le \rho \le \frac{2}{3}(k-1)$.

Consider sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho }{m}+1,\frac{k-1}{m})$ where $gcd(k-1,\rho )=m$. We claim that the red shaded area is a subset of ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho }{m}+1,\frac{k-1}{m})$.

Let $l_6,l_7$ and $l_8$ be the following lines:

• $l_6$ is the line passing through $c_{0,\frac{\rho }{m},\frac{k-1}{m}}$ and $c_{1,\frac{\rho }{m}+1,\frac{k-1}{m}}$,

• $l_7$ is the line passing through $c_{0,\frac{\rho }{m},\frac{k-1}{m}}$ and $c_{1,\rho +1,k}$,

• $l_8$ is the line passing through $c_{0,\frac{\rho }{m},\frac{k-1}{m}}$ and $c_{1,\frac{\rho }{m},\frac{k-1}{m}}$.

Let $m_6,m_7,m_8$ be the slopes of $l_6,l_7,l_8$, respectively, see Figure 28. Let A be the crossing point between $l_2$ and $l_5$ and let B be the crossing point between $l_5$ and $l_8$, see Figure 28.

Figure 28. Sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho }{m}+1,\frac{k-1}{m})$. The upper black dot is point A and the lower black dot is B.

To get the claim, we need to show that ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k-2}{l})$ and the r-coordinate of A is greater than the r-coordinate of B. By (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), the slopes of $c_{0,\frac{\rho -1}{l},\frac{k-2}{l}}$, $c_{1,\frac{\rho -1}{l},\frac{k-2}{l}}$ and $m_8<m_7<m_6$ are as follows: $m_6$It follows that $m_7$. The point A is the solution of the systems $m_8$Then, the r-coordinate of A is (44) $\begin{array}{rl}{m}_6& =1+\frac{\rho c(k-1-\rho -m)}{(k-1{)}^2},\\ m_7& =1-\frac{\rho [k-c(k-1-\rho \left)\right]}{k(k-1)}\text{ and}{m}_8=\frac{\rho c(k-1-\rho )}{(k-1{)}^2}.\end{array}$(44) The point B is the solution of the systems $m_8\le m_7\le m_6$Then, the r-coordinate of B is $r-1=\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right)\text{ and}r-\frac{\rho }{k}=\left(1+\frac{\rho c(k-\rho -n)}{k^2}\right)s.$We claim that $\begin{array}{r}{r}_A=1+\frac{(k+1-c)(k+1)\left[\frac{k^2+\rho c(k-\rho -n)}{k+1}-k(k-\rho )\right]}{c{k}^2+\rho c^2(k-\rho -n)+(k+1-c)(k+1)(k{)}^2}.\end{array}$. By simplification, it is equivalent to show that (45) $r-1=\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right)\text{ and}r-\frac{\rho }{k-1}=\frac{\rho c(k-\rho -1)}{(k-1{)}^2}s.$(45) Since $r_B=1+\frac{(k+1-c)(k+1)\left[\frac{\rho c(k-\rho -1)}{k+1}-(k-1)(k-\rho -1)\right]}{\rho c^2(k-\rho -1)+(k+1-c)(k+1)(k-1{)}^2}.$ and $r_A-r_B>0$, the inequality (46) $\begin{array}{r}(k-\rho -1)\left[\right(k-1\left)\right(k^2-\rho cn)-\rho c(k-\rho )-(k+1-c\left)k^2\rho \right]\\ +\frac{k+1-c}{c}\left[\right(k-1{)}^2{k}^2-\rho k(k^2-1)]+(k+1-c\left)\right(k-1{)}^2\rho (k-\rho -n)>0\end{array}$(46) implies the inequality (45(45) $r-1=\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right)\text{ and}r-\frac{\rho }{k-1}=\frac{\rho c(k-\rho -1)}{(k-1{)}^2}s.$(45) ). Note that $\rho \le \frac{2}{3}(k-1)$, so $k-p-1\ge \frac{k-1}{3}$. Then, (47) $\begin{array}{r}{k}^{2}c-\frac{2}{3}(k-1)c^2(n-\frac{2}{3})-\frac{2}{3}{c}^{2}k+(k+1-c)\left[k^2\left(1-\frac{2}{3}c\right)-2k\right]>0\end{array}$(47) implies the previous inequality. The left-hand side of the inequality (47(47) $\begin{array}{r}{k}^{2}c-\frac{2}{3}(k-1)c^2(n-\frac{2}{3})-\frac{2}{3}{c}^{2}k+(k+1-c)\left[k^2\left(1-\frac{2}{3}c\right)-2k\right]>0\end{array}$(47) ) can be considered as a quadratic polynomial $n=gcd(\rho ,k)\le \frac{k}{2}$with variable c and fixed k. Then, the following properties hold:

• coefficient of $n-\frac{2}{3}\le \frac{k}{2}-\frac{2}{3}$ is nonnegative,

• slope of the polynomial is negative at c = 0 and 1,

• the values of the function are positive at c = 0 and 1.

Since $\begin{array}{r}\left(\frac{k-4}{9}\right)c^2+\left(2k-\frac{2}{3}(k+1)k^2\right)c+k^3-k^2-2k>0\end{array}$, the inequality (47(47) $\begin{array}{r}{k}^{2}c-\frac{2}{3}(k-1)c^2(n-\frac{2}{3})-\frac{2}{3}{c}^{2}k+(k+1-c)\left[k^2\left(1-\frac{2}{3}c\right)-2k\right]>0\end{array}$(47) ) holds. We get the claim $\left(\frac{k-4}{9}\right)c^2+\left(2k-\frac{2}{3}(k+1)k^2\right)c+k^3-k^2-2k$. Hence, $c^2$where $0<c\le 1$ and $r_A-r_B>0$.

Case II: ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}\subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho }{n}+1,\frac{k}{n}\right)\cup {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho }{m}+1,\frac{k-1}{m}\right),$.

In this case, we construct a sub-triangle $gcd(\rho ,k)=n$ where $gcd(k-1,\rho )=m$. We claim that the red shaded area is a subset of $\frac{2}{3}(k-1)\le \rho \le k-1$. Let D be the line ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k-2}{l})$ and the line passing through $gcd(k-2,\rho -1)=l$ and ${\mathrm{△}}_{\mathbf{r}}(1,\frac{\rho -1}{l}+1,\frac{k-2}{l})$. Let $l_5$ and $c_{0,\frac{\rho -1}{l},\frac{k-2}{l}}$ be slopes of the lines as follows:

• $c_{1,\frac{\rho -1}{l},\frac{k-2}{l}}$ is the slope of the line passing through $m_9,m_{10}$ and $m_{11}$,

• $m_9$ is the slope of the line passing through $c_{0,\frac{\rho -1}{l},\frac{k-2}{l}}$ and $c_{1,\frac{\rho -1}{l}+1,\frac{k-2}{l}}$,

• $m_{10}$ is the slope of the line passing through $c_{0,\frac{\rho -1}{l},\frac{k-2}{l}}$ and $c_{1,\rho +1,k}$,

see Figure 29. We need to show that $m_{11}$ and the r-coordinate of A is greater than the r-coordinate of D. By the simultaneous points formula (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), $c_{0,\frac{\rho -1}{l},\frac{k-2}{l}}$and $c_{1,\frac{\rho -1}{l}+1,\frac{k-2}{l}}$It follows that $m_{11}<m_{10}<m_9$. Note that the formula for the r-coordinate of A is given by (44(44) $\begin{array}{rl}{m}_6& =1+\frac{\rho c(k-1-\rho -m)}{(k-1{)}^2},\\ m_7& =1-\frac{\rho [k-c(k-1-\rho \left)\right]}{k(k-1)}\text{ and}{m}_8=\frac{\rho c(k-1-\rho )}{(k-1{)}^2}.\end{array}$(44) ). The point D is the solution of the systems $m_9=1+\frac{(\rho -1)c(k-\rho -1-l)}{(k-2{)}^2},m_{10}=1+\frac{k^2-2k\rho +c(\rho -1)(k-\rho -1)}{k(k-2)},$Thus the r-coordinate of D is $m_{11}=\frac{(\rho -1)c(k-\rho -1)}{(k-2{)}^2}.$We claim that $m_{11}<m_{10}<m_9$. By simplification, it is equivalent to show that (48) $r-1=\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right)\text{ and}r-\frac{\rho -1}{k-2}=\frac{c(\rho -1)(k-\rho -1)}{(k-2{)}^2}s.$(48) Since $r_D=1+\frac{(k+1-c)(k+1)[\frac{c(\rho -1)(k-\rho -1)}{k+1}-(k-2\left)\right(k-\rho -1\left)\right]}{c^2(\rho -1)(k-\rho -1)+(k+1-c)(k+1)(k-2{)}^2}.$, it suffices to show that $r_A-r_D\ge 0$Note that $\begin{array}{rl}& (k+1-c)\\ & \times \left[\frac{k(k-2)}{c}(2k^2-k-2k\rho -2\rho )+\rho (k-\rho -n)(k-2{)}^2-k^2(\rho -1\left)\right(k-\rho -1)\right]\\ & +(k-\rho -1)\left[\right(k-2\left)\right(k^2+\rho c(k-\rho -n))-k(k-\rho \left)c\right(\rho -1\left)\right]\ge 0.\end{array}$, it is enough to show (49) $(k-\rho -1)\left[\right(k-2\left)\right(k^2+\rho c(k-\rho -n))-k(k-\rho \left)c\right(\rho -1\left)\right]\ge 0$(49) The inequality (49(49) $(k-\rho -1)\left[\right(k-2\left)\right(k^2+\rho c(k-\rho -n))-k(k-\rho \left)c\right(\rho -1\left)\right]\ge 0$(49) ) holds when c = 0. For c = 1, since $\frac{k(k-2)}{c}(2k^2-k-2k\rho -2\rho )+\rho (k-\rho -n)(k-2{)}^2-k^2(\rho -1\left)\right(k-\rho -1)\ge 0.$, we get $k-\rho -n\ge 0$Since the left-hand side of (49(49) $(k-\rho -1)\left[\right(k-2\left)\right(k^2+\rho c(k-\rho -n))-k(k-\rho \left)c\right(\rho -1\left)\right]\ge 0$(49) ) can be considered as a linear function of variable c, the inequality (49(49) $(k-\rho -1)\left[\right(k-2\left)\right(k^2+\rho c(k-\rho -n))-k(k-\rho \left)c\right(\rho -1\left)\right]\ge 0$(49) ) holds for $\begin{array}{r}(k-2)(2k^2-k-2k\rho -2\rho )-ck(\rho -1)(k-\rho -1)\ge 0.\end{array}$, i.e. $\frac{2}{3}(k-1)\le \rho \le k-1$. Therefore, $\begin{array}{rl}0& \le (k-2)(k+4)-\frac{(2k-5)(k-1)}{9},\\ & \le (k-2)(2k^2-k-2k\rho -2\rho )-k(\rho -1)(k-\rho -1).\end{array}$where $0<c\le 1$ and $r_A-r_D\ge 0$.

Figure 29. Sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,\rho +1,k)\cap {\mathrm{△}}_{k+1}\subseteq {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho }{n}+1,\frac{k}{n}\right)\cup {\mathrm{△}}_{\mathbf{r}}\left(1,\frac{\rho -1}{l}+1,\frac{k-2}{l}\right),$ and three lineslopes, m₉, m₁₀ and m₁₁. The upper blue dot is point A (same point as in Figure 28). The lower black dot is point D, the crossing point between two lines: theline l₅ and the line passing through $gcd(\rho ,k)=n$ and$gcd(k-2,\rho -1)=l$.

The following result addresses the gap along the horizontal boundary.

Lemma 5.8

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. For $k\ge 4$ and $2\le \sigma \le k-1$, ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}$ is covered by stable sub-triangles.

Proof.

Let $n=gcd(\sigma ,k)$, $l=gcd(\sigma -1,k-2)$, and $q=gcd(\sigma -1,k-1)$. We consider ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}$ as having two distinct parts; the part that intersects ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$ and the part that intersects ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\mathrm{\setminus }{\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$. Since ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$ is stable by Theorem 3.3, we need to show that ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}\cap {\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\mathrm{\setminus }{\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$ (the blue shaded region in Figure 30) is covered by a stable sub-triangle. The proof will be separated into two cases, $2\le \sigma \le \frac{k}{5}$ and $\frac{k}{5}\le \sigma \le k-1$.

Figure 30. Case I: $2\le \sigma \le k/5$. Blue shaded region is ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}\cap {\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\mathrm{\setminus }{\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$. The red triangle is ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$.

Case I: $2\le \sigma \le k/5$. Let $A_1,A_2,A_3$, and $A_4$ be the following points:

• $A_1$ is the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $r=s+\frac{k-\sigma -1}{k-2}$,

• $A_2$ is the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and the line passing through $c_{\sigma ,k,k}$ and $c_{\frac{\sigma }{n}-1,\frac{k}{n}-1,\frac{k}{n}}$,

• $A_3$ is the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $r=s+\frac{k-\sigma }{k}$,

• $A_4$ is the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $s=\frac{\sigma -1}{k-2}$.

Note that the left boundary of each ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma -1}{l},\frac{k-2}{l},\frac{k-2}{l})$ and ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{n},\frac{k}{n},\frac{k}{n})$ has slope less than 1 by Proposition 5.4. To prove the claim that the blue region in Figure 30 is a subset of ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma -1}{l},\frac{k-2}{l},\frac{k-2}{l})$, it suffices to compare the s-coordinates of points $A_1$, $A_3$ and $A_4$, i.e. show that $s_{A_1}<s_{A_3}<s_{A_4}=\frac{\sigma -1}{k-2}.$Figure 30 is a visualization of the claim.

By the definitions of the points $A_1$ and $A_3$, we get $s_{A_1}=\frac{(k\sigma -2k+\sigma +1)(k+1)}{\left(\right(k+1{)}^2-ck\left)\right(k-2)}\text{ and}{s}_{A_3}=\frac{(k\sigma -k+\sigma )(k+1)}{\left(\right(k+1{)}^2-ck)k}.$It follows that $s_{A_1}<s_{A_3}$ for $2\le \sigma \le k/5$. Since $\frac{(k\sigma -k+\sigma )(k+1)}{\left(\right(k+1{)}^2-ck)k}<\frac{(k\sigma -k+\sigma )(k+1)}{\left(\right(k+1{)}^2-k)k}<\frac{\sigma -1}{k-2},$we get $s_{A_3}<\frac{\sigma -1}{k-2}.$Case II: $k/5\le \sigma \le k-1$. In this case, we claim that the blue region in Figure 30 is covered by ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma -1}{q},\frac{k-1}{q},\frac{k-1}{q})$. Let $B_4$ be the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and the line passing through $c_{\sigma -1,k-1,k-1}$ and $c_{\frac{\sigma -1}{q},\frac{k-1}{q}-1,\frac{k-1}{q}}$. We claim that the s-coordinate of point $A_3$ is less than the s-coordinate of point $B_4$. Figure 31 is a visualization of this claim. By Proposition 5.1 and the definition of $B_4$, we get $s_{B_4}=\frac{(k^2-1-c(\sigma -1\left)k\right)(\sigma -1)(k+1)}{c^{2}k(\sigma -1{)}^2+(k^2-1{)}^2-c(\sigma -1)(k-1)(k+1{)}^2}.$Let $A=c^{2}k(\sigma -1{)}^2+(k^2-1{)}^2-c(\sigma -1)(k-1)(k+1{)}^2-(k^2-1-c(\sigma -1)k\left)\right((k+1{)}^2-ck)$. Then, $\begin{array}{rl}A& =-2(k^2-1)(k+1)+c(k+1)\left(k\right(k-1)+(\sigma -1\left)\right(k+1\left)\right)\\ & -c^{2}k(\sigma -1)(k-\sigma +1)\\ & <-2(k^2-1)(k+1)+c(k+1)\left(k\right(k-1)+(\sigma -1\left)\right(k+1\left)\right)\\ & \le -2(k^2-1)(k+1)+(k+1)\left(k\right(k-1)+(\sigma -1\left)\right(k+1\left)\right)\\ & =-(k+1)\left[\right(k+1\left)\right(k-\sigma +1)-2]\le 0.\end{array}$Since A<0, it follows that $\frac{1}{(k+1{)}^2-ck}<\frac{k^2-1-c(\sigma -1)k}{c^{2}k(\sigma -1{)}^2+(k^2-1{)}^2-c(\sigma -1)(k-1)(k+1{)}^2}.$This inequality implies that $s_{A_3}<s_{B_3}$. Therefore, the blue regions covered by stable sub-triangles.

Combining the previous lemmas, we have that sub-triangles in all gaps are covered.

Lemma 5.9

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. For $2\le \rho \le k$ and $1\le \sigma \le k-1$, ${\mathrm{△}}_{\mathbf{r}}(1,\rho ,k)\cap {\mathrm{△}}_{k+1}$, ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$ are covered by stable sub-triangles.

The following will confirm that ${\mathrm{△}}_k$ (defined in Definition 5.6) is covered by stable sub-triangles.

Lemma 5.10

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. For $k\ge 3$, ${\mathrm{△}}_k$ is covered by stable sub-triangles.

Proof.

This lemma will be proved by induction. For k = 3, ${\mathrm{△}}_3$ is shown in Figure 32, where point A is $c_{1,2,3}$, point B is the solution of $r=s+\frac{1}{3}$ and $r=\frac{2cs}{9}+\frac{2}{3}$, and point C is the solution of $r=s+\frac{1}{3}$ and $r-1=3(1-\frac{3}{c})(s-\frac{1}{3})$. Then, $\begin{array}{rl}A& =\left(\frac{3}{9-c},\frac{6}{9-c}\right),\\ B& =\left(\frac{3}{9-2c},\frac{3}{9-2c}+\frac{1}{3}\right),\text{ and}C=\left(\frac{9-c}{3(9-2c)},\frac{18-3c}{3(9-2c)}\right).\end{array}$Thus the points A, B, C are in a stable sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,2,2)$, i.e. the stable sub-triangle for k = 2.

Figure 31. Case II: $k/5\le \sigma \le k-1$. The integer q denotes the greatest common denominator of $\sigma -1$ and k−1.

Figure 32. The shaded area is ${\mathrm{△}}_3$. It is covered by the stable sub-triangle ${\mathrm{△}}_{\mathbf{r}}(1,2,2)$, the largest (yellow) sub-triangle shown in Figure 24.

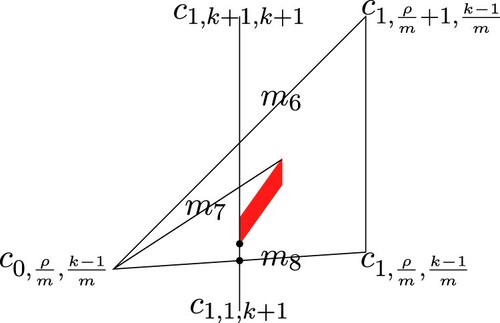
It suffices for the inductive step to show that the gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$, see Figure 33, is covered by stable sub-triangles. We separate the gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ into three parts as follows:

• The vertical gap is the area bounded by four lines: the line passing through $c_{1,k+1,k+1}$ and $c_{1,1,k+1}$, the line passing through $c_{1,k,k}$ and $c_{1,1,k}$, the line passing through $c_{0,k,k+1}$ and $c_{k,k,k+1}$, and the line passing through $c_{0,1,k+1}$ and $c_{k,k+1,k+1}$.

• The horizontal gap is the area bounded by four lines: the line passing through $c_{0,k,k+1}$ and $c_{k,k,k+1}$, the line passing through $c_{0,k-1,k}$ and $c_{k-1,k-1,k}$, the line passing through $c_{1,k+1,k+1}$ and $c_{1,1,k+1}$, and the line passing through $c_{k,k+1,k+1}$ and $c_{0,1,k+1}$.

• The oblique gap is the area bounded by four lines: the line passing through $c_{0,1,k}$ and $c_{k-1,k,k}$, the line passing through $c_{0,1,k+1}$ and $c_{k,k+1,k+1}$, the line passing through $c_{0,k,k+1}$ and $c_{k,k,k+1}$, and the line passing through $c_{1,k+1,k+1}$ and $c_{1,1,k+1}$.

First, we consider the vertical gap and let $1\le j\le k-2$.Let $l=gcd(j,k-1)$. Let $l_1,l_2,l_3$ and $l_4$ be lines as follows:

• $l_1$ is the line passing through $c_{1,k+1,k+1}$ and $c_{1,1,k+1}$,

• $l_2$ is the line passing through $c_{0,j+1,k}$ and $c_{1,j+1,k}$,

• $l_3$ is the line passing through $c_{0,j,k}$ and $c_{1,j+1,k}$,

• $l_4$ is the line passing through $c_{0,j,k-1}$ and $c_{1,\frac{j}{l},\frac{k-1}{l}}$.

By Lemma 5.9, the regions ${\mathrm{△}}_{\mathbf{r}}(1,j+2,k)\cap {\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k)\cap {\mathrm{△}}_{k+1}$ (the blue shaded areas in Figure 34) are covered by stable sub-triangles. To show that the entire vertical gap is covered by stable sub-triangles, we further need to show that the region bounded by $l_1,l_2$ and $l_3$ (the red area in Figure 34) is covered by ${\mathrm{△}}_{\mathbf{r}}(1,\frac{j}{l}+1,\frac{k-1}{l})$. Note that ${\mathrm{△}}_{\mathbf{r}}(1,\frac{j}{l}+1,\frac{k-1}{l})$ is a stable sub-triangle by Theorem 3.3. Let $B_1$ be the crossing point between $l_1$ and $l_2$, $A_1$ be the crossing point between $l_1$ and $l_3$ and $A_2$ be the crossing point between $l_1$ and $l_4$. To prove that the red area in Figure 34 is covered by ${\mathrm{△}}_{\mathbf{r}}(1,\frac{j}{l}+1,\frac{k-1}{l})$, we show the following:

Figure 33. The gap between ${\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_k$.

Figure 34. The vertical gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$. The blue shaded areas are covered by stable sub-triangles by Lemma 5.9. The green triangle is ${\mathrm{△}}_{\mathbf{r}}(1,j+1,k-1)$. The brown triangle is ${\mathrm{△}}_{\mathbf{r}}(1,\frac{j}{l}+1,\frac{k-1}{l})$ where $l=gcd(j,k-1)$.

Claim 1

The slope of the line passing through $c_{0,j,k-1}$ and $B_1$ is less than or equal 1.

Claim 2

The r-coordinate of $A_1$ is greater than the r-coordinate of $A_2$, i.e. $r_{A_1}>r_{A_2}$.

We first prove Claim 1. By (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), it follows that $B_1$ is the solution of (50) $\begin{array}{r}\begin{array}{rl}r-1& =\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right),\\ \text{ and}r-\frac{j+1}{k}& =\frac{(j+1)c(k-j-1)}{k^2}s.\end{array}\end{array}$(50) Then, the r-coordinate of $B_1$ is (51) $\begin{array}{r}{r}_{B_1}=1+\frac{\frac{(k+1)(k+1-c)}{c}(k-j-1)\left(\right(j+1)c-k(k+1\left)\right)}{\frac{(k+1)(k+1-c)}{c}{k}^2(k+1)+(j+1)c(k-j-1)(k+1)}.\end{array}$(51) Let $s_{B_1}$ be the s-coordinate of $B_1$. Since $c_{0,j,k-1}=(0,\frac{j}{k-1})$, to prove Claim 1 we need to show that $r_{B_1}-s_{B_1}\le 1.$This inequality is equivalent to $r_{B_1}\left(c-\frac{k^2}{(j+1)(k-j-1)}\right)+\frac{k}{k-j-1}\le \frac{cj}{k-1},$by using (50(50) $\begin{array}{r}\begin{array}{rl}r-1& =\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right),\\ \text{ and}r-\frac{j+1}{k}& =\frac{(j+1)c(k-j-1)}{k^2}s.\end{array}\end{array}$(50) ). It is the same as showing (52) $\begin{array}{r}{r}_{B_1}\le 1+\frac{k^2(k-1)-c(j+1)(k-j-1{)}^2-(k-1\left)k\right(j+1)}{(k-1)\left(c\right(j+1\left)\right(k-j-1)-k^2)}.\end{array}$(52) Since (51(51) $\begin{array}{r}{r}_{B_1}=1+\frac{\frac{(k+1)(k+1-c)}{c}(k-j-1)\left(\right(j+1)c-k(k+1\left)\right)}{\frac{(k+1)(k+1-c)}{c}{k}^2(k+1)+(j+1)c(k-j-1)(k+1)}.\end{array}$(51) ) provides the exact value of $r_{B_1}$, showing (52(52) $\begin{array}{r}{r}_{B_1}\le 1+\frac{k^2(k-1)-c(j+1)(k-j-1{)}^2-(k-1\left)k\right(j+1)}{(k-1)\left(c\right(j+1\left)\right(k-j-1)-k^2)}.\end{array}$(52) ) is equivalent to prove (53) $\begin{array}{rl}& \frac{(k+1)(k+1-c)(k-j-1)\left(k\right(k+1)-(j+1\left)c\right)}{(k+1)(k+1-c)k^2(k+1)+(j+1)c^2(k-j-1)(k+1)}\\ & \ge \frac{k^2(k-1)-c(j+1)(k-j-1{)}^2-(k-1\left)k\right(j+1)}{(k-1)(k^2-c(j+1\left)\right(k-j-1\left)\right)}.\end{array}$(53) It is equivalent to showing (54) $\begin{array}{rl}& c^2(k+1-c)(k+1)(j+1{)}^2(k-j-1{)}^2(k-1)\\ & +c(k+1-c)(k+1)(j+1)(k-j-1)\left[\right(k-j-1\left)\right(k^3+1)-k(k-1\left)\right]\\ & -c^2(k-j-1)(k+1)(j+1)\left[k^2\right(k-1)-(k-1\left)k\right(j+1\left)\right]\\ & +c^3(k-j-1{)}^3(k+1\left)\right(j+1{)}^2\ge 0\end{array}$(54) Since $k+1-c\ge k$ and $c^3(k-j-1{)}^3(k+1\left)\right(j+1{)}^2\ge 0$, the inequality (55) $\begin{array}{rl}& ck(k+1)\left[c\right(j+1{)}^2(k-j-1{)}^2(k-1)\\ & +(j+1)(k-j-1)\left(\right(k-j-1\left)\right(k^3+1)-k(k-1\left)\right)]\\ & -ck(k+1)c(k-j-1{)}^2(j+1\left)k\right(k-1)\ge 0\end{array}$(55) implies (54(54) $\begin{array}{rl}& c^2(k+1-c)(k+1)(j+1{)}^2(k-j-1{)}^2(k-1)\\ & +c(k+1-c)(k+1)(j+1)(k-j-1)\left[\right(k-j-1\left)\right(k^3+1)-k(k-1\left)\right]\\ & -c^2(k-j-1)(k+1)(j+1)\left[k^2\right(k-1)-(k-1\left)k\right(j+1\left)\right]\\ & +c^3(k-j-1{)}^3(k+1\left)\right(j+1{)}^2\ge 0\end{array}$(54) ). By multiplying $1/\left(ck\right(k+1\left)\right)$ to (55(55) $\begin{array}{rl}& ck(k+1)\left[c\right(j+1{)}^2(k-j-1{)}^2(k-1)\\ & +(j+1)(k-j-1)\left(\right(k-j-1\left)\right(k^3+1)-k(k-1\left)\right)]\\ & -ck(k+1)c(k-j-1{)}^2(j+1\left)k\right(k-1)\ge 0\end{array}$(55) ) and simplifying, we get (56) $\begin{array}{r}(j+1)(k-j-1)\left[\right(k-j-1\left)\right(k^3+1)-k(k-1\left)\right]-c(k-j-1{)}^3(k-1\left)\right(j+1)\ge 0.\end{array}$(56) This inequality holds for $0<c\le 1$. Hence, Claim 1 holds.

Next, we will prove Claim 2, i.e. the r-coordinate of $A_1$ is greater than the r-coordinate of $A_2$. Let $r_{A_1}$ and $r_{A_2}$ be the r-coordinates of $A_1$ and $A_2$, respectively. By (43(43) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=\left(\frac{\sigma }{k-\frac{c\sigma }{k}(k-\rho )},\frac{\rho }{k-\frac{c\sigma }{k}(k-\rho )}\right)=\left(\frac{\sigma k}{k^2-c\sigma (k-\rho )},\frac{\rho k}{k^2-c\sigma (k-\rho )}\right).\end{array}$(43) ), $A_1$ is the solution of $\begin{array}{rl}& r-1=\frac{(k+1)(k+1-c)}{-c}\left(s-\frac{1}{k+1}\right),\\ \text{ and}& r-\frac{j}{k}=\left(1+\frac{jc(k-j-1)}{k^2}\right)s.\end{array}$Then, $r_{A_1}=1+\frac{\frac{(k+1)(k+1-c)}{c}\left(jk\right(k+1)+jc(k-j-1)-k^3)}{\frac{(k+1)(k+1-c)}{c}{k}^2(k+1)+(k^2+jc(k-j-1\left)\right)(k+1)}.$Point $A_2$ is the solution of $\begin{array}{rl}r-1& =\frac{(k+1)(k+1-c)}{-c}(s-\frac{1}{k+1}),\\ \text{ and}r-\frac{j}{k-1}& =\frac{cj(k-j-1)}{(k-1{)}^2}s.\end{array}$Then, $r_{A_2}=1+\frac{\frac{(k+1)(k+1-c)}{c}\left[\right(k-1\left)\right(k+1)j+cj(k-j-1)-(k-1{)}^2(k+1)]}{\frac{(k+1)(k+1-c)}{c}(k+1)(k-1{)}^2+cj(k-j-1\left)\right(k+1)}.$Showing $r_{A_1}-r_{A_2}\ge 0$ is equivalent to prove the following inequality: (57) $\begin{array}{rl}& \frac{k+1-c}{c}k(k-1)\left(k\right(k-j-1)-j)-(k+1-c)j(k-j-1)(2k-1)\\ & +(k-j-1)\left(k^2\right(k-1)-jc(k-j-1\left)\right)\ge 0.\end{array}$(57) This inequality is equivalent to (58) $\begin{array}{rl}& k^2(k-1)\left(k\right(k-j-1)-j)+(k-j-1)\left(k^2\right(k-1)-(k+1\left)\right(2k-1\left)j\right)c\\ & -j(k-j-1{)}^2{c}^2\ge 0.\end{array}$(58) The left-hand side of (58(58) $\begin{array}{rl}& k^2(k-1)\left(k\right(k-j-1)-j)+(k-j-1)\left(k^2\right(k-1)-(k+1\left)\right(2k-1\left)j\right)c\\ & -j(k-j-1{)}^2{c}^2\ge 0.\end{array}$(58) ) is a quadratic polynomial function in variable c where $0\le c\le 1$. The polynomial satisfies the following:

• the coefficient of $c^2$ is negative,

• the slopes at c = 0 and c = 1 are both negative,

• its values at c = 0 and c = 1 are both positive.

Thus, (58(58) $\begin{array}{rl}& k^2(k-1)\left(k\right(k-j-1)-j)+(k-j-1)\left(k^2\right(k-1)-(k+1\left)\right(2k-1\left)j\right)c\\ & -j(k-j-1{)}^2{c}^2\ge 0.\end{array}$(58) ) is achieved, so $r_{A_1}-r_{A_2}\ge 0$. Hence, Claim 2 holds. Since the slope of the line passing $c_{0,j,k-1}$ and $c_{1,\frac{j}{l}+1,\frac{k-1}{l}}$ is greater than 1 by Proposition 5.3 and since Claims 1 and 2 hold, it follows that the red area in Figure 34 is covered by ${\mathrm{△}}_{\mathbf{r}}(1,\frac{j}{l}+1,\frac{k-1}{l})$. Therefore, the entire vertical gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ is covered by stable sub-triangles.

Next, we consider the horizontal gap and let $\sigma =2,\dots ,k-3$. Let $q=gcd(\sigma ,k-1)$. Let $l_5,l_6$, and $l_7$ be lines as follows:

• $l_5$ is the line passing through $c_{\sigma ,k,k}$ and $c_{\sigma ,k-1,k}$,

• $l_6$ is the line passing through $c_{\sigma ,k-1,k}$ and $c_{\sigma +1,k,k}$,

• $l_7$ is the line passing through $c_{\sigma +1,k,k}$ and $c_{\frac{\sigma }{q},\frac{k-1}{q}-1,\frac{k-1}{q}}$.

By Lemma 5.9, the regions ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k,k)\cap {\mathrm{△}}_{k+1}$ and ${\mathrm{△}}_{\mathbf{r}}(\sigma +1,k,k)\cap {\mathrm{△}}_{k+1}$ (the blue shaded areas in Figure 35) are covered by stable sub-triangles. We claim that the region bounded by $l_5,l_6$, and $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ (the red shaded triangle in Figure 35) is covered by ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{q},\frac{k-1}{q},\frac{k-1}{q})$. Let $a_{\sigma }$ be the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $r-1=s-\frac{\sigma }{k-1}$, $A_{\sigma }$ be the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $l_5$, $B_{\sigma }$ be the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $l_6$, and $b_{\sigma }$ be the crossing point between $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s$ and $l_7$.Since the slope of the line passing through $c_{\frac{\sigma }{q},\frac{k-1}{q},\frac{k-1}{q}}=c_{\sigma ,k-1,k-1}$ and $c_{\frac{\sigma }{q}-1,\frac{k-1}{q}-1,\frac{k-1}{q}}$ is less than 1 by Proposition 5.4, it suffices to prove the claim by showing that $s_{a_{\sigma }}<s_{A_{\sigma }}\text{ ~~ and ~~ }{s}_{B_{\sigma }}<s_{b_{\sigma }}$where $s_{a_{\sigma }},s_{A_{\sigma }},s_{B_{\sigma }},s_{b_{\sigma }}$ denote the s-coordinates of $a_{\sigma }$, $A_{\sigma }$, $B_{\sigma }$ and $b_{\sigma }$, respectively. Figure 35 is a visualization of this claim.

Figure 35. The horizontal gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$. The blue shaded areas are covered by stable sub-triangles by Lemma 5.9. The green triangle is ${\mathrm{△}}_{\mathbf{r}}(\sigma ,k-1,k-1)$. The brown triangle is ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{q},\frac{k-1}{q},\frac{k-1}{q})$ where $q=gcd(\sigma ,k-1)$.

Point $a_{\sigma }$ is the solution of $r-1=s-\frac{\sigma }{k-1}\text{ and}r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s.$Then, $s_{a_{\sigma }}=\frac{(k+1)\left(\sigma \right(k+1)-k+1)}{(k-1)\left(\right(k+1{)}^2-ck)}.$Point $A_{\sigma }$ is the solution of $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s\text{ and}r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}\left(s-\frac{\sigma }{k}\right).$Then, $s_{A_{\sigma }}=\frac{(k+1)\sigma (k-c\sigma +1)}{(k+1{)}^2(k-c\sigma )-c^2{\sigma }^2}.$Since $B_{\sigma }$ is the solution of $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s\text{ and}r-1=\frac{k^2-c\sigma k}{k^2-c\sigma (\sigma +1)}\left(s-\frac{\sigma +1}{k}\right),$we get $s_{B_{\sigma }}=\frac{(k+1)(k^2-c\sigma (\sigma +1)-(k-c\sigma \left)\right(\sigma +1\left)\right(k+1\left)\right)}{ck(k^2-c\sigma (\sigma +1\left)\right)-(k^2-c\sigma k)(k+1{)}^2}.$Point $b_{\sigma }$ is the solution of $r-\frac{k}{k+1}=\frac{ck}{(k+1{)}^2}s\text{ and}r-1=-\frac{(k-1-c\sigma )(k-1)}{c{\sigma }^2}\left(s-\frac{\sigma }{k-1}\right).$Thus $s_{b_{\sigma }}=\frac{(k+1)\sigma (k^2-1-c\sigma k)}{c^{2}k{\sigma }^2+(k-1-c\sigma )(k-1)(k+1{)}^2}.$Lemma 5.12 implies $s_{a_{\sigma }}<s_{A_{\sigma }}$ and $s_{B_{\sigma }}<s_{b_{\sigma }}$. Hence, the red shaded triangle in Figure 35 is covered by ${\mathrm{△}}_{\mathbf{r}}(\frac{\sigma }{q},\frac{k-1}{q},\frac{k-1}{q})$ which is a stable sub-triangle. Therefore, the entire horizontal gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ is covered by stable sub-triangles.

Next, we consider the oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$. There are four steps to prove how the oblique gap is covered by stable sub-triangles.

Step 1: We will show that the intersection of the vertical and oblique gaps and the intersection of the horizontal and oblique gaps are covered by ${\mathrm{△}}_{\mathbf{r}}(1,2,k)$ and ${\mathrm{△}}_{\mathbf{r}}(k-1,k,k)$. Let $A_1$ be the lowest corner of the former intersection and $A_2$ be the highest corner of the latter intersection. The two red shaded areas in Figure 36 are a visualization of the intersections. We note that the slope of the line segment from $c_{0,1,k}$ to $c_{1,2,k}$ is greater than 1. To complete this step, we need to show that $A_1\in {\mathrm{△}}_{\mathbf{r}}(1,2,k)$ and $A_2\in {\mathrm{△}}_{\mathbf{r}}(k-1,k,k)$. Point $A_1$ is the solution of $r=s+\frac{1}{k+1}$and $r-1=-\frac{(k+1-c)(k+1)}{c}\left(s-\frac{1}{k+1}\right).$Then, $\begin{array}{rl}{A}_1& =(s_{A_1},\\ r_{A_1})& :=\left(\frac{(k+1-c)(k+1)+ck}{(k+1)(c+(k+1-c\left)\right(k+1\left)\right)},\frac{(k+1-c)(k+1)+ck}{(k+1)(c+(k+1-c\left)\right(k+1\left)\right)}+\frac{1}{k+1}\right).\end{array}$Point $A_2$ is the solution of $r=s+\frac{1}{k+1}$and $r-\frac{k-1}{k}=\frac{c(k-1)}{k^2}s.$Then, $A_2=(s_{A_2},r_{A_2}):=\left(\frac{k^3-k^2-k}{(k+1)(k^2-c(k-1\left)\right)},\frac{k^3-k^2-k}{(k+1)(k^2-c(k-1\left)\right)}+\frac{1}{k+1}\right).$

Let $B_1$ be the crossing point of $r=s+\frac{1}{k+1}$ and the line passing through $c_{0,1,k}$ and $c_{1,1,k}$ and let $B_2$ be the crossing point of $r=s+\frac{1}{k+1}$ and the line passing through $c_{k-1,k,k}$ and $c_{k-1,k-1,k}$. To show $A_1\in {\mathrm{△}}_{\mathbf{r}}(1,2,k)$ and $A_2\in {\mathrm{△}}_{\mathbf{r}}(k-1,k,k)$, we need to show that $s_{B_1}<s_{A_1}\text{ and}{s}_{A_2}<s_{B_2}.$Figure 37 is a visualization what we need to show. By the definition of $B_1$, $B_2$ and Propositions 5.2 and 5.1, we get the s-coordinates of $B_1$ and $B_2$ as follows: $s_{B_1}=\frac{k}{(k+1)(k^2-c(k-1\left)\right)}$and $s_{B_2}=\frac{k(k^2-1)-c(k-1{)}^2}{(k+1)(k^2-c(k-1\left)\right)}.$Since $\frac{(k+1{)}^2-c}{(k+1{)}^2-ck}>\frac{k}{k^2-c(k-1)},$we get $s_{A_1}>s_{B_1}$. Since $c<(1-c)k^2+2ck,$we obtain $\frac{k^3-k^2-k}{k^2-c(k-1)}<\frac{k(k^2-1)-c(k-1{)}^2}{k^2-c(k-1)}.$This implies $s_{A_2}<s_{B_2}$.

Figure 36. The corners of oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ where the four green shaded areas called $G_1$, $G_2$, $G_{k-3}$, $G_{k-2}$, respectively from the bottom corner.

Figure 37. A visualization of the claim to show that $A_1\in {\mathrm{△}}_{\mathbf{r}}(1,2,k)$ and $A_2\in {\mathrm{△}}_{\mathbf{r}}(k-1,k,k)$.

For Steps 2, 3 and 4 below, we define the following:

• $G_{\sigma }$ denotes the region bounded by $r=s+\frac{1}{k}$, $r=s+\frac{1}{k+1}$, $r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}(s-\frac{\sigma }{k})$, and $r-\frac{\sigma +1}{k}=\frac{c(\sigma +1)(k-\sigma -1)}{k^2}s$,

• $D_{\sigma }$ denotes the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}(s-\frac{\sigma }{k})$,

• $E_{\sigma }$ denotes the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma +1}{k}=\frac{c(\sigma +1)(k-\sigma -1)}{k^2}s$,

where $\sigma =1,\dots ,k-2$.

Step 2: Let $\sigma =1,2,k-3,k-2$. The green regions shown in Figure 36 are a visualization of $G_1$, $G_2$, $G_{k-3}$, $G_{k-2}$. In this step, we claim the following: (59) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma ,\sigma +1,k-2)\text{ for}\sigma =1,2\end{array}$(59) and (60) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma -1,\sigma ,k-2)\text{ for}\sigma =k-3,k-2\end{array}$(60)

We first prove (59(59) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma ,\sigma +1,k-2)\text{ for}\sigma =1,2\end{array}$(59) ). Let $\sigma =1,2$. Let $d_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma }{k-2}=\frac{c\sigma (k-2-\sigma )}{(k-2{)}^2}s$ and let $e_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k-2-c\sigma )(k-2)}{c{\sigma }^2}(s-\frac{\sigma }{k-2})$. We claim that the points $D_{\sigma }$ and $E_{\sigma }$ are in ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k-2)$. Figure 38 is a visualization of this claim. We will prove this by comparing the s-coordinates of the points $d_{\sigma },D_{\sigma }$ and $e_{\sigma },E_{\sigma }$. Point $D_{\sigma }$ is the solution of $r=s+\frac{1}{k+1}$and $r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}\left(s-\frac{\sigma }{k}\right).$Then, $D_{\sigma }=(s_{D_{\sigma }},r_{D_{\sigma }}):=\left(\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}+\frac{1}{k+1}\right).$The s-coordinate of $d_{\sigma }$ is as follows: $s_{d_{\sigma }}=\frac{(k-2)\left(\sigma \right(k+1)-k+2)}{(k+1)\left[\right(k-2{)}^2-c\sigma (k-2-\sigma )]}.$By the formulas for $s_{d_{\sigma }}$ and $s_{D_{\sigma }}$, we get $s_{d_{\sigma }}<s_{D_{\sigma }}$ for $\sigma =1,2$. Point $E_{\sigma }$ is the solution of $r=s+\frac{1}{k+1}$and $r-\frac{\sigma +1}{k}=\frac{c(\sigma +1)(k-\sigma -1)}{k^2}s.$Then, $\begin{array}{rl}{E}_{\sigma }& =(s_{E_{\sigma }},r_{E_{\sigma }})\\ & :=\left(\frac{\sigma k^2+\sigma k+k}{\left(k+1\right)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]},\frac{\sigma k^2+\sigma k+k}{\left(k+1\right)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]}+\frac{1}{k+1}\right).\end{array}$We get the s-coordinate of $e_{\sigma }$ as follows: $s_{e_{\sigma }}=\frac{\sigma (k-2)(k+1)-c{\sigma }^2}{(k+1)\left[\right(k-2{)}^2-c\sigma (k-2-\sigma )]}.$It is elementary to check that $s_{E_{\sigma }}<s_{e_{\sigma }}$ for $\sigma =1,2$. Then, (59(59) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma ,\sigma +1,k-2)\text{ for}\sigma =1,2\end{array}$(59) ) holds.

Figure 38. A part of the oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ for $\sigma =1,2$.

Next, we will prove (60(60) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma -1,\sigma ,k-2)\text{ for}\sigma =k-3,k-2\end{array}$(60) ). Let $\sigma =k-3,k-2$. Let $d_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma -1}{k-2}=\frac{c(\sigma -1)(k-1-\sigma )}{(k-2{)}^2}s$ and let $e_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k-2-c(\sigma -1\left)\right)(k-2)}{c(\sigma -1{)}^2}(s-\frac{\sigma -1}{k-2})$.

The s-coordinates of the points $d_{\sigma },D_{\sigma },E_{\sigma },e_{\sigma }$ are as follows: $\begin{array}{rl}{s}_{d_{\sigma }}& =\frac{(k-2)\left[\right(\sigma -1\left)\right(k+1)-k+2]}{(k+1)\left[\right(k-2{)}^2-c(\sigma -1)(k-1-\sigma )]},\\ s_{D_{\sigma }}& =\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\\ s_{E_{\sigma }}& =\frac{\sigma k^2+\sigma k+k}{(k+1)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]},\\ s_{e_{\sigma }}& =\frac{(\sigma -1)(k-2)(k+1)-c(\sigma -1{)}^2}{(k+1)\left[\right(k-2{)}^2-c(\sigma -1)(k-1-\sigma )]}.\end{array}$Figure 39 is a visualization of $d_{\sigma },D_{\sigma },E_{\sigma },e_{\sigma }$ for $\sigma =k-3,k-2$. For $\sigma =k-3,k-2$, we get $s_{d_{\sigma }}<s_{D_{\sigma }}$ and $s_{E_{\sigma }}<s_{e_{\sigma }}$. Hence, we get (60(60) $\begin{array}{r}{G}_{\sigma }\subseteq \mathrm{△}(\sigma -1,\sigma ,k-2)\text{ for}\sigma =k-3,k-2\end{array}$(60) ).

Figure 39. A part of the oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ for $\sigma =k-3,k-2$.

Step 3: Let $3\le \sigma \le k-4$. In this step, we will show that $G_{\sigma }$ is covered by ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k-1)$ for $k=4,\dots ,10$. This step will be proved in Lemma 5.11 below.

Step 4: Let $3\le \sigma \le k-4$ and $k\ge 11$. In this step, we the proof will depend on the value of c. There are two cases to be considered; $0\le c\le 0.5$ and $0.5\le c\le 1$.

Case I: $0\le c\le 0.5$. We claim that the points $D_{\sigma },E_{\sigma }$ are in ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k-1)$. Let $d_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma }{k-1}=\frac{c\sigma (k-1-\sigma )}{(k-1{)}^2}s$ and let $e_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k-1-c\sigma )(k-1)}{c{\sigma }^2}(s-\frac{\sigma }{k-1})$. Figure 40 is a visualization of $d_{\sigma },D_{\sigma },E_{\sigma },e_{\sigma }$. The s-coordinates of $d_{\sigma },D_{\sigma },E_{\sigma },e_{\sigma }$ are the following: (61) $\begin{array}{rl}{s}_{d_{\sigma }}& =\frac{(k-1)\left[\sigma \right(k+1)-k+1]}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]},\end{array}$(61) (62) $\begin{array}{rl}{s}_{D_{\sigma }}& =\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\end{array}$(62) (63) $\begin{array}{rl}{s}_{E_{\sigma }}& =\frac{\sigma k^2+\sigma k+k}{(k+1)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]},\end{array}$(63) (64) $\begin{array}{rl}{s}_{e_{\sigma }}& =\frac{\sigma k^2-\sigma -c{\sigma }^2}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}.\end{array}$(64) By Lemma 5.13 below, we get $s_{d_{\sigma }}<s_{D_{\sigma }}$ and $s_{E_{\sigma }}<s_{e_{\sigma }}$. Then, we obtain that $D_{\sigma },E_{\sigma }\in {\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k-1).$Case II: $0.5\le c\le 1$. We define the following:

• $G_{\sigma }^{\prime }$ denotes the region bounded by $r=s+\frac{1}{k}$, $r=s+\frac{1}{k+1}$, $r-1=-\frac{(k+1-c\sigma )(k+1)}{c{\sigma }^2}(s-\frac{\sigma }{k+1})$, and $r-\frac{\sigma +1}{k+1}=\frac{c(\sigma +1)(k-\sigma )}{(k+1{)}^2}s$,

• $D_{\sigma }^{\prime }$ denotes the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k+1-c\sigma )(k+1)}{c{\sigma }^2}(s-\frac{\sigma }{k+1})$,

• $E_{\sigma }^{\prime }$ denotes the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma +1}{k+1}=\frac{c(\sigma +1)(k-\sigma )}{(k+1{)}^2}s$,

where $\sigma =3,\dots ,k-3$. We will show that $G_{\sigma }^{\prime }$ is covered by ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$. Since $k\ge 11$ and $0.5\le c\le 1$, the point $c_{\sigma ,\sigma +1,k+1}=(s,r)$ satisfies the inequality $r-s>\frac{1}{k}$. Then, it suffices to show that $D_{\sigma }^{\prime },E_{\sigma }^{\prime }$ are in ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$. Let $d_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-\frac{\sigma }{k}=\frac{c\sigma (k-\sigma )}{k^2}s$ and let $e_{\sigma }$ be the solution of $r=s+\frac{1}{k+1}$ and $r-1=-\frac{(k-c\sigma )k}{c{\sigma }^2}(s-\frac{\sigma }{k})$. Figure 41 is a visualization of $d_{\sigma },D_{\sigma }^{\prime },E_{\sigma }^{\prime },e_{\sigma }$.

Figure 40. A part of the oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ for $\sigma =3,\dots ,k-4$ and $0\le c\le 0.5$. The blue shaded region is $G_{\sigma }$.

Figure 41. A part of the oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ for $\sigma =3,\dots ,k-3$ and $0.5\le c\le 1$. The blue shaded region is $G_{\sigma }^{\prime }$.

Point $D_{\sigma }^{\prime }$ is the solution of $r=s+\frac{1}{k+1}$and $r-1=-\frac{(k+1-c\sigma )(k+1)}{c{\sigma }^2}\left(s-\frac{\sigma }{k+1}\right).$Then, (65) $\begin{array}{rl}{D}_{\sigma }^{\prime }& =(s_{D_{\sigma }^{\prime }},r_{D_{\sigma }^{\prime }})\\ & :=\left(\frac{\sigma (k+1{)}^2-c{\sigma }^2}{\left(k+1\right)\left[\right(k+1{)}^2-c\sigma (k-\sigma +1)]},\frac{\sigma (k+1{)}^2-c{\sigma }^2}{\left(k+1\right)\left[\right(k+1{)}^2-c\sigma (k-\sigma +1)]}+\frac{1}{k+1}\right).\end{array}$(65) The s-coordinate of $d_{\sigma }$ is as follows: $s_{d_{\sigma }}=\frac{k\left(\sigma \right(k+1)-k)}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}.$Point $E_{\sigma }^{\prime }$ is the solution of $r=s+\frac{1}{k+1}$and $r-\frac{\sigma +1}{k+1}=\frac{c(\sigma +1)(k-\sigma )}{(k+1{)}^2}s.$Then, (66) $\begin{array}{r}{E}_{\sigma }^{\prime }=(s_{E_{\sigma }^{\prime }},r_{E_{\sigma }^{\prime }}):=\left(\frac{\sigma \left(k+1\right)}{(k+1{)}^2-c(\sigma +1\left)\right(k-\sigma )},\frac{\sigma \left(k+1\right)}{(k+1{)}^2-c(\sigma +1\left)\right(k-\sigma )}+\frac{1}{k+1}\right).\end{array}$(66) The s-coordinate of $e_{\sigma }$ is as follows: $s_{e_{\sigma }}=\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}.$By Lemma 5.14 below, we obtain $s_{d_{\sigma }}<s_{D_{\sigma }}$ and $s_{E_{\sigma }}<s_{e_{\sigma }}$. Then, $D_{\sigma },E_{\sigma }\in {\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k).$By Steps 1-4, the entire oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ is covered by (67) $\begin{array}{r}\bigcup _{\begin{array}{c}i=k-2\\ 1\le \sigma \le i-1\end{array}}^k{\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,i).\end{array}$(67) By Lemma 5.9, it follows that the set in (67(67) $\begin{array}{r}\bigcup _{\begin{array}{c}i=k-2\\ 1\le \sigma \le i-1\end{array}}^k{\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,i).\end{array}$(67) ) is covered by stable sub-triangles. Therefore, the entire oblique gap between ${\mathrm{△}}_k$ and ${\mathrm{△}}_{k+1}$ is covered stable sub-triangles.

We next state and prove the Lemmas 5.11, 5.12, 5.13, and 5.14 that were used above in the proof of Lemma 5.10.

Lemma 5.11

Let f be a negative linear feedback function, $f\left(x\right)=-cx$ where $0<c\le 1$. Let k and σ be positive numbers, $7\le k\le 10$, $\sigma =3,\dots ,k-4$. Then, $G_{\sigma }$ (the blue shaded regions in Figure 40) defined at the end of Step 1 in the previous lemma is covered by ${\mathrm{△}}_{\mathbf{r}}(\sigma ,\sigma +1,k)$.

Proof.

By (61(61) $\begin{array}{rl}{s}_{d_{\sigma }}& =\frac{(k-1)\left[\sigma \right(k+1)-k+1]}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]},\end{array}$(61) )–(64(64) $\begin{array}{rl}{s}_{e_{\sigma }}& =\frac{\sigma k^2-\sigma -c{\sigma }^2}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}.\end{array}$(64) ), the s-coordinates of $d_{\sigma }$, $D_{\sigma }$, $E_{\sigma }$, and $e_{\sigma }$ are follows: $\begin{array}{rl}{s}_{d_{\sigma }}& =\frac{(k-1)\left[\sigma \right(k+1)-k+1]}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]},\\ s_{D_{\sigma }}& =\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\\ s_{E_{\sigma }}& =\frac{\sigma k^2+\sigma k+k}{(k+1)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]},\\ s_{e_{\sigma }}& =\frac{\sigma k^2-\sigma -c{\sigma }^2}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}.\end{array}$The cases $7\le k\le 10$, $\sigma =3,\dots ,k-4$ can be checked individually [28].

For each case, it follows that $s_{d_{\sigma }}<s_{D_{\sigma }}$ and $s_{E_{\sigma }}<s_{e_{\sigma }}$ for any $0<c\le 1$.

Lemma 5.12

Let k and σ be positive integers such that $2\le \sigma \le k-3$. Then, the following inequalities hold: (68) $\begin{array}{rl}\frac{\sigma (k+1)-k+1}{(k-1)\left(\right(k+1{)}^2-ck)}& <\frac{\sigma (k-c\sigma +1)}{(k+1{)}^2(k-c\sigma )-c^2{\sigma }^2},\end{array}$(68) (69) $\begin{array}{rl}\frac{k^2-c\sigma (\sigma +1)-(k-c\sigma )(\sigma +1)(k+1)}{ck(k^2-c\sigma (\sigma +1\left)\right)-(k^2-c\sigma k)(k+1{)}^2}& <\frac{\sigma (k^2-1-c\sigma k)}{c^{2}k{\sigma }^2+(k-1-c\sigma )(k-1)(k+1{)}^2}\end{array}$(69) for $0<c\le 1$.

Proof.

Let $A=\left(\sigma \right(k+1)-k+1)(k+1{)}^2(k-c\sigma )-\sigma (k-c\sigma +1\left)\right(k-1\left)\right(\left(k+1{)}^2-ck\right)$. The expression A can be rewritten as a quadratic polynomial in variable c for fixed k and σ: $\begin{array}{rl}A& =-(k+1{)}^2(k^2-k\sigma -k-q)+c\sigma (k+1\left)\right[(k^2-1)(\sigma +1)-\sigma (k+1{)}^2+(k-1\left)k\right]\\ & -c^2{\sigma }^{2}k(k-1).\end{array}$The polynomial has the following properties:

• the coefficient of $c^2$ is negative,

• its values at c = 0 and c = 1 are both negative,

• the slopes at c = 0 and c = 1 are both positive.

Thus A<0. It implies that $\frac{\sigma (k+1)-k+1}{(k-1)\left(\right(k+1{)}^2-ck)}<\frac{\sigma (k-c\sigma +1)}{(k+1{)}^2(k-c\sigma )}.$Then, (68(68) $\begin{array}{rl}\frac{\sigma (k+1)-k+1}{(k-1)\left(\right(k+1{)}^2-ck)}& <\frac{\sigma (k-c\sigma +1)}{(k+1{)}^2(k-c\sigma )-c^2{\sigma }^2},\end{array}$(68) ) holds.

Next, we claim that (70) $\begin{array}{r}\frac{k^2\sigma +k\sigma +k-ck\sigma (\sigma +1)}{k^2(k+1{)}^2-ck(\sigma (k+1{)}^2+k^2)}<\frac{(k^2-1)\sigma -c{\sigma }^{2}k}{(k^2-1{)}^2-c\sigma (k^2-1\left)\right(k+1)}.\end{array}$(70) Let $\begin{array}{rl}B& =[k\sigma +\sigma +1-c\sigma (\sigma +1\left)\right]\left[\right(k^2-1{)}^2-c\sigma (k^2-1)(k+1)]\\ & -\left[\right(k^2-1)\sigma -c{\sigma }^{2}k]\left[k\right(k+1{)}^2-c\left(\sigma \right(k+1{)}^2+k^2\left)\right].\end{array}$For fixed k and σ, B can be rewritten as a quadratic polynomial in variable c: $\begin{array}{rl}B& =-(k^2-1)(k+1)(k\sigma -k+\sigma +1)+c\sigma (2k^3\sigma -k^3+3k^2\sigma +k-\sigma )\\ & +c^2{\sigma }^2(k^3\sigma +k^3-3k\sigma -k-2\sigma -1).\end{array}$The polynomial has the following properties:

• the coefficient of $c^2$ is positive,

• its values at c = 0 and c = 1 are both negative,

• the slopes at c = 0 and c = 1 are both positive.

Then, inequality (70(70) $\begin{array}{r}\frac{k^2\sigma +k\sigma +k-ck\sigma (\sigma +1)}{k^2(k+1{)}^2-ck(\sigma (k+1{)}^2+k^2)}<\frac{(k^2-1)\sigma -c{\sigma }^{2}k}{(k^2-1{)}^2-c\sigma (k^2-1\left)\right(k+1)}.\end{array}$(70) ) holds. Since $c^{2}k\sigma (\sigma +1)>c^{2}k{\sigma }^2$ and (70(70) $\begin{array}{r}\frac{k^2\sigma +k\sigma +k-ck\sigma (\sigma +1)}{k^2(k+1{)}^2-ck(\sigma (k+1{)}^2+k^2)}<\frac{(k^2-1)\sigma -c{\sigma }^{2}k}{(k^2-1{)}^2-c\sigma (k^2-1\left)\right(k+1)}.\end{array}$(70) ) holds, we get $\begin{array}{rl}& \frac{k^2\sigma +k\sigma +k-ck\sigma (\sigma +1)}{c^{2}k\sigma (\sigma +1)+k^2(k+1{)}^2-ck(\sigma (k+1{)}^2+k^2)}\\ & <\frac{(k^2-1)\sigma -c{\sigma }^{2}k}{c^{2}k{\sigma }^2+(k^2-1{)}^2-c\sigma (k^2-1\left)\right(k+1)}.\end{array}$This result implies (69(69) $\begin{array}{rl}\frac{k^2-c\sigma (\sigma +1)-(k-c\sigma )(\sigma +1)(k+1)}{ck(k^2-c\sigma (\sigma +1\left)\right)-(k^2-c\sigma k)(k+1{)}^2}& <\frac{\sigma (k^2-1-c\sigma k)}{c^{2}k{\sigma }^2+(k-1-c\sigma )(k-1)(k+1{)}^2}\end{array}$(69) ).

Lemma 5.13

Let k and σ be positive integers such that $k\ge 11$ and $3\le \sigma \le k-4$. For $0\le c\le 0.5$, the following inequalities hold: (71) $\begin{array}{rl}\frac{(k-1)\left[\sigma \right(k+1)-k+1]}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}& <\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\end{array}$(71) (72) $\begin{array}{rl}\frac{\sigma k^2+\sigma k+k}{(k+1)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]}& <\frac{\sigma k^2-\sigma -c{\sigma }^2}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}.\end{array}$(72)

Proof.

Let g, h, i be functions on $[3,k-4]$ such that $\begin{array}{rl}g\left(x\right)& =x(k^3-k+c{k}^3-2c{k}^2+ck)-x^3\left[c\right(k+1)+c^2(k-1\left)\right]+c^2{x}^4-(k-1{)}^2{k}^2,\\ h\left(x\right)& =g^{\prime }\left(x\right)=k^3-k+c{k}^3-2c{k}^2+ck-3x^{2}c(k+1+c(k-1\left)\right)+4c^2{x}^3,\\ i\left(x\right)& =h^{\prime }\left(x\right)=-6xc(k+1+c(k-1\left)\right)+12c^2{x}^2.\end{array}$Note that $\begin{array}{rl}g\left(3\right)& =-k^4+k^3(5+3c)-k^2(6c+1)-k(27c^2+24c+3)+108c^2-27c,\\ g(k-4)& =-k^3(3c^2-5c+2)+k^2(36c^2-27c-2)\\ & -k(144c^2-12c-4)+192c^2+64c,\\ h\left(3\right)& =k^3(1+c)-2c{k}^2-k(27c^2+26c+1)+135c^2-27c,\\ h(k-4)& =k^3(c-1{)}^2+c{k}^2(19-21c)+k(120c^2-23c-1)-208c^2-48c,\end{array}$and $\begin{array}{rl}i\left(x\right)& =c\left[6cx\right(2x-k+1)-6x(k+1\left)\right],\\ & \le c\left[3x\right(2x-k+1)-6x(k+1\left)\right],\\ & =-3cx(3k-1)<0.\end{array}$By using the conditions of k and c, it is obvious that $g\left(3\right),g(k-4)$ are negative and $h\left(3\right),h(k-4)$ are positive. Since $i\left(x\right)<0$ and $h\left(3\right),h(k-4)$ are positive, $h\left(x\right)>0$ on $[3,k-4]$. Since $h\left(x\right)>0$ and $g\left(3\right),g(k-4)$ are negative, $g\left(x\right)<0$ on $[3,k-4]$. Showing $g\left(x\right)<0$ on $[3,k-4]$ is equivalent to showing (71(71) $\begin{array}{rl}\frac{(k-1)\left[\sigma \right(k+1)-k+1]}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}& <\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]},\end{array}$(71) ).

Next, let $A_1=(\sigma k^2+\sigma k+k)\left(\right(k-1{)}^2-c\sigma (k-1-\sigma ))-(\sigma k^2-\sigma -c{\sigma }^2\left)\right(k^2-c(\sigma +1)(k-\sigma -1))$. Then $\begin{array}{rl}{A}_1& =(\sigma k^2+\sigma k+k)(k-1{)}^2-(\sigma k^2-\sigma )k^2+c\sigma (k^3-k^2(\sigma +2)\\ & +k\sigma (\sigma +1)+(\sigma +1{)}^2)-c^2(\sigma +1)(k-\sigma -1){\sigma }^2,\\ & \le (\sigma k^2+\sigma k+k)(k-1{)}^2-(\sigma k^2-\sigma )k^2\\ & +c\sigma (k^3-k^2(\sigma +2)+k\sigma (\sigma +1)+(\sigma +1{)}^2),\\ & \le -0.5\left(k^3\right(\sigma -2)+k(k{\sigma }^2-{\sigma }^3+2k\sigma -{\sigma }^2+4k-2\sigma +2)-\sigma (\sigma +1{)}^2),\\ & <0.\end{array}$Since $A_1<0$, we get (72(72) $\begin{array}{rl}\frac{\sigma k^2+\sigma k+k}{(k+1)[k^2-c(\sigma +1\left)\right(k-\sigma -1\left)\right]}& <\frac{\sigma k^2-\sigma -c{\sigma }^2}{(k+1)\left[\right(k-1{)}^2-c\sigma (k-1-\sigma )]}.\end{array}$(72) ).

Lemma 5.14

Let k and σ be positive integers such that $k\ge 11$ and $3\le \sigma \le k-3$. For $0.5\le c\le 1$, the following inequalities hold: (73) $\begin{array}{rl}\frac{k\left(\sigma \right(k+1)-k)}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}& <\frac{\sigma (k+1{)}^2-c{\sigma }^2}{(k+1)\left[\right(k+1{)}^2-c\sigma (k-\sigma +1)]},\end{array}$(73) (74) $\begin{array}{rl}\frac{\sigma (k+1)}{(k+1{)}^2-c(\sigma +1\left)\right(k-\sigma )}& <\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}.\end{array}$(74)

Proof.

Let $B_1=\left(\sigma \right(k+1)-k)\left[\right(k+1{)}^2-c\sigma (k-\sigma +1)]-(\sigma (k+1{)}^2-c{\sigma }^2)(k^2-c\sigma (k-\sigma \left)\right)$, then $\begin{array}{rl}{B}_1& =-(k+1{)}^2(\sigma k^2+k-\sigma (k+1))+c\sigma [(k^3-1)\sigma -k^2({\sigma }^2-2\sigma -1)\\ & -k({\sigma }^2+2\sigma -1)]-c^2{\sigma }^3(k-\sigma ),\\ & \le -(k+1{)}^2(\sigma k^2+k-\sigma (k+1))+c\sigma [(k^3-1)\sigma -k^2({\sigma }^2-2\sigma -1)\\ & -k({\sigma }^2+2\sigma -1)],\\ & <-(k+1{)}^2(\sigma k^2+k-\sigma (k+1))+c{\sigma }^2(k^3-1),\\ & <k^2(\sigma k^2+k-\sigma (k+1\left)\right)+c\sigma k^3,\\ & =-k^2\left(\sigma k\right(k-1)+k-\sigma -{\sigma }^{2}k)<0.\end{array}$Since $B_1<0$, inequality (73(73) $\begin{array}{rl}\frac{k\left(\sigma \right(k+1)-k)}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}& <\frac{\sigma (k+1{)}^2-c{\sigma }^2}{(k+1)\left[\right(k+1{)}^2-c\sigma (k-\sigma +1)]},\end{array}$(73) ) holds. Let $B_2=\sigma (k+1{)}^2(k^2-c\sigma (k-\sigma ))-(\sigma k(k+1)-c{\sigma }^2\left)\right[(k+1{)}^2-c(\sigma +1\left)\right(k-\sigma \left)\right]$. Then $\begin{array}{rl}{B}_2& =-\sigma k(k+1{)}^2+c\sigma (k+1\left)\right(k^2-\sigma k+\sigma +{\sigma }^2)-c^2{\sigma }^2(\sigma +1\left)\right(k-\sigma ),\\ & \le -\sigma k(k+1{)}^2+c\sigma (k+1\left)\right(k^2-\sigma k+\sigma +{\sigma }^2),\\ & =-\sigma (k+1)\left[\right(1-c)k^2+k+c\sigma (k-c-\sigma \left)\right]<0.\end{array}$Since $B_2<0$, it implies that inequality (74(74) $\begin{array}{rl}\frac{\sigma (k+1)}{(k+1{)}^2-c(\sigma +1\left)\right(k-\sigma )}& <\frac{\sigma k(k+1)-c{\sigma }^2}{(k+1)[k^2-c\sigma (k-\sigma \left)\right]}.\end{array}$(74) ) holds.

Let a point $(s,r)\in T$. Then $(s,r)\in {\mathrm{△}}_k$ for some k. By Lemma 5.10, it follows that the point $(s,r)$ is covered by a stable sub-triangle. We have now proved Theorem B.

6. Conclusion and discussion

In Theorem thmA, we have fully characterized the stability k-cyclic solutions for $(s.r)$ in all boundary sub-triangles for any negative feedback. For the order of events sr1 they are always neutrally stable. For the order rs1, the stability is completely determined by the index $i=\sigma$ or $k-\rho$. Solutions are asymptotically stable if i and k are relatively prime and neutral otherwise.

We have shown in Theorem thmB that for linear negative feedback the stable boundary triangles completely cover the parameter triangle $\mathrm{△}$.

Thus the model predicts that there will always exist an asymptotically stable clustered solution regardless of parameter values. Numerics show that this is also true for many forms of nonlinear feedback. See Figures 44 and 45. In [39], it was shown that for any negative feedback the synchronized solution is unstable. In [2], it was shown that the ‘uniform solution’, i.e. a steady-state periodic solution with cells spread out maximally around the circle is also unstable in most cases. Thus it appears that for negative feedback systems of this form and any parameter values, a k cluster solution will be the only stable periodic solution. This is what we always observe in simulations starting from random initial conditions -- a k cluster periodic solution emerges with roughly the same number of cells in each cluster (see [5] and [32]). The universality of this result is important because for these models, as with many biological systems, the parameter values are hard to estimate from first principles.

Figure 42. An overlay of all stable sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\left(I\right)=-0.27I$.

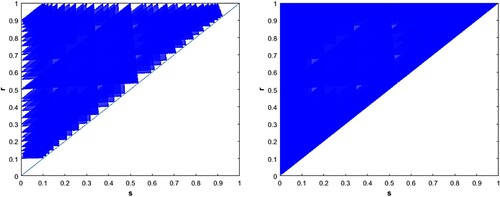
Figure 43. An overlay of all stable sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\left(I\right)=-I$.

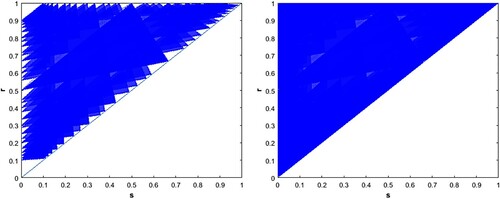
Figure 44. An overlay of all stable sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\left(I\right)=-I/(2-I)$.

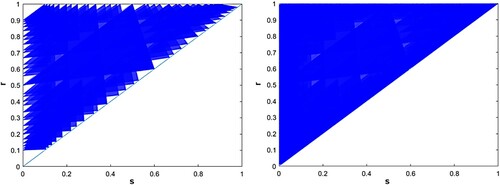
Figure 45. An overlay of all stable sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\left(I\right)=-3I^2+2I^3$. Note that the graph of this function is S-shaped.

In the following figures, we show visualizations for overlays of stable sub-triangles. The figures were generated using a MATLAB program by the following process:

• We first consider linear negative feedback functions and then some examples of nonlinear negative feedback functions.

• For each k where $k=2,\dots ,m$, the program constructs stable sub-triangles (blue shaded sub-triangles) by using the vertex formula (34(34) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=(x_{\sigma +1},x_{\rho +1})=(\sigma d,\rho d)=\left(\frac{\sigma }{k+{\text{β}}_{\sigma ,k}(k-\rho )},\frac{\rho }{k+{\text{β}}_{\sigma ,k}(k-\rho )}\right).\end{array}$(34) ) and Theorems 3.1 and 3.3. Note that these two results provide all stable sub-triangles among the boundary sub-triangles.

• Then, the program displays in one plot all the constructed stable boundary sub-triangles.

We provide two types of overlays; k ranges from 2 to 10 and k ranges from 2 to 100. Note here that the lighter blue regions in all figures throughout this section are the area that some parts of stable sub-triangles do not overlap other stable sub-triangles. These are the exception rather than the rule, indicating that for most parameter values there exist multiple stable cyclic solutions (with different values of k).

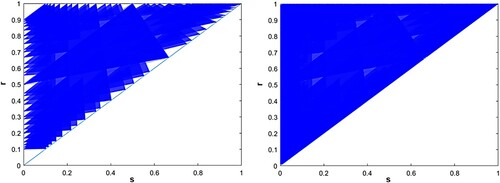
For negative linear feedback functions $f\left(I\right)=-0.27I$ and $f\left(I\right)=-I$, Figures 42 and 43 are overlays of stable regions for $k=2,\dots ,10$ and $k=2,\dots ,100$.

In Figures 44 and 45, we show overlays of stable regions for two nonlinear feedback functions $f\left(I\right)=-I/(2-I)$ and $f\left(I\right)=-3I^2+2I^3$. For both of these examples and many others that we examined, the parameter triangle is fully covered by stable sub-triangles. Thus we believe that the conclusion of Theorem thmB holds far beyond the linear case.

We note from Figures 16 and 21 and those in this section that most of the area of $\mathrm{△}$ is already covered with stable sub-triangles with small k. While larger k are theoretically possible, they are expected to be of little consequence for three reasons: (1) the parameter sets where they exist grow small as k increases (they are on the boundary of $\mathrm{△}$), (2) these sets are often overlapped by stability regions with fewer clusters and (3) the amount of feedback exerted by a single cluster would decrease like 1/k as k increases and at some point would be insufficient to overcome the noise in the system. The number of cells, n, in a bioreactor with a litre of fluid is on the order of ${10}^{10}$, so for practical purposes $k\ll n$.

We observe that there are some negative nonlinear feedback functions such that some points in $\mathrm{△}$ are not covered by any stable boundary sub-triangle. By Theorems 3.1 and 3.3 and the vertex formula of sub-triangles (34(34) $\begin{array}{r}{c}_{\sigma ,\rho ,k}=(x_{\sigma +1},x_{\rho +1})=(\sigma d,\rho d)=\left(\frac{\sigma }{k+{\text{β}}_{\sigma ,k}(k-\rho )},\frac{\rho }{k+{\text{β}}_{\sigma ,k}(k-\rho )}\right).\end{array}$(34) ), if there exist a positive integer $k\ge 2$ and a subset G of ${\mathrm{△}}_k$ (${\mathrm{△}}_k$ is defined in Definition 5.6) such that G is not covered by stable boundary sub-triangles for $l\le k$, then G is not covered by any stable boundary sub-triangle. For $f\left(I\right)=-\sqrt{I}$, Figure 46 suggests that there are regions in $\mathrm{△}$ that are not covered by any stable boundary sub-triangles. This feedback function has the features that it is not Lipschitz and it is not bounded below by the functions covered in Theorem thmB. We also observe in Figure 47 that for a particular negative feedback function $f\left(I\right)=-0.1\arctan \left(50\right(I-0.22\left)\right)-0.14801$ that is Lipschitz and bounded below by the function $-I$, the union of stable boundary sub-triangles for all $k\ge 2$ does not cover the interior of $\mathrm{△}$.

Figure 46. An overlay of all stable sub-triangles for $k=2,\dots ,10$ (left) and for $k=2,\dots ,100$ (right) with feedback function $f\left(I\right)=-\sqrt{I}$. The white holes in the plot on the right show that for this function not every parameter point is covered by an asymptotically stable boundary sub-triangle.

Figure 47. An overlay of all stable sub-triangles for $k=2,\dots ,10$ with feedback function $f\left(I\right)=-0.1\arctan \left(50\right(I-0.22\left)\right)-0.14801$. The white area inside the red circle is the set of points that cannot be covered by any stable boundary sub-triangle since the area is not covered by any stable boundary sub-triangle for $l\le 10$.

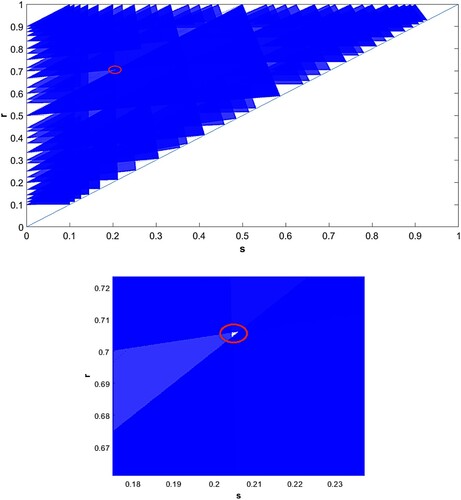
Whether Theorem thmB can be extended more generally is an open question. The numerical results shown in Figures 46 and 47 make it clear that for some non-linear negative feedback functions the stable boundary sub-triangles alone do not fully cover the parameter triangle. As discussed in [2], there are a few exceptional interior sub-triangles that are stable. It is possible that these stable interior sub-triangles cover any holes. In [29,30], the stability of exceptional triangles was proved for k = 9 and $k=14$. Further, they showed that for k prime, some interior sub-triangles can become stable for larger feedback. The indices of these sub-triangles satisfy certain number theoretic relations. Since the holes in the figures appear only for larger feedback, it is possible that these exceptional sub-triangles cover some or all of the holes.

Numerical simulations, i.e. running the model for some $(s,r)$ in the holes that appear show that even in the holes in the figures, the solutions always converge to some clustered solution.

In light of these considerations, settling the conjecture fully appears to be complicated.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Appendix. List of symbols

$z_i\left(t\right)\in [0,1)$	=	coordinate of a cell
$X_i\left(t\right)\in [0,1)$	=	coordinate of a cluster
$x_i\in [0,1)$	=	initial condition of a cluster, i.e. $x_i=X_i\left(0\right)$
k	=	number of clusters in the cell cycle
S	=	interval $[0,s)$ on the cycle for a real number $s\in (0,1)$
R	=	interval $[r,1)$ on the cycle for a real number $r\in (0,1)$
σ	=	number of clusters inside S at the initial time
ρ	=	number of clusters in $[0,r)$ (outside R) at the initial time
$f\left(I\right)$	=	feedback function
${\text{β}}_{\sigma }={\text{β}}_{\sigma ,k}=f\left(\frac{\sigma }{k}\right)$	=	a particular value of the feedback function when σ clusters are in the S region, from the total number of k clusters
$\omega =\frac{{\text{β}}_{\sigma }-{\text{β}}_{\sigma -1}}{1+{\text{β}}_{\sigma -1}}$	=
$\theta =-\omega$	=
Π	=	Poincaré return map for the system with clusters
F	=	partial return map, a factor of Π
$\mathrm{△}$	=	parameter triangle, set of points $(s,r)$ such that 0<s<r<1
${\mathrm{△}}_{\mathbf{r}}(\sigma ,\rho ,k)$	=	sub-triangle (isosequential region) corresponding to the k-cyclic solutions with order of events $\mathbf{r}\mathbf{s}\mathbf{1}$ and initial conditions where σ clusters lie in S and ρ clusters are outside R
${\mathrm{△}}_{\mathbf{s}}(\sigma ,\rho ,k)$	=	sub-triangle corresponding to the k-cyclic solutions with order of events $\mathbf{s}\mathbf{r}\mathbf{1}$ and initial conditions where σ clusters lie in S and ρ clusters are outside R
${\mathrm{△}}_k$	=	triangle bounded by $r-1=-k\left(\frac{k-c}{c}\right)(s-\frac{1}{k})$, $r-\frac{k-1}{k}=\frac{c(k-1)}{k^2}s$, and $r=s+\frac{1}{k}$ if a real number $c\ne 0$ (Section 3.2). If c = 0 (zero feedback in Section 3.1), it represents a triangle bounded by $s=\frac{1}{k}$, $r=\frac{k-1}{k}$, and $r=s+\frac{1}{k}$. s