Dynamics of autotroph–mixotroph interactions with the intraguild predation structure

Abstract

A mathematical model with the intraguild predation structure is proposed to describe the interactions of autotrophs and mixotrophs containing light and nutrients in a well-mixed aquatic ecosystem. The dissipation, existence and stability of equilibria of the model are proved, and the ecological reproductive indexes for the extinction, survival and coexistence of autotrophs and mixotrophs are established. We also consider the influence of Holling type functional responses and abiotic factors on the coexistence and biomass of autotrophs and mixotrophs. It is shown that the intraguild predation structure is beneficial to phytoplankton biodiversity and provides an explanation for the phytoplankton paradox.

Keywords:

• Autotrophs
• mixotrophs
• intraguild predation
• light
• nutrients

1. Introduction

Algae, as typical phytoplankton, are the primary producer of organic compounds in the whole aquatic ecosystem. They form the basis of energy flow and material circulation in lakes or oceans. Algae mainly consist of two parts: autotrophs (autotrophic algae) and mixotrophs (mixotrophic algae). Autotrophs synthesize organic matters through photosynthesis to supply their own growth [1, 11, 17, 18]. Mixotrophs as the combination of autotrophic and heterotrophic nutrition not only use photosynthesis to combine inorganic matters into organic matters, but also feed on microorganisms to meet their growth [2, 3].

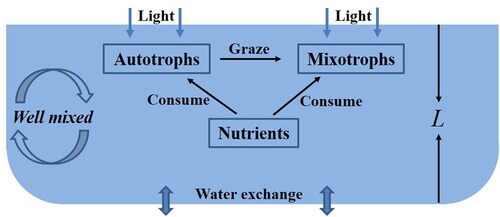
The interaction of autotrophs and mixotrophs is complicated containing competition and predation (see Figure 1). The growth of autotrophs is affected by nutrition and light [1, 10, 23, 29]. There is no obvious dichotomy for mixotrophs as producers or consumers. In general, autotrophic activities and heterotrophic activities of mixotrophs are carried out at the same time. In the autotrophic situation, the metabolism of mixotrophs is also limited by light and nutrients. This indicates that in this case, autotrophs and mixotrophs compete for light [2, 14] or nutrients [15, 16, 24, 25]. Mixotrophs in the heterotrophic nutrition can ingest micro-autotrophs [14, 24, 25].

Figure 1. The interactions between autotrophs and mixotrophs.

Intraguild predation is a ubiquitous ecological phenomenon in natural ecosystems [5, 20]. It describes a relationship in which the predator not only consumes the prey, but also shares the same resource with the prey. From the relationship between autotrophs and mixotrophs, they form an intraguild predation structure. Previous studies have shown that autotrophs and mixotrophs compete only for nutrients [15, 16, 24, 25] or only for light [14]. Light comes from the water surface and gradually weakens with the depth of the water [4, 19, 23]. Nutrients come from the bottom of the lake, and spread to the whole lake with the turbulence [6, 27, 28]. Due to the importance of nutrients and light on the metabolism of autotrophs and mixotrophs [1, 23, 29], it is essential to investigate the intraguild predation structure between autotrophs and mixotrophs with nutrients and light.

According to the above considerations and the existing research results, we propose and analyse a mathematical model of autotroph–mixotroph interactions with the intraguild predation structure. Our model contains the effect of light and nutrients. Through the analysis of the model, we investigate the dynamical behaviours for the survival, extinction and coexistence of autotrophs and mixotrophs, and consider Holling type functional responses, light and nutrients on the coexistence of autotrophs and mixotrophs. Here, we also try to study the ‘Paradox of the Plankton’ based on the model. This paradox, proposed by Hutchinson [9], generally describes that the diversity of phytoplankton deviates from the limitation of the available abiotic resources in the same ecological niche.

Algal blooms are a natural ecological phenomenon of algae mass-breeding in the water source. It seriously affects aquatic ecological communities, water quality, and even threatens people's health. Algal blooms are caused by many reasons, including biotic and abiotic factors [1, 27, 29]. The motivation of this paper is to explore the effect of biotic and abiotic factors on the blooms of autotrophic algae and mixotrophic algae. Based on our model, we will consider the biomass density of autotrophs and mixotrophs with the change of some important environmental parameters.

We construct this paper as follows. In Section 2, a dynamical model describing the interaction of autotrophs and mixotrophs is established in the intraguild predation structure. Then, we study dynamical features of this model containing dissipation of the solutions, the existence and stability of non-negative stable solutions in Section 3. In Section 4, by using some numerical simulations, we investigate the effect of abiotic and biotic factors on the coexistence and density of autotrophs and mixotrophs at a steady state with biologically reasonable parameters, and it explains their effects in phytoplankton biodiversity and blooms. Section 5 summarizes our results and proposes some research prospects to be studied in the future.

2. The model

We establish a dynamical model with the intraguild predation structure to describe the interactions of autotrophs and mixotrophs containing light and nutrients. Here, we consider a well-mixed aquatic environment such as a water column [7, 8, 14] or epilimnion in lakes [23, 29]. Let z represent the water depth coordinate. Then z = 0 denotes the water surface, and z = L denotes the bottom of the water column or epilimnion. Our model consists of three ordinary differential equations and one algebraic equation, characterizing the rate of change for autotrophs (A), mixotrophs (M) and dissolved nutrients (N) and light intensity ($I(x,A,M)$). Table 1 lists the information on variables and parameters of the model.

Table 1. The variables and parameters of model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ).

Symbol	Meaning	Value	Unit	Source
t	Time	Variable	day
A	Biomass density of autotrophs	Variable	mgC/m${}^3$
M	Biomass density of mixotrophs	Variable	mgC/m${}^3$
N	Dissolved nutrient concentration	Variable	mgP/m${}^3$
$r_1$	Maximum specific production rate of autotrophs	1	day${}^{-1}$	[14]
$r_2$	Maximum specific production rate of mixotrophs	0.4	day${}^{-1}$	[14]
$I_{in}$	Light intensity at the surface	400	µmol quanta/(m${}^2$s)	[22]
$N_{in}$	Concentration of dissolved nutrients at the bottom of the water column or epilimnion	80	mgP/m${}^3$	[23]
$m_1$	Loss rate of autotrophs	0.05	day${}^{-1}$	[14]
$m_2$	Loss rate of mixotrophs	0.05	day${}^{-1}$	[14]
$h_1$	Half-saturation light intensity for autotrophs	200	µmol quanta/(m${}^2$s)	[14]
$h_2$	Half-saturation light intensity for mixotrophs	250	µmol quanta/(m${}^2$s)	[14]
${\gamma }_1$	Half-saturation constant for nutrient production of autotrophs	1.5	mgP/m${}^3$	[23]
${\gamma }_2$	Half-saturation constant for nutrient production of mixotrophs	2	mgP/m${}^3$	Assumption
${\theta }_1$	Phosphorus to carbon quota of autotrophs	0.008	mgP/mgC	[22, 23]
${\theta }_2$	Phosphorus to carbon quota of mixotrophs	0.006	mgP/mgC	[2]
$k_0$	Background light attenuation coefficient	0.5	m${}^{-1}$	[22, 23]
$k_1$	Light absorbance of autotrophs	0.0003	m${}^2$/mgC	[22, 23]
$k_2$	Light absorbance of mixotrophs	0.0003	m${}^2$/mgC	Assumption
$v_1$	Autotroph sinking velocity	0.08	m/day	[22, 23]
$v_2$	Mixotroph sinking velocity	0.08	m/day	[22, 23]
D	Water exchange rate	0.02	m·day${}^{-1}$	[23]
a	Attack rate of mixotrophs on autotrophs	0.05	day${}^{-1}$	[14]
e	Conversion rate of autotrophs to mixotrophs	0.83	–	[2]
β	Half-saturation constant for autotroph ingestion	100	mgC/m${}^3$	Assumption
α	Curvature of Holling type functional responses	2	–	[24, 25]
${\delta }_1$	Proportion of nutrient in autotrophs losses that is recycled	0.5	–	[21]
${\delta }_2$	Proportion of nutrient in mixotrophs losses that is recycled	0.5	–	[21]
L	Depth of the water	10	m	Assumption

Light from the water surface is absorbed by the water body and phytoplankton. The light intensity at depth z can be described by the Lambert–Beer law [7] as $I(z,A,M)=I_{in}\exp (-k_{0}z-(k_{1}A+k_{2}M)z),0<z<L.$The growth of autotrophs or mixotrophs in the autotrophic situation are limited by the light intensity $I(z,A,M)$ and dissolved nutrients N. It takes the form of multiplication of the two [8, 23, 29] and is expressed as $r_i{H}_i(I_{in},A,M)F_i(N)=r_i\frac{1}{L}{\int }_0^L{\tilde{H}}_i(I(z,A,M))\mathrm{d}z{F}_i(N),i=1,2.$Here, we assume that ${\tilde{H}}_i,F_i$ satisfy (1) $\begin{array}{rl}& {\tilde{H}}_i(0)=0,0\le {\tilde{H}}_i<1,\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }A}<0\mathrm{and}\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }M}<0,i=1,2,\\ & F_i(0)=0,0\le F_i<1,F_i^{\prime }(N)>0\mathrm{and}\underset{N\to \mathrm{\infty }}{lim}{F}_i(N)=1,i=1,2.\end{array}$(1) Typical expressions for ${\tilde{H}}_i$ and $F_i$ are Monod functions [8, 23]: (2) ${\tilde{H}}_i(I(z,A,M))=\frac{I(z,A,M)}{I(z,A,M)+h_i},F_i(N)=\frac{N}{N+{\gamma }_i},i=1,2.$(2) In the heterotrophic condition, mixotrophs supply their own growth by ingesting autotrophic organisms [14, 24, 25]. The predation rate of mixotrophs to autotrophs is $G(A)$, where $G(A)$ is assumed to satisfy $G(0)=0,G^{\prime }(A)>0.$Based on the principle of ecological stoichiometry [11], the conversion rate satisfies $e\le min\{{\theta }_1/{\theta }_2,1\}$.

The reduction of biomass of autotrophs and mixotrophs mainly contains lost biomass $m_{1}A,m_{2}M$ due to death and respiration, sinking biomass $v_{1}A/L,v_{2}M/L$ and water exchange biomass $DA/L,DM/L$ [23]. In addition, the predation of mixotrophs will also lead to the decline of autotrophic biomass.

The change of dissolved nutrients N consists of three parts. The first part depends on consumption by autotrophs and mixotrophs with a consumption rate ${\theta }_i{r}_i{H}_i(I_{in},A,M)F_i(N),i=1,2.$The second part is nutrient recycling from the loss of autotrophic and mixotrophic with recycling proportion ${\delta }_1,{\delta }_2$ and the nutrients to carbon quota ${\theta }_1,{\theta }_2$. The last part is nutrient exchange $(D/L)(N_{in}-N)$ at the bottom of the water column or epilimnion, where $N_{in}$ is a fixed nutrient input concentration.

According to the above discussion, we have the following autotroph–mixotroph interaction model in a well-mixed aquatic environment: (3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) Considering the biological significance of (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ), we assume that all the parameters in Table 1 are positive and ${\delta }_1,{\delta }_2\in [0,1],0<e\le min\{{\theta }_1/{\theta }_2,1\}$. By using rigorous mathematical arguments, we can draw the conclusion that for any positive initial value, (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) admits a unique positive solution defined for all $t\ge 0$.

3. Qualitative analysis

In this section, we explore the dynamics of (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) containing dissipation of the solutions, the existence and stability of non-negative steady-state solutions. The following theorem concludes the positive invariance and dissipation of the solutions of model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ).

Theorem 3.1

The system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) is dissipative.

Proof.

Let $W=N+{\theta }_{1}A+{\theta }_{2}M$, which is the total nutrients in system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ). A direct calculation gives $\begin{array}{rl}\frac{\mathrm{d}W}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-W)-\frac{{\theta }_1{v}_{1}A+{\theta }_2{v}_{2}M}{L}\\ & -(1-{\delta }_1){\theta }_1{m}_{1}A-(1-{\delta }_1){\theta }_2{m}_{2}M-a({\theta }_1-e{\theta }_2)G(A)M\\ & \le \frac{D}{L}(N_{in}-W).\end{array}$This implies that $lim\underset{t\to \mathrm{\infty }}{sup}W(t)\le N_{in}$ and the system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) is dissipative.

Let $\mathrm{\Delta }:=\{(A,M,N)\in {\mathbb{R}}_{+}^3|N+{\theta }_{1}A+{\theta }_{2}M\le N_{in}\}.$It follows from Theorem 3.1 that Δ is a global attracting region of system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) and positively invariant.

3.1. Semi-trivial steady states

It follows from (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) that the possible non-negative semi-trivial steady states are listed below:

1. Nutrient-only semi-trivial steady state $E_0:(0,0,N_{in})$.

2. Nutrient-autotroph semi-trivial steady state $E_a:(A_a,0,N_a)$, where $A_a,N_a$ satisfy (4) $\begin{array}{rl}& r_1{F}_1(N)H_1(I_{in},A,0)-m_1-\frac{v_1+D}{L}=0,\\ & \frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A=0.\end{array}$(4)

3. Nutrient-mixotroph semi-trivial steady state $E_m:(0,M_m,N_m)$, where $M_m,N_m$ satisfy $\begin{array}{rl}& r_2{F}_2(N)H_2(I_{in},0,M)-m_2-\frac{v_2+D}{L}=0,\\ & \frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M=0.\end{array}$

We define the following ecological reproductive indexes for autotrophs and mixotrophs: $R_0^A:=\frac{r_1{F}_1(N_{in})H_1(I_{in},0,0)}{m_1+(v_1+D)/L},R_0^M:=\frac{r_2{F}_2(N_{in})H_2(I_{in},0,0)}{m_2+(v_2+D)/L}$and $\begin{array}{rl}{R}_1^A& :=\frac{r_1{F}_1(N_m)H_1(I_{in},0,M_m)-a{G}^{\prime }(0)M_m}{m_1+(v_1+D)/L},\\ R_1^M& :=\frac{r_2{F}_2(N_a)H_2(I_{in},A_a,0)+eaG(A_a)}{m_2+(v_2+D)/L}.\end{array}$As an indicator of viability for autotrophs or mixotrophs, $R_i^A(R_i^M)$, i = 0, 1, describe the average number of new autotrophs (mixotrophs) produced by one cubic metre of autotrophs (mixotrophs) in a life cycle of autotrophs (mixotrophs). In the following discussion, it is shown that $R_i^A$ and $R_i^M$, i = 0, 1 are four critical values for autotrophs and mixotrophs to invade aquatic ecosystems, respectively.

The following result shows that (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) always has a unique nutrient-only semi-trivial steady state $E_0$, which is also stable in terms of the ecological reproductive index $max\{R_0^A,R_0^M\}<1$.

Theorem 3.2

$E_0$ always exists and it is globally asymptotically stable if $max\{R_0^A,R_0^M\}<1$, while $E_0$ is unstable if $max\{R_0^A,R_0^M\}>1$.

Proof.

It is clear that $E_0$ always exists. The Jacobian matrix at $E_0$ is $J(E_0)=\left(\begin{array}{ccc}{a}_{11}& 0& 0\\ 0& a_{22}& 0\\ a_{31}& a_{32}& -D/L\end{array}\right),$where $\begin{array}{rl}{a}_{11}& =r_1{F}_1(N_{in})H_1(I_{in},0,0)-m_1-\frac{v_1+D}{L},a_{31}={\delta }_1{\theta }_1{m}_1-{\theta }_1{r}_1{F}_1(N_{in})H_1(I_{in},0,0),\\ a_{22}& =r_2{F}_2(N_{in})H_2(I_{in},0,0)-m_2-\frac{v_2+D}{L},a_{32}={\delta }_2{\theta }_2{m}_2-{\theta }_2{r}_2{F}_2(N_{in})H_2(I_{in},0,0).\end{array}$If $max\{R_0^A,R_0^M\}<1$, then real parts of all the eigenvalues of the characteristic equation of $J(E_0)$ are negative. This implies that $E_0$ is locally asymptotically stable. On the contrary, if $max\{R_0^A,R_0^M\}>1$, then $E_0$ is unstable.

It follows from Theorem 3.1 that $lim\underset{t\to \mathrm{\infty }}{sup}N(t)\le N_{in}$. From (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ), we have $\frac{\mathrm{d}A}{\mathrm{d}t}\le r_1{F}_1(N_{in})H_1(I_{in},0,0)A-m_{1}A-\frac{v_1+D}{L}A$for sufficiently large t. This means that $lim\underset{t\to \mathrm{\infty }}{sup}A(t)=0$ if $R_0^A<1$. The second Equation of (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) becomes $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M\\ & \le r_2{F}_2(N_{in})H_2(I_{in},0,0)M-m_{2}M-\frac{v_2+D}{L}M.\end{array}$By the comparison theorem, $lim\underset{t\to \mathrm{\infty }}{sup}M(t)=0$ if $R_0^M<1$. By using the theory of asymptotical autonomous systems [13], model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) can reduce to a limiting system $\frac{\mathrm{d}N}{\mathrm{d}t}=\frac{D}{L}(N_{in}-N).$This implies that $\underset{t\to \mathrm{\infty }}{lim}N(t)=N_{in}$ and $E_0$ is globally attractive. Then $E_0$ is globally asymptotically stable.

Remark 3.1

$max\{R_0^A,R_0^M\}$ is a critical value for algae to survive in a well-mixed aquatic environment. It is affected by the nutrient input concentration $N_{in}$ and the water surface light intensity $I_{in}$. It can be observed directly that $max\{R_0^A,R_0^M\}$ is increasing with respect to $N_{in}$ and $I_{in}$. This means that the high light intensity and nutrient input concentration are conducive to the invasion of algae.

Theorem 3.3

1. $E_a$ exists and is unique if and only if $R_0^A>1$ .

2. If $R_1^M<1$, then $E_a$ is locally asymptotically stable, while $E_a$ is unstable if $R_1^M>1$.

Proof.

From (4(4) $\begin{array}{rl}& r_1{F}_1(N)H_1(I_{in},A,0)-m_1-\frac{v_1+D}{L}=0,\\ & \frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A=0.\end{array}$(4) ), we have $\begin{array}{rl}& {\mathrm{\Lambda }}_1(A):=N_{in}-\left[\frac{L(1-{\delta }_1){\theta }_1{m}_1+(v_1+D){\theta }_1}{D}\right]A,\\ & {\mathrm{\Lambda }}_2(A):=F^{-1}\left(\frac{m_1+(v_1+D)/L}{r_1{H}_1(I_{in},A,0)}\right).\end{array}$Note that ${\mathrm{\Lambda }}_1(A)$ is strictly monotone decreasing with respect to A with $\underset{A\to 0^{+}}{lim}{\mathrm{\Lambda }}_1(A)=N_{in}.$ It follows from (1(1) $\begin{array}{rl}& {\tilde{H}}_i(0)=0,0\le {\tilde{H}}_i<1,\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }A}<0\mathrm{and}\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }M}<0,i=1,2,\\ & F_i(0)=0,0\le F_i<1,F_i^{\prime }(N)>0\mathrm{and}\underset{N\to \mathrm{\infty }}{lim}{F}_i(N)=1,i=1,2.\end{array}$(1) ) that ${\mathrm{\Lambda }}_2(A)$ is strictly monotone increasing with respect to A with $\underset{A\to 0^{+}}{lim}{\mathrm{\Lambda }}_2(A)=F^{-1}\left(\frac{m_1+(v_1+D)/L}{r_1{H}_1(I_{in},0,0)}\right).$Then there exists a unique positive $A_a$ such that ${\mathrm{\Lambda }}_1(A_a)={\mathrm{\Lambda }}_2(A_a)$ if and only if $R_0^A>1$. From the first equality of (4(4) $\begin{array}{rl}& r_1{F}_1(N)H_1(I_{in},A,0)-m_1-\frac{v_1+D}{L}=0,\\ & \frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A=0.\end{array}$(4) ), $N_a$ can be explicitly solved.

The Jacobian matrix at $E_a$ is $J(E_a)=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ 0& a_{22}& 0\\ a_{31}& a_{32}& a_{33}\end{array}\right),$where $\begin{array}{rl}{a}_{11}& =r_1{F}_1(N_a)\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }A}{A}_a,a_{12}=r_1{F}_1(N_a)\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }M}{A}_a-aG(A_a),\\ a_{13}& =r_1{F}_1^{\prime }(N_a)H_1{A}_a,a_{22}=r_2{F}_2(N_a)H_2-m_2-\frac{v_2+D}{L}+eaG(A_a),\\ a_{31}& ={\delta }_1{\theta }_1{m}_1-{\theta }_1{r}_1{F}_1(N_a)(\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }A}{A}_a+H_1),a_{33}=-\frac{D}{L}-{\theta }_1{r}_1{F}_1^{\prime }(N_a)H_1{A}_a,\\ a_{32}& ={\delta }_2{\theta }_2{m}_2-{\theta }_1{r}_1{F}_1(N_a)\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }M}{A}_a-{\theta }_2{r}_2{F}_2(N_a)H_2.\end{array}$From (1(1) $\begin{array}{rl}& {\tilde{H}}_i(0)=0,0\le {\tilde{H}}_i<1,\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }A}<0\mathrm{and}\frac{\mathrm{\partial }{\tilde{H}}_i}{\mathrm{\partial }M}<0,i=1,2,\\ & F_i(0)=0,0\le F_i<1,F_i^{\prime }(N)>0\mathrm{and}\underset{N\to \mathrm{\infty }}{lim}{F}_i(N)=1,i=1,2.\end{array}$(1) ), we have $H_1(0,0,0)=0,0\le H_1(I_{in},A,M)<1,\frac{\mathrm{\partial }{H}_1(I_{in},A,M)}{\mathrm{\partial }A}<0,\frac{\mathrm{\partial }{H}_1(I_{in},A,M)}{\mathrm{\partial }M}<0.$A direct calculation gives $\begin{array}{rl}& a_{11}+a_{33}=r_1{F}_1(N_a)\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }A}{A}_a-\frac{D}{L}-{\theta }_1{r}_1{F}_1^{\prime }(N_a)H_1{A}_a<0,\\ & a_{11}{a}_{33}-a_{13}{a}_{31}=-\frac{D}{L}{r}_1{F}_1(N_a)\frac{\mathrm{\partial }{H}_1}{\mathrm{\partial }A}{A}_a+{\theta }_1{r}_1((1-{\delta }_1)m_1+\frac{D}{L})F_1^{\prime }(N)H_1{A}_a>0.\end{array}$If $R_1^M<1$, then $a_{22}<0$. To conclude, we have $a_{11}+a_{33}<0,a_{11}{a}_{33}-a_{13}{a}_{31}>0,a_{22}<0.$This shows that the real parts of all the eigenvalues of the characteristic equation of $J(E_a)$ are negative. Hence we conclude that if $R_1^M<1$, then $E_a$ is locally asymptotically stable; Conversely, if $R_1^M>1$, then $E_a$ is unstable.

Remark 3.2

The conclusion in Theorem 3.3 reveals that $R_0^A$ is a critical value for autotrophs from extinction to survival. If $R_1^M<1$, then autotrophs win the competition in the intraguild predation and dominate the whole aquatic ecosystem. This implies that $R_1^M$ is a threshold value for mixotrophs to survive in the water ecosystem in the presence of autotrophs.

Theorem 3.4

1. $E_m$ exists and is unique if and only if $R_0^M>1$ .

2. If $R_1^A<1$, then $E_m$ is locally asymptotically stable, while $E_m$ is unstable if $R_1^A>1$.

Proof.

The proof of (i) has many similarities with Theorem 3.3. Then, we omit the proof process here. The Jacobian matrix at $E_m$ is $J(E_m)=\left(\begin{array}{ccc}{a}_{11}& 0& 0\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right),$where $\begin{array}{rl}{a}_{11}& =r_1{F}_1(N_m)H_1-m_1-\frac{v_1+D}{L}-a{G}^{\prime }(0)M_m,a_{22}=r_2{F}_2(N_m)\frac{\mathrm{\partial }{H}_2}{\mathrm{\partial }M}{M}_m,\\ a_{21}& =r_2{F}_2(N_m)\frac{\mathrm{\partial }{H}_2}{\mathrm{\partial }A}{M}_m+ea{G}^{\prime }(0)M_m,a_{23}=r_2{F}_2^{\prime }(N_m)H_2{M}_m,\\ a_{32}& ={\delta }_2{\theta }_2{m}_2-{\theta }_2{r}_2{F}_2(N_m)(\frac{\mathrm{\partial }{H}_2}{\mathrm{\partial }M}{M}_m+H_2),a_{33}=-\frac{D}{L}-{\theta }_2{r}_2{F}_2^{\prime }(N_m)H_2{M}_m,\\ a_{31}& ={\delta }_1{\theta }_1{m}_1-{\theta }_1{r}_1{F}_1(N_m)H_1-{\theta }_2{r}_2{F}_2(N_m)\frac{\mathrm{\partial }{H}_2}{\mathrm{\partial }A}{M}_m.\end{array}$Similar to the proof of Theorem 3.3, we prove that the real parts of eigenvalues of $J(E_m)$ are all negative if $R_1^A<1$, which means that $E_m$ is locally asymptotically stable. On the contrary, $E_m$ is unstable if $R_1^A>1$.

Remark 3.3

Theorem 3.4 shows that $E_m$ exists if $R_0^M>1$ and $R_0^M$ is the index of threshold determining the survival of mixotrophs. Here, we only obtain the local stability of $E_m$. Actually, our numerical simulations indicate that $E_m$ should be globally asymptotically stable. This means that if $R_1^A<1$, then mixotrophs win the competition in the intraguild predation structure. Autotrophs invade successfully only when $R_1^A>1$.

3.2. Coexistence steady states

This subsection is to explore the existence of the coexistence solution $E_c:(A_c,M_c,N_c)$ by using the method of repellers and persistence in Zhao [30].

We first consider the following autotroph-nutrient model and mixotroph-nutrient model: (5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) and (6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) From Theorem 3.1, we find that the sets ${\mathrm{\Delta }}_1=\{(A,N)\in {\mathbb{R}}_{+}^2|N+{\theta }_{1}A\le N_{in}\},{\mathrm{\Delta }}_2=\{(M,N)\in {\mathbb{R}}_{+}^2|N+{\theta }_{2}M\le N_{in}\}$are global attracting regions and positively invariant sets of (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) and (6(6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) ), respectively. We next show the global asymptotic stability of the positive steady states of (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) and (6(6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) ).

Lemma 3.5

1. If $R_0^A>1$, then model (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) holds a unique positive equilibrium ${\overline{E}}_a(A_a,N_a)$, which is globally asymptotically stable;

2. If $R_0^M>1$, then model (6(6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) ) holds a unique positive equilibrium ${\overline{E}}_m(M_m,N_m)$, which is globally asymptotically stable.

Proof.

The uniqueness, existence and local asymptotic stability of ${\overline{E}}_a,{\overline{E}}_m$ can be obtained from Theorems 3.3 and 3.4. We show that there is no periodic orbit of (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) in ${\mathrm{\Delta }}_1$ by using Dulac's criterion. Let $\begin{array}{rl}{K}_1(A,N)& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ K_2(A,N)& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A.\end{array}$Choose $D(A,N)=1/A$ as a Dulac function. Then $\frac{\mathrm{\partial }(D{K}_1(A,N))}{\mathrm{\partial }A}+\frac{\mathrm{\partial }(D{K}_2(A,N))}{\mathrm{\partial }N}=r_1{F}_1(N)\frac{\mathrm{\partial }{H}_1(I_{in},A,0)}{\mathrm{\partial }A}-\frac{D}{AL}-{\theta }_1{r}_1{F}_1^{\prime }(N)H_1<0.$This implies that (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) has no positive periodic orbit in ${\mathrm{\Delta }}_1$. When $R_0^A>1$, $\overline{E}$ is globally asymptotically stable for (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ) by using the Poincare–Bendixson criterion. Similarly, ${\overline{E}}_m$ is also globally asymptotically stable for (6(6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) ) when $R_0^M>1$.

In order to study the existence of $E_c$, we assume that $\mathrm{\Phi }(t):\mathrm{\Delta }\to \mathrm{\Delta }$ is the semiflow generated by system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) and $\mathrm{\Phi }(t)(A(0),M(0),N(0))=(A(t),M(t),N(t))$ for all $t\ge 0$ with the initial value $(A(0),M(0),N(0))\in {\mathbb{R}}_{+}^3$. Let $\begin{array}{rl}{\mathrm{\Delta }}_0& :=\{(A,M,N)\in \mathrm{\Delta }:A>0\mathrm{and}M>0\},\\ \mathrm{\partial }{\mathrm{\Delta }}_0& :=\mathrm{\Delta }\setminus {\mathrm{\Delta }}_0=\{(A,M,N)\in \mathrm{\Delta }:A=0\mathrm{or}M=0\}\end{array}$and $\mathrm{\Lambda }:=\{(A_0,M_0,N_0)\in \mathrm{\partial }{\mathrm{\Delta }}_0:\mathrm{\Phi }(t)(A_0,M_0,N_0)\in \mathrm{\partial }{\mathrm{\Delta }}_0\mathrm{for}\mathrm{all}t\in {\mathbb{R}}^{+}\}.$From Theorem 3.1 and uniqueness of solutions, Δ and ${\mathrm{\Delta }}_0$ are positively invariant for system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ).

We are in a position to establish the existence of the coexistence steady-state solution $E_c$.

Theorem 3.6

Assume that $R_0^A>1$, $R_0^M>1$. If $R_1^A>1$ and $R_1^M>1$, then system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) is uniformly persistent with respect to $({\mathrm{\Delta }}_0,\mathrm{\partial }{\mathrm{\Delta }}_0)$ in the sense that there is a positive constant $ϵ>0$ such that $\underset{t\to \mathrm{\infty }}{lim inf}A(t)>ϵ\mathrm{and}\underset{t\to \mathrm{\infty }}{lim inf}M(t)>ϵ.$Moreover, system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) has at least one positive steady state solution $E_c$.

Proof.

We first prove that the omega limit set $\omega (q)=\{E_0,E_a,E_m\}$ of the orbit with the initial value $q(A_0,M_0,N_0)\in \mathrm{\partial }{\mathrm{\Delta }}_0$. For any $q(A_0,M_0,N_0)\in \mathrm{\partial }{\mathrm{\Delta }}_0$, we have $\mathrm{\Phi }(t)q\in \mathrm{\partial }{\mathrm{\Delta }}_0$ and consider the following three cases: (1) $A_0=0,M_0=0$; (2) $A_0=0,M_0\ne 0$; (3) $A_0\ne 0,M_0=0$.

Case (1): $A_0=0,M_0=0$. Then, we get $A(t,q)=0$ and $M(t,q)=0$ for any $t\ge 0$. From Theorem 3.2, $(A(t,q),M(t,q),N(t,q))\to (0,0,N_b)$ as $t\to \mathrm{\infty }$;

Case (2): $A_0=0,M_0\ne 0$. Then, we obtain $A(t,q)=0$ for any $t\ge 0$. This shows that $(M(t,q),N(t,q))$ satisfies (6(6) $\begin{array}{rl}\frac{\mathrm{d}M}{\mathrm{d}t}& =r_2{F}_2(N)H_2(I_{in},0,M)M-m_{2}M-\frac{v_2+D}{L}M,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_2{\theta }_2{m}_{2}M-{\theta }_2{r}_2{F}_2(N)H_2(I_{in},0,M)M.\end{array}$(6) ). By Lemma 3.5, $(M(t,q),N(t,q))\to (M_m,N_m)$ as $t\to \mathrm{\infty }$;

Case (3): $A_0\ne 0,M_0=0$. Then, we have $M(t,q)=0$ for any $t\ge 0$ and $(A(t,q),N(t,q))$ satisfies (5(5) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =r_1{F}_1(N)H_1(I_{in},A,0)A-m_{1}A-\frac{v_1+D}{L}A,\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\frac{D}{L}(N_{in}-N)+{\delta }_1{\theta }_1{m}_{1}A-{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,0)A\end{array}$(5) ). From Lemma 3.5, we have $(A(t,q),N(t,q))\to (A_a,N_a)$ as $t\to \mathrm{\infty }$.

In view of cases (1)–(3), we have $\omega (q)=\{E_0,E_a,E_m\}$ for any $q\in \mathrm{\partial }{\mathrm{\Delta }}_0$. From $R_0^A>1$ and $R_1^M>1$, we let $\begin{array}{rl}{\delta }_1& =\frac{1}{2}(r_1{F}_1(N_{in})H_1(I_{in},0,0)-m_1-\frac{v_1+D}{L})>0,\\ {\delta }_2& =\frac{1}{2}(r_2{F}_2(N_a)H_2(I_{in},A_a,0)+eaG(A_a)-m_2-\frac{v_2+D}{L})>0.\end{array}$We then show that $E_0,E_a,E_m$ are uniform weak repellers for ${\mathrm{\Delta }}_0$. Then it follows that there exists a $\epsilon >0$ so that (7a) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_0)\ge \epsilon ,\end{array}$(7a) (7b) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_a)\ge \epsilon ,\end{array}$(7b) (7c) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_m)\ge \epsilon \end{array}$(7c) for any $q(A_0,M_0,N_0)\in {\mathrm{\Delta }}_0$ and $t\ge 0$. If (7a(7a) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_0)\ge \epsilon ,\end{array}$(7a) ) does not hold, then there exists a $q^0\in {\mathrm{\Delta }}_0$ such that $\underset{t\to \mathrm{\infty }}{lim sup}\text{dist}(\mathrm{\Phi }(t)q^0,E_0)<{\delta }_1.$This means that there exists a $T_1>0$ such that (8) $|N(t,q^0)-N_{in}|<{\delta }_1,|A(t,q^0)|<{\delta }_1\mathrm{for}\mathrm{all}t\ge T_1.$(8) Then $r_1{F}_1(N)H_1(I_{in},A,0)-m_1-\frac{v_1+D}{L}>r_1{F}_1(N_{in})H_1(I_{in},0,0)-m_1-\frac{v_1+D}{L}-{\delta }_1={\delta }_1$and $\frac{\mathrm{d}A(t,q^0)}{\mathrm{d}t}>{\delta }_{1}A(t,q^0)$for any $t\ge T_1$. This shows that $A(t,q^0)\to \mathrm{\infty }$ as $t\to \mathrm{\infty }$, which is a contradiction to (8(8) $|N(t,q^0)-N_{in}|<{\delta }_1,|A(t,q^0)|<{\delta }_1\mathrm{for}\mathrm{all}t\ge T_1.$(8) ).

Assume that (7b(7b) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_a)\ge \epsilon ,\end{array}$(7b) ) does not hold, then there exists a $q^a\in {\mathrm{\Delta }}_0$ and $T_2>0$ such that $\underset{t\to \mathrm{\infty }}{lim sup}\text{dist}(\mathrm{\Phi }(t)q^a,E_a)<{\delta }_2$and (9) $|N(t,q^a)-N_a|<{\delta }_2,|A(t,q^a)-A_a|<{\delta }_2,|M(t,q^a)|<{\delta }_2\mathrm{for}\mathrm{all}t\ge T_2.$(9) Note that $\begin{array}{rl}& r_2{F}_2(N)H_2(I_{in},A,M)+eaG(A)-m_2-\frac{v_2+D}{L}\\ & >r_2{F}_2(N_a)H_2(I_{in},A_a,0)+eaG(A_a)-m_2-\frac{v_2+D}{L}-{\delta }_2={\delta }_2\end{array}$for all $t\ge T_2$. Hence $\mathrm{d}M(t,q^a)/\mathrm{d}t>{\delta }_{2}M(t,q^a)$ and $M(t,q^a)\to \mathrm{\infty }$ as $t\to \mathrm{\infty }$. This is a contradiction with (9(9) $|N(t,q^a)-N_a|<{\delta }_2,|A(t,q^a)-A_a|<{\delta }_2,|M(t,q^a)|<{\delta }_2\mathrm{for}\mathrm{all}t\ge T_2.$(9) ). Similarly, (7c(7c) $\begin{array}{rl}& \underset{t\to \mathrm{\infty }}{lim sup}\mathrm{dist}(\mathrm{\Phi }(t)q,E_m)\ge \epsilon \end{array}$(7c) ) holds.

It follows from Theorem 3.1 that $\mathrm{\Phi }(t)$ is point dissipative and compact, and then $\mathrm{\Phi }(t)$ has a global attractor in Δ. From the above analysis, we obtain the following conclusions: (i) $\{E_0,E_a,E_m\}$ is disjoint, compact, and isolated invariant sets in $\mathrm{\partial }{\mathrm{\Delta }}_0$; (ii) ${\cup }_{q\in \mathrm{\partial }{\mathrm{\Delta }}_0}\omega (q)=\{E_0,E_a,E_m\}$; (iii) $E_0$, $E_a$ and $E_m$ are isolated in Δ; (iv) no subset of $E_0$, $E_a$ and $E_m$ forms a cycle in $\mathrm{\partial }{\mathrm{\Delta }}_0$; (v) $W^s(E_i)\cap {\mathrm{\Delta }}_0=\mathrm{\varnothing }$, i = 0, a, m, where $W^s(E_i)$ is the stable set of $E_i$. By Theorem 1.3.1 in Zhao [30], we have $\mathrm{\Phi }(t):\mathrm{\Delta }\to \mathrm{\Delta }$ is uniformly persistent with respect to $({\mathrm{\Delta }}_0,\mathrm{\partial }{\mathrm{\Delta }}_0)$. According to Theorem 1.3.6 in Zhao [30], there exists a global attractor for $\mathrm{\Phi }(t)$ in ${\mathrm{\Delta }}_0$ and $\mathrm{\Phi }(t)$ has at least one fixed point $(A_c,M_c,N_c)\in {\mathrm{\Delta }}_0$, which is a coexistence steady state solution of system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ). This completes the proof.

Remark 3.4

In the intraguild predation structure, autotrophs and mixotrophs can coexist in an aquatic ecosystem if the conditions of Theorem 3.6 hold. This suggests that the intraguild predation is an important ecological mechanism in aquatic communities. It is beneficial to phytoplankton biodiversity, and provides an explanation for the phytoplankton paradox.

Remark 3.5

$R_i^A,R_i^M>1$, i = 0, 1 are only sufficient conditions for the coexistence of autotrophs and mixotrophs. If this condition does not hold, they can also coexist, such as region ${\mathrm{\Delta }}_4\cup {\mathrm{\Delta }}_5$ in Figure 2. In the next section, our numerical simulations show the coexistence form of autotrophs and mixotrophs is either a positive steady-state solution or a positive periodic solution.

Figure 2. The parameter regions in the $(m_1,m_2)$-plane about the survival of autotrophs and mixotrophs. Here, other parameters are from Table 1.

4. Autotroph and mixotroph coexistence and density

Algae are widely distributed in various aquatic ecosystems, ranging from lakes, rivers to oceans. The coexistence of autotrophic algae and mixotrophic algae in the intraguild predation structure plays an important role in maintaining algal biodiversity and explaining the phytoplankton paradox [14, 24, 25]. The coexistence mechanism can be significantly influenced by some biotic and abiotic factors, such as the structure of functional response functions, light intensity and nutrients input. It is meaningful to investigate the influence of these factors on the coexistence of autotrophs and mixotrophs. The algal biomass density is an essential indicator for forewarning algal blooms and evaluating water quality. Another purpose of the section is to consider the effects of environmental factors on the biomass density of autotrophs and mixotrophs.

In the following discussion, some numerical simulations are done to explore the coexistence and biomass density of autotrophs and mixotrophs based on parameters in biologically reasonable ranges listed in Table 1. Here, there are several parameter values that we assume. Due to the simultaneous autotrophic and heterotrophic activities of mixotrophs, they have lower nutrient and light absorption rates than autotrophs. Hence it is biologically reasonable to assume that ${\gamma }_2\ge {\gamma }_1$, $k_2\le k_1$. The value of β is chosen from the autotrophic biomass density in our numerical simulations. The research background of the current paper is a well-mixed aquatic environment such as shallow lakes or epilimnion. This means that L = 10 m is also consistent with the realistic aquatic environment.

4.1. Autotroph and mixotroph coexistence

We first consider the effect of different functional responses on the coexistence of autotrophs and mixotrophs. To facilitate the following analysis, in view of Theorems 3.2, 3.3, 3.4 and 3.6, we denote $\begin{array}{rl}& m_1^{\ast \ast }:=r_1{F}_1(N_{in})H_1(I_{in},0,0)-(v_1+D)/L,\\ & m_2^{\ast \ast }:=r_2{F}_2(N_{in})H_2(I_{in},0,0)-(v_2+D)/L,\\ & m_1^{\ast }:=r_1{F}_1(N_m)H_1(I_{in},0,M_m)-a{G}^{\prime }(0)M_m-(v_1+D)/L,\\ & m_2^{\ast }:=r_2{F}_2(N_a)H_2(I_{in},A_a,0)+eaG(A_a)-(v_2+D)/L\end{array}$and divide the parameter space of $(m_1,m_2)$ as follows: $\begin{array}{rl}& {\mathrm{\Delta }}_0:=\{(m_1,m_2):m_1>m_1^{\ast \ast },m_2>m_2^{\ast \ast }\},\\ & {\mathrm{\Delta }}_1:=\{(m_1,m_2):0<m_1<m_1^{\ast \ast },m_2>m_2^{\ast }\},\\ & {\mathrm{\Delta }}_2:=\{(m_1,m_2):0<m_2<m_2^{\ast \ast },m_1>m_1^{\ast }\},\\ & {\mathrm{\Delta }}_3:=\{(m_1,m_2):0<m_1<min\{m_1^{\ast \ast },m_1^{\ast }\},0<m_2<min\{m_2^{\ast \ast },m_2^{\ast }\}\},\\ & {\mathrm{\Delta }}_4:=\{(m_1,m_2):0<m_1<m_1^{\ast \ast },m_2^{\ast \ast }<m_2<m_2^{\ast }\},\\ & {\mathrm{\Delta }}_5:=\{(m_1,m_2):0<m_1<m_1^{\ast \ast },m_2^{\ast }<m_2<m_2^{\ast \ast }\}.\end{array}$Here, $m_i^{\ast \ast },m_i^{\ast },i=1,2$ are the critical loss rates for autotrophs and mixotrophs from extinction to survival in an aquatic ecosystem.

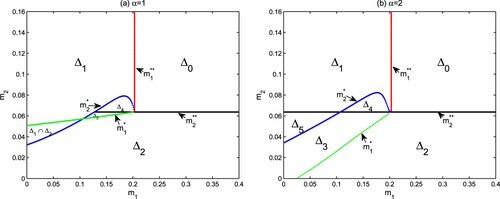
The functional responses are the most important component between predator and prey. Choose (2(2) ${\tilde{H}}_i(I(z,A,M))=\frac{I(z,A,M)}{I(z,A,M)+h_i},F_i(N)=\frac{N}{N+{\gamma }_i},i=1,2.$(2) ) and let (10) $G(A)=\frac{A^{\alpha }}{{\beta }^{\alpha }+A^{\alpha }}.$(10) We consider two classical functional responses: $\alpha =1$ (Holling type II functional response) and $\alpha =2$ (Holling type III functional response). Figure 2 shows the parameter regions in the $(m_1,m_2)$-plane about survival of autotrophs and mixotrophs for different Holling type functional responses. The extinction of both autotrophs and mixotrophs with nutrients reaching the fixed external dissolved nutrients $N_{in}$ ($E_0$) can occur if autotrophic and mixotrophic loss rates are very large (see ${\mathrm{\Delta }}_0$ and Theorem 3.2). The coexistence of autotrophs and dissolved nutrients with the extinction of mixotrophs ($E_1$), and the coexistence of mixotrophs and dissolved nutrients with the extinction of autotrophs ($E_2$) are both possible outcomes of model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) for different parameter ranges (see ${\mathrm{\Delta }}_1$, ${\mathrm{\Delta }}_2$ and Theorems 3.3, 3.4). Autotrophs, mixotrophs and nutrients appear together in aquatic ecosystems (see ${\mathrm{\Delta }}_3$ and Theorem 3.6). The numerical simulations indicate that there are bistable structures in regions ${\mathrm{\Delta }}_1\cap {\mathrm{\Delta }}_2$ and ${\mathrm{\Delta }}_5$, and autotrophs and mixotrophs also coexist in ${\mathrm{\Delta }}_4$.

Model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) has extremely complex dynamic behaviours. From Figure 3, one can see that there are two bistable cases for different values α. The first case is that the semi-trivial steady states $E_a$ and $E_m$ are bistable in ${\mathrm{\Delta }}_1\cap {\mathrm{\Delta }}_2$ with respect to different initial values and $\alpha =1$ (see Figure 3(a)). This is due to the competition between autotrophs and mixotrophs for light and nutrients. Another case is that $E_a$ and $E_c$ or an oscillatory periodic solution are bistable in ${\mathrm{\Delta }}_5$ for $\alpha =2$ (see Figure 3(b,c)). This suggests that the initial values of the model can also determine the coexistence of autotrophs and mixotrophs. From the point of view of actual ecosystems, the initial biomass of autotrophic algae and mixotrophic algae directly affects the final results of competition and coexistence between them.

Figure 3. Bistability of model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ). (a) $E_a$ and $E_m$ are bistable in ${\mathrm{\Delta }}_1\cap {\mathrm{\Delta }}_2$ for $I_{in}=400$, $m_1=0.02$, $m_2=0.04$; (b) $E_a$ and $E_c$ are bistable in ${\mathrm{\Delta }}_5$ for $I_{in}=400$, $m_1=0.05$, $m_2=0.05$; (c) $E_a$ and a positive periodic solution are bistable in ${\mathrm{\Delta }}_5$ for $I_{in}=150$, $m_1=0.05$, $m_2=0.05$. Here, other parameters are from Table 1.

By comparing (a) and (b) in Figure 2, one can observe that there are similarities and many differences between Holling type II functional response ($\alpha =1$) and Holling type III functional response ($\alpha =2$). They all have four situations: algae extinction, only autotrophs, only mixotrophs and coexistence. But there are also some differences between them. One difference is that there are a bistable region ${\mathrm{\Delta }}_1\cap {\mathrm{\Delta }}_2$ of $E_a$ and $E_m$ for $\alpha =1$, and a bistable region ${\mathrm{\Delta }}_5$ of $E_a$ and $E_c$ or a positive periodic solution for $\alpha =2$. Another difference is that autotrophs and mixotrophs have a larger coexistence area ${\mathrm{\Delta }}_3\cup {\mathrm{\Delta }}_4$ for $\alpha =2$. This means that Holling III type functional response is conducive to the coexistence of autotrophs and mixotrophs under the framework of intraguild predation.

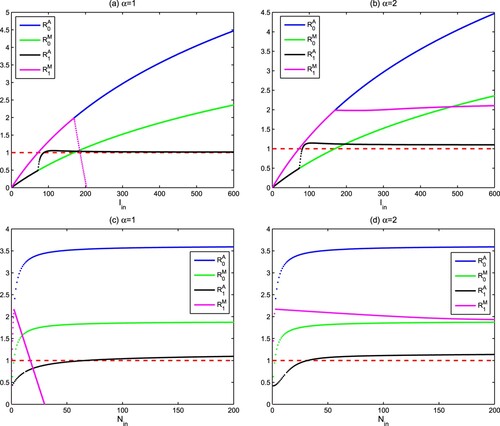
The water surface light intensity $I_{in}$ and the nutrient input concentration $N_{in}$ are two important abiotic factors in aquatic ecosystems. They will change with the seasons and climate. Figure 4 shows the influence of $I_{in}$ and $N_{in}$ on the ecological reproductive indexes $R_i^A,R_i^M$, i = 0, 1 for different Holling type functional responses. From Figure 4(a,c), it is found that $R_0^A,R_0^M,R_1^A$ will increase and exceed the threshold 1 if $I_{in}$ and $N_{in}$ raise. While $R_1^M$ exhibits a rapid increase above 1, followed by a rapid decrease below 1. This makes the region with $R_{\ast }:=min\{R_0^A,R_0^M,R_1^A,R_1^M\}>1$ very small. On the contrary, it can be seen from Figure 4(b) that there is a unique threshold value about light $I_{in}^{\ast }$ so that $R_{\ast }>1$ if $I_{in}>I_{in}^{\ast }$. Similarly there also is a unique threshold value about nutrient $N_{in}^{\ast }$ so that $R_{\ast }>1$ if $N_{in}>N_{in}^{\ast }$ (see Figure 4(d)). The above analysis shows that high light intensity $I_{in}$ and nutrient concentration $N_{in}$ are beneficial to the existence of autotrophs and mixotrophs for Holling III type functional response. This research also suggests that the intraguild predation structure can be used to explain the phytoplankton paradox, especially when (10(10) $G(A)=\frac{A^{\alpha }}{{\beta }^{\alpha }+A^{\alpha }}.$(10) ) is Holling III type functional response.

Figure 4. Influence of the water surface light intensity $I_{in}$ and the nutrient input concentration $N_{in}$ on the ecological reproductive indexes $R_i^A,R_i^M$, i = 0, 1. (a,b) $N_{in}=80$; (c,d) $I_{in}=400$. Here, $m_2=0.6$ and other parameters are from Table 1.

4.2. Biomass density

The biomass density of autotrophic algae and mixotrophic algae as an important indicator of algal blooms is closely related to some important environmental parameters. For example, L and D are parameters relevant to water depth and movement; $I_{in}$ and $k_0$ are parameters about light; $N_{in},{\theta }_1,{\theta }_2$ are parameters related to nutrients; ${\delta }_1,{\delta }_2$ are parameters related to water temperature and organic carbon degradation; Parameter a describes the heterotrophic activity of mixotrophs. In the following study, we use the Holling type II functional response ($\alpha =2$) and explore the effects of environmental factors in system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) on the density of autotrophs and mixotrophs.

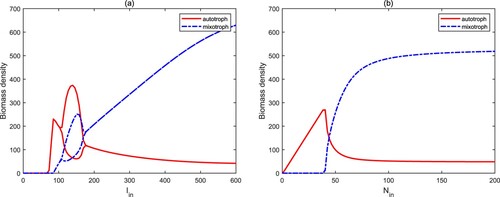
From Figure 5(a), one can observe that if the surface light density $I_{in}$ is very low, both autotrophic algae and mixotrophic algae will become extinct ($E_0$). As light intensity increases gradually, autotrophs can invade the aquatic ecosystems and occupy a dominant position ($E_a$). When the light intensity is high, there is a regime transition from autotrophs to mixotrophs, and mixotrophs dominate the whole aquatic ecosystems. In this process, the numerical bifurcation diagram implies that there exist two stability switches for $I_{in}$. Figure 5(b) shows a similar process for the nutrient input concentration $N_{in}$ from $E_0$, $E_a$ to $E_c$. 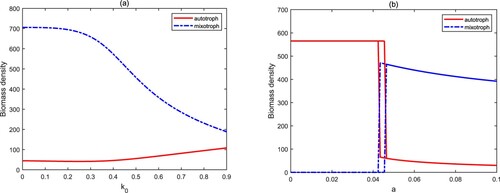The reason for the above phenomenons is that although high light intensity and nutrient input concentration are conducive to the growth of autotrophs and mixotrophs, the high biomass of mixotrophic algae will cause the rapid decrease of the biomass of autotrophic algae due to the predation between the two. Therefore, mixotrophic algae are more prone to blooms for high light intensity and nutrient concentration because of intraguild predation.

Figure 5. Bifurcation diagrams of autotrophs and mixotrophs for $I_{in}\in (0,600)$ and $N_{in}\in (0,200)$. Here, other parameters are from Table 1.

The light attenuation coefficient $k_0$ is used to describe the turbidity of water quality. From Figure 6(a), we find that the increase of $k_0$ causes a positive effect on autotrophs and a negative effect on mixotrophs. This means that the clear water is more favourable for mixotrophs in the framework of intraguild predation. The attack rate a is an important parameter to assess the heterotrophic activity of mixotrophs. Figure 6(b) shows three stages: autotroph-only $E_a$, the bistability of $E_a$ and $E_c$ and the coexistence $E_c$. When the value of a is low, which implies that mixotrophs mainly carry out autotrophic activities, the biomass of autotrophs is high, but that of mixotrophs is low. This suggests that autotrophs are a powerful competitor and limit the growth of mixotrophs in an aquatic ecosystem since mixotrophs have a lower growth rate. When the attack rate a varies in high level, we observed the opposite phenomenon because of the enhancement of predation. In the bistable stage, the final biomass density of autotrophs and mixotrophs is directly determined by their initial biomass. Therefore, high heterotrophic activity raises the probability of mixotrophic algal blooms, and conversely, the possibility of autotrophic algal blooms will increase.

Figure 6. Bifurcation diagrams of autotrophs and mixotrophs for $k_0\in (0.1,0.9)$ and $a\in (0,0.1)$. Here, other parameters are from Table 1.

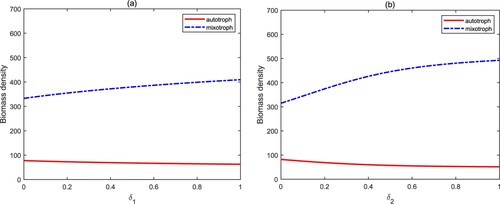
The parameter ${\delta }_1$ and ${\delta }_2$ describe the nutrient recycling proportions, which are closely related and proportional to the degradation rate of bacterial organic carbon and the internal temperature of the water. It has been shown that the increase of the nutrient recycling proportion causes a sharp increase in the biomass of algae, and finally leads to the occurrence of algal blooms [27, 28]. Figure 7 exhibits a different situation from the past. The biomass density of autotrophs and mixotrophs does not change, or only slightly increases. This is mainly attributed to the intraguild predation structure between autotrophs and mixotrophs. Mixotrophs control autotrophic algae by predation. On the contrary, autotrophs suppress mixotrophic algae through competition.

Figure 7. Bifurcation diagrams of autotrophs and mixotrophs for ${\delta }_1\in (0,1)$ and ${\delta }_2\in (0,1)$. Here, other parameters are from Table 1.

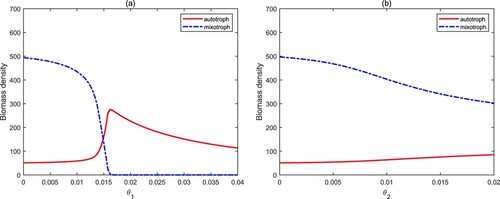
The quota of nutrients to carbon in algal cells describes the quality of algae, and it is constantly changing [10, 11, 17]. From Figure 8(a), we find that when ${\theta }_1$ varies in low level, the biomass density of mixotrophs is higher than that of autotrophs when they coexist. Although the growth of autotrophs needs lower nutrients, which means that they should have higher biomass, the biomass of autotrophs did not increase significantly. This is mainly due to the predation of mixotrophs. When ${\theta }_1$ increases in high level, we get an opposite result. Mixotrophs are extinct, and autotrophs have become a dominator in aquatic ecosystems. In this case, autotrophs consume more nutrients, leading to the extinction of mixotrophs through competition. In comparison, ${\theta }_2$ only causes little effect on the biomass density of autotrophs and mixotrophs (see Figure 8(b)).

Figure 8. Bifurcation diagrams of autotrophs and mixotrophs for ${\theta }_1\in (0,0.04)$ and ${\theta }_2\in (0,0.02)$. Here, other parameters are from Table 1.

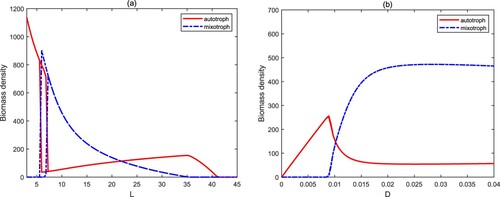
The water depth L has an important effect on the biomass density of autotrophs and mixotrophs. With the increase of the water depth L, model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) has four situations: autotroph-only $E_a$, the bistability of $E_a$ and $E_c$, the coexistence $E_c$, and the extinction $E_0$ (see Figure 9(a)). Their total biomass is gradually decreasing. It also confirms once again that the shallow aquatic systems are more prone to algal blooms. The exchange rate D characterizes the water movement, which is mainly caused by wind and the density difference of water body. A low value of D means less nutrient input. Mixotrophs are extinct since they are at a disadvantage in competing with autotrophs for nutrients. The high exchange rate (D) is conducive to the coexistence of autotrophs and mixotrophs, and mixotrophs have more biomass (see Figure 9(b)).

Figure 9. Bifurcation diagrams of autotrophs and mixotrophs for $D\in (0,0.04)$ and $L\in (0,30)$. Here, other parameters are from Table 1.

In summary, we let BDA represents the biomass density of autotrophic algae, and BDM represents the biomass density of mixotrophic algae. PAB characterizes the probability of autotrophic algal blooms, and PMB describes the probability of mixotrophic algal blooms. The influence of partial parameters on the growth of autotrophs and mixotrophs can be summarized in Table 2.

Table 2. Example of a table showing that its caption is as wide as the table itself and justified.

Parameters	BDA	BDM	PAB	PMB	Parameters	BDA	BDM	PAB	PMB
$I_{in}$ ↑	↑↓	↑	↑↓	↑	$N_{in}$↑	↑↓	↑	↑↓	↑
$k_0$ ↑	NSE	↓	NSE	↓	a ↑	↓	↑	↓	↑
${\delta }_1$ ↑	NSE	NSE	NSE	NSE	${\delta }_2$ ↑	NSE	↑	NSE	↑
${\theta }_1$ ↑	↑↓	↓	↑↓	↓	${\theta }_2$↑	NSE	↓	NSE	↓
D ↑	↑↓	↑	↑↓	↑	L ↑	↓↑↓	↑↓	↓↑↓	↑↓

Note: ↑, increasing; ↓, decreasing; NSE, no significant effect.

5. Conclusion and discussion

In this paper, we propose and investigate a mathematical model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) describing the interactions of autotrophs (autotrophic algae) and mixotrophs (mixotrophic algae) with the intragulid predation structure in a well-mixed aquatic environment. Mixotrophs compete with autotrophs for light and nutrients, and also consume micro-autotrophs. The ecological reproductive indexes for the extinction, survival and coexistence of autotrophs and mixotrophs are rigorously derived. All possible results of system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) are described in terms of parameters $(m_1,m_2)$ and summarized in Figure 2. This research indicates that the intraguild predation structure is beneficial to phytoplankton biodiversity, and provides an explanation for the phytoplankton paradox.

The different Holling type functional responses and some important environmental parameters could influence the coexistence and the biomass density of autotrophs and mixotrophs. Our results show that Holling III type functional response is conducive to the coexistence of autotrophs and mixotrophs under the intraguild predation structure. There exists the critical light intensity $I_{in}$ and the critical nutrient input concentration $N_{in}$ that affect the coexistence of autotrophs and mixotrophs (see Figure 4). The effect of environmental factors on the metabolism of autotrophs and mixotrophs is complicated (see Table 2). These results are helpful for protecting water quality and evaluating algae blooms.

The coexistence mechanism of autotrophs and mixotrophs is very complex. It has stable positive steady-state solutions, periodic solutions generated by Hopf bifurcation and double Hopf bifurcations, and multiple stability switches. In the theoretical analysis, we only prove the existence of positive steady-state solutions. Rigorously proving the remaining coexistence mechanism is an interesting and important question. Ecological stoichiometry is a very important method and tool, including energy flow and element cycle [10, 11, 18, 23]. Previous studies have considered stoichiometric autotroph–mixotroph interactions without light [15, 16, 24, 25]. It is of interest to add stoichiometric mechanism into system (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ) to investigate some new findings.

The turbulence of the lake changes with the water depth [26]. In the upper layer, algae mixes better since the turbulence is intense, while the turbulence is relatively small in the lower layer, and algae exhibit spatial heterogeneity. The interesting problem is to explore the interactions of autotrophs and mixotrophs with light and nutrients in a water ecosystem with spatial heterogeneity. In view of the present analysis and model (3(3) $\begin{array}{rl}\frac{\mathrm{d}A}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{autotrophs}}{\underbrace{r_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{loss}}{\underbrace{m_{1}A}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_1+D}{L}A}}-\underset{\mathrm{predation}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{aG(A)M,}}\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\underset{\mathrm{growth}\mathrm{of}\mathrm{mixotrophs}}{\underbrace{r_2{F}_2(N)H_2(I_{in},A,M)M+eaG(A)M}}-\underset{\mathrm{loss}}{\underbrace{m_{2}M}}-\underset{\mathrm{sinking}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{v_2+D}{L}M,}}\\ \frac{\mathrm{d}N}{\mathrm{d}t}& =\underset{\mathrm{nutrient}\mathrm{input}\mathrm{and}\mathrm{exchange}}{\underbrace{\frac{D}{L}(N_{in}-N)}}+\underset{\mathrm{nutrient}\mathrm{recycling}}{\underbrace{{\delta }_1{\theta }_1{m}_{1}A+{\delta }_2{\theta }_2{m}_{2}M}}\\ & -\underset{\mathrm{consumption}\mathrm{by}\mathrm{autotrophs}}{\underbrace{{\theta }_1{r}_1{F}_1(N)H_1(I_{in},A,M)A}}-\underset{\mathrm{consumption}\mathrm{by}\mathrm{mixotrophs}}{\underbrace{{\theta }_2{r}_2{F}_2(N)H_2(I_{in},A,M)M}}.\end{array}$(3) ), there are more interesting ecological problems worthy of careful discussion. For example, adding dissolved inorganic carbon [28], zooplankton and fishes [11, 12] and the effect of toxic plankton species [6].

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research is partially supported by the National Natural Science Foundation of China [grant numbers 11801052 and 11971088], the Natural Science Foundation of Liaoning Province [grant number 2019-ZD-1056], the Natural Science Foundation of Heilongjiang Province [grant number LH2019A022] and the Fundamental Research Funds for the Central Universities [grant number 3132022202].