Control analysis of virotherapy chaotic system

Abstract

In this work, we consider a chaotic system that plays a vital role in the treatment of cancer by injection of a virus externally. Due to the sensitivity of this disease, most of its treatments are highly risky. Therefore, we have designed control inputs using adaptive and passive control techniques for virotherapy. Both controllers are designed to bring global stability to the cancer system with the aid of a quadratic Lyapunov function. Furthermore, we use simulations to verify our controllers. Moreover, we show that our adaptive control technique gives better results in comparison.

Keywords:

• Sections
• tumor cells
• Lyapunov function
• chaos
• adaptive control
• passive control
• stability

1. Introduction

Cancer remains a high priority of research due to its prevalence, treatment difficulties, and high mortality rate. In late 19${}^{\mathrm{th}}$ century, the removal of tumors by surgical operations and radiation was common but was not effective as hoped [24]. The failure of these two treatments was due to the uncontrollable growth and recurring nature of cancer cells. During the last two decades, the study of cancer has accelerated not only biologists, but among mathematician as well. In Saleem et al. [22] several mathematical models are used to analyse the interaction of tumor cells with healthy cells, the immune system and with viruses. These mathematical models facilitated investigations into the growth rate of cancer and its prognosis and treatment. Using a bifurcation analysis of a modified tomorrow growth model, Wei [26] observed chemotherapy-induced damage may cause a microscopic tumor. In 2018, Maddali1 et al. [12] studied chaotic dynamics caused by the mutual interaction of cancer cells with immune cells and healthy host cells. Eftimie et al. [5] investigated oncolytic therapy with the addition of viruses in the system. A mathematical model for the growth dynamics of infected and uninfected tumors is considered by Malinzi et al. [15].

Sensitivity to initial conditions is a significant characteristic of chaos [11, 17]. Chaos plays a remarkable role in the field of biology [4], engineering [21], finance [8], quantum mechanics [20], weather forecasting [18] and physical sciences [13]. Regardless of any positive aspects of chaos, its occurrence in cancer patients may cause difficulties as the unpredictable growth rate of tumor cells in the body [23] and predicting cardiac arrhythmia [2]. These pros and cons of chaos lead to the introduction of new subject; control of chaos [17]. Since the pioneering work of Ott, Grebogi and Yorke in ${20}^{\mathrm{th}}$ century, the control and synchronization of chaos have become an active field for scientific research [6]. A variety of productive control and synchronization [7] approaches have been implemented, such as sliding [3], adaptive [9, 25], optimal [16], active [19], passive [1], feedback linearization [10] control techniques. It is important to mention that the main aim of all the control techniques appearing in literature is to overcome chaos and gain global stability. In the adaptive control technique, controllers are designed by using parameter estimation and low complexity algorithms. Virotherapy [24] is the most recent and effective treatment regimen in which external viruses are injected for the removal of a tumor and to stimulate the immune system. The main hurdle in virus therapy is that all viruses have pre-existing antibodies and the challenging task is to choose the right virus. However, in 2017, Malinzi showed that cancer can be treated with a mixture of chemotherapy and virotherapy [14]. However, recent research and clinical trials have shown that virotherapy has fewer side effects on patients and is less toxic towards healthy cells than chemotherapy. The target of virotherapy treatments is to lower the number of tumor cells by increasing the concentration of infected cells to the highest level. Virotherapy is extremely nonlinear because of its dependence on cancer cells disintegration and virus transmission rates. A model introduced by Soufiani [24] in 2017 is described by the three differential equations (1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) In this model, tumor cells are classified into uninfected cells $u(t)$, infected cells $w(t)$ and the virus population $v(t)$, whereas r is the effective growth rate for uninfected cells, σ is the death rate of infected cells, K is the carrying capacity, p shows inter-cellular fusion, k is constant rate of virus transmission, α is the virus production rate by replication of infected cells and ω gives constant rate of virus eradication are the involved parameters in our considered model. System (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) is chaotic for parameter values; K = 2139, $ϵ=2$, k = 0.05, r = 0.6, p = 0.02, $\sigma =0.1$, $\alpha =6.6$ and $\omega =1.3$.

In aforementioned paragraphs, we have discussed that virotheraphy is one of the treatments for cancer. But, along with its importance it has side effects with injecting dangerous virus and consequently life of a patient can be in danger. Therefore, keeping in mind its drawback, we have introduced two control inputs for Virotherphy chaotic model to bring stability and save lives.

This paper is organized as follows. In Sections 2 and 3, we design control inputs by using adaptive and passive control techniques. We compare the results obtained from adaptive and passive control techniques in Section 4, and concluding remarks appear in Section 5.

2. Adaptive control

In this section, we use adaptive techniques to attain the global stability of the system at fixed points. The main components of this technique are the creation of an error dynamical system and the construction of a Lyapunov functions. We consider a modification of system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) (2) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw+{\theta }_1,\\ & \dot{w}=kuv-\sigma w+{\theta }_2,\\ & \dot{v}=\alpha w-\omega v-kuv+{\theta }_3,\end{array}$(2) where ${\theta }_i$; i = 1, 2, 3 are adaptive control input rates for bringing stability to the virotherapy process in such a way that infected cell, uninfected cell and virus populations converge to the desired stable points with the passage of time. These control inputs can be designed with the help of an error dynamical system and an updating law (9(9) $\{\begin{array}{l}\dot{\hat{k}}=e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})+c_4{e}_k,\\ \dot{\hat{p}}=e_1(-uw+\overline{u}\overline{w})+c_5{e}_p,\\ \dot{\hat{\sigma }}=-e_2^2+c_6{e}_{\sigma },\\ \dot{\hat{\alpha }}=e_2{e}_3+c_7{e}_{\alpha },\\ \dot{\hat{\omega }}=-e_3^2+c_8{e}_{\omega },\end{array}$(9) ). Denote an equilibria of the virotherapy system by $(\overline{u},\overline{w},\overline{v})$ and introduce the error terms (3) $\{\begin{array}{l}{e}_1=u-\overline{u},\\ e_2=w-\overline{w},\\ e_3=v-\overline{v}.\end{array}$(3) Now, differentiating Equation (3(3) $\{\begin{array}{l}{e}_1=u-\overline{u},\\ e_2=w-\overline{w},\\ e_3=v-\overline{v}.\end{array}$(3) ), we get a dynamical system for the error terms (4) $\begin{array}{rl}& \dot{e_1}=r{e}_1+\frac{r[-u(u+w{)}^{ϵ}+\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}]}{K^{ϵ}}+k[\overline{u}\overline{v}-uv]+p[\overline{u}\overline{w}-uw]+{\theta }_1,\\ & \dot{e_2}=k(uv-\overline{u}\overline{v})-\sigma e_2+{\theta }_2,\\ & \dot{e_3}=\alpha e_2-\omega e_3+k(-uv+\overline{u}\overline{v})+{\theta }_3.\end{array}$(4) In this technique parameters involved in system are unknown and time-dependent. Therefore, arbitrary parameters $\hat{\sigma }$, $\hat{k}$, $\hat{p}$, $\hat{\alpha }$, $\hat{\omega }$ are introduced for σ, k, p, α and ω, respectively. Control terms with respect to error terms (3(3) $\{\begin{array}{l}{e}_1=u-\overline{u},\\ e_2=w-\overline{w},\\ e_3=v-\overline{v}.\end{array}$(3) ) are (5) $\begin{array}{rl}& {\theta }_1=-r{e}_1-\frac{r[-u(u+w{)}^{ϵ}+\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}]}{K^{ϵ}}-\hat{k}[\overline{u}\overline{v}-uv]-\hat{p}[\overline{u}\overline{w}-uw]-c_1{e}_1,\\ & {\theta }_2=-\hat{k}(uv-\overline{u}\overline{v})+\hat{\sigma }{e}_2-c_2{e}_2,\\ & {\theta }_3=-\hat{\alpha }{e}_2+\hat{\omega }{e}_3-\hat{k}(-uv+\overline{u}\overline{v})-c_3{e}_3,\end{array}$(5) where $c_i>0$ for i = 1, 2, 3. We get the following error dynamical system by putting Equation (5(5) $\begin{array}{rl}& {\theta }_1=-r{e}_1-\frac{r[-u(u+w{)}^{ϵ}+\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}]}{K^{ϵ}}-\hat{k}[\overline{u}\overline{v}-uv]-\hat{p}[\overline{u}\overline{w}-uw]-c_1{e}_1,\\ & {\theta }_2=-\hat{k}(uv-\overline{u}\overline{v})+\hat{\sigma }{e}_2-c_2{e}_2,\\ & {\theta }_3=-\hat{\alpha }{e}_2+\hat{\omega }{e}_3-\hat{k}(-uv+\overline{u}\overline{v})-c_3{e}_3,\end{array}$(5) ) into Equation (4(4) $\begin{array}{rl}& \dot{e_1}=r{e}_1+\frac{r[-u(u+w{)}^{ϵ}+\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}]}{K^{ϵ}}+k[\overline{u}\overline{v}-uv]+p[\overline{u}\overline{w}-uw]+{\theta }_1,\\ & \dot{e_2}=k(uv-\overline{u}\overline{v})-\sigma e_2+{\theta }_2,\\ & \dot{e_3}=\alpha e_2-\omega e_3+k(-uv+\overline{u}\overline{v})+{\theta }_3.\end{array}$(4) ) (6) $\{\begin{array}{l}\dot{e_1}=e_k[\overline{u}\overline{v}-uv]+e_p[\overline{u}\overline{w}-uw]-c_1{e}_1,\\ \dot{e_2}=e_k(-\overline{u}\overline{v}+uv)-e_{\sigma }{e}_2-c_2{e}_2,\\ \dot{e_3}=e_{\alpha }{e}_2-e_{\omega }{e}_3+e_k(-uv+\overline{u}\overline{v})-c_3{e}_3,\end{array}$(6) where $e_p$, $e_k$, $e_{\sigma }$, $e_{\omega }$ and $e_{\alpha }$ are the error terms associated with the estimated parameters as defined by $e_k=k-\hat{k}$, $e_p=p-\hat{p}$, $e_{\sigma }=\sigma -\hat{\sigma }$, $e_{\alpha }=\alpha -\hat{\alpha }$, $e_{\omega }=\omega -\hat{\omega }$. Taking derivative of each error term, we obtain $\{\begin{array}{l}\dot{e_k}=-\dot{\hat{k}}(t),\\ \dot{e_p}=-\dot{\hat{p}}(t),\\ \dot{e_{\sigma }}=-\dot{\hat{\sigma }}(t),\\ \dot{e_{\alpha }}=-\dot{\hat{\alpha }}(t),\\ \dot{e_{\omega }}=-\dot{\hat{\omega }}(t).\end{array}$In order to obtain an updating law, we use a quadratic Lyapunov function (7) $L(\mathbf{e})=\frac{1}{2}(e_1^2+e_2^2+e_3^2+e_k^2+e_p^2+e_{\sigma }^2+e_{\alpha }^2+e_{\omega }^2).$(7) Clearly, $L(e)$ is greater than or equal to zero and to be negative definite, we require its derivative (8) $\begin{array}{rl}& \dot{L}=-c_1{e}_1^2-c_2{e}_2^2-c_3{e}_3^2+e_k[e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})-\dot{\hat{k}}]\\ & +e_p[e_1(-uw+\overline{u}\overline{w})-\dot{\hat{p}}]+e_{\sigma }[-e_2^2-\dot{\hat{\sigma }}]+e_{\alpha }[e_2{e}_3-\dot{\hat{\alpha }}]+e_{\omega }[-e_3^2-\dot{\hat{\omega }}]\end{array}$(8) to satisfy $\dot{L}(e)\le 0$. Therefore, in view of Equation (8(8) $\begin{array}{rl}& \dot{L}=-c_1{e}_1^2-c_2{e}_2^2-c_3{e}_3^2+e_k[e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})-\dot{\hat{k}}]\\ & +e_p[e_1(-uw+\overline{u}\overline{w})-\dot{\hat{p}}]+e_{\sigma }[-e_2^2-\dot{\hat{\sigma }}]+e_{\alpha }[e_2{e}_3-\dot{\hat{\alpha }}]+e_{\omega }[-e_3^2-\dot{\hat{\omega }}]\end{array}$(8) ), we can attain this by the following updating law (9) $\{\begin{array}{l}\dot{\hat{k}}=e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})+c_4{e}_k,\\ \dot{\hat{p}}=e_1(-uw+\overline{u}\overline{w})+c_5{e}_p,\\ \dot{\hat{\sigma }}=-e_2^2+c_6{e}_{\sigma },\\ \dot{\hat{\alpha }}=e_2{e}_3+c_7{e}_{\alpha },\\ \dot{\hat{\omega }}=-e_3^2+c_8{e}_{\omega },\end{array}$(9) where $c_4$, $c_5$, $c_6$, $c_7$ and $c_8$ are positive gain constants. There are several techniques for calculating these gain constants. However, we require only that $c_i$ > 0, $i=1,2,3\dots ,8$ for simplicity. Now, substituting Equation (9(9) $\{\begin{array}{l}\dot{\hat{k}}=e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})+c_4{e}_k,\\ \dot{\hat{p}}=e_1(-uw+\overline{u}\overline{w})+c_5{e}_p,\\ \dot{\hat{\sigma }}=-e_2^2+c_6{e}_{\sigma },\\ \dot{\hat{\alpha }}=e_2{e}_3+c_7{e}_{\alpha },\\ \dot{\hat{\omega }}=-e_3^2+c_8{e}_{\omega },\end{array}$(9) ) into Equation (8(8) $\begin{array}{rl}& \dot{L}=-c_1{e}_1^2-c_2{e}_2^2-c_3{e}_3^2+e_k[e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})-\dot{\hat{k}}]\\ & +e_p[e_1(-uw+\overline{u}\overline{w})-\dot{\hat{p}}]+e_{\sigma }[-e_2^2-\dot{\hat{\sigma }}]+e_{\alpha }[e_2{e}_3-\dot{\hat{\alpha }}]+e_{\omega }[-e_3^2-\dot{\hat{\omega }}]\end{array}$(8) ) to get (10) $\dot{L}=-c_1{e}_1^2-c_2{e}_2^2-c_3{e}_3^2-c_4{e}_k^2-c_5{e}_p^2-c_6{e}_{\sigma }^2-c_7{e}_{\alpha }^2-c_8{e}_{\omega }^2$(10) which clearly is a negative definite function. Hence, we get that solution of system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) is asymptotically stable with the updating law (9(9) $\{\begin{array}{l}\dot{\hat{k}}=e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})+c_4{e}_k,\\ \dot{\hat{p}}=e_1(-uw+\overline{u}\overline{w})+c_5{e}_p,\\ \dot{\hat{\sigma }}=-e_2^2+c_6{e}_{\sigma },\\ \dot{\hat{\alpha }}=e_2{e}_3+c_7{e}_{\alpha },\\ \dot{\hat{\omega }}=-e_3^2+c_8{e}_{\omega },\end{array}$(9) ).

In Figure 1, it can be observed that trajectories of error terms converge to zero asymptotically. In other words, when error terms approach zero, state variables start moving towards the desired point. In Figure 2, estimated parameters converge to the original values. To plot updated law (9(9) $\{\begin{array}{l}\dot{\hat{k}}=e_1(-uv+\overline{u}\overline{v})+e_2(uv-\overline{u}\overline{v})+e_3(-uv+\overline{u}\overline{v})+c_4{e}_k,\\ \dot{\hat{p}}=e_1(-uw+\overline{u}\overline{w})+c_5{e}_p,\\ \dot{\hat{\sigma }}=-e_2^2+c_6{e}_{\sigma },\\ \dot{\hat{\alpha }}=e_2{e}_3+c_7{e}_{\alpha },\\ \dot{\hat{\omega }}=-e_3^2+c_8{e}_{\omega },\end{array}$(9) ), initial conditions are considered as $\hat{k}=4$, $\hat{p}=1$, $\hat{\sigma }=1$, $\hat{\alpha }=3$, $\hat{\omega }=10$. As these estimated parameter values approach towards their original values, chaotic trajectories start converging toward their desired point.

3. Passive feedback

In this section, chaotic virotheraphy system is controlled about equilibria using passive control function ${{\rm Y}}_1(t)$ for Equation (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) (11) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-pwu+{{\rm Y}}_1,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(11) Here ${{\rm Y}}_1$ is the control input for our considered chaotic system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ), which is designed on the basis of Feedback Linearization. In similar way as adaptive technique, the error dynamics for system (11(11) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-pwu+{{\rm Y}}_1,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(11) ) is defined as (12) $\begin{array}{rl}\dot{e_1}& =r{e}_1+\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(e_1+\overline{u})(e_1+e_2+\overline{u}+\overline{w}{)}^{ϵ}]\\ & +k(-e_1{e}_3-e_1\overline{v}-e_3\overline{u})+p(-e_2{e}_1-e_2\overline{u}-e_1\overline{w})+{{\rm Y}}_1,\\ \dot{e_2}& =k{e}_1{e}_3+k{e}_1\overline{v}-(\sigma +c_1)e_2,\\ \dot{e_3}& =-\omega e_3-k{e}_1{e}_3-k\overline{v}{e}_1-c_1{e}_3,\end{array}$(12) where error state variable $e_1$ is considered as output, $z_1$=$e_2$ and $z_2$=$e_3$. Error dynamics system in the form of $z_1$, $z_2$ and output Y can be rewritten as (13) $\begin{array}{rl}\dot{z_1}& =kY{z}_2+kY\overline{v}-(\sigma +c_1)z_1,\\ \dot{z_2}& =-\omega z_2-kY{z}_2-k\overline{v}Y-c_1{z}_2,\\ \dot{Y}& =rY+\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(Y+\overline{u})(Y+z_1+\overline{u}+\overline{w}{)}^{ϵ}]\\ & +k(-Y{z}_2-Y\overline{v}-z_2\overline{u})+p(-z_{1}Y-z_1\overline{u}-Y\overline{w})+{{\rm Y}}_1.\end{array}$(13) According to passive control normal form, Equation (13(13) $\begin{array}{rl}\dot{z_1}& =kY{z}_2+kY\overline{v}-(\sigma +c_1)z_1,\\ \dot{z_2}& =-\omega z_2-kY{z}_2-k\overline{v}Y-c_1{z}_2,\\ \dot{Y}& =rY+\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(Y+\overline{u})(Y+z_1+\overline{u}+\overline{w}{)}^{ϵ}]\\ & +k(-Y{z}_2-Y\overline{v}-z_2\overline{u})+p(-z_{1}Y-z_1\overline{u}-Y\overline{w})+{{\rm Y}}_1.\end{array}$(13) ) can be written as (14) $f(z)=\left[\begin{array}{c}-(c_1+\sigma )z_1\\ -(\omega +c_1)z_2\end{array}\right],g(z,Y)=\left[\begin{array}{c}k{z}_2+k\overline{v}\\ -k{z}_2-k\overline{v}\end{array}\right],\varphi (z,Y)=1$(14) and (15) $\begin{array}{rl}h(z,Y)& =rY+\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(Y+\overline{u})(Y+z_1+\overline{u}+\overline{w}{)}^{ϵ}]\\ & +k(-Y{z}_2-Y\overline{v}-z_2\overline{u})+p(-z_{1}Y-z_1\overline{u}-Y\overline{w}).\end{array}$(15) Storage function for passive control method is considered as (16) $S(z,Y)=W(z)+\frac{Y^2}{2},$(16) where $W(z)=\frac{1}{2}(z_1^2+z_2^2)$ is Lyapunov function of $f(z)$ coupled with $W(0)=0$ and (17) $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}S(z,Y)& =\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}\dot{z}+Y\dot{Y}\\ & =\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}f(z)+\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}g(z,Y)Y+h(z,Y)Y+\varphi (z,Y)Yp.\end{array}$(17) To ensure existence of stability for solution of system (11(11) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-pwu+{{\rm Y}}_1,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(11) ), we differentiate Equation (16(16) $S(z,Y)=W(z)+\frac{Y^2}{2},$(16) ) and get (18) $\begin{array}{rl}\dot{W}(z)& =\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}f(z)=\left[\begin{array}{cc}{z}_1& z_2\end{array}\right]\left[\begin{array}{c}-(c_1+\sigma )z_1\\ -(\omega +c_1)z_2\end{array}\right]\\ & =-(c_1+\sigma )z_1^2-(\omega +c_1)z_2^2.\end{array}$(18) Therefore, $\dot{W}(z)\le 0$ for all real values and hence we achieve global stability of $f(z)$. Hence, zero dynamics of controlled system (13(13) $\begin{array}{rl}\dot{z_1}& =kY{z}_2+kY\overline{v}-(\sigma +c_1)z_1,\\ \dot{z_2}& =-\omega z_2-kY{z}_2-k\overline{v}Y-c_1{z}_2,\\ \dot{Y}& =rY+\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(Y+\overline{u})(Y+z_1+\overline{u}+\overline{w}{)}^{ϵ}]\\ & +k(-Y{z}_2-Y\overline{v}-z_2\overline{u})+p(-z_{1}Y-z_1\overline{u}-Y\overline{w})+{{\rm Y}}_1.\end{array}$(13) ) is asymptotically stable and is a minimum phase system. According to passive control theory controller is designed to make system passive as (19) ${{\rm Y}}_1=\varphi (z,Y{)}^{-1}(-h(z,Y)-{(\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}g(z,Y))}^T-\beta Y+\mu ).$(19) Here β is positive real number and μ is an external signal. Using $\varphi (z,Y)$, $h(z,Y)$ into Equation (19(19) ${{\rm Y}}_1=\varphi (z,Y{)}^{-1}(-h(z,Y)-{(\frac{\mathrm{\partial }W(z)}{\mathrm{\partial }z}g(z,Y))}^T-\beta Y+\mu ).$(19) ), control function can be achieved as $\begin{array}{rl}{{\rm Y}}_1& =-rY-\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(Y+\overline{u})(Y+z_1+\overline{u}+\overline{w}{)}^{ϵ}]-k(-Y{z}_2-Y\overline{v}-z_2\overline{u})\\ & -p(-z_{1}Y-z_1\overline{u}-Y\overline{w})-k{z}_2{z}_1-k\overline{v}{z}_1+k{z}_2^2+k{z}_2\overline{v}-\beta Y+\mu .\end{array}$For convenience, writing the system in form of error terms; $e_1=Y$, $e_2=z_1$ and $e_3=z_2$, yield (20) $\begin{array}{rl}{{\rm Y}}_1& =-r{e}_1-\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(e_1+\overline{u})(e_1+e_2+\overline{u}+\overline{w}{)}^{ϵ}]\\ & -k(-e_1{e}_3-e_1\overline{v}-e_3\overline{u})-p(-e_1{e}_2-e_2\overline{u}-e_1\overline{w})\\ & -k{e}_3{e}_2-k\overline{v}{e}_2+k{e}_3^2+k{e}_3\overline{v}-\beta e_1+\mu .\end{array}$(20) Equation (20(20) $\begin{array}{rl}{{\rm Y}}_1& =-r{e}_1-\frac{r}{K^{ϵ}}[\overline{u}(\overline{u}+\overline{w}{)}^{ϵ}-(e_1+\overline{u})(e_1+e_2+\overline{u}+\overline{w}{)}^{ϵ}]\\ & -k(-e_1{e}_3-e_1\overline{v}-e_3\overline{u})-p(-e_1{e}_2-e_2\overline{u}-e_1\overline{w})\\ & -k{e}_3{e}_2-k\overline{v}{e}_2+k{e}_3^2+k{e}_3\overline{v}-\beta e_1+\mu .\end{array}$(20) ) gives the control function to control chaos that appears in virotherapy.

Figure 1. Tracking of error terms converging to origin.

Figure 2. Estimated parameters converge to original parameter values.

4. Numerical simulation results

In this section, our aim is to demonstrate graphical results of adaptive and passive control techniques obtained in sections 2 and 3. For this purpose, parameter values are considered as K = 2139, $ϵ=2$, k = 0.05, r = 0.6, p = 0.02, $\sigma =0.1$, $\alpha =6.6$ and $\omega =1.3$ along with initial conditions $u(0)=9.02$, $w(0)=0$ and $v(0)=200$.

For these initial conditions and parameter values, trajectories of system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) show unpredictable behaviour. For adaptive control, positive gain constants are selected as $c_i=2.8$ for $i=1,2,\dots ,8$.

Figure 3 represents global stability of uninfected tumor cells u, infected tumor cells w and virus cells v about fixed points $E_1=(0,0,0)$, $E_2=(2139,0,0)$ and $E_3=(0.4,2.22,11.11)$ when adaptive controllers are introduced into original system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ).

Figure 3. Trajectories approaching towards $E_1$, $E_2$ and $E_3$ using adaptive control.

Figure 4. Trajectories approaching towards $E_1$, $E_2$ and $E_3$ using passive control.

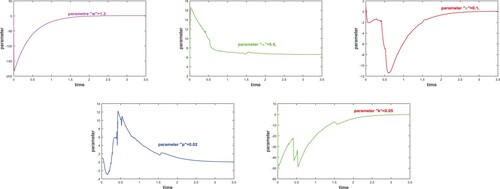
Figure 4 illustrates the convergence of trajectories towards fixed points when passive feedback controller is activated at t = 0. On the other hand, constant used in control function is designed through passive technique, considered as $\beta =2.4$ and external signal $\mu =0$. Figures 3 and 4 verify the analytical results obtained in sections 2 and 3, respectively. Now, to analyze the control method for transient speed, control effort and convergence time, we plot each state variable using both techniques.

From Figure 5, it is observed that control obtained for chaotic system through adaptive technique is more efficient than passive technique. Further, it is observed that controller designed in virotheraphy becomes effective in less time using adaptive control technique, while passive control function takes more time in comparison. In Figure 6, control of chaos and convergence to equilibrium point $E_2=(2139,0,0)$ is achieved faster for adaptive method instead of passive. It is also observed that, trajectories in both cases start with oscillation of large amplitude but control inputs at t = 0.1 and t = 0.9, using adaptive and passive control techniques, respectively control the systems and converge to their point. In Figures 5–7, it it is noticed that trajectories of system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) are stabilizing towards equilibria $E_3=(0.4,2.22,11.11)$ is target for virotheraphy treatment, because at this point virus replication rate increases, while population of uninfected tumor cells decreases and converges to its lowest state. Third equilibrium point, (21) $E_3=(\frac{\sigma \omega }{k(\alpha -\sigma )},\frac{r\omega }{[(\alpha -\sigma )k+\rho \omega ]}[1-\frac{(U+W{)}^e}{K^e}],\frac{\alpha -\sigma }{\omega U})$(21) represent the partial success of virotherapy. However, if virotherapy fails, then its cure state can be achieved through global stability about equilibria $E_3$. This point state can be reached when (22) $\frac{\sigma \omega }{k(\alpha -\sigma )}\le K.$(22) The term; $k\alpha$ indicates infection rate or the release of virions, whereas its population in the cure state is a consequence of assuming a continuous constant dosage. Moreover, the term $\sigma \omega$ represents virus elimination by death of infected cells. Hence, $E_3$ reaches when the infection rate is more than virus elimination. In the present work, we have proved in Sections 2 and 3 that if system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) is controlled about $E_3$ then population of uninfected tumor cells decreases. Thus, from clinical point of view, our findings indicate that regeneration of infected cells can improve treatment.

5. Conclusion

In this paper, global stability for virotheraphy system is investigated using adaptive and passive control techniques. In both cases, we used the concept of Lyapunov stability. Passive control method coupled with feedback is used to attain convergence of virotheraphy model. Analytical work and graphical simulations confirm that both methods successfully achieve the control of virotherapy system. But, adaptive controller works faster in comparison.

Figure 5. Comparison of adaptive and passive control inputs for each state variables using equilibria; $E_1=(0,0,0)$.

Figure 6. Comparison of adaptive and passive control inputs for each state variables using equilibria; $E_2=(2139,0,0)$.

Figure 7. Comparison of adaptive and passive control inputs for each state variables using equilibria; $E_3=(0.4,2.22,11.11)$.

Virotherapy shows complex behaviour due to chaotic growth of tumor cells and virus decomposition rate. In this article, we used chaos control regimens to suppress chaoticity and converge the state variables toward the target point at which tumor cells are minimized. Global stability towards steady state $E_1=(0,0,0)$ and $E_3=(0.4,2.22,11.11)$ shows the complete removal of tumor and partial success of therapy, whereas convergence towards $E_2=(2139,0,0)$ refers to incurable stage at which population of tumor cells converges to maximum level. Moreover, stabilizing trajectories of system (1(1) $\begin{array}{rl}& \dot{u}=ru[1-\frac{(u+w{)}^{ϵ}}{K^{ϵ}}]-kuv-puw,\\ & \dot{w}=kuv-\sigma w,\\ & \dot{v}=\alpha w-\omega v-kuv.\end{array}$(1) ) towards equilibria $E_3=(0.4,2.22,11.11)$ is the target state for virotheraphy treatment. At $E_3$ virus replication rate increases, while population of uninfected tumor cells decreases and converges to its lowest state.

Compliance with ethical standards

Ethical approval: This paper does not contain any studies with human participants or animals performed by any of the author.

Acknowledgements

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

MATLAB is used for graphs and tedious calculations in this work; codes are available upon reasonable request from corresponding author.