Time and frequency behaviour in TSR and PPT evaluation for flash thermography^*

^*The paper is an extended version of the publication presented at Thermosense conference and referenced as [6]. In the first part it is investigated, what is the difference using the theoretical Fourier transformation and the numerical FFT calculation for flash thermography results. The next part compares the defect depth calculation in TSR and PPT, and the influence of a couple of parameters is investigated. As this analysis is done based on FEM simulation, the last section shows also measurement results on steel sample with flat bottom hole defects.

Abstract

Subsurface defects can be detected by flash thermography evaluating the temperature response at the surface. Many techniques have been developed in the past to localise defects and also to estimate their depth and size. Two of the most established methods are TSR and PPT, whereby TSR analyses the data in the time domain, and PPT evaluates the signal in the frequency domain. In order to get the data in the frequency domain, Fourier transformation, especially FFT is used to calculate the phase shift for the different frequencies. The usage of FFT assumes a periodic signal or a temporal signal limited in time. As this is not the case for the temperature signal after a short pulse heating, the transformation to the frequency domain generates some errors. Therefore parameters as e.g. sampling frequency or time duration of evaluation have to be selected carefully. Even if many publications have been already dealing with this topic, in this paper a new approach is attempted by comparing the temporal behaviour as it is handled by the TSR technique with the frequency behaviour calculated by PPT. The results are interpreted with the help of simulation and measurements for flat bottom hole samples are also presented.

Keywords:

• Flash thermography
• thermal wave
• defect detection
• TSR
• PPT

1. Introduction

In the last years flash thermography has been established as a non-destructive testing method for detection of subsurface defects in many different materials, from metals to CFRP. Many publications have already proved that instead of taking one single image with the best temperature contrast, evaluating the whole infrared image sequence produces a much better signal-to-noise ratio (SNR) and therefore much better detectability of defects [1]. In the last years many techniques have been developed. One of them is TSR [2] where the measured data are investigated in the time domain. The other technique, PPT [3] evaluates the temperature response in the frequency domain. In order to get the data in the frequency domain, Fourier transformation, especially FFT is used to calculate the phase shift for the different frequencies. The usage of FFT assumes a periodic signal or a temporal signal limited in time. As this is not the case for the temperature signal after a short pulse heating, the transformation to the frequency domain generates some errors. Therefore parameters as e.g. sampling frequency or time duration have to be selected carefully [4–6]. In the next sections this paper deals with the consequences of using FFT instead of a Fourier transformation and how this affects the PPT evaluations. Both PPT and TSR allow the possibility of estimating the depth of a defect. In the paper different parameters are investigated for both techniques how they influence this estimation. At the end of the paper, measurement results are also presented, but the main focus of the paper is on the theoretical investigation in terms of simulations and analytical calculations.

2. Fourier transformation of the temperature

2.1. Semi-infinite body

After an infinitesimal short heating pulse, after a so-called Dirac-delta pulse, the surface temperature of a semi-infinite body with adiabatic assumption is described by the equation [7](1)

where Q is the applied heat amount, k the thermal conductivity, α the thermal diffusivity and t denotes the time. The Fourier transformation of this function results in(2)

and its phase is(3)

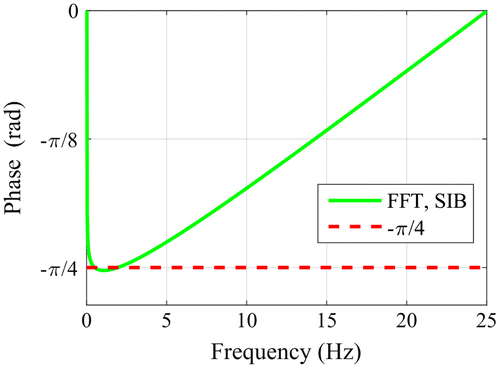
for all the frequencies. As the Dirac delta heating corresponds to a heating with all the frequencies, the angle of the Fourier transformation shows, that independently of the frequency, each wave has a phase shift of −π/4 related to the excitation.

For the PPT evaluation measured data will be evaluated by FFT instead of Fourier transformation. In this case the integration limit of the transformation does not go to infinity, but it is calculated only for the finite temporal range of 0 … t_end of the measurement and it is resulting in the Fourier transformation of a periodic function repeating the part of t = 0 … t_end. This means that the spectrum received with FFT is discretised, its base frequency is(4)

and the spectrum contains the multiples of this base frequency.

The recorded temperature data are not continuous, but discretised with the recording frequency f_s of the infrared camera:(5)

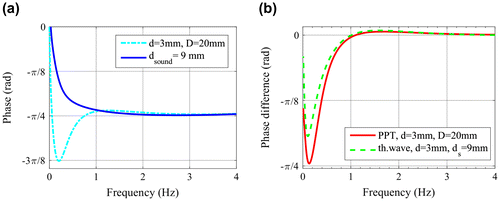
where dt is the time step of the discretization and N the number of the recorded steps. This causes a limitation for the spectrum. Based on the Nyquist theorem only the half of the spectrum contains real information and for the frequency f = 0 Hz and for f = f_s/2 the phase is equal to zero, as it is also shown in Figure 1. On the other hand this means, that using FFT, instead of the theoretical value of constant −π/4 a function is obtained, which starts and ends at zero and only at low frequencies it has a value around −π/4.

Figure 1. Comparison of the phase calculated by Fourier transformation and by FFT for a semi-infinite body (f_s = 50 Hz) after a Dirac delta heating and under adiabatic circumstances.

2.2. Finite body

In the case of a finite body with a thickness of d, the heat is reflected from the back and front sides of the sample. Assuming a reflection factor of 1, the surface temperature can be written as [7](6)

The Fourier transformation of one term results(7)

where(8)

and μ is the thermal diffusion length of a wave with the angular frequency ω. Summing up all the reflected terms the Fourier transformation of the surface temperature of a finite body gives(9)

and its phase is(10)

If x = 0 then Φ_fib,inst,(z = 0) = −π/2, and if x = π then Φ_fib,inst,(z = 0) = −π/4, where x depends on material parameters and on the thickness d. It is to note that in experiments a phase difference to a sound surface, in ideal case to a semi-infinity body is observed. As phase difference is equal to the ratio of both Fourier transformations, it can be calculated as(11)

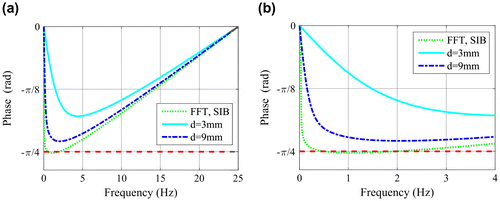
Since the phase of F(T_sib,inst,0(t)) is equal to −π/4 independently of the frequency (see Equation (3(3) )), this division means a shifting by −π/4. In Figure 2(a) this phase difference is shown. If the sound part of a sample is not semi-infinite but has a thickness of d_s, then the phase difference between this and the defect thickness d is regarded. Figure 2(b) compares Φ_fib,inst(z = 0) for two different thicknesses, where typical steel material parameters have been used for the calculation. The two curves cross each other, when x = π for the thinner finite body, that means at the frequency of(12)

Figure 2. Phase of the surface temperature of a finite body obtained by Fourier transformation according to Equation (10(10) ); a: on the x-axis is the dimensionless x parameter which is the double of the so-called thermal thickness; b: calculated for two different thicknesses using typical steel parameters.

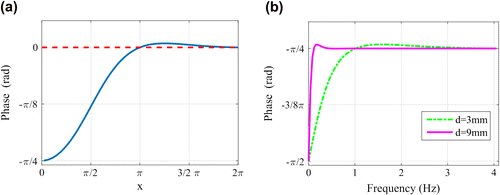
Therefore, at this frequency the phase difference between these two finite bodies is zero.

Calculating the phase of the finite body response with FFT instead of Fourier transformation, the same problem is encountered as by the semi-infinite body: at f = 0 Hz and at f = f_s/2 the phase is zero instead of −π/2 and −π/4, respectively, as it is shown in Figure 3(a). In Figure 3(b) the same curves are depicted as in Figure 3(a), but in close up to the frequency range of 0–4 Hz. Comparing now Figures 2(b) and 3(b) it is to note that the curves look very differently calculated by Fourier transformation (Figure 2(b)) or by FFT (Figure 3(b)) and in the latter one the two curves nowhere cross each other, therefore, no zero phase difference can be observed.

Figure 3. a: Phase of the surface temperature calculated by FFT (f_s = 50 Hz) for semi-infinity body and for two finite bodies; b: the same curves as in Figure a but in close up for the same range of 0–4 Hz as in Figure 2(b).

3. Phase of a thermal wave

3.1. Semi-infinite body

Applying a harmonic heating at the surface of a semi-infinity body as(13)

and after solving the differential equation of heat flow and taking only the AC part for the excitation frequency results in [7].(14)

For z = 0, that means at the surface, the phase of the thermal wave is −π/4 independently of the frequency, similarly as in Equation (3(3) ), as it has been obtained from the Fourier transformation of the instantaneous heating of a semi-infinite body.

3.2. Finite body

Taking a finite body with thickness of d, the thermal wave is reflected from the back and front side causing a phase difference between reference and sample signal [8].(15)

where R_g and R_b are the reflection factors at the back and the front sides, respectively. Assuming on both sides a reflection factor of 1, this expression can be simplified and the same equation as Equation (11(11) ) is obtained. The case, when R_g and R_b have different values from unity, is investigated in another paper [9].

On the other hand that means that the phase depending on the dimensionless x parameter, see Equation (8(8) ), looks the same as shown in Figure 2(a): at x = 0 it has a value of −π/4 and for large x it tends to 0. The zero-crossings occur if x = mπ, where m is an integer. The 1st zero-crossing (x = π), is quite visible. The 2nd zero-crossing (x = 2π), is not so significant any more due to the exponential damping of the thermal wave.

The wavelength of the thermal wave can be expressed as λ = 2πμ, therefore the physical meaning of the zero-crossing is that(16)

as it is generally valid for destructive interference of waves. Additionally, the zero-crossings occur at the frequencies of(17)

Figure 4(a) shows the temperature at the surface of a finite body after an instantaneous heating in double logarithmical scale. It is well known that temperature in this representation is decreasing first with −1/2 slope corresponding the semi-infinite behaviour. As the heat is trapped in the finite body thickness, the temperature tends to the constant value of(18)

Figure 4. a: Normalised temperature increase after a Dirac delta heating; b: phase of a thermal wave in the same finite body.

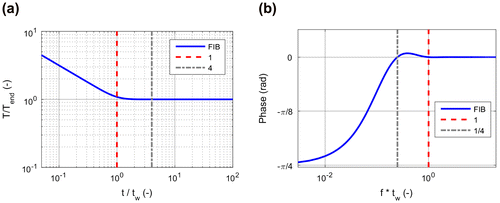
and the time, when the saturation starts, can be expressed as(19)

In Figure 4(a) the temperature has been normalised to T_end and on the x-axis the dimensionless parameter t/t_w is displayed. On the other hand, t_w is the reciprocal value of the 2nd zero-crossing frequency (see Equation (17(17) )) i.e. t_w is the cycle duration belonging to the 2nd zero-crossing. In Figure 4(a) and (b) they are marked by red dash lines, respectively. The 1st zero-crossing frequency and its cycle duration of 4t_w are marked by grey dash lines in Figure 4(a) and (b). Expressed on other way: at the 1st zero-crossing frequency d = λ/4 and at the 2nd zero-crossing d = λ/2. The temperature saturation above the defect starts at t = t_w when the thickness d is equal to λ/2, belonging to the 2nd zero-crossing frequency, causing at this frequency a destructive interference.

3.3. Phase difference of thermal waves

If in a finite body with a sound thickness of d_s a defect in a depth of d should be detected, then the phase difference between both thermal waves reflected from d_s and d depth is investigated. Figure 5 demonstrates such a case, where d = 3 mm and d_s = 9 mm. As the phase of the wave is strongly damped (see Equations (11(11) ) and (15(15) )), the zero-crossing is mainly determined by the phase of the thermal wave reflected from the defect depth d, calculated by Equation (12(12) ).

Figure 5. Phase of thermal waves for a defect depth of d = 3 mm, for a sound thickness of d_s = 9 mm and the difference of these two phases.

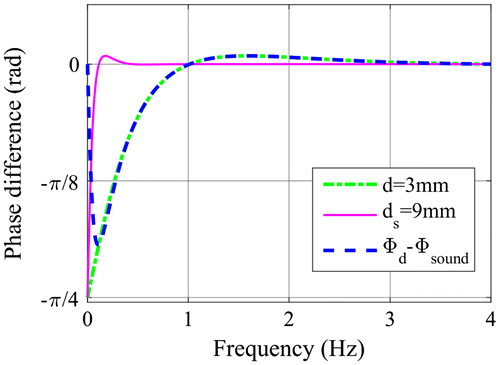
The phase difference has a positive maximum, which can be determined by derivation of Equation (11(11) ) and resulting x_max = 5/4π and Φ_max ~ 0.028. The phase difference has a negative minimum occurring approximately there, where the thermal wave in the sound part has the 1st zero-crossing, i.e. at x_min = d/d_s*π. For the thickness ratio of d/d_s = 1/3 results a Φ_min ~ −0.6. Therefore the phase contrast, which means the absolute value of the phase difference at the minimum (Φ_min) is about 22 times larger than at the positive maximum (Φ_max).

4. Phase calculations for bottom hole defects

In the previous sections analytical calculations have been performed assuming a 1-dimensional model. To investigate the heat flow around defects with a finite lateral extension, FEM simulations have been setup and calculated with multiphysics simulator ANSYS [10]. Figure 6(a) shows such a model with a defect diameter of 20 mm. For the simulation, and also for the previous analytical calculations, typical steel material has been used: k = 40 W/m K, density ρ = 8400 kg/m³, specific heat capacity c = 460 J/kg K. The heating pulse duration in this model was 10 ms and the time step during the cooldown was 20 ms, corresponding to 50 Hz sampling frequency. In other simulation models the pulse length (see Section 7.2) and the sampling frequency (see Section 7.5) have been varied to investigate their effects on the results. The gridding size was set to a 10th of the defect depth, which means 0.3 × 0.3 mm² for d = 3 mm. Additional simulations were carried out with grid size of 0.15 × 0.15 mm² and 0.075 × 0.075 mm² and the results with the higher grid resolutions were mainly identical to the first one.

Figure 6. a: FEM simulation model of bottom hole (d = 3 mm, d_s = 9 mm, diameter D = 20 mm); b: temperature increase after instantaneous heating calculated for different defect sizes (d = 3 mm, d_s = 9 mm).

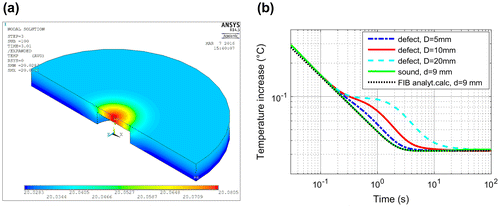
The temperature at the surface decreases first with the −1/2 slope as in the semi-infinite body, then the heat accumulates above the defect building a kind of plateau in the temperature vs. time plot. Then the accumulated heat above the defect flows laterally away and the temperature decreases again until the same temperature is achieved in the whole sample, this time is denoted as t_e. Figure 6(b) demonstrates that the smaller the defect size, the quicker the trapped heat flows laterally away. Therefore the quicker the temperature starts to decrease and the shorter is the temperature plateau. And at the end the quicker a homogeneous temperature at the surface is achieved, which means, t_e is shorter for small defect sizes. In Figure 6(b) also the temperature for a finite body calculated with Equation (6(6) ) is shown. In the early time a small difference can be observed between the simulated sound surface signal and the analytically calculated one. The analytical model assumes a Dirac delta heating with an infinitesimal short heating pulse, in contrast to the simulation with a 10 ms heating pulse, which causes a slight deviation from the −1/2 slope straight line at the beginning.

Calculating the phase with FFT for the sound part, the phase vs. frequency curve is identical with the one obtained for finite body, compare in Figure 3(b) and in Figure 7(a). But for the defect the phase vs. frequency function looks very differently: for the finite body with the thickness d = 3 mm and with infinite lateral extension, the phase function was monotonously decreasing in the frequency range of 0–4 Hz (see Figure 3(b)). But for the defect with finite lateral extension it has first a minimum and then it is crossing the phase function of the sound part (see Figure 7(a)). The difference of both phases shown in Figure 7(a) is depicted in Figure 7(b) and compared with the phase difference curve obtained for the thermal waves (see also in Figure 5). The phase difference function calculated for the bottom hole defect has a similar form as the one for the thermal waves, but the zero crossing and the minimum value are slightly different. It is important to note, that this zero crossing is caused by the finite lateral size of the defect, as the phase curves for infinite lateral size, as in Figure 3, was a monotonous function without a crossing of the phase curve of the sound part. The lateral extension of the defect and the temperature decrease due to the lateral heat flow cause this zero-crossing in the phase function calculated with FFT. Therefore the phase difference function with FFT becomes only similar to the thermal waves due to the finite lateral size of the defect.

Figure 7. a: Phase calculated with FFT for the bottom hole defect FEM model; b: phase difference of both functions in Figure a compared with the phase difference of the thermal waves as shown in Figure 5.

In Figure 7(b) the difference between the phase contrast functions has mainly two reasons:

•	In PPT the numerical method of FFT is used, assuming a periodic function or function limited in time, which is not valid for the temperature vs. time function after a short pulse heating.
•	The phase contrast for the thermal wave does not take into account the lateral size of the defect, it is based only on a 1D calculation. As the lateral heat flow around the defect has a significant effect at low frequencies on the phase contrast, there is a difference to observe between the two curves.

It is to note that the here presented results are calculated for steel material parameters. In the case of other materials, e.g. for plastic the observation time and the sampling frequency have to be adjusted according to the much lower thermal conductivity and diffusivity values. As the thermal diffusivity of the plastic is about two orders of magnitudes less than of steel, the observation time has to be set about two magnitudes larger than for a steel sample with the same geometry. The sampling frequency for plastic may be set two magnitudes less than for steel, and in this way the number of the images is the same for both materials. So long only ideal adiabatic conditions are taken into account, the analytical and FEM simulation results with the normalising as shown in Figure 4 become identical for both materials. Therefore, the here presented results are not only valid for steel, but also other isotropic materials with appropriate scaling of the measurement parameters. This topic is investigated in more detail in another publication [9].

5. Blind frequency

In the lock-in technique the surface is heated by a periodically changing intensity according to Equation (13(13) ) and the answer obtained from the specimen is evaluated only for the excitation frequency. Therefore the lock-in measurement results are very similar to the analytical solution for thermal waves. It has been observed [11,12] that the phase images of the lock-in technique have higher depth resolution than its amplitude images. The depth resolution of the phase is about 1.5–2μ, where μ is the thermal diffusion length.

For PPT evaluations the term ‘blind frequency’ is often used [4,5,13], ‘as a limiting frequency at which the defect presents enough phase contrast to be detected on the phase spectra’. It has been published [13] that the blind frequency and the defect depth are correlating by(20)

where C₁ has been called as a correlation constant, which is in the range of 1.5–2.

Assuming the 1st zero crossing frequency of the thermal wave (see Equations (12(12) ) and (17(17) )) as the blind frequency, then d = λ/4 (Equation (16(16) )) results in a value of(21)

6. TSR results

With the TSR technique [2,14] the data are evaluated in the time domain instead of in the frequency domain. If the temperature time function is plotted in double logarithmical scale, as e.g. in Figure 6(b), then its first and second derivatives can be calculated as(22) (23)

Taking the first logarithmical derivative of the temperature for semi-infinite body, described by Equation (1(1) ), results(24)

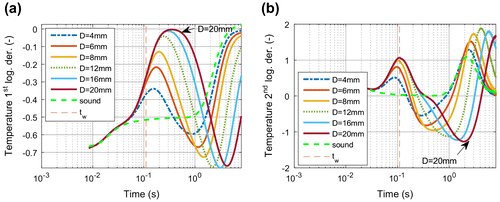
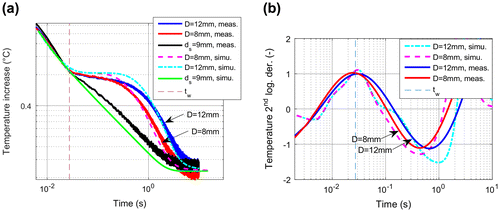
The first derivative for finite body, see Equation (6(6) ), starts also with a value of −1/2 and when the heat starts to accumulate above the defect at time t_w and tending to the constant value of T_end, then the derivative changes to 0. The inflexion point is at time t_w, therefore the 2nd derivative has its maximum at this time. Figure 8 compares these functions with the ones obtained for the simulated model of Figure 6(a). As the trapped heat above the defect flows laterally away, the 1st derivative decreases, causing a minimum in the 2nd derivative. The 1st and 2nd derivative of the analytical curve and the simulated one for the sound surface fit very well, only at the beginning, shortly after the heating pulse is a difference to observe. This is caused by the rather low time resolution of 1/50 Hz = 0.02 s in the simulation model. Other simulations with higher sampling frequency (see e.g. in Section 7.5) show better fit also for short times.

Figure 8. Temperature (left), its 1st derivative (mid) and its 2nd derivative (right) for the simulation model with 20 mm diameter and 3 mm defect depth in a 9 mm thick sound steel material. As comparison also the analytically calculated functions for a finite body with 9 mm thickness are plotted.

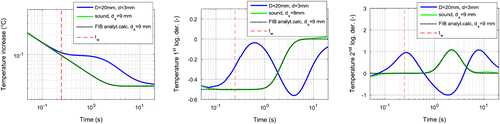
As in TSR the first and second derivatives are used, which are mainly visualising the heat flow, the effects of inhomogeneous heating are therefore well suppressed, similarly to the PPT evaluation. As measured data due to noise cannot be directly differentiated, polynomial fitting is suggested [2] as a preprocessing step. Regarding the optimum polynomial degree for the fitting, different investigations have been published [15]. If the used degree is too high, then the fitted line is strongly affected by noise. On the other hand, if the polynomial degree is too low, then it does not follow well enough the measured curve. Consequently, it can occur that a not correctly fitted polynomial has its inflexion point or its maximum at a different position as the original curve would have.

Another possibility is to use line smoothing instead of polynomial fitting. For example filtering with weighted averaging over the neighbouring points can be appropriate. The smoothed curves can be differentiated to obtain the 1st and 2nd derivative images, without encountering the problem with selection of the correct polynomial degree. On the other hand, the polynomial fitting of TSR has the advantage, that it provides the opportunity to store only the polynomial factors for each pixel, which needs much less storage than the original infrared image sequence. And from the coefficients it is possible to reconstruct the denoised temperature images [2].

It is to note that in this paper a generic Matlab routine is used to perform polynomial fitting. However, TSR is a patented method [2] that is only available in software programmes sold by its developers, using optimised, proprietary algorithms. While the generic approach is adequate for the purposes of the comparison performed in this paper, it is not the authorised, commercial version.

Figure 9 shows the first and second derivatives calculated for a couple of FEM models with different defect sizes. It can be observed that

•	The 2nd derivative has a maximum at tw, as at this point of time the temperature starts to saturate and tends to remain constant;
•	If the defect’s aspect ratio is so small, that no real temperature plateau occurs, then this maximum of the 2nd derivative is shifted to shorter time, as it has been also shown in [16];
•	The 2nd derivative has later a negative minimum which corresponds to the time when the accumulated heat above the defect starts to flow laterally away, therefore this time position correlates with the size of the defect.

Figure 9. 1st (a) and 2nd (b) derivative of temperature curves for models with different defect sizes (defect depth = 2 mm).

7. Determination of the defect depth

As has been shown in the previous sections, the first zero-crossing frequency f_z of the thermal wave (see Equation (17(17) )) and the maximum of the second logarithmical derivative (see Equation (19(19) )) correspond with the defect depth:(25)

Hence the blind frequency in the PPT technique is the numerically with FFT calculated frequency, where the phase contrast is zero, it corresponds to f_z of the thermal wave. Therefore it can be used for the estimation of the defect depth. In the next sections different parameters are investigated how they affect in PPT and in TSR techniques the determination of this depth value.

7.1. Dependency on time duration

For the PPT technique the end of the evaluation or observation time (t_end) determines the base frequency (see Equation (4(4) )), therefore for low frequencies a long measurement time is required. Additionally, the necessary time duration has also an effect on the zero-crossing frequency, as it is demonstrated in Figure 10(a). It shows the phase calculated for the FEM simulation model of Figure 6(a) with different time durations:

•	If tend < tw then the temperature vs. time curves for the defect and for the sound surface are identical and no phase difference can be observed (tend = 0.245 s curve in Figure 10(a);
•	If tend is on the accumulation plateau, then there is a phase difference, but no zero crossing, similarly to the finite bodies with infinite lateral extension (tend = 2 s curve in Figure 10(a);
•	If tend is in the range, where the temperature is decreasing above the defect due the lateral heat flow, then there is a zero-crossing, but it is lower than the zero-crossing frequency of the thermal wave (tend = 5 s curve in Figure 10(a));
•	The time point, when the temperature becomes equal over the whole sample surface, is called te. If tend > te, then the zero crossing of the FFT occurs at larger frequency than the one from the thermal waves (tend = 20 s and tend = 100 s curves in Figure 10(a)). Additionally, in order to detect the significant negative minimum, tend should be at least as long, that the temperature above the defect and at the sound surface are mainly equal (te).

Figure 10. a: Phase contrast calculated for the FEM simulation model of Figure 6(a) regarding different time durations; b: ratio of the calculated defect depth to the real depth plotted vs. t_end.

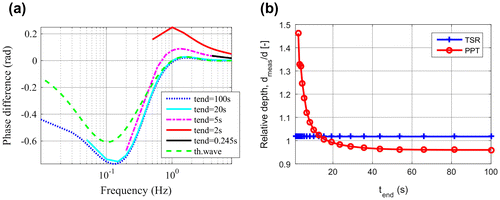
From the zero crossing frequency a defect depth can be calculated (see Equation (25(25) )), which is shown in Figure 10(b). If the time duration t_end is too short, then the defect depth is overestimated by the PPT technique, and in the case of long t_end, the depth is slightly underestimated.

In the case of TSR the evaluation time t_end has to be larger than t_w, that means a difference between the sound surface and the defect should be observable in the temperature response. If this is the case, then the maximum of the 2nd derivative can be used for defect depth estimation, which is very close to the real depth, independently of t_end (see Figure 10(b)).

7.2. Dependency on pulse length

The derivations in the previous sections have assumed a Dirac delta heating. Real measurements cannot have infinitesimal short pulse, and it is well known [17] that shortening of the heating pulse is significant, especially for shallow defects, where the temperature response occurs shortly after the excitation.

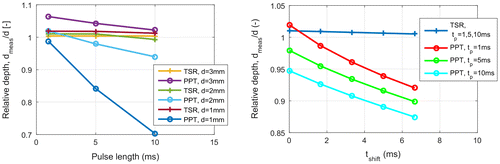
Simulation models with 1, 5 and 10 ms heating pulse have been calculated to investigate this effect, see Figure 11(a). In the case of TSR the effect is negligible small, as mainly it means only a small time shifting. In contrast, the zero crossing frequency of PPT is strongly affected by the pulse length. The longer the pulse and the shallower the depth, the larger is the error of the depth calculation.

Figure 11. a: Ratio of the calculated defect depth to the real depth versus heating pulse length, defect depth = 1–3 mm, aspect ratio of defect diameter to depth is equal to 6 for all the simulated models; b: relative depth depending on the shifting of the starting time (D = 12 mm, d = 2 mm).

7.3. Dependency on evaluation start

If the heating is not Dirac delta pulse, then the temperature versus time function in double logarithmical scale does not start with a straight line with −1/2 slope, as it has been shown in Figure 4(a). In case of a pulse heating with finite duration the temperature slightly deviates from this line. It is a usual technique to shift the starting time of the evaluation a little bit, approximately with the half of the heating pulse, in order to obtain the temperature vs. time function closer to the theoretical straight line. For this reason, it has been investigated how this shifting of the starting time affects the determination of the defect depth.

Figure 11(b) shows the results of these calculations. In the case of TSR no influence can be observed, as the curves are shifted by couple of ms, therefore the t_w value is shifted only by this very short time. The defect depth determined from PPT is significantly influenced by this shifting and the error of the calculation is even increased due to the shifting.

7.4. Dependency on defect size

If the defect size is small, then the trapped heat above the defect flows quickly laterally away and no temperature plateau occurs. As it is visible in Figure 9(b), and it has been also shown already by other authors [16], the maximum of the 2nd derivative is shifted to shorter times, which results in an underestimation of the defect depth, see Figure 12(b).

Figure 12. a: Phase contrast for different defect sizes, calculated for the same models as in Figure 8; b: relative depth depending on the aspect ratio (d = 2 mm, D = 4–20 mm).

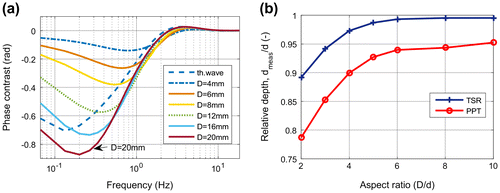
The zero crossing frequency depends also on the defect size: small defects cause higher zero-crossing, see Figure 12(a). This causes an underestimation of the defect depth similarly to TSR (see Figure 12(b)).

It is interesting to note, that the larger the defect is, the larger negative phase contrast occurs at small frequencies (see Figure 12(a)). The smaller a defect is, the earlier t_e, i.e. an equalised temperature at the surface is achieved (see also in Figure 6(b)). As the frequency of the minimum phase contrast correlates with the reciprocal value of t_e, the shifting of the minimum to higher frequency with smaller defect diameter is well understandable.

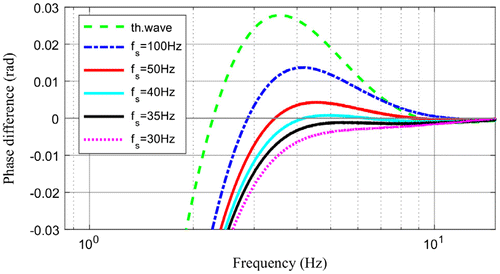
7.5. Dependency on sampling frequency

As has been shown in Section 2 the sampling frequency defines the maximal frequency of the spectrum obtained by FFT. Additionally it has also an influence on the resolution of the phase vs. frequency function: the higher the sampling frequency the better is the resolution in the high frequency range. This has a stronger effect, if the defect depth is less, which means the zero crossing frequency is higher. For a good resolution of shallow defects high sampling frequency is necessary, as t_w, the starting time of accumulation takes place earlier. Figure 13 shows in close-up the zero-crossing for the defect depth of 2 mm calculated with different sampling frequencies. With lower sampling frequency the resolution becomes less, the zero-crossing calculated by FFT is shifted farer away from the theoretical value of the thermal wave, and also the maximum value of the phase contrast becomes less and less with lower sampling frequency.

Figure 13. Phase contrast in the vicinity of the zero crossing calculated with different sampling frequencies (d = 2 mm, D = 20 mm, t_end = 100 s).

7.6. Dependency on noise

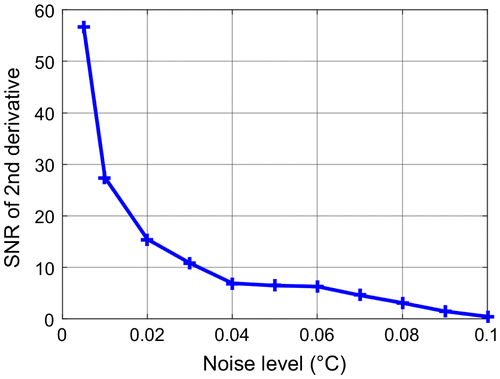
In order to investigate how noise affects the phase contrast, random noise in different levels has been added to the simulated results. The noise was generated by random numbers in a given range specifying its peak-to-peak value. Figure 14(a) shows the phase contrast (d = 3 mm, D = 20 mm) calculated for a noisy model with low noise level of 0.005 °C. At low frequencies the noise is very well suppressed due to the FFT, but for high frequencies the noise becomes more and more dominant. The phase contrast itself is much lower for high frequency due to the strongly damping of the thermal wave. Hence the additional large influence of the noise and due to the decreasing signal, a correct determination of the zero-crossing becomes very difficult. Figure 14(b) shows how SNR for the phase contrast changes with increasing noise level at the position of the minimum phase contrast (f = 0.13 Hz) and at the maximum (f = 1.67 Hz). The signal is much higher at low frequency (see also in Section 3.3) than at higher frequencies, and on the other hand the noise is better suppressed at low frequencies. Therefore small and shallow defects can be well detected at low frequencies, but the positive maximum at higher frequency may be too noisy for a possible detection.

Figure 14. a: Phase contrast with additional random noise (noise level = 0.005 °C); b: SNR of the phase contrast at the negative minimum (f = 0.13 Hz) and at the positive maximum (f = 1.67 Hz).

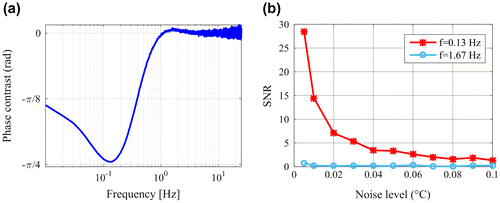
Figure 15 shows three phase images, received for the same simulation model as in Figure 14(a) with additional noise. At frequency 0.13 Hz the phase contrast has its minimum value (and the highest maximum absolute value) and the defect is excellently detectable. At f = 1.67 Hz the phase above the defect is higher than at the sound surface and the positive maximum is achieved (Figure 15(c)). But the noise, even as it has the same level as for Figure 15(a), dominates the phase image.

Figure 15. Phase images for the simulated model with additional noise (noise level = 0.005 °C, D = 20 mm, d = 3 mm, d_s = 9 mm, steel material parameters); a: at the frequency of the negative phase contrast minimum; b: at the zero crossing frequency; c: at the positive phase contrast maximum.

In Figure 15(b) the phase image at the zero crossing frequency is shown. It is to note, that phase in the midpoint of the defect is the same as at the sound surface, but at the boundary of the defect, due to the lateral flow, the phase is negative. This demonstrates an additional problem determining a zero crossing frequency: it is different over the whole defect. In the case of an artificial symmetrical defect the midpoint can be well used, but for an arbitrary defect shape it is questionable which points should be selected. As it has been noted in [18], the blind frequency depends also on the shape of the defect.

In the case of TSR additional noise is very well suppressed due to the polynomial fitting. Figure 16 shows two 2nd derivative images for the same case, as Figure 15 showed the phase images. Figure 16(a) is at the time of t_w, which means at the maximum of the 2nd derivative, and Figure 16(b) shows the situation when the 2nd derivative has its minimum. In both cases the noise is well reduced and not noticeable at all.

Figure 16. 2nd derivative images at the maximum (a) and at the minimum (b), calculated for the same noisy model as in Figure 15.

Figure 17 shows how the SNR at the maximum (t = t_w) decreases with additional noise level. Comparing Figures 17 and 14(b) it can be observed that the signal-to-noise ratios are very similar for both techniques. The SNR of the 2nd derivative is slightly higher, but it has been shown [19,20] that the SNR for PPT can be improved, if the FFT calculation is applied with TSR reconstructed noised reduced images.

Figure 17. SNR of the 2nd derivative at t_w = 0.24 s versus additional noise (d = 3 mm, D = 20 mm)

8. Measurement results

In a 9 mm thick steel plate flat bottom holes (FBHs) with different diameters and with different remaining wall thicknesses have been created. Even if real defects, as e.g. cavities in castings, are holes inside the material, they are difficult to manufacture artificially. Instead of that, FBHs are used to create failures with defined geometry. Flat bottom holes are a kind of ‘best case’ scenario for detectability [16]. The difference between the signals from flat bottom holes and cavities in many cases is negligible, as far the effusivity ratio of the host material and the included air is large. This topic is investigated in more detail in another publication [9].

For the measurements a flash lamp with a full width half maximum duration of 1 ms and 6 kJ energy has been used. The infrared camera with a cooled InSb detector has in full window mode with 383 Hz a pixel resolution of 320 × 256. Using half image size the speed of 600 Hz has been set to get a better resolution for shallow defects. Its spectral range is specified with 1.5–5.1 μm. Between the flash lamp and the sample a plate has been placed, which lets radiation only in the visible range through, but not in the infrared spectrum of the camera, in order to reduce the ‘after glow’ effect of the flash.

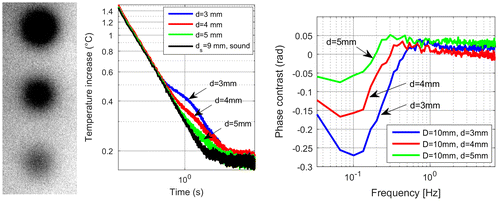
In the first sample three FBHs with 10 mm diameter and remaining wall thicknesses of d = 3, 4 and 5 mm have been manufactured. Figure 18 shows the phase image, the temperature vs. time functions and the phase contrast for these three FBHs. The trend of the phase contrast functions corresponds to the expected values: the deeper the defect, the lower the zero crossing frequency. But their values are significantly less than the theoretical values. On the one hand, the aspect ratios for these FBHs are between 2 and 3.3 and no temperature plateaus occurs, therefore their defect depth is difficult to determine as it has been shown in Section 7.4. On the other hand, the pulse of the flash lamp decreases exponentially and has a significantly longer tail than it is assumed in the simulations. This distorts also the measurement results, as it has been shown in Section 7.2.

Figure 18. left: phase image at f = 0.1 Hz of three FBHs with 10 mm diameter and with remaining wall thickness d = 3,4,5 mm from top to bottom, respectively; mid: temperature vs. time function for these defects; right: phase contrast calculated by PPT for the same measurement.

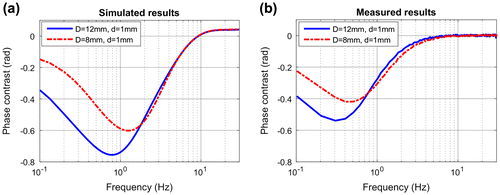
In another sample two FBHs with remaining wall thickness of 1 mm and with 12 and 8 mm diameters have been created. As the aspect ratio of these FBHs is 12 and 8, accordingly the temperature plateau is quite visible. Figure 19(a) compares the simulation and measurement temperature vs. time functions, which fit quite well. Hence t_w, calculated from the 2nd derivatives corresponds also with the expected value of 0.027 s (see Figure 19(b)). The phase contrast curves (see Figure 20) show the expected trends, but similarly to the previous measurements the zero crossing frequency is less than expected. The main reason for this is the not infinitesimal short heating pulse, and as it has been shown, the PPT calculation is very sensitive to this.

Figure 19. a: Comparison of measured and simulated temperature curves (a) and their 2nd logarithmical derivatives (b) for two defects with a remaining wall thickness of 1 mm and defect diameter 12 and 8 mm.

Figure 20. Comparison of phase contrast results based on the simulated (a) and measured (b) temperature for the same defects as in Figure 19.

9. Summary and conclusion

PPT and TSR are two well established methods to evaluate measurement results after short heating pulse and both techniques can be well used to detect even shallow and small defects. For both techniques similar SNR values can be achieved: in the case of TSR the best images can be obtained with the 2nd derivative image at the time of t_w, which also means that the defect can be detected already in a very early time [21]. For PPT the best SNR occurs at the negative minimum, which can be only observed if the measurement is recorded as long as the temperature above the defect and the sound surface is already equalised, which on the other hand requires a long recording duration.

Additionally to the pure localisation of a defect, an important question is how deep and how large it is. Both techniques, PPT and TSR, can be well used to estimate defect size, but this question is not handled in this paper, some investigations have been made in another publication [6].

With the TSR technique the defect depth can be determined from the maximum of the 2nd derivative. In the case of PPT this calculation is much more difficult. Physically the zero-crossing frequency contains this information, but it is affected by a couple of factors, therefore its exact determination from measurements encounters different difficulties. Additionally, in PPT always a comparison to a sound point is required, only the difference of these two phases exhibits a zero-crossing frequency. In contrast, TSR and the calculation of the 2nd derivative are done for each pixel separately and no selection of a sound reference point is required. Table 1 summarizes this comparison of both techniques.

Table 1. Comparison of PPT and TSR technique.

	PPT	TSR
	Evaluation in frequency domain	Evaluation in time domain
Effects of inhomogeneous heating well suppressed	Yes	Yes
Subsurface defects can be detected	Appr. up to the same aspect ratio defects can be detected by both techniques
Image with best SNR usually obtained	At low frequency with negative phase contrast	2nd derivative image at t = tw
Estimation of the detect depth	Based on the frequency (fb) when the phase contrast is zero:	Based on the time (tw) when the 2nd derivative has a maximum:
	Defect depth estimation is influenced by many factors	Defect depth calculation is mainly independent of most of the factors
Reference sound point	For defect depth detection a reference sound point is necessary	2nd derivative is calculated for each pixel separately, no reference point is necessary
Necessary observation time	Long: tend ≥ te (time when temperature at the whole top surface is equalised)	Short: tend > tw

Disclosure statement

No potential conflict of interest was reported by the author.

Notes

^* The paper is an extended version of the publication presented at Thermosense conference and referenced as [6]. In the first part it is investigated, what is the difference using the theoretical Fourier transformation and the numerical FFT calculation for flash thermography results. The next part compares the defect depth calculation in TSR and PPT, and the influence of a couple of parameters is investigated. As this analysis is done based on FEM simulation, the last section shows also measurement results on steel sample with flat bottom hole defects.