Developing design principles to enhance pre-service teachers’ understanding of number structure and mathematical equivalence in early grade mathematics

Abstract

Research on mathematical equivalence, and to some extent, on number structure in early grade mathematics, has shown that most students at primary and secondary levels understand these concepts instrumentally rather than relationally. The study reported in this paper uses a design research approach to explore both mathematical equivalence and number structure in a primary pre-service teacher education programme at a university in South Africa and reports on an intervention strategy intended to culminate in developing design principles comprising guidelines for the effective teaching of number structure and mathematics equivalence in primary pre-service teacher education programmes. The mixed method study comprises 70 first-year primary pre-service teachers (PSTs) and a teacher educator. The PSTs wrote pre- and post-tests, and were interviewed following the pre-test. Skemp’s notion of relational and instrumental understanding guided the design of the intervention and the analysis of the data. The results from the study indicates that PSTs’ understanding of the notion of equivalence is similar to what has been reported for students in schools, and that there were some learning gains in the post-test results. Based on the findings from the study in general, some emergent design principles are proposed.

Keywords:

• Mathematical equivalence
• number structure
• design principles
• early grade mathematics
• equal sign
• instrumental and relational understanding
• design research

Introduction

Research into the state of primary education in South Africa has indicated that a good number of learners fall behind by as much as 2–3 years below their actual grade by the time they are in Grade 6 (see Hartley, 2007; Spaull & Kotze, 2015; Mohohlwane & Taylor, 2015; Human, Van der Walt, Posthuma, 2015). It is evident that this cumulative growth in knowledge gap starts in the early grades (see, for example, research by Fritz et al., 2020). While these learning gaps cannot solely be attributed to one factor, they raise questions about the teacher’s role in creating meaningful opportunities for learning mathematics in early grade classrooms in South Africa and the extent to which teachers teach for understanding in these grades. Research into teaching and learning in the early grades in South Africa has repeatedly shown a lack of coherence in the teaching of mathematics and a decline into choral responses that are not helpful in developing conceptual understanding in learners (Venkat & Adler, 2012; Ndabezitha, 2022). Several reasons have been put forward to explain this incoherence in teaching and these learning gaps in the early grades, and how both are precipitated by knowledge gaps that teachers themselves demonstrate (Askew, Bowie, & Venkat, 2019; Venkat & Spaull, 2015). What this also points to is the question regarding teacher education and how these teachers are enculturated into teaching mathematics in the early grades. In this vein, Michael Fullan’s (1993) anecdote, that teacher education has the honour of being simultaneously the worst problem and the best solution in education, comes to mind.

In light of research evidence that the mathematics content knowledge of teachers in the Foundation Phase (FP)—Grades R–3—needs strengthening, the Maths Wits Connect-Primary (WMC-P) project embarked on a design research and development project aimed at improving Foundation Phase, and Intermediate Phase (Grades 4–7) pre-service teachers’ content knowledge that will see them better equipped to teach, with understanding, different critical concepts in mathematics. The focus in the inaugural year of the project has been on additive reasoning, and will shift to multiplicative reasoning and geometric reasoning in subsequent years. The project is motivated by two key goals: first, to gain an understanding of the content knowledge gaps in first year pre-service teachers (PSTs) on these different concepts in mathematics, and secondly, based on our understanding of key gaps in PSTs’ understanding of these concepts, to develop design principles for teaching these concepts in such a way that attends to these conceptual gaps.

Located in the Foundation Phase teacher education programme, the research reported in this paper focuses on mathematical equivalence and number structure, two concepts which rely on additive reasoning for comprehension. These concepts have been researched for many decades with most research bemoaning the poor grasp of number structure, equivalence and/or the equal sign in mathematics across several grades with some researchers concluding that far less attention is paid to these important and foundational notions in mathematics (Essien, 2009; Essien & Setati, 2006; Knuth, Stephens, McNeil, & Alibali 2006; Pournara & Sanders, 2020). In stressing the importance of mathematical equivalence, McNeil, Fyfe and Dunwiddie (2015: 423) argue that ‘[a] formal understanding of [mathematical equivalence] involves knowing that numbers, measurements, and expressions can be represented in a variety of equal and interchangeable ways’. As Mason, Stevens and Watson (2009), as well as Mulligan and Mitchelmore (2009) argue, structure permeates the whole of mathematics at every stage and for every age, and is of critical importance in developing mathematics competence in children. Research (see for example Mulligan, 2002; Tondorf & Prediger, 2022) has shown that young children who understand structure in mathematics acquire deep conceptual understanding and perform better than those with an underlying poor understanding of mathematical structure. Concerning the notion of equivalence, studies conducted in the Senior Phase (Grades 7–9) in South Africa continue to show how a poor understanding of the notion of mathematical equivalence has proved detrimental to the understanding of algebra (Essien & Setati, 2006; Pournara & Sanders, 2020). Barbe, Bosch, Espinoza and Gascon (2005) argues that the moment of first encounter is important for a successful understanding of a didactic process (or processes of study) involving a concept. In South Africa, as in many parts of the world, number structure and the notion of equivalence are first introduced in the Foundation Phase. Knowledge on how to organise the learners’ first encounter with a particular concept is crucial to the type of internalisation that occurs in the learners.

A critical issue picked up by the WMC-P project team while researching in primary schools is the lack of attention to getting learners to appreciate and work with the underlying number structure (Venkat & Askew, 2018). Venkat and Askew (2018) argue that in the absence of deliberate attention to structuring, particularly where this relates to number, learners are robbed of the opportunity to abstract the relations between the properties of the number system being studied. Working from a sociocultural perspective, they (Venkat and Askew) found that there are several mediational means that can be employed in instruction, namely, mediating with artefacts, inscriptions, and talk and gestures (to build mathematical and learning connections, and for generating and validating solutions).

Understanding that PSTs tend to teach how they have been taught, it was incumbent upon the WMC-P project to investigate ways in which instruction can foreground and focus PSTs’ attention on number structure and mathematical equivalence. The space in which Venkat and Askew (2018) envisage these mediational means to play out is primarily in the example space opened up by the teacher. For this reason, in developing the principles for the design of the course on how to prepare pre-service mathematics teachers better to effectively teach number structure and mathematical equivalence, attention to careful selection of examples featured prominently in relation to providing varied examples that took into account progression from simple to complex examples.

In light of the challenges highlighted above with respect to number structuring and equivalence, the following specific questions inform the present study reported in this paper:

1. What gaps can be seen in first year Foundation phase PSTs’ knowledge on the concept of number structure and mathematical equivalence?

2. What learning gains (if any) can be seen in PSTs’ content knowledge following a carefully designed intervention focusing on number structure and mathematical equivalence?

3. In light of the answers to RQs 1 and 2 above, what principles can be formulated to inform the design of a course on how to better prepare pre-service mathematics teachers to effectively teach number structure and mathematical equivalence?

In the two sections that follow, we provide background information on early grade teaching and learning of Mathematics in South Africa more generally, and the teacher education programme at the research institution specifically.

Early Grade Teaching and Learning of Mathematics in South Africa

As indicated in the introductory section, over the past decade, most research conducted in South Africa into teachers’ mathematical content knowledge has been on in-service primary teachers, and in particular, on Intermediate Phase (Grades 4–6) teachers (e.g. Carnoy & Chisholm, 2008; Venkat & Spaull, 2015). With these studies reporting on substantial gaps in upper primary teachers’ mathematical content knowledge, there has been a shift in attention towards pre-service teacher education and its role in enhancing prospective teachers’ mathematical content knowledge.

The Initial Teacher Education Research Project is a study that examined pre-service primary mathematics teacher education programmes across five different pre-service primary mathematics teacher education programmes in South Africa. It reported on big differences in pre-service course offerings related to mathematics (Bowie & Reed, 2016) and highlighted the need, not only to work across concepts, but also to include assessment items that will provide insights into pre-service teachers’ higher and lower-cognitive-demand skills. In taking up this challenge, Bowie, Venkat and Askew (2019) conducted an exploratory study into pre-service teachers’ mathematical content knowledge and reported on the results of an assessment administered to test prospective teachers’ (n = 488 first year students; n = 282 fourth year students) higher and lower-cognitive-demand skills. A key finding of this study was that, although the fourth year students performed better on the lower-cognitive-demand items, there was very little difference in the performance of the first and fourth year cohorts on the higher-cognitive-demand items. Included amongst the higher-cognitive-demand whole number items was the following mathematical equivalence task:

Fill in the number to make the number sentence true 623 − 298 = 622 −?

The difficulties experienced by both cohorts on this higher-cognitive-demand item led Bowie, Venkat and Askew (2019) to conclude that ‘many student teachers at both first and fourth year university level experience difficulty working structurally with numbers, and with making sense of whole-number problem situations’ (p. 293). In light of the insights provided by Bowie et al.’s (2019) study, we look to delineate in this paper emergent design principles that can inform the teaching of mathematical equivalence and number structure in pre-service teacher education.

The Primary Teacher Education Programme at Wits University

In 2018, the PrimTED standards and norms were designed to create a collective approach to what should be taught in Primary Schools regarding developing Number Sense across universities. The promulgation of these standard and norms precipitated changes in how teacher education programmes introduce, arrange and approach concepts, in particular, Additive Reasoning. Following careful consideration and adoption of the PrimTED standards and norms by the Wits School of Education, we illustrate in Table 1 the differences between the BEd mathematics curriculum offered prior to 2018 and the curriculum offered from 2018 to date.

Table 1. Difference between BEd primary mathematics curricula

Difference between the previous and current BEd primary school mathematics curriculum
Prior to 2018	2018–2022
First year	First year and second year
Intemediate Phase (IP) and Foundation Phase (FP) cohorts of students were taught mathematical concepts in the Maths Division	IP and FP cohorts of students were taught together by lecturers in both the Maths Division and the Foundation Phase Division. In the first two years, the focus has been on the domains of number and geometry respectively, with IP and FP students attending together
Second, third and fourth year	Third and fourth year
IP and FP cohorts of students were taught mathematics methodology courses either in the Maths Division or in the Foundation Phase Division	IP and FP students are split according to their phases, focusing on the teaching of number and geometry. In year 3 the focus is on how number should be taught and in Year 4 the focus is on how geometry should be taught. FP students are taught by the Foundation Phase Division while the IP students are taught by the Maths Division

Additive reasoning is currently being taught over two weeks in two one-hour lectures and two one-hour tutorials each. Until the onset of our study, in the two weeks, instructional emphasis has been on the rules governing additive reasoning, particularly where these rules relate to subtraction, and using models and representations (part–part–whole diagrams, 100 number chart, number lines, simplified pictorials), as well as calculation methods (column methods: traditional and extended format) and calculation strategies (near doubles, compensation, bridging through 10).

In the section that follows, we delineate our theoretical framework informed by what we have outlined in the previous two sections.

Theoretical Orientation

The theoretical stance that informs our study is based on Skemp’s notion of understanding. One of the central assumptions of the Skempian theory of understanding is that understanding has a subjective nature since it involves assimilation into the proper schema (Skemp, 1971). Skemp (1976) distinguishes between relational understanding and instrumental understanding of mathematical concepts. By relational understanding, Skemp alludes to an in-depth and adaptive understanding of a mathematical concept that goes beyond the mere application of rules to arrive at answers. By instrumental understanding, he refers to the mere application of rules to arrive at answers without consideration of why the rules work.

More recently, Carpenter et al. (2005) have used the terms computational perspective of arithmetic vs. a perspective of arithmetic in which relations are prominent to express the dichotomy between Skemp’s relational and instrumental understanding. They call the perspective of arithmetic in which relations are prominent relational thinking and argue that it denotes paying attention to the relationships and fundamental properties of operations and using these ‘to transform mathematical expressions rather than simply calculating an answer following a prescribed sequence of procedures’ (Capenter et al., 2005: 54). The example they provide to illustrate this is particularly illuminating: using the example of the number sentence: 8 + 4 = __ + 5, they argue that learners who provide an answer of 12 see the equal sign as a do-something symbol. On the other hand, learners who provide the correct answers may do it in two ways. First, the focus can be on adding 8 and 4 and figuring out which number added to 5 produces the sum of 8 and 4; second, the focus can be on the number sentence as a whole by recognising that 5 is one more than 4 and as such, the missing number must be one less than 8. Carpenter et al. (2005) argue that while both strategies focus on the equal sign as a relation, in the first the focus is on ‘computation specific to the problem to calculate the answer’ (p. 54) while the second shows a holistic view of the equation, and thus, a deep level of understanding of the number structure that uses number relationships to arrive at the correct answer. Along this line of thinking, Matthews, Rittle-Johnson, McEldoon, and Taylor (2012) developed Mathematical Equivalence Knowledge Construct Map for further disaggregating ‘equivalence knowledge’ by level of complexity ranging from operational (lowest level) to relational (highest level) levels, as shown in Table 2.

Table 2. Construct map for mathematical equivalence knowledge (Matthews et al., 2012: 224)

Level	Description	Core equation structure(s)
Level 4 Comparative Relational	Successfully solve and evaluate equations by comparing the expressions on the two sides of the equal sign, including using compensatory strategies and recognising transformations that maintain equality. Consistently generate a relational interpretation of the equal sign	Equations that can be most efficiently solved by applying simplifying transformations. For example, without adding 67 + 86, can you tell if the number sentence ‘67 + 86 = 68 + 85’ is true or false?
Level 3 Basic Relational	Successfully solve, evaluate and encode equation structures with operations on both sides of the equal sign. Recognise relational definition of the equal sign as correct	Operations on both sides: a + b = c + d a + b − c = d + e
Level 2 Flexible Operational	Successfully solve, evaluate and encode atypical equation structures that remain compatible with an operational view of the equal sign	Operations on the right: c = a + b No operations: a = a
Level 1 Rigid Operational	Only successful with equations with an operations-equals-answer structure, including solving, evaluating and encoding equations with this structure. Define the equal sign operationally	Operations on left: a + b = c (including when blank is before the equal sign)

To expound further on the distinction between instrumental and relational understanding, we draw on Mason et al.’s (2009) argument that instrumental understanding for fluency in procedures is of little value if learners only understand procedures without an ‘appreciation of the mathematical structures which make them effective’ (p. 11). In short, it is an appreciation of structures that underpins relational understanding. In this light, in our study, we do not view one form of understanding as necessarily superior to the other. Instead, we see both forms of understanding as complementary. We draw on the different contructs from Skemp (1971), Carpenter et al. (2005), and Matthews et al. (2012) to understand data generated from our study.

Methodological Approach

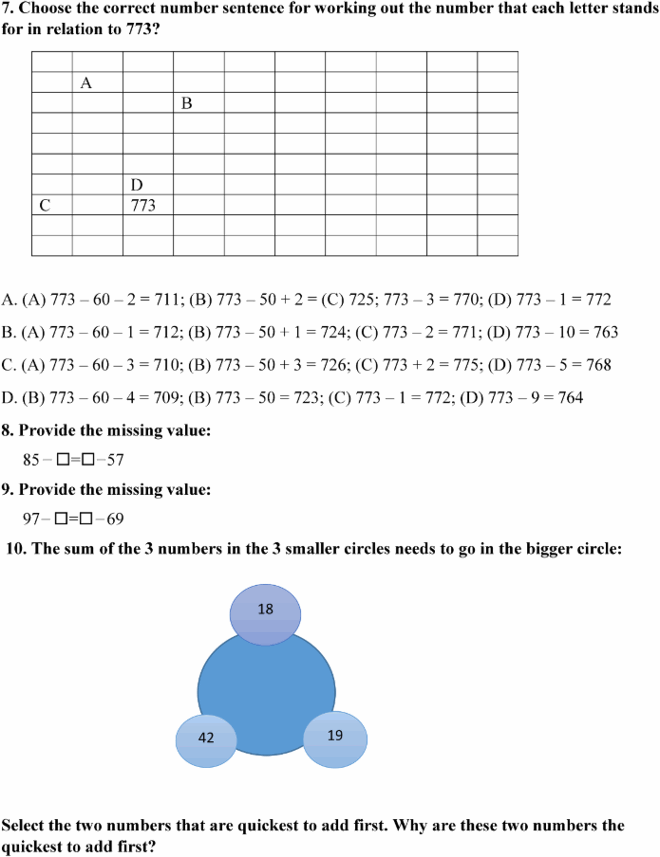
Against this backdrop, our study uses the design research approach—also called education design research—an iterative research process which Reeves (2006) described as consisting of four stages. According to Reeves, McKenney and Herrington (2011), the education design research approach has the dual objectives of ‘developing creative approaches to solving human teaching, learning, and performance problems while at the same time constructing a body of design principles that can guide future development efforts’ (p. 55). To add to this, Prediger, Quasthoff, Vogler, and Heller (2015) contend that a good theoretical base for the specific content (in our case the notion of equivalence and number structure) is important. Our project uses the four phases of design research as shown in Figure 1. In the last stage, the cumulative work for the present study would be to derive learning design principles comprising guidelines for an effective pedagogic approach to teaching number structure and mathematics equivalence in pre-service teacher education programmes.

Figure 1. Four stages of design research (Reeves, 2006: 59)

Amiel and Reeves (2008) argue that the ultimate goal of using the design research approach is to build stronger connections between educational research and real-world problems. For this study, we operationalise this building of stronger connection as the teaching of number structure and mathematics equivalence with understanding so that all PSTs (regardless of their level of attainment) would be better prepared to teach these concepts in mathematics.

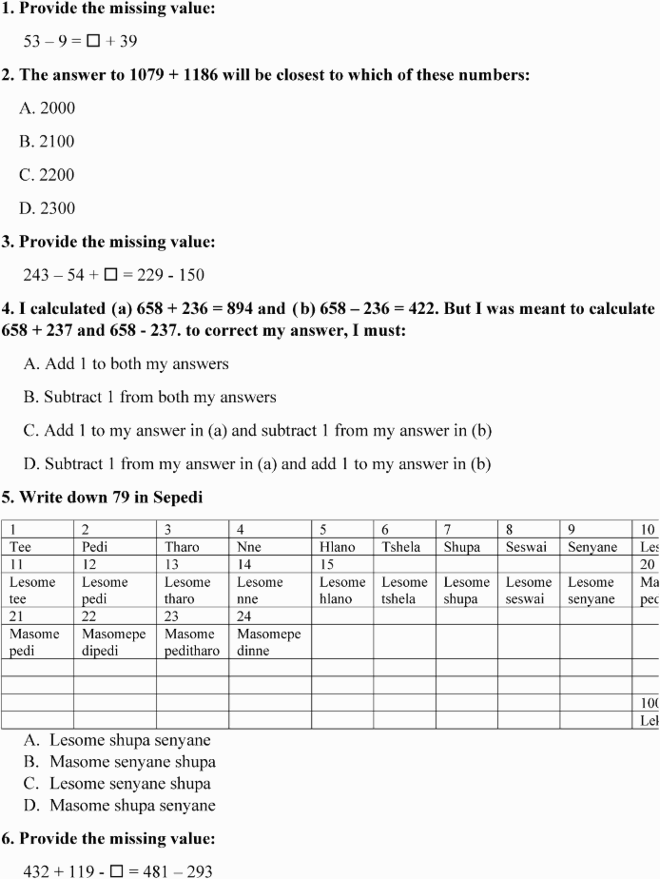
Phase 1 as per the stages of design research consisted in identifying the problem through a carefully designed pre-test consisting of 27 items (10 of these are provided in the Appendix) related to equivalence and number structure, then analysing the pre-test to establish how 70 FP PSTs understand number structure and the notion of equivalence. An interview with selected PSTs (n = 25) was also conducted. The interview was aimed at determining how they answered particular questions during the test. Both pre-test and interviews gave us an understanding of the problems related to equivalence and number structure and fed into the design of the intervention as explained below.

In Phase 2 (see the second stage in Figure 1), based on the results of the worst-performing items, lessons were designed on the two functions of the equal sign. The first function was that the equal sign produced the answer to additive tasks. The second function of the equal sign is that the equal sign creates equivalence. The design lessons supported the student’s development in their area of weakness within additive tasks. We collaboratively developed ways to improve the quality of teaching (and learning) of both concepts through carefully selected/developed examples. The development of the lessons was guided by two principles—using the idea of balance and the number line, and using Skemps’ notion of instrumental and relational understanding as a theoretical lens to inform the selection/development of the examples to be used in class. The PSTs were taught in two classes and one tutorial focusing on using the equal sign in solving additive tasks.

Phase 3 of our research consisted of implementing the carefully selected/developed examples from Phase 2. The design of the first lesson was focused on the equal sign as a way of producing the answer. So, the first approach used diagrams such as 100 number charts and number lines to solve additive tasks. After that, expanded notation focusing on using place values was used in producing the answers, followed by the use of column addition and subtraction. The final aspect of the lesson was looking at two types of subtraction, namely, taking away and difference.

The second lesson focused on how the equal sign creates equivalence. Equivalence was taught through the use of pictures in which both sides of the equal signs needed to be balanced, whether the number sentences were addition or subtraction. The pictures took the forms of apples and, later in the lesson, blocks. Part–part–whole (PPW) diagrams that would assist in showing equivalence were used. Equivalence was encouraged between the first and second levels of the PPW diagrams. So, the focus was placed on the length of each block. The length of the top and bottom bars was used to enforce the notion of equivalence. Another diagram used was a double numberline, a diagram in which two number lines of the same length are placed on top of each other. The use of the double number line lent itself to supporting a deep understanding of equivalence whenever the one numberline represented one side of the equal sign, and the other number line represented the other side of the equal sign.

With the double number line now backgrounded, the final representation focused on symbols only, ranging from one-digit numbers to three-digit numbers. On the left-hand side (LHS), three numbers were seen, and the right-hand side (RHS) only had one number known with a space for the second number. In solving the task, common numbers from both sides would be written down, and then the knowns would be added, followed by adding in the unknown. For example, 32 + 17 + 28 = _ + 28; in the next line, ‘28’ would be written on both sides of the equal sign _ + 28 = _ + 28. Then 32 + 17 would be added to give 49 and added to the 28 on the LHS to make 77. Without calculations, the student should see that, on the LHS, 49 was added to the 28. Therefore 49 is added to 28 on the RHS. Then both numbers are added to produce the same answer on the LHS and RHS; in this instance, both sides are 77. This process was applied to other addition and subtraction tasks, containing three numbers on the RHS and two on the left side.

Finally, equivalence was used to reinforce the emphasis on reasoning. Reasoning, in this case, was defined as using the answers to the previous calculation to assist in solving the next calculation. For example, 9 + 6 = 15; what will 9 + 7 = __ be? What was promoted is that equivalence can be used to solve the answer. Therefore, if 1 is added to the 6 to make the 7, one needs to add 1 to the 15 to make 16 without adding 9 + 7 from the start. The reasoning is that one can make both sides equivalent by adding 1. The second lecture focused on developing equivalence between the RHS and LHS of the equal signs using different representations instead of producing an answer.

In Phase 3, we administered a post-test to understand the cognitive gains from pre-test to post-test. The post-test was exactly the same as the pre-test.

Phase 4 of our study involved a reflection by the WMC-P Project team on possible learning design principles comprising guidelines for teaching number structure and mathematical equivalence with understanding. Given the iterative nature of design research, and the fact that this is our first year of implementation, we look to repeat the four stages of design research again for another two cycles (years) before providing more definitive design principles. As such, the design principles at this stage are only emergent.

Quantitative Analysis of Data

In the quantitative analysis, we attempt to answer the following research questions:

1. What gaps can be seen in first year Foundation phase Pre-service teachers’ knowledge on the concept of number structure and mathematical equivalence?

2. What learning gains (if any) can be seen in PSTs’ content knowledge following a carefully designed intervention focusing on number structure and mathematical equivalence?

In order to analyse the content knowledge gaps and the learning gains, we first engaged with what counts as ‘desirable’ content knowledge for teaching. By desirable content knowledge, we mean an acceptable level of content knowledge that is adequate to enable one effectively teach a particular content (in our case mathematical equivalence and number structure). In their re-analysis of SACMEQ 2007 teacher test in South Africa, Venkat and Spaull (2015) considered a score of above 60% as an indication of desirable mathematics content knowledge with a majority of test items at the intermediate phase. In our study, 27 test items focusing on number structure and equivalence were administered to 70 FP PSTs. Out of the 27 items, 24 (85%) were at the FP level and four (15%) at the Intermediate phase level. Since most of the items are at the FP level, we consider scores above 70% to indicate desirable content knowledge for teaching the concept of equivalence in this study. We acknowledge that 70% of correct answers for an item is low to be considered a level of teaching attainment, with 85% of items at the Foundation phase level. To unpack the extent of the content knowledge gap, we also focused on items’ difficulty levels. We decided on items with scores below 65% correct answers as difficult items. We used the benchmark of 65% based on PSTs’ performance in both pre- and post-tests.

Results and Findings

RQ1: What gaps can be seen in first-year Foundation phase Pre-service teachers’ knowledge on the concept of number structure and mathematical equivalence?

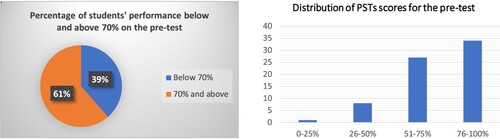
Figure 2a shows that only 61% of the first year FP PSTs attained desirable content knowledge on the concepts of number structure and mathematical equivalence. This finding raised serious concerns as content knowledge is necessary for teaching since teachers cannot teach what they do not know (Ball, Thames, & Phelps, 2008). Figure 2b provides a summary of distribution of PSTs’ scores for the pre-test.

Figure 2. Percentage of Foundation Phase pre-service teachers attaining desirable content knowledge for teaching equivalence

To further unpack the extent of the knowledge gaps of the PSTs, we focus on test items in the pre-test with the lowest performance. Table 1 shows 10 out of 27 test items with PSTs’ performance at 65% correct answers and below. In addition to gaining insight on the areas of difficulty by the PSTs, we also used the 10 items to explore possible shift in the post-test. We decided to look at the gains between the pre- and post-tests by only focussing on these 10 items. Table 3 shows the items where 65% or fewer of the students could answer correctly in the pre-test. We are also interested in the improvements we can see in the post-test after the intervention.

Table 3. Percentage of test items with FP PSTs score 65% and below in the pre-test

S/N	Test items	Correct responses out of 70	Percentage correct answers
1	53 − 9 = __ + 39	46	65
2	The answer to 1079 + 1186 will be closest to which of these numbers: (a) 2000, (b) 2100, (c) 2200, (d) 23,000	44	62
3	243 − 54 + __ = 229 – 150	43	61
4	I calculated (a) 658 + 236 = 894 and (b) 658 − 236 = 422. But I was meant to calculate 658 + 237 and 658 − 237. To correct my answer I must:	41	58
5	Number words from 1 to 24 are given in Sepedi. Use the number structure write down 79 in words in Sipedi	38	54
6	432 + 119 − __ = 481 – 293	36	51
7	A number chart is provided with the number 773 written down. Use the position of 773 to write down values for given positions marked as A, B, C and D	30	42
8	85 − __ = __  − 57	25	35
9	97 − ­__ = __ − 69	22	31
10	Select the two numbers that are quickest to add first (18, 19 and 42) and provide the reason	14	20

Collectively, the findings indicate serious gaps in Foundation Phase PSTs’ content knowledge for teaching the concept of number structure and equivalence. The questions where they performed the worst were questions 7–10. For example, for the last item, with only 20% correct answers, PSTs were asked to select the two numbers (18, 19 and 42) that were quickest to add. In most cases, 18 and 19 were provided as the answer, with some students reasoning that 18 and 19 were the smaller of the three numbers involved. However, a student with a good understanding of number structure would reason that the two numbers are 2 and 1 less than 20, and so the result will be 3 less than 40. Alternatively, they would see 18 and 42 as easier numbers to add since they will produce a number that is a multiple of 10.

To answer the question of what the content knowledge gaps of the first-year Foundation phase PSTs are on the concept of mathematical equivalence, we can say that the students did not understand how to fill in a missing number if they had to fill two missing numbers on each side of the equivalence sign and still maintain equivalence.

RQ 2: What learning gains (if any) can be seen in PSTs content knowledge following a carefully designed intervention focusing on number structure and mathematical equivalence?

To understand learning gains, we compared FP PSTs’ pre- and post-tests performance. Figure 3 shows a shift in the performance of attainment of desirable content knowledge for teaching equivalence from 61% to 86% (a difference of 25 percentage points)

Figure 3. A comparison of the percentage of Foundation Phase pre-service teachers attaining desirable content knowledge for teaching equivalence in the pre- and post-test

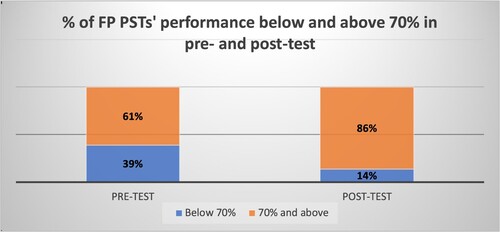
Regarding the shift in difficult items, Table 3 shows a shift in percentage positive points across the 10 items mentioned in Table 1. High changes (in items 7–10), medium shifts (in items 1–3 and 6), and low shifts (in items 4 and 5) can be seen in Table 4.

Table 4. Differences in terms of changes in percentage positive points (see the Appendix for the full versions of questions)

S/N	Test items	Percentage of correct answers (pre-test)	Percentage of correct answers (post-test)	Differences (post–pre) in percentage points
1	53 − 9 = __ + 39	65	79	14
2	The answer to 1079 + 1186 will be closest to which of these numbers: (a) 2000, (b) 2100, (c) 2200, (d) 23,000	62	77	15
3	243 − 54 + __ = 229 – 150	61	72	11
4	I calculated (a) 658 + 236 = 894 and (b) 658 − 236 = 422. But I was meant to calculate 658 + 237 and 658 − 237. To correct my answer I must:	58	61	3
5	Number words from 1 to 24 are given in Sepedi. Use the number structure to write down 79 in word in Sipedi.	54	61	7
6	432 + 119 − __ = 481 − 293	51	72	21
7	A number chart is provided with the number 773 written down. Use the position of 773 to write down values for given positions marked as A, B, C and D	42	93	51
8	85 − __ = __  − 57	35	75	39
9	97 − ­__ = __ − 69	31	79	48
10	Select the two numbers that are quickest to add first (42, 19 and 18) and provide the reason	20	46	27

The most positive gain was in item 7 where the percentage point gain was 51. This suggested that the intervention helped students to underatnd the relationship between 773 and other numbers on the number square. What is interesting to notice is that the difference between the percentage point gains of questions 8 and 9 differs that much (question 8, a 39 persentage points and question 9, a 48 percentage point difference).

To further understand the significance of the difference in performance between the pre- and post-test, we conducted a paired data Wilcoxon signed-rank test since both datasets are not gaussian. Brase and Brase (2011) give guidelines to determine normality by arguing that the distributions must comply with certain conditions. We applied the conditions of Brace and Brase and found that both datasets (pre- and post-tests) are not gaussian. The Wilcoxon signed-rank is an alternative to the parametric t-test that does not require the datasets to be gaussian (Oyeka & Ebuh, 2012).

The null hypothesis—H₀ In the sample, the central tendencies (medians in the case of the Wilcoxon signed ranked test) of the two dependent datasets are the same.

Using SPSS, the Wilcoxon signed-rank analysis showed that, with a 95% confidence level (or 0.05 level of significance), we can reject the H₀, which indicates a statistically significant difference in performance between the pre- and post-test (see Table 5).

Table 5. Summary of paired data Wilcoxon signed-rank

	Null hypothesis	Test	Significance^a	Decision
1	The median of differences between pre- and post-test equals 0	Related-samples Wilcoxon signed rank test	<0.001	Reject the null hypothesis

^aThe significance level is 0.050.

It must be noted that the above quantitative analysis of our data was not geared towards making claims that the intervention strategy worked (or did not work). We will engage with this later.

Qualitative Analysis

In the qualitative analysis, we drew on the quantitative analysis by categorising the 10 questions into three groups: high shifts (in items 7–10); medium shifts (in items 1–3 and 6); and low shifts (in items 4 and 5).

In terms of the questions that had high positive gains from pre- to post-test, question 7 was the highest with a percentage point gain of 51%. In the pre-test, the most common incorrect answers were (A) 773 − 60 – 2 = 711; (B) 773 – 50 + 2 = (C) 725; 773 − 3 = 770; (D) 773 − 1 = 772, with most PSTs indicating during interviews that they did not know what the question required of them. While it can be argued that the gains in the post-test are due to familiarity with the question post the intervention, it was helpful to us to understand that PSTs had a limited grasp of the 100 number chart in such a way that they were unable to generalise this understanding to an extended number chart like the one in question 7. Questions 8 and 9 saw a positive percentage point gains of 39 and 48% respectively and are particularly instructive in engaging with the PSTs’ understanding of equivalence. Matthews et al. (2012) argue that students who successfully solve question 8/9-type questions (questions with operations on both sides of the equal sign) are beginning to hold a basic relational view of the equal sign, ‘although it coexists with an operational view’ (p. 225). In the pre-test, our data revealed that only 25 out of 70 students (for question 8) and 22 out of 79 (for question 9) were on the basic relational level. A wide range of incorrect answers was noted in the pre-test, but the common answer in both questions was 28 (which could have been found by subtracting 57 from 85 (question 8) and by subtracting 69 from 97 (question 9). Pre-service teachers who carried out this procedure to arrive at an answer of 28 in both questions were unable to provide justification for their solution strategy during interviews. As indicated previously, research into the understanding of the notion of equivalence in South Africa has shown the prevalence of the operational view of the equal sign in primary (e.g. McAuliffe, Tambara & Simsek, 2020) and high school students (e.g. Essien & Setati, 2006). Our research has revealed that this instrumental understanding of the equal sign is also held by pre-service primary school teachers. In Question 10, two of the most common incorrect responses were 42 and 18 because they are even numbers and 18 and 19 because they are the smallest numbers. While both answers are mathematically correct, the rationale for adding each set of numbers focuses on computations specific to the problem (Carpenter et al., 2005) and does not work with an understanding that uses number relationships to arrive at the numbers that are quickest to add.

With regards to the medium shift questions, in question 1 (53 − 9 = __ + 39), we still see an operational view of the equal sign at play given that in the pre-test, the most incorrect responses offered by students in this question was 44. In the post-test, even though there was a shift of 14 percentage points in this question, those PSTs who still incorrectly solved question 1 still had 44 as a response. In question 2, which asked which number would be closest to 1079 + 1186, there was a shift of 15 percentage points, and the common incorrect response in the pre-test and the post-test was 2200. The PSTs did not seem to realise that 2265 is closer to 2300 since 265 is closer to 300 than 200. While this question may be a number-structure question, it is in essence also an equivalence question. In fact, Matthews et al. (2012) places a question like this at the Comparative Relational Level—the most sophisticated/advanced knowledge of equality. Question 6 saw an 11% shift. The two common incorrect responses in the pre-test were 79 and 189. The PSTs who answered 79 got to the answer by subtracting 150 from 229 and those who got 189 did so by subtracting 54 from 243. Again, no mathematical reason for this procedure was put forward during interviews.

Questions 4 and 5 saw the least gains (3 and 7 percentage point gains respectively). Question 4 is another example of a comparative relational level question (level 4 of Matthews et al.’s (2012) construct map for knowledge of equality). Understanding number structure as well as a good grasp of equivalence is important to successfully answer this question. The most common incorrect response was A—‘add 1 to both my answers’. This could be due to the fact that the numbers in each sum were increased by 1. In question 5 (see the Appendix), the most common incorrect answer in both pre- and post-tests was Lesome shupa senyane. These questions have to do with understanding number structure. The lesson here for the WMC-P Project is that the focus on number structure while teaching additive reasoning needs to be reinforced. In doing this, the transparent number structure in the African languages as described by Mostert (2019) can be harnessed to reinforce the concepts of addition, number structure and equivalence.

Discussions and Concluding Remarks

Our study has revealed that the concepts of mathematical equivalence and number structure also pose problems to pre-service teachers. As indicated previously, in the design of the current PST education programme, unlike in the past where the focus was more on producing the correct answers when teaching additive relations, the focus in our Project is currently on how to produce the answer and on how to make explicit (and consciously so) equivalence relations. While the former is an instrumental approach to teaching, the latter approach can be seen as a relational approach to the teaching of the notion of equivalence. While the intention of our study is not to draw conclusions about the impact or the effectiveness of the intervention, what both the statistical and qualitative analyses have shown is that, with the intervention, the students have been able to make some significant learning gains as far as their understanding of number structure and mathematical equivalence are concerned. From our study, we can draw on the following emerging principles which will further guide our design research study in subsequent years.

1. Attend more consciously to the notion of equivalence relations when teaching additive reasoning rather than on students’ fluency in producing the correct answers. In doing this, the key is on the use of different representations and models that have the potential of supporting sense-making.

2. Developg questions that promote reasoning with relations over quick calculation, that is, tasks that foster an appreciation for the equal sign as an equivalence relation.

3. Deliberately refocus PST’s attention towards understanding relations between numbers as a means to developing PST’s appreciation of number structure through carefully chosen tasks that are more explicitly on mathematics equivalence.

In conclusion, one useful approach to improving learners’ understanding of the notion of mathematical equivalence noted by McNeil et al. (2015) is to design teacher professional development programmes in such a way that mathematics equivalence is developed ‘by way of explicit, discursive justification processes’ (p. 424). However, they are quick to argue that the disadvantages of such an approach are that it is time intensive and requires dedication from a team of well-trained, highly motivated teachers and educational researchers, which makes replication difficult. The advantage of using a design research approach is that these drawbacks are circumvented. Firstly, in terms of replication, the key driving force for our study is not to show that our intervention has worked (or has not worked). The overall aim of our research and development project is to develop design principles that will guide the future teaching of mathematics equivalence and number structure, and, for this reason, we did not deem it necessary to have a control group. Our belief is that these principles will afford teacher education programmes with better ways of teaching mathematical equivalence. Ultimately, in terms of replication and to a large extent, time, our study is also concerned with what we can learn from our pedagogic approach on additive reasoning that can be transferred to other content domains (multiplicative reasoning, geometric reasoning, etc.) that are at the core of primary teacher education programmes.

Acknowledgements

This work is based on the research supported by the National Research Foundation South African Numeracy Chair at Wits (grant number 74703). Any opinion, finding and conclusion or recommendation expressed in this material is that of the authors and the National Research Foundation does not accept any liability in this regard.

Disclosure Statement

No potential conflict of interest was reported by the authors.

Appendix: Pre-and Post-test Instruments