Transfer of squeezed coherent state using quantum teleportation of continuous variables

Abstract

Quantum entanglement states in continuous-variable quantum teleportation can transfer any quantum state. However, errors occur in the quantum states before and after the transfer in scientific experiments because generating a perfect quantum entanglement is physically unattainable. This paper limits the quantum states transferred to squeezed coherent states and introduces a controller to classical information transfer in continuous-variable quantum teleportation to improve transfer accuracy. Under such a setup, we derived the optimal controller that maximizes the fidelity, independent of the measurement results and the value of the displacement of the squeezed coherent state.

Keywords:

• Quantum control
• quantum teleportation
• squeezed coherent state

1. Introduction

Quantum teleportation is a method of transporting an unknown quantum state from one place to another by using quantum entanglement and classical communication. Some of the applications of quantum teleportation are communication technology and quantum computers. Bennett et al. in 1993 [1] published a detailed paper on quantum teleportation technology, while the University of Innsbruck in 1997 [2] performed the first successful experiment on the transfer of a quantum state described by a discrete variable. In 1998, the California Institute of Technology conducted an experiment on the teleportation of quantum states of continuous variables [3] using the optical scheme of quantum teleportation proposed in Ref. [4]. This continuous variable (CV) teleportation has no condition for transferring the quantum state. The transfer is possible if the source can generate the transferred quantum state. As for the generation of quantum states, the generation methods for typical quantum states, such as coherent states and squeezed states, have been established. The field of quantum feedback control [5] investigates various ways of generating quantum states. In recent years, the third-order phase gates using quantum gate teleportation have been studied [6]. The third-order phase gate is necessary to make arbitrary Hamiltonians act and is essential for realizing quantum control theory.

There are several factors that reduce the fidelity of CV teleportation experiments. For example, thermal noise, detection efficiency, and energy loss are common in many experiments. There is also another factor unique to CV quantum teleportation, such as the inability to achieve ideal quantum entanglement in experiments. As a method to reduce such errors, the application of gain adjustment to classical communication in CV teleportation has been studied.

In Ref. [3], they derived the gain to reduce the error caused by imperfect detection efficiency. To reduce the error caused by imperfect entanglement through gain adjustment, it is necessary to limit the quantum states to be transferred. There have been studies in Ref. [7–9] on gain tuning to maximize fidelity when the quantum state to be transferred is restricted to a coherent state. In Ref. [10], they showed that the error due to incomplete quantum entanglement can be completely eliminated by optimally adjusting the gain when the quantum state is qubit. However, little research has been done on the case of transferring squeezed coherent states.

In this work, we introduce a feedforward controller with extended gain adjustments into classical communication to maximize the fidelity when the quantum state transferred is a squeezed coherent state. This scheme loses the advantage of transferring an unknown quantum state that conventional quantum teleportation has. However, the security against information leakage that quantum communication offers remains. In this paper, we assume CV teleportation with no noise, perfect detection efficiency, and the error due to imperfect entanglement are considered.

This paper is organized as follows. In Section 2, we define some of the operators used in this paper. Section 3 describes the teleportation scheme in Schrödinger picture and its fidelity that is needed to design the controller. In Section 4, the optimal controller is derived for the case of transferring a squeezed coherent state. The conclusions are discussed in Section 5.

2. Definition of operators

In this section, we define some of the operators used in this paper.

2.1. Creation and annihilation operators

The annihilation operator ${\hat{a}}_{\mathit{k}\sigma }$ and the creation operator ${\hat{a}}_{\mathit{k}\sigma }^{†}$ in quantized electromagnetic waves are defined by (1) $\begin{array}{rl}{\hat{a}}_{\mathit{k}\sigma }& \equiv \sqrt{\frac{{ϵ}_0}{2\hslash {\omega }_{\mathit{k}}}}\left[{\omega }_{\mathit{k}}{\hat{\mathcal{A}}}_{\sigma }\right(\mathit{k},t)+i\frac{1}{{ϵ}_0}{\hat{\pi }}_{\sigma }(\mathit{k},t\left)\right],\end{array}$(1) (2) $\begin{array}{rl}{\hat{a}}_{\mathit{k}\sigma }^{†}& \equiv \sqrt{\frac{{ϵ}_0}{2\hslash {\omega }_{\mathit{k}}}}\left[{\omega }_{\mathit{k}}{\hat{\mathcal{A}}}_{\sigma }^{†}\right(\mathit{k},t)-i\frac{1}{{ϵ}_0}{\hat{\pi }}_{\sigma }^{†}(\mathit{k},t\left)\right],\end{array}$(2) where ${ϵ}_0$ is the dielectric constant of vacuum, ω is the frequency of electromagnetic wave, ℏ is the Dirac constant, $\mathit{k}$ is the wavenumber vector, and $\sigma \in \{0,1\}$ is the variable to distinguish the polarization direction. Also, ${\hat{\mathcal{A}}}_{\sigma }(\mathit{k},t)$ is the σ component of the vector potential $\mathcal{A}(\mathit{k},t)$, which is a spatial Fourier transform of the generalized coordinates, canonically quantized in the Coulomb gauge. The ${\hat{\pi }}_{\sigma }(\mathit{k},t)$ is the canonically quantized generalized momentum ${\pi }_{\sigma }(\mathit{k},t)$ defined by ${\pi }_{\sigma }(\mathit{r},t)\equiv {ϵ}_0\dot{{\mathcal{A}}_{\sigma }}(\mathit{k},t)$. These operators are distinguished by each $\mathit{k}$ and σ, but in this paper, we assume that ideal single-mode light is used, and subsequently, we will not distinguish between them by $\mathit{k}$ and σ.

2.2. Quadrature operators

Using the creation and annihilation operators, we define the quadratures $\hat{x}$ and $\hat{p}$ as follows: $\hat{x}\equiv \sqrt{\frac{\hslash }{2\omega }}(\hat{a}+{\hat{a}}^{†}),\hat{p}\equiv \frac{1}{i}\sqrt{\frac{\mathrm{\hslash \omega }}{2}}(\hat{a}-{\hat{a}}^{†}).$These, when solved for the creation and annihilation operators, are given by (3) $\hat{a}=\sqrt{\frac{1}{2\mathrm{\hslash \omega }}}(\omega \hat{x}+i\hat{p}),{\hat{a}}^{†}=\sqrt{\frac{1}{2\mathrm{\hslash \omega }}}(\omega \hat{x}-i\hat{p}).$(3) This corresponds to the single-mode version of Equations (1(1) $\begin{array}{rl}{\hat{a}}_{\mathit{k}\sigma }& \equiv \sqrt{\frac{{ϵ}_0}{2\hslash {\omega }_{\mathit{k}}}}\left[{\omega }_{\mathit{k}}{\hat{\mathcal{A}}}_{\sigma }\right(\mathit{k},t)+i\frac{1}{{ϵ}_0}{\hat{\pi }}_{\sigma }(\mathit{k},t\left)\right],\end{array}$(1) ) and (2(2) $\begin{array}{rl}{\hat{a}}_{\mathit{k}\sigma }^{†}& \equiv \sqrt{\frac{{ϵ}_0}{2\hslash {\omega }_{\mathit{k}}}}\left[{\omega }_{\mathit{k}}{\hat{\mathcal{A}}}_{\sigma }^{†}\right(\mathit{k},t)-i\frac{1}{{ϵ}_0}{\hat{\pi }}_{\sigma }^{†}(\mathit{k},t\left)\right],\end{array}$(2) ) with ${ϵ}_0=1$. From now on, we assume an appropriate unit system. We also assume that $\hslash =1/2$ and $\omega =1$. In summary, we obtain the following relations. $\hat{a}=\hat{x}+i\hat{p},{\hat{a}}^{†}=\hat{x}-i\hat{p}.$

2.3. Displacement and squeeze operators

The displacement operator $\hat{D}\left(\alpha \right)$ is defined as follows: $\hat{D}\left(\alpha \right)\equiv e^{\alpha {\hat{a}}^{†}-{\alpha }^{\ast }\hat{a}},\alpha \in \mathbb{C},$where α is a complex number called the displacement. $\hat{D}\left(\alpha \right)$ satisfies the relations $\hat{D}\left(\alpha \right)\hat{D}\left(\text{β}\right)=\hat{D}(\alpha +\text{β})$ and ${\hat{D}}^{†}\left(\alpha \right)=\hat{D}(-\alpha )$.

The squeeze operator $\hat{S}\left(r\right)$ is defined by $\hat{S}\left(r\right)\equiv \exp \left[\frac{1}{2}\right(r^{\ast }{\hat{a}}^2-r{\hat{a}}^{†2}\left)\right],r\in \mathbb{C},$where $r=|r|e^{\mathrm{i\varphi }}$ is the squeezing parameter for the phase ϕ. Since we can set $\varphi =0$ by appropriately rotating the coordinates, we consider r is a real number in this paper. The action of the squeeze operator represents a degenerate optical parametric process.

The displacement and squeeze operators satisfy the following exchange relation. (4) $\hat{D}\left(\alpha \right)\hat{S}\left(r\right)=\hat{S}\left(r\right)\hat{D}\left(\overline{\alpha }\right),$(4) where $\overline{\alpha }=\mathrm{\alpha cosh}r+{\alpha }^{\ast }\sinh r$.

3. Quantum teleportation of continuous variables

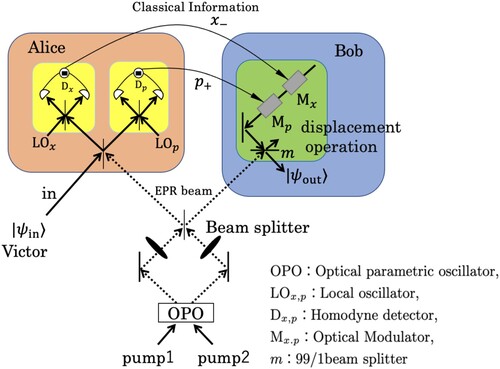
This section describes a protocol for CV quantum teleportation in Schrödinger picture [11]. Figure 1 shows a conceptual diagram of the CV teleportation system [3]. In the teleportation system, Alice can send quantum information to Bob. First, the half-beamsplitter mixes two independent squeezing fields, that is, $\hat{S}\left(r\right)|0〉$ and $\hat{S}(-r)|0〉$, with the squeezing parameter r to form an quantum entanglement called EPR ( Einstein–Podolsky–Rosen) state between Alice and Bob. The state of the EPR entanglement between Alice and Bob is (5) $|\mathrm{EPR}{〉}_{\mathrm{AB}}=\sqrt{1-q^2}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n{〉}_{\mathrm{A}}\otimes |n{〉}_{\mathrm{B}},$(5) where $|n{〉}_{\mathrm{A}}$ and $|n{〉}_{\mathrm{B}}$ are energy eigenstates with photon number n for Alice and Bob, respectively, and $q=\tanh r$ is a variable indicating the degree of entanglement, and entanglement is maximal when $\underset{r\to \mathrm{\infty }}{lim}q=1$. Victor sends a beam, whose state is $|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}$, to Alice, where $|{\psi }_{\mathrm{in}}〉$ is a state we want to send to Bob. Then, the overall state in the teleportation system becomes (6) $|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\otimes \sqrt{1-q^2}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n{〉}_{\mathrm{A}}\otimes |n{〉}_{\mathrm{B}}.$(6)

Figure 1. Conceptual diagram of teleportation system.

Then, as shown in Figure 1, the EPR beam and the beam with $|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}$ at Alice are input to a half beam splitter. Then, two set of the balanced homodyne detectors measure the physical quantities ${\hat{x}}_{\mathrm{V}}-{\hat{x}}_{\mathrm{A}}$ and ${\hat{p}}_{\mathrm{V}}+{\hat{p}}_{\mathrm{A}}$. The states in Alice and Victor are then projected on the states corresponding to measured values. The measured values of physical quantity ${\hat{x}}_{\mathrm{V}}-{\hat{x}}_{\mathrm{A}}$ and ${\hat{p}}_{\mathrm{V}}+{\hat{p}}_{\mathrm{A}}$ are $x_{-}$ and $p_{+}$, respectively. After the balanced homodyne measurements in Alice, the state of the beams in Victor and Alice are (7) $|\text{β}{〉}_{\mathrm{VA}}=\frac{1}{\sqrt{\pi }}\sum _{n=0}^{\mathrm{\infty }}{\hat{D}}_{\mathrm{V}}\left(\text{β}\right)|n{〉}_{\mathrm{V}}\otimes |n{〉}_{\mathrm{A}},$(7) where $\text{β}=x_{-}+i{p}_{+}$. Then, Bob's state is given by taking the inner product of $|\text{β}{〉}_{\mathrm{VA}}$ and Equation (6(6) $|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\otimes \sqrt{1-q^2}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n{〉}_{\mathrm{A}}\otimes |n{〉}_{\mathrm{B}}.$(6) ) such that (8) $\begin{array}{rl}{}_{\mathrm{VA}}〈\text{β}& |(|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\otimes \sqrt{1-q^2}\sum _{n^{\mathrm{\prime }}=0}^{\mathrm{\infty }}{q}^{n^{\mathrm{\prime }}}|n^{\prime }{〉}_{\mathrm{A}}\otimes |n^{\prime }{〉}_{\mathrm{B}})\\ & =\frac{1}{\sqrt{\pi }}\sum _{n=0}^{\mathrm{\infty }}{}_{\mathrm{V}}〈n|\otimes {}_{\mathrm{A}}〈n|{\hat{D}}_{\mathrm{V}}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\\ & \otimes \sqrt{1-q^2}\sum _{n^{\prime }=0}^{\mathrm{\infty }}{q}^{n^{\prime }}|n^{\prime }{〉}_{\mathrm{A}}\otimes |n^{\prime }{〉}_{\mathrm{B}}\\ & =\sqrt{\frac{1-q^2}{\pi }}\sum _{n=0}^{\mathrm{\infty }}〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}〉q^n|n{〉}_{\mathrm{B}}\\ & =\sqrt{\frac{1-q^2}{\pi }}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},\end{array}$(8) note that Equation (8(8) $\begin{array}{rl}{}_{\mathrm{VA}}〈\text{β}& |(|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\otimes \sqrt{1-q^2}\sum _{n^{\mathrm{\prime }}=0}^{\mathrm{\infty }}{q}^{n^{\mathrm{\prime }}}|n^{\prime }{〉}_{\mathrm{A}}\otimes |n^{\prime }{〉}_{\mathrm{B}})\\ & =\frac{1}{\sqrt{\pi }}\sum _{n=0}^{\mathrm{\infty }}{}_{\mathrm{V}}〈n|\otimes {}_{\mathrm{A}}〈n|{\hat{D}}_{\mathrm{V}}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{V}}\\ & \otimes \sqrt{1-q^2}\sum _{n^{\prime }=0}^{\mathrm{\infty }}{q}^{n^{\prime }}|n^{\prime }{〉}_{\mathrm{A}}\otimes |n^{\prime }{〉}_{\mathrm{B}}\\ & =\sqrt{\frac{1-q^2}{\pi }}\sum _{n=0}^{\mathrm{\infty }}〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}〉q^n|n{〉}_{\mathrm{B}}\\ & =\sqrt{\frac{1-q^2}{\pi }}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},\end{array}$(8) ) is not normalized. Finally, applying the displacement operation by $\hat{D}\left(\text{β}\right)$ to the state at Bob based on the measurement result β completes the teleportation from Alice to Bob. This displacement operation uses an optical modulator and a 99/1 beam splitter. The final Bob's state is (9) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left(\text{β}\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},$(9) where N is a normalization factor. If ideal EPR entanglement is used in this teleportation, then $r\to \mathrm{\infty }$, $q\to 1$ and $\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\to \hat{I}$ hold. Therefore, the right-hand side of Equation (9(9) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left(\text{β}\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},$(9) ) converges to $|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}}$. This means that the teleportation system has successfully transferred the continuous variable. Even in the case of q<1 with $q\ne 0$, from Equation (9(9) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left(\text{β}\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},$(9) ), the information of the quantum state $|{\psi }_{\mathrm{in}}〉$ that we wanted to send appears in the teleportation output, and thus quantum teleportation has succeeded to some extent. To evaluate the accuracy of quantum teleportation, we use the fidelity F defined as follows: (10) $F\equiv 〈{\psi }_{\mathrm{in}}|{\hat{\rho }}_{\mathrm{out}}|{\psi }_{\mathrm{in}}〉,$(10) where ${\hat{\rho }}_{\mathrm{out}}$ is the density operator of Bob's output state by quantum teleportation. If the output state is a pure state, then $F=|〈{\psi }_{\mathrm{in}}|{\psi }_{\mathrm{out}}〉{|}^2$ holds.

4. Quantum teleportation of squeezed coherent state

4.1. Problem setting

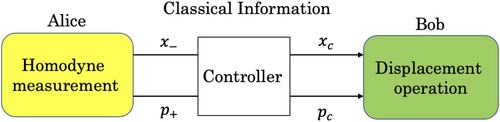
As we have already seen in Section 3 that a simple way to increase the value of fidelity F in continuous variable teleportation is increasing the squeezing parameter r of the squeezed field used to generate EPR entanglement. Note that increasing r implies increasing q in Equation (9(9) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left(\text{β}\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},$(9) ). However, since $r=\mathrm{\infty }$ is physically unattainable in reality, this simple way has a limit to the increase of F. Therefore, in this study, we consider raising the value of F by introducing a feedforward controller into classical communication, as shown in Figure 2. Then, we perform the displacement operation by $\hat{D}({\text{β}}_c=x_c+i{p}_c)$ considering the squeezing parameter r and the measured value β. Assume that the measured value $\text{β}=x_{-}+i{p}_{+}$ and the controller output ${\text{β}}_c=x_c+i{p}_c$ satisfy the following relation. (11) $\left[\begin{array}{c}{x}_c\\ p_c\end{array}\right]={\mathcal{C}}_1\left[\begin{array}{c}{x}_{-}\\ p_{+}\end{array}\right]+{\mathcal{C}}_2,$(11) where ${\mathcal{C}}_1\in {\mathbb{R}}^{2\times 2}$ and ${\mathcal{C}}_2\in {\mathbb{R}}^2$ are coefficient matrices. When the state to be transferred $|{\psi }_{\mathrm{in}}〉$ is unknown, ${\text{β}}_c=\text{β}$ is optimal, so that the controller does not make sense. In this paper, we assume a squeezed coherent state as a known state to be transferred. The general form of the squeezed coherent state is given by (12) $|r_{\mathrm{in}},\alpha 〉=\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉,$(12) where $r_{\mathrm{in}}$ is the squeezing parameter, $\alpha =x_{\alpha }+i{p}_{\alpha }$ is the displacement, and $|0〉$ is the vacuum state. Letting $s=\sinh r_{\mathrm{in}}$ and $c=\cosh r_{\mathrm{in}}$, the photon number expansion of Equation (12(12) $|r_{\mathrm{in}},\alpha 〉=\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉,$(12) ) is as follows [12]: (13) $|r_{\mathrm{in}},\alpha 〉=C\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\alpha }{\sqrt{2cs}}\right){\left(\frac{s}{2c}\right)}^{n/2}|n〉.$(13) Note that $H_n(\cdot )$ is a Hermitian polynomial, C is the normalization factor, which is given below. (14) $C=\frac{1}{\sqrt{c}}\exp (-\frac{1}{2}(|\alpha {|}^2-\frac{s}{c}{\alpha }^2)).$(14) The strong point of this problem setting is that it offers flexibility in transferring other quantum states. With this approach, the additional operation we introduced is only the conversion of classical information, and the quantum operations performed by Alice and Bob are the same as in the conventional scheme. Therefore, if Alice wants to transfer a known quantum state other than the squeezed coherent state, Alice only needs to change the conversion applied to the classical information to one suitable for that quantum state. Furthermore, if Alice wants to send an unknown quantum state, it is possible to transfer the quantum state by reverting to the conventional scheme without performing the conversion on the classical information.

Figure 2. Install the controller.

4.2. Optimal controller

Our aim is to transfer the squeezed coherent state $|{\psi }_{\mathrm{in}}〉=\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉$ from Equation (12(12) $|r_{\mathrm{in}},\alpha 〉=\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉,$(12) ) by maximizing the fidelity. To accomplish this aim, we have the following theorem.

Theorem 4.1

Given the squeezing parameter $r_{\mathrm{in}}$ and the displacement α, consider the feedforward controller in Equation (11(11) $\left[\begin{array}{c}{x}_c\\ p_c\end{array}\right]={\mathcal{C}}_1\left[\begin{array}{c}{x}_{-}\\ p_{+}\end{array}\right]+{\mathcal{C}}_2,$(11) ), where (15) ${\mathcal{C}}_1=\left[\begin{array}{cc}{g}_x& 0\\ 0& g_p\end{array}\right],{\mathcal{C}}_2=\left[\begin{array}{c}{x}_{\alpha }(c-s)(1-g_x)\\ p_{\alpha }(c+s)(1-g_p)\end{array}\right]$(15) with $c=\cosh r_{\mathrm{in}}$, $s=\sinh r_{\mathrm{in}}$, $q_{\mathrm{in}}=\tanh r_{\mathrm{in}}$, $A=\mathrm{cs}(1-q^2{q}_{\mathrm{in}}^2)$, $g_x=\frac{q{q}_{\mathrm{in}}}{A(1-q_{\mathrm{in}})+q^2{q}_{\mathrm{in}}^2},g_p=\frac{q{q}_{\mathrm{in}}}{A(1+q_{\mathrm{in}})-q^2{q}_{\mathrm{in}}^2}.$Then, the fidelity is (16) $F=\frac{\sqrt{1-q^4{q}_{\mathrm{in}}^2}}{c(1-q^2{q}_{\mathrm{in}}^2)},$(16) which is a maximum when transferring the squeezed coherent state $|{\psi }_{\mathrm{in}}〉$.

Proof.

From $|{\psi }_{\mathrm{in}}〉=\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉$ and Equation (9(9) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left(\text{β}\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})|{\psi }_{\mathrm{in}}{〉}_{\mathrm{B}},$(9) ), the output state at Bob $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}$ is as follows: (17) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left({\text{β}}_c\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉.$(17) Letting $\overline{\alpha }=\mathrm{\alpha c}-{\alpha }^{\ast }s$, $\gamma =\overline{\alpha }-\text{β}$, $\overline{\gamma }=\mathrm{\gamma c}+{\gamma }^{\ast }s$ and using the exchange relation in Equation (4(4) $\hat{D}\left(\alpha \right)\hat{S}\left(r\right)=\hat{S}\left(r\right)\hat{D}\left(\overline{\alpha }\right),$(4) ), we can rewrite Equation (17(17) $|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}=N\hat{D}\left({\text{β}}_c\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\alpha \right)|0〉.$(17) ) such that (18) $\begin{array}{rl}|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}& =N\hat{D}\left({\text{β}}_c\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{D}(-\text{β})\hat{D}\left(\overline{\alpha }\right)\hat{S}\left(r_{\mathrm{in}}\right)|0〉\\ & =N\hat{D}\left({\text{β}}_c\right)\sum _{n=0}^{\mathrm{\infty }}{q}^n|n〉〈n|\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left(\overline{\gamma }\right)|0〉.\end{array}$(18) Using Equation (13(13) $|r_{\mathrm{in}},\alpha 〉=C\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\alpha }{\sqrt{2cs}}\right){\left(\frac{s}{2c}\right)}^{n/2}|n〉.$(13) ), we obtain (19) $\begin{array}{rl}|{\psi }_{\mathrm{out}}{〉}_{\mathrm{B}}& =\hat{D}\left({\text{β}}_c\right)C_0\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\overline{\gamma }}{\sqrt{2cs}}\right)\\ & \times {\left(\frac{q^2{q}_{\mathrm{in}}}{2}\right)}^{n/2}|n〉,\end{array}$(19) where $C_0$ is a normalization factor satisfying the following normalization conditions. (20) $\begin{array}{r}|C_0{|}^2\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}{H}_n\left(\frac{{\overline{\gamma }}^{\ast }}{\sqrt{2cs}}\right)H_n\left(\frac{\overline{\gamma }}{\sqrt{2cs}}\right){\left|\frac{q^2{q}_{\mathrm{in}}}{2}\right|}^n=1.\end{array}$(20) Using Mehler's Hermite polynomial formula: (21) $\begin{array}{rl}& \sum _{n=0}^{\mathrm{\infty }}\frac{H_n\left(x\right)H_n\left(y\right)}{n!}{\left(\frac{1}{2}w\right)}^n\\ & =(1-w^2{)}^{-1/2}\exp \left[\frac{2\mathrm{xyw}-(x^2+y^2)w^2}{1-w^2}\right],\end{array}$(21) Equation (20(20) $\begin{array}{r}|C_0{|}^2\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}{H}_n\left(\frac{{\overline{\gamma }}^{\ast }}{\sqrt{2cs}}\right)H_n\left(\frac{\overline{\gamma }}{\sqrt{2cs}}\right){\left|\frac{q^2{q}_{\mathrm{in}}}{2}\right|}^n=1.\end{array}$(20) ) can be transformed into the following equation for $|C_0{|}^2$. $\begin{array}{rl}|C_0{|}^2& =\sqrt{1-q^4{q}_{\mathrm{in}}^2}\\ & \times \exp [-q^2{q}_{\mathrm{in}}\frac{2|\overline{\gamma }{|}^2-({\overline{\gamma }}^{\ast 2}+{\overline{\gamma }}^2)q^2{q}_{\mathrm{in}}}{2\mathrm{cs}(1-q^4{q}_{\mathrm{in}}^2)}].\end{array}$The fidelity F is $|〈{\psi }_{\mathrm{in}}|{\psi }_{\mathrm{out}}〉{|}^2$ from Equation (10(10) $F\equiv 〈{\psi }_{\mathrm{in}}|{\hat{\rho }}_{\mathrm{out}}|{\psi }_{\mathrm{in}}〉,$(10) ). On the other hand, we can obtain the same value of the fidelity by computing $|〈{\psi }_{\mathrm{out}}^{\mathrm{\prime }}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉{|}^2$ using the following two equations instead. (22) $\begin{array}{rl}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉& =\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left({\overline{\gamma }}_c\right)|0〉,\end{array}$(22) (23) $\begin{array}{rl}|{\psi }_{\mathrm{out}}^{\mathrm{\prime }}〉& =C_0\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\overline{\gamma }}{\sqrt{2cs}}\right){\left(\frac{q^2{q}_{\mathrm{in}}}{2}\right)}^{n/2}|n〉,\end{array}$(23) where ${\gamma }_c=\overline{\alpha }-{\text{β}}_c$ and ${\overline{\gamma }}_c={\gamma }_{c}c+{\gamma }_c^{\ast }s$. From Equation (13(13) $|r_{\mathrm{in}},\alpha 〉=C\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\alpha }{\sqrt{2cs}}\right){\left(\frac{s}{2c}\right)}^{n/2}|n〉.$(13) ), the photon number expansion of Equation (22(22) $\begin{array}{rl}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉& =\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left({\overline{\gamma }}_c\right)|0〉,\end{array}$(22) ) is given by $|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉=C_1\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{{\overline{\gamma }}_c}{\sqrt{2cs}}\right){\left(\frac{q_{\mathrm{in}}}{2}\right)}^{n/2}|n〉.$Here, from Equation (14(14) $C=\frac{1}{\sqrt{c}}\exp (-\frac{1}{2}(|\alpha {|}^2-\frac{s}{c}{\alpha }^2)).$(14) ), $C_1$ satisfies (24) $C_1=\frac{1}{\sqrt{c}}\exp (-\frac{1}{2}(|\overline{{\gamma }_c}{|}^2-q_{\mathrm{in}}{\overline{{\gamma }_c}}^2)).$(24) As a result, the inner product of Equations (22(22) $\begin{array}{rl}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉& =\hat{S}\left(r_{\mathrm{in}}\right)\hat{D}\left({\overline{\gamma }}_c\right)|0〉,\end{array}$(22) ) and (23(23) $\begin{array}{rl}|{\psi }_{\mathrm{out}}^{\mathrm{\prime }}〉& =C_0\sum _{n=0}^{\mathrm{\infty }}\frac{1}{\sqrt{n!}}{H}_n\left(\frac{\overline{\gamma }}{\sqrt{2cs}}\right){\left(\frac{q^2{q}_{\mathrm{in}}}{2}\right)}^{n/2}|n〉,\end{array}$(23) ), $〈{\psi }_{\mathrm{out}}^{\mathrm{\prime }}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉$ is (25) $C_0^{\ast }{C}_1\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}{H}_n\left(\frac{{\overline{\gamma }}_c}{\sqrt{2cs}}\right)H_n\left(\frac{{\overline{\gamma }}^{\ast }}{\sqrt{2cs}}\right){\left(\frac{q{q}_{\mathrm{in}}}{2}\right)}^n.$(25) Using Equation (21(21) $\begin{array}{rl}& \sum _{n=0}^{\mathrm{\infty }}\frac{H_n\left(x\right)H_n\left(y\right)}{n!}{\left(\frac{1}{2}w\right)}^n\\ & =(1-w^2{)}^{-1/2}\exp \left[\frac{2\mathrm{xyw}-(x^2+y^2)w^2}{1-w^2}\right],\end{array}$(21) ), we obtain (26) $〈{\psi }_{\mathrm{out}}^{\mathrm{\prime }}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉=\frac{C_0^{\ast }}{\sqrt{c(1-q^2{q}_{\mathrm{in}}^2)}}\exp \left[\frac{f\left({\gamma }_c\right)}{2A}\right],$(26) where $f\left({\gamma }_c\right)=q{q}_{\mathrm{in}}\{2{\overline{\gamma }}_c{\overline{\gamma }}^{\ast }-({\overline{\gamma }}_c^2+{\overline{\gamma }}^{\ast 2}\left)q{q}_{\mathrm{in}}\right\}+A(q_{\mathrm{in}}{\overline{\gamma }}_c^2-|{\overline{\gamma }}_c{|}^2)$. Since $\overline{\alpha }=x_{\alpha }(c-s)+i{p}_{\alpha }(c+s)={\overline{x}}_{\alpha }+i{\overline{p}}_{\alpha }$, ${\overline{x}}_c=(c+s)({\overline{x}}_{\alpha }-x_c)$, ${\overline{p}}_c=(c-s)({\overline{p}}_{\alpha }-p_c)$, ${\overline{x}}_{-}=(c+s)({\overline{x}}_{\alpha }-x_{-})$, ${\overline{p}}_{+}=(c-s)({\overline{p}}_{\alpha }-p_{+})$, ${\overline{\gamma }}_c={\overline{x}}_c+i{\overline{p}}_c$, and $\overline{\gamma }={\overline{x}}_{-}+i{\overline{p}}_{+}$, we obtain $\begin{array}{rl}\mathrm{Re}f(x_c,p_c)& ={\overline{x}}_c^2\{-q^2{q}_{\mathrm{in}}^2+A(q_{\mathrm{in}}-1\left)\right\}+{\overline{x}}_c\left(2q{q}_{\mathrm{in}}{\overline{x}}_{-}\right)\\ & +{\overline{p}}_c^2\{q^2{q}_{\mathrm{in}}^2-A(q_{\mathrm{in}}+1\left)\right\}+{\overline{p}}_c\left(2q{q}_{\mathrm{in}}{\overline{p}}_{+}\right)\\ & -q^2{q}_{\mathrm{in}}^2({\overline{x}}_{-}^2-{\overline{p}}_{+}^2).\end{array}$Then, the maximizer $(x_c,p_c)$ of $\mathrm{Re}f(x_c,p_c)$ is $(\frac{q{q}_{\mathrm{in}}(x_{-}-x_{\alpha }(c-s\left)\right)}{A(1-q_{\mathrm{in}})+q^2{q}_{\mathrm{in}}^2},\frac{q{q}_{\mathrm{in}}(p_{+}-p_{\alpha }(c+s\left)\right)}{A(1+q_{\mathrm{in}})-q^2{q}_{\mathrm{in}}^2}).$Rewriting these in the form of Equation (11(11) $\left[\begin{array}{c}{x}_c\\ p_c\end{array}\right]={\mathcal{C}}_1\left[\begin{array}{c}{x}_{-}\\ p_{+}\end{array}\right]+{\mathcal{C}}_2,$(11) ), we obtain Equation (15(15) ${\mathcal{C}}_1=\left[\begin{array}{cc}{g}_x& 0\\ 0& g_p\end{array}\right],{\mathcal{C}}_2=\left[\begin{array}{c}{x}_{\alpha }(c-s)(1-g_x)\\ p_{\alpha }(c+s)(1-g_p)\end{array}\right]$(15) ).

When $\mathrm{Re}f$ takes a maximum value, the fidelity F is also takes a maximum value. Thus, the controller (11(11) $\left[\begin{array}{c}{x}_c\\ p_c\end{array}\right]={\mathcal{C}}_1\left[\begin{array}{c}{x}_{-}\\ p_{+}\end{array}\right]+{\mathcal{C}}_2,$(11) ) with Equation (15(15) ${\mathcal{C}}_1=\left[\begin{array}{cc}{g}_x& 0\\ 0& g_p\end{array}\right],{\mathcal{C}}_2=\left[\begin{array}{c}{x}_{\alpha }(c-s)(1-g_x)\\ p_{\alpha }(c+s)(1-g_p)\end{array}\right]$(15) ) is an optimal controller for transferring squeezed coherent states. We can derive the value of F from Equation (26(26) $〈{\psi }_{\mathrm{out}}^{\mathrm{\prime }}|{\psi }_{\mathrm{in}}^{\mathrm{\prime }}〉=\frac{C_0^{\ast }}{\sqrt{c(1-q^2{q}_{\mathrm{in}}^2)}}\exp \left[\frac{f\left({\gamma }_c\right)}{2A}\right],$(26) ) when applying the optimal controller and obtain Equation (16(16) $F=\frac{\sqrt{1-q^4{q}_{\mathrm{in}}^2}}{c(1-q^2{q}_{\mathrm{in}}^2)},$(16) ).

From Equation (16(16) $F=\frac{\sqrt{1-q^4{q}_{\mathrm{in}}^2}}{c(1-q^2{q}_{\mathrm{in}}^2)},$(16) ), we obtain $\mathrm{\partial F}/\mathrm{\partial r}\ge 0$ and $\mathrm{\partial F}/\mathrm{\partial }{r}_{\mathrm{in}}\le 0$, which implies that the optimal fidelity F increases monotonically for r and decreases monotonically for $r_{\mathrm{in}}$. In other words, the larger the squeezing parameter r used to generate the entanglement, the higher the fidelity, and the larger the squeezing parameter $r_{\mathrm{in}}$ of the quantum state transferred, the lower the fidelity. This result holds even with the conventional scheme. The physical meaning of this result is intuitively understandable from Equation (5(5) $|\mathrm{EPR}{〉}_{\mathrm{AB}}=\sqrt{1-q^2}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n{〉}_{\mathrm{A}}\otimes |n{〉}_{\mathrm{B}},$(5) ), which is the EPR entanglement formula. The coefficient $q^n$ in Equation (5(5) $|\mathrm{EPR}{〉}_{\mathrm{AB}}=\sqrt{1-q^2}\sum _{n=0}^{\mathrm{\infty }}{q}^n|n{〉}_{\mathrm{A}}\otimes |n{〉}_{\mathrm{B}},$(5) ) represents the degree of entanglement for the n-photon number state, and when r is finite, i.e. q<1, the energy entanglement $q^n$ decreases as the photon number n increases. Thus, the higher the energy of the state transferred, the more error is introduced in the transferred information. In the case of transferring a squeezed coherent state, the larger the squeezing parameter $r_{\mathrm{in}}$, the higher the expected energy, and hence the larger $r_{\mathrm{in}}$, the lower the fidelity.

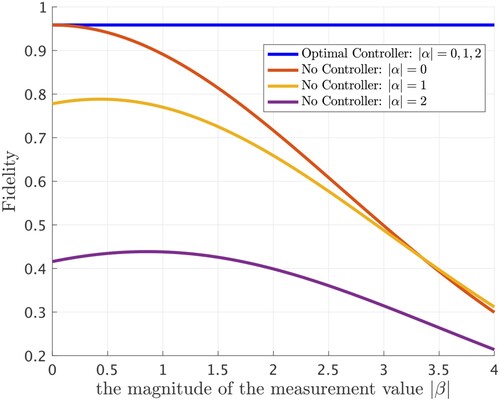
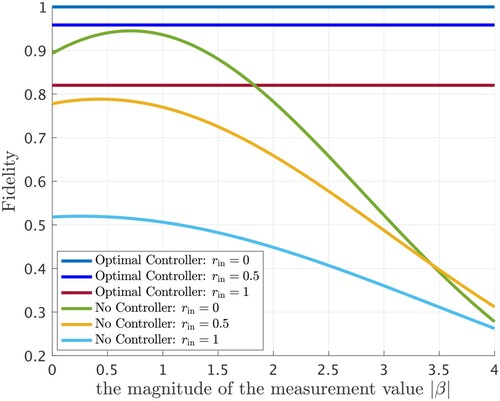
Figure 3 shows the relationship between the magnitude of the measured value $|\text{β}|$, displacement $|\alpha |$, and the fidelity calculated numerically when r = 0.8 and $r_{\mathrm{in}}=0.5$. Figure 4 shows the relationship between $|\text{β}|$, squeezing parameter $r_{\mathrm{in}}$, and the fidelity calculated numerically when r = 0.8 and $|\alpha |=1$. The fidelity without gain and controllers in CV quantum teleportation depends on the magnitude of measured value $|\text{β}|$ and displacement $|\alpha |$. As shown in Equation (16(16) $F=\frac{\sqrt{1-q^4{q}_{\mathrm{in}}^2}}{c(1-q^2{q}_{\mathrm{in}}^2)},$(16) ), Figures 3 and 4, when we use the controller, the values $|\text{β}|$ and $|\alpha |$ do not affect the value of the fidelity, while the squeezing parameter does affect. In particular, when $r_{\mathrm{in}}=0$, i.e. when the state to be transferred is the coherent state $|{\psi }_{\mathrm{in}}〉=\hat{D}\left(\alpha \right)|0〉$, the teleportation is always possible with F = 1 regardless of the squeezing parameter r of the EPR entanglement.

Figure 3. The relationship between the magnitude of the measured value $|\text{β}|$, displacement $|\alpha |$, and the fidelity when r = 0.8 and $r_{\mathrm{in}}=0.5$.

Figure 4. The relationship between the magnitude of the measured value $|\text{β}|$, squeezing parameter $r_{\mathrm{in}}$, and the fidelity when r = 0.8 and $|\alpha |=1$.

5. Conclusion

In the CV quantum teleportation, we have introduced a feedforward controller in classical communication, where the state transferred is known. The proposed controller increases the fidelity other than increasing the squeezing parameter of EPR entanglement. We derived the optimal controller and fidelity when the state transferred is a squeezed coherent state, and shown that the transfer is always more accurate than the conventional method without being affected by measurements. Such teleportation with constant accuracy unaffected by measurements might be applicable to analysing disturbances that are difficult to model numerically.

As a future work, we will design a controller that takes into account the phase of the squeezing parameter r, energy loss, and measurement efficiency, which were not considered in this study.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Aoi Fujimoto

Aoi Fujimoto He received his B.S. degree from Meiji University, Japan, in 2023. He has been a Master's Student at the School of Science and Technology, Meiji University. His research interests include quantum control.

Hiroyuki Ichihara

Hiroyuki Ichihara He received his B.S., M.S., and Ph.D. degrees from Meiji University, Japan, in 1995, 1997, and 2000, respectively. From 2002 to 2009, he was an Assistant Professor of the Department of Systems Design and Informatics, Kyushu Institute of Technology. In 2019, he has been a Professor of the Department of Mechanical Engineering Informatics, Meiji University. His research interests include robust control and numerical optimization in control. He is a member of IEEE.